Developing a 3D Hydrodynamic and Water Quality Model for Floating Treatment Wetlands to Study the Flow Structure and Nutrient Removal Performance of Different Configurations

Abstract

Floating treatment wetlands (FTWs) are widely used in surface water. The nutrient removal performance depends on both physical processes and chemical/biological transformations in FTWs. However, research describing the coupling processes of hydrodynamic and water quality in the system remains limited. Therefore, a coupled three-dimensional model of hydrodynamic and water quality for FTWs was developed based on the Environmental Fluid Dynamics Code (EFDC). Additional plant drag terms were added to the momentum equations to simulate the suspended canopy effect, and the chemical/biological processes occurring in FTWs were integrated into the original water quality equations simultaneously. The fully calibrated model was used to compare the hydrodynamic characteristics and nutrient removal performance of seven FTW configurations. The modeling results showed that the main stream would turn to the bottom and side of the plant root zone because of the block in FTWs. The differences in the hydrodynamic characteristics among the seven configurations led to a difference in water quality improvement effects. Segmenting a single FTW into a pair of parallel FTWs could achieve the maximum nitrogen and phosphorus mass removal. The results of the study are useful for designing an optimal FTW configuration in surface water.

1. Introduction

Floating treatment wetlands (FTWs) consist of emergent vegetation established upon a floating structure and have proved to be an effective and promising remediation technology for the removal of nutrients from surface water systems [1,2]. A large number of studies have demonstrated that FTWs could enhance the removal of suspended solids [3], nutrients [4], organic matter [5], metals [6] and algae [7]. The excellent nutrient removal performance benefits from the physical and chemical/biological processes occurring in the plant zone of the FTWs [8,9].

A physical experiment is a basic method to explore the hydrodynamic characteristics and nutrient removal processes that occur in FTWs. However, it is difficult to consider both processes as they are limited by space scale, time scale and numerous uncertain factors, such as temperature, wind and precipitation. On the one hand, some water quality models, which describe the physical and chemical/biological processes in FTWs, have been developed [10,11,12]. For example, Wang et al. [13] developed a FTWMOD model, which consisted of a plant growth module, a nitrogen dynamic module and a phosphorus dynamics module.

On the other hand, some researchers have tried to develop a hydrodynamic aquatic model, using Delft3D-FLOW, EFDC and Fluent, to study the effects of plants on hydrodynamic characteristics [9,14,15,16], without considering the chemical/biological processes caused by plants in FTWs. Therefore, a group of coupled models of hydrodynamics and water quality emerged. For example, Machado et al. [17] used numerical modeling with a reactive tracer to study the flow through the plant root zone, with the goal of determining which configuration of FTWs demonstrated higher nutrient removal performance. Sabokrouhiyeh et al. [18] developed a two-dimensional depth-averaged model to identify optimal vegetation distributions. However, the complex chemical/biological processes occurring in the plant zone of the FTWs were simplified as a degradation coefficient. An integrated model that considers both the flow and the complex chemical/biological processes is still unavailable thus far.

FTWs were always deployed in groups in surface water systems [19,20]. An unreasonable arrangement of FTWs might lead to dead-zones and associated short-circuiting in the FTW system [2,21,22], which could reduce the residential time and the rate of flow through the plant root zone, resulting in reduced nutrient removal performance. When two FTWs were arranged in series, the main stream turned from the upper water to the bottom water when flowing through the upstream FTW, resulting in a decrease in the inflow mass to the downstream FTW. Machado et al. [17] reported that the mass removal by the downstream FTW was 2.7% less than the upstream FTW. Previous studies indicated that a reasonable FTW arrangement could improve the nutrient removal performance. The goal of this study was to develop a 3D hydrodynamic and water quality model to study the flow structure and nutrient removal performance of different FTW configurations.

2. Materials and Methods

2.1. EFDC Description

The Environmental Fluid Dynamics Code (EFDC), developed by Hamrick (1992) [23], is capable of simulating one-, two- or three-dimensional hydrodynamic, sediment transport and water quality of rivers, lakes and reservoirs. Based on the assumption of vertical hydrostatic pressure and Boussinesq approximation, the following continuity equations and momentum equations are proposed [23].

The continuity equations:

$$\frac{\partial (m\zeta )}{\partial t}+\frac{\partial \left(m_{x}Hu\right)}{\partial x}+\frac{\partial \left(m_{x}Hv\right)}{\partial y}+\frac{\partial (mw)}{\partial z}=Q_H$$

(1)

$$\frac{\partial (m\zeta )}{\partial t}+\frac{\partial \left(m_{y}H{\displaystyle {\int }_0^{1}u}dz\right)}{\partial x}+\frac{\partial \left(m_{x}H{\displaystyle {\int }_0^{1}v}dz\right)}{\partial y}={\displaystyle {\int }_0^1{Q}_H}dz$$

(2)

The momentum equations:

$$\begin{array}{l}\frac{\partial (mHu)}{\partial t}+\frac{\partial \left(m_{y}Huu\right)}{\partial x}+\frac{\partial \left(m_{x}Hvu\right)}{\partial y}+\frac{\partial (mwu)}{\partial z}-\left(mf+v\frac{\partial m_y}{\partial x}-u\frac{\partial m_x}{\partial y}\right)Hv\hfill \\ =-m_{y}H\frac{\partial (g\zeta +p)}{\partial x}-m_y\left(\frac{\partial h}{\partial x}-z\frac{\partial H}{\partial x}\right)\frac{\partial p}{\partial z}+\frac{\partial }{\partial z}\left(m\frac{1}{H}{A}_v\frac{\partial u}{\partial v}\right)+Q_u-F_{u}H\hfill \end{array}$$

(3)

$$\begin{array}{l}\frac{\partial (mHv)}{\partial t}+\frac{\partial \left(m_{y}Huv\right)}{\partial x}+\frac{\partial \left(m_{x}Hvv\right)}{\partial y}+\frac{\partial (mwu)}{\partial z}+\left(mf+v\frac{\partial m_y}{\partial x}-u\frac{\partial m_x}{\partial y}\right)Hu\hfill \\ =-m_{x}H\frac{\partial (g\zeta +p)}{\partial y}-m_x\left(\frac{\partial h}{\partial y}-z\frac{\partial H}{\partial y}\right)\frac{\partial p}{\partial z}+\frac{\partial }{\partial z}\left(m\frac{1}{H}{A}_v\frac{\partial u}{\partial z}\right)+Q_v-F_{v}H\hfill \end{array}$$

(4)

$$\frac{\partial p}{\partial z}=gH\frac{\rho -{\rho }_0}{{\rho }_0}$$

(5)

where H = h + ζ is the total water depth, h is the equilibrium water depth and ζ is surface displacement from the equilibrium; u, v and w are water velocity in the x, y and z directions, respectively; m_x and m_y are metric coefficients, m = m_x · m_y; Q_H is water inflow/outflow from the external sources; p is the physical pressure in excess of the reference density hydrostatic pressure; A_v is the vertical turbulent momentum mixing coefficient; Q_u and Q_v are the source and sink terms; F_u and F_v are extensions to the original equations to represent the plant drag force, respectively.

2.2. Development of a Hydrodynamic and Water Quality Model for FTWs

Based on the basic hydrodynamic module of EFDC, additional plant drag terms were added to simulate the effect of FTWs on flow structure. The plant drag force was modeled using F_u and F_v as Equations (6) and (7) [24]:

$$F_u=\frac{1}{2}{C}_D\rho au\sqrt{u^2+v^2+w^2}$$

(6)

$$F_v=\frac{1}{2}{C}_D\rho av\sqrt{u^2+v^2+w^2}$$

(7)

where C_D is the drag coefficient, $\rho$ is the density of the water column and a is the projected area of the canopy per unit volume.

Then, based on the basic water quality module of EFDC, the chemical/biological processes occurring in FTWs were integrated into the original water quality equations as source/sink terms. Here follows a condensed description of the water quality model for FTWs (FTWMOD). For detailed equations for the chemical/biological processes of plants, nitrogen and phosphorus, refer to the previous study [13]. The FTWMOD consists of three interconnected submodels: (1) a plant growth submodel; (2) a nitrogen dynamics submodel; and (3) a phosphorus dynamics submodel. The plant growth submodel incorporates two state variables, namely shoot biomass and root biomass. Organic nitrogen, ammonia nitrogen and nitrate nitrogen in the water column are modeled in the nitrogen dynamic submodel. Organic phosphorus and phosphate in the water column are modeled in the phosphorus dynamics submodel.

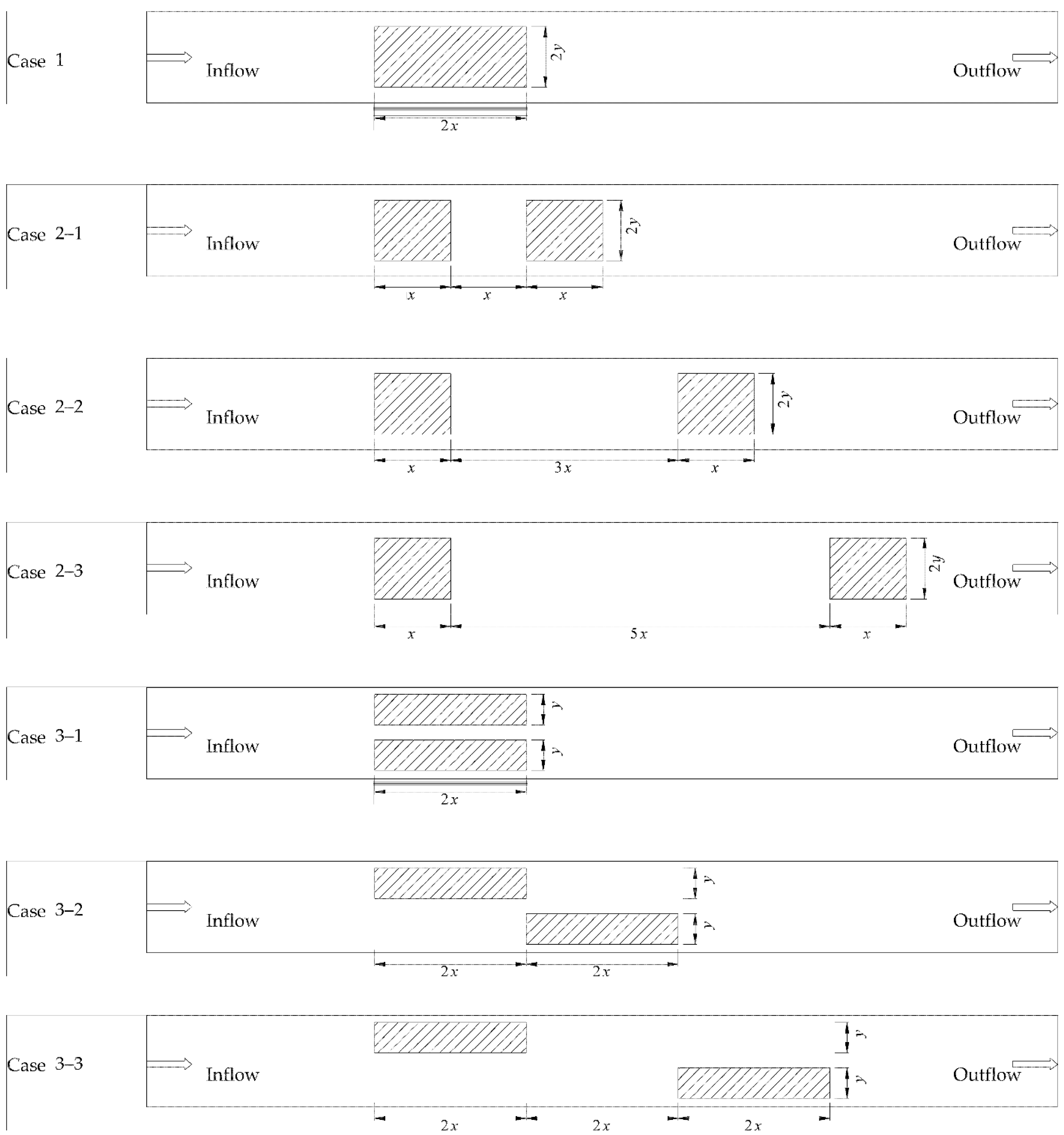
2.3. Expression of FTW in Model

In the model, the study area is generally divided into several grids, where the plant species in the FTWs, if they exist, can be defined. For each species, the corresponding planting density, root length, root diameter and drag coefficient can be set. Once the model is run, the plant species for each grid is first determined in the horizontal direction. Because FTWs can fluctuate with the water level, the grid that the FTWs occupy is dynamic and is determined according to the current water depth and the length of plant roots at each time step. Then, based on the plant properties and hydrodynamic characteristics, the plant drag force and the quality of nutrient removal from the water are calculated.

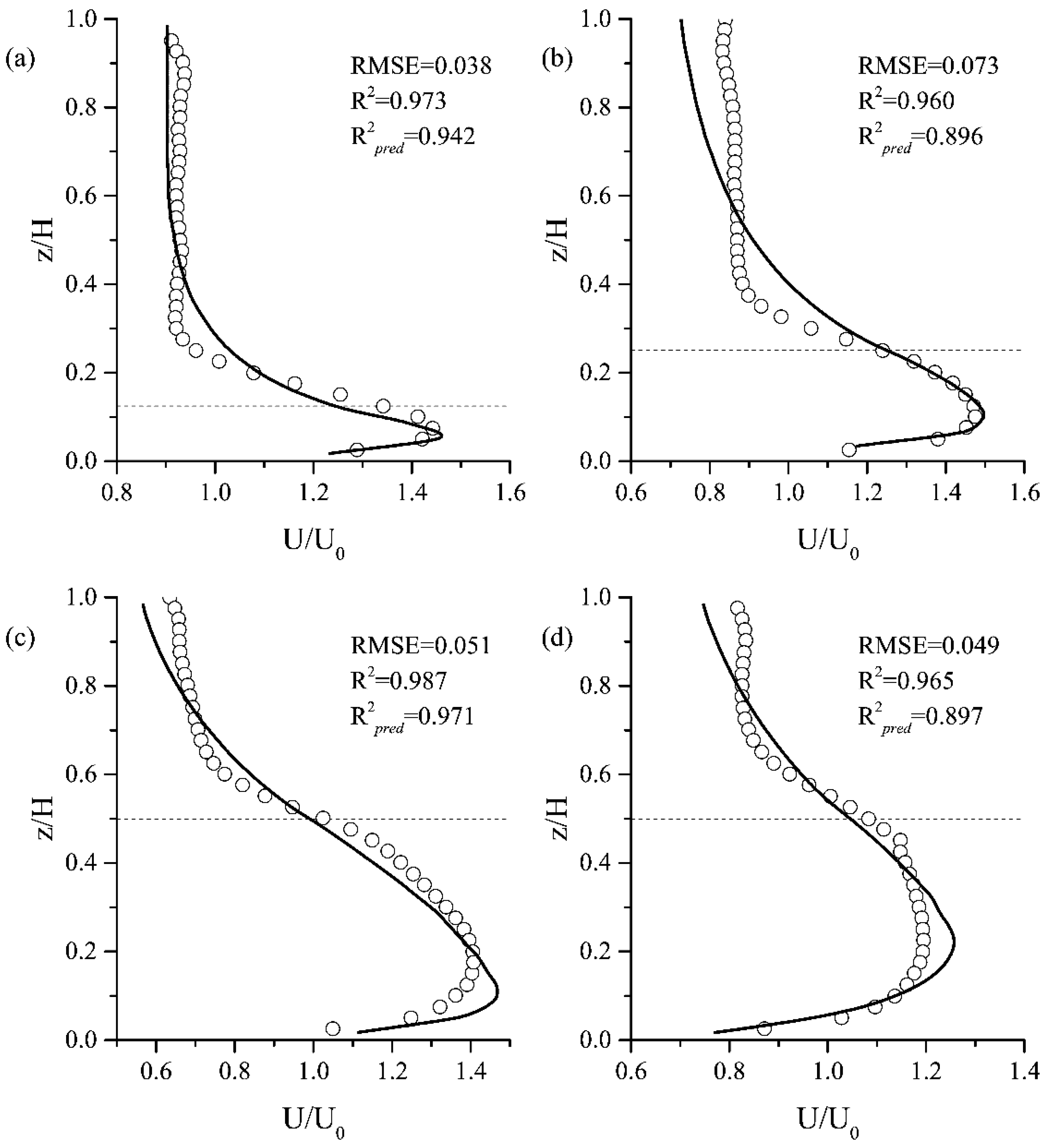
2.4. Calibration and Validation

The hydrodynamic model and water quality model for FTWs were calibrated separately due to the lack of relevant literature and experimental data for the simultaneous measurement of hydrodynamic and water quality data. The calibrated water quality model for FTWs in the previous study was used in the present study. Data for calibrating the hydrodynamic model were taken from laboratory experiments described by Plew [25] and were also used as calibrating data in other studies [9,24]. Results from four experiments (here termed B2, B5, B13 and B15) provide data for evaluating the hydrodynamic mode of FTWs. These experiments were conducted under steady flow conditions in an open channel flume with a length of 6.0 m and a width of 0.6 m. The plants used in the experiments, covering all the effective areas of the flume, were generalized as aluminum cylinders with a diameter of 9.54 mm. The basic conditions of the four experimental runs are listed in

Table 1. Basic condition of the B2, B5, B13 and B15 experimental runs.

Run	H (mm)	hg (mm)	L (mm)	B (mm)	a (m2/m3)	Q (L/s)
B2	200	175	150	50	1.272	7.1
B5	200	150	150	50	1.272	7.8
B13	200	100	150	50	1.272	10.1
B15	200	100	200	100	0.477	10.3

Note. H is the water depth, h_g is the root length immersed in water, L and B are the streamwise and cross-stream spacing between plants, a is the projected area per unit volume, Q is the flow rate.

. The plant density in B2, B5 and B13 was the same, but the root length immersed in water was 175, 150 and 100 mm, respectively, and the flow rate was 7.1, 7.8 and 10.1 L/s, respectively. The root length immersed in water and the flow rate in B13 and B15 were the same, but the projected area per unit volume was 1.272 and 0.477 m²/m³, respectively, which meant the plant density was different. All the data described in this section were only used for model calibration and validation.

The three-dimensional hydrodynamic and water quality coupling model for B2, B5, B13 and B15 experimental runs was established. The size of the model mesh was 5.0 × 5.0 cm² in the horizontal direction, and the water was evenly divided into 30 layers in the vertical direction, which suggested that the model had a total grid of 43,200. The roughness height was set to 0.001 m according to the previous study [24]. When the root length immersed in water was 175 mm (B2), the plant ranged from layer 5 to layer 30 (from bottom to top); when the root length immersed in water was 150 mm (B5), the plant ranged from layer 9 to layer 30; when the root length immersed in water was 100 mm (B13 and B15), the plant ranged from layer 16 to 30. After the model ran stably, the horizontal velocity along the vertical direction in the flume 4 m from the inlet was exported for comparison with the experimental data.

The root mean square error (RMSE), the coefficient of determination (R²) and the Predicted R-Squared (R²_pred) were applied to evaluate the deviation between the experimental data and the simulation data:

$$\mathrm{RMSE}=\sqrt{\frac{{\displaystyle {\sum }_{i=1}^N{\left(M_i-S_i\right)}^2}}{N}}$$

(8)

$$R^2={\left[\frac{N{\displaystyle {\sum }_{i=1}^N{M}_i{S}_i}-\left({\displaystyle {\sum }_{i=1}^N{M}_i}\right)\left({\displaystyle {\sum }_{i=1}^N{S}_i}\right)}{\sqrt{N{\displaystyle {\sum }_{i=1}^N{M}_i{}^2-{\left({\displaystyle {\sum }_{i=1}^N{M}_i}\right)}^2}}\sqrt{N{\displaystyle {\sum }_{i=1}^N{S}_i{}^2-{\left({\displaystyle {\sum }_{i=1}^N{S}_i}\right)}^2}}}\right]}^2$$

(9)

$$R_{pred}^2=1-\left[\frac{{{\displaystyle {\sum }_{i=1}^N\left(M_i-S_i\right)}}^2}{{{\displaystyle {\sum }_{i=1}^N\left(S_i-\overline{M}\right)}}^2}\right]$$

(10)

where M_i and S_i are the experimental data and simulation data, respectively; $\overline{M}$ is the average value of the experimental data; and N is the number of data sets.

2.5. Model Application

To study the influence of the flow structure and the nutrient removal performance of different FTW configurations, the following seven typical cases were put forward in the open channel flume according to the layout form and spacing of the FTWs (Figure 1). A single large FTW was positioned in the channel flume in case 1. A single large FTW was evenly segmented into two smaller FTWs in series, and had distances of x, 3x and 5x in case 2–1, case 2–2 and case 2–3, respectively (x is the length of the two smaller FTWs). A single large FTW was evenly segmented into two smaller FTWs, which were interlaced at a distance of 0, 2x and 4x. For all cases, FTWs were arranged at a distance of 1.5 m from the inflow port to make sure that the water flow through the FTWs was steady. The root length immersed in water was 100 mm, and the area of the FTWs was 0.4 m², occupying 11.1% of the water surface area. The inflow rate in all cases was 7.2 L/s with the same concentrations of NH₄⁺–N (1.0 mg/L), NO₃⁻–N (1.0 mg/L), OrgN (1.0 mg/L), PO₄³⁻–P (0.1 mg/L) and OrgP (0.1 mg/L), while the water level at the outlet was maintained at 200 mm.

Because of the short contact time between nutrients and FTWs in the model application, the quality of the nutrients removed per unit time was used to evaluate the water quality improvement, which was also applied to practical engineering [26]. After the model ran stably, the quality of the nitrogen removed by FTWs within one day was calculated as:

$$\mathrm{N}\_\mathrm{removal}={\displaystyle {\int }_0^1\left(\mathrm{Plant}\_\mathrm{N}+\mathrm{Sed}\_\mathrm{N}+\mathrm{Denit}\_\mathrm{N}\right)}\hspace{0.17em}dt$$

(11)

$$\mathrm{Plant}\_\mathrm{N}={\displaystyle {\int }_S\left(LPLNM·{\mathrm{B}}_{\mathrm{SH}}\left(t,s\right)+LPLNM·{\mathrm{B}}_{\mathrm{RO}}\left(t,s\right)\right)}\hspace{0.17em}ds$$

(12)

$$\mathrm{Sed}\_\mathrm{N}={\displaystyle {\int }_{\Omega }KNSED·\mathrm{OrgN}\left(t,x\right)d}x$$

(13)

$$\mathrm{Denit}\_\mathrm{N}={\displaystyle {\int }_{\Omega }Denit·{\mathrm{NO}}_3\left(t,x\right)}\hspace{0.17em}dx$$

(14)

where N_removal is the quality of nitrogen removed by FTWs within one day; Plant_N is the net nitrogen content absorbed by plants; Sed_N is the accumulated nitrogen content in sediment; Denit_N is the nitrogen content removed via denitrification; LPLNM is the ratio of nitrogen to plant biomass; B_SH and B_RO are the shoot and root biomass of the plants, respectively; KNSED is the sedimentation rate of OrgN; Denit is the denitrification rate; OrgN and NO₃ are the contents of organic nitrogen and nitrate nitrogen in the water column, s is the plane coordinate of the area covered with FTWs; x is the three-dimensional coordinate of the whole area.

The quality of the nitrogen removed by FTWs within one day was calculated as:

$$\mathrm{P}\_\mathrm{removal}={\displaystyle {\int }_0^1\left(\mathrm{Plant}\_\mathrm{P}+\mathrm{Sed}\_\mathrm{P}\right)}\hspace{0.17em}dt$$

(15)

$$\mathrm{Plant}\_\mathrm{P}={\displaystyle {\int }_S\left(LPLPM·{\mathrm{B}}_{\mathrm{SH}}\left(t,s\right)+LPLPM·{\mathrm{B}}_{\mathrm{RO}}\left(t,s\right)\right)}\hspace{0.17em}ds$$

(16)

$$\mathrm{Sed}\_\mathrm{P}={\displaystyle {\int }_{\Omega }\left(KPSED·\mathrm{OrgP}\left(t,x\right)+KPCO·{\mathrm{PO}}_4\left(t,x\right)\right)}\hspace{0.17em}dx$$

(17)

where P_removal is the quality of the phosphorus removed by FTWs within one day; Plant_P is the net phosphorus content absorbed by plants; Sed_P is the accumulated phosphorus content in sediment; LPLPM is the ratio of phosphorus to plant biomass; KPSED is the sedimentation rate of OrgP; KPCO is the ratio of coprecipitation of PO₄³⁻–P.

3. Results and Discussion

3.1. Calibration and Validation Results

The simulation data about the horizontal velocity was exported and compared with the experimental data (Figure 2). The R², R²_pred and the RMSE were 0.973, 0.942 and 0.038 in B2; 0.960, 0.896 and 0.0378 in B5; 0.987, 0.971 and 0.051 in B13; and 0.965, 0.897 and 0.049 in B15, respectively. These results demonstrated the good performance of the hydrodynamic model for FTWs.

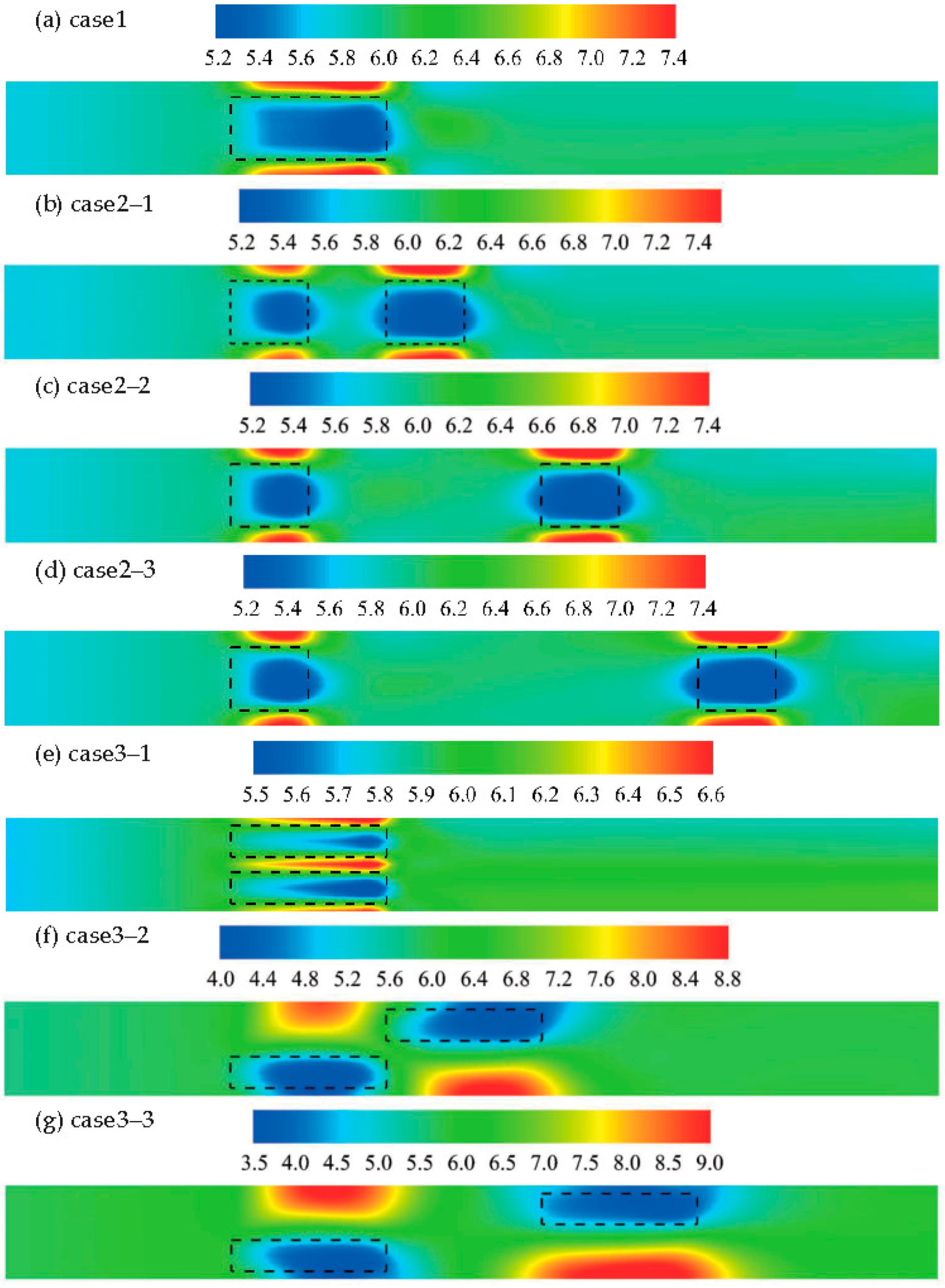
3.2. Flow Structure Comparison of Different FTW Configurations

The depth-averaged plane flow field and the horizontal velocity along the direction of the water depth are shown in Figure 3 and Figure 4, respectively. When a single large FTW was positioned in the channel flume (case 1), the main stream turned to the side and the bottom of the FTWs when entering the plant zone. The water flow velocity was minimized at the end of the FTW with an average of 5.09 cm/s, compared to 7.86 cm/s on the lateral sides of the FTW. As shown in Figure 4, because of the blocking of plant roots, the water flow velocity in the range of plant roots (4.97 cm/s) was lower than at the bottom (6.86 cm/s).

When a single large FTW was evenly segmented into two smaller FTWs in series (case 2–1, 2–2 and 2–3), the main stream turned to the side and the bottom of the FTWs when entering the plant zone of both FTWs. The three cases had similar flow characteristics around the first FTW, where the average velocity in and out of the range of plant roots was 4.84 cm/s and 5.22 cm/s, respectively. However, the average velocity in the plant zone of the second FTW increased with the distance of the two FTWs, which was 3.77 cm/s, 3.87 cm/s and 4.97 cm/s in case 2–1, 2–2 and 2–3, respectively.

When a single large FTW was evenly segmented into two smaller interlaced FTWs (case 3–1, 3–2 and 3–3), the average velocity in the range of plant roots of the upper FTW increased with the distance of the two staggered FTWs, which was 4.63 cm/s, 3.76 cm/s and 3.71 cm/s in case 3–1, 3–2 and 3–3, respectively. However, the average velocity in the range of plant roots of the lower FTW was reduced to 3.41 cm/s and 3.05 cm/s, respectively, when the distance of the two staggered FTWs was 2x (case 3–2) and 4x (case 3–3).

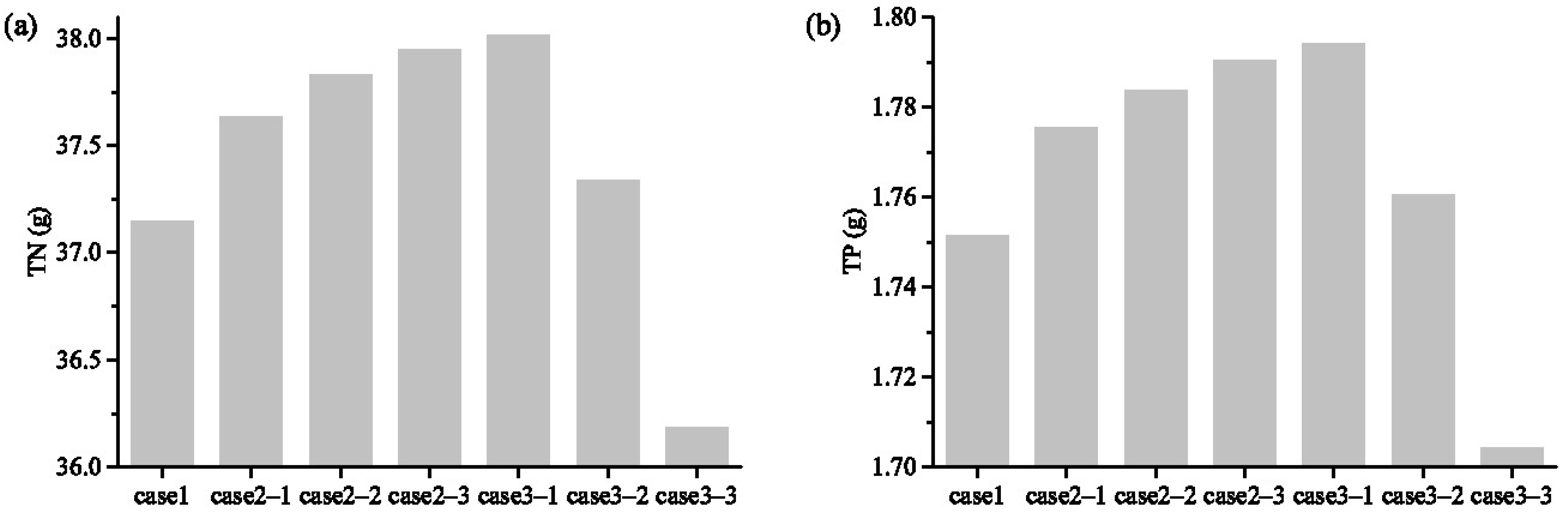
3.3. Nutrient Removal Performance Comparison of Different FTW Configurations

The quality of the nutrients removed per unit time in seven test cases is shown in Figure 5. When a single large FTW was positioned in the channel flume (case 1), the quality of TN and TP removed per unit time was 20.73 g and 0.97 g, respectively.

When a single large FTW was evenly segmented into two smaller FTWs in series (case 2–1, 2–2 and 2–3), the quality of the nutrients removed increased with the distance of the upper and lower FTWs. When the distance between the two FTWs was x, 3x and 5x, the removal quality of TN increased by 88.78 mg, 111.23 mg and 129.58 mg, respectively, compared with case 1; the removal quality of TP increased by 4.17 mg, 5.22 mg and 6.08 mg, respectively, compared with case 1.

When the two evenly segmented FTWs were arranged in parallel (case 3–1), the removal quality of TN and TP increased by 870.12 mg and 42.46 mg, respectively, which were the highest among all test cases. However, when the distance of the two staggered FTWs was increased, the nutrient removal performance declined substantially.

The center distance of two continuously arranged FTWs is an important factor for nutrient removal performance. A previous study proved that the fraction of flow entering the root zone of the FTW depended on the center distance [27]. When the center distance was 0.5 L, L and 11 L, where L was the length of the FTW along the flow direction, the percentages of the flow entering the root zone were 18 ± 8%, 52 ± 4% and 73 ± 2%, respectively [27]. When the percentage of flow entering the root zone increased, the nutrient removal performance should also be theoretically increased. This conclusion was consistent with Rao et al. [28], who found that when the center distance of two FTWs increased from 30 cm to 45 cm, the nutrient removal efficiency increased 20–40%. However, as the center distance increased, the surface area of the FTWs would inevitably be reduced in certain systems. Liu et al.’s study indicated that if the FTWs were continuously arranged with a center distance of 2–3 L in the whole area, then the system would have the highest nutrient removal performance [27].

Compared with FTWs deployed in series, FTWs deployed in a staggered formation had a greater impact on the flow structure, and the influence decreased along with the space between the two FTWs [29]. A higher turbulence intensity was beneficial to the absorption and diffusion of nutrients [8]. Computational fluid dynamics simulation results showed that when a single large FTW was evenly segmented into two smaller FTWs in parallel, the nutrient removal efficiency increased from 60% to 64% [17], which is consistent with our result.

4. Conclusions

This study developed a mathematical model by coupling both the hydrodynamic and chemical/biological processes in FWTs, which was then used to study the flow structure and nutrient removal performance of different FTW configurations. The main conclusions are as follows:

• The calibration and validation results showed that the simulation results could be well matched with the experimental results. The hydrodynamic characteristics in FTWs could be described properly by the model.
• When two FTWs were deployed in series, the percentage of the flow entering the root zone of the downstream FTW would increase with the center distance of two FTWs, resulting in higher TN and TP removal performance.
• When two FTWs were deployed in parallel, the system had the highest TN and TP removal performance.

The model has potential for widespread application in FTW investigations and combines hydrodynamic and water quality to permit a comprehensive assessment of FTW arrangement in stormwater ponds and rivers. However, the model performance was only examined using a channel flume experiment; therefore, further examination of the model should be performed using a field-scale application. A field experiment will be planned in a stormwater pond or river to explore both the hydrodynamic characteristics and the nutrient removal performance, which could be helpful for improving the model.