Combined PV-Wind Hosting Capacity Enhancement of a Hybrid AC/DC Distribution Network Using Reactive Control of Convertors and Demand Flexibility
Abstract
:1. Introduction
1.1. Motivation
1.2. Literature Review
1.3. Contributions and Organization
- Proposing a stochastic and linearized model for the HC problem of HRES (PV-WT) (sizing in multi-candidate locations) in the hybrid AC/DC distribution network.
- Utilizing the reactive power control of VSCs (QSVC) as an ANM scheme for increasing the HC and reducing the network energy losses.
- Including the DFP in the proposed formulation in order to achieve the objectives of the problem.
- Presenting a multi-objective, multi-source, and multi-period optimization framework (increasing HC and reducing energy losses) based on ɛ-constraint and fuzzy satisfying methods.
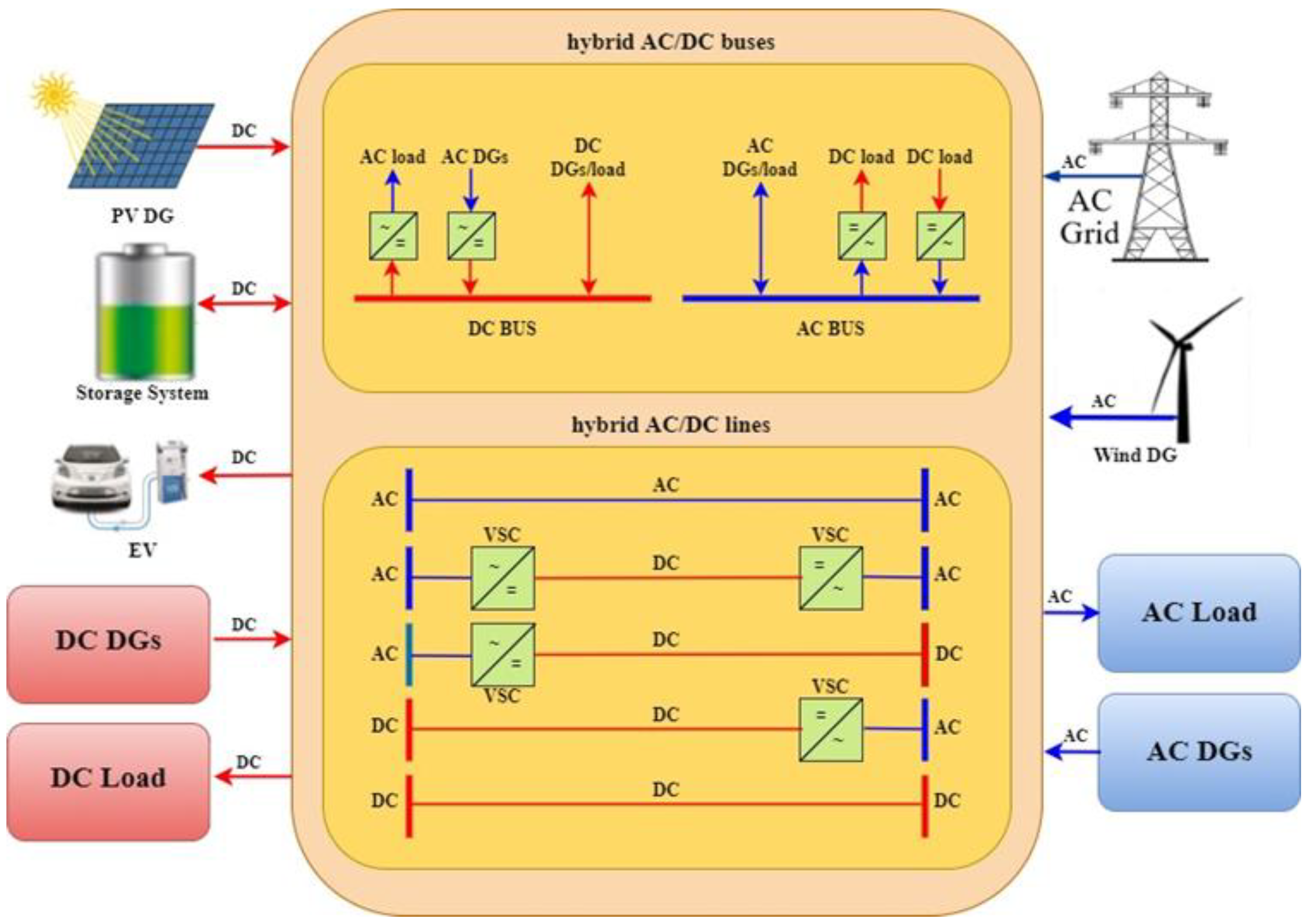
2. Structure of a Hybrid AC/DC Distribution Network
3. Uncertainty Modeling
3.1. Modeling of RESs Uncertainty
3.2. Two-Stage Stochastic Optimization Modeling
4. Problem Formulation
4.1. Objective Functions
4.2. Constraints
4.2.1. Power Flow Equations of AC Distribution Network
4.2.2. Power Flow Equations of DC Distribution Network
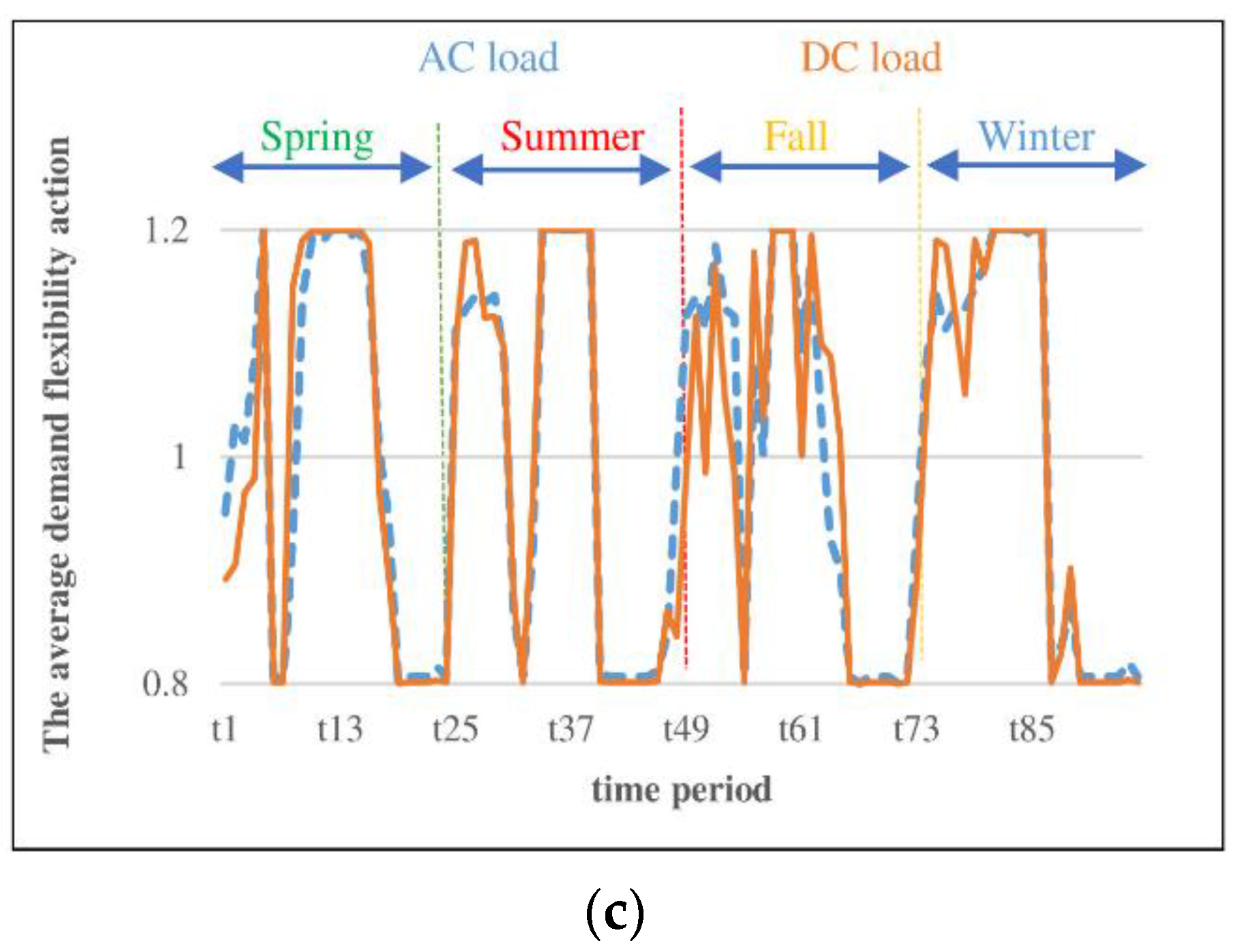
4.2.3. DFP Equations
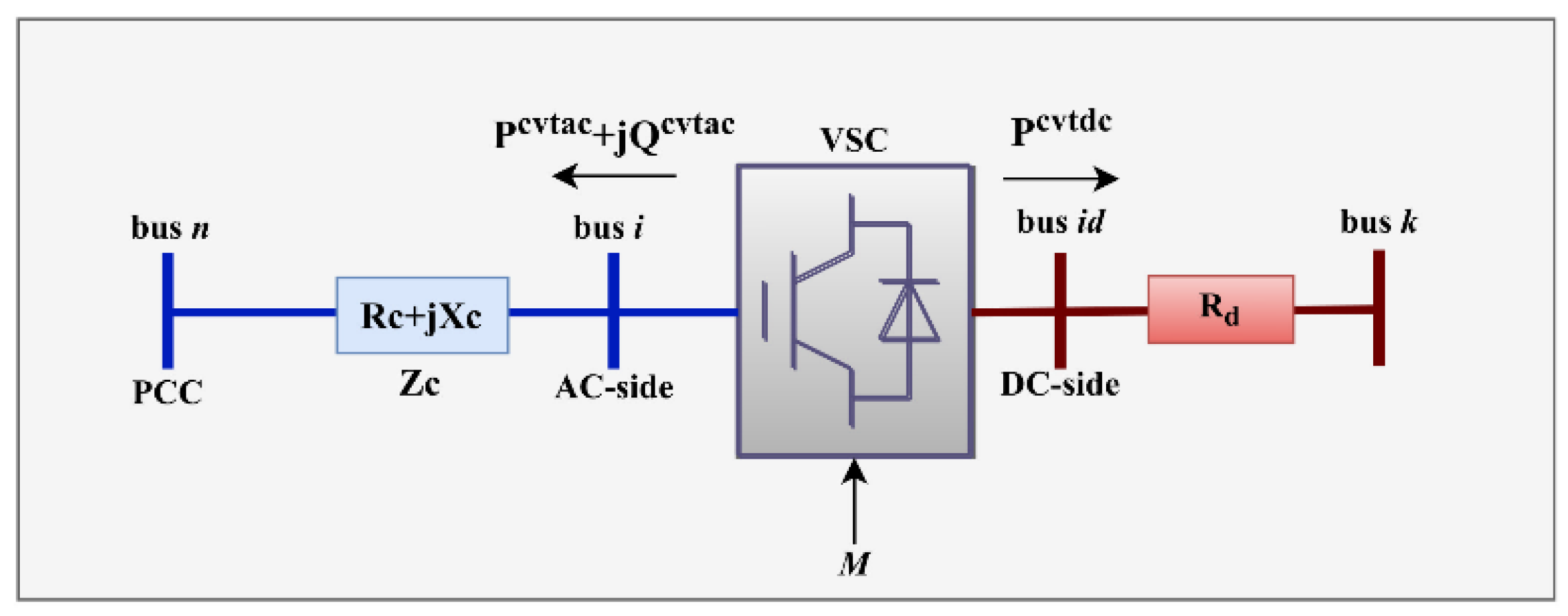
4.2.4. Modeling of VSC
4.3. Linearization
- (1)
- The typical power flow equations in AC and DC distribution networks that are illustrated in (9), (10), and (29), are nonlinear and non-convex. Reasonably, utilizing these power flow terms in the optimization problems is difficult. Therefore, they are linearized by taking into consideration two practical assumptions. The first one is regarding the bus voltage magnitudes, in an AC and DC distribution system, to be close to the nominal value The second assumption is that the voltage angle difference through the AC line is tiny, leading to the trigonometric estimates, i.e., and [37]. In addition, the voltage magnitude at bus i and id can be represented as the summation of the nominal voltage and a minor deviation , i.e., .
- (2)
- The modulation index (M) of each VSC should be limited in order to prevent over-modulation and excessive harmonics. The upper limit of M can be selected as and the lower limit as , which is usually the upper and lower voltage limits, i.e., 0.95 p.u and 1.05 p.u, respectively. By defining the variable , the upper and lower limits of H are considered equal to 1.1 and 1. Additionally, by defining () and dH equal to 0.05, the value of the new variable, i.e., , is limited to . So, we have [37].
- (3)
- The variables , and θ have small values and therefore their multiplication can be considered to be zero [37].
4.4. Multi-Objective Optimization
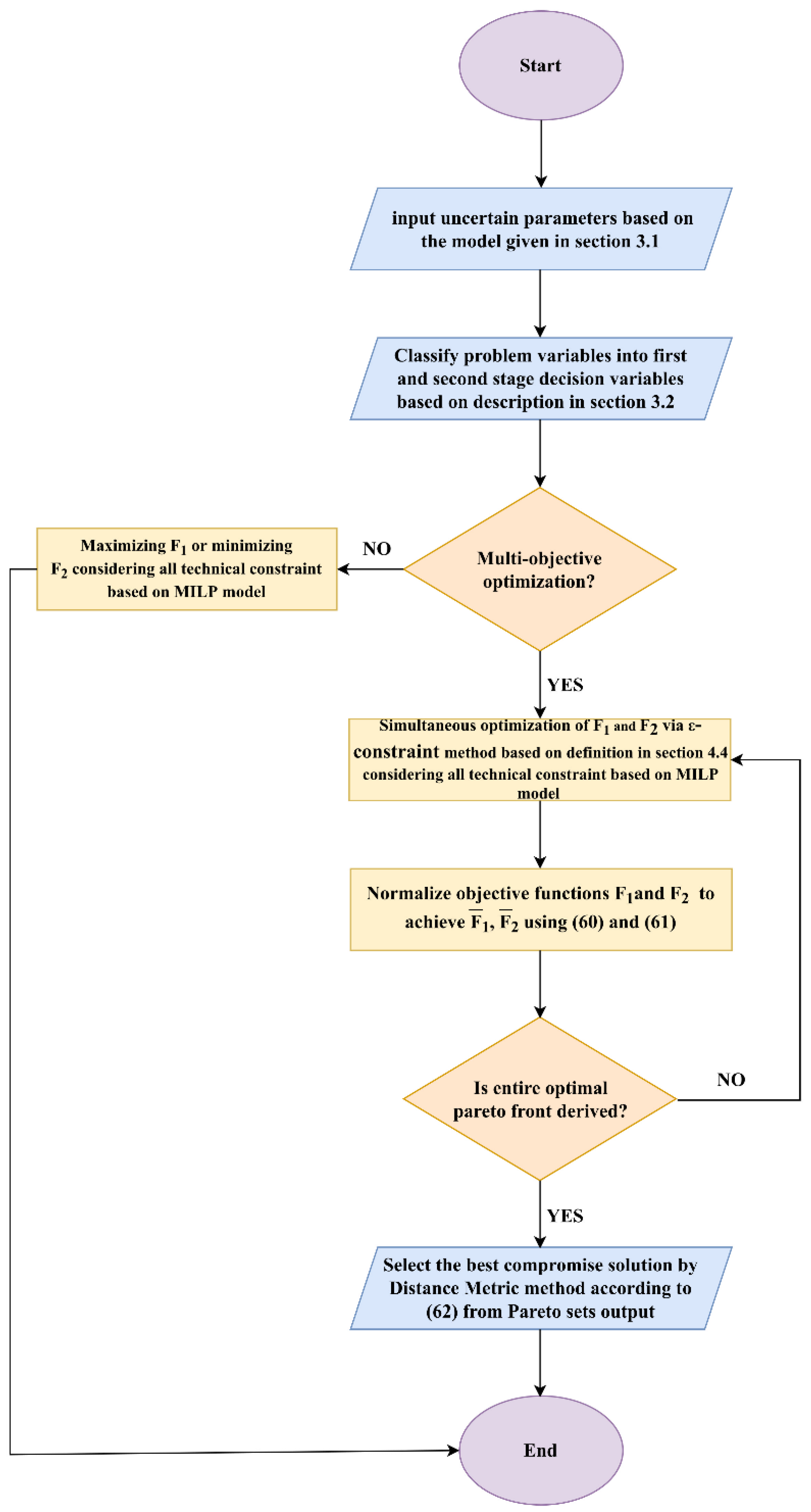
4.5. Solution Procedure
5. Simulation Results
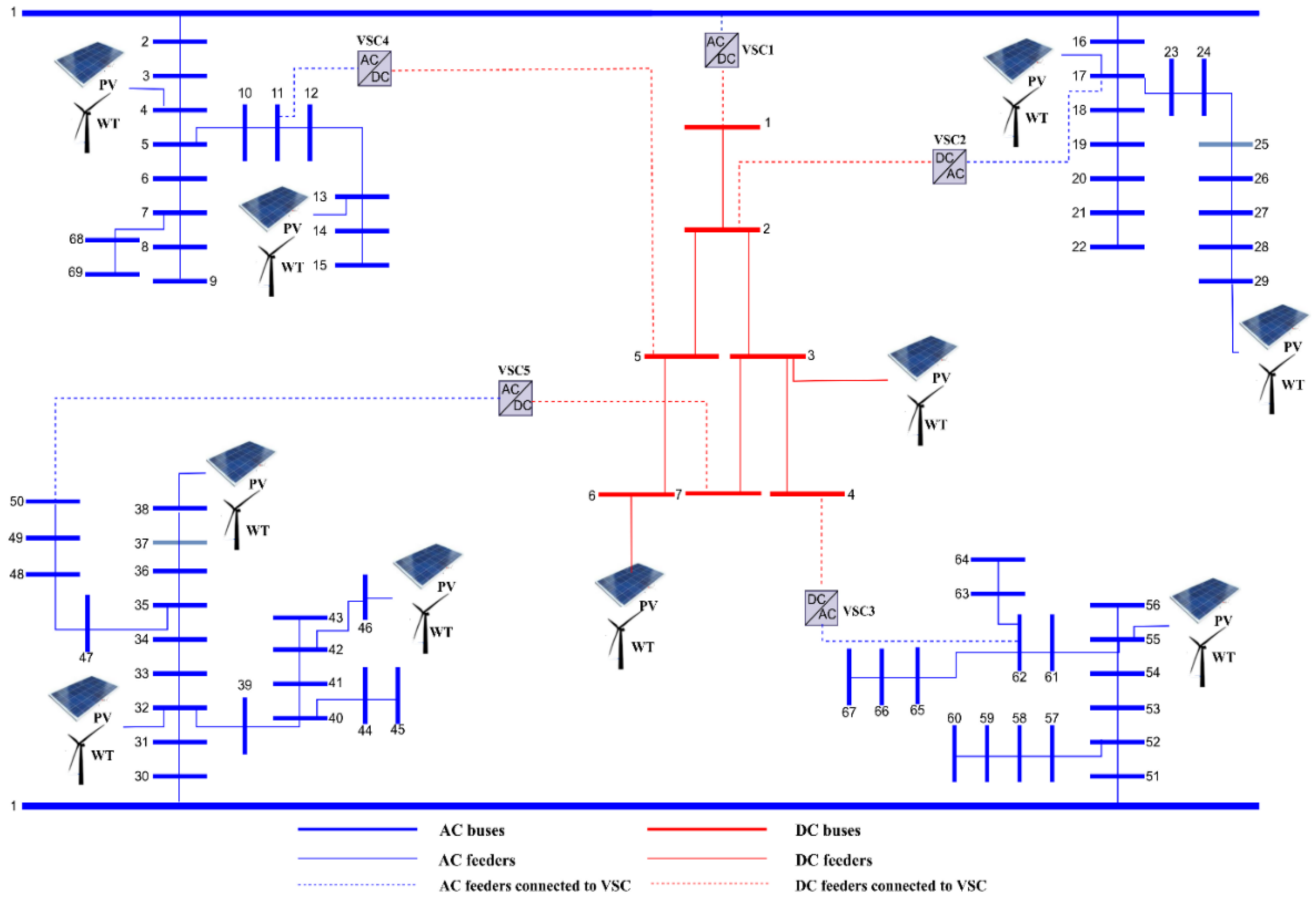
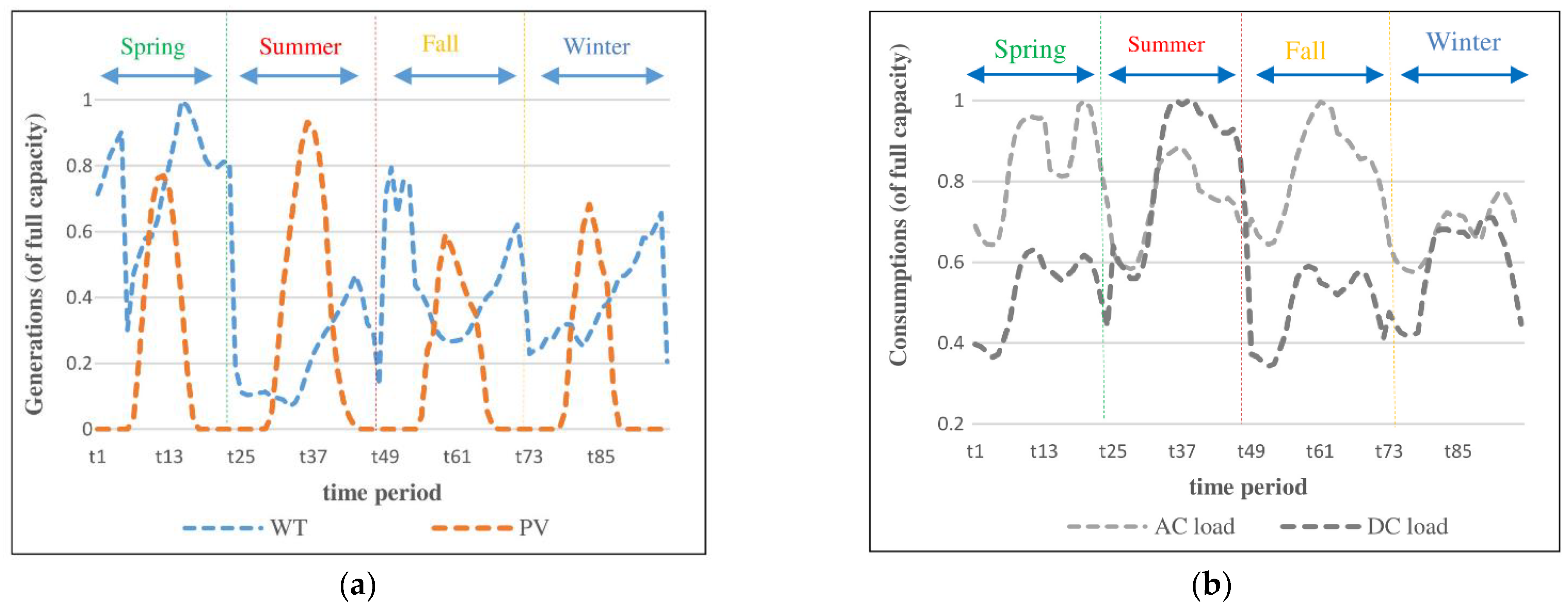
5.1. Input Data
5.2. Case Studies
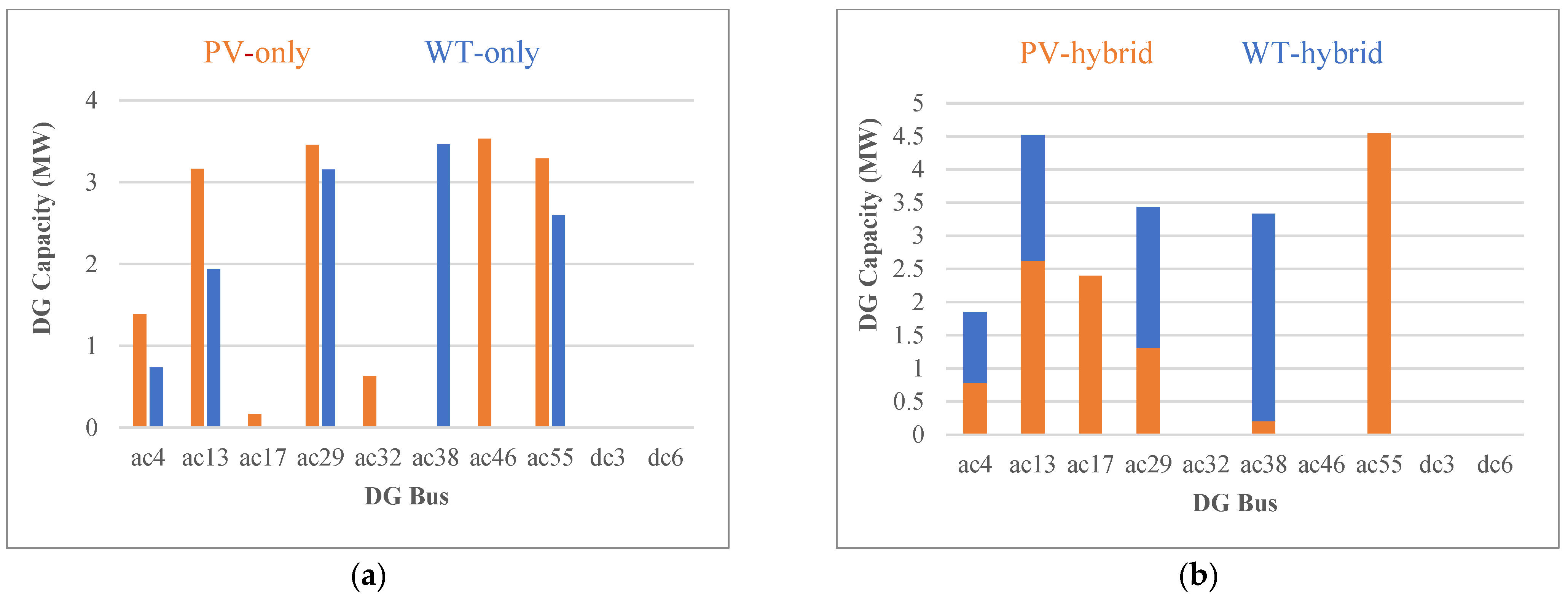
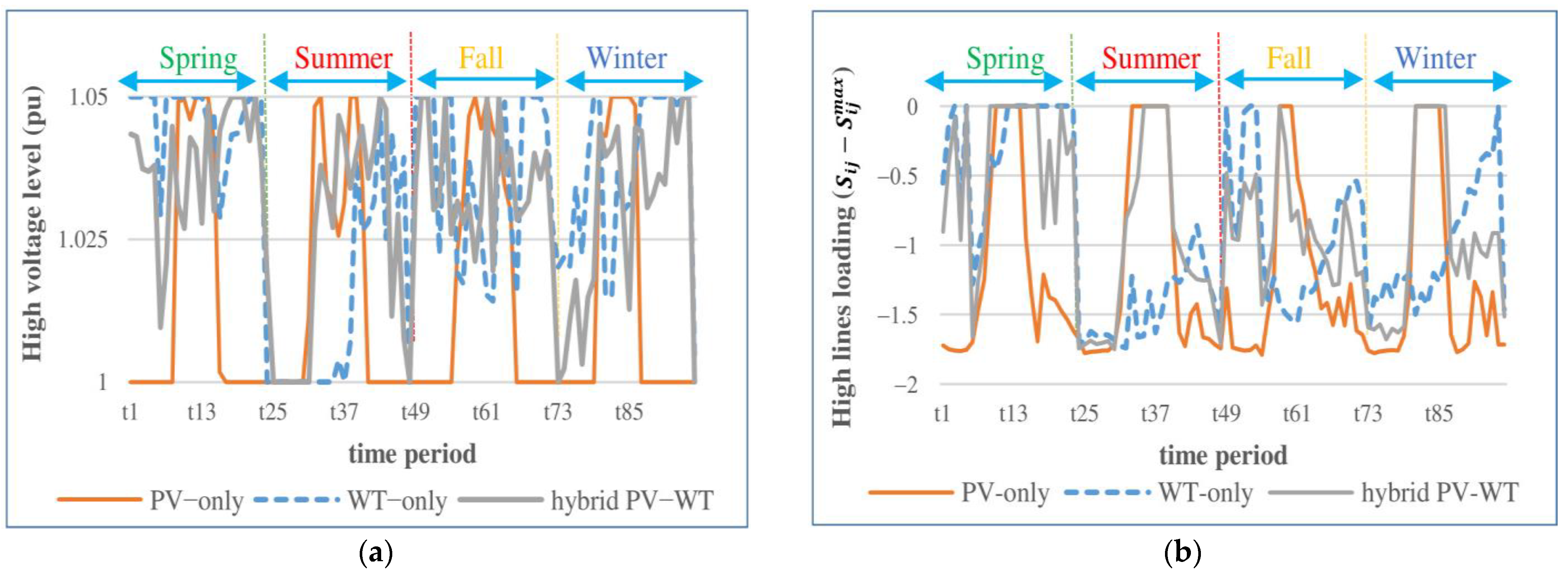
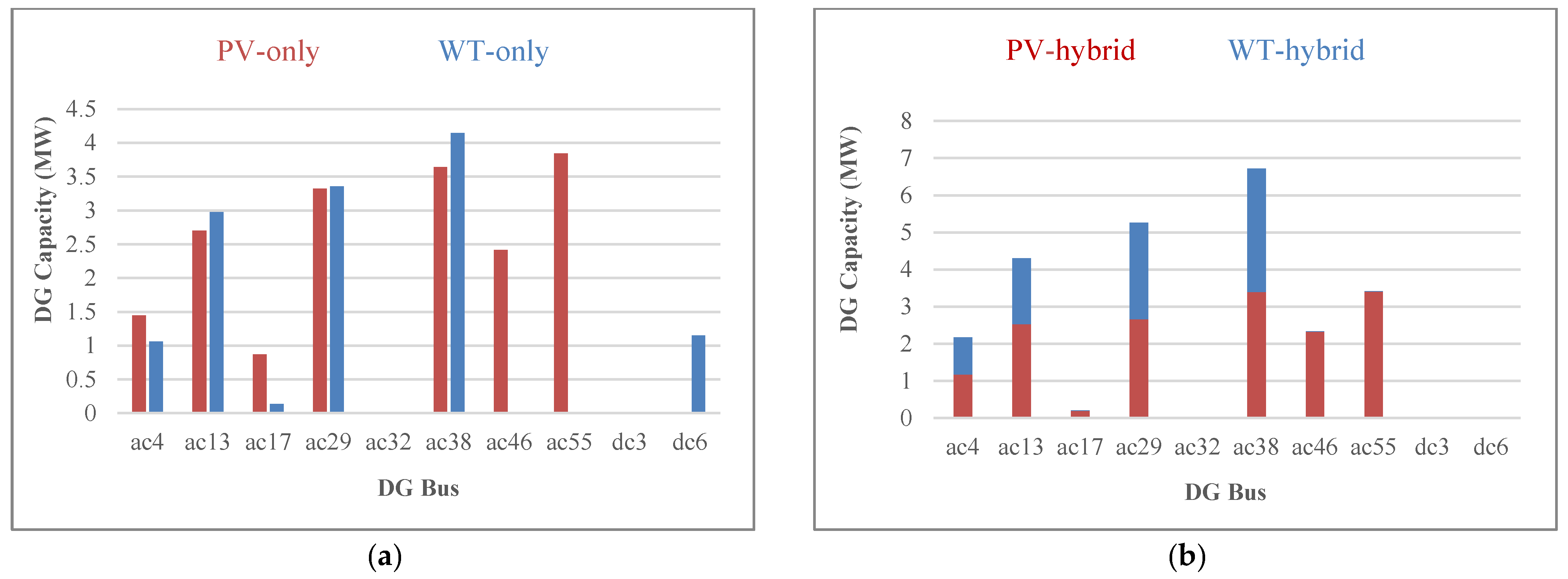
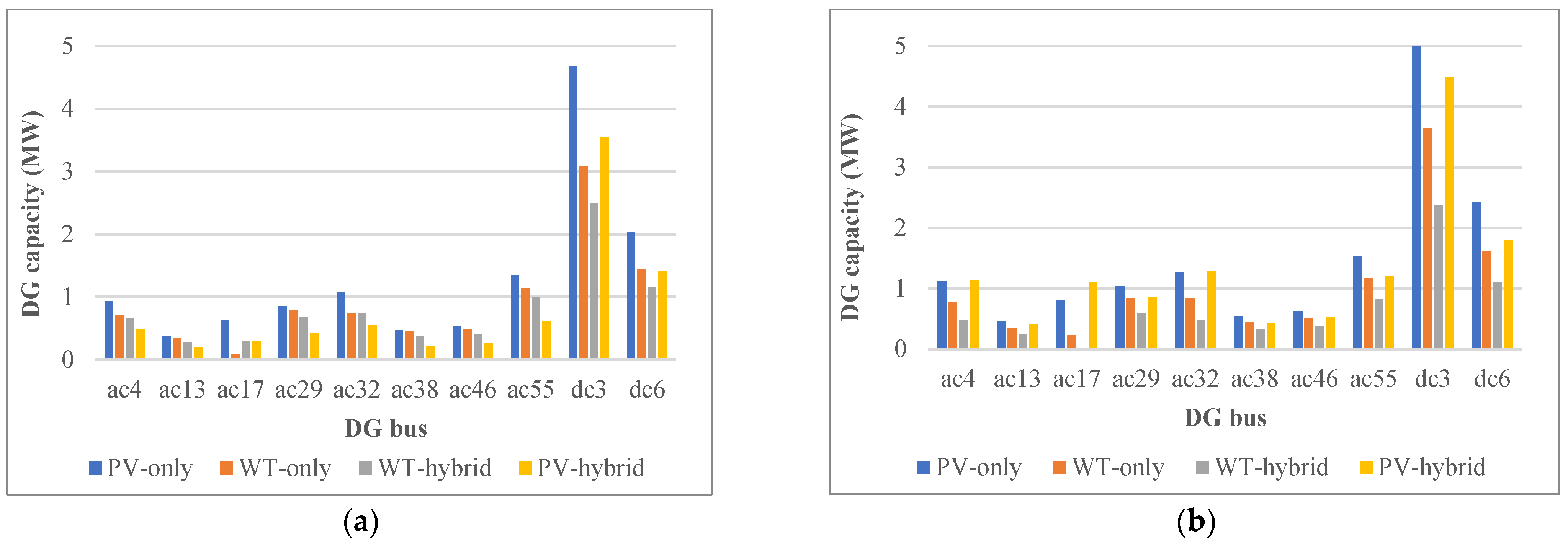
5.3. Case Study 1: Maximizing Hybrid PV-WT HC without DFP and with/without QVSC
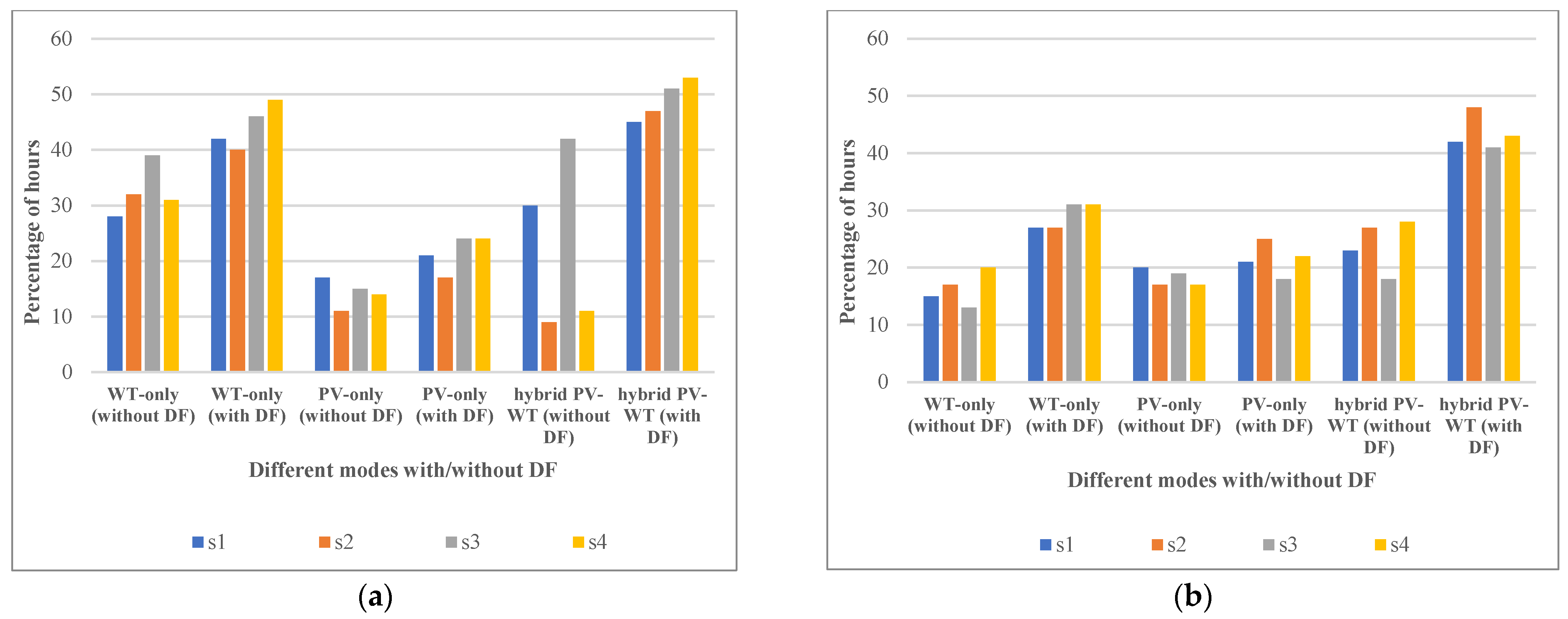
5.4. Case 2: Maximizing Hybrid PV-WT HC with DFP and with/without QVSC
5.5. Case Study 3: Minimization of Losses for Hybrid PV-WT with/without DFP and QVSC
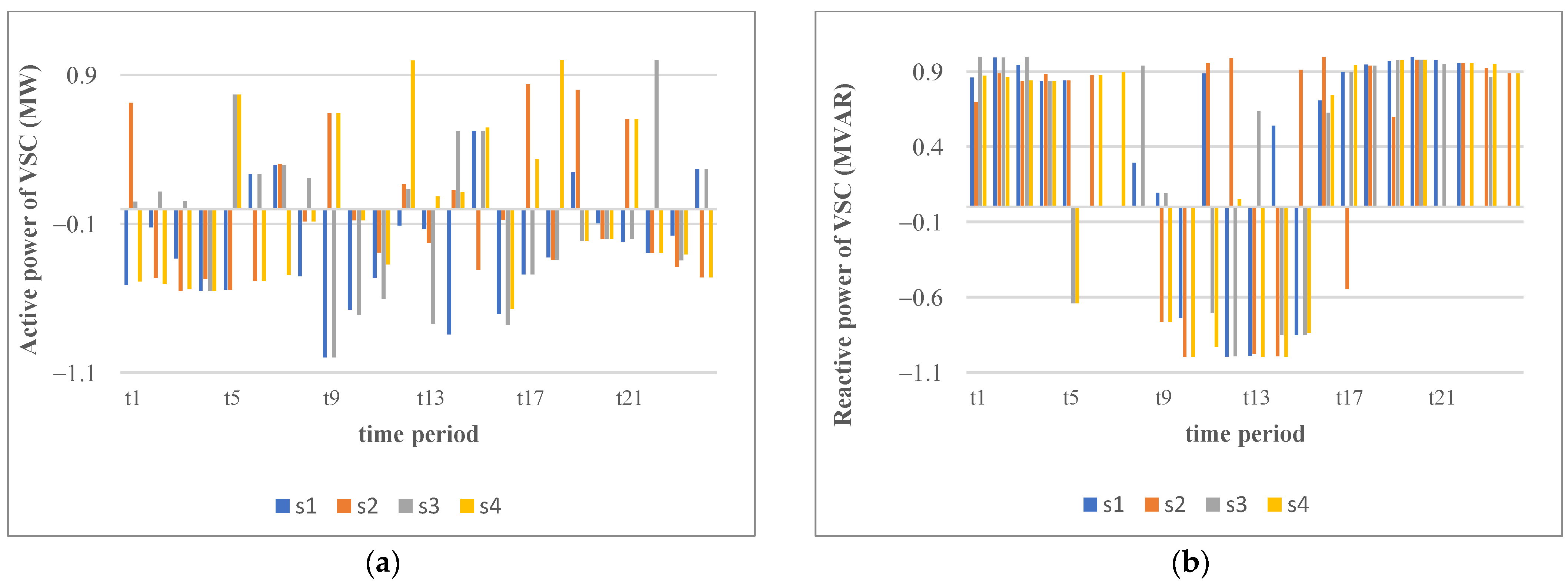
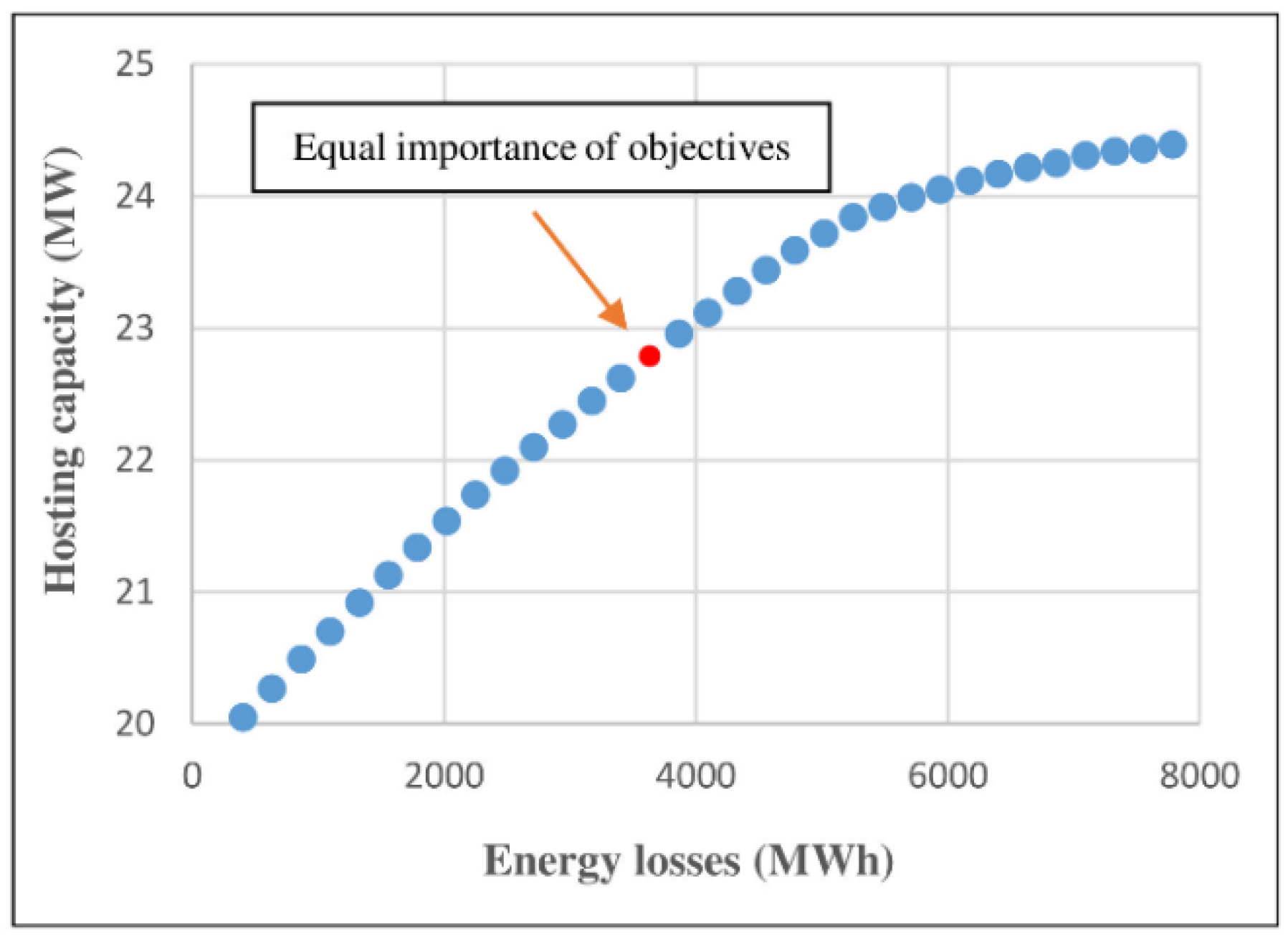
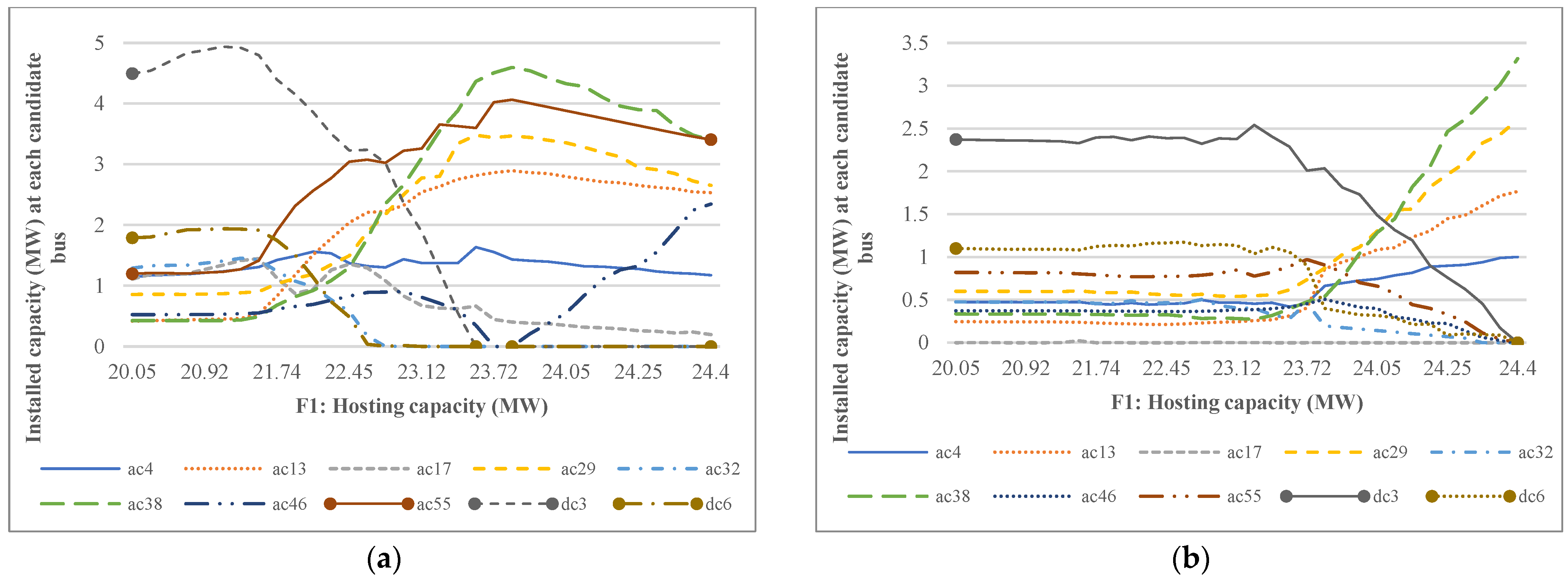
5.6. Case Study 4: Optimization of Hybrid PV-WT HC and Losses with the DFP and QVSC
5.7. Economic Analysis
5.8. Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| Indices | |
| : | Indices of the AC buses. |
| , | Indices of the DC buses. |
| Index of the hours. | |
| Index of the scenarios. | |
| Index of the feeders. | |
| Sets | |
| Set of substation buses in the network. | |
| Set of scenarios in the operation period. | |
| Set of hours in the operation period. | |
| Set of candidate AC/DC buses for installing PV. | |
| Set of candidate AC/DC buses for installing WT. | |
| Set of candidate AC/DC buses for installing the VSC. | |
| Set of AC/DC distribution buses. | |
| Set of demand buses in AC/DC network. | |
| Set of distribution buses participating in the DFP in AC/DC network. | |
| Variables | |
| WT/PV installed capacity in the bus i of the AC network (MW). | |
| WT/PV installed capacity in bus id of the DC network (MW). | |
| Active/reactive power of WT/PV in the bus i at time t and scenario s in AC network (MW/MVAR). | |
| Active power of WT/PV in bus id at time t and scenario s in DC network (MW). | |
| Curtailed power of WT/PV in the bus i at time t and scenario s in AC network (MW). | |
| Curtailed power of WT/PV in the bus id at time t and scenario s in DC network (MW). | |
| Active/reactive demand of bus i considering DFP at time t in AC network (MW/MVAR). | |
| Active power demand in the bus id considering DFP at time t in DC network (MW). | |
| DFP in the bus i/id of AC/DC network at time t. | |
| Net active/reactive power injection to the bus i at time t and scenario s (MW/MVAR). | |
| Net active power injection to the bus id at time t and scenario s (MW). | |
| Active/reactive power of VSC connected to bus i at time t and scenario s (MW/MVAR). | |
| Active power losses of VSC connected to bus i at time t and scenario s (MW). | |
| Active power of VSC connected to bus id at time t and scenario s in DC network (MW). | |
| Active/reactive power flowing line ij in AC network at time t and scenario s (MW). | |
| Active power flowing line id.jd in DC network at time t and scenario s (MW). | |
| Active/reactive losses of AC lines connected between i and j at time t and scenario s (MW/MVAR). | |
| Active losses of DC lines connected between id and jd at time t and scenario s (MW). | |
| Active power losses of AC/DC network at time t and scenario s (MW). | |
| Voltage magnitude/angle of bus i at time t and scenario s in AC network. | |
| Voltage magnitude of bus id at time t and scenario s in DC network. | |
| Variable used in the linearization process for the DC network. | |
| Deviation of Voltage magnitude at bus i and id in AC/DC network. | |
| Parameters | |
| Magnitude/angle of the element ij of the admittance matrix of AC network. | |
| Conductance/susceptance/ MVA rating of the line connecting bus i and j. | |
| Conductance/ MW rating of the line connecting between bus id and jd in DC network. | |
| Min/ Max active power imported from the upstream grid (MW). | |
| Min/ Max reactive power imported from the upstream grid (MVAR). | |
| WT/PV power generation at time t and scenario s (percentage of the full capacity). | |
| Minimum/Maximum reactive power generation by WT/PV sources in the bus i (MVAR). | |
| Power factor of WT and PV located in the bus i at time t and scenario s. | |
| The upper limit for acceptable generation energy curtailment at bus i/id in AC/DC network. | |
| A binary parameter that indicates the participation of bus i/id in DFP in the AC/DC network. | |
| Base (without DFP) active power in the bus id for time t in DC network (MW). | |
| Base (without DFP) active/reactive power in the bus i at time t (MW/MVAR). | |
| Upper/lower boundary of DFP at bus i/id in AC/DC network. | |
| Ψi | Power factor angle of VSC connected to bus i in AC network. |
References
- Bagherzadeh, L.; Shayeghi, H.; Pirouzi, S.; Shafie-khah, M.; Catalão, J.P. Coordinated flexible energy and self-healing management according to the multi-agent system-based restoration scheme in active distribution network. IET Renew. Power Gener. 2021, 15, 1765–1777. [Google Scholar] [CrossRef]
- Chen, H.; Gao, L.; Zhang, Z. Multi-objective optimal scheduling of a microgrid with uncertainties of renewable power generation considering user satisfaction. Int. J. Electr. Power Energy Syst. 2021, 131, 107142. [Google Scholar] [CrossRef]
- Hossain, M.; Jahid, A.; Islam, K.Z.; Alsharif, M.H.; Rahman, M. Multi-objective optimum design of hybrid renewable energy system for sustainable energy supply to a green cellular networks. Sustainability 2020, 12, 3536. [Google Scholar] [CrossRef]
- Hussain, M.; Gao, Y. A review of demand response in an efficient smart grid environment. Electr. J. 2018, 31, 55–63. [Google Scholar] [CrossRef]
- Venkatesan, C.; Kannadasan, R.; Alsharif, M.H.; Kim, M.-K.; Nebhen, J. A novel multiobjective hybrid technique for siting and sizing of distributed generation and capacitor banks in radial distribution systems. Sustainability 2021, 13, 3308. [Google Scholar] [CrossRef]
- Rabiee, A.; Mohseni-Bonab, S.M. Maximizing hosting capacity of renewable energy sources in distribution networks: A multi-objective and scenario-based approach. Energy 2017, 120, 417–430. [Google Scholar] [CrossRef]
- Bajaj, M.; Singh, A.K. Performance assessment of hybrid active filtering technique to enhance the hosting capacity of distorted grids for renewable energy systems. Int. J. Energy Res. 2022, 46, 2783–2809. [Google Scholar] [CrossRef]
- Mulenga, E.; Bollen, M.H.; Etherden, N. A review of hosting capacity quantification methods for photovoltaics in low-voltage distribution grids. Int. J. Electr. Power Energy Syst. 2020, 115, 105445. [Google Scholar] [CrossRef]
- Estorque, L.K.L.; Pedrasa, M.A.A. Utility-scale DG planning using location-specific hosting capacity analysis. In Proceedings of the 2016 IEEE Innovative Smart Grid Technologies-Asia (ISGT-Asia), Melbourne, VIC, Australia, 28 November–1 December 2016; pp. 984–989. [Google Scholar]
- Capitanescu, F.; Ochoa, L.F.; Margossian, H.; Hatziargyriou, N.D. Assessing the potential of network reconfiguration to improve distributed generation hosting capacity in active distribution systems. IEEE Trans. Power Syst. 2014, 30, 346–356. [Google Scholar] [CrossRef]
- Sun, W.; Harrison, G.P. Wind-solar complementarity and effective use of distribution network capacity. Appl. Energy 2019, 247, 89–101. [Google Scholar] [CrossRef] [Green Version]
- Ali, A.; Mahmoud, K.; Lehtonen, M. Maximizing hosting capacity of uncertain photovoltaics by coordinated management of OLTC, VAr sources and stochastic EVs. Int. J. Electr. Power Energy Syst. 2021, 127, 106627. [Google Scholar] [CrossRef]
- Xu, X.; Xu, Z.; Li, J.; Zhao, J.; Xue, L. Optimal Placement of Voltage Regulators for Photovoltaic Hosting Capacity Maximization. In Proceedings of the 2018 IEEE Innovative Smart Grid Technologies-Asia (ISGT Asia), Singapore, 22–25 May 2018; pp. 1278–1282. [Google Scholar]
- Fachrizal, R.; Ramadhani, U.H.; Munkhammar, J.; Widén, J. Combined PV–EV hosting capacity assessment for a residential LV distribution grid with smart EV charging and PV curtailment. Sustain. Energy Grids Netw. 2021, 26, 100445. [Google Scholar] [CrossRef]
- Kazemi-Robati, E.; Sepasian, M.S.; Hafezi, H.; Arasteh, H. PV-hosting-capacity enhancement and power-quality improvement through multiobjective reconfiguration of harmonic-polluted distribution systems. Int. J. Electr. Power Energy Syst. 2022, 140, 107972. [Google Scholar] [CrossRef]
- Xiao, J.; Li, Y.; Qiao, X.; Tan, Y.; Cao, Y.; Jiang, L. Enhancing Hosting Capacity of Uncertain and Correlated Wind Power in Distribution Network with ANM Strategies. IEEE Access 2020, 8, 189115–189128. [Google Scholar] [CrossRef]
- Rawa, M.; Abusorrah, A.; Al-Turki, Y.; Mekhilef, S.; Mostafa, M.H.; Ali, Z.M.; Aleem, S.H.A. Optimal allocation and economic analysis of battery energy storage systems: Self-consumption rate and hosting capacity enhancement for microgrids with high renewable penetration. Sustainability 2020, 12, 10144. [Google Scholar] [CrossRef]
- Divshali, P.H.; Söder, L. Improving PV dynamic hosting capacity using adaptive controller for STATCOMs. IEEE Trans. Energy Convers. 2018, 34, 415–425. [Google Scholar] [CrossRef]
- Hamidi, A.; Nazarpour, D.; Golshannavaz, S. Smart grid adds to renewable resources hosting capacity: Collaboration of plug-in hybrid electric vehicles in volt/VAr control process. Int. J. Energy Res. 2018, 42, 601–615. [Google Scholar] [CrossRef]
- Ding, F.; Mather, B. On distributed PV hosting capacity estimation, sensitivity study, and improvement. IEEE Trans. Sustain. Energy 2016, 8, 1010–1020. [Google Scholar] [CrossRef]
- Panda, A.; Aviso, K.B.; Mishra, U.; Nanda, I. Impact of optimal power generation scheduling for operating cleaner hybrid power systems with energy storage. Int. J. Energy Res. 2021, 45, 14493–14517. [Google Scholar] [CrossRef]
- Monforti, F.; Huld, T.; Bódis, K.; Vitali, L.; D’isidoro, M.; Lacal-Arántegui, R. Assessing complementarity of wind and solar resources for energy production in Italy. A Monte Carlo approach. Renew. Energy 2014, 63, 576–586. [Google Scholar] [CrossRef]
- Hoicka, C.E.; Rowlands, I.H. Solar and wind resource complementarity: Advancing options for renewable electricity integration in Ontario, Canada. Renew. Energy 2011, 36, 97–107. [Google Scholar] [CrossRef]
- Ajeigbe, O.A.; Munda, J.L.; Hamam, Y. Towards maximising the integration of renewable energy hybrid distributed generations for small signal stability enhancement: A review. Int. J. Energy Res. 2020, 44, 2379–2425. [Google Scholar] [CrossRef]
- Liu, D.; Wang, C.; Tang, F.; Zhou, Y. Probabilistic assessment of hybrid wind-PV hosting capacity in distribution systems. Sustainability 2020, 12, 2183. [Google Scholar] [CrossRef] [Green Version]
- Soroudi, A.; Rabiee, A.; Keane, A. Distribution networks’ energy losses versus hosting capacity of wind power in the presence of demand flexibility. Renew. Energy 2017, 102, 316–325. [Google Scholar] [CrossRef] [Green Version]
- Ikeda, S.; Ohmori, H. Evaluation for maximum hosting capacity of distributed generation considering active network management. Int. J. Electr. Electron. Eng. Telecommun. 2018, 7, 96–102. [Google Scholar] [CrossRef] [Green Version]
- Alvarez-Herault, M.-C.; N’doye, N.; Gandioli, C.; Hadjsaid, N.; Tixador, P. Meshed distribution network vs. reinforcement to increase the distributed generation connection. Sustain. Energy Grids Netw. 2015, 1, 20–27. [Google Scholar] [CrossRef]
- Zhang, L.; Chen, Y.; Shen, C.; Tang, W.; Liang, J. Releasing more capacity for EV integration by DC medium voltage distribution lines. IET Power Electron. 2017, 10, 2116–2123. [Google Scholar] [CrossRef]
- Chaudhary, S.K.; Guerrero, J.M.; Teodorescu, R. Enhancing the capacity of the AC distribution system using DC interlinks—A step toward future DC grid. IEEE Trans. Smart Grid 2015, 6, 1722–1729. [Google Scholar] [CrossRef]
- Kaipia, T.; Salonen, P.; Lassila, J.; Partanen, J. Application of low voltage DC-distribution system—A techno-economical study. In Proceedings of the 19th International Conference on Electricity Distribution CIRED, Vienna, Austria, 21–24 May 2007; pp. 21–24. [Google Scholar]
- Ahmed, H.M.; Eltantawy, A.B.; Salama, M.M. A planning approach for the network configuration of AC-DC hybrid distribution systems. IEEE Trans. Smart Grid 2016, 9, 2203–2213. [Google Scholar] [CrossRef]
- Delkhosh, H.; Moghaddam, M.P.; Ghaedi, M. Multi-Objective Sizing of Energy Storage Systems (ESSs) and Capacitors in a Distribution System. In Proceedings of the 2020 10th Smart Grid Conference (SGC), Kashan, Iran, 16–17 December 2020; pp. 1–6. [Google Scholar]
- Soares, J.; Canizes, B.; Ghazvini, M.A.F.; Vale, Z.; Venayagamoorthy, G.K. Two-stage stochastic model using benders’ decomposition for large-scale energy resource management in smart grids. IEEE Trans. Ind. Appl. 2017, 53, 5905–5914. [Google Scholar] [CrossRef]
- Conejo, A.J.; Carrión, M.; Morales, J.M. Decision Making under Uncertainty in Electricity Markets; Springer: New York, NY, USA, 2010. [Google Scholar]
- Beerten, J.; Cole, S.; Belmans, R. Generalized steady-state VSC MTDC model for sequential AC/DC power flow algorithms. IEEE Trans. Power Syst. 2012, 27, 821–829. [Google Scholar] [CrossRef] [Green Version]
- Ahmed, H.M.; Salama, M.M. Energy management of AC–DC hybrid distribution systems considering network reconfiguration. IEEE Trans. Power Syst. 2019, 34, 4583–4594. [Google Scholar] [CrossRef]
- Maghouli, P.; Hosseini, S.H.; Buygi, M.O.; Shahidehpour, M. A multi-objective framework for transmission expansion planning in deregulated environments. IEEE Trans. Power Syst. 2009, 24, 1051–1061. [Google Scholar] [CrossRef]
- Rosenthal, R. GAMS, A User’s Guide; GAMS Development Corporation: Washington, DC, USA, 2012. [Google Scholar]
- Chen, Y.-L. An interactive fuzzy-norm satisfying method for multi-objective reactive power sources planning. IEEE Trans. Power Syst. 2000, 15, 1154–1160. [Google Scholar] [CrossRef]
- Lotfi, H.; Khodaei, A. Hybrid AC/DC microgrid planning. Energy 2017, 118, 37–46. [Google Scholar] [CrossRef]



| MILP Model | Multi Objectives Framework | Hybrid RESs | RESs Uncertainty | Stochastic Model | Hybrid AC/DC Network | Tools | |||
|---|---|---|---|---|---|---|---|---|---|
| DFP | ANM (QVSC) | ANM (Others) | |||||||
| [6] | ✘ | ✓ | ✘ | ✓ | ✓ | ✘ | ✘ | ✘ | ✓ |
| [11] | ✘ | ✘ | ✓ | ✘ | ✘ | ✘ | ✘ | ✘ | ✓ |
| [12] | ✘ | ✘ | ✘ | ✓ | ✓ | ✘ | ✘ | ✘ | ✓ |
| [13] | ✓ | ✓ | ✘ | ✘ | ✘ | ✘ | ✘ | ✘ | ✓ |
| [14] | ✘ | ✘ | ✘ | ✘ | ✘ | ✘ | ✘ | ✘ | ✓ |
| [15] | ✘ | ✓ | ✘ | ✓ | ✘ | ✘ | ✘ | ✘ | ✓ |
| [16] | ✓ | ✓ | ✘ | ✓ | ✓ | ✘ | ✘ | ✘ | ✓ |
| [17] | ✘ | ✓ | ✘ | ✘ | ✘ | ✘ | ✘ | ✘ | ✓ |
| [19] | ✘ | ✘ | ✘ | ✘ | ✘ | ✘ | ✘ | ✘ | ✓ |
| [20] | ✘ | ✘ | ✘ | ✘ | ✘ | ✘ | ✘ | ✘ | ✓ |
| [25] | ✘ | ✘ | ✓ | ✓ | ✘ | ✘ | ✘ | ✘ | ✓ |
| [26] | ✘ | ✓ | ✘ | ✘ | ✘ | ✘ | ✓ | ✘ | ✓ |
| [27] | ✘ | ✘ | ✘ | ✘ | ✘ | ✘ | ✓ | ✘ | ✓ |
| Current paper | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ |
| Case Study | Stochastic (Uncertainties) | RESs | Objectives | Tools | ||||
|---|---|---|---|---|---|---|---|---|
| WT Only | PV Only | Hybrid PV-WT | Max HC | Min Losses | DFP | ANM (QVSC) | ||
| 1 | ✓ | ✓ | ✓ | ✓ | ✓ | ✘ | ✘ | ✓✘ |
| 2 | ✓ | ✓ | ✓ | ✓ | ✓ | ✘ | ✓ | ✓✘ |
| 3 | ✓ | ✓ | ✓ | ✓ | ✘ | ✓ | ✓✘ | ✓✘ |
| 4 | ✓ | ✘ | ✘ | ✓ | ✓ | ✓ | ✓ | ✓ |
| RESs | WT Capacity (MW) | PV Capacity (MW) | Total HC (MW) | Energy of Sources (GWh) | Energy Curtailment (GWh) | Energy Losses (GWh) | Energy Exchange by VSC (GWh) |
|---|---|---|---|---|---|---|---|
| WT-only | 11.89 | - | 11.89 | 46.35 | 4.63 | 5.45 | 35.50 |
| PV-only | - | 15.63 | 15.63 | 27.48 | 2.74 | 4.52 | 29.15 |
| Hybrid PV-WT | 8.21 | 11.85 | 20.06 | 52.89 | 5.27 | 5.51 | 34.78 |
| RESs | WT Capacity (MW) | PV Capacity (MW) | Total HC (MW) | Energy of Sources (GWh) | Energy Curtailment (GWh) | Energy Losses (GWh) | Energy Exchange by VSC (GWh) |
|---|---|---|---|---|---|---|---|
| WT-only | 12.83 | - | 12.83 | 50.01 | 5.00 | 6.08 | 30.81 |
| PV-only | - | 18.25 | 18.25 | 32.08 | 3.20 | 4.79 | 32.64 |
| Hybrid PV-WT | 8.69 | 15.69 | 24.39 | 61.47 | 6.14 | 7.55 | 44.46 |
| RESs | Without DFP | With DFP | ||
|---|---|---|---|---|
| HC (MW) | Energy Losses (MWh) | HC (MW) | Energy Losses (MWh) | |
| WT-only | 9.35 | 649.23 | 10.43 | 574.10 |
| PV-only | 12.99 | 984.50 | 15.61 | 854.23 |
| Hybrid PV-WT | 16.16 | 475.97 | 20.05 | 405.00 |
| DFP | RESs | Additional Cost of Converters ($) | HC (MW) |
|---|---|---|---|
| Without DFP | WT-only | 0 | 11.89 |
| PV-only | 101,595 | 15.63 | |
| PV and WT in AC and DC network (multi-location/ hybrid mode) | 77,025 | 20.06 | |
| PV in DC network and WT in AC network (single-location/ hybrid mode) | 0 | 19.37 | |
| With DFP | WT-only | 4830 | 12.83 |
| PV-only | 118,625 | 18.25 | |
| PV and WT in AC and DC network (multi-location/ hybrid mode) | 101,985 | 24.39 | |
| PV in DC network and WT in AC network (single-location/ hybrid mode) | 0 | 21.81 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Taghavi, M.; Delkhosh, H.; Parsa Moghaddam, M.; Sheikhi Fini, A. Combined PV-Wind Hosting Capacity Enhancement of a Hybrid AC/DC Distribution Network Using Reactive Control of Convertors and Demand Flexibility. Sustainability 2022, 14, 7558. https://doi.org/10.3390/su14137558
Taghavi M, Delkhosh H, Parsa Moghaddam M, Sheikhi Fini A. Combined PV-Wind Hosting Capacity Enhancement of a Hybrid AC/DC Distribution Network Using Reactive Control of Convertors and Demand Flexibility. Sustainability. 2022; 14(13):7558. https://doi.org/10.3390/su14137558
Chicago/Turabian StyleTaghavi, Moein, Hamed Delkhosh, Mohsen Parsa Moghaddam, and Alireza Sheikhi Fini. 2022. "Combined PV-Wind Hosting Capacity Enhancement of a Hybrid AC/DC Distribution Network Using Reactive Control of Convertors and Demand Flexibility" Sustainability 14, no. 13: 7558. https://doi.org/10.3390/su14137558
APA StyleTaghavi, M., Delkhosh, H., Parsa Moghaddam, M., & Sheikhi Fini, A. (2022). Combined PV-Wind Hosting Capacity Enhancement of a Hybrid AC/DC Distribution Network Using Reactive Control of Convertors and Demand Flexibility. Sustainability, 14(13), 7558. https://doi.org/10.3390/su14137558






