Green Mining Strategy Selection via an Integrated SWOT-PEST Analysis and Fuzzy AHP-MARCOS Approach

Abstract

Deciding on an appropriate development strategy is one of the most crucial aspects of the mining industry’s green transition. This research introduces a novel integrated decision support model that can be applied to analyze various environmental factors and determine development strategies. In this study, a strengths, weaknesses, opportunities, and threats (SWOT) analysis is employed from multiple perspectives, including political, economic, social, and technological (PEST), to assess the internal and external factors that influence green mining. The fuzzy analytic hierarchy process (AHP) is used to analyze the factor weights quantitatively, and the fuzzy Measurement of Alternatives and Ranking according to Compromise Solution (MARCOS) method is used to rank and select development strategies. According to the results, “grasp the trend of green development and improve the protection and exploitation level of mineral resources” is found to be the final optimal strategy. Comparative analysis and sensitivity analysis confirmed the accuracy of the model and the case study results.

1. Introduction

Global companies are driven to make a green transformation due to escalating ecological degradation and pollution [1]. Under the government’s severe resource and environmental policies, as well as the fiercely competitive market, green development has become an unavoidable trend [2]. The green development model is an important path towards “intensive and economical utilization of resources, reduction of environmental damage, improvement of labor productivity, and enhancement of sustainable development capabilities” [3]. A healthy ecological environment has become the focus of the government and society more than ever [4]. Mining, as an industry that pollutes and destroys the environment, is much worse [5,6]. It has become a critical industry to address as part of the process of achieving green development. Mining not only provides employment and income, but it is also the pillar of the energy supply chain [7]. Mining companies used to focus on mining productivity and profit margins, with the environment being the least important issue. This development model resulted in the continuing deterioration of the mining area’s ecological environment, significant waste of mineral resources [8,9], and negative social consequences. The situation is changing due to the background of the gradual depletion of resources and the growing popularity of green concepts. Resources and environmental protection have now been elevated to become the top priority in mining, based on the construction of a long-term sustainable profit model [10].

As mining activities involve the whole life cycle from exploration to production, closure, and restoration, it makes the green transformation of mines a multi-dimensional, long-term process [11]. Traditional technologies and conceptions have given way to a new, more sustainable production model in this process [12]. Developed mining countries such as in Europe and the United States put forward the concept with the same connotation as green mining as early as the 19th century, but, initially, it was limited to the greening of the mining environment [13]. In China, the specific concept of green mining was first proposed by Qian in 2003 for coal mines [14]. Subsequently, the government proposed a series of policy requirements for green practices in mines. The overall goal of establishing a fundamental pattern of green mines was put forward in 2009 in China [15]. Later, in 2016, it was proposed to form a new pattern of green mines and the establishment of 661 green mine pilot units was approved [16]. In 2018, the green mine construction standards of nine major industries were proposed, and the green mine construction began to be standardized [17]. Nowadays, the fundamental pattern of green mine construction has a general outline, but it is confronting complicated political, economic, social, and technological considerations at home and abroad in its new stage of growth and promotion. In recent years, with the dual background of building an innovative country and a green development strategy, some new concepts, such as developing smart mines and tailless mines [18], have been proposed. Some challenges, such as deep mining, the comprehensive utilization of resources, and ecological restoration, have made partial breakthroughs and innovations [19], and the release and implementation of a series of policy incentive documents have forced mining enterprises to re-examine their development model, promote the establishment of green mine transformation, and gain a competitive edge [20].

Due to differences in mine scale, category, area, and other factors, decision makers in mining companies have gaps in the transformation strategies they can choose as a part of the process of pursuing green transformation [21]. Therefore, it is not only technology that drives green transformation but also the planning and selection of development strategies [22]. However, because the mining industry is such a complicated system, strategic planning and decision making are challenging [23]. It is necessary for mining companies to analyze their internal and external influencing factors and implement the right strategy at the right time and place in order to maintain dynamic competitiveness [24], which can only be achieved through holistic strategic planning. There are few such studies in the context of China’s mining development. Therefore, from this perspective, this study uses SWOT as the most basic tool for strategic analysis and selection. After the introduction, the second part of the article presents the literature review. The third part introduces the methodology and proposes an AHP-MARCOS strategic decision analysis model based on SWOT-PEST analysis, and the fourth part presents a case study. The next section compares three methods, namely MARCOS, FTOPSIS, and FMABAC, to verify the accuracy of the case analysis and conduct a sensitivity analysis. Finally, the conclusions and prospects of this study are presented.

2. Literature Review

SWOT analysis is a well-known analysis method in modern strategic management and planning. Using the SWOT analysis method to make strategic decisions based on the research objectives and current environment of the research object can make full use of strengths, eliminate weaknesses, seize opportunities, and deal with threats [25], resulting in a positive match between internal and external factors [26]. The SWOT analysis was developed in the 1960s [27] and is now extensively utilized in various industries, such as construction, energy, e-commerce, etc. Yuan [28] provided critical strategies for construction waste management in the construction industry based on SWOT analysis. Terrados et al. [29] conducted strategic planning for renewable energy development with the help of a SWOT analysis tool. Zhao et al. [30] introduced SWOT analysis to explore strategies for high-level development of China’s e-commerce industry. Novikov [31] employed SWOT to analyze the high-tech strategic development of manufacturing enterprises. Kolbina [32] and Bohari et al. [33] conducted a SWOT analysis of the food business. SWOT analysis is applicable in the energy sector. Liu et al. [34] identified the influencing factors of the low-carbon economy development of mining companies through SWOT analysis, proposed a framework structure for developing a low-carbon economy, and constructed a new development model of mines. Nikolaou and Evangelino [35] used SWOT tools to analyze the problems faced in the practice of environmental management in Greek mines. Jiskani et al. [36] used a multi-criteria-based SWOT analysis of sustainable planning for the mining and mineral industry in Pakistan. The environmental factors of traditional SWOT analysis are complex. To classify the complex factors clearly and provide a reference for subsequent strategy formulation, Dong et al. [37] integrated the variables of the selected environmental factors into politics, the economy, society, and technology by introducing the PEST tool, which provides a clear direction for the analysis of SWOT environmental factors [38].

A single SWOT analysis, on the other hand, can give a subjective qualitative assessment of development competitiveness [39], which is the foundation for strategy formulation. However, a single SWOT analysis cannot completely evaluate the strategic decision-making process [40] since it is impossible to determine the relative influence of various factors on strategic decision making by quantifying the importance of these factors. Therefore, many researchers have extensively combined SWOT analysis with other quantitative evaluation approaches. Multi-criteria decision making (MCDM) is the most used method, such as the analytic hierarchy process (AHP), the analytical network (ANP), etc., which determines the relative significance of the various factors in the proposed strategy [41] and overcomes the shortcomings of traditional SWOT analysis. Considering that real-life decision-making processes are frequently ambiguous, fuzzy logic may be used in MCDM. The AHP technique has become the most prominent MCDM method in mining research due to its ease of use, high repeatability, support for group decision making, and ability to apply to fuzzy sets [42]. In addition, the AHP technique allows the SWOT model to be incorporated into the hierarchy to quantify the factors [43]. According to studies, combining the SWOT analysis approach with the fuzzy AHP method helps handle decision-making challenges in a variety of sectors. For example, Erdogan and Kara [44] integrated SWOT and Fuzzy AHP models to analyze Turkey’s maritime transport strategy options, Buyukozkan et al. [45] studied healthy tourism strategy options, and Solangi et al. [46] explored Pakistan’s sustainable energy strategic planning. Most of the above studies are based on case studies, showing that SWOT combined with the AHP methods can be successfully applied to case studies. It is reasonable to use SWOT analysis combined with Fuzzy AHP method for quantitative research in this study.

For strategic decision making, this study employs a new ranking method, Measurement of Alternatives and Ranking According to Compromise (MARCOS), which was proposed by Stevic et al. [47] in 2020 and was subsequently improved by Stankovic et al. [48]. Despite the fact that the MARCOS method is a relatively new method, due to its advantages of stability and applicability in different MCDM methods, scientific articles using the MARCOS method have been published frequently in recent years and it has been applied in a variety of fields [49,50], but its application in the mining field is very limited. The use of the MARCOS approach in the mining area, as well as embedding PEST into a SWOT tool for a full internal and external factor analysis to create the Fuzzy AHP hierarchy, are the contributions and originality of this research.

3. Methodology

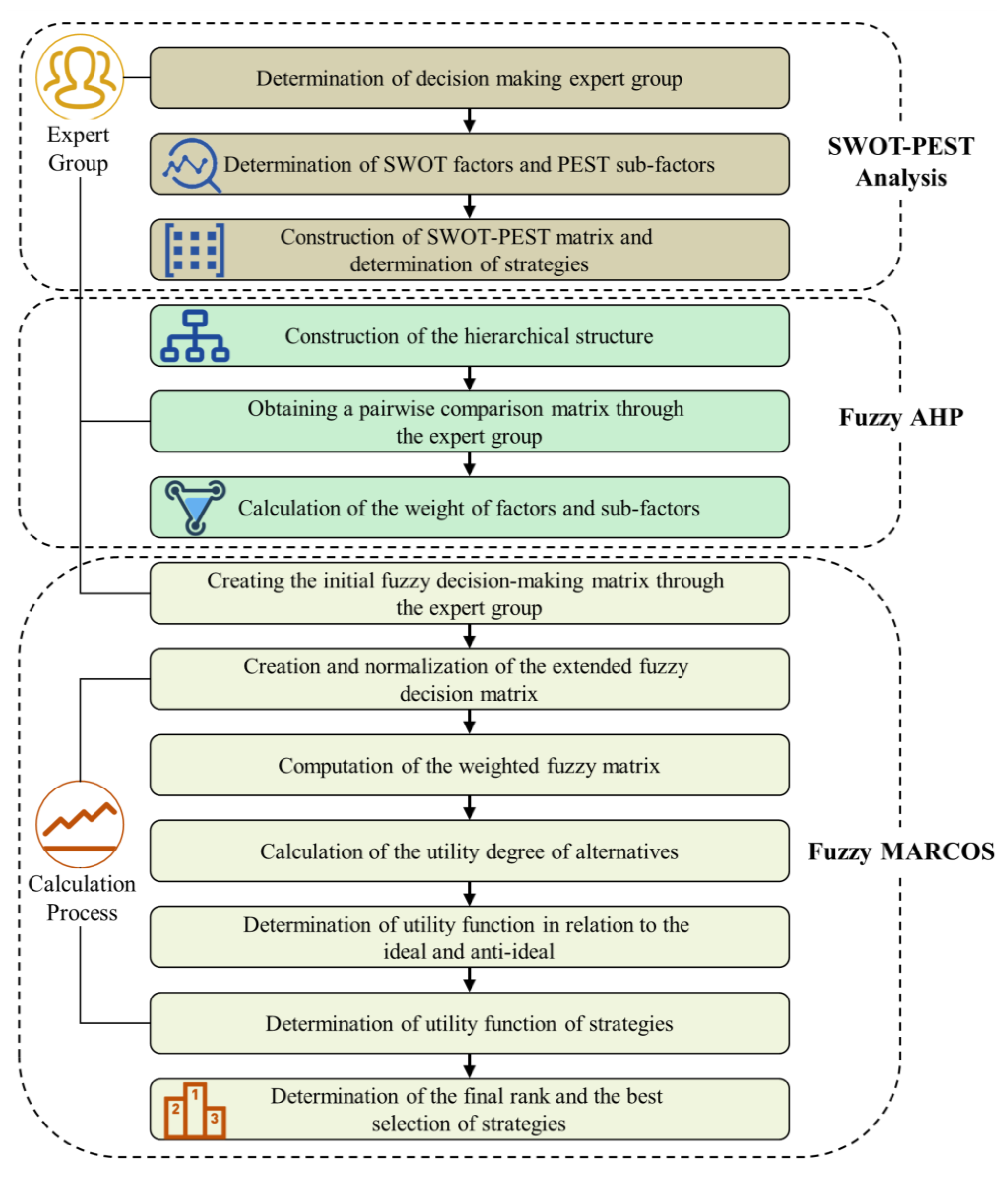
This section presents the implemented analytical model, the proposed decision-making method, and other preparations to deepen the connection between the theoretical frameworks. First, the SWOT-PEST analysis method is described, then the Fuzzy set theory is introduced, further introducing the complete steps of Fuzzy AHP, and finally the Fuzzy MARCOS method and its steps are described. In the proposed method, AHP is used to obtain criterion weights, and MARCOS is employed to evaluate and rank the alternatives. AHP is easy to use, repeatable, and supports group decision making in a hierarchical structure, while MARCOS is characterized by flexibility when considering compromise solutions based on relative importance. The combination of two methods makes the model less complex even when there are a large number of criteria or alternatives. Figure 1 depicts the phases of the proposed integrated decision model.

3.1. SWOT-PEST Analysis

SWOT analysis is a useful technique for environmental analysis. It can summarize the internal and external situations of the research object, as well as examine its strengths, weaknesses, opportunities, and threats. It can lead to several more scientific and comprehensive observations. This approach can be used as a guide for developing strategic plans.

PEST analysis is a method for macro-environmental analysis that utilizes environmental scanning to investigate four factors in the total environment: political, economy, society, and technology. It is one of the most significant models for macro-environmental analysis. It assesses the impact of these factors on strategic objectives and strategy formulation by using factor analysis in four aspects to comprehend the macro environment as a whole.

It is not appropriate to analyze an object’s development just based on external or internal aspects when there are several contributing factors. As shown in

Table 1. PEST-embedded SWOT analysis.

PEST	SWOT
	Strengths	Weaknesses	Opportunities	Threats
Politics	SP	WP	OP	TP
Economy	SE	WE	OE	TE
Society	SS	WS	OS	TS
Technology	ST	WT	OT	TT

and Figure 2, this work develops a SWOT-PEST matrix analysis model from the perspective of a comprehensive paradigm to obtain numerous environmental factors. The SWOT-PEST analysis approach combines SWOT and PEST analysis, in which internal factors (strengths and weaknesses) and external macro-environmental factors (opportunities and threats) are included for systematic investigation and analysis. Policy, economy, society, and technology are put into the SWOT analysis framework to consider and systematically analyze the strengths, weaknesses, opportunities, and threats to obtain a comprehensive and clear overview of the environmental factors at hand, and to serve as a foundation for strategy formulation.

3.2. Utilized Fuzzy-Based Method

3.2.1. Preliminaries of Fuzzy Set Theory

To cope with the uncertainty or ambiguity of objects, L.A. Zadeh developed the fuzzy set theory in 1965 [51].

A fuzzy set $\tilde{A}=\left\{\left(x,{\mu }_{\tilde{A}}\left(x\right)\right)|x\in X\right\}$ is a set of ordered pairs, X is a subset of real numbers R, where ${\mu }_{\tilde{A}}\left(x\right)$ is called the membership function, which assigns each object x a membership level from zero to one [52].

Fuzzy set theory has been widely employed to handle practical situations in which decision makers must examine and deal with inaccurate data since its conception. Different fuzzy numbers can be chosen depending on multiple realities. TFN is a specific case of trapezoidal fuzzy numbers that occurs when the two most promising values of a trapezoidal fuzzy number are the same value. Due to its computational simplicity and ability to enable representation and information processing in fuzzy environments [53], triangular fuzzy numbers (TFNs) are employed in many applications. TFNs are typically employed to record the ambiguity of parameters relevant to the decision-making process. They are represented by boundaries rather than clear numbers to reflect the uncertainty decision makers encounter in pairwise comparison matrices. The membership function of a triangular fuzzy number, denoted as $\tilde{A}=(l ,m u)$, is as follows

$${\mu }_{\tilde{A}}(x)=\{\begin{array}{l}0\hspace{1em}\hspace{1em} if x\le l\hfill \\ \frac{x-l}{m-l}\hspace{1em} if l\le x\le m\hfill \\ \frac{u-x}{u-m}\hspace{1em}if m\le x\le u\hfill \\ 0\hspace{1em}\hspace{1em} if x\le u\hfill \end{array}$$

(1)

A triangular fuzzy number $\tilde{A}$ is a possible range with upper and lower bounds, where m is the most likely value [54]. Consider two TFNS, $\tilde{A}=(a_1, a_2, a_3)$ and $\tilde{B}=(b_1, b_2, b_3)$, the main operational laws [55] for two triangular fuzzy numbers A and B are as follows

$$\tilde{A}\oplus \tilde{B}=(a_1, a_2, a_3)\oplus (b_1, b_2, b_3)=(a_1+b_1, a_2+b_2, a_3+b_3)$$

(2)

$$\tilde{A}\otimes \tilde{B}=(a_1, a_2, a_3)\otimes (b_1, b_2, b_3)=(a_1{b}_1, a_2{b}_2, a_3{b}_3)$$

(3)

$$\lambda \otimes \tilde{A}=\lambda \otimes (a_1, a_2, a_3)=(\lambda a_1, \lambda a_2, \lambda a_3)\hspace{1em}\lambda >0, \lambda \in R$$

(4)

$${\tilde{A}}^{-1}=(\frac{1}{a_3}, \frac{1}{a_2}, \frac{1}{a_1})$$

(5)

3.2.2. Fuzzy AHP Approach

There are several improved models for fuzzy AHP. Reference [56] compares the advantages and disadvantages of different Fuzzy AHP methods. This study adopts the method proposed by Chang [57], which has been applied in various fields because of its low computational complexity and wide applicability. Let $\tilde{A}={({\tilde{a}}_{ij})}_{m\times n}$ be a fuzzy pairwise comparison matrix, where ${\tilde{a}}_{ij}=(l_{ij}, m_{ij}, u_{ij})$. The steps of Chang’s method can be described as follows:

Step 1: Calculate the value of the fuzzy synthetic extent with respect to the i-th object of the k-level index as follows

$${\tilde{V}}_i^k={\displaystyle \sum _{j=1}^n{\tilde{a}}_{ij}^k}\otimes {\left[{\displaystyle \sum _{i=1}^n{\displaystyle \sum _{j=1}^n{\tilde{a}}_{ij}^k}}\right]}^{-1}, i=1, 2, \dots , n$$

(6)

Step 2: Calculate the degree of possibility between two fuzzy synthetic extent values. The degree of possibility is defined as follows

$$P\left(V_1>V_2\right)=height(V_1\cap V_2)=\{\begin{array}{l}0\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em} if l_2\ge u_1\hfill \\ \frac{l_2-u_1}{(m_1-u_1)-(m_2-l_2)}\hspace{1em}\hspace{1em}\hspace{1em}otherwise\hfill \\ 1\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em} if m_1\ge m_2\hfill \end{array}$$

(7)

Step 3: The degree of possibility for a fuzzy number to be greater than the other k fuzzy numbers can be defined as follows

$$\begin{array}{l}P(V\ge V_1, V_2, \dots , V_k)=P[(V\ge V_1) and (V\ge V_2) and \dots and (V\ge V_k)]\\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em} =\min P(V\ge V_i)\hspace{1em}i=1, 2, \dots , k\end{array}$$

(8)

Step 4: Assume that $d^{\prime }(C_i)=\min P(V_i>V_k)$ for k = 1, 2, …, n (i ≠ k). Then the weight vector can be given as follows

$${W^{\prime }}_C={[d^{\prime }(C_1), d^{\prime }(C_2), \dots ,d^{\prime }(C_n)]}^T$$

(9)

where C_i (i = 1, 2, …, n).

Step 5: The normalized weight vector needs to be obtained through normalization

$$W_C={[d(C_1), d(C_2), \dots ,d(C_n)]}^T$$

(10)

Step 6: Repeat the procedures above to obtain the weight W_i of the next level indicator; then the total weight of the indicator is calculated as follows

$$T{W}_i=W_C\times W_i$$

(11)

3.2.3. Fuzzy MARCOS Approach

The Measurement of Alternatives and Ranking according to Compromise Solution (MARCOS) is a new multi-criteria analysis method. The MARCOS approach is based on a predetermined connection between alternatives and their reference values, which represent ideal and anti-ideal points. For decision making, the MARCOS method employs a utility function, which represents alternatives to ideal and anti-ideal solutions. The optimal alternative is the one that is closest to the ideal solution while being the farthest from the anti-ideal solution. A fuzzy version of the MARCOS method was proposed by Torkayesh, AE et al. [58]. The steps of the method are as follows:

Step 1: The decision maker constructs an initial decision matrix based on the linguistic terms of the alternatives under multiple criteria.

Step 2. Construct an extended initial fuzzy matrix by defining ideal (AI) and anti-ideal (AAI) solutions.

The anti-ideal solution (AAI) and the ideal solution (AI) are obtained by applying Equations (12) and (13)

$$\tilde{A}(AAI)=\{\begin{array}{c}\underset{i}{\min }{x}_{ij}\hspace{1em}if j\in B\\ \underset{i}{\max }{x}_{ij}\hspace{1em}if j\in C\end{array}$$

(12)

$$\tilde{A}(AI)=\{\begin{array}{c}\underset{i}{\max }{x}_{ij}\hspace{1em}if j\in B\\ \underset{i}{\min }{x}_{ij}\hspace{1em}if j\in C\end{array}$$

(13)

where B represents the benefit criterion that needs to be maximized, and C represents the cost criterion that needs to be minimized.

Step 3: Normalize the initial fuzzy decision matrix. Depending on the criteria involved, normalize using Equation (14)

$$\tilde{n}=(n_{ij}^l, n_{ij}^m, n_{ij}^u)=\{\begin{array}{c}(\frac{x_{id}^l}{x_{ij}^u}, \frac{x_{id}^l}{x_{ij}^m}, \frac{x_{id}^l}{x_{ij}^l})\hspace{1em}if j\in C\\ (\frac{x_{ij}^l}{x_{id}^u}, \frac{x_{ij}^m}{x_{id}^u}, \frac{x_{ij}^u}{x_{id}^u})\hspace{1em}if j\in B\end{array}$$

(14)

where l, m, u are the parameters in the triangular fuzzy number, respectively.

Step 4: Calculate the weighted fuzzy matrix $\tilde{V}$ by multiplying the normalized matrix $\tilde{n}$ by the weight coefficient ${\tilde{w}}_j$ of the indicator according to Equation (15).

$${\tilde{v}}_{ij}=(v_{ij}^l, v_{ij}^m, v_{ij}^u)={\tilde{n}}_{ij}\otimes {\tilde{w}}_j=(n_{ij}^l\times w_j^l, n_{ij}^m\times w_j^m, n_{ij}^u\times w_j^u)$$

(15)

Step 5: The calculation of the ${\tilde{S}}_i$ matrix implies the sum of values by rows (alternatives), including the anti-ideal and ideal solution by applying Equation (16)

$${\tilde{S}}_i={\displaystyle \sum _{i=1}^n{\tilde{v}}_{ij}}$$

(16)

Step 6: Calculation of the utility degree of alternatives ${\tilde{K}}_i^{}$. The utility degrees of an alternative in relation to the anti-ideal and ideal solution are obtained by using Equations (17) and (18).

$${\tilde{K}}_i^{-}=(\frac{{\tilde{s}}_i}{{\tilde{s}}_{ai}})=(\frac{s_i^l}{s_{ai}^u}, \frac{s_i^m}{s_{ai}^u}, \frac{s_i^u}{s_{ai}^u})$$

(17)

$${\tilde{K}}_i^{+}=(\frac{{\tilde{s}}_i}{{\tilde{s}}_{id}})=(\frac{s_i^l}{s_{id}^u}, \frac{s_i^m}{s_{id}^u}, \frac{s_i^u}{s_{id}^u})$$

(18)

Step 7: Calculate the fuzzy matrix ${\tilde{T}}_i$ and $\tilde{D}$ by using Equations (19) and (20)

$${\tilde{T}}_i={\tilde{t}}_i=(t_i^l, t_i^m, t_i^u)={\tilde{K}}_i^{-}+K_i^{+}=({\tilde{k}}_i^{-l}+{\tilde{k}}_i^{+l},{\tilde{k}}_i^{-m}+{\tilde{k}}_i^{+m},{\tilde{k}}_i^{-u}+{\tilde{k}}_i^{+u})$$

(19)

$$\tilde{D}=(d^l, d^m, d^u)=\underset{i}{\max }{\tilde{t}}_{ij}$$

(20)

Step 8: Defuzzify the fuzzy number $\tilde{D}$ by using Equation (21)

$$d{f}_{def}=\frac{l+4m+u}{6}$$

(21)

Step 9: Determine the utility functions for the ideal and anti-ideal solutions via Equations (22) and (23)

$$f({\tilde{K}}_i^{+})=\frac{{\tilde{K}}_i^{-}}{d{f}_{def}}=(\frac{k_i^{-l}}{d{f}_{def}}, \frac{k_i^{-m}}{d{f}_{def}}, \frac{k_i^{-u}}{d{f}_{def}})$$

(22)

$$f({\tilde{K}}_i^{-})=\frac{{\tilde{K}}_i^{+}}{d{f}_{def}}=(\frac{k_i^{+l}}{d{f}_{def}}, \frac{k_i^{+m}}{d{f}_{def}}, \frac{k_i^{+u}}{d{f}_{def}})$$

(23)

where ${\tilde{K}}_i^{-}$, ${\tilde{K}}_i^{+}$, $f({\tilde{K}}_i^{+})$, $f({\tilde{K}}_i^{-})$ should be defuzzified.

Step 10: Determine the utility functions of alternatives: utility functions f(K_i) of alternatives are obtained through Equation (24)

$$f(K_i)=\frac{K_i^{+}+K_i^{-}}{1+\frac{1-f(K_i^{+})}{f(K_i^{+})}+\frac{1-f(K_i^{-})}{f(K_i^{-})}}$$

(24)

Step 11: Rank the alternatives according to their final utility value.

4. Case Study

In this section, the applicability of the proposed model is demonstrated through a case study. All countries throughout the world are developing sustainable development models that are tailored to their own needs, and the mining sector is experiencing a transformation towards sustainable green development and has achieved certain results in the past few years. Through the establishment of a long-term policy mechanism, mine resources and environmental problems have been improved to a certain extent. Today, China has innovatively developed and adopted modern mining technologies, implemented green concepts in mines, issued a series of green mine construction guidelines, and set up some green mine demonstration sites. It is necessary to determine an appropriate development strategy for the green transformation of mines under this trend.

4.1. SWOT-PEST Analysis of Green Mining in China

China’s green mining development strategy is influenced by the combination of internal and external environments. This study adopts the PEST-embedded SWOT analysis method to identify the internal and external factors of the slow progress of green mine construction, and construct a specific SWOT analysis matrix. Through the analysis, various major strengths and opportunities for the development of green mining technology, as well as weaknesses and threats in the development process of green mining, are discovered.

To provide data for strategy analysis, we conducted extensive literature research on relevant themes and approaches. Based on the survey results, as shown in Figure 3, an analysis matrix with four strengths, four weaknesses, four opportunities, and four threats was identified by employing a SWOT-PEST analysis. Green mining strategies were given based on interviews with the expert group. DM1 has more than three decades of experience in the mining industry, specializing in mining development in China. DM2 has extensive experience in the Chinese mining sector. DM3 has extensive experience in researching the sustainable development of China’s mining industry. Each of the three professionals has significant mining expertise and experience.

4.2. Determining the Weights of Criteria by Fuzzy AHP

The evaluation criteria for the alternatives must be defined initially in Fuzzy AHP. We constructed a hierarchical model (Figure 4) containing the objective layer, the criterion layer, the sub-criteria layer, and the strategy layer, as shown in Figure 3, with one objective, four criteria, sixteen sub-criteria, and eight methods, based on the influencing factors identified by the SWOT-PEST study.

Followed by the identification of the criteria and sub-criteria, different priority weights for each criterion and sub-criteria are determined by linguistic comparison terms and their equivalent triangular fuzzy numbers (TFN), which are defined by Khazaeni [53] in

Table 2. Fuzzy Fundamental Scale.

Linguistic Term	Fuzzy Number	Triangular Fuzzy Scale	Reciprocal Fuzzy Scale
Equally significant (ES)	$\tilde{1}$	(1, 1, 1)	(1, 1, 1)
Weakly more significant (WMS)	$\tilde{3}$	(1, 3, 5)	(1/5, 1/3, 1)
Strongly more significant (SMS)	$\tilde{5}$	(3, 5, 7)	(1/7, 1/5, 1/3)
Very strongly significant (VSS)	$\tilde{7}$	(5, 7, 9)	(1/9, 1/7, 1/5)
Absolutely significant (AS)	$\tilde{9}$	(7, 9, 9)	(1/9, 1/9, 1/7)

.

Table 3. The fuzzy comparison matrix of criteria with respect to the objective.

Criteria	S	W	O	T	Criteria Weight
S	ES		VSS	SMS	0.353
W	SMS	ES	WMS		0.164
O			ES	WMS	0.273
T		AS		ES	0.210

(C.R. = 0.001 < 0.1).

,

Table 4. The fuzzy comparison matrix of sub-criteria with respect to criteria S.

Sub-Criteria	SP	SE	SS	ST	Relative Weight
SP	ES	WMS			0.377
SE		ES	SMS		0.286
SS	VSS		ES	SMS	0.117
ST	SMS	WMS		ES	0.220

(C.R. = 0.043 < 0.1).

,

Table 5. The fuzzy comparison matrix of sub-criteria with respect to criteria W.

Sub-Criteria	WP	WE	WS	WT	Relative Weight
WP	ES	WMS	VSS		0.166
WE		ES		SMS	0.291
WS		SMS	ES	SMS	0.170
WT	WMS			ES	0.373

(C.R. = 0.045 < 0.1).

,

Table 6. The fuzzy comparison matrix of sub-criteria with respect to criteria O.

Sub-Criteria	OP	OE	OS	OT	Relative Weight
OP	ES	WMS	SMS		0.221
OE		ES	MS	SMS	0.217
OS			ES	WMS	0.338
OT	VSS			ES	0.224

(C.R. = 0.073 < 0.1).

and

Table 7. The fuzzy comparison matrix of sub-criteria with respect to criteria T.

Sub-Criteria	TP	TE	TS	TT	Relative Weight
TP	ES		VSS	SMS	0.131
TE	SMS	ES	WMS		0.257
TS			ES	WMS	0.430
TT		AS		ES	0.182

(C.R. = 0.039 < 0.1).

show the fuzzy comparison matrices for the criterion and sub-criteria and the calculated weights. The consistency check results show that all calculated C.R. values satisfy C.R. < 0.1. Therefore, all evaluations obtained from the panel are consistent. There is no need to repeat the evaluation process.

The standard weight results obtained by the fuzzy AHP method are shown in

Table 8. Weights of criteria and sub-criteria.

Criteria	Criteria Weight	Sub-Criteria	Relative Weight	Overall Weight
S	0.353	SP	0.377	0.134
		SE	0.286	0.101
		SS	0.117	0.041
		ST	0.220	0.078
W	0.164	WP	0.166	0.027
		WE	0.291	0.048
		WS	0.170	0.028
		WT	0.373	0.061
O	0.273	WP	0.221	0.060
		OE	0.217	0.059
		OS	0.338	0.092
		OT	0.224	0.061
T	0.210	TP	0.131	0.028
		TE	0.257	0.054
		TS	0.430	0.090
		TT	0.182	0.038

. Furthermore, Figure 5 shows the distribution of the SWOT indicator weights based on overall weights.

4.3. Ranking the Strategies by Fuzzy MARCOS

The determined set of suitable strategies given in Table 5 is used in this section. The expert group evaluated alternative strategies based on the SWOT-PEST sub-criteria using the language terms listed in

Table 9. Valuation scale for strategies.

Linguistic Term	TFN
Extremely poor (EP)	(1, 1, 1)
Very poor (VP)	(1, 1, 3)
Poor (P)	(1, 3, 3)
Medium poor (MP)	(3, 3, 5)
Medium (M)	(3, 5, 5)
Medium good (MG)	(5, 5, 7)
Good (G)	(5, 7, 7)
Very good (VG)	(7, 7, 9)
Extremely good (EG)	(7, 9, 9)

[48]. A consensus process was applied during the evaluations. The evaluations of the expert group concerning the strategies are given in

Table 10. Evaluation of green mining strategies by the group of experts.

GMS	SP	SE	SS	ST	WP	WE	WS	WT	OP	OE	OS	OT	TP	TE	TS	TT
S1	EG	EG	EG	EG	MG	G	G	MG	EG	EG	G	EG	MG	EG	G	MG
S2	M	MG	MG	G	MG	MG	G	VG	EG	EG	EG	VG	G	G	VG	MG
S3	EG	MG	MG	EG	G	G	EG	MG	EG	EG	EG	G	M	EG	MG	G
S4	EG	VG	EG	EG	G	EG	VG	G	EG	EG	EG	EG	P	EG	EG	M
S5	G	VG	G	G	G	VG	EG	G	VG	EG	VG	VG	VG	VG	G	M
S6	EG	G	G	EG	EG	G	EG	EG	EG	VG	EG	EG	EG	VG	G	G
S7	MG	VP	VG	P	EG	MG	EG	G	MG	VP	M	MP	EG	VG	EG	MG
S8	MG	MG	MG	G	M	G	G	VG	EG	EG	EG	G	EG	EG	G	M

.

For the SWOT-PEST model, the S and W factors are benefit-type, and the W and T factors are cost-type. Therefore, the fuzzy anti-ideal solution and the fuzzy ideal solution are obtained by using Equations (12) and (13); then the extended initial fuzzy matrix is constructed, and the extended initial fuzzy matrix is then normalized using Equation (14).

The weighted fuzzy matrix $\tilde{V}$ is obtained through Equation (15), where the overall weights of the SWOT factors given in Table 8 are used, and ${\tilde{S}}_i$, representing the sum of the elements of the weighted fuzzy matrix, is obtained using Equation (16), as shown in

Table 11. The sum of the elements of the weighted fuzzy matrix.

${\tilde{\mathit{S}}}_{\mathit{i}}$	$({\tilde{\mathit{s}}}_{\mathit{i}}^{\mathit{l}}, {\tilde{\mathit{s}}}_{\mathit{i}}^{\mathit{m}}, {\tilde{\mathit{s}}}_{\mathit{i}}^{\mathit{u}})$	${\tilde{\mathit{S}}}_{\mathit{i}}$	$({\tilde{\mathit{s}}}_{\mathit{i}}^{\mathit{l}}, {\tilde{\mathit{s}}}_{\mathit{i}}^{\mathit{m}}, {\tilde{\mathit{s}}}_{\mathit{i}}^{\mathit{u}})$
${\tilde{S}}_{aai}$	(0.387, 0.443, 0.561)	${\tilde{S}}_5$	(0.590, 0.665, 0.795)
${\tilde{S}}_1$	(0.632, 0.786, 0.844)	${\tilde{S}}_6$	(0.603, 0.717, 0.791)
${\tilde{S}}_2$	(0.559, 0.686, 0.764)	${\tilde{S}}_7$	(0.446, 0.502, 0.633)
${\tilde{S}}_3$	(0.608, 0.733, 0.819)	${\tilde{S}}_8$	(0.590, 0.660, 0.825)
${\tilde{S}}_4$	(0.647, 0.761, 0.894)	${\tilde{S}}_{ai}$	(0.700, 0.841, 1.000)

below.

The utility degree of ${\tilde{K}}_i^{-}$, ${\tilde{K}}_i^{+}$ in relation to the anti-ideal and ideal solution are calculated by Equations (17) and (18), and, in addition, the fuzzy matrix ${\tilde{T}}_i$ value is obtained by Equation (19). It is necessary to use Equation (20) to find the maximum t_i and $\tilde{D}$ = (1.800, 2.710, 3.588), and then use Equation (21) to defuzzify the number $\tilde{D}$ to obtain the number $d{f}_{def}$ = 2.705.

According to the obtained utility degree ${\tilde{K}}_i^{+}$ and $d{f}_{def}$, the utility function $f({\tilde{K}}_i^{+})$ about the ideal can be obtained by applying Equation (22), and similarly, according to the obtained utility degree ${\tilde{K}}_i^{-}$ and $d{f}_{def}$, the utility function $f({\tilde{K}}_i^{-})$ about the anti-ideal can be obtained by applying Equation (23): it is shown in the following

Table 12. Obtained ${\tilde{K}}_i^{+}$, ${\tilde{K}}_i^{-}$, and ${\tilde{T}}_i$ values.

I	${\tilde{\mathit{K}}}_{\mathit{i}}^{+}$	${\tilde{\mathit{K}}}_{\mathit{i}}^{-}$	${\tilde{\mathit{T}}}_{\mathit{i}}$	$\mathit{f}({\tilde{\mathit{K}}}_{\mathit{i}}^{+})$	$\mathit{f}({\tilde{\mathit{K}}}_{\mathit{i}}^{-})$
1	(0.632, 0.935, 1.206)	(1.126, 1.775, 2.181)	(1.758, 2.710, 3.387)	(0.416, 0.656, 0.806)	(0.234, 0.346, 0.446)
2	(0.559, 0.816, 1.092)	(0.996, 1.549, 1.974)	(1.554, 2.364, 3.066)	(0.368, 0.572, 0.730)	(0.206, 0.302, 0.404)
3	(0.608, 0.871, 1.170)	(1.084, 1.654, 2.116)	(1.692, 2.525, 3.285)	(0.401, 0.611, 0.782)	(0.225, 0.322, 0.432)
4	(0.647, 0.905, 1.277)	(1.153, 1.719, 2.310)	(1.800, 2.624, 3.588)	(0.426, 0.635, 0.854)	(0.239, 0.335, 0.472)
5	(0.590, 0.791, 1.136)	(1.052, 1.502, 2.055)	(1.642, 2.293, 3.192)	(0.389, 0.555, 0.760)	(0.218, 0.292, 0.420)
6	(0.603, 0.853, 1.130)	(1.075, 1.619, 2.044)	(1.677, 2.472, 3.175)	(0.397, 0.599, 0.756)	(0.223, 0.315, 0.418)
7	(0.446, 0.597, 0.905)	(0.795, 1.134, 1.637)	(1.241, 1.732, 2.542)	(0.294, 0.419, 0.605)	(0.165, 0.221, 0.335)
8	(0.590, 0.785, 1.179)	(1.051, 1.490, 2.132)	(1.641, 2.275, 3.310)	(0.389, 0.551, 0.788)	(0.218, 0.290, 0.436)

.

Defuzzify ${\tilde{K}}_i^{-}$, ${\tilde{K}}_i^{+}$, $f({\tilde{K}}_i^{+})$, and $f({\tilde{K}}_i^{-})$ by Equation (21) to obtain sharp values $K_i^{-}$, $K_i^{+}$, $f(K_i^{+})$, and $f(K_i^{-})$. Finally, the utility function $f(K_i)$ of the alternatives is obtained by Equation (24), and the alternatives are sorted according to the value of the utility function. The final results are shown in

Table 13. Final results of fuzzy MARCOS method and ranking of the GMS.

GMS	${\mathit{K}}_{\mathit{i}}^{+}$	${\mathit{K}}_{\mathit{i}}^{-}$	$\mathit{f}({\mathit{K}}_{\mathit{i}}^{+})$	$\mathit{f}({\mathit{K}}_{\mathit{i}}^{-})$	$\mathit{f}({\mathit{K}}_{\mathit{i}})$	Order
S1	0.930	1.735	0.641	0.344	0.768	1
S2	0.819	1.527	0.565	0.303	0.576	5
S3	0.877	1.636	0.605	0.324	0.672	3
S4	0.924	1.723	0.637	0.342	0.757	2
S5	0.815	1.519	0.562	0.301	0.569	7
S6	0.857	1.599	0.591	0.317	0.639	4
S7	0.623	1.161	0.429	0.230	0.315	8
S8	0.818	1.524	0.563	0.302	0.574	6

, and the strategies are ranked as S1 > S4 > S3 > S6 > S2 > S8 > S5 > S7. A comparative and sensitivity analysis was performed to confirm these results and is shown in the next section.

The results indicate that the most important dimensions that mines should focus on are the strengths and opportunities associated with GM. The criteria weights obtained through the fuzzy AHP method are shown in Table 3, with a total percentage of 52% for strengths and weaknesses and 48% for opportunities and threats. It shows that internal (strengths and weaknesses) factors and external (opportunities and threats) factors have almost equal importance. Table 10 and Figure 5 show that SP, SE, OS, TS, and ST are the five factors with the highest global weights, indicating that with increased government policy support (SP), positive economic conditions (SE), and a surging demand for resources (OS), Chinese mining companies should take its innovative national strategy as a starting point and make improving its R&D capacity for green technology innovation in mines a development priority (ST) in order to avoid being caught in a global mining environmental pollution problem in the long term (TS). The GMS ranking order indicates that the three most important digital conversion strategies are S1, S4, and S3. These are “Grasp the trend of green development and improve the protection and development level of mineral resources”, “Strengthen technological research and development, improve technological innovation capabilities, and focus on the development of green technologies”, and “Absorb the advanced organization and management experience of developed countries in the mining industry, and standardize and improve the mine green guarantee mechanism”.

5. Validation of Results and Sensitivity Analysis

Result validation and sensitivity analysis are carried out in two processes in this section.

5.1. Comparison with Other Approaches

It is necessary to compare the results obtained by Fuzzy MARCOS with those acquired by using other fuzzy methods in order to validate the results of this study [47]. Therefore, two methods, fuzzy MABAC (Multiple Attribute Boundary Approximate Area Comparison) and TOPSIS (Technique for Order Performance Through Similarity to Ideal Solutions), are used to test the accuracy of the results obtained by the fuzzy MARCOS method.

The results of the comparative analysis are shown in Figure 6; the y-axis represents the ranking, with shorter histograms indicating higher rankings. Comparing the ranking of the fuzzy MARCOS method and the fuzzy TOPSIS method, the change in the ranking results of the eight strategies is the exchange of two groups of adjacent strategies. Comparing the fuzzy MARCOS method and the fuzzy MABAC method, the change in the ranking results of the eight strategies is the order of the last three strategies, and the other orders are the same.

The overall results show that there is little difference between the ranking results of these strategies. The results of the fuzzy MARCOS method are basically the same as those of FMABAC and FTOPSISs. It can be seen that the results obtained by the fuzzy MARCOS method are accurate.

5.2. Sensitivity Analysis

The sensitivity analysis is conducted by changing the weights of criteria to evaluate the impact of individual criteria on prioritization [59]. Therefore, this study changed the weights of the SWOT criteria to investigate the impact of changing the criteria weights on GMS’s prioritization. For this purpose, five cases are determined by changing the weight of the SWOT criteria. In one case, the weights of the four SWOT criteria are set to be equal (0.250), and in the other four cases, only one criterion was set to be relatively important (0.400) [60], while the others remained the same (0.200). Different cases of SWOT criteria weights are given in

Table 14. Different weights of the SWOT criteria in different cases.

Criteria	Initial Value	C1	C2	C3	C4	C5
S	0.353	0.250	0.400	0.200	0.200	0.200
W	0.164	0.250	0.200	0.400	0.200	0.200
O	0.273	0.250	0.200	0.200	0.400	0.200
T	0.210	0.250	0.200	0.200	0.200	0.400

.

Then, the fuzzy MARCOS method is applied to the weights determined for each case, and, furthermore, the utility function f(K) value is updated according to the weights.

Table 15. The weights of the SWOT factors in different cases.

Factors	Relative Weight	C0	C1	C2	C3	C4	C5
SP	0.377	0.134	0.094	0.151	0.075	0.075	0.075
SE	0.286	0.101	0.072	0.114	0.057	0.057	0.057
SS	0.117	0.041	0.029	0.047	0.023	0.023	0.023
ST	0.220	0.078	0.055	0.088	0.044	0.044	0.044
WP	0.166	0.027	0.042	0.033	0.066	0.033	0.033
WE	0.291	0.048	0.073	0.058	0.116	0.058	0.058
WS	0.170	0.028	0.043	0.034	0.068	0.034	0.034
WT	0.373	0.061	0.093	0.075	0.149	0.075	0.075
OP	0.221	0.060	0.055	0.044	0.044	0.088	0.044
OE	0.217	0.059	0.054	0.043	0.043	0.087	0.043
OS	0.338	0.092	0.085	0.068	0.068	0.135	0.068
OT	0.224	0.061	0.056	0.045	0.045	0.090	0.045
TP	0.131	0.028	0.033	0.026	0.026	0.026	0.052
TE	0.257	0.054	0.064	0.051	0.051	0.051	0.103
TS	0.430	0.090	0.108	0.086	0.086	0.086	0.172
TT	0.182	0.038	0.046	0.036	0.036	0.036	0.073

presents the GMS utility function values obtained. Based on the updated utility function value, a ranking of the GMS is obtained.

Table 16. The obtained f(K) and strategy ordering in different cases.

GMS	C0		C1		C2		C3		C4		C5
	f(Ki)	Order	f(Ki)	Order	f(Ki)	Order	f(Ki)	Order	f(Ki)	Order	f(Ki)	Order
S1	0.768	1	0.803	1	0.827	1	0.793	1	0.802	1	0.779	1
S2	0.576	5	0.618	6	0.543	7	0.626	4	0.671	5	0.629	6
S3	0.672	3	0.743	2	0.718	3	0.725	2	0.767	3	0.760	2
S4	0.757	2	0.722	3	0.745	2	0.665	3	0.771	2	0.701	3
S5	0.569	7	0.623	5	0.606	5	0.593	7	0.644	7	0.645	5
S6	0.639	4	0.666	4	0.682	4	0.603	5	0.712	4	0.665	4
S7	0.315	8	0.308	8	0.272	8	0.355	8	0.272	8	0.339	8
S8	0.574	6	0.605	7	0.544	6	0.601	6	0.654	6	0.617	7

shows the new ranking order of GMS under different cases. Here, to compare with the initial study, C0 is added to indicate the preliminary results of the study.

Figure 7 presents the distribution of the GMS rankings from an overall perspective. The results obtained show that there is little variation in the prioritization among these cases, and these small differences do not affect the validity of the study. The initial results of this study using the fuzzy MARCOS method can be confirmed. Furthermore, “Grasp the trend of green development and improve the protection and exploitation level of mineral resources” is the most appropriate GMS in all cases.

6. Conclusions

In view of the importance of the mining industry’s green transformation and the driving force of strategic planning for the green transformation, it is essential to take measures to conduct research on the strategic decision making of green mine construction. Accordingly, this study supports this decision making by constructing a new SWOT-PEST matrix and a decision support model. The proposed decision support model and the SWOT-PEST matrix are validated using China’s green mining construction case. The SWOT-PEST tool was used to conduct a comprehensive analysis of internal and external driving and hindering factors, resulting in the identification of four main criteria and 16 sub-criteria. Then the interaction of these factors was studied, and eight macro strategies were formulated. The group expert decision making based on fuzzy terms is introduced to make the decision-making process more scientific and rational. A comprehensive selection of strategies is carried out using two steps: the fuzzy AHP and fuzzy MARCOS method based on SWOT-PEST analysis. Firstly, the importance and weight of SWOT-PEST factors are determined by fuzzy AHP. Then, the recently proposed Fuzzy MARCOS method is adopted for strategy ranking. Finally, the fuzzy TOPSIS and the fuzzy MABAC methods are used to verify the results of the fuzzy MARCOS method. The impact of the SWOT factor weights on the results is evaluated by sensitivity analysis, which verifies the robustness of the proposed method. This paper’s major contributions can be summarized as follows:

• To the best of the authors’ knowledge, this paper is the first combined method of study using quantitative SWOT-PEST analysis based on the combined fuzzy AHP and fuzzy MARCOS methods.
• The SWOT-PEST, a combined analysis tool, is used for the first time to create a hierarchical index system for selecting green mining development strategies, which provides a systematic quantitative framework for selecting green mining development strategies and fills a research gap in this area.
• A case study was carried out concerning the mining industry in China. For green mining, policy support is the prerequisite, technological innovation is the key link, and organization and management are the basic guarantees.

This study provides a systematic quantitative framework for selecting green mining strategies. The model can be applied not only in the mining sector, but also in other industries by analyzing distinct factors and strategies. In the future, it is possible to investigate whether and how to formulate an extended version of the fuzzy analysis.