Comparative Efficiency and Sensitivity Analysis of AC and DC Power Distribution Paradigms for Residential Localities
Abstract
:1. Introduction
Innovative Aspects of the Current Research Effort
2. Modeling of the Systems
2.1. Distribution of Load Using Normal Distribution for Non-Fixed Category of Load
2.1.1. Off Load Method
2.1.2. On/Off Method for Fixed Category Load
2.2. Mathematical Modeling
2.2.1. DC System
2.2.2. AC System
2.3. Sensitivity Analysis
2.3.1. PV Capacity Variation
2.3.2. PEC Efficiency Variation
3. Main Results
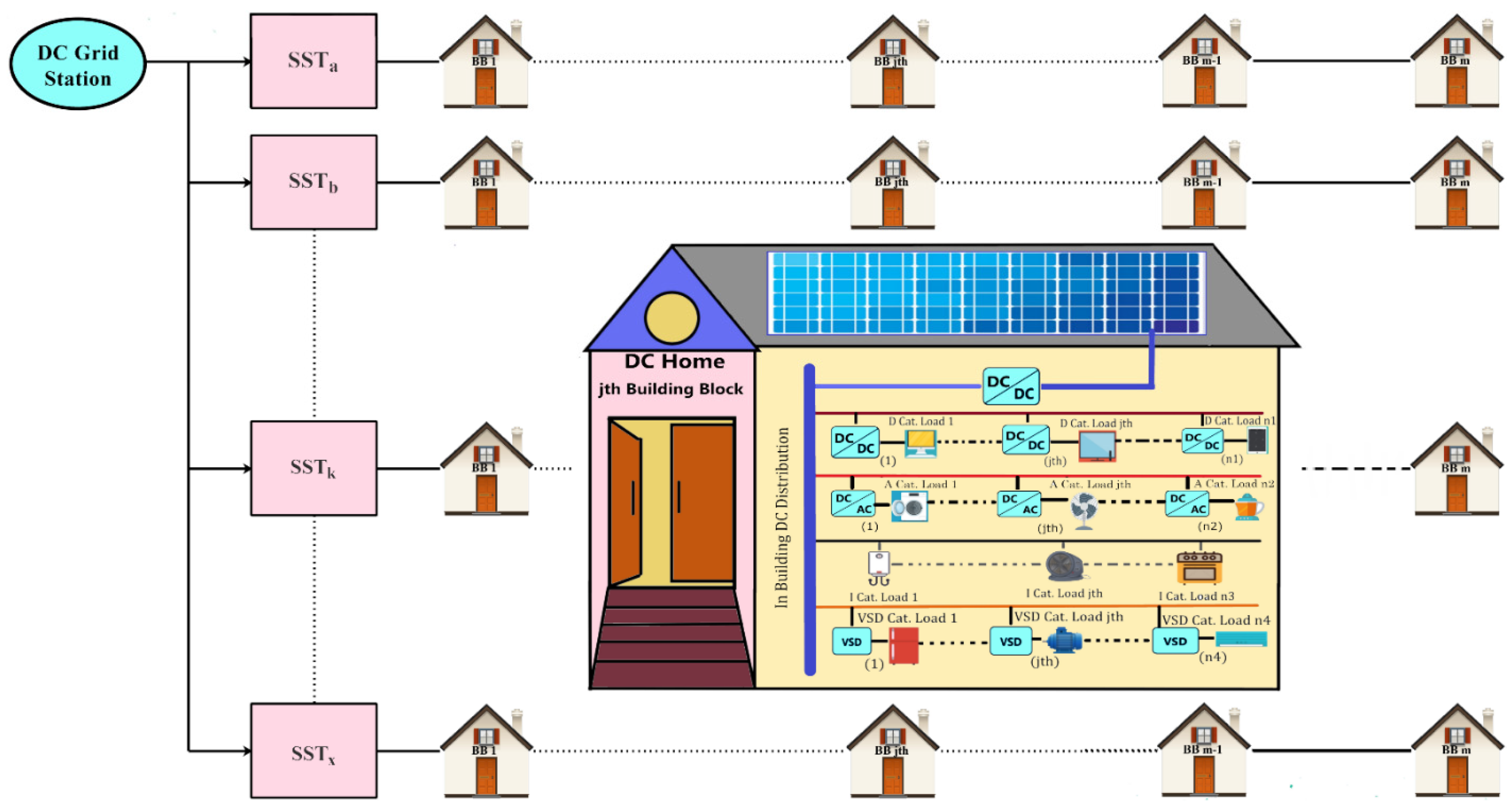
3.1. Structural Visualization of Scenarios in Both Systems
3.2. Comparative Efficiency Analysis of Both Systems
3.3. Comparative Sensitivity Analysis on Both Systems
3.4. Discussion
4. Conclusions and Future Recommendations
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| Power Electronic Converter | PEC |
| High Voltage Direct Current | HVDC |
| Brushless Direct Current | BLDC |
| Variable Speed Drive | VSD |
| Electric Power Research Institute | EPRI |
| Building Block | BB |
| Transformer | XFMR |
| Solid State Transformer | SST |
| time | t |
| Input Power | Pi |
| AC Load | A |
| DC Load | D |
| Independent Load | I |
| Efficiency | |
| Standard Deviation | SD |
| Loss Factor | |
| DC to DC | dd |
| AC to DC | ad |
| DC to AC | da |
| Reactive Power | q |
| Active Power | p |
| Load | l |
| Inverter loss-installed at solar | SA |
| Coefficients of curve fitting tool equation | |
| Output | out |
| Input | in |
Appendix A. Sensitivity Analysis Curves of AC and DC Distribution Systems




























References
- Sulzberger, C.L. Triumph of ac-from Pearl Street to Niagara. IEEE Power Energy Mag. 2003, 1, 64–67. [Google Scholar] [CrossRef]
- McPherson, S.S. War of the Currents: Thomas Edison vs. Nikola Tesla; Twenty-First Century Books: Chicago, IL, USA, 2012. [Google Scholar]
- Allerhand, A. A contrarian history of early electric power distribution [scanning our past]. In Proceeding of the IEEE; IEEE: Piscataway, NJ, USA, 2017; Volume 105, pp. 768–778. [Google Scholar]
- McNichol, T. AC/DC: The Savage Tale of the First Standards War; John Wiley & Sons: Hoboken, NJ, USA, 2011. [Google Scholar]
- Fairley, P. DC versus AC: The second war of currents has already begun [in my view]. IEEE Power Energy Mag. 2012, 10, 103–104. [Google Scholar] [CrossRef]
- Dastgeer, F.; Gelani, H.E.; Anees, H.M.; Paracha, Z.J.; Kalam, A. Analyses of efficiency/energy-savings of DC power distribution systems/microgrids: Past, present and future. Int. J. Electr. Power Energy Syst. 2019, 104, 89–100. [Google Scholar] [CrossRef]
- Capasso, C.; Rubino, G.; Rubino, L.; Veneri, O. Power architectures for the integration of photovoltaic generation systems in DC-microgrids. Energy Procedia 2019, 159, 34–41. [Google Scholar] [CrossRef]
- Musasa, K.; Nwulu, N.I.; Gitau, M.N.; Bansal, R.C. Review on DC collection grids for offshore wind farms with high-voltage DC transmission system. IET Power Electron. 2017, 10, 2104–2115. [Google Scholar] [CrossRef]
- Singh, M.; Khadkikar, V.; Chandra, A.; Varma, R.K. Grid interconnection of renewable energy sources at the distribution level with power-quality improvement features. IEEE Trans. Power Deliv. 2010, 26, 307–315. [Google Scholar] [CrossRef]
- Owusu, P.A.; Sarkodie, S. A review of renewable energy sources, sustainability issues and climate change mitigation. Cogent Eng. 2016, 3, 1167990. [Google Scholar] [CrossRef]
- Alassi, A.; Bañales, S.; Ellabban, O.; Adam, G.; MacIver, C. HVDC transmission: Technology review, market trends and future outlook. Renew. Sustain. Energy Rev. 2019, 112, 530–554. [Google Scholar] [CrossRef]
- Shinde, M.P.; Helonde, J.B. An Overview of HVDC Power Transmission System with Voltage Source Converter. Int. J. Recent Innov. Trends Comput. Commun. 2018, 6, 240–244. [Google Scholar]
- Gerber, D.L.; Liou, R.; Brown, R. Energy-saving opportunities of direct-DC loads in buildings. Appl. Energy 2019, 248, 274–287. [Google Scholar] [CrossRef] [Green Version]
- Thomas, B.A. Edison revisited: Impact of DC distribution on the cost of LED lighting and distributed generation. In Proceedings of the 2010 Twenty-Fifth Annual IEEE Applied Power Electronics Conference and Exposition (APEC), Palm Springs, CA, USA, 21–25 February 2010; IEEE: Piscataway, NJ, USA, 2010. [Google Scholar]
- Rathikrindi, K.S.; Paramasivam, S.; Sandeep, L. Energy saving opportunities through variable frequency drive for commercial air conditioners. In Proceedings of the 2018 4th International Conference on Electrical Energy Systems (ICEES), Chennai, India, 7–9 February 2018; IEEE: Piscataway, NJ, USA, 2018. [Google Scholar]
- Kamran, M.; Bilal, M.; Mudassar, M. DC home appliances for DC distribution system. Mehran Univ. Res. J. Eng. Technol. 2017, 36, 881–890. [Google Scholar] [CrossRef]
- NakuÃ, L.; Spahiu, A. Saving energy by replacing IM with BLDC MOTOR in fan application. Eur. J. Electr. Eng. Comput. Sci. 2018, 2. [Google Scholar] [CrossRef]
- Brenguier, J.; Vallet, M.; Vaillant, F. Efficiency gap between AC and DC electrical power distribution system. In Proceedings of the 2016 IEEE/IAS 52nd Industrial and Commercial Power Systems Technical Conference (I&CPS), Detroit, MI, USA, 1–5 May 2016; IEEE: Piscataway, NJ, USA, 2016. [Google Scholar]
- Fregosi, D.; Ravula, S.; Brhlik, D.; Saussele, J.; Frank, S.; Bonnema, E.; Scheib, J.; Wilson, E. A comparative study of DC and AC microgrids in commercial buildings across different climates and operating profiles. In Proceedings of the 2015 IEEE First International Conference on DC Microgrids (ICDCM), Atlanta, GA, USA, 7–10 June 2015; IEEE: Piscataway, NJ, USA, 2015. [Google Scholar]
- Gerber, D.L.; Vossos, V.; Feng, W.; Marnay, C.; Nordman, B.; Brown, R. A simulation-based efficiency comparison of AC and DC power distribution networks in commercial buildings. Appl. Energy 2018, 210, 1167–1187. [Google Scholar] [CrossRef] [Green Version]
- Manandhar, U.; Ukil, A.; Jonathan, T.K.K. Efficiency comparison of DC and AC microgrid. In Proceedings of the 2015 IEEE Innovative Smart Grid Technologies-Asia (ISGT ASIA), Bangkok, Thailand, 3–6 November 2015; IEEE: Piscataway, NJ, USA, 2016. [Google Scholar]
- Siraj, K.; Khan, H.A. Dc distribution for residential power networks—A framework to analyze the impact of voltage levels on energy efficiency. Energy Rep. 2020, 6, 944–951. [Google Scholar] [CrossRef]
- Atia, H.R.; Shakya, A.; Tandukar, P.; Tamrakar, U.; Hansen, T.M.; Tonkoski, R. Efficiency analysis of AC coupled and DC coupled microgrids considering load profile variations. In Proceedings of the 2016 IEEE International Conference on Electro Information Technology (EIT), Grand Forks, ND, USA, 19–21 May 2016; IEEE: Piscataway, NJ, USA, 2016. [Google Scholar]
- Sirsi, R.; Prasad, S.; Sonawane, A.; Lokhande, A. Efficiency comparison of AC distribution system and DC distribution system in microgrid. In Proceedings of the 2016 International Conference on Energy Efficient Technologies for Sustainability (ICEETS), Nagercoil, India, 7–8 April 2016; IEEE: Piscataway, NJ, USA, 2016. [Google Scholar]
- Vossos, V.; Garbesi, K.; Shen, H. Energy savings from direct-DC in US residential buildings. Energy Build. 2014, 68, 223–231. [Google Scholar] [CrossRef]
- Boeke, U.; Wendt, M. DC power grids for buildings. In Proceedings of the 2015 IEEE First International Conference on DC Microgrids (ICDCM), Atlanta, GA, USA, 7–10 June 2015; IEEE: Piscataway, NJ, USA, 2015. [Google Scholar]
- Weiss, R.; Ott, L.; Boeke, U. Energy efficient low-voltage DC-grids for commercial buildings. In Proceedings of the 2015 IEEE First International Conference on DC Microgrids (ICDCM), Atlanta, GA, USA, 7–10 June 2015; IEEE: Piscataway, NJ, USA, 2015. [Google Scholar]
- Viitanen, J.; Halonen, L. Electrical efficiency study of alternating current and direct current power topologies in office building with integrated photovoltaics in Matlab-Simulink environment. J. Renew. Sustain. Energy 2014, 6, 033123. [Google Scholar] [CrossRef] [Green Version]
- Hammerstrom, D.J. AC versus DC distribution systemsdid we get it right? In Proceedings of the 2007 IEEE Power Engineering Society General Meeting, Tampa, FL, USA, 24–28 June 2007; IEEE: Piscataway, NJ, USA, 2007. [Google Scholar]
- Nilsson, D.; Sannino, A. Efficiency analysis of low-and medium-voltage DC distribution systems. In Proceedings of the IEEE Power Engineering Society General Meeting, Denver, CO, USA, 6–10 June 2004; IEEE: Piscataway, NJ, USA, 2005. [Google Scholar]
- Montoya, O.D.; Serra, F.M.; De Angelo, C.H. On the efficiency in electrical networks with ac and dc operation technologies: A comparative study at the distribution stage. Electronics 2020, 9, 1352. [Google Scholar] [CrossRef]
- Ahmad, F.; Dastgeer, F.; Gelani, H.E.; Khan, S.; Nasir, M. Comparative Analyses of Residential Building Efficiency for AC and DC Distribution Networks. Bull. Pol. Acad. Sci. Tech. Sci. 2021, 69, e136732. [Google Scholar]
- Dastgeer, F.; Gelani, H.E. A Comparative analysis of system efficiency for AC and DC residential power distribution paradigms. Energy Build. 2017, 138, 648–654. [Google Scholar] [CrossRef]
- Gelani, H.E.; Dastgeer, F.; Siraj, K.; Nasir, M.; Niazi, K.A.K.; Yang, Y. Efficiency comparison of AC and DC distribution networks for modern residential localities. Appl. Sci. 2019, 9, 582. [Google Scholar] [CrossRef] [Green Version]
- Gelani, H.E.; Dastgeer, F. Efficiency analyses of a DC residential power distribution system for the modern home. Adv. Electr. Comput. Eng. 2015, 15, 135–143. [Google Scholar] [CrossRef]
- Gelani, H.E.; Nasir, M.; Dastgeer, F.; Hussain, H. Efficiency comparison of alternating current (AC) and direct current (DC) distribution system at residential level with load characterization and daily load variation. Proc. Pak. Acad. Sci. A. Phys. Comput. Sci. 2017, 54, 111–118. [Google Scholar]
- Rasheed, A.; Khan, S.; Gelani, H.E.; Dastgeer, F. AC vs. DC Home: An Efficiency Comparison. In Proceedings of the 2019 International Symposium on Recent Advances in Electrical Engineering (RAEE), Islamabad, Pakistan, 28–29 August 2019; IEEE: Piscataway, NJ, USA, 2019. [Google Scholar]
- Glasgo, B.; Azevedo, I.L.; Hendrickson, C. How much electricity can we save by using direct current circuits in homes? Understanding the potential for electricity savings and assessing feasibility of a transition towards DC powered buildings. Appl. Energy 2016, 180, 66–75. [Google Scholar] [CrossRef] [Green Version]
- Electric Power Research Institute (EPRI). End Use Load Shapes Data. 2012–2013. Available online: https://loadshape.epri.com/enduse (accessed on 11 May 2022).
- Table 2—2015 Residential Energy End-Use Splits, by Fuel Type (QuadrillionBtu). Available online: http://buildingsdatabook.eren.doe.gov/TableView.aspx? (accessed on 11 May 2022).
- Instantaneous Power Consumption of Appliances. Available online: https://www.daftlogic.com/information-appliance-power-consumption.htm (accessed on 11 May 2022).
- How Much Power is Consumed by Computer. Available online: https://www.kompulsa.com/much-power-computers-consume/ (accessed on 11 May 2022).
- How Much Power Do Your Appliances Use? Available online: https://www.wholesalesolar.com/solar-information/power-table (accessed on 11 May 2022).
- Typical Power Rating of Common Electrical Equipment. Available online: https://www.sgs-engineering.com/help-advice/typical-power-ratings-of-common-electrical-equipment/ (accessed on 11 May 2022).
- RECOM RACG150-12S 150 W AC-DC Converter. Available online: https://recom-power.com/pdf/Powerline_AC-DC/RACG150.pdf (accessed on 11 May 2022).
- CUI INC PDRB-300-24 300 W AC-DC Converter. Available online: https://www.cui.com/product/internal-ac-dc-power-supplies/din-rail/pdrb-300-series (accessed on 11 May 2022).
- MORNINGSTAR SI-300-115V-UL SI-300-220 V 300 W DC-AC Inverter. Available online: https://ww.morningstarcorp.com/products/suresine/ (accessed on 11 May 2022).
- SUNGROW SG8K-D 8000 W DC/AC Inverter. Available online: https://ww.gemenergy.com.au/wp-content/uploads/2019/12/SG8K-D-Datasheet.pdf (accessed on 11 May 2022).
- CALEX 24S12.12QSW (ROHS) 150 W DC-DC Converter. Available online: http://calex.com/pdf/qsw.pdf (accessed on 11 May 2022).
- TOSHIBA RD024 300 W Isolated DC-DC Converter. Available online: https://toshiba.semicon-storage.com/ap-en/semiconductor/designdevelopment/referencedesign/articles/300w-Isolated-dc-dc_powermanagement_rd024.html (accessed on 11 May 2022).
- Texas Instruments 600 W DC-AC Inverter Reference Design. Available online: http://www.ti.com/tool/TIDM-HV-1PH-DCAC?keyMatch=TIDM-HV-1PH-DCAC&tisearch=Search-EN-everything&usecase=GPN#Technical%20Documents (accessed on 11 May 2022).
- SMA SB1700 1700 W DC-AC Inverter. Available online: https://www.eco-logisch.nl/pdfupload/SMA%20SB%201700.pdf (accessed on 11 May 2022).
- ABB String Inverter PVI-5000-TL-OUTD 5000 W DC-AC Inverter. Available online: https://library.e.abb.com/public/056a93c2644e4f15b55475647c6e0156/PVI-5000-ENRev%20E.pdf (accessed on 11 May 2022).
- Baldwin, T.L.; Turk, R.J.; Myers, K.S.; Gentle, J.P.; Bush, J.W. Transformer Efficiency Assessment—Okinawa, Japan; U.S. Department of Energy: Portland, OR, USA, 2012. [Google Scholar] [CrossRef] [Green Version]
- ApECOR 200 kW Bidirectional DC-DC. Available online: http://apecor.com/pages/products/highpower/apecor_ev_bidirectional_dcdc.pdf (accessed on 11 May 2022).
- Lukhwareni, T.; Dobzhanskyi, O.; Gouws, R. Solar power pumping system for domestic appliances. In Proceedings of the Twenty-Second Domestic Use of Energy, Cape Town, South Africa, 1–2 April 2014; pp. 1–6. [Google Scholar] [CrossRef]
- Dastgeer, F.; Anees, H.M.; Gelani, H.E.; Amjad, K.; Javeed, M.R. A basic mathematical testbed for energy efficiency analyses of DC power distribution systems/microgrids. Bull. Electr. Eng. Inform. 2021, 10, 1484–1494. [Google Scholar] [CrossRef]










| Research Work | Load Modelling | Multiple Voltage Levels | Load Variation with Respect to Time | Conductor/Cable Losses | Energy Storage (Battery) | Renewable Energy Resources (PV System) | Analysis on Partial Loading | Perform for Residential/Commercial | Comparison with AC System | PEC Efficiency Variation | PV Capacity Variation | Result |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| [30] | - | - | - | ✔ | - | - | - | Commercial | ✔ | - | - | AC is better than DC. The study is performed on low and medium voltage networks |
| [29] | ✔ | - | - | - | - | ✔ | - | Residential | ✔ | - | - | DC is better. The study is performed with fixed PEC efficiency |
| [35] | ✔ | - | ✔ | - | - | - | ✔ | Residential | - | ✔ | - | DC is feasible. Loss comparison is performed allowing load variation. |
| [18] | ✔ | - | - | ✔ | ✔ | ✔ | ✔ | Residential | ✔ | ✔ | - | DC is feasible up to some extent. The authors proposed almost equal efficiency for AC and DC at low voltage distribution scale. |
| [38] | - | - | ✔ | - | ✔ | ✔ | ✔ | Residential | ✔ | ✔ | - | DC is better. The study is performed by considering all loads as DC without considering PEC efficiency variation |
| [25] | - | - | ✔ | - | ✔ | ✔ | ✔ | Residential | ✔ | - | - | DC is better. The study is performed by considering and PEC efficiency variation |
| [33] | ✔ | - | ✔ | - | - | - | - | Residential | ✔ | ✔ | - | AC and DC are comparable. Efficiency of PECs is varied in fix range. |
| [24] | - | - | - | - | - | - | - | Residential | ✔ | - | - | DC is better. Limited loads selection and fixed PEC efficiency |
| [23] | - | - | ✔ | - | - | ✔ | - | Residential | ✔ | - | - | AC is better. Load variation is considered, however, the effect of load variation on PEC efficiency is not considered |
| [27] | - | ✔ | ✔ | - | - | ✔ | - | Commercial | ✔ | - | - | DC is better. Hardware based analysis is performed with limited loads |
| [19] | - | - | ✔ | - | - | ✔ | - | Commercial | ✔ | - | - | DC is better. Seasonal effect is considered, however, certain basic parameters related to load and PEC are missing. |
| [26] | - | - | - | ✔ | - | ✔ | - | Commercial | ✔ | - | - | DC is better. A total of 230 V AC is compared against 380 V Dc with limited scenarios and loads. |
| [21] | ✔ | ✔ | - | - | - | - | - | Residential | ✔ | - | - | DC is feasible. Limited scenario with constant loads and fixed PEC efficiency |
| [34] | ✔ | - | ✔ | ✔ | - | ✔ | - | Residential | ✔ | ✔ | ✔ | DC is better. Time based study is performed with averaged load models, the loads are categorized according to the power demand |
| [22] | - | ✔ | - | ✔ | - | ✔ | - | Residential | ✔ | - | - | DC shows better efficiency at different voltage levels. The comparative analysis is performed on the basis of voltage levels. |
| [13] | ✔ | ✔ | - | - | - | - | - | Residential/Commercial | - | - | - | DC shows better energy savings with DC loads. The comparison is performed with futuristic approach, by considering DC loads only. |
| [20] | ✔ | - | ✔ | ✔ | ✔ | ✔ | ✔ | Commercial | ✔ | - | ✔ | DC shows better efficiency about 9.9% in base case while 17.9% in best case. |
| [23] | - | - | ✔ | - | - | ✔ | - | Residential | ✔ | - | - | AC shows better efficiency as compared to DC |
| [28] | - | ✔ | ✔ | ✔ | ✔ | ✔ | - | Commercial | ✔ | - | - | Efficiency of AC and DC is comparable and depend upon voltage level of DC mainly. |
| [31] | - | ✔ | ✔ | ✔ | - | - | - | Distribution level | ✔ | - | - | With DC is more efficient regarding energy losses, voltage profiles than its AC counterpart |
| [32] | ✔ | - | ✔ | - | - | ✔ | - | Residential | ✔ | ✔ | ✔ | AC System shows better efficiency during the presence of PV solar system |
| [37] | ✔ | - | ✔ | - | - | - | - | Residential | ✔ | - | - | DC shows better efficiency with separate and bulk PEC topologies. |
| Serial No. | Category | Energy Used (Quad. Btu) | Energy Usage Converted to % |
|---|---|---|---|
| 1 | Space Heating | 0.42 | 8.8 |
| 2 | Water Heating | 0.48 | 10 |
| 3 | Space Cooling | 1.02 | 21.3 |
| 4 | Lighting | 0.53 | 11.1 |
| 5 | Refrigeration | 0.45 | 9.4 |
| 6 | Electronics | 0.33 | 6.9 |
| 7 | Wet Cleaning | 0.33 | 6.9 |
| 8 | Cooking | 0.11 | 2.3 |
| 9 | Computers | 0.19 | 4 |
| 10 | Other | 0.94 | 19.6 |
| Serial No. | Appliances | Load Ratings (W) | Category | Load Type |
|---|---|---|---|---|
| 1 | Indoor Lights | 13 W per light | Fixed | D |
| 2 | Television | 120–130 | Fixed | D |
| 3 | Computer | 4–250 | Non-Fixed | D |
| 4 | Dishwasher | 1200–1500 | Fixed | A |
| 5 | Clothe Dryer | 1000–4000 | Non-Fixed | A |
| 6 | Clothe Washer | 500 | Fixed | A |
| 7 | Air Conditioner | 1000–6000 | Non-Fixed | VSD |
| 8 | Refrigerator | 100–220 | Non-Fixed | VSD |
| 9 | Cooking Equip. | 2150 | Fixed | I |
| 10 | Water Heater | 3000 | Fixed | I |
| 11 | Space Heater | 2000–3000 | Fixed | I |
| Serial No. | Appliances | Category | Required PEC Ratings (Maximum) | PEC for DC System | PEC for AC System |
|---|---|---|---|---|---|
| 1 | Indoor Lights | D | 300 W | DC/DC | AC/DC |
| 2 | Television | D | 150 W | DC/DC | AC/DC |
| 3 | Computer | D | 300 W | DC/DC | AC/DC |
| 4 | Dishwasher | A | 1700 W | DC/AC | N/A |
| 5 | Clothe Dryer | A | 5000 W | DC/AC | N/A |
| 6 | Clothe Washer | A | 600 W | DC/AC | N/A |
| 7 | Air Conditioner | VSD | 8000 W | DC/AC | VSD |
| 8 | Refrigerator | VSD | 300 W | DC/AC | VSD |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Erteza Gelani, H.; Dastgeer, F.; Ali Shah, S.A.; Saeed, F.; Hassan Yousuf, M.; Afzal, H.M.W.; Bilal, A.; Chowdhury, M.S.; Techato, K.; Channumsin, S.; et al. Comparative Efficiency and Sensitivity Analysis of AC and DC Power Distribution Paradigms for Residential Localities. Sustainability 2022, 14, 8220. https://doi.org/10.3390/su14138220
Erteza Gelani H, Dastgeer F, Ali Shah SA, Saeed F, Hassan Yousuf M, Afzal HMW, Bilal A, Chowdhury MS, Techato K, Channumsin S, et al. Comparative Efficiency and Sensitivity Analysis of AC and DC Power Distribution Paradigms for Residential Localities. Sustainability. 2022; 14(13):8220. https://doi.org/10.3390/su14138220
Chicago/Turabian StyleErteza Gelani, Hasan, Faizan Dastgeer, Sayyad Ahmad Ali Shah, Faisal Saeed, Muhammad Hassan Yousuf, Hafiz Muhammad Waqas Afzal, Abdullah Bilal, Md. Shahariar Chowdhury, Kuaanan Techato, Sittiporn Channumsin, and et al. 2022. "Comparative Efficiency and Sensitivity Analysis of AC and DC Power Distribution Paradigms for Residential Localities" Sustainability 14, no. 13: 8220. https://doi.org/10.3390/su14138220
APA StyleErteza Gelani, H., Dastgeer, F., Ali Shah, S. A., Saeed, F., Hassan Yousuf, M., Afzal, H. M. W., Bilal, A., Chowdhury, M. S., Techato, K., Channumsin, S., & Ullah, N. (2022). Comparative Efficiency and Sensitivity Analysis of AC and DC Power Distribution Paradigms for Residential Localities. Sustainability, 14(13), 8220. https://doi.org/10.3390/su14138220









