A Study of Contact Pressure with Thermo-Mechanical Coupled Action for a Full-Dimensional PEMFC Stack

Abstract

The contact pressure between bipolar plates (BPPs) and a membrane electrode assembly (MEA) has a key impact on Proton Exchange Membrane Fuel Cell (PEMFC) performance. However, it is difficult to obtain the contact pressure combined with operating temperature action via the finite element analysis (FEA) model, resulting in limited calculation resources for the problem of multiscale and thermo-mechanical coupled action in a full-dimensional fuel cell stack. This paper establishes an equivalent stiffness model for contact pressure, which could be predicted simply and quickly compared with the FEA model. Then, this presented model is validated by experimentation with a full-dimensional fuel cell stack assembled with 10 cells using pressure-sensitive film. The error between the presented model and the experimentation of the full-dimensional stack is a maximum of 4.41%. This work provides important insight into thermo-mechanical coupled action, as less empirical testing is required to identify the contact pressure in a full-dimensional fuel cell stack.

1. Introduction

Nowadays, the importance of sustainability in energy supply is growing, with an increasing impact on the environment. For this reason, renewable energy plays an increasingly important role in the industry, especially the automotive sector. Since the PEMFC has the advantages of being emissions-free and having high efficiency, fast startup, quick refueling, etc. [1,2,3], it is a promising alternative to fossil fuels in the automotive sector [4]. Although there are still some impediments in commercialization, such as cost, duration, and cold start [5], with proper design and management, the PEMFC is a practical way to reach the goal of sustainable development [6,7,8].

In the automotive sector, there is a growing need for research on the optimization of fuel cell stack performance. Although the field of PEMFC stack performance optimization is quite broad, the contact pressure on the multi-contact interface between the BPP and MEA must be especially well-controlled, since it greatly influences the electron transportation and fuel supply [9,10], thereby affecting the output characteristics [11].

Too small a contact pressure may cause a high contact electrical resistance on the multi-contact interface of the BPP ribs and gas diffusion layer (GDL), increasing the ohmic loss [12,13]. Otherwise, if the contact pressure is too large, the GDL is over-compressed, leading to concentration loss of the fuel cell performance [14] and even mechanical damage to the MEA [15]. In addition, the operational temperature is higher in a PEMFC stack for a better electrochemical reaction. However, a high temperature causes the MEA, sealant, and other components to expand under the constraint of the stack assembly force; thus, the thermo-mechanical coupled action of contact pressure needs to be further identified [16,17].

At present, contact pressure analysis is mainly carried out in two aspects: experimental research and numerical simulation. Selamet et al. [18] conducted experiments using pressure-sensitive film on a single cell to obtain the contact pressure. The results of the pressure-sensitive film are further presented as a 3D pressure distribution map, which is helpful to reveal the contact pressure behavior. Alizadeh et al. [19] studied the influence of endplate thickness, material, and number of cells on the contact pressure through experiments and a finite element model, thereby providing a theoretical basis with the contact pressure value for the assembly design of a fuel cell stack.

Carral et al. [20] developed an FEA model to study the assembly process of a PEMFC stack on the mechanical properties of the MEA. The presented model was used to analyze the contact pressure, contact resistance and porosity of the GDL. The greater the number of cells in the fuel cell stack, the more uniform the contact pressure. Peng et al. [21] used a PCB board to observe the electrical density in different areas on multi-contact interfaces. Different clamping bolt torques of 4 N·m, 6 N·m, and 8 N·m were applied, and it was found that when the bolt torque is large, the electric density is more uniform. Uzundurukan et al. [22] converted bolt torque into contact pressure on a flat plate via FEA numerical simulations and experiments. They found that the contact pressure is important to improve the fuel cell stack power. Optimal contact pressure is beneficial to avoid excessive deformation of the MEA and to ensure high porosity of the GDL.

Yan et al. [23] used an FEA model to simulate a five-fuel cell stack with different contact pressures of 0.5 MPa, 1.5 MPa, 2.5 MPa, and 3.5 MPa. The fuel cell output power was the largest with a contact pressure of 1.5 MPa. They also found that a higher contact pressure is beneficial to heat conduction, improving the uniformity of the temperature field and avoiding local hot spots. Weng et al. [24] studied the contact pressure between the metal BPP and GDL under different clamping forces. A polarization curve test and electrochemical spectrum (EIS) experiment were carried out. It was found that the fuel cell performance under 200 kgf was the best, and the overall electrochemical impedance was significantly smaller. Movahedi et al. [25] studied the effect of GDL thickness on the optimal contact pressure. The results show that the optimal contact pressure is quite different for different GDL thicknesses.

There is no doubt that FEA numerical simulation combined with experimentation is an available method to identify the contact pressure for a fuel cell stack; however, most current studies using FEA models are high in cost and require enormous calculation resources [26]. It is also not affordable to simulate the multiscale problems and related thermo-mechanical coupled action in a full-dimensional fuel cell stack.

For this reason, theoretical methodologies for full-dimensional fuel cell stacks are valuable for efficient analysis. Lin et al. [27,28] developed an equivalent stiffness model consisting of numerous elastic elements in either series or parallel connections of a large PEMFC stack. The presented model was validated by an FEA model, and the error was less than 1%. Ahmad et al. [29] validated an equivalent stiffness model using polarization data and pressure-sensitive films for contact pressure; the error between the model and the experimental results was a maximum of 6.4%, considering the tolerance relevant to the stack assembly and gas pressure difference. Yu et al. [30] established a simplified beam model to simulate the deflection of endplates for the contact pressure and obtained an appropriate flexural rigidity of endplates with proper endplate thickness. Qiu et al. [31] also proposed an effective continuous equivalent model to identify contact pressure on the GDLs; experiments with dimensional error metallic BPPs were carried out and were in good agreement with the numerical results. Carral et al. [32] predicted the endplate strain and displacement by using Euler–Bernoulli beam theory. The endplate deflection leads to contact pressure concentration and over-compression on the MEA. The experimental results measured by strain gauge sensors were consistent with the beam theory.

Most current studies regarding contact pressure in a large fuel cell stack are based on numerous empirical tests. Unfortunately, there are only a few effective theoretical methods that contribute to identifying contact pressure for the whole stack model, especially in a full-dimensional fuel cell stack. Moreover, a fuel cell stack with an electrochemical reaction has operating temperature effects, but the thermo-mechanical coupled action of contact pressure has not yet been solved in these presented models.

In this paper, an equivalent stiffness model of contact pressure for a full-dimensional PEMFC stack is studied. The contact pressure and structural deformation of the fuel cell components are revealed under the clamping force of the fuel cell stack. Thermal expansion of the fuel cell components is also considered in the presented model, which is experimentally validated by a full-dimensional fuel cell stack with 10 cells using pressure-sensitive films. The error between the experimental and theoretical results of the presented model is evaluated. The focus of this work is to validate the effectiveness of this equivalent stiffness model with thermo-mechanical coupled action of the contact pressure for a full-dimensional fuel cell stack.

2. An Equivalent Stiffness Model with Thermo-Mechanical Coupled Action of Contact Pressure for a Full-Dimensional Fuel Cell Stack

2.1. An Equivalent Stiffness Model for a PEMFC Stack

A PEMFC stack is mainly composed of current collection plates, endplates, and N_j single cells. Each cell consists of a cathode BPP, an anode BPP, an MEA, and sealants. An example of such a stack is shown in Figure 1.

When fuel cell stacks are assembled by clamping force with steel belts, the fuel cell components are structurally compressed along the assembly direction, which can be regarded as an elastic bar subjected to compression, as well as fuel cell components. The equivalent axial stiffness is

$$\mathrm{k}=\frac{\mathrm{EA}}{\mathrm{l}}$$

(1)

where k is the equivalent stiffness, E is the elastic modulus, A is the cross-sectional area, and l is the length of the structure along the axial direction.

Since the contact pressure on the multi-contact interfaces which affects the fuel cell performance is along the direction of fuel cell stack assembly, the equivalent stiffness of a fuel cell stack with several basic components can be obtained by Equation (1). Firstly, a single fuel cell composed of a flow field area and sealing area is presented.

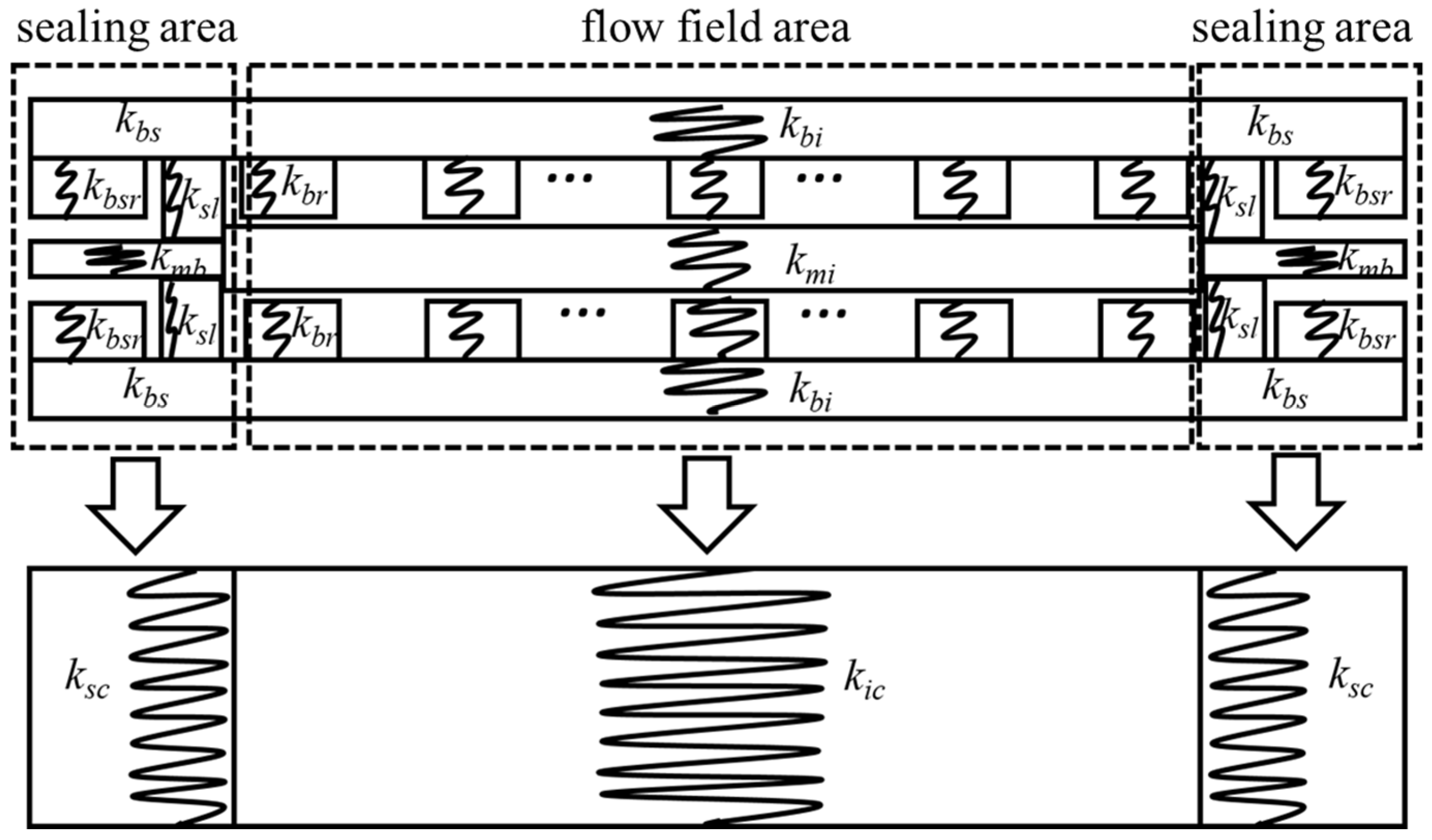
As shown in Figure 2, the flow field area composed of the BPP base, BPP ribs, and MEA can be regarded as equivalent springs in series. The sealing area is composed of a BPP base, BPP ribs, MEA frame, and sealants is regarded as equivalent springs connected in series and parallel.

The equivalent stiffness of the flow field area is

$${\mathrm{k}}_{\mathrm{ic}}=\frac{{\mathrm{k}}_{\mathrm{bi}}{\mathrm{K}}_{\mathrm{mr}}}{{\mathrm{k}}_{\mathrm{bi}}{+2\mathrm{K}}_{\mathrm{mr}}}$$

(2)

where k_ic is the total equivalent stiffness of the flow field area; k_bi is the equivalent stiffness of the BPP base; K_mr represents the equivalent stiffness of the BPP ribs and MEA in series connection, K_mr = N_rk_brk_mi/(N_rk_br + 2k_mi); N_r is the number of BPP ribs; k_br is the equivalent stiffness of the BPP ribs; and k_mi is the equivalent stiffness of the MEA.

The total equivalent stiffness of the sealing area k_sc is

$${\mathrm{k}}_{\mathrm{sc}}=\frac{{\mathrm{k}}_{\mathrm{mb}}{\mathrm{K}}_{\mathrm{bsl}}}{{\mathrm{K}}_{\mathrm{bsl}}{+2\mathrm{k}}_{\mathrm{mb}}}$$

(3)

where k_mb is the equivalent stiffness of the MEA frame; K_bsl represents the equivalent stiffness of the BPP base, BPP rib, and sealant in series or parallel connection, K_bsl = k_bsk_slr/(k_bs + k_slr); k_slr represents the equivalent stiffness of the BPP rib and the sealant in parallel connection, k_slr = k_sl + k_bsr; k_bs is the equivalent stiffness of the BPP base in the sealing area; k_sl is the equivalent stiffness of sealants; and k_bsr is the equivalent stiffness of the BPP ribs in the sealing area.

The single cell is composed of equivalent springs of two sealing areas K_sc and one flow field area K_ic in parallel, so the equivalent stiffness of the single cell K_cj is

$${\mathrm{k}}_{\mathrm{cj}}{=\mathrm{k}}_{\mathrm{ic}}{+2\mathrm{k}}_{\mathrm{sc}}$$

(4)

For the whole stack, in addition to the large numbers of cells, there are also current collection plates and endplates. The connections of these equivalent springs are in series, so the equivalent stiffness of the whole fuel cell stack is

$${\mathrm{k}}_{\mathrm{st}}=\frac{1}{{\mathrm{N}}_{\mathrm{j}}\frac{1}{{\mathrm{k}}_{\mathrm{cj}}}+2\frac{1}{{\mathrm{k}}_{\mathrm{cc}}}+2\frac{1}{{\mathrm{k}}_{\mathrm{ep}}}}$$

(5)

where N_j is the number of cells, k_cc is the equivalent stiffness of the current collection plate, and k_ep is the equivalent stiffness of endplates.

2.2. Contact Pressure Based on the Equivalent Stiffness Model

The schematic structure of the entire equivalent stiffness model for the fuel cell stack with clamping force is shown in Figure 3.

For the assembled fuel cell stack, the clamping force is applied by steel belts. The following equation is obtained:

$${\mathrm{F}}_{\mathrm{bl}}{=\mathrm{N}}_{\mathrm{bl}}{\mathrm{k}}_{\mathrm{bl}}{\Delta \mathrm{y}}_{\mathrm{bl}}{=\mathrm{F}}_{\mathrm{st}}{=\mathrm{k}}_{\mathrm{st}}{\Delta \mathrm{y}}_{\mathrm{st}}$$

(6)

where F_bl and F_st are, respectively, the force values of the steel belts and the fuel cell stack; N_bl is the number of steel belts; k_bl is the equivalent stiffness of the steel belts; and Δy_bl and Δy_st are their respective structural deformations.

For the j^th cell in the fuel cell stack, the following equation is obtained:

$${\mathrm{F}}_{\mathrm{cj}}{=\mathrm{k}}_{\mathrm{cj}}{\Delta \mathrm{y}}_{\mathrm{cj}}{=\mathrm{F}}_{\mathrm{st}}{=\mathrm{k}}_{\mathrm{st}}{\Delta \mathrm{y}}_{\mathrm{st}}$$

(7)

where F_cj is the force on the j^th cell, and Δy_cj is the deformation of the j^th cell. Then, the deformation of the j^th cell is

$${\Delta \mathrm{y}}_{\mathrm{cj}}=\frac{{\mathrm{k}}_{\mathrm{st}}}{{\mathrm{k}}_{\mathrm{cj}}}{\Delta \mathrm{y}}_{\mathrm{st}}$$

(8)

Since each cell is composed of two sealing areas and one flow field area in parallel, as shown in Figure 2, the forces applied in the flow field area F_ic and the sealing area F_sc can be respectively calculated using the following equations:

$${\mathrm{F}}_{\mathrm{ic}}{=\mathrm{k}}_{\mathrm{ic}}{\Delta \mathrm{y}}_{\mathrm{cj}}=\frac{{\mathrm{k}}_{\mathrm{st}}{\Delta \mathrm{y}}_{\mathrm{st}}}{{1+2\mathsf{\beta }}_{\mathrm{si}}}$$

(9)

$${\mathrm{F}}_{\mathrm{sc}}{=\mathrm{k}}_{\mathrm{sc}}{\Delta \mathrm{y}}_{\mathrm{cj}}=\frac{{\mathrm{k}}_{\mathrm{st}}{\Delta \mathrm{y}}_{\mathrm{st}}}{{2+\mathsf{\beta }}_{\mathrm{is}}}$$

(10)

where β_si = k_sc/k_ic and β_is = k_ic/k_sc.

The force applied to the sealants is

$${\mathrm{F}}_{\mathrm{sl}}=\frac{{\mathrm{k}}_{\mathrm{sl}}}{{\mathrm{k}}_{\mathrm{slr}}}{\mathrm{F}}_{\mathrm{sc}}=\frac{{\mathrm{k}}_{\mathrm{st}}{\Delta \mathrm{y}}_{\mathrm{st}}}{\left({2+\mathsf{\beta }}_{\mathrm{is}}\right){\mathsf{\beta }}_{\mathrm{rs}}}$$

(11)

where β_rs = k_slr/k_sl.

The deformation of the MEA is

$${\Delta \mathrm{y}}_{\mathrm{mi}}=\frac{{\mathrm{F}}_{\mathrm{ic}}}{{\mathrm{k}}_{\mathrm{mi}}}=\frac{{\mathrm{k}}_{\mathrm{st}}{\Delta \mathrm{y}}_{\mathrm{st}}}{{\mathrm{k}}_{\mathrm{mi}}\left({1+2\mathsf{\beta }}_{\mathrm{si}}\right)}$$

(12)

The deformation of the sealants is

$${\Delta \mathrm{y}}_{\mathrm{sl}}=\frac{{\mathrm{F}}_{\mathrm{sl}}}{{\mathrm{k}}_{\mathrm{slr}}}=\frac{{\mathrm{k}}_{\mathrm{st}}{\Delta \mathrm{y}}_{\mathrm{st}}}{{(2+\mathsf{\beta }}_{\mathrm{is}}{)\mathsf{\beta }}_{\mathrm{rs}}{\mathrm{k}}_{\mathrm{slr}}}$$

(13)

The contact pressure on the BPP ribs is

$${\mathsf{\sigma }}_{\mathrm{bp}}=\frac{{\mathrm{F}}_{\mathrm{ic}}}{{\mathrm{N}}_{\mathrm{r}}{\mathrm{A}}_{\mathrm{br}}}=\frac{1}{\left({1+2\mathsf{\beta }}_{\mathrm{si}}\right)}\frac{{\mathrm{k}}_{\mathrm{st}}{\Delta \mathrm{y}}_{\mathrm{st}}}{{\mathrm{N}}_{\mathrm{r}}{\mathrm{A}}_{\mathrm{br}}}$$

(14)

where N_rA_br is the total contact area of the BPP ribs with the MEA.

The contact pressure on the MEA is

$${\mathsf{\sigma }}_{\mathrm{mi}}=\frac{{\mathrm{F}}_{\mathrm{ic}}}{{\mathrm{A}}_{\mathrm{mi}} }=\frac{1}{\left({1+2\mathsf{\beta }}_{\mathrm{si}}\right)}\frac{{\mathrm{k}}_{\mathrm{st}}{\Delta \mathrm{y}}_{\mathrm{st}}}{{\mathrm{A}}_{\mathrm{mi}}}$$

(15)

where A_mi is the total contact area of the MEA with the BPP ribs. The MEA and BPP ribs are a pair of contact interfaces. Then, A_mi = N_rA_br and σ_bp = σ_mi.

The contact pressure on sealants is

$${\mathsf{\sigma }}_{\mathrm{sl}}=\frac{{\mathrm{F}}_{\mathrm{sl}}}{ {\mathrm{A}}_{\mathrm{sl}}}=\frac{1}{\left({2+\mathsf{\beta }}_{\mathrm{is}}\right)}\frac{1}{{\mathsf{\beta }}_{\mathrm{rs}}}\frac{{\mathrm{k}}_{\mathrm{st}}{\Delta \mathrm{y}}_{\mathrm{st}}}{{\mathrm{A}}_{\mathrm{sl}}}$$

(16)

where A_sl is the contact area of sealants with the MEA frame.

The above-established equations represent the interrelationships between the deformation of each component, the contact pressure, and the clamping force. These equivalent models can be used not only to predict the equivalent contact pressure value quickly, but also to evaluate whether the clamping force is reasonable. That is, if the optimal contact pressure is obtained by experiments, then the optimal clamping force can also be calculated based on the above equations.

2.3. Contact Pressure Based on the Equivalent Stiffness Model with Thermo-Mechanical Coupled Action

The fuel cell stack is generally assembled at room temperature, but during the actual fuel cell electrochemical reaction, the operating temperature is much higher than room temperature, mainly due to the electrochemical heat release and the ohmic loss. The operating temperature of the fuel cell stack can generally reach 80 °C to 95 °C. Due to the different thermal expansion coefficients, the deformation of each fuel cell component caused by thermal expansion leads to increased contact pressure with thermo-mechanical coupled action.

Contact pressure based on the equivalent stiffness model should be reconsidered with thermo-mechanical coupled action, especially in full-dimensional fuel cell stacks. For experimental validation with a steady operational temperature using pressure-sensitive film, the operating temperature distribution of the presented equivalent stiffness model is uniform, so the deformation of each fuel cell component caused by thermal expansion is linear.

In the flow field area, the deformation caused by thermal expansion is mainly due to the MEA and BPPs. The deformation Δl_ic of the flow field area caused by the thermal expansion is

$${\Delta \mathrm{l}}_{\mathrm{ic}}{=(2\mathsf{\alpha }}_{\mathrm{b}}{\mathrm{l}}_{\mathrm{b}}{+\mathsf{\alpha }}_{\mathrm{mi}}{\mathrm{l}}_{\mathrm{mi}})\Delta \mathrm{T}$$

(17)

where α_mi is the linear thermal expansion coefficient of the MEA; α_b is the linear thermal expansion coefficient of the BPP; l_b is the thickness of the BPP in the flow field region, which includes the thickness of the BPP base and BPP ribs; and l_mi is the thickness of the MEA.

In the sealing area, the deformation caused by thermal expansion is mainly due to sealants and BPPs. The thermal expansion deformation of the MEA frame is negligible due to its small thickness. The deformation Δl_sc of the sealing area caused by the thermal expansion is

$${\Delta \mathrm{l}}_{\mathrm{sc}}{=(2\mathsf{\alpha }}_{\mathrm{b}}{\mathrm{l}}_{\mathrm{bs}}{+\mathsf{\alpha }}_{\mathrm{sl}}{\mathrm{l}}_{\mathrm{sl}})\Delta \mathrm{T}$$

(18)

where α_sl is the linear thermal expansion coefficient of the sealant, l_bs is the thickness of the BPP in the sealing area, and l_sl is the thickness of the sealant. The deformation Δl_sc of each cell caused by thermal expansion is

$${\Delta \mathrm{l}}_{\mathrm{cj}}=\frac{{2\mathrm{k}}_{\mathrm{sc}}{\Delta \mathrm{l}}_{\mathrm{sc}}{+\mathrm{k}}_{\mathrm{ic}}{\Delta \mathrm{l}}_{\mathrm{ic}}}{{2\mathrm{k}}_{\mathrm{sc}}{+\mathrm{k}}_{\mathrm{ic}}}$$

(19)

The deformation Δl_st of the entire fuel cell stack caused by thermal expansion is

$${\Delta \mathrm{lst}=2(\Delta \mathrm{l}}_{\mathrm{cc}}{+\Delta \mathrm{l}}_{\mathrm{ep}}{)+\mathrm{N}}_{\mathrm{j}}{\Delta \mathrm{l}}_{\mathrm{cj}}$$

(20)

where Δl_cc and Δl_ep are individual deformations due to thermal expansion for the current collection plates and endplates.

The initial height before assembly and the assembled height after assembly of the fuel cell stack are defined as y₀ and y₁, and the final height of the fuel cell stack after assembly considering the operating temperature action is y′₁. If there is no operating temperature action, the initial heights of the fuel cell stack before and after assembly by clamping force are represented as

$${\mathrm{y}}_1{=\mathrm{y}}_0-{\Delta \mathrm{y}}_{\mathrm{st}}$$

(21)

With the operating temperature action, the final height of the fuel cell stack is represented by

$${{\mathrm{y}}^{\prime }}_1{=\mathrm{y}}_0{+\Delta \mathrm{ly}}_{st}-{\Delta {\mathrm{y}}^{\prime }}_{\mathrm{st}}$$

(22)

Δy′_st is the total deformation of the fuel cell stack considering the thermal expansion. If the release of the clamping steel belts is neglected, the final height of the fuel cell stack considering the operating temperature is the same as the assembled height; that is, y′₁ = y₁. Then, based on Equations (21) and (22), the total deformation Δy′_st of the fuel cell stack considering the thermal expansion can be obtained.

$${\Delta {\mathrm{y}}^{\prime }}_{\mathrm{st}}{=\Delta \mathrm{y}}_{\mathrm{st}}{+\Delta \mathrm{ly}}_{\mathrm{st}}$$

(23)

Since the total clamping force of a fuel cell stack transforms into compression force applied on each cell, even considering the thermal expansion of each fuel cell component, we have

$${{\mathrm{F}}^{\prime }}_{\mathrm{st}}{=\mathrm{k}}_{\mathrm{st}}{\Delta {\mathrm{y}}^{\prime }}_{\mathrm{st}}{={\mathrm{F}}^{\prime }}_{\mathrm{cj}}{=\mathrm{k}}_{\mathrm{cj}}{\Delta {\mathrm{y}}^{\prime }}_{\mathrm{cj}}$$

(24)

where F′_st and F′_cj are, respectively, the clamping force of the fuel cell stack and the compression force on each cell considering the thermal expansion; and Δy′_cj is the corresponding total deformation of each cell considering the thermal expansion. Based on Equations (23) and (24), Δy′_cj is obtained as

$${\Delta {\mathrm{y}}^{\prime }}_{\mathrm{cj}}=\frac{{\mathrm{k}}_{\mathrm{st}}}{{\mathrm{k}}_{\mathrm{cj}}}{\Delta {\mathrm{y}}^{\prime }}_{\mathrm{st}}=\frac{{\mathrm{k}}_{\mathrm{st}}}{{\mathrm{k}}_{\mathrm{cj}}}{(\Delta \mathrm{y}}_{\mathrm{st}}+\Delta \mathrm{l})$$

(25)

Based on Equations (9)–(11), the force in the flow field area F′_ic and the lealants F′_sl with operating temperature action are represented, respectively, as

$${{\mathrm{F}}^{\prime }}_{\mathrm{ic}}{=\mathrm{k}}_{\mathrm{ic}}{\Delta {\mathrm{y}}^{\prime }}_{\mathrm{cj}}=\frac{{\mathrm{k}}_{\mathrm{st}}}{{1+2\mathsf{\beta }}_{\mathrm{si}}}{(\Delta \mathrm{y}}_{\mathrm{st}}+\Delta \mathrm{l})$$

(26)

$${{\mathrm{F}}^{\prime }}_{\mathrm{sl}}{=\mathrm{k}}_{\mathrm{sl}}{\Delta {\mathrm{y}}^{\prime }}_{\mathrm{sl}}=\frac{{\mathrm{k}}_{\mathrm{st}}}{{(2+\mathsf{\beta }}_{\mathrm{is}}{)\mathsf{\beta }}_{\mathrm{rs}}}{(\Delta \mathrm{y}}_{\mathrm{st}}+\Delta \mathrm{l})$$

(27)

Based on Equations (12) and (13), The total deformation values of the MEAs Δy′_mi and the sealants Δy′_sl with operating temperature action are

$${\Delta {\mathrm{y}}^{\prime }}_{\mathrm{mi}}=\frac{{{\mathrm{F}}^{\prime }}_{\mathrm{mi}}}{{\mathrm{k}}_{\mathrm{mi}}}=\frac{{\mathrm{k}}_{\mathrm{st}}}{{\mathrm{k}}_{\mathrm{mi}}\left({1+2\mathsf{\beta }}_{\mathrm{si}}\right)}\left({\Delta \mathrm{y}}_{\mathrm{st}}+\Delta \mathrm{l}\right)$$

(28)

$${\Delta {\mathrm{y}}^{\prime }}_{\mathrm{sl}}=\frac{{\mathrm{k}}_{\mathrm{st}}}{{(2+\mathsf{\beta }}_{\mathrm{is}}{)\mathsf{\beta }}_{\mathrm{rs}}{\mathrm{k}}_{\mathrm{slr}}}{(\Delta \mathrm{y}}_{\mathrm{st}}+\Delta \mathrm{l})$$

(29)

Based on Equations (14)–(16), the contact pressure values on the BPP ribs σ′_bp, MEA σ′_mi, and sealant σ′_sl with operating temperature action are

$${{\mathsf{\sigma }}^{\prime }}_{\mathrm{bp}}=\frac{{{\mathrm{F}}^{\prime }}_{\mathrm{ic}}}{{\mathrm{N}}_{\mathrm{r}}{\mathrm{A}}_{\mathrm{br}}}=\frac{{\mathrm{k}}_{\mathrm{st}}}{{(1+2\mathsf{\beta }}_{\mathrm{si}}{)\mathrm{N}}_{\mathrm{r}}{\mathrm{A}}_{\mathrm{br}}}{(\Delta \mathrm{y}}_{\mathrm{st}}+\Delta \mathrm{l})$$

(30)

$${{\mathsf{\sigma }}^{\prime }}_{\mathrm{mi}}=\frac{{{\mathrm{F}}^{\prime }}_{\mathrm{ic}}}{{\mathrm{A}}_{\mathrm{mi}}}=\frac{{\mathrm{k}}_{\mathrm{st}}}{{(1+2\mathsf{\beta }}_{\mathrm{si}}{)\mathrm{A}}_{\mathrm{mi}}}{(\Delta \mathrm{y}}_{\mathrm{st}}+\Delta \mathrm{l})$$

(31)

$${{\mathsf{\sigma }}^{\prime }}_{\mathrm{sl}}=\frac{{{\mathrm{F}}^{\prime }}_{\mathrm{sl}}}{{\mathrm{A}}_{\mathrm{sl}}}=\frac{{\mathrm{k}}_{\mathrm{st}}}{{(2+\mathsf{\beta }}_{\mathrm{is}}{)\mathsf{\beta }}_{\mathrm{rs}}{\mathrm{A}}_{\mathrm{sl}}}{(\Delta \mathrm{y}}_{\mathrm{st}}+\Delta \mathrm{l})$$

(32)

Based on these established equations considering the thermal expansion of the fuel cell components, the contact pressure in a full-dimensional fuel cell stack is obtained. Next, we experimentally validate this presented model using a full-dimensional fuel cell stack.

3. Experimental Validation of Contact Pressure in a Full-Dimensional Fuel Cell Stack

The experimental validation of the contact pressure was carried out in a full-dimensional fuel cell stack with 10 cells. The fuel cell stack was assembled with a gas cylinder to clamp the endplates, current collector plates, and cells with steel belts, as shown in Figure 4. The materials of the main fuel cell components are shown in

Table 1. Material properties of the fuel cell components in the experimental fuel cell stack.

Component	Material	Elastic Modulus/GPa	Poisson	Thermal Expansion Coefficient/10−6·K−1
Current collector plate	Copper	100	0.33	16.6
Endplate	Epoxy resin	2.6	0.3	137
Bipolar plate	Graphite	10	0.25	7.9
Sealant	Olefin resin	5.5	0.49	77
MEA frame	Polyethylene	18	0.33	60
MEA	Polymer material	0.021	0.1	123

. The applied clamping force was converted into applied pressure on the endplates by the gas cylinder according to

$$\mathrm{F}=\mathrm{P}\times \mathrm{S}$$

(33)

where S = π × R², in which R is the piston radius of the gas cylinder, which is 0.1 m. P is the operational gas pressure, which is 0.6 MPa. The clamping force applied to the fuel cell stack was 18.84 kN in this experimentation.

According to the theoretical results from the equivalent stiffness model, the experimental contact pressure was below 2.5 MPa. Fujifilm’s pressure-sensitive film (LLW) with a range of 0.5–2.5 MPa was selected. Pressure-sensitive films were installed on the cathode side of the first, third, fifth, seventh, and ninth cells in the stack. A schematic of the installation of pressure-sensitive films is shown in Figure 5, where the dotted lines represent the locations of the inserted pressure-sensitive films.

After the stack was assembled and connected to the test bench of the fuel cell stack, the cooling water temperature was set to 50 °C to heat the stack for steady-operating temperature action as shown in Figure 6.

Certain holes were precut in each pressure-sensitive film, corresponding to the positions of the inlet and outlet of water cooling for the fuel cell stack to ensure that the cooling water could flow and warm up the stack. A diagram of the inlets and outlets in the BPP is shown in Figure 7.

After the contact pressure experiment using the pressure-sensitive film, the stack was disassembled, and the pressure-sensitive films were removed and examined. An example of the experimental results of the pressure-sensitive film at the location of the ninth cell is shown in Figure 8a. Due to the obvious difference in the contact pressure level in the flow field area and the sealing area, the captured result of the pressure-sensitive film was divided into two parts—the flow field area and the sealing area—corresponding to the equivalent stiffness model and analyzed separately, as shown in Figure 8b,c. The contact pressure in the zone without impression is lower than 0.5 MPa. The deeper the red color, the closer the contact pressure is to 2.5 MPa.

Furthermore, the tested contact pressure values should be identified to validate the equivalent stiffness model. According to the operational methodology and temperature property of the pressure-sensitive film, there are corresponding relationship curves between the color density and contact pressure value at different temperatures. The curves are provided by the manufacturer of the pressure-sensitive film and could be used to read the contact pressure value. A color reading program can be written to quantitatively analyze the pressure values, as shown in Figure 9.

The experimental results of contact pressure at different locations were identified, and the contact pressure results of the flow field area and sealing area are shown in

Table 2. Tested contact pressure results of the pressure-sensitive film in the flow field area.

Cell Number of Pressure-Sensitive Film	Maximum Pressure /MPa	Mean Pressure /MPa	Standard Deviation /MPa
1	1.8408	1.1013	0.3416
3	2.1379	1.0854	0.3243
5	1.8734	1.1185	0.3515
7	1.9547	1.1287	0.3633
9	1.9710	1.1298	0.3635

and

Table 3. Tested contact pressure results of the pressure-sensitive film in the sealing area.

Cell Number of Pressure-Sensitive Film	Maximum Pressure /MPa	Mean Pressure /MPa	Standard Deviation /MPa
1	2.1834	1.2316	0.3120
3	1.9547	1.1704	0.2998
5	1.9873	1.2038	0.2934
7	1.9873	1.2103	0.3072
9	1.9873	1.2293	0.3068

.

The mean contact pressure of each cell in the flow field area is shown in Figure 10. It was found that the mean contact pressure of each cell was nearly the same, showing that the fuel cell stack was well-assembled. The mean contact pressure at the ninth cell was higher than that at the others; as this cell is closer to the lower endplate, this is mainly due to the deflection of endplates under the clamping force of steel belts.

The mean contact pressure in the sealing area is shown in Figure 11. It was found that the mean contact pressure in the sealing area was a little higher than the contact pressure in the flow area due to the thin sealing area of the experimental fuel cell stack. Furthermore, the mean contact pressure in the sealing area near the endplates on both sides of the fuel cell stack was higher than that elsewhere due to the relatively large deflection of the endplates with the clamping force of the fuel cell stack.

On the other hand, the theoretical contact pressure, considering the operational temperature action based on the equivalent stiffness model, was also identified based on Equations (31) and (32) for validation with the experimental results. The contact pressure values are also presented in the flow field area and the sealing area.

Firstly, the contact pressure in the flow field area obtained by the equivalent stiffness model was identified as 1.08 MPa based on Equation (31). Since the equivalent stiffness model is considered to be linear, the contact nonlinear characteristics of the multi-contact interface are neglected, so the contact pressure value obtained by the stiffness model is constant. The theoretical mean contact pressure and experimental mean contact pressure in the flow field area are shown in Figure 12.

The theoretical contact pressure result errors when compared to the experimental results using pressure-sensitive film at the first, third, fifth, seventh, and ninth cells were 1.93%, 0.50%, 3.44%, 4.31%, and 4.41%, respectively. It was found that the equivalent stiffness model results were in good agreement with the experimental results. The maximum error was 4.41%.

Secondly, the theoretical contact pressure in the sealing area was identified as 1.187 MPa based on Equation (32). The theoretical mean contact pressure and experimental mean contact pressure in the sealing area are shown in Figure 13.

The errors of the different cells were 3.62%, 1.42%, 1.4%, 1.93%, and 3.44%, respectively. It was found that the equivalent stiffness model results were also in good agreement with the experimental results. The maximum error was 3.62%.

Based on the contact pressure analysis of the equivalent stiffness model and experimentation considering the operational temperature action in a full-dimensional fuel cell stack, the errors in both the flow field and sealing areas were within 5%. The effectiveness of the equivalent stiffness model of the contact pressure with thermo-mechanical coupled action was thus validated by the experiment in a full-dimensional fuel cell stack.

In contrast to the huge calculation resources required by the FEA model, and its time-consuming nature, the equivalent stiffness model provides a simple and quick calculation method to obtain the contact pressure for a full-dimensional fuel cell stack. Unlike other equivalent models, this study presents the contact pressure with thermo-mechanical coupled action between the contact pressure and operating temperature of the fuel cell stack, which well predicts the mechanical behavior in a full-dimensional fuel cell stack.

4. Conclusions

In this study, an equivalent stiffness model for identifying the contact pressure with thermo-mechanical coupled action was proposed and validated against experiments on a full-dimensional fuel cell stack using pressure-sensitive film. The contact pressure values obtained by the equivalent stiffness model were compared to the experimental results, and the maximum error was within 5%. Compared with the FEA, the presented equivalent model could greatly save on cost and time, while providing an accurate result and important insights into the contact mechanical behavior of a full-dimensional fuel cell stack.

In detail, at first, each component of the fuel cell stack, such as the endplates, BPPs, MEAs, and sealants, was equivalent to springs based on the established equivalent stiffness model. The equivalent contact pressure value and structural deformation of each component were individually obtained and combined with the contact area on the multi-contact interface.

Then, bearing in mind the fuel cell operational temperature, the thermal expansion deformation was considered, and the equivalent stiffness model of contact pressure with thermo-mechanical coupled action for a full-dimensional fuel cell stack was then established to identify the contact pressure value.

Finally, the equivalent stiffness model of contact pressure with thermo-mechanical coupled action was validated by an experiment using pressure-sensitive film in a full-dimensional fuel cell stack with 10 cells; the equivalent stiffness model was effective, and the errors were within 5% on the multi-contact interface.

Based on this equivalent stiffness model with thermo-mechanical coupled action, the bottleneck problem of contact pressure identification in a full-dimensional fuel cell stack can be solved. The FEA model often requires huge calculation resources and presents convergence problems, while the presented equivalent model can predict the contact pressure simply and quickly. With effective contact pressure prediction, we have the ability to effectively control the assembly quality and optimize the performance of full-dimensional fuel cell stacks.