Large Scale Energy Signature Analysis: Tools for Utility Managers and Planners
Abstract
:1. Introduction
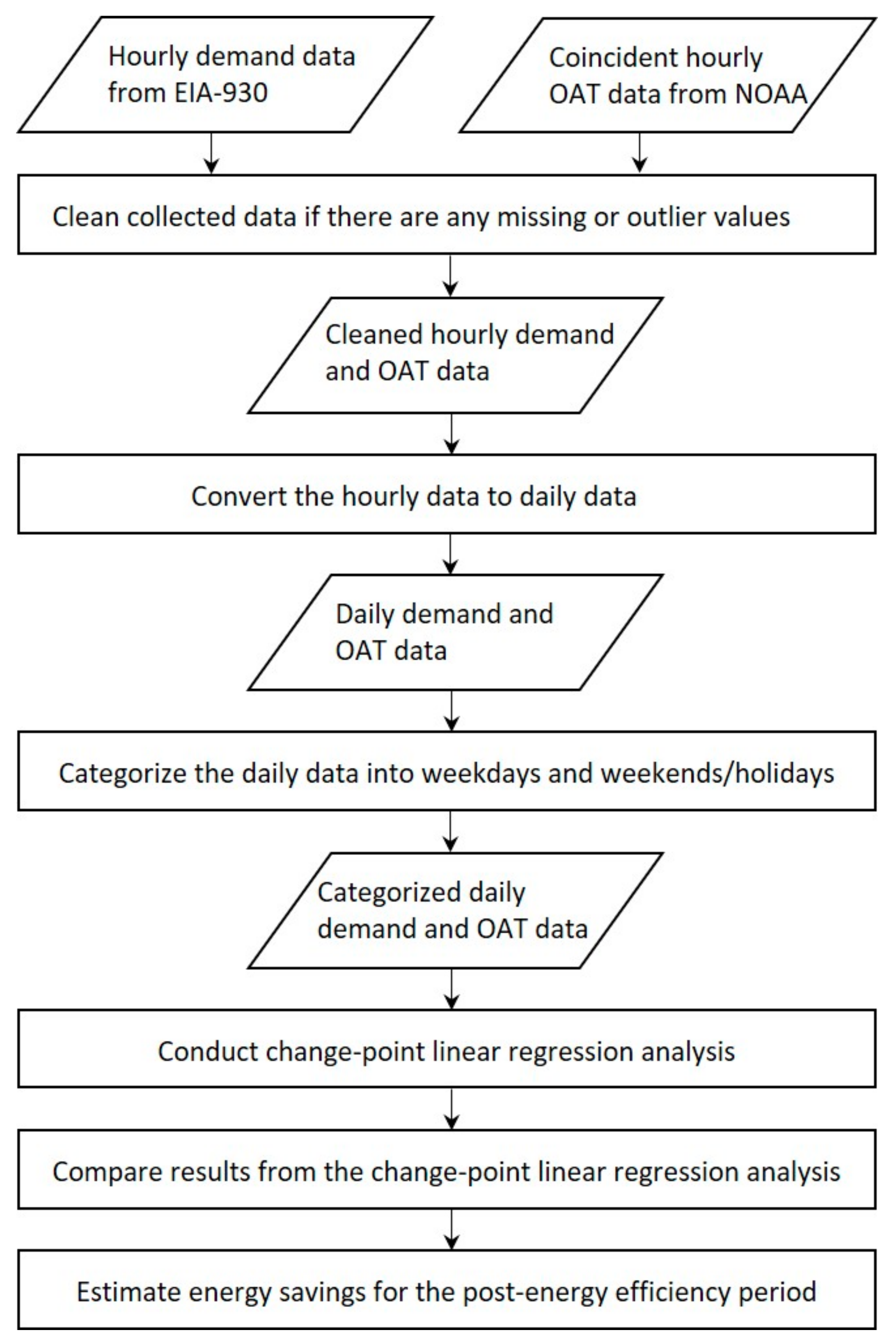
2. Materials and Methods
2.1. Electricity Demand Data
2.2. Selected BA
- -
- Hourly interval electricity demand data (MW) for 14 BAs were collected for the one-year period from January 2016 to December 2016. For further analysis, hourly interval electricity demand data (MW) for four BAs were collected for the two periods: July 2015 to June 2016 and July 2017 to June 2018. In addition, the corresponding hourly outside air temperature (OAT) (°C) data were collected for each BA [30];
- -
- Blank, zero, and minus values from hourly electricity demand data were considered as missing values. Outliers were then removed for hourly electricity demand data. If hourly demand was above two times of the maximum value and below the half of the minimum value during the year, the hourly demand was considered as an outlier. When missing and outlier data exist in a day for hourly electricity demand data, the day was handled as a missing and outlier day, respectively. In addition, missing data were filled in for the hourly outside air temperature data using a linear interpolation method when missing data were found [31];
- -
- Hourly data were converted to daily data. The hourly demand data were added and the hourly OAT data were averaged for the daily intervals;
- -
- The daily data were organized by dividing the data into the two categories: weekdays (WDs) and weekends/holidays (WEs);
- -
- Change-point linear regression analysis was conducted using the ASHRAE Inverse Modeling Toolkit (IMT) [32] to find a balance-point temperature, a heating or cooling slope (weather-dependent electricity demand), and weather-independent electricity demand for each BA;
- -
- The results from the change-point analysis were compared for 14 BAs. Furthermore, four BAs were compared with two different periods, which assumed that the periods were pre- and post-energy efficiency program periods, respectively. In addition, energy savings were estimated using a weather-adjusted method [9] for four BAs during a post-energy efficiency program period.
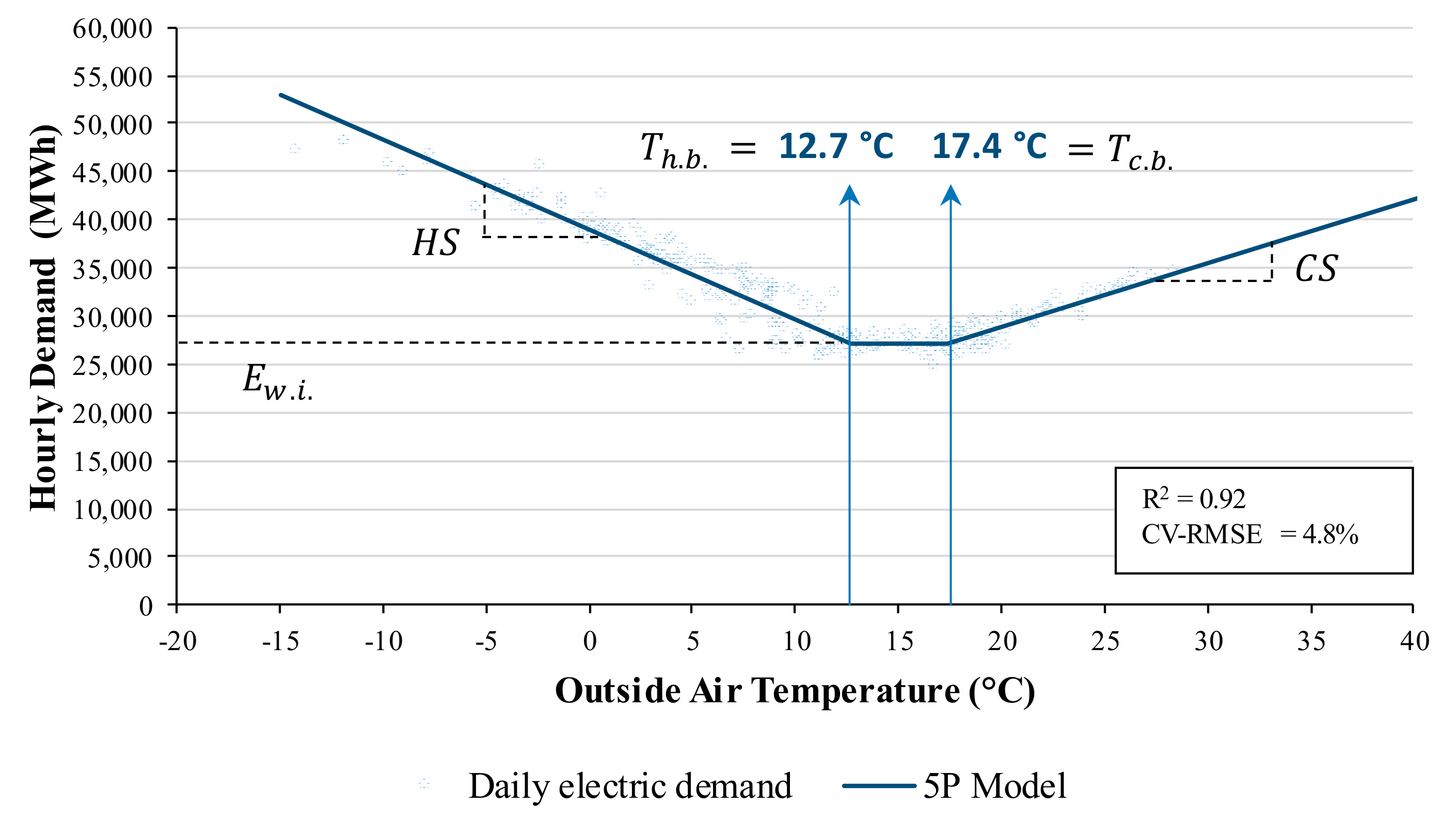
2.3. Model
3. Results
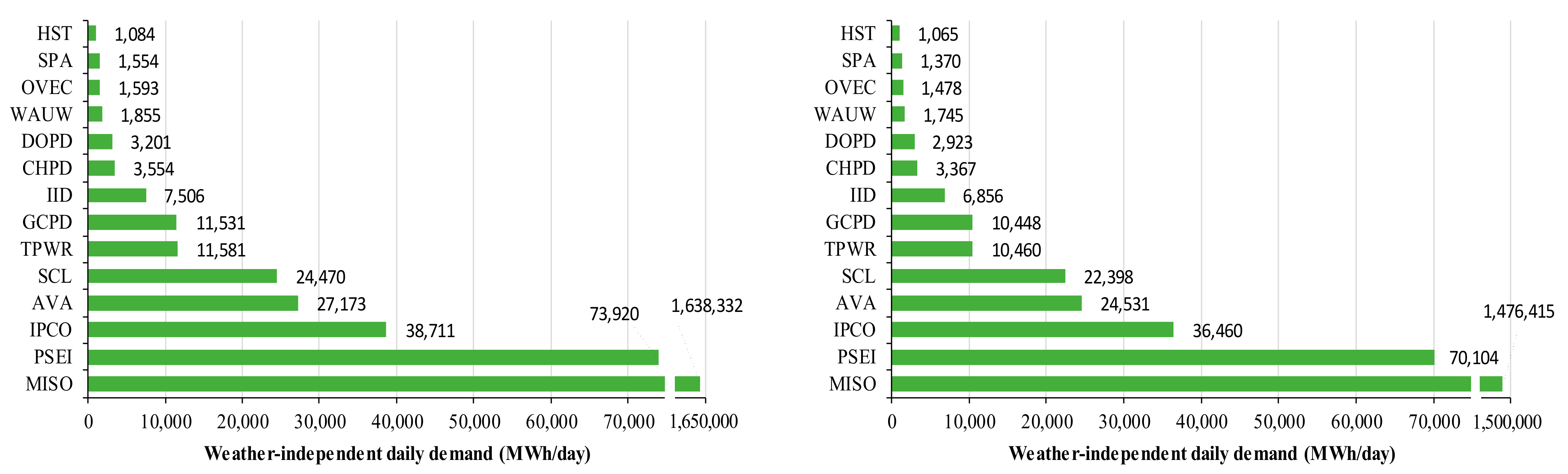
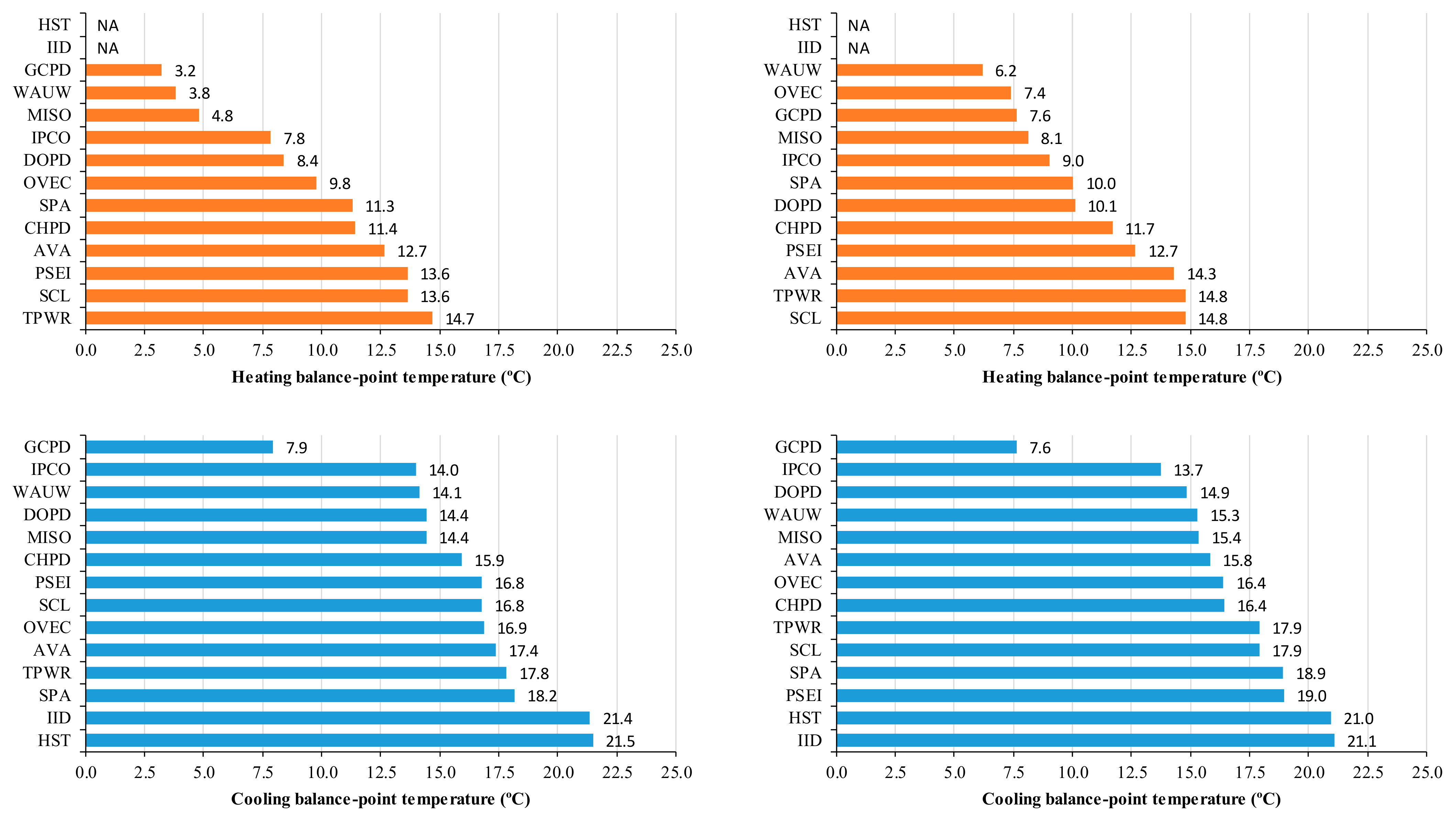
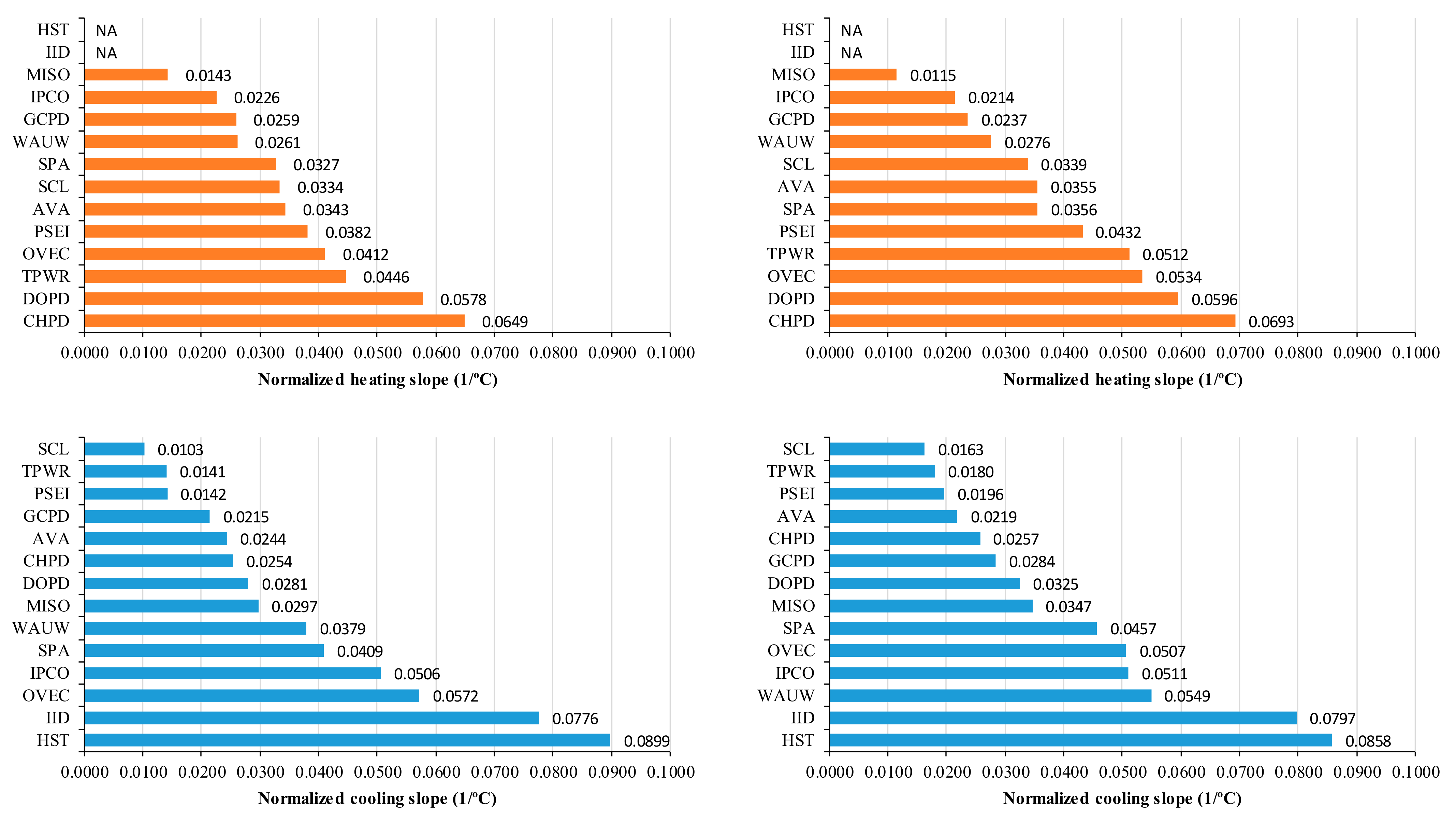
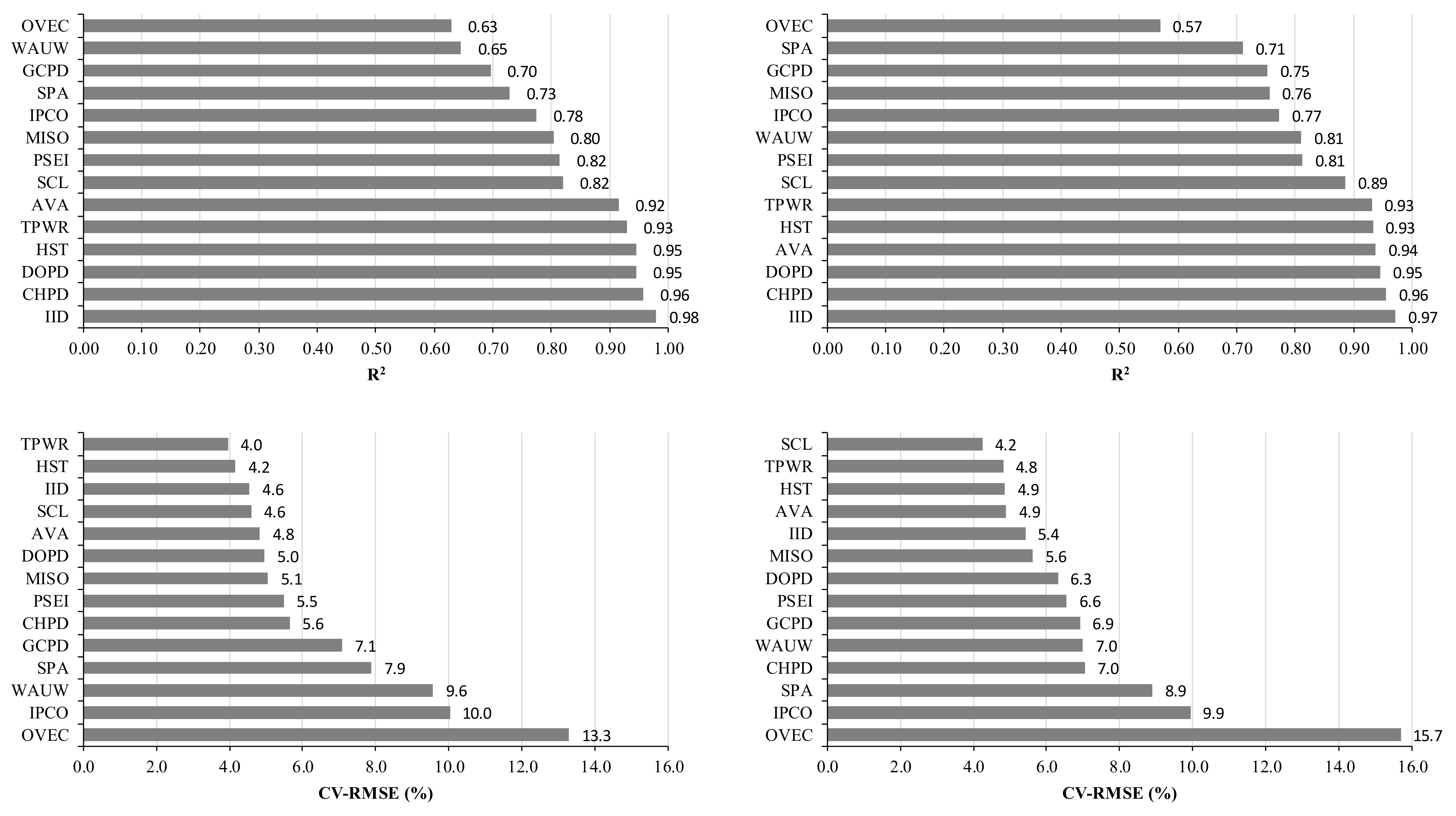
3.1. Results from the Energy Signature Analysis for 14 BAs
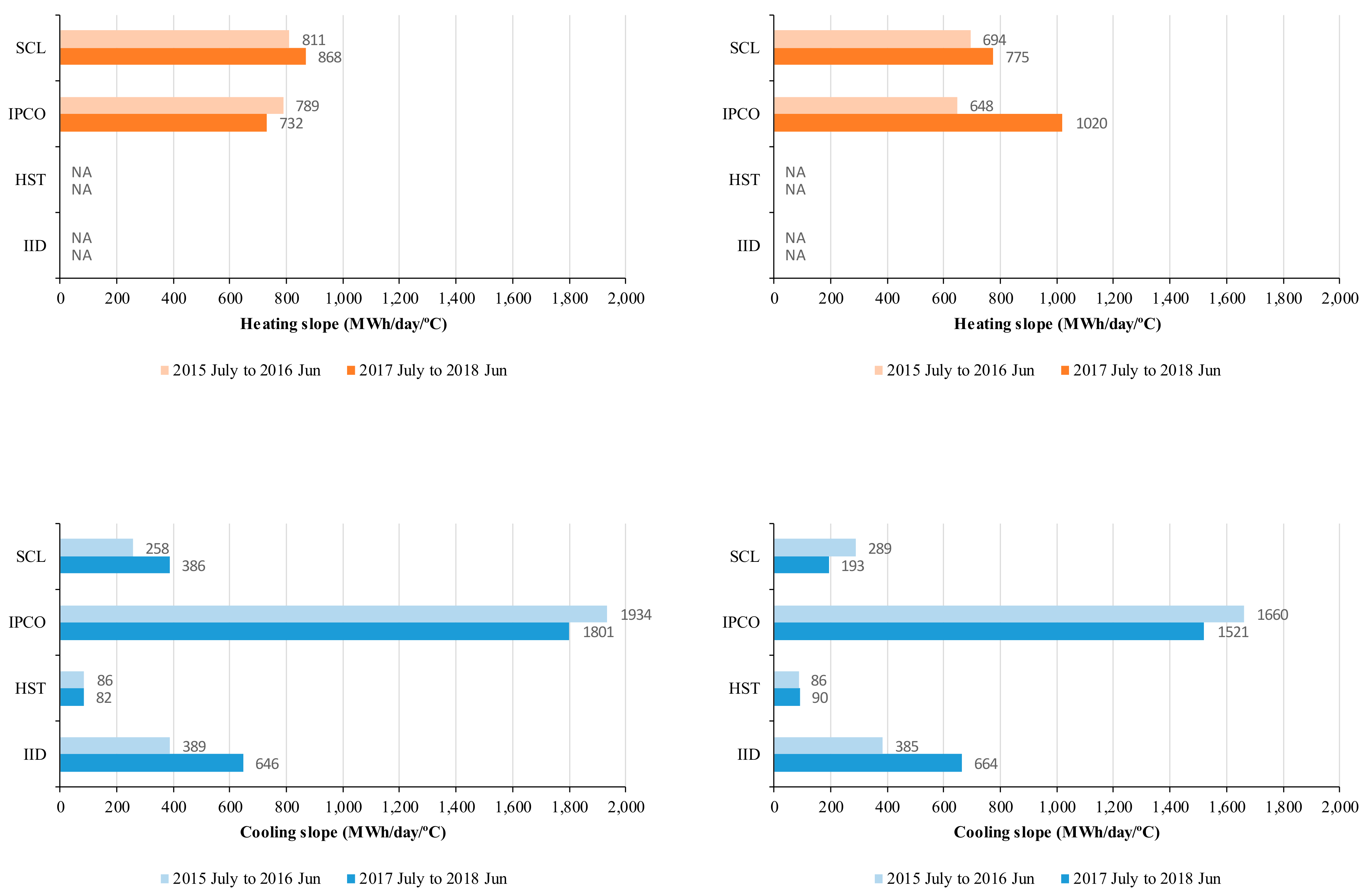
3.2. Results from the Energy Signature Analysis for Four BAs for the Two Different Periods
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- ACEEE. State and Utility Policy. Available online: https://www.aceee.org/program/utilities (accessed on 27 June 2022).
- Austin Energy Rebates & Incentives. Available online: https://savings.austinenergy.com/rebates/ (accessed on 27 June 2022).
- Idaho Power Ways to Save. Available online: https://www.idahopower.com/energy-environment/ways-to-save/ (accessed on 27 June 2022).
- Berg, W.; Ribeiro, D. Saving Watts to Save Drops: Inclusion of Water Efficiency in Energy Efficiency Programs; American Council for an Energy-Efficient Economy: Washington, DC, USA, 2018. [Google Scholar]
- Bukarica, V.; Tomšić, Ž. Energy Efficiency Policy Evaluation by Moving from Techno-Economic towards Whole Society Perspective on Energy Efficiency Market. Renew. Sustain. Energy Rev. 2017, 70, 968–975. [Google Scholar] [CrossRef]
- ACEEE. State and Local Policy Database. Available online: https://database.aceee.org/ (accessed on 27 June 2022).
- Hayes, S.; Baum, N.; Herndon, G. Energy Efficiency: Is the United States Improving? American Council for an Energy-Efficient Economy: Washington, DC, USA, 2013. [Google Scholar]
- Perez, K.X.; Cetin, K.; Baldea, M.; Edgar, T.F. Development and Analysis of Residential Change-Point Models from Smart Meter Data. Energy Build. 2017, 139, 351–359. [Google Scholar] [CrossRef] [Green Version]
- Kissock, J.K.; Reddy, T.A.; Claridge, D.E. Ambient-Temperature Regression Analysis for Estimating Retrofit Savings in Commercial Buildings. ASME J. Sol. Energy Eng. 1998, 120, 168–176. [Google Scholar] [CrossRef]
- Kissock, K.J.; Eger, C. Measuring Industrial Energy Savings. Appl. Energy 2008, 85, 347–361. [Google Scholar] [CrossRef]
- ASHRAE. Chapter 19. Energy Estimating and Modeling Methods. In ASHRAE Handbook—Fundamentals; ASHRAE: Atlanta, GA, USA, 2017. [Google Scholar]
- Fumo, N.; Rafe Biswas, M.A. Regression Analysis for Prediction of Residential Energy Consumption. Renew. Sustain. Energy Rev. 2015, 47, 332–343. [Google Scholar] [CrossRef]
- Raffio, G.; Isambert, O.; Mertz, G.; Schreier, C.; Kissock, K. Targeting Residential Energy Assistance. In Proceedings of the ASME 2007 Energy Sustainability Conference, Long Beach, CA, USA, 27–30 July 2007; pp. 489–495. [Google Scholar]
- Gianniou, P.; Reinhart, C.; Hsu, D.; Heller, A.; Rode, C. Estimation of Temperature Setpoints and Heat Transfer Coefficients among Residential Buildings in Denmark Based on Smart Meter Data. Build. Environ. 2018, 139, 125–133. [Google Scholar] [CrossRef]
- Eriksson, M.; Akander, J.; Moshfegh, B. Investigating Energy Use in a City District in Nordic Climate Using Energy Signature. Energies 2022, 15, 1907. [Google Scholar] [CrossRef]
- Ding, Y.; Ivanko, D.; Cao, G.; Brattebø, H.; Nord, N. Analysis of Electricity Use and Economic Impacts for Buildings with Electric Heating under Lockdown Conditions: Examples for Educational Buildings and Residential Buildings in Norway. Sustain. Cities Soc. 2021, 74, 103253. [Google Scholar] [CrossRef]
- Aragon, V.; James, P.A.B.; Gauthier, S. The Influence of Weather on Heat Demand Profiles in UK Social Housing Tower Blocks. Build. Environ. 2022, 219, 109101. [Google Scholar] [CrossRef]
- Ali, M.T.; Mokhtar, M.; Chiesa, M.; Armstrong, P. A Cooling Change-Point Model of Community-Aggregate Electrical Load. Energy Build. 2011, 43, 28–37. [Google Scholar] [CrossRef]
- Wang, Z.; Hong, T.; Li, H.; Ann Piette, M. Predicting City-Scale Daily Electricity Consumption Using Data-Driven Models. Adv. Appl. Energy 2021, 2, 100025. [Google Scholar] [CrossRef]
- US EIA. U.S. Electric System Operating Data. Available online: https://www.eia.gov/realtime_grid/#/status?end=20180830T17 (accessed on 30 August 2018).
- US EIA. About the EIA-930 Data. Available online: https://www.eia.gov/electricity/gridmonitor/about (accessed on 27 June 2022).
- US EIA. Hourly Electric Grid Monitor. Available online: https://www.eia.gov/electricity/gridmonitor/dashboard/electric_overview/US48/US48 (accessed on 29 April 2022).
- Ruggles, T.H.; Farnham, D.J.; Tong, D.; Caldeira, K. Developing Reliable Hourly Electricity Demand Data through Screening and Imputation. Sci. Data 2020, 7, 155. [Google Scholar] [CrossRef] [PubMed]
- Büyükalaca, O.; Bulut, H.; Yılmaz, T. Analysis of Variable-Base Heating and Cooling Degree-Days for Turkey. Appl. Energy 2001, 69, 269–283. [Google Scholar] [CrossRef] [Green Version]
- US EIA. Hourly Information on U.S. Electricity Supply, Demand, and Flows Is Now Available. Available online: https://www.eia.gov/todayinenergy/detail.php?id=27212 (accessed on 27 August 2018).
- US EIA. EIA-930 Data Users Guide and Known Issues; US EIA: Washington, DC, USA, 2018. [Google Scholar]
- US EIA. U.S. Electric Power Regions. Available online: https://www.eia.gov/todayinenergy/detail.php?id=27152 (accessed on 6 August 2018).
- US EIA. Select Balancing Authority. Available online: https://www.eia.gov/electricity/gridmonitor/dashboard/electric_overview/US48/US48 (accessed on 27 June 2022).
- ICC. 2018 International Energy Conservation Code; ICC: Washington, DC, USA, 2017. [Google Scholar]
- NOAA. Data Tools: Local Climatological Data (LCD). Available online: https://www.ncdc.noaa.gov/cdo-web/datatools/lcd (accessed on 1 July 2018).
- Long, N. Real-Time Weather Data Access Guide; National Renewable Energy Laboratory: Golden, CO, USA, 2006. [Google Scholar]
- Kissock, K.; Haberl, J.S.; Claridge, D.E. Inverse Modeling Toolkit: User’s Guide (ASHRAE Final Report for RP-1050); ASHRAE: Atlanta, GA, USA, 2001. [Google Scholar]
- ASHRAE. ASHRAE Guideline 14-2014; ASHRAE: Atlanta, GA, USA, 2014. [Google Scholar]
- Research Into Action; QuEST; Stetz Consulting; Kolderup Consulting; Warren Energy Engineering; Left Fork Energy; Consulting, S. Regression for M & V: Reference Guide; Bonneville Power Administration (BPA): Portland, OR, USA, 2011. [Google Scholar]
- Henseler, J.; Ringle, C.M.; Sinkovics, R.R. The Use of Partial Least Squares Path Modeling in International Marketing. In New Challenges to International Marketing; Sinkovics, R.R., Ghauri, P.N., Eds.; Advances in International Marketing; Emerald Group Publishing Limited: Bingley, UK, 2009; Volume 20, pp. 277–319. ISBN 978-1-84855-468-9. [Google Scholar]
- Idaho Power. Demand-Side Management 2017 Annual Report; Idaho Power: Boise, ID, USA, 2018. [Google Scholar]
- Idaho Power. Demand-Side Management 2018 Annual Report; Idaho Power: Boise, ID, USA, 2019. [Google Scholar]
- US EIA. Idaho Electricity Profile 2017—Table 1. Available online: https://www.eia.gov/electricity/state/archive/2017/idaho/ (accessed on 28 June 2022).
- US EIA. Idaho Electricity Profile 2018—Table 1. Available online: https://www.eia.gov/electricity/state/archive/2018/idaho/ (accessed on 28 June 2022).
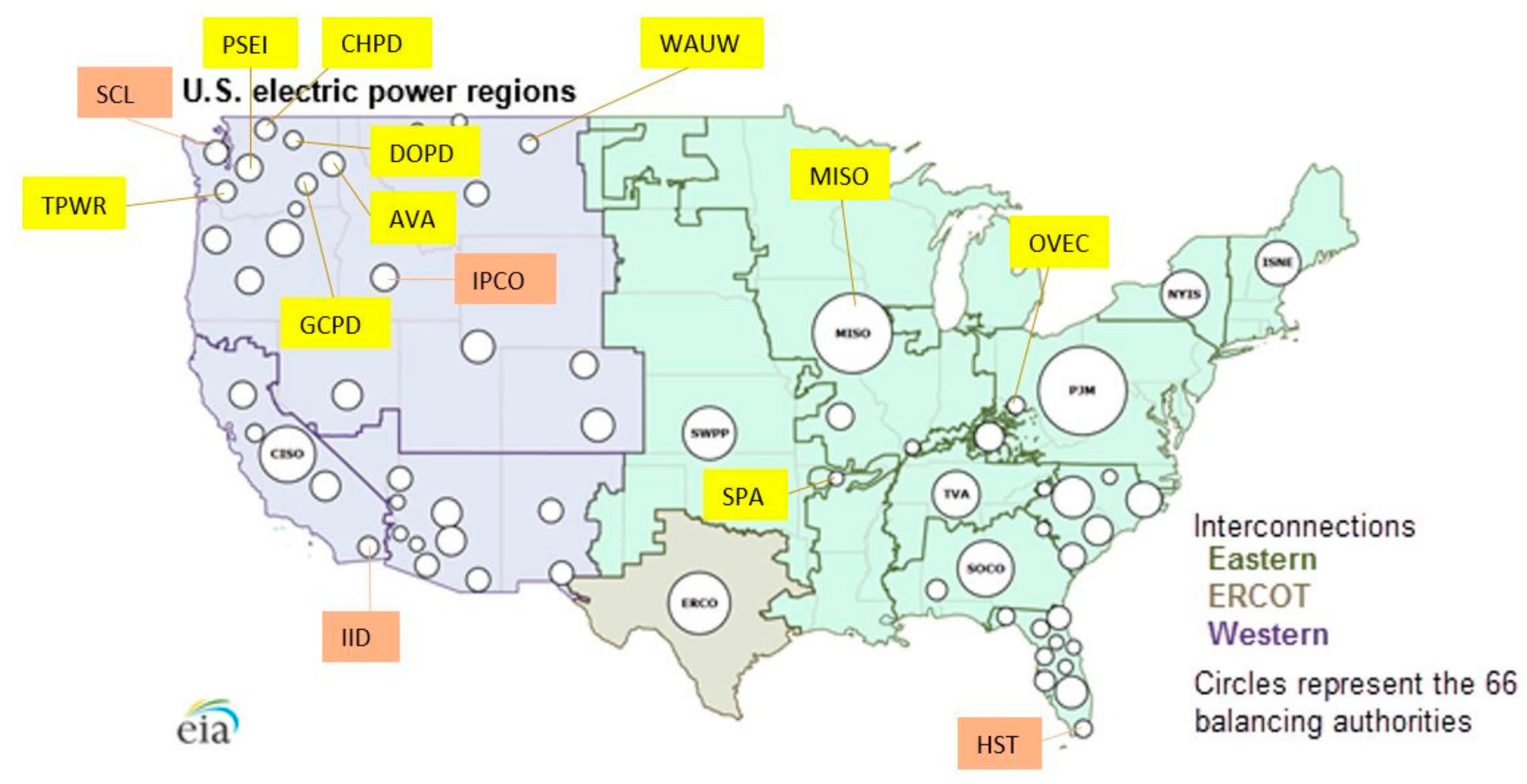



| BA | Region | IECC Climate Zone | Weather Data (NOAA) Location, State |
|---|---|---|---|
| Seattle City Light (SCL) | Northwest | 4C | Seattle-Tacoma, WA |
| City of Tacoma, Department of Public Utilities, Light Division (TPWR) | Northwest | 4C | Seattle-Tacoma, WA |
| Puget Sound Energy, Inc. (PSEI) | Northwest | 5B | Seattle-Tacoma, WA |
| Public Utility District No. 2 of Grant County, Washington (GCPD) | Northwest | 5B | Spokane, WA |
| Avista Corporation (AVA) | Northwest | 5B | Spokane, WA |
| Public Utility District No. 1 of Chelan County (CHPD) | Northwest | 5B | Omak, WA |
| PUD No. 1 of Douglas County (DOPD) | Northwest | 5B | Omak, WA |
| Idaho Power Company (IPCO) | Northwest | 5B | Boise, ID |
| Western Area Power Administration—Upper Great Plains West (WAUW) | Northwest | 6B | Glasgow, MT |
| Imperial Irrigation District (IID) | California | 2B | EL Centro, CA |
| Southwestern Power Administration (SPA) | Central | 4A | Harrison, AR |
| Ohio Valley Electric Corporation (OVEC) | Mid-Atlantic | 4A | Cincinnati, OH |
| City of Homestead (HST) | Florida | 1A | Miami, FL |
| Midcontinent Independent System Operator, Inc. (MISO) | Midwest | 5A | Des Moines, IA |
| BA | Weather Data (NOAA), State | WD/WE | Missing/ Outlier Days | Used model | °C) | °C) | R2 | CV-RMSE (%) | |||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| SCL | Seattle-Tacoma, | WD | 4/0 | 5P | 13.6 | 16.8 | −817.6 | 251.7 | −0.0334 | 0.0103 | 24,469.7 | 0.82 | 4.6% |
| WA | WE | 2/0 | 5P | 14.8 | 17.9 | −758.3 | 364.6 | −0.0339 | 0.0163 | 22,398.0 | 0.89 | 4.2% | |
| TPWR | Seattle-Tacoma, | WD | 0/0 | 5P | 14.7 | 17.8 | −516.9 | 162.8 | −0.0446 | 0.0141 | 11,580.6 | 0.93 | 4.0% |
| WA | WE | 0/0 | 5P | 14.8 | 17.9 | −535.5 | 188.0 | −0.0512 | 0.0180 | 10,459.5 | 0.93 | 4.8% | |
| PSEI | Seattle-Tacoma, | WD | 3>/0 | 5P | 13.6 | 16.8 | −2,822.1 | 1,047.5 | −0.0382 | 0.0142 | 73,919.6 | 0.82 | 5.5% |
| WA | WE | 2/0 | 5P | 12.7 | 19.0 | −3,026.7 | 1,375.6 | −0.0432 | 0.0196 | 70,104.2 | 0.81 | 6.6% | |
| GCPD | Spokane, | WD | 0/0 | 5P | 3.2 | 7.9 | −298.7 | 247.7 | −0.0259 | 0.0215 | 11,531.3 | 0.70 | 7.1% |
| WA | WE | 0/0 | 4P | 7.6 | 7.6 | −247.4 | 297.0 | −0.0237 | 0.0284 | 10,448.0 | 0.75 | 6.9% | |
| AVA | Spokane, | WD | 0/2 | 5P | 12.7 | 17.4 | −933.1 | 661.7 | −0.0343 | 0.0244 | 27,173.4 | 0.92 | 4.8% |
| WA | WE | 0/2 | 5P | 14.3 | 15.8 | −871.3 | 537.2 | −0.0355 | 0.0219 | 24,531.3 | 0.94 | 4.9% | |
| CHPD | Omak, | WD | 0/0 | 5P | 11.4 | 15.9 | −230.6 | 90.3 | −0.0649 | 0.0254 | 3554.2 | 0.96 | 5.6% |
| WA | WE | 0/0 | 5P | 11.7 | 16.4 | −233.2 | 86.5 | −0.0693 | 0.0257 | 3366.6 | 0.96 | 7.0% | |
| DOPD | Omak, | WD | 11/0 | 5P | 8.4 | 14.4 | −185.0 | 89.8 | −0.0578 | 0.0281 | 3201.2 | 0.95 | 5.0% |
| WA | WE | 4/0 | 5P | 10.1 | 14.9 | −174.1 | 94.9 | −0.0596 | 0.0325 | 2922.8 | 0.95 | 6.3% | |
| IPCO | Boise, | WD | 1/7 | 5P | 7.8 | 14.0 | −873.1 | 1,960.0 | −0.0226 | 0.0506 | 38,710.9 | 0.78 | 10.0% |
| ID | WE | 2/3 | 5P | 9.0 | 13.7 | −780.9 | 1,861.6 | −0.0214 | 0.0511 | 36,459.9 | 0.77 | 9.9% | |
| WAUW | Glasgow | WD | 28/1 | 5P | 3.8 | 14.1 | −48.5 | 70.4 | −0.0261 | 0.0379 | 1,855.2 | 0.65 | 9.6% |
| MT | WE | 30/0 | 5P | 6.2 | 15.3 | −48.2 | 95.8 | −0.0276 | 0.0549 | 1744.7 | 0.81 | 7.0% | |
| IID | EL Centro, | WD | 5/0 | 3P | 21.4 | 21.4 | 0.0 | 582.6 | 0.0000 | 0.0776 | 7506.4 | 0.98 | 4.6% |
| CA | WE | 5/0 | 3P | 21.1 | 21.1 | 0.0 | 546.7 | 0.0000 | 0.0797 | 6856.4 | 0.97 | 5.4% | |
| SPA | Harrison, | WD | 0/0 | 5P | 11.3 | 18.2 | −50.8 | 63.6 | −0.0327 | 0.0409 | 1553.8 | 0.73 | 7.9% |
| AR | WE | 0/0 | 5P | 10.0 | 18.9 | −48.8 | 62.6 | −0.0356 | 0.0457 | 1370.1 | 0.71 | 8.9% | |
| OVEC | Cincinnati, | WD | 0/1 | 5P | 9.8 | 16.9 | −65.6 | 91.1 | −0.0412 | 0.0572 | 1592.7 | 0.63 | 13.3% |
| OH | WE | 1/0 | 5P | 7.4 | 16.4 | −79.0 | 74.9 | −0.0534 | 0.0507 | 1477.5 | 0.57 | 15.7% | |
| HST | Miami, | WD | 3/0 | 3P | 21.5 | 21.5 | 0.0 | 97.4 | 0.0000 | 0.0899 | 1084.3 | 0.95 | 4.2% |
| FL | WE | 0/0 | 3P | 21.0 | 21.0 | 0.0 | 91.4 | 0.0000 | 0.0858 | 1064.9 | 0.93 | 4.9% | |
| MISO | Des Moines | WD | 2/0 | 5P | 4.8 | 14.4 | −23,450.9 | 48,687.5 | −0.0143 | 0.0297 | 1,638,332.9 | 0.80 | 5.1% |
| IA | WE | 1/0 | 5P | 8.1 | 15.4 | −17,020.5 | 51,193.9 | −0.0115 | 0.0347 | 1,476,414.6 | 0.76 | 5.6% |
| BA | Period | WD/WE | Measured (MWh) | Adjusted Baseline (MWh) | Difference (MWh) | Difference (%) |
|---|---|---|---|---|---|---|
| SCL | July 2015–June 2016 | WD | 6,806,550 | |||
| WE | 2,874,378 | |||||
| Total | 9,680,928 | |||||
| July 2017–June 2018 | WD | 6,413,611 | 6,502,737 | −89,126 | −1.4% | |
| WE | 2,672,695 | 2,720,224 | −47,529 | −1.7% | ||
| Total | 9,086,306 | 9,222,961 | −136,655 | −1.5% | ||
| IPCO | July 2015–June 2016 | WD | 11,899,065 | |||
| WE | 4,974,351 | |||||
| Total | 16,873,416 | |||||
| July 2017–June 2018 | WD | 10,934,425 | 11,050,100 | −115,675 | −1.0% | |
| WE | 4,751,940 | 4,818,318 | −66,378 | −1.4% | ||
| Total | 15,686,365 | 15,868,418 | −182,053 | −1.1% | ||
| HST | July 2015–June 2016 | WD | 328,037 | |||
| WE | 150,258 | |||||
| Total | 478,295 | |||||
| July 2017–June 2018 | WD | 352,822 | 350,636 | 2186 | 0.6% | |
| WE | 156,657 | 157,539 | −882 | −0.6% | ||
| Total | 509,479 | 508,176 | 1303 | 0.3% | ||
| IID | July 2015–June 2016 | WD | 2,331,221 | |||
| WE | 923,900 | |||||
| Total | 3,255,121 | |||||
| July 2017–June 2018 | WD | 2,338,633 | 2,132,910 | 205,723 | 9.6% | |
| WE | 972,205 | 863,453 | 108,752 | 12.6% | ||
| Total | 3,310,838 | 2,996,362 | 314,476 | 10.5% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Oh, S.; Gardner, J.F. Large Scale Energy Signature Analysis: Tools for Utility Managers and Planners. Sustainability 2022, 14, 8649. https://doi.org/10.3390/su14148649
Oh S, Gardner JF. Large Scale Energy Signature Analysis: Tools for Utility Managers and Planners. Sustainability. 2022; 14(14):8649. https://doi.org/10.3390/su14148649
Chicago/Turabian StyleOh, Sukjoon, and John F. Gardner. 2022. "Large Scale Energy Signature Analysis: Tools for Utility Managers and Planners" Sustainability 14, no. 14: 8649. https://doi.org/10.3390/su14148649
APA StyleOh, S., & Gardner, J. F. (2022). Large Scale Energy Signature Analysis: Tools for Utility Managers and Planners. Sustainability, 14(14), 8649. https://doi.org/10.3390/su14148649







