Cognitive IoT Vision System Using Weighted Guided Harris Corner Feature Detector for Visually Impaired People
Abstract
:1. Introduction
2. Related Work
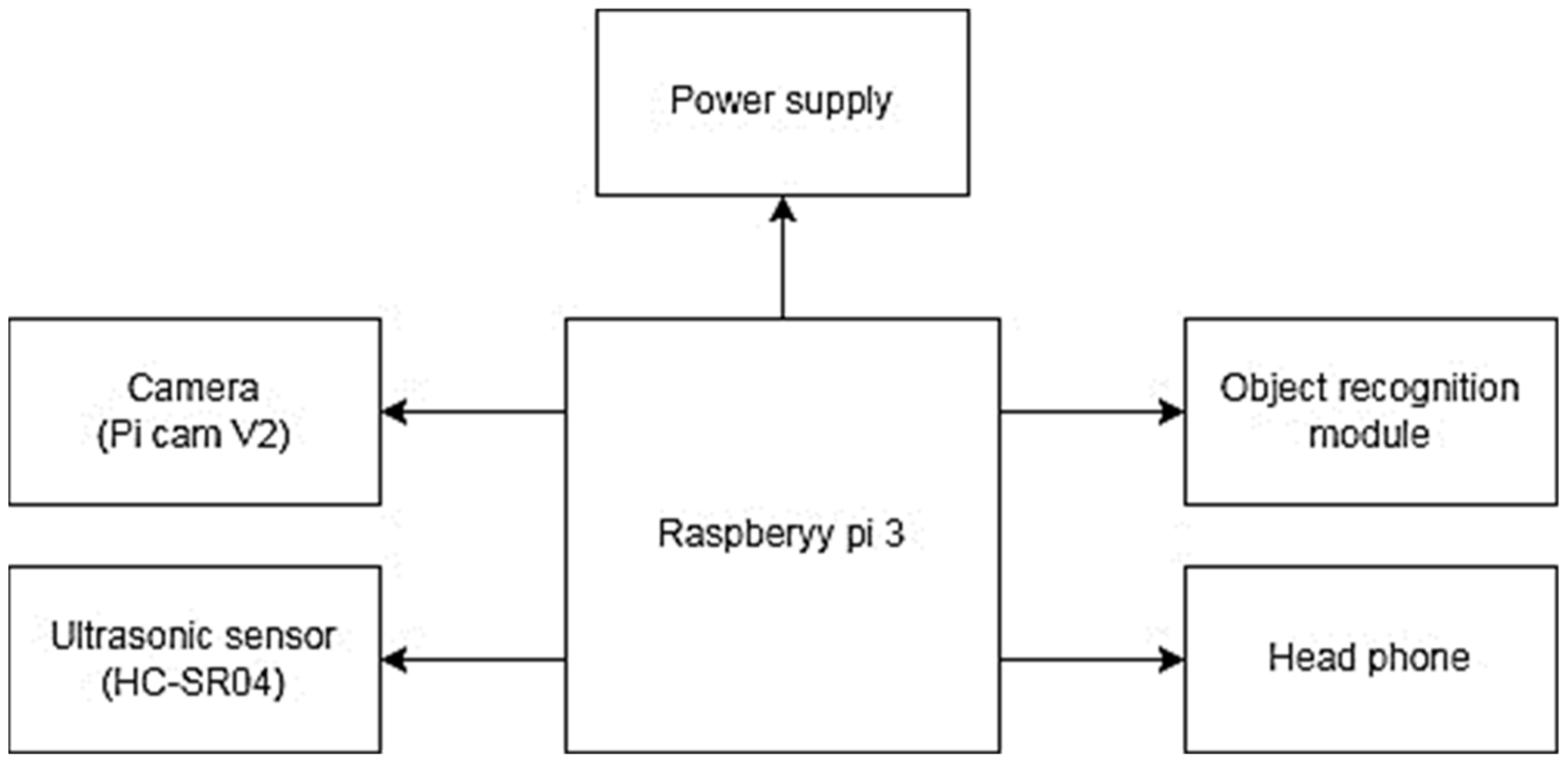
3. Proposed Vision System for Visually Impaired People
3.1. Object Recognition Module
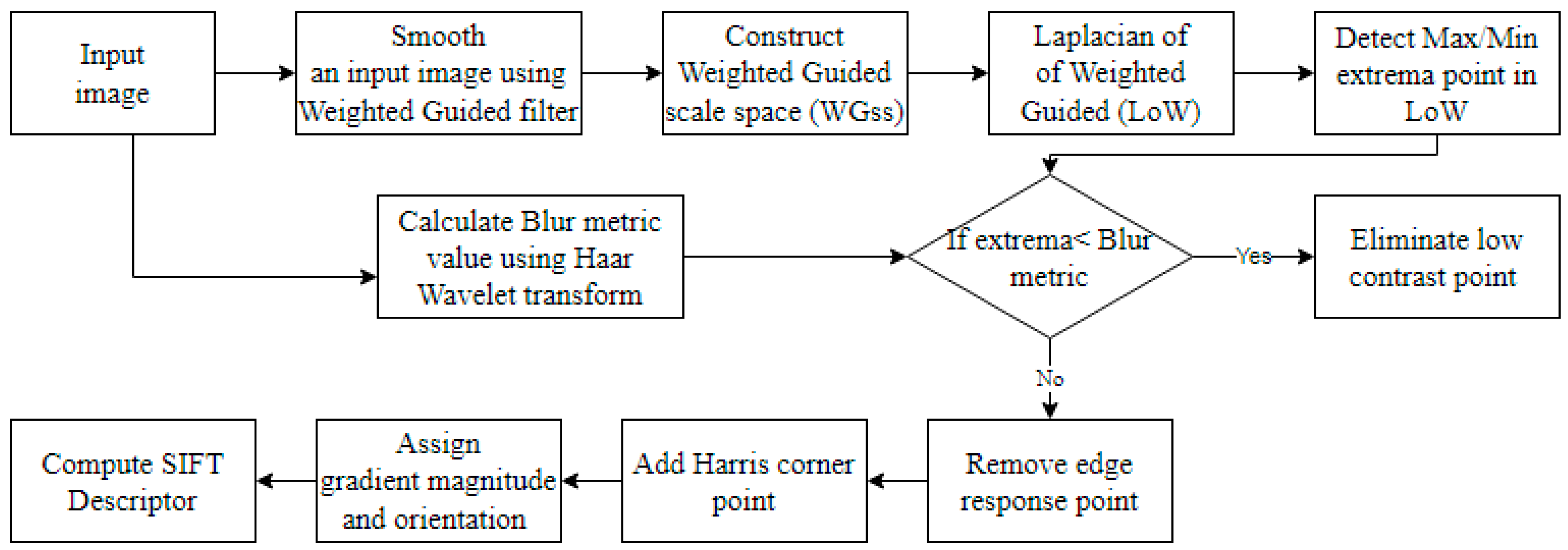
Feature Extraction Using Proposed WGHCFD Detector
- Stage 1: The Weighted Guided scale space construction (WGss)
- Stage 2: Feature point Localization
- Step 1: Perform level 3 decomposition of the input image using Haar wavelet transform.
- Step 2: Construct an edge map for each scale using Equation (6):
- Step 3: Partition the edge maps and find local maxima Emaxi (i = 1, 2, 3).
- Step 4: Calculate blur metric value.
- Stage 3: Feature point Magnitude and Orientation Assignment
- Stage 4: Generate Descriptor
4. Qualitative Analysis of the Proposed WGHCFD
4.1. Performance Measures
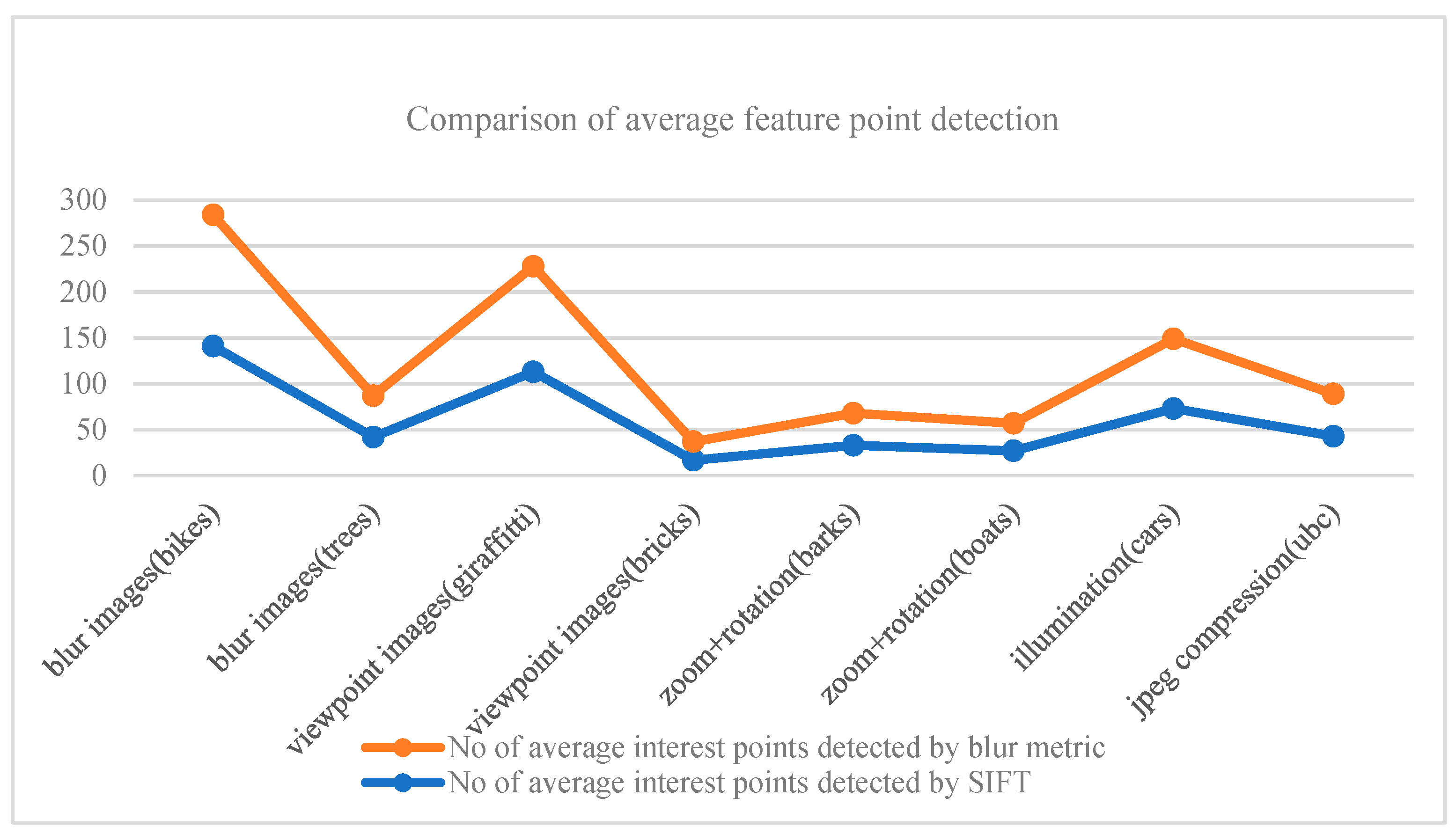
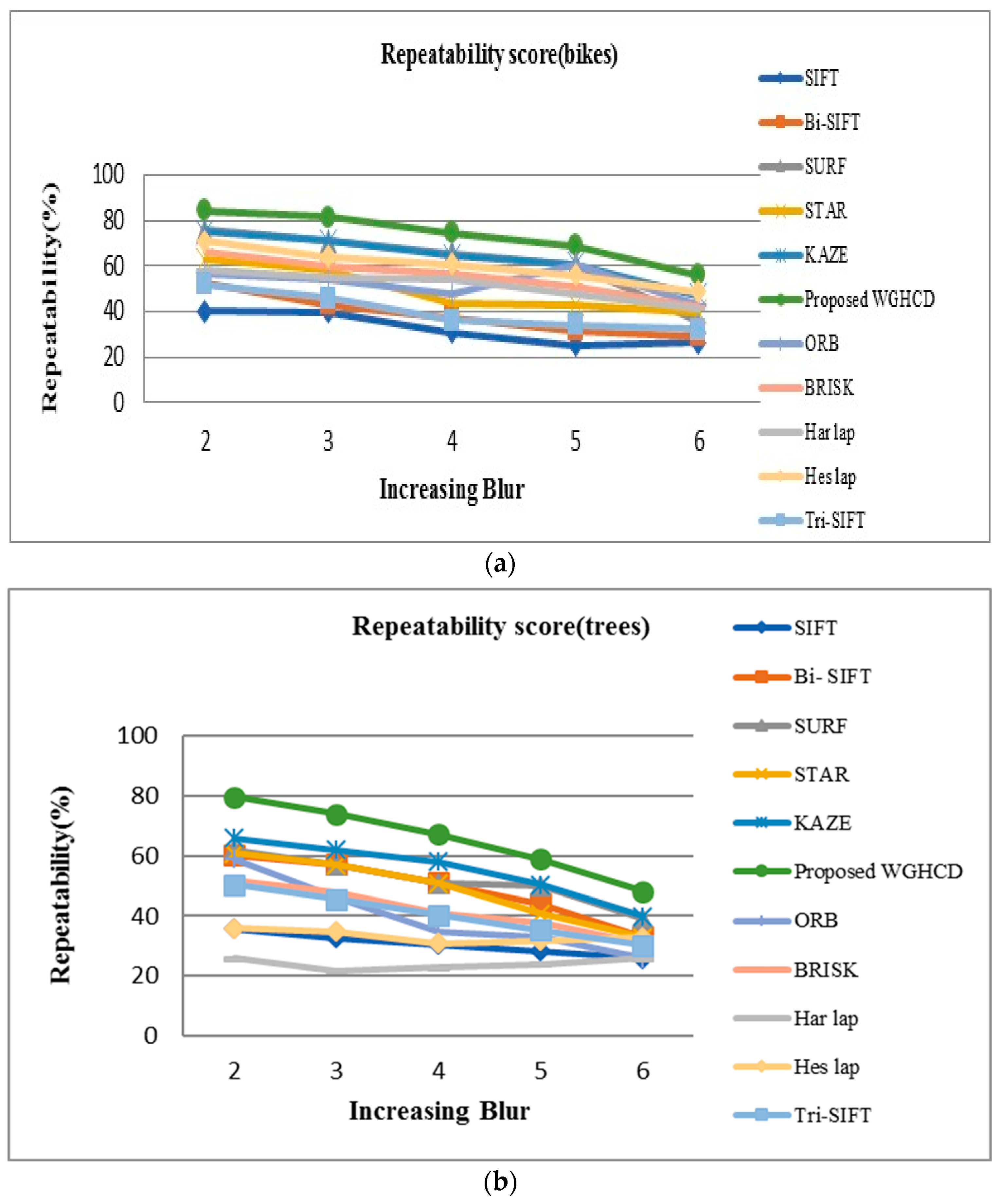
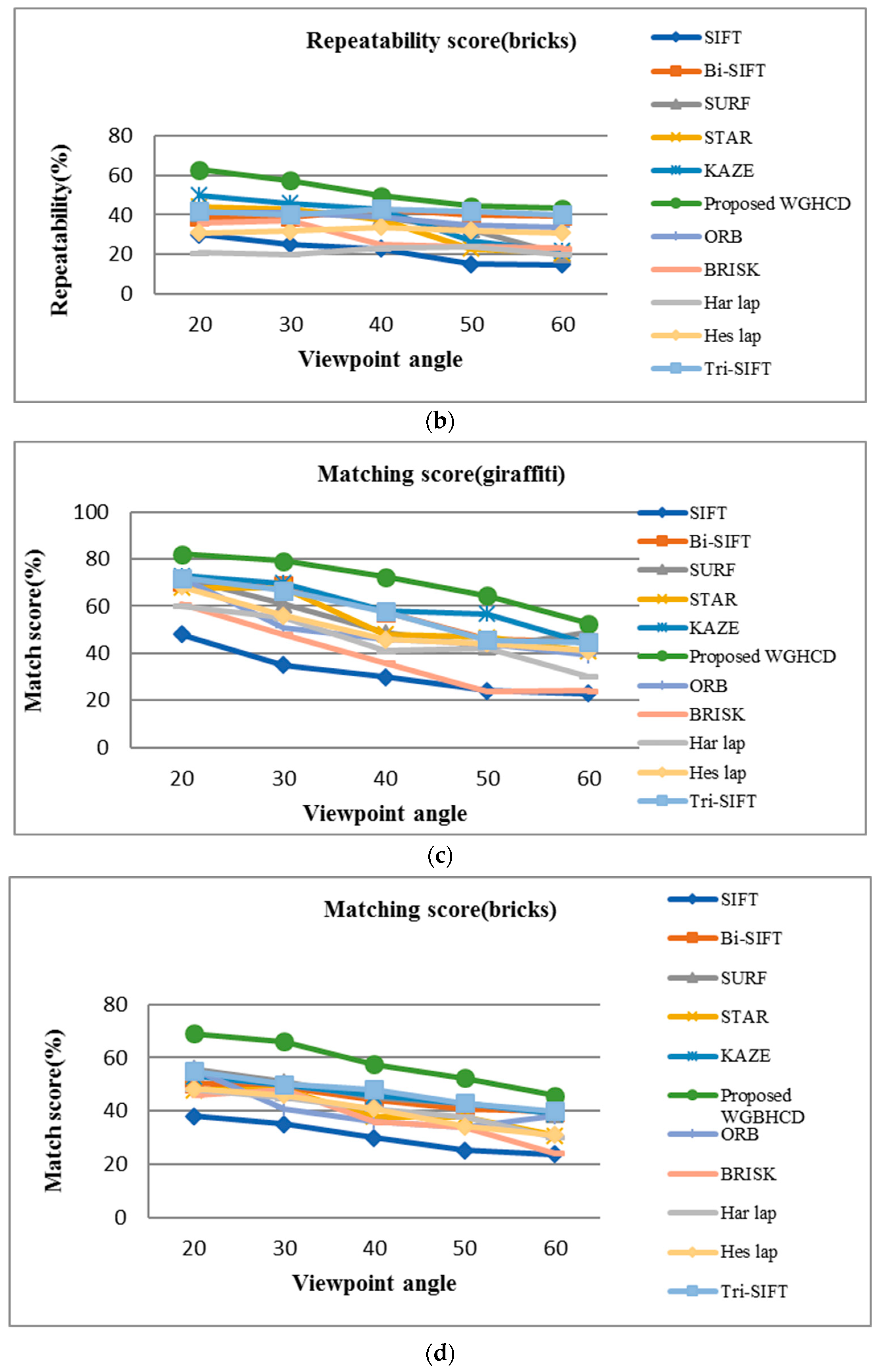
4.2. Experimental Result Analysis
4.2.1. Blur Change Images
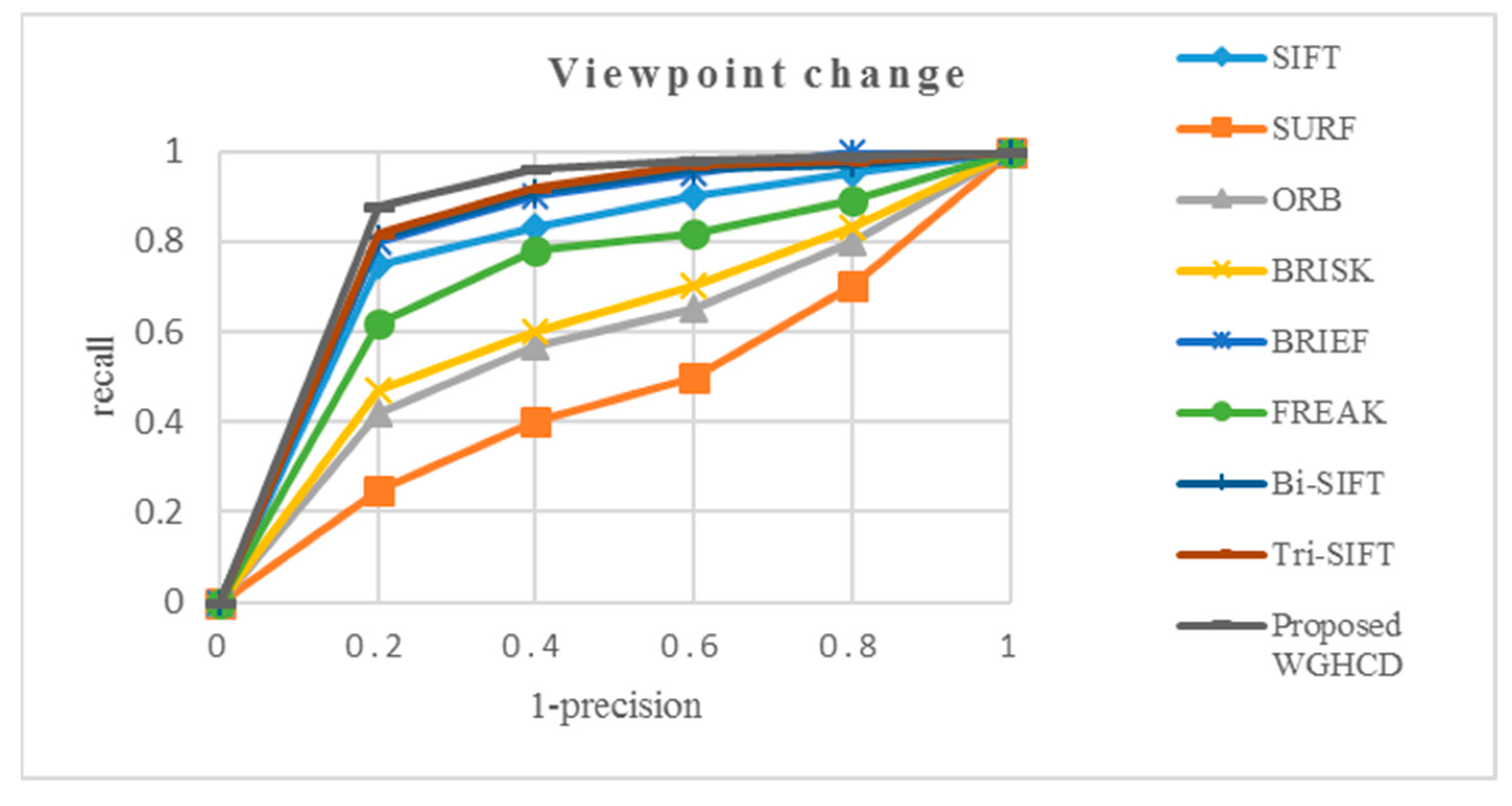
4.2.2. Viewpoint Change Images
4.2.3. Zoom+Rotation Change Images
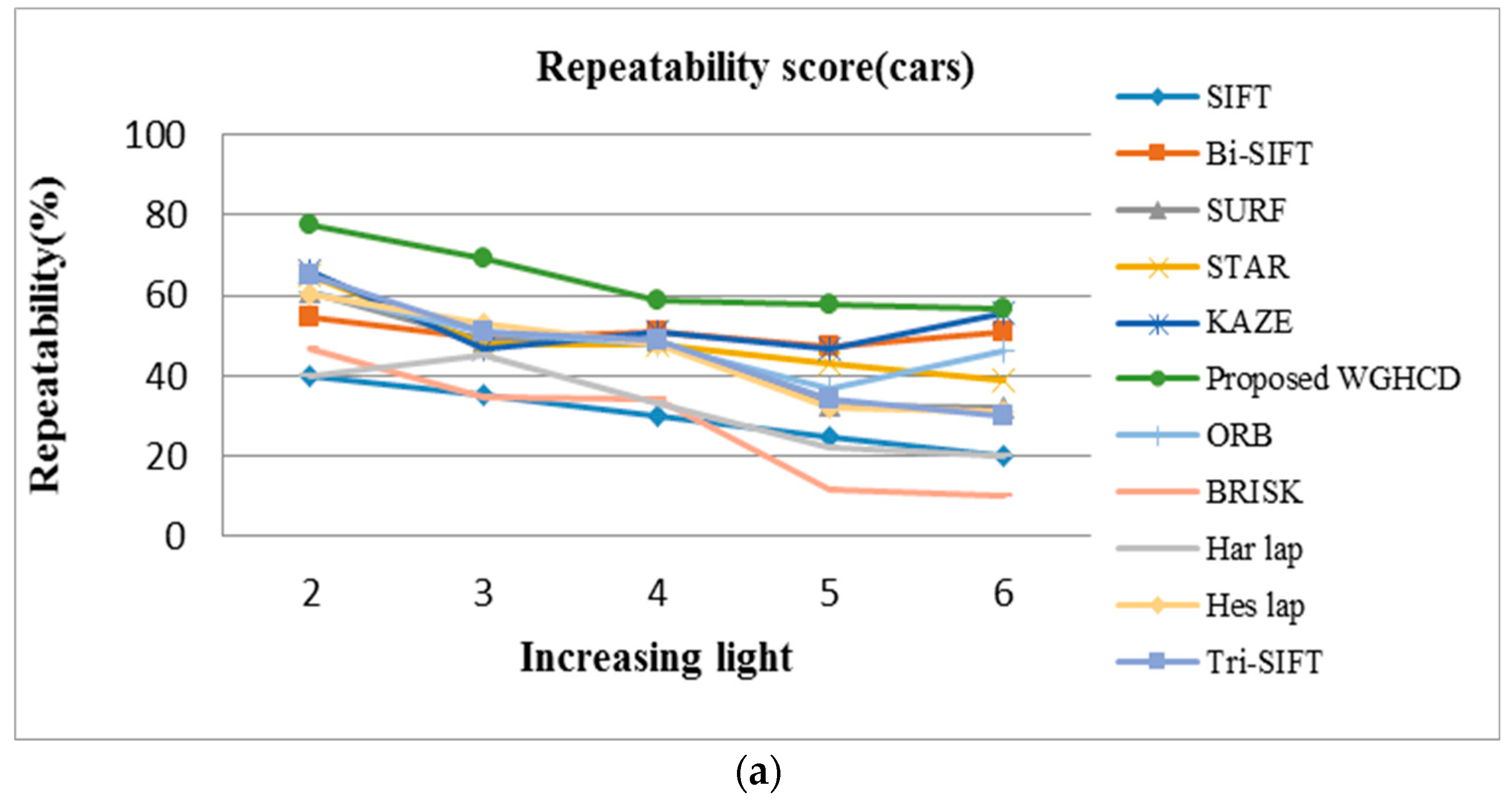
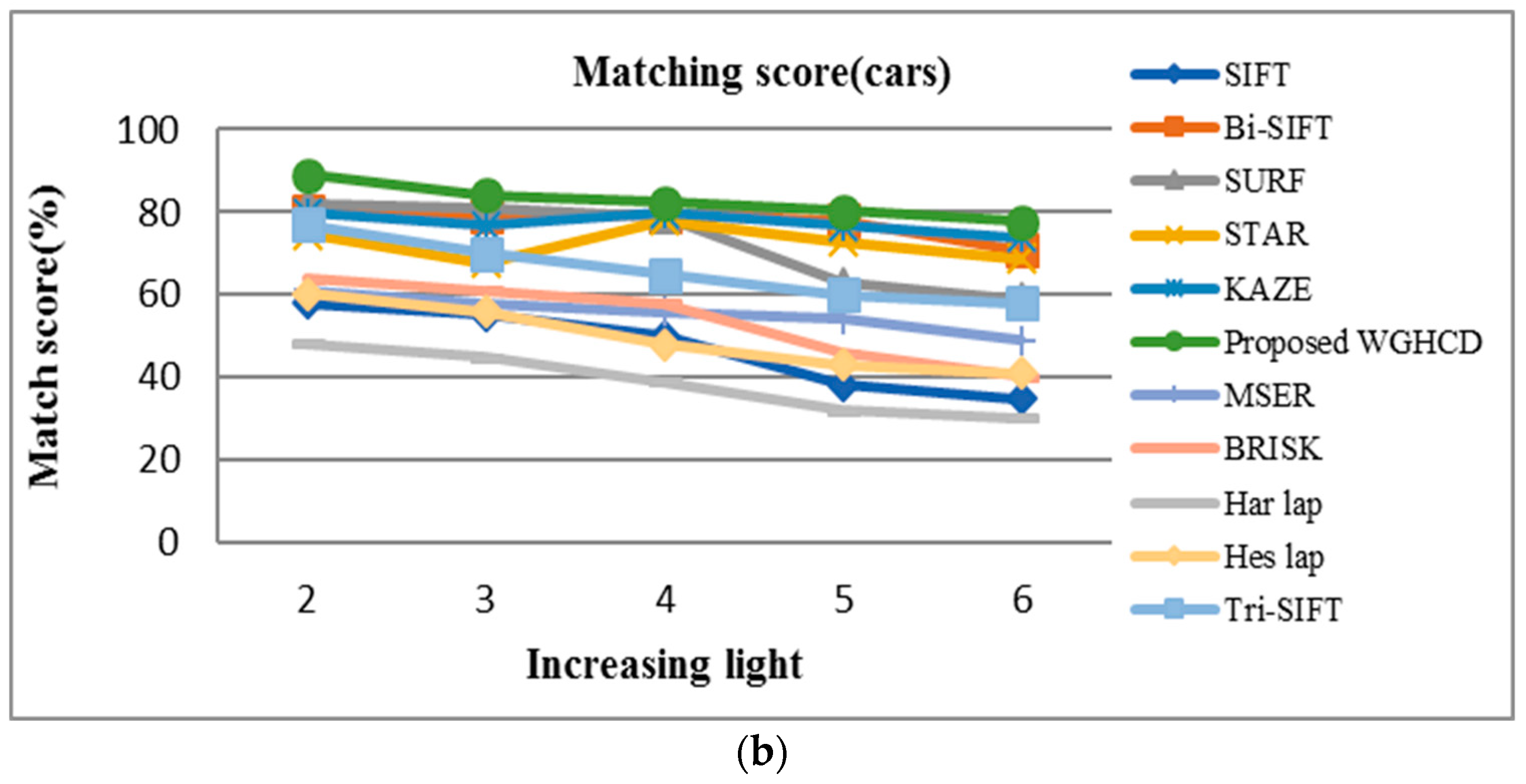
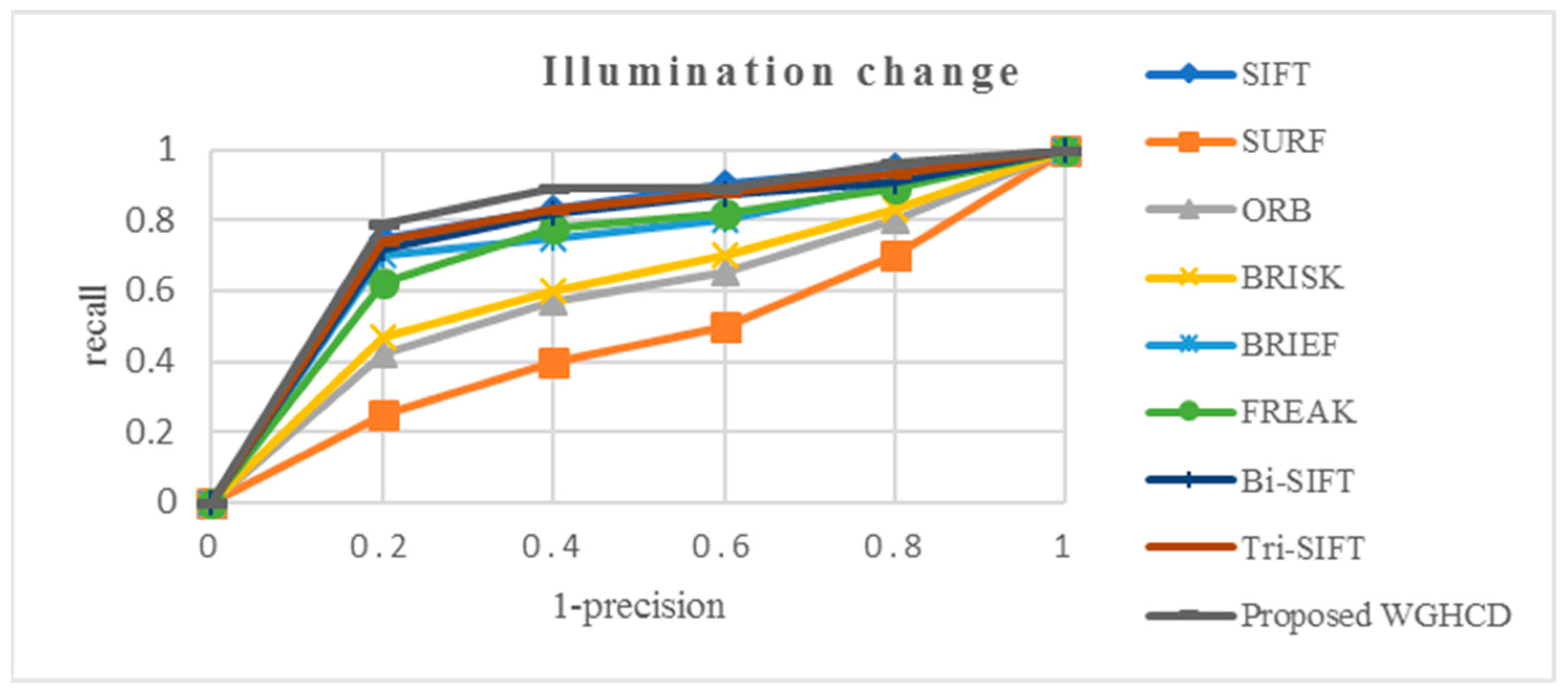
4.2.4. Illumination Change Images
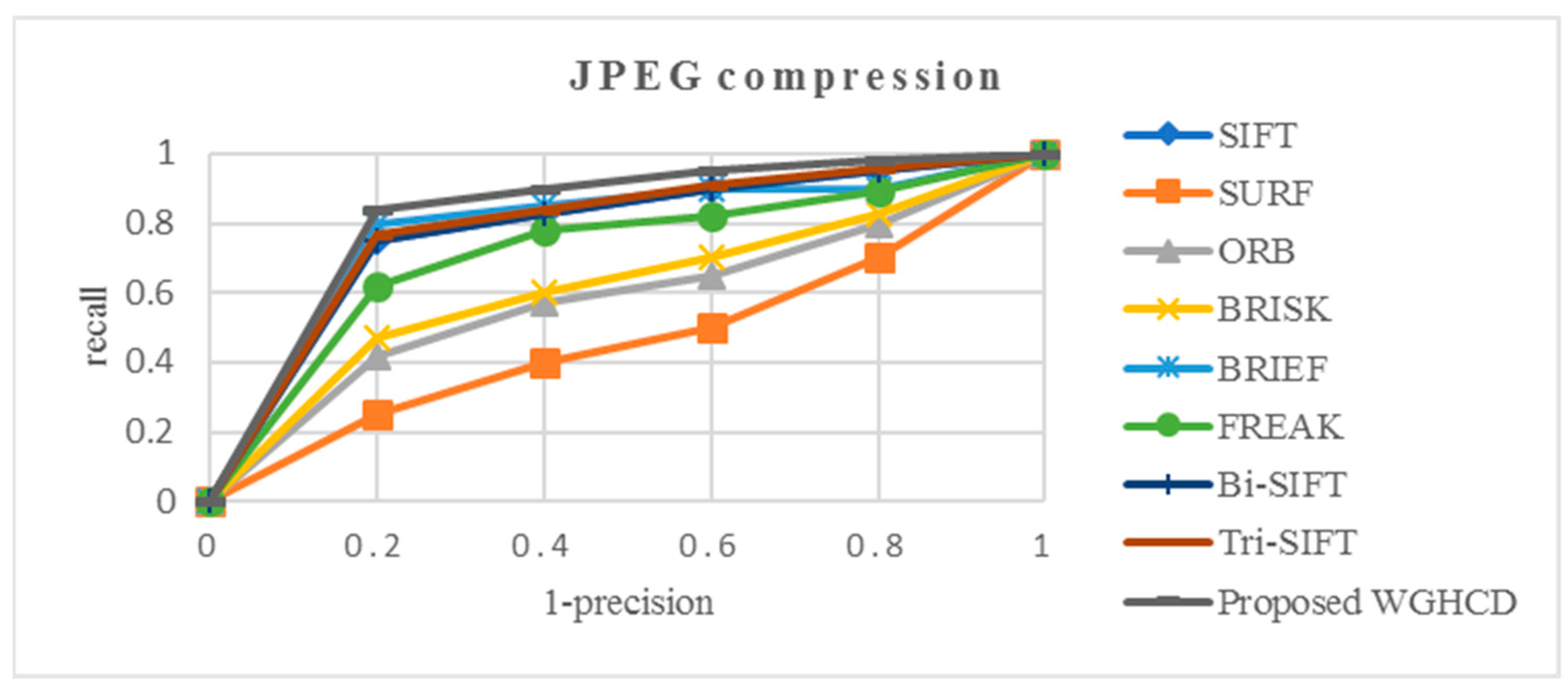
4.2.5. JPEG Compression Images
4.3. WGHCFD for Object Recognition Applications
5. Conclusions and Future Work
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Shanthi, K.G. Smart Vision using Machine learning for Blind. Int. J. Adv. Sci. Technol. 2020, 29, 12458–12463. [Google Scholar]
- Rahman, M.A.; Sadi, M.S. IoT Enabled Automated Object Recognition for the Visually Impaired. Comput. Methods Programs Biomed. Update 2021, 1, 100015. [Google Scholar] [CrossRef]
- Afif, M.; Ayachi, R.; Said, Y.; Pissaloux, E.; Atri, M. An Evaluation of RetinaNet on Indoor Object Detection for Blind and Visually Impaired Persons Assistance Navigation. Neural Process. Lett. 2020, 51, 2265–2279. [Google Scholar] [CrossRef]
- Lowe, D.G. Distinctive image features from scale-invariant interest points. Int. J. Comput. Vis. 2004, 60, 91–110. [Google Scholar] [CrossRef]
- Zhang, J.; Chen, G.; Jia, Z. An image stitching algorithm based on histogram matching and SIFT algorithm. Int. J. Pattern Recognit. Artif. Intell. 2017, 31, 1754006. [Google Scholar] [CrossRef] [Green Version]
- Arth, C.; Bischof, H. Real-time object recognition using local features on a DSP-based embedded system. J. Real-Time Image Process. 2008, 3, 233–253. [Google Scholar] [CrossRef]
- Zhou, H.; Yuan, Y.; Shi, C. Object tracking using SIFT features and mean shift. Comput. Vis. Image Underst. 2009, 113, 345–352. [Google Scholar] [CrossRef]
- Sirmacek, B.; Unsalan, C. Urban area and building detection using SIFT keypoints and graph theory. IEEE Trans. Geosci. Remote Sens. 2009, 47, 1156–1167. [Google Scholar] [CrossRef]
- Chang, L.; Duarte, M.M.; Sucar, L.E.; Morales, E.F. Object class recognition using SIFT and Bayesian networks. Adv. Soft Comput. 2010, 6438, 56–66. [Google Scholar]
- Soni, B.; Das, P.K.; Thounaojam, D.M. Keypoints based enhanced multiple copy-move forgeries detection system using density-based spatial clustering of application with noise clustering algorithm. IET Image Process. 2018, 12, 2092–2099. [Google Scholar] [CrossRef]
- Lodha, S.K.; Xiao, Y. GSIFT: Geometric scale invariant feature transform for terrain data. Int. Soc. Opt. Photonics 2006, 6066, 60660L. [Google Scholar]
- Ke, Y.; Sukthankar, R. PCA-SIFT: A more distinctive representation for local image descriptors. CVPR 2004, 4, 506–513. [Google Scholar]
- Abdel-Hakim, A.E.; Farag, A.A. CSIFT: A SIFT descriptor with color invariant characteristics. Comput. Vis. Pattern Recognit. 2006, 2, 1978–1983. [Google Scholar]
- Morel, J.M.; Yu, G. ASIFT: A new framework for fully affine invariant image comparison. SIAM J. Imaging Sci. 2009, 2, 438–469. [Google Scholar] [CrossRef]
- Mikolajczyk, K.; Schmid, C. A performance evaluation of local descriptors. IEEE Trans. Pattern Anal. Mach. Intell. 2005, 27, 1615–1630. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Rosten, E.; Drummond, T. Machine learning for high-speed corner detection. In Proceedings of the European Conference on Computer Vision (ECCV), Graz, Austria, 7–13 May 2006; pp. 430–443. [Google Scholar]
- Agrawal, M.; Konolige, K.; Blas, M.R. Censure: Center surround extremas for realtime feature detection and matching. In Proceedings of the European Conference on Computer Vision, Marseille, France, 12–18 October 2008; pp. 102–115. [Google Scholar]
- Bay, H.; Andreas, E.; Tuytelaars, T.; Van Gool, L. Speeded-Up Robust Features (SURF). Comput. Vis. Image Underst. 2008, 110, 346–359. [Google Scholar] [CrossRef]
- Alcantarilla, P.F.; Bartoli, A.; Davison, A.J. KAZE features. In Proceedings of the European Conference on Computer Vision, Florence, Italy, 7–13 October 2012; pp. 214–227. [Google Scholar]
- Leutenegger, S.; Chli, M.; Siegwart, R.Y. BRISK: Binary robust invariant scalable keypoints. In Proceedings of the IEEE International Conference on Computer Vision (ICCV 2011), Barcelona, Spain, 6–13 November 2011; pp. 2548–2555. [Google Scholar]
- Rublee, M.E.; Rabaud, V.; Konolige, K.; Bradski, G.R. ORB: An efficient alternative to SIFT or SURF. ICCV 2011, 11, 2. [Google Scholar]
- Huang, M.; Mu, Z.; Zeng, H.; Huang, H. A novel approach for interest point detection via Laplacian-of-bilateral filter. J. Sens. 2015, 2015, 685154. [Google Scholar] [CrossRef]
- Şekeroglu, K.; Soysal, O.M. Comparison of SIFT, Bi-SIFT, and Tri-SIFT and their frequency spectrum analysis. Mach. Vis. Appl. 2017, 28, 875–902. [Google Scholar] [CrossRef]
- Ghahremani, M.; Liu, Y.; Tiddeman, B. FFD: Fast Feature Detector. IEEE Trans. Image Process. 2021, 30, 1153–1168. [Google Scholar] [CrossRef]
- Calonder, M.; Lepetit, V.; Strecha, C.; Fua, P. BRIEF: Binary robust independent elementary features. In Proceedings of the European Conference on Computer Vision, Heraklion, Crete, Greece, 5–11 September 2010. [Google Scholar]
- Alahi, A.; Ortiz, R.; Vandergheynst, P. Freak: Fast retina keypoint. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition 2012, Providence, RI, USA, 16–21 June 2012; pp. 510–517. [Google Scholar]
- Simo-Serra, E.; Torras, C.; Moreno-Noguer, F. DaLI: Deformation and Light Invariant Descriptor. Int. J. Comput. Vis. 2015, 115, 115–136. [Google Scholar] [CrossRef]
- Weng, D.W.; Wang, Y.H.; Gong, M.M.; Tao, D.C.; Wei, H.; Huang, D. DERF: Distinctive efficient robust features from the biological modeling of the P ganglion cells. IEEE Trans. Image Process. 2015, 24, 2287–2302. [Google Scholar] [CrossRef] [PubMed]
- Kim, W.; Han, J. Directional coherence-based spatiotemporal descriptor for object detection in static and dynamic scenes. Mach. Vis. Appl. 2017, 28, 49–59. [Google Scholar] [CrossRef]
- Sadeghi, B.; Jamshidi, K.; Vafaei, A.; Monadjemi, S.A. A local image descriptor based on radial and angular gradient intensity histogram for blurred image matching. Vis. Comput. 2019, 35, 1373–1391. [Google Scholar] [CrossRef]
- Yu, Q.; Zhou, S.; Jiang, Y.; Wu, P.; Xu, Y. High-Performance SAR Image Matching Using Improved SIFT Framework Based on Rolling Guidance Filter and ROEWA-Powered Feature. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2019, 12, 920–933. [Google Scholar] [CrossRef]
- DeTone, D.; Malisiewicz, T.; Rabinovich, A. Superpoint: Selfsupervised interest point detection and description. In Proceedings of the 2018 IEEE/CVF Conference on Computer Vision and Pattern Recognition Workshops (CVPRW), Salt Lake City, UT, USA, 18–22 June 2018; pp. 224–236. [Google Scholar]
- Jingade, R.R.; Kunte, R.S. DOG-ADTCP: A new feature descriptor for protection of face identification system. Expert Syst. Appl. 2022, 201, 117207. [Google Scholar] [CrossRef]
- Yang, W.; Xu, C.; Mei, L.; Yao, Y.; Liu, C. LPSO: Multi-Source Image Matching Considering the Description of Local Phase Sharpness Orientation 2022. IEEE Photonics J. 2022, 14, 7811109. [Google Scholar] [CrossRef]
- Dusmanu, M. D2-net: A trainable CNN for joint description and detection of local features. In Proceedings of the 2019 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Long Beach, CA, USA, 15–20 June 2019; pp. 8092–8101. [Google Scholar]
- Li, Z.; Zheng, J.; Zhu, Z.; Yao, W.; Wu, S. Weighted guided image filtering. IEEE Trans. Image Process. 2015, 24, 120–129. [Google Scholar]
- He, K.; Sun, J.; Tang, X. Guided image filtering. IEEE Trans. Pattern Anal. Mach. Intell. 2013, 35, 1397–1409. [Google Scholar] [CrossRef]
- Tong, H.; Li, M.; Zhang, H.; Zhang, C. Blur detection for digital images using wavelet transform. In Proceedings of the IEEE International Conference on Multimedia and Expo (ICME 2004), Taipei, Taiwan, 27–30 June 2004; pp. 17–20. [Google Scholar]
- Harris, C.; Stephens, M. A combined corner and edge detection. In Proceedings of the fourth alvey vision conference (UK, 1988), Manchester, UK, 31 August–2 September 1988; pp. 147–151. [Google Scholar]
- Mikolajczyk, K. Oxford Data Set. Available online: http://www.robots.ox.ac.uk/~vgg/research/affine (accessed on 24 May 2022).
- Schmid, C.; Mohr, R.; Bauckhage, C. Evaluation of interest point detectors. Int. J. Comput. Vis. 2000, 37, 151–172. [Google Scholar] [CrossRef] [Green Version]










| Detectors | Feature Detector Type | Scale-Invariant | Rotation Invariant |
|---|---|---|---|
| Harris–Laplace (2004) | Corner + Partial blob | Yes | Yes |
| Hessian–Laplace (2004) | Partial corner + Blob | Yes | Yes |
| SIFT (2004) | Partial corner + Blob | Yes | Yes |
| FAST (2006) | Corner | No | Yes |
| STAR (2008) | Blob | Yes | Yes |
| ORB (2011) | Corner | Yes | Yes |
| BRISK (2011) | Corner | Yes | Yes |
| Bi-SIFT (2015) | Blob | Yes | Yes |
| Tri-SIFT (2017) | Blob | Yes | Yes |
| FFD (2021) | Blob | Yes | No |
| Methods | Scale-Space | Orientation | Descriptor Generation | Feature Size | Robustness |
|---|---|---|---|---|---|
| SIFT (2004) | DoG | Local gradient histogram | Local gradient histogram | 128 | Brightness, contrast, rotation, scale, affine transforms, noise |
| GLOH (2005) | No | No | Log-polar location grid in radial direction | 128 | Brightness, contrast, rotation, scale, affine transforms, noise |
| SURF (2006) | Box filter | Haar wavelet responses | Haar wavelet responses | 64 | Scale, rotation, illumination, noise |
| BRIEF (2010) | No | No | Intensity comparison of pixel pairs in the random sampling pattern using a Gaussian distribution | 256 | Brightness, contrast |
| ORB (2011) | Gaussian image pyramid | Intensity calculation | centroid Oriented BRIEF descriptor | 256 | Brightness, contrast, rotation, limited scale |
| BRISK (2011) | Gaussian image pyramid | Average of the local gradient | Intensity comparison of pixels in concentric circles pattern | 512 | Brightness, contrast, rotation, scale |
| FREAK (2012) | No | Average of the local gradient | Intensity comparison of pixels in the retina sampling pattern | 256 | Brightness, contrast, rotation, scale, viewpoint |
| DaLI (2015) | No | No | Heat Kernel Signature | 128 | Non-rigid deformations and photometric changes |
| Bi-SIFT (2015) | LoB | Local gradient histogram | Local gradient histogram | 128 | Brightness, contrast, rotation, scale, affine transforms, noise |
| DERF (2015) | Convolve gradient maps of grid points using DoG | DoG convoluted gradient orientation maps | Sampling the gradient orientation maps | 536 | Scale and rotation |
| HiSTDO (2016) | No | The dominant orientation and coherence based on the space-time local gradient field | Normalized gradient-based histogram | Depend on image/video | Background clutter, brightness change and camera noise. |
| Tri-SIFT (2017) | DoT | Local gradient histogram | Local gradient histogram | 128 | Brightness, contrast, rotation, scale, affine transforms, noise |
| RAGIH (2018) | No | No | Radial and angular gradient intensity histogram | 120 | Robustness to rotation and scale changes in a blurred image |
| ROEWA (2019) | Nonlinear multiscale space | Gradient histogram | GLOH descriptor | 128 | Speckle noise and complex deformation |
| DOG–ADTCP (2022) | Modified DOG and Angle Directional Ternary Co-relation pattern (ADTCP) | Local gradient histogram | Local gradient histogram | 128 | Illumination and rotation |
| LPSO (2022) | Gaussian spatial maximum moment map | Phase orientation feature calculation | Histogram of phase sharpness orientation features | 200 | Illumination and rotation |
| Method | Number of Recognized Images | Recognition Rate (%) |
|---|---|---|
| SIFT | 838/1010 | 83 |
| Bi-SIFT | 959/1010 | 95 |
| SURF | 929/1010 | 92 |
| Tri-SFT | 969/1010 | 96 |
| ORB | 776/1010 | 76.9 |
| BRISK | 888/1010 | 88 |
| BRIEF | 898/1010 | 89 |
| FREAK | 929/1010 | 92 |
| DOG–ADTCP | 959/1010 | 95 |
| Proposed WGHCFD | 1007/1010 | 99.8 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rajendran, M.; Stephan, P.; Stephan, T.; Agarwal, S.; Kim, H. Cognitive IoT Vision System Using Weighted Guided Harris Corner Feature Detector for Visually Impaired People. Sustainability 2022, 14, 9063. https://doi.org/10.3390/su14159063
Rajendran M, Stephan P, Stephan T, Agarwal S, Kim H. Cognitive IoT Vision System Using Weighted Guided Harris Corner Feature Detector for Visually Impaired People. Sustainability. 2022; 14(15):9063. https://doi.org/10.3390/su14159063
Chicago/Turabian StyleRajendran, Manoranjitham, Punitha Stephan, Thompson Stephan, Saurabh Agarwal, and Hyunsung Kim. 2022. "Cognitive IoT Vision System Using Weighted Guided Harris Corner Feature Detector for Visually Impaired People" Sustainability 14, no. 15: 9063. https://doi.org/10.3390/su14159063
APA StyleRajendran, M., Stephan, P., Stephan, T., Agarwal, S., & Kim, H. (2022). Cognitive IoT Vision System Using Weighted Guided Harris Corner Feature Detector for Visually Impaired People. Sustainability, 14(15), 9063. https://doi.org/10.3390/su14159063








