Development and Evaluation of a Prototype Self-Propelled Crop Sprayer for Agricultural Sustainability in Small Farms
Abstract
:1. Introduction
2. Materials and Methods
2.1. Development of Sprayer
2.1.1. Power Sizing
2.1.2. Sizing of Hydraulic System for Spray Boom Movement
Hydraulic Pump Force Calculations
Hydraulic Cylinder Calculations
2.1.3. Turning Radius Calculation
2.1.4. Spray Pump Calculations
2.2. Laboratory Evaluation
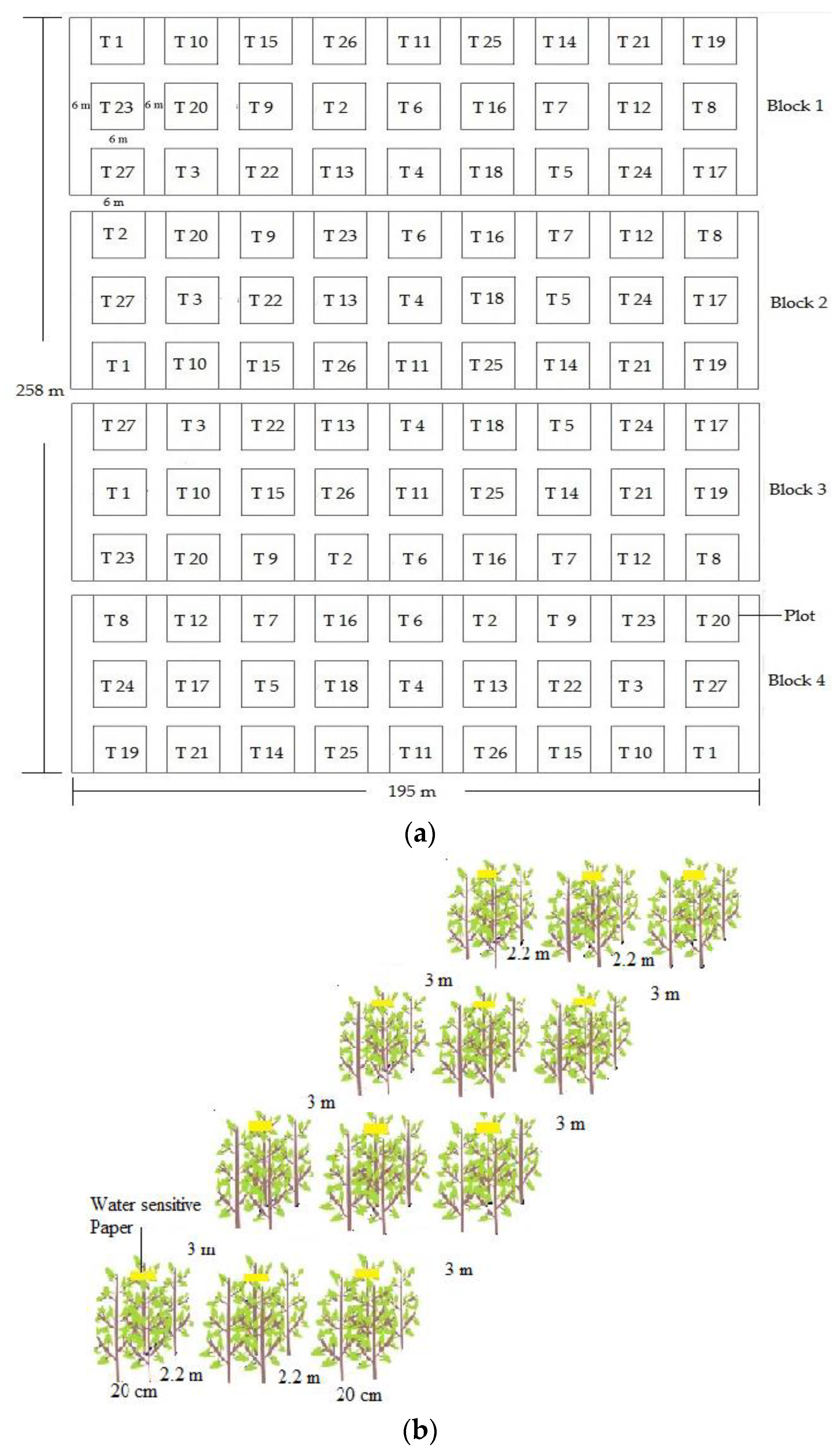
Experimental Design
2.3. Field Evaluation
2.3.1. Experimental Site
2.3.2. Experimental Design
2.3.3. Data Analysis
2.4. Field Efficiency
2.5. Economic Analysis
3. Results and Discussion
3.1. Laboratory Evaluation
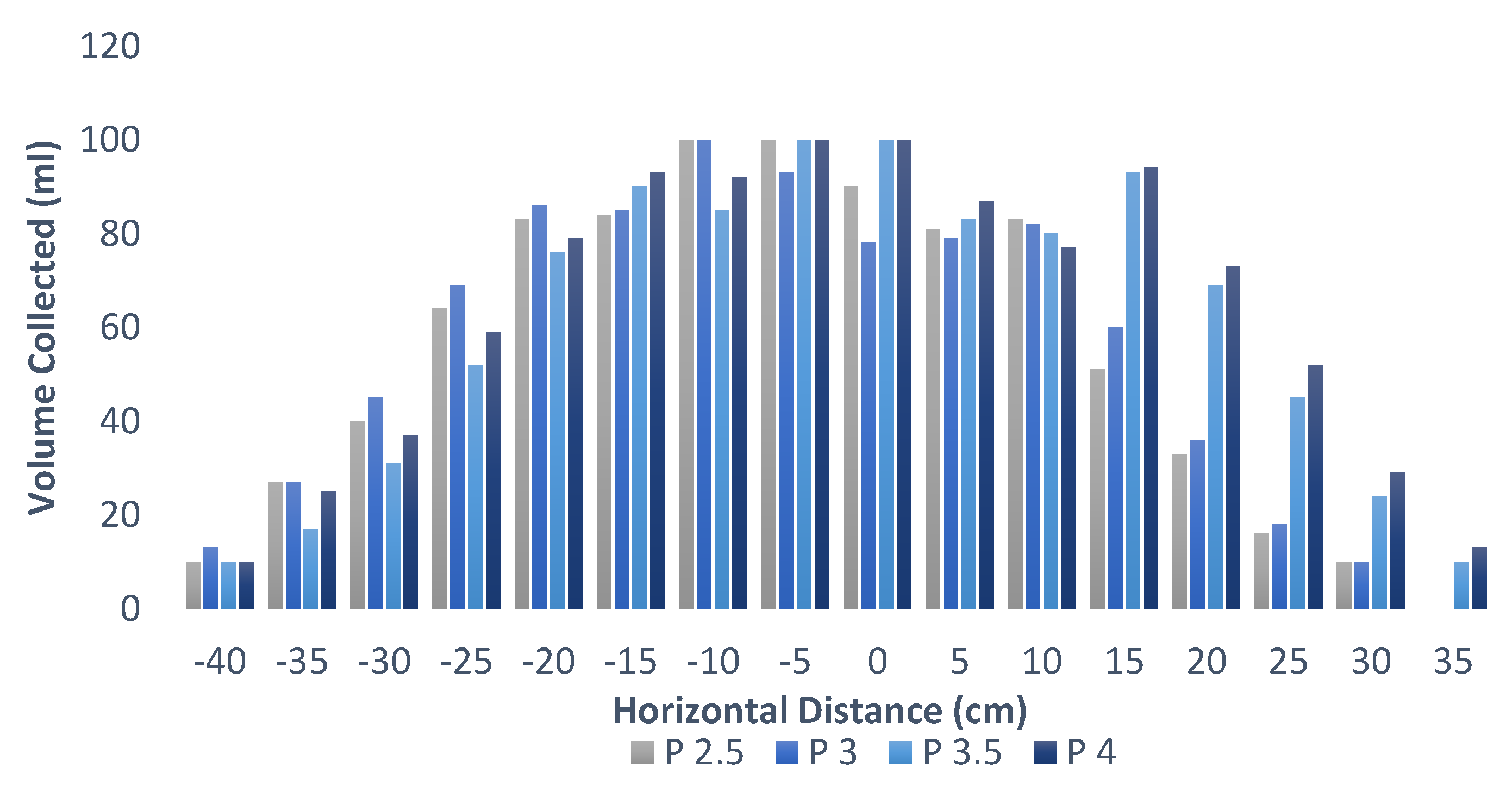
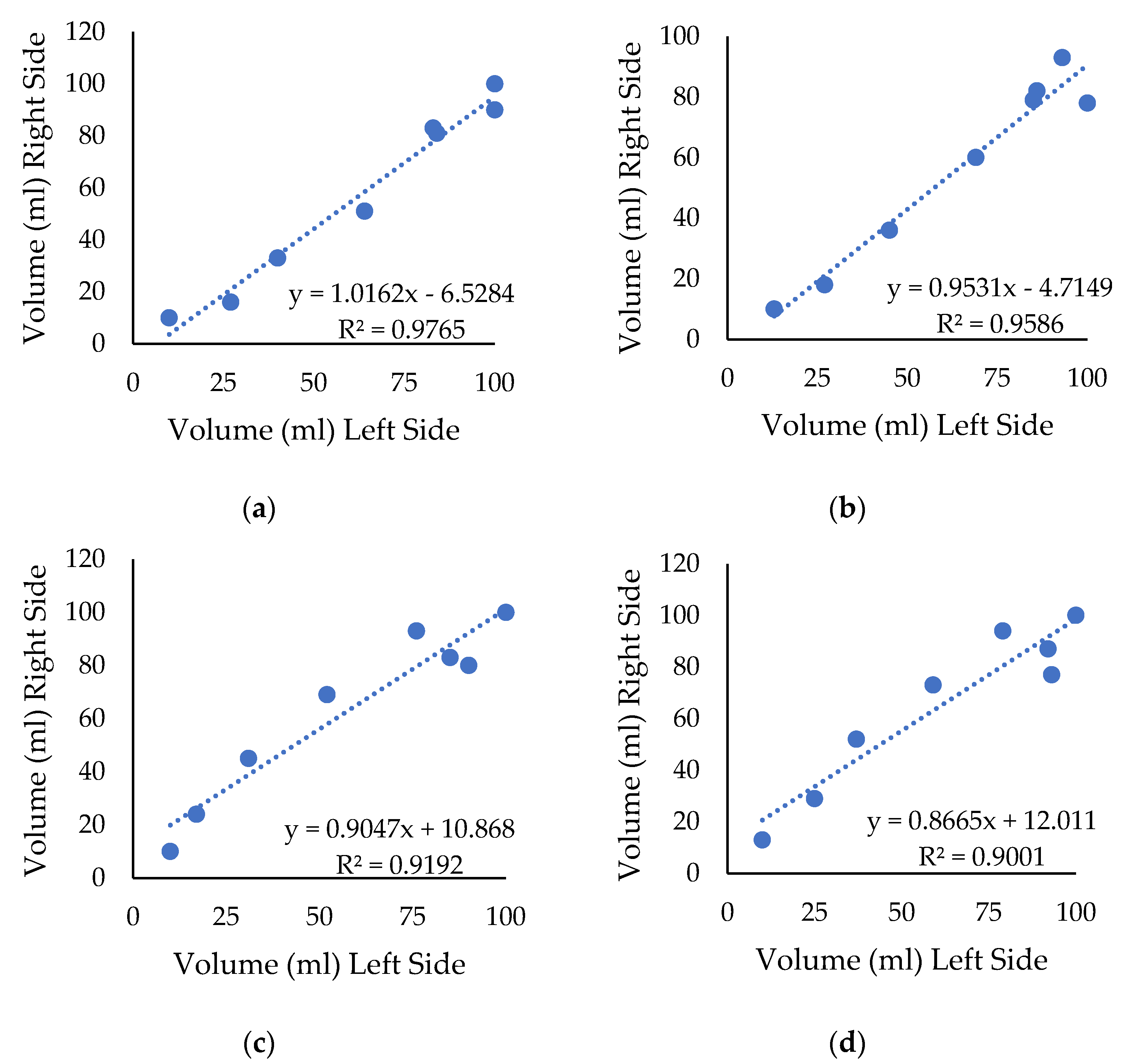
Effect of Pressure on Spray Symmetry of Nozzle
3.2. Field Evaluation
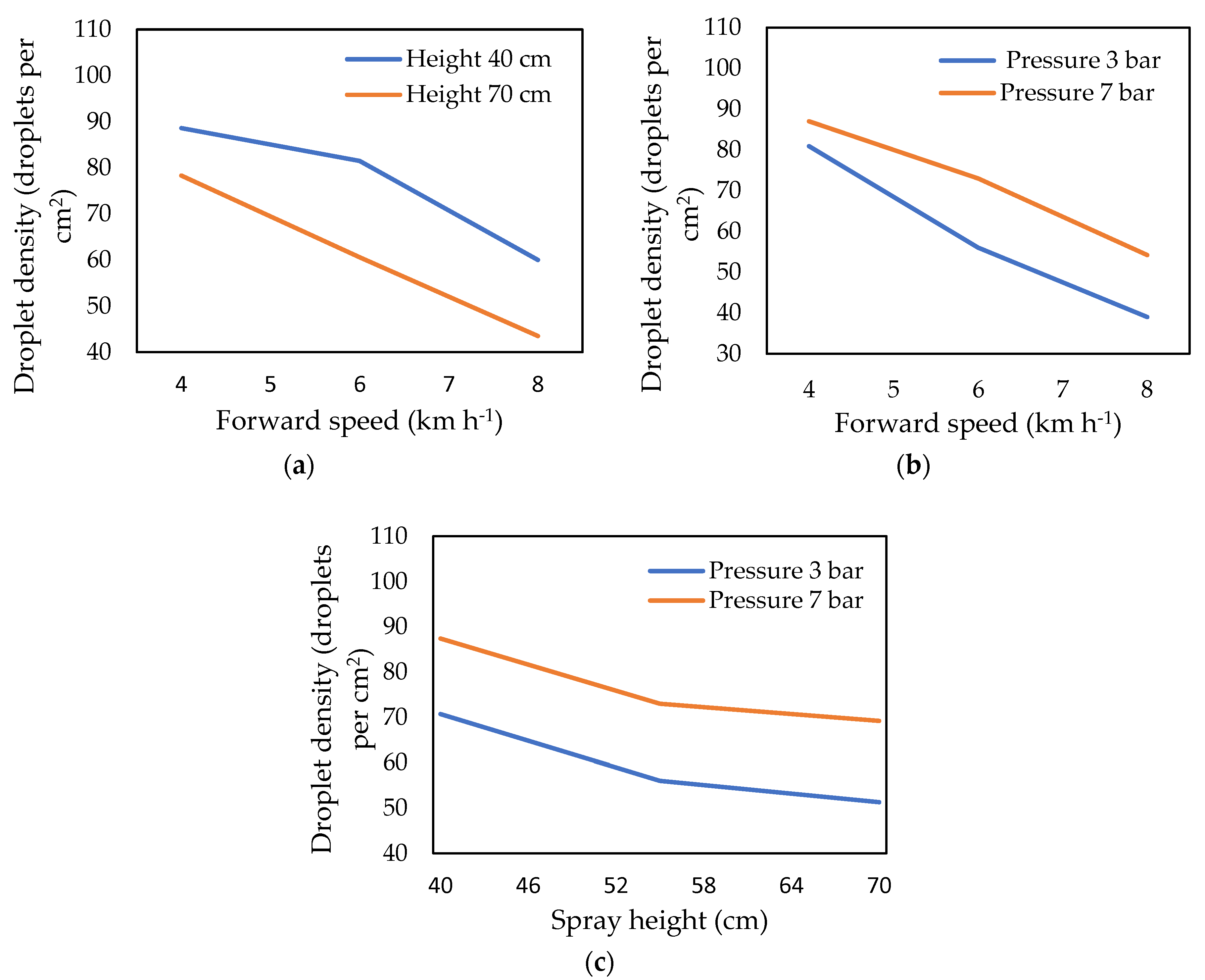
3.2.1. Effect of Spray Treatments on Droplet Density of Sprayer
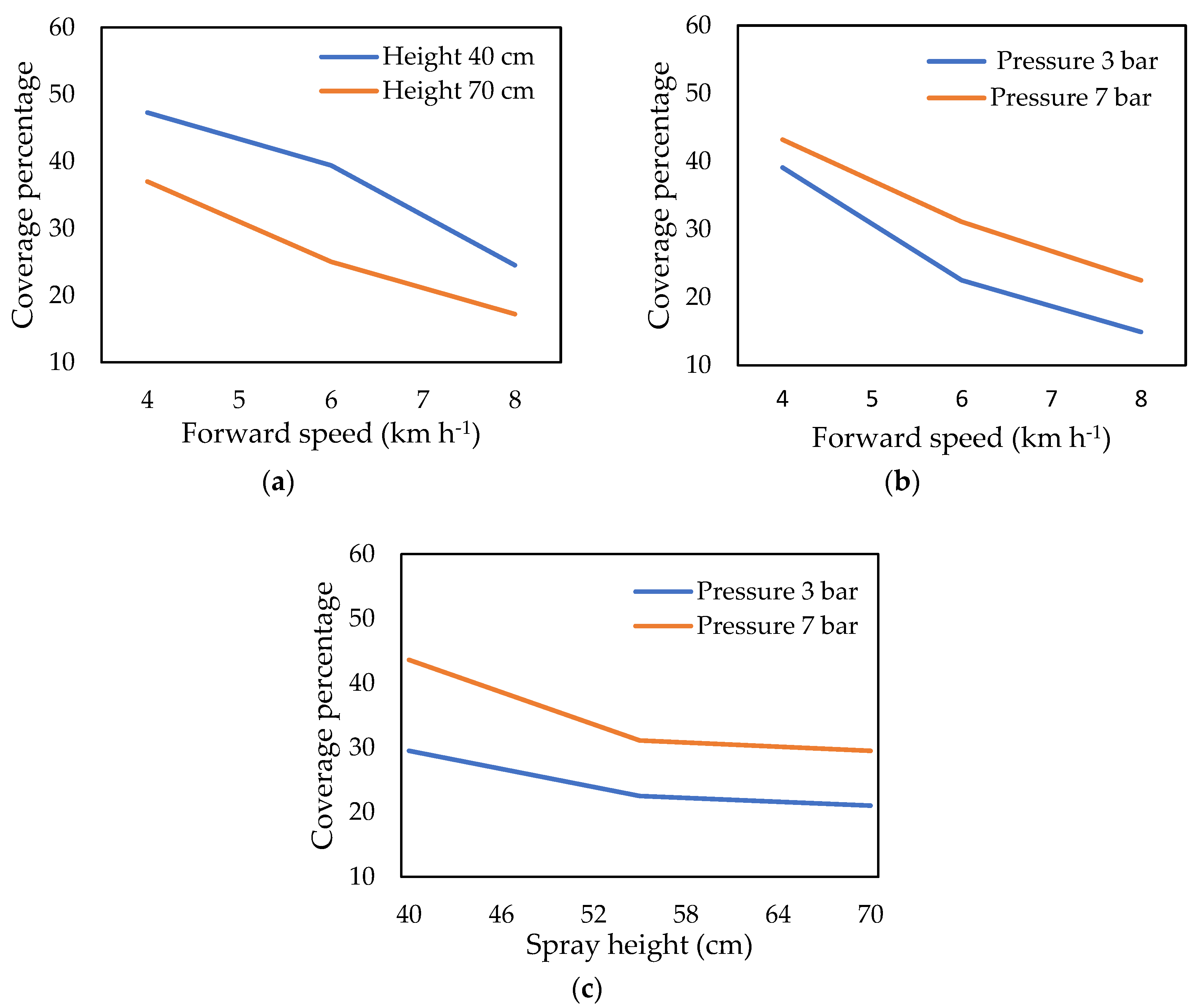
3.2.2. Effect of Spray Treatments on Coverage Percentage of Sprayer
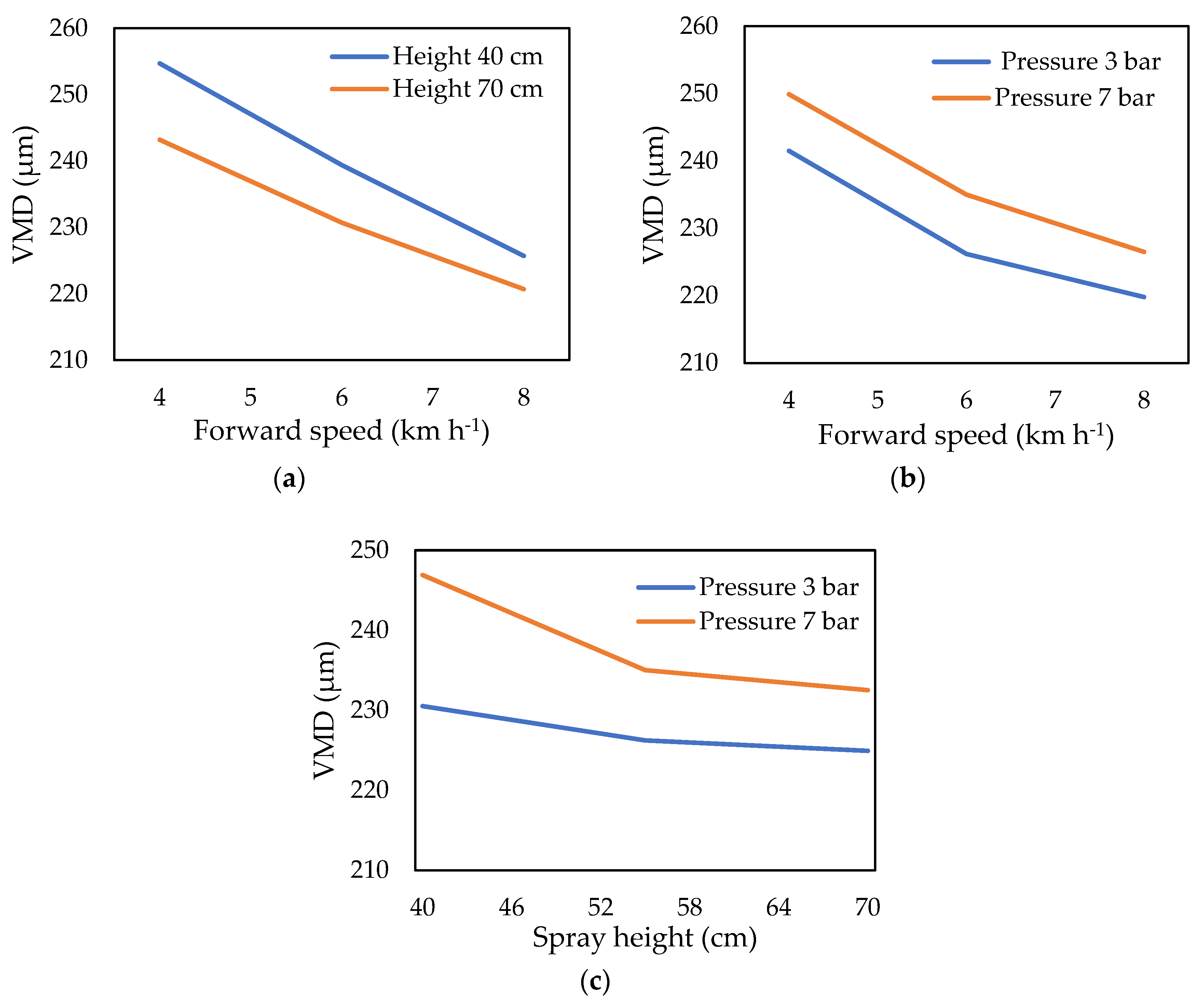
3.2.3. Effect of Spray Treatments on VMD of Sprayer
3.3. Optimization of Spraying Parameters
3.4. Field Efficiency
3.5. Economic Analysis
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Fan, S.; Chan-Kang, C. Is small beautiful? Farm size, productivity, and poverty in Asian agriculture. Agric. Econ. 2005, 32, 135–146. [Google Scholar] [CrossRef] [Green Version]
- Zaidi, S. Issues in Pakistan’s Economy: A Political Economy Perspective, 3rd ed.; Oxford University Press: Oxford, UK, 2015. [Google Scholar]
- Phambra, A.M.; Tahir, S.; Imran, M. Small farms and the current structure of farmland holding in Pakistan. Pak. J. Econ. Stud. 2020, 3, 47–64. [Google Scholar]
- Chauhan, N.S.; Mohapatra, P.K.J.; Pandey, K.P. Improving energy productivity in paddy production through benchmarking—An application of data envelopment analysis. Energy Conv. Manag. 2006, 47, 1063–1085. [Google Scholar] [CrossRef]
- Singh, G. Estimation of a mechanization index and its impact on production and economic factors—A case study in India. Biosyst. Eng. 2006, 93, 99–106. [Google Scholar] [CrossRef]
- Bourguet, D.; Guillemand, T. The hidden and external costs of pesticide use. Sustain. Agric. Rev. 2016, 19, 35–120. [Google Scholar]
- Yadav, I.C.; Devi, N.L.; Syed, J.H.; Cheng, Z.; Li, J.; Zhang, G.; Jones, K.C. Current status of persistent organic pesticide residues in air, water, and soil, and their possible effect on neighboring countries: A comprehensive review of India. Sci. Total Environ. 2015, 511, 123–137. [Google Scholar] [CrossRef]
- Rincon, V.J.; Sánchez-Hermosilla, J.; Páez, F.; Pérez-Alonso, J.; Callejón, A.J. Assessment of the influence of working pressure and application rate on pesticide spray application with a hand-held spray gun on greenhouse pepper crops. Crop Prot. 2017, 96, 7–13. [Google Scholar] [CrossRef]
- Braekman, P.; Foque, D.; Messens, W.; Van Labeke, M.C.; Pieters, J.G.; Nuyttens, D. Effect of spray application technique on spray deposition in greenhouse strawberries and tomatoes. Pest Manag. Sci. 2010, 66, 203–212. [Google Scholar] [CrossRef] [PubMed]
- Pergher, G.; Gubiani, R.; Tonetto, G. Foliar deposition and pesticide losses from three air-assisted sprayers in a hedgerow vineyard. Crop Prot. 1997, 16, 25–33. [Google Scholar] [CrossRef]
- Cunningham, G.P.; Harden, J. Reducing spray volumes applied to mature citrus trees. Crop Prot. 1998, 17, 289–292. [Google Scholar] [CrossRef]
- Farooq, M.; Salyani, M. Spray penetration into the citrus tree canopy from two air-carrier sprayers. Trans. ASABE 2002, 45, 1287–1293. [Google Scholar] [CrossRef]
- Salyani, M.; Sweeb, R.D.; Farooq, M. Comparison of string and ribbon samplers in orchard spray applications. Trans. ASABE 2006, 49, 1705–1710. [Google Scholar] [CrossRef]
- Braekman, P.; Foque, D.; Van Labeke, M.C.; Pieters, J.G.; Nuyttens, D. Influence of spray application technique on spray deposition in Greenhouse Ivy pot plants grown on hanging shelves. HortScience 2009, 44, 1921–1927. [Google Scholar] [CrossRef] [Green Version]
- Nuyttens, D.; Windey, S.; Sonck, B. Optimization of a vertical spray boom for greenhouse spray applications. Biosyst. Eng. 2004, 89, 417–423. [Google Scholar] [CrossRef]
- Nuyttens, D.; Windey, S.; Sonck, B. Comparison of operator exposure for five different greenhouse spraying applications. J. Agric. Saf. Health 2004, 10, 187–195. [Google Scholar] [CrossRef] [PubMed]
- Nuyttens, D.; Braekman, P.; Windey, S.; Sonck, B. Potential dermal pesticide exposure affected by greenhouse spray application technique. Pest Manag. Sci. 2009, 65, 781–790. [Google Scholar] [CrossRef]
- Chen, Y.; Mao, E.; Li, W.; Zhang, S.; Song, Z.; Yang, S.; Chen, J. Design and experiment of a high-clearance self-propelled sprayer chassis. Int. J. Agric. Biol. Eng. 2020, 13, 71–80. [Google Scholar] [CrossRef]
- Qiu, W.; Li, X.L.; Li, C.C.; Ding, W.M.; Lv, X.L.; Liu, Y.D. Design and test of a novel crawler-type multi-channel air-assisted orchard sprayer. Int. J. Agric. Biol. Eng. 2020, 13, 60–67. [Google Scholar] [CrossRef]
- Ma, C.; Li, G.; Peng, Q. Design and Test of a Jet Remote Control Spraying Machine for Orchards. AgriEngineering 2021, 3, 797–814. [Google Scholar] [CrossRef]
- Cai, J.C.; Wang, X.; Gao, Y.Y.; Yang, S.; Zhao, C.J. Design and performance evaluation of a variable-rate orchard sprayer based on a laser-scanning sensor. Int. J. Agric. Biol. Eng. 2019, 12, 51–57. [Google Scholar] [CrossRef]
- Penido, E.C.C.; Teixeira, M.M.; Fernandes, H.C.; Monteiro, P.B.; Cecon, P.R. Development, and evaluation of a remotely controlled and monitored self-propelled sprayer in tomato crops. Rev. Cienc. Agron. 2019, 50, 8–17. [Google Scholar] [CrossRef]
- Teejet®. A User’s Guide to Spray Nozzles; Teejet Technologies: Glendale Heights, IL, USA, 2013; 60p, Available online: https://www.teejet.com/CMSImages/TEEJET/documents/bulletins/spray-application/LI-TJ178_a-users-guide-to-spray-nozzles.pdf (accessed on 30 December 2013).
- Teejet®. Spray Nozzles. Teejet Technologies. Available online: https://www.teejet.com/spray_application/nozzles.aspx (accessed on 30 December 2018).
- Sanchez-Hermosilla, J.; Paez, F.; Rincon, V.J.; Carvajal, F. Evaluation of the effect of spray pressure in hand-held sprayers in a greenhouse tomato crop. Crop Prot. 2013, 54, 121–125. [Google Scholar] [CrossRef]
- Rehman, T.; Khan, M.U.; Tayyab, M.; Akram, M.W.; Faheem, M. Current status and overview of farm mechanization in Pakistan—A review. Agric. Eng. Int. 2016, 18, 83–93. [Google Scholar]
- Matthews, G.A. Attitudes, and behaviours regarding use of crop protection products—A survey of more than 8500 smallholders in 26 countries. Crop Prot. 2008, 27, 834–846. [Google Scholar] [CrossRef]
- Sanchez-Hermosilla, J.; Rincon, V.J.; Paez, F.; Fernandez, M. Comparative spray deposits by manually pulled trolley sprayer and spray gun in greenhouse tomato crops. Crop Prot. 2012, 31, 119–124. [Google Scholar] [CrossRef]
- Sangale, K.A.; Shinde, D.D. Design of hydraulic power transmission system of a heavy-duty vehicle. Int. Adv. Res. J. Sci. Eng. Technol. 2016, 3, 79–81. [Google Scholar]
- Engineering ToolBox. Rolling Resistance. 2008. Available online: https://www.engineeringtoolbox.com/rolling-friction-resistance-d_1303.html (accessed on 30 December 2008).
- Zhu, H.; Salyani, M.; Fox, R.D. A portable scanning system for evaluation of spray deposit distribution. Comput. Electron. Agric. 2011, 76, 38–43. [Google Scholar] [CrossRef]
- Hoffmann, W.C.; Hewitt, A.J. Comparison of three imaging systems for water-sensitive papers. Appl. Eng. Agric. 2005, 21, 961–964. [Google Scholar] [CrossRef]
- Wang, G.; Lan, Y.; Qi, H.; Chen, P.; Hewitt, A.; Han, Y. Field evaluation of an unmanned aerial vehicle (UAV) sprayer: Effect of spray volume on deposition and the control of pests and disease in wheat. Pest Manag. Sci. 2019, 75, 1546–1555. [Google Scholar] [CrossRef] [PubMed]
- Fernandes, A.P.; Parreira, R.S.; Ferreira, M.C.; Romani, G.N. Characterization of the deposition profile and droplet diameter and optimization of spacing between nozzles in the spray boom. Agric. Eng. 2007, 27, 728–733. [Google Scholar]
- Ferreira, M.C.; Costa, G.M.; Silva, A.R.; Tagliari, S.R.A. Qualitative factors of the hydraulic power tip ADGA-110015 for agricultural spraying. Agric. Eng. 2007, 27, 471–478. [Google Scholar]
- Roman, R.A.A.; Ferreira, M.C.; Carvalho, G.F.G.; Baggio, M.V. Spraying distribution, symmetry of fan, and droplet size of spray nozzles TF-VS2. Planta Daninha 2010, 28, 897–905. [Google Scholar]
- National Association of State Departments of Agriculture. National Pesticide Applicator Certification Core Manual, 2nd ed.; National Association of State Departments of Agriculture: Washington, DC, USA, 2014.
- Carroll, J. The Effects of Sprayer Speed and Droplet Size on Herbicide Burndown Efficacy. Master’s Thesis, University of Arkansas, Fayetteville, AR, USA, 2017. Available online: https://scholarworks.uark.edu/etd/2435/ (accessed on 1 September 2021).
- Khan, F.A.; Ghafoor, A.; Khan, M.A.; Chattha, U.M.; Kouhanestani, F.K. Parameter Optimization of Newly Developed Self-Propelled Variable Height Crop Sprayer Using Response Surface Methodology (RSM) Approach. Agriculture 2022, 12, 408. [Google Scholar] [CrossRef]
- Sayinci, B.; Demir, B.; Acik, N. Comparison of spray nozzles in terms of spray coverage and drop distribution at low volume. Turk. J. Agric. For. 2020, 44, 262–270. [Google Scholar] [CrossRef]
- Ferguson, J.C.; Chechetto, R.G.; Hewitt, A.J.; Chauhan, B.S.; Adkins, S.W.; Kruger, G.R.; O’Donnell, C.C. Assessing the deposition and canopy penetration of nozzles with different spray qualities in an oat (Avena sativa L.) canopy. Crop Prot. 2016, 81, 14–19. [Google Scholar] [CrossRef] [Green Version]
- Koszel, M. Influence of fan flat nozzles wears degree on drop tracks size. Res. Agric. Eng. 2009, 55, 39–44. [Google Scholar] [CrossRef] [Green Version]
- Nansen, C.; Ferguson, J.C.; Moore, J.; Groves, L.; Emery, R.; Garel, N.; Hewitt, A. Optimizing pesticide spray coverage using a novel web and smartphone tool, snap card. Agron. Sustain. Dev. 2015, 35, 1075–1085. [Google Scholar] [CrossRef]
- Ranta, O.; Marian, O.; Muntean, M.V.; Molnar, A.; Ghețe, A.; Crisan, V.; Stanila, S.; Rittner, T. Quality Analysis of Some Spray Parameters When Performing Treatments in Vineyards in Order to Reduce Environment Pollution. Sustainability 2021, 13, 7780. [Google Scholar] [CrossRef]
- TeeJet Technologies. Spray Application: Overview. Available online: https://www.teejet.com/CMSImages/TEEJET/documents/catalogs/cat51a_us.pdf (accessed on 30 December 2014).
- Shirwal, S.; Veerangouda, M.; Palled, V.; Sushilendra; Hosamani, A.; Krishnamurthy, D. Studies on Operational Parameters of Different Spray Nozzles. Int. J. Curr. Microbiol. Appl. Sci. 2020, 9, 1267–1281. [Google Scholar] [CrossRef]
- Azizpanah, A.; Rajabipour, A.; Alimardani, R.; Kheiralipour, K.; Ghamari, B.; Mohammadi, V. Design, construction, and evaluation of a sprayer drift measurement system. Agric. Eng. Int. 2015, 17, 138–146. [Google Scholar]
- ASABE S572.1; Spray Nozzle Classification by Droplet Spectra. American Society of Agricultural and Biological Engineers: St. Joseph, MI, USA, 2009; 3p.
- Wang, G.; Lan, Y.; Yuan, H.; Qi, H.; Chen, P.; Ouyang, F.; Han, Y. Comparison of Spray Deposition, Control Efficacy on Wheat Aphids and Working Efficiency in the Wheat Field of the Unmanned Aerial Vehicle with Boom Sprayer and Two Conventional Knapsack Sprayers. Appl. Sci. 2019, 9, 218. [Google Scholar] [CrossRef] [Green Version]
- Water-Sensitive Paper Check Your Spray Coverage. Available online: https://www.syngenta.com.au/awri (accessed on 19 April 2021).
- Ahmad, D.; Afzal, M. Estimating the economic perspective of cotton crop in southern Punjab of Pakistan. Int. J. Adv. Appl. Sci. 2018, 5, 50–55. [Google Scholar] [CrossRef]
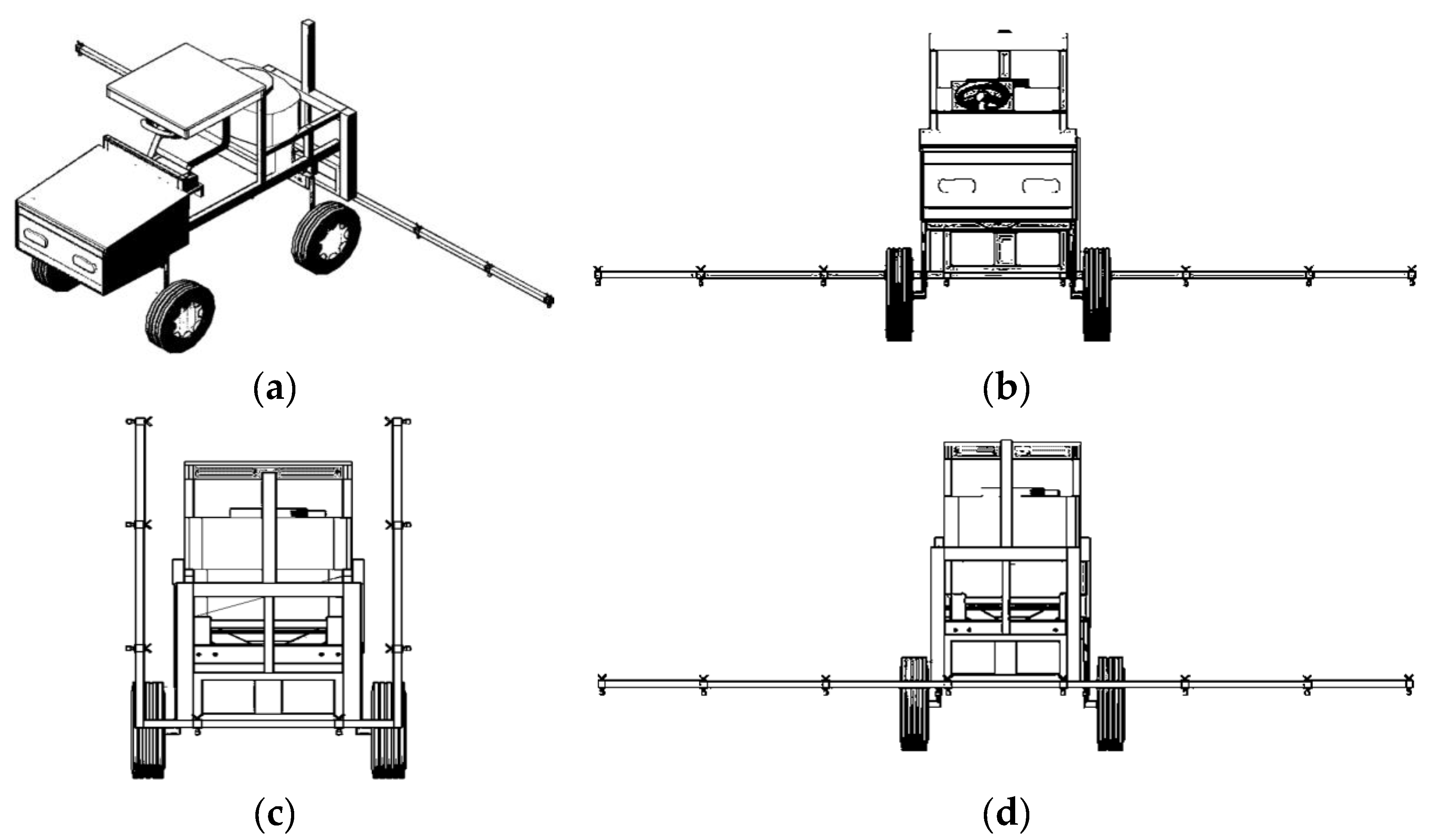
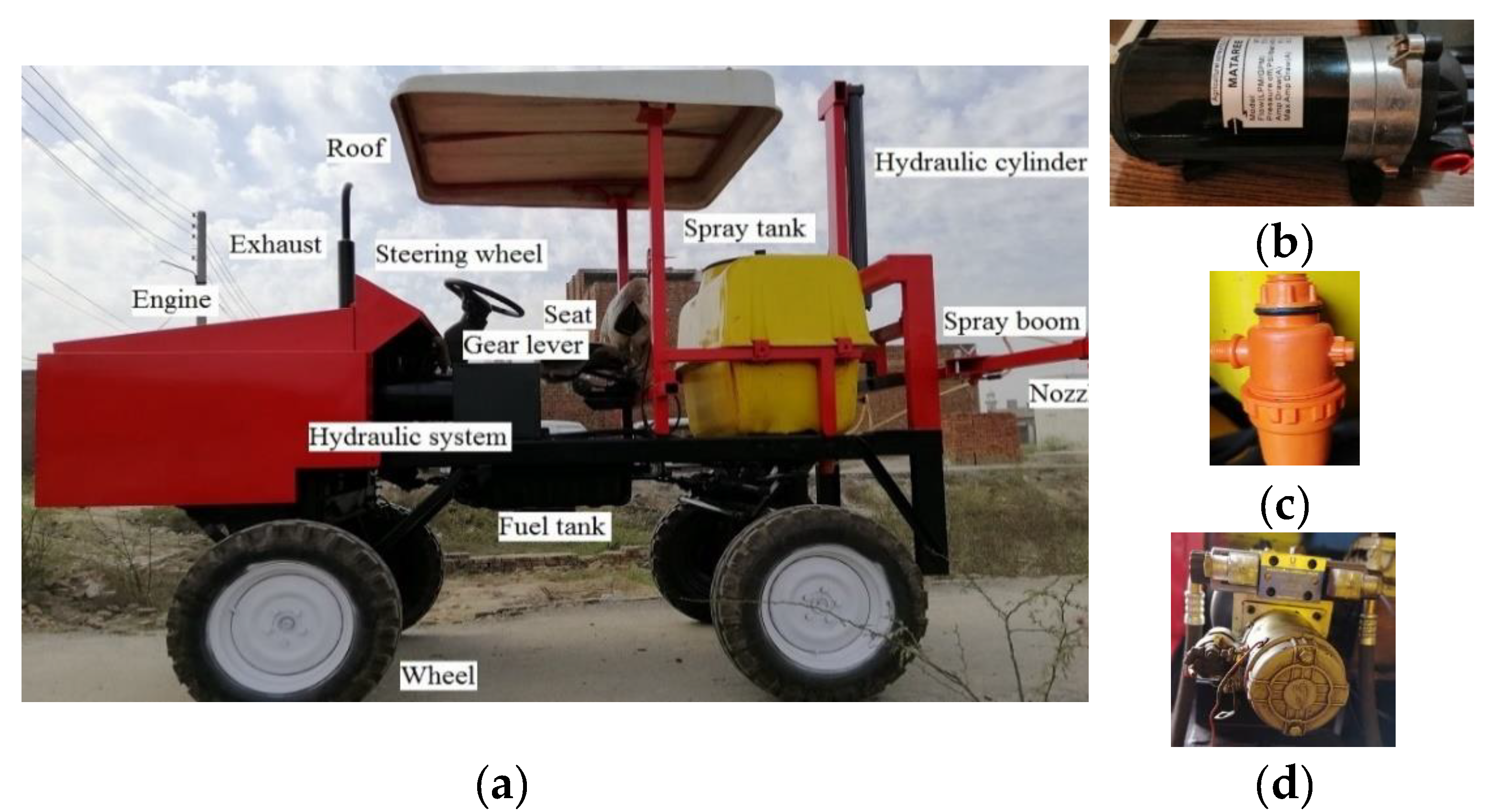
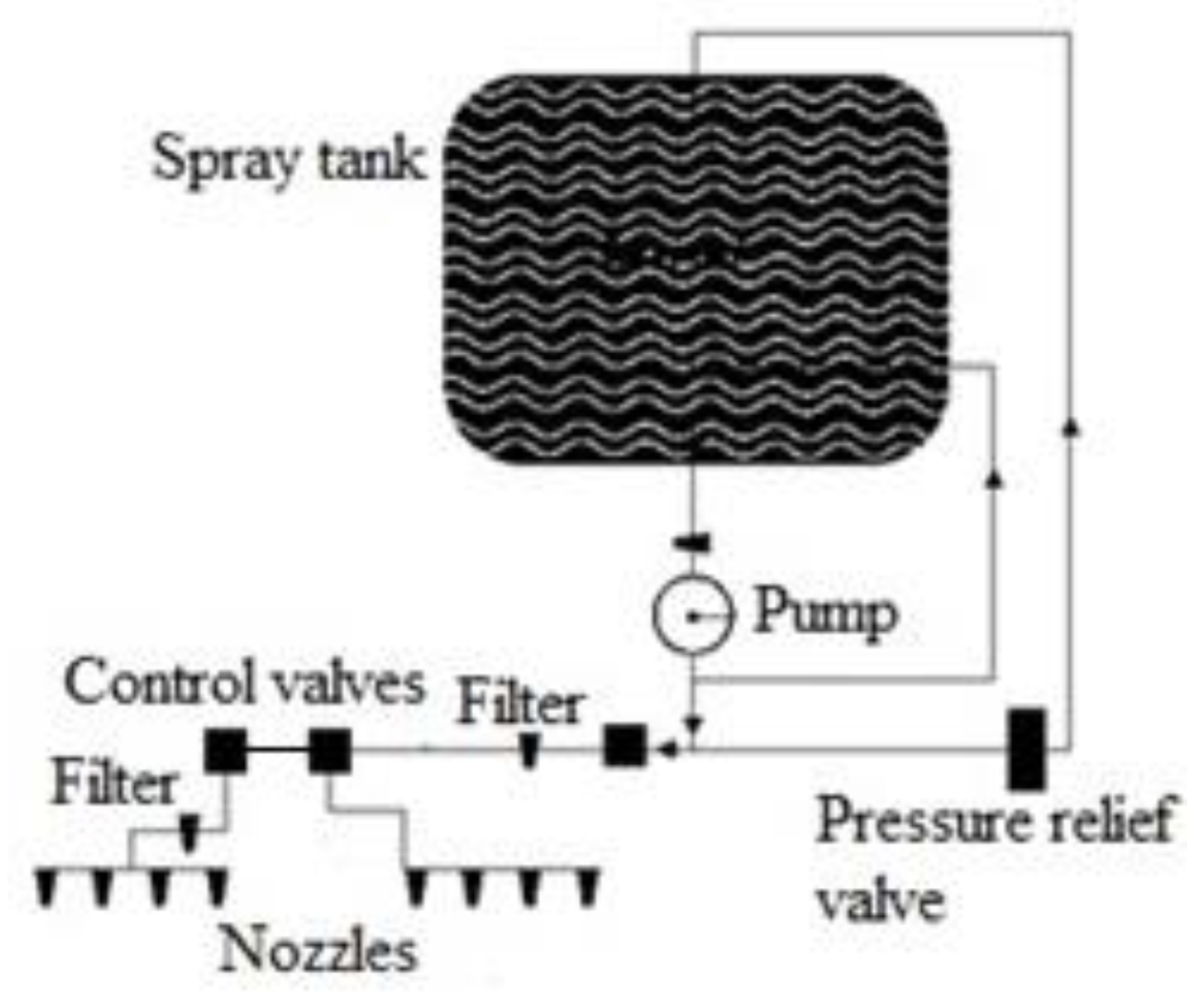
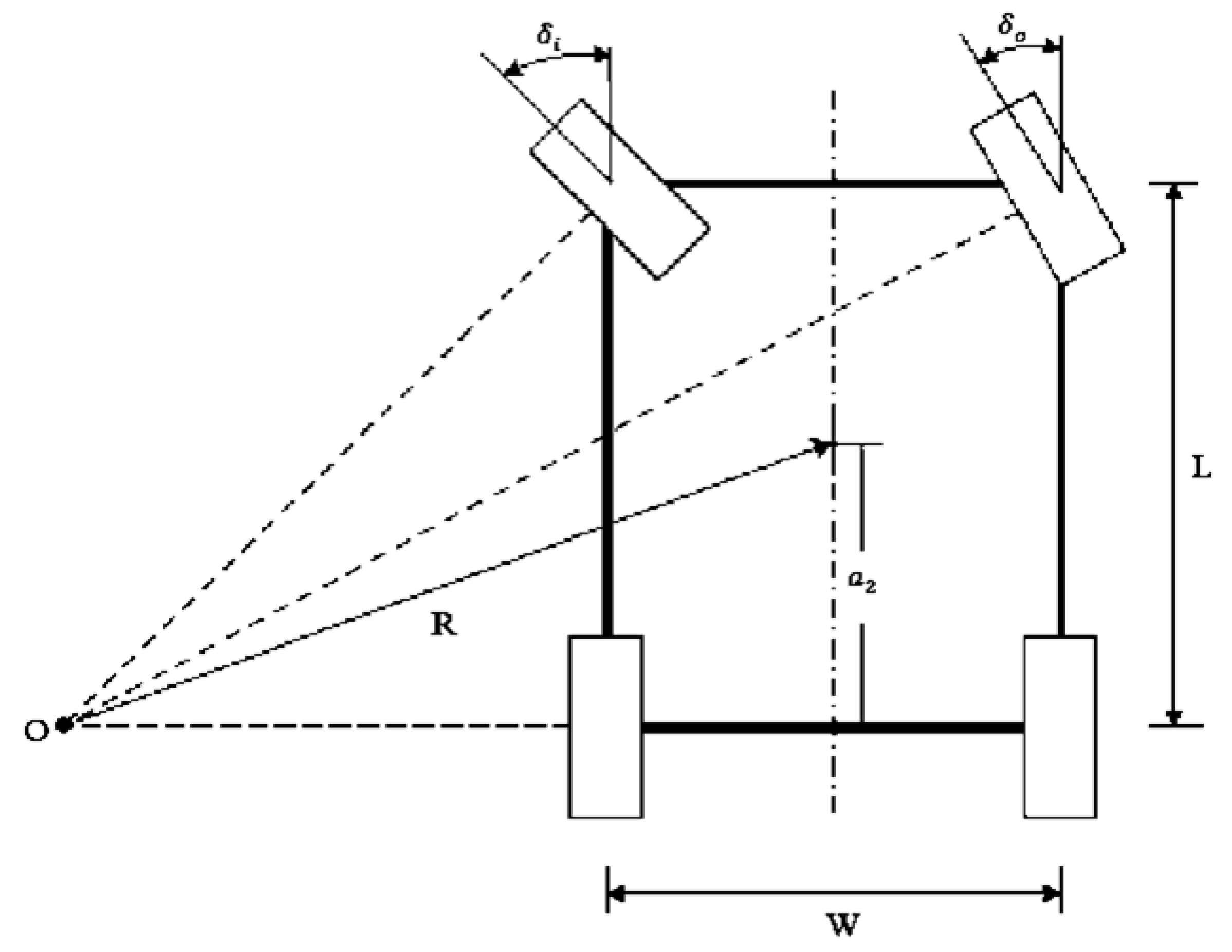


| Items | Specifications | Detailed Specifications | |
|---|---|---|---|
| Structure | Self-propelled | – | |
| Overall frame sizes | 2845 × 1017 × 2440 mm | Mild steel, material grade SAE 4130 | |
| Machine weight | 1090 kg | – | |
| Wheelbase | 1753 mm | – | |
| Ground clearance | 762–915 mm | – | |
| Track width | 1676 mm | ||
| Turning mode | Rack & pinion steering | ||
| Minimum turning radius | 3056 mm | ||
| Nozzle height from the ground | 458–1220 mm | – | |
| Engine power | 20 hp | Model 2105D, 2-cylinder, closed water cooling, straight-line four-stroke, speed 1500 rpm | |
| Driving mode | Automatic gear shift | – | |
| Tire | Four tire | Tire pressure 2 bar | |
| Liquid tank | 300 L | Polyethylene (PE) | |
| Nozzle | Hollow cone | ASJ (HC8002), size 15 × 7 mm, spray angle 80° | |
| Hydraulic system | Type | DC power pack | – |
| Motor | 12-V | – | |
| Power | 1600 W | – | |
| Pump type | Gear pump | – | |
| Reservoir capacity | 8 L | – | |
| Max flow rate | 5.6 L min−1 | – | |
| Max Pressure | 176 bar | – | |
| Hydraulic cylinder length | 1220 mm | – | |
| Spray boom | Lifting mode | Hydraulic drive | – |
| Folding mode | Manual drive | – | |
| Spray boom | 6096 mm | – | |
| Spray pump | Type | Diaphragm pump | Model-BYT-7A111, Volt-12 V |
| Pressure | 24 bar | – | |
| Flow rate | 22 L min−1 | – | |
| Trt. No. | Treatment Abbreviation | Treatment Variables | ||
|---|---|---|---|---|
| Forward Speed (km h−1) | Spray Height (cm) | Spray Pressure (bar) | ||
| T1 | S1H1P1 | 4 | 40 | 3 |
| T2 | S1H1P2 | 4 | 40 | 5 |
| T3 | S1H1P3 | 4 | 40 | 7 |
| T4 | S1H2P1 | 4 | 55 | 3 |
| T5 | S1H2P2 | 4 | 55 | 5 |
| T6 | S1H2P3 | 4 | 55 | 7 |
| T7 | S1H3P1 | 4 | 70 | 3 |
| T8 | S1H3P2 | 4 | 70 | 5 |
| T9 | S1H3P3 | 4 | 70 | 7 |
| T10 | S2H1P1 | 6 | 40 | 3 |
| T11 | S2H1P2 | 6 | 40 | 5 |
| T12 | S2H1P3 | 6 | 40 | 7 |
| T13 | S2H2P1 | 6 | 55 | 3 |
| T14 | S2H2P2 | 6 | 55 | 5 |
| T15 | S2H2P3 | 6 | 55 | 7 |
| T16 | S2H3P1 | 6 | 70 | 3 |
| T17 | S2H3P2 | 6 | 70 | 5 |
| T18 | S2H3P3 | 6 | 70 | 7 |
| T19 | S3H1P1 | 8 | 40 | 3 |
| T20 | S3H1P2 | 8 | 40 | 5 |
| T21 | S3H1P3 | 8 | 40 | 7 |
| T22 | S3H2P1 | 8 | 55 | 3 |
| T23 | S3H2P2 | 8 | 55 | 5 |
| T24 | S3H2P3 | 8 | 55 | 7 |
| T25 | S3H3P1 | 8 | 70 | 3 |
| T26 | S3H3P2 | 8 | 70 | 5 |
| T27 | S3H3P3 | 8 | 70 | 7 |
| Response Variables | Source of Variance | SS | df | MS | F | p |
|---|---|---|---|---|---|---|
| Droplet density | Between groups | 0.84 | 2 | 0.42 | 0.004 | 0.10 * |
| Coverage | Between groups | 7.33 | 2 | 3.65 | 0.101 | 0.90 |
| VMD | Between groups | 1.52 | 2 | 0.76 | 0.02 | 0.979 |
| Response Variables | Kolmogorov-Smirnova | ||
|---|---|---|---|
| Statistic | df | Sig. | |
| Droplet Density | 0.100 | 324 | <0.001 * |
| Coverage Percentage | 0.077 | 324 | <0.001 |
| VMD | 0.098 | 324 | <0.001 |
| Treatment No. | Treatment Abbreviation | Droplet Density (Droplets cm−2) |
|---|---|---|
| T1 | S1H1P1 | 85.6 ± 3.76 c |
| T2 | S1H1P2 | 88.6 ± 3.53 b |
| T3 | S1H1P3 | 97.4 ± 3.21 a |
| T4 | S1H2P1 | 80.9 ± 3.09 e |
| T5 | S1H2P2 | 84.9 ± 2.97 cd |
| T6 | S1H2P3 | 87 ± 3.22 bc |
| T7 | S1H3P1 | 69 ± 3.43 h |
| T8 | S1H3P2 | 78.3 ± 3.55 f |
| T9 | S1H3P3 | 82.8 ± 2.89 de |
| T10 | S2H1P1 | 70.7 ± 3.18 gh |
| T11 | S2H1P2 | 81.5 ± 3.25 e |
| T12 | S2H1P3 | 87.4 ± 3.68 bc |
| T13 | S2H2P1 | 56 ± 3.98 k |
| T14 | S2H2P2 | 64.7 ± 3.61 i |
| T15 | S2H2P3 | 73 ± 3.34 g |
| T16 | S2H3P1 | 51.3 ± 2.87 l |
| T17 | S2H3P2 | 60.6 ± 3.48 j |
| T18 | S2H3P3 | 69.2 ± 3.87 h |
| T19 | S3H1P1 | 42.8 ± 3.59 n |
| T20 | S3H1P2 | 60 ± 2.99 j |
| T21 | S3H1P3 | 68.7 ± 3.23 h |
| T22 | S3H2P1 | 39 ± 3.56 o |
| T23 | S3H2P2 | 48 ± 3.82 m |
| T24 | S3H2P3 | 54.2 ± 3.46 k |
| T25 | S3H3P1 | 31.3 ± 3.71 p |
| T26 | S3H3P2 | 43.5 ± 3.83 n |
| T27 | S3H3P3 | 48.4 ± 3.97 m |
| Source of Variance | SS | df | MS | F | p-Value | Fcrit | Results |
|---|---|---|---|---|---|---|---|
| Treatment | 98,984.22 | 26 | 3807 | 396.9 | 1.54 | Significant * | |
| Crop block | 50.08352 | 2 | 25 | 2.6 | 0.075559 | 3.03 | Not significant |
| Treatment × Crop block | 296.8031 | 52 | 5.70 | 0.6 | 0.9867 | 1.39 | Not significant |
| Error | 2331.038 | 243 | 9.60 | ||||
| Total | 101,662.1 | 323 |
| Treatment No. | Treatment Abbreviation | Coverage Percentage |
|---|---|---|
| T1 | S1H1P1 | 43.9 ± 1.63 c |
| T2 | S1H1P2 | 47.3 ± 1.59 b |
| T3 | S1H1P3 | 55.9 ± 1.47 a |
| T4 | S1H2P1 | 39.1 ± 1.65 f |
| T5 | S1H2P2 | 41.6 ± 1.73 de |
| T6 | S1H2P3 | 43.2 ± 1.41 cd |
| T7 | S1H3P1 | 31.9 ± 1.53 h |
| T8 | S1H3P2 | 37 ± 1.92 g |
| T9 | S1H3P3 | 40.6 ± 1.88 ef |
| T10 | S2H1P1 | 29.5 ± 1.67 ij |
| T11 | S2H1P2 | 39.4 ± 1.39 f |
| T12 | S2H1P3 | 43.6 ± 1.55 c |
| T13 | S2H2P1 | 22.5 ± 1.46 m |
| T14 | S2H2P2 | 26.7 ± 1.75 k |
| T15 | S2H2P3 | 31.1 ± 1.38 hi |
| T16 | S2H3P1 | 21 ± 1.53 mn |
| T17 | S2H3P2 | 25 ± 1.89 kl |
| T18 | S2H3P3 | 29.5 ± 1.78 ij |
| T19 | S3H1P1 | 17.2 ± 1.32 o |
| T20 | S3H1P2 | 24.5 ± 1.43 l |
| T21 | S3H1P3 | 29.1 ± 1.49 j |
| T22 | S3H2P1 | 14.9 ± 1.72 p |
| T23 | S3H2P2 | 19.8 ± 1.65 n |
| T24 | S3H2P3 | 22.5 ± 1.82 m |
| T25 | S3H3P1 | 13.1 ± 1.52 p |
| T26 | S3H3P2 | 17.2 ± 1.73 o |
| T27 | S3H3P3 | 20 ± 1.40 n |
| Source of Variance | SS | df | MS | F | p-Value | Fcrit | Results |
|---|---|---|---|---|---|---|---|
| Treatment | 39,590.12 | 26 | 1522.7 | 290.8 | 1.54 | Significant * | |
| Crop block | 21.48969 | 2 | 10.7 | 2.05 | 0.130693 | 3.03 | Not significant |
| Treatment × Crop block | 176.1436 | 52 | 3.4 | 0.64 | 0.969285 | 1.39 | Not significant |
| Error | 1272.393 | 243 | 5.2 | ||||
| Total | 41,060.15 | 323 |
| Treatment No. | Treatment Abbreviation | VMD (µm) |
|---|---|---|
| T1 | S1H1P1 | 245 ± 2.54 f |
| T2 | S1H1P2 | 254.2 ± 2.21 b |
| T3 | S1H1P3 | 261.4 ± 2.32 a |
| T4 | S1H2P1 | 241.5 ± 2.45 h |
| T5 | S1H2P2 | 246.3 ± 2.16 de |
| T6 | S1H2P3 | 249.9 ± 1.97 c |
| T7 | S1H3P1 | 234.5 ± 2.28 j |
| T8 | S1H3P2 | 243.2 ± 2.34 g |
| T9 | S1H3P3 | 245.3 ± 2.53 ef |
| T10 | S2H1P1 | 230.5 ± 2.03 lm |
| T11 | S2H1P2 | 239.8 ± 2.11 i |
| T12 | S2H1P3 | 246.9 ± 1.98 d |
| T13 | S2H2P1 | 226.2 ± 2.46 n |
| T14 | S2H2P2 | 230 ± 2.37 m |
| T15 | S2H2P3 | 235 ± 2.42 j |
| T16 | S2H3P1 | 224.9 ± 2.51 op |
| T17 | S2H3P2 | 230.7 ± 2.39 lm |
| T18 | S2H3P3 | 232.5 ± 2.27 k |
| T19 | S3H1P1 | 221 ± 2.13 r |
| T20 | S3H1P2 | 225.7 ± 2.05 no |
| T21 | S3H1P3 | 231.4 ± 2.27 kl |
| T22 | S3H2P1 | 219.8 ± 2.21 r |
| T23 | S3H2P2 | 223.4 ± 2.47 q |
| T24 | S3H2P3 | 226.5 ± 2.31 n |
| T25 | S3H3P1 | 217.1 ± 2.56 s |
| T26 | S3H3P2 | 220.7 ± 2.09 r |
| T27 | S3H3P3 | 223.8 ± 2.23 pq |
| Source of Variance | SS | df | MS | F | p-Value | Fcrit | Results |
|---|---|---|---|---|---|---|---|
| Treatment | 42,168.6 | 26 | 1621.9 | 900.74 | 1.54 | Significant * | |
| Crop block | 2.77858 | 2 | 1.389 | 0.77 | 0.4634 | 3.03 | Not significant |
| Treatment × Crop block | 107.4631 | 52 | 2.066 | 1.14 | 0.2443 | 1.39 | Not significant |
| Error | 437.5425 | 243 | 1.800 | ||||
| Total | 42,716.38 | 323 |
| Tank Capacity | Spray Area (Mean ± SE *) | Spray Time (Mean ± SE *) | Effective Field Capacity | Field Efficiency |
|---|---|---|---|---|
| (L) | (ha) | (h) | (ha h−1) | (%) |
| 300 | 0.90 ± 0.06 | 0.41 ± 0.03 | 2.19 | 61 |
| Fixed Cost | |
|---|---|
| Depreciation | $300 per year |
| Interest @ 12% | $360 per year |
| Fixed cost | $660 per year |
| Annual spray area assumed Total Fixed cost per hectare | 3285 hectares per year $660/3285 = $0.20 ha−1 |
| Variable cost | |
| Repair and Maintenance @ 15% | $450 per year |
| Driver charges @ $7.5/8 h/day | $1400 per year |
| Fuel Charges @ $0.70/liter | $3416 per year |
| Variable cost | $5266 per year |
| Annual spray area assumed | 3285 hectares per year |
| Total variable cost | $5266/3285 = $1.60 ha−1 |
| Total spraying cost | |
| Total spraying cost (Fixed + Variable) | $0.20 + $1.60/ha = $1.80 ha−1 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ghafoor, A.; Khan, F.A.; Khorsandi, F.; Khan, M.A.; Nauman, H.M.; Farid, M.U. Development and Evaluation of a Prototype Self-Propelled Crop Sprayer for Agricultural Sustainability in Small Farms. Sustainability 2022, 14, 9204. https://doi.org/10.3390/su14159204
Ghafoor A, Khan FA, Khorsandi F, Khan MA, Nauman HM, Farid MU. Development and Evaluation of a Prototype Self-Propelled Crop Sprayer for Agricultural Sustainability in Small Farms. Sustainability. 2022; 14(15):9204. https://doi.org/10.3390/su14159204
Chicago/Turabian StyleGhafoor, Abdul, Fraz Ahmad Khan, Farzaneh Khorsandi, Muhammad Azam Khan, Hafiz Muhammad Nauman, and Muhammad Usman Farid. 2022. "Development and Evaluation of a Prototype Self-Propelled Crop Sprayer for Agricultural Sustainability in Small Farms" Sustainability 14, no. 15: 9204. https://doi.org/10.3390/su14159204
APA StyleGhafoor, A., Khan, F. A., Khorsandi, F., Khan, M. A., Nauman, H. M., & Farid, M. U. (2022). Development and Evaluation of a Prototype Self-Propelled Crop Sprayer for Agricultural Sustainability in Small Farms. Sustainability, 14(15), 9204. https://doi.org/10.3390/su14159204






