Regional Flood Frequency Analysis of the Sava River in South-Eastern Europe
Abstract
:1. Introduction
2. Research Area
3. Data
4. Methods
4.1. L-Moments Estimation for RFFA
4.2. Trend Estimation
5. Results and Discussion
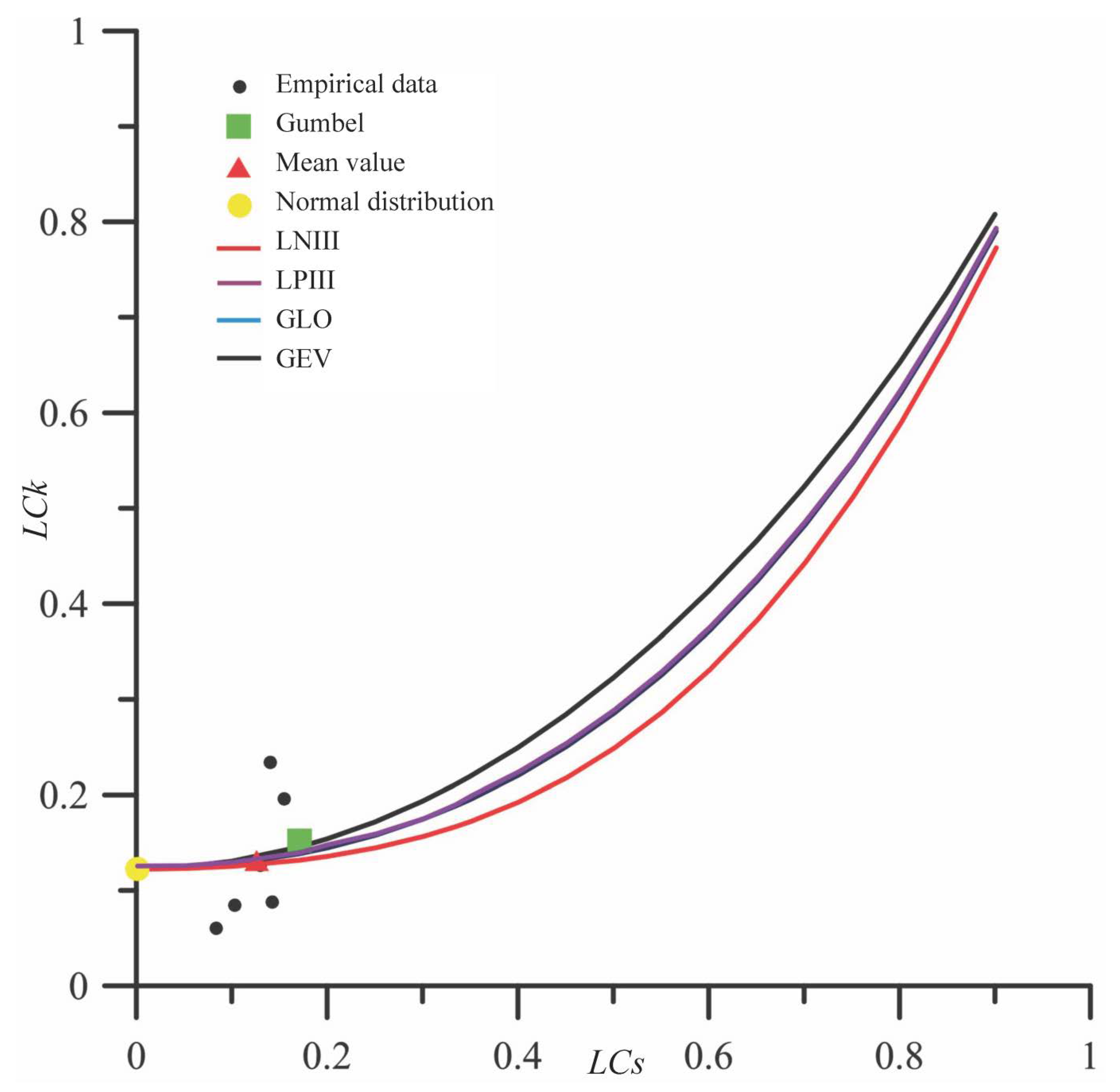
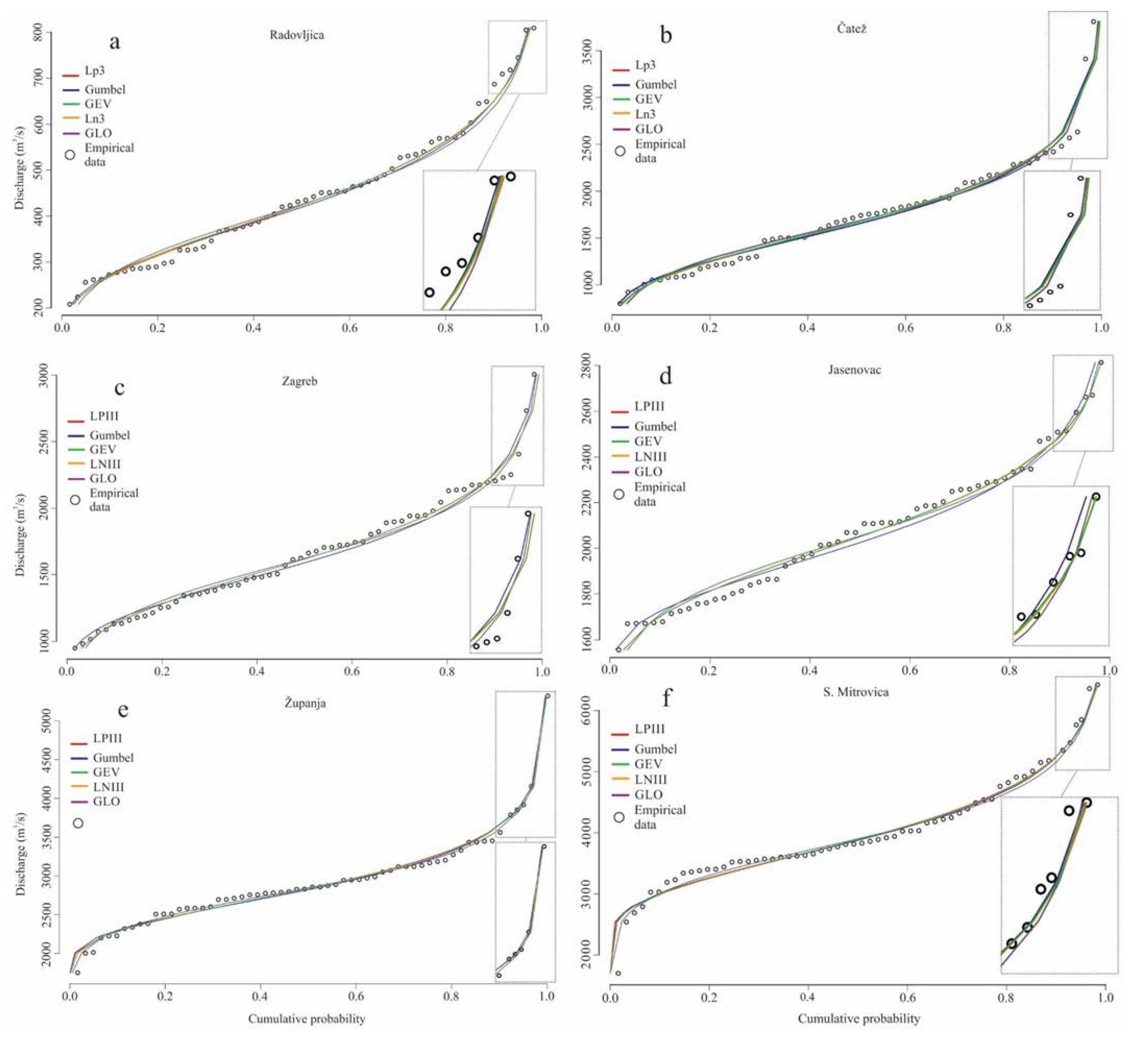
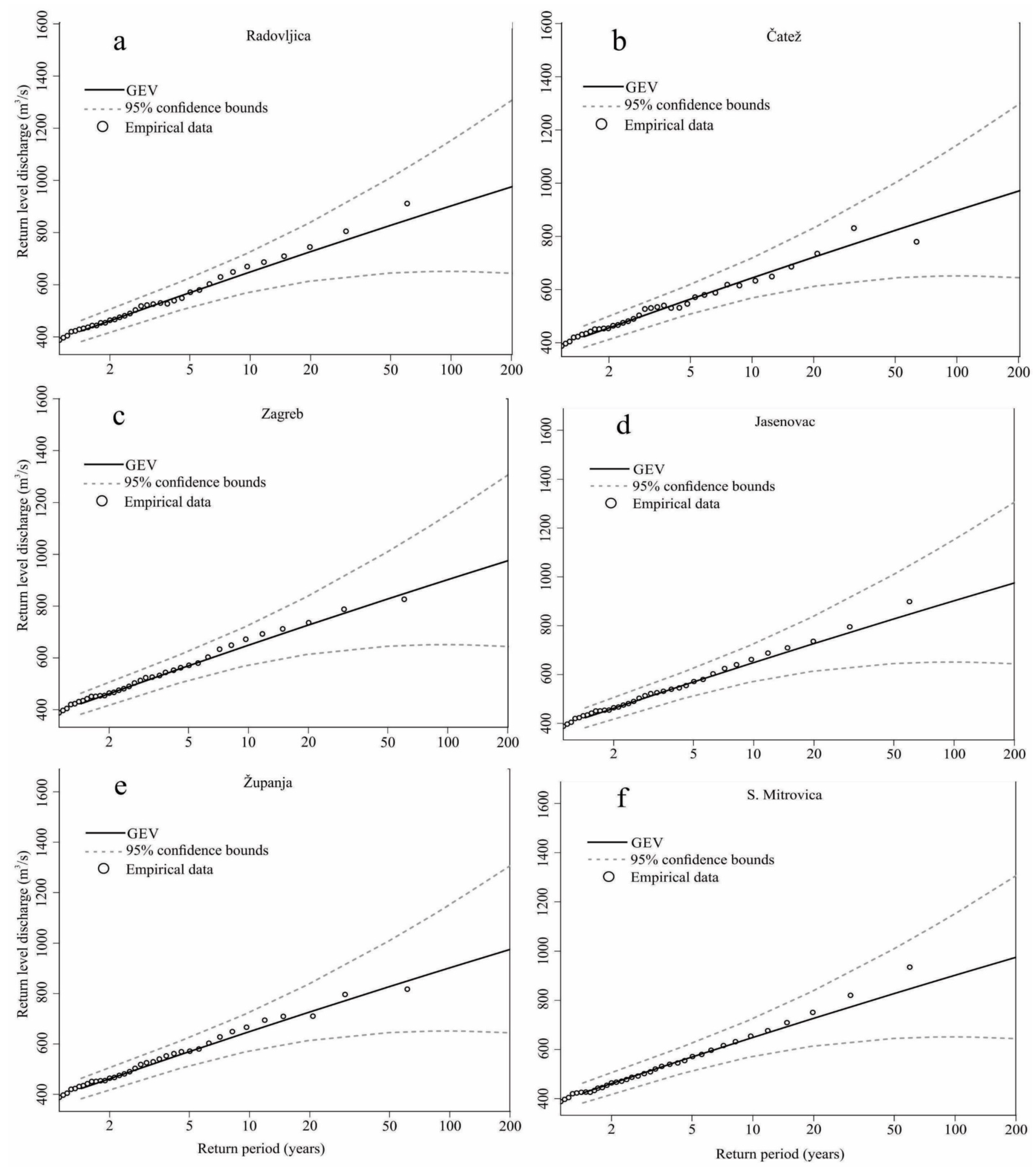
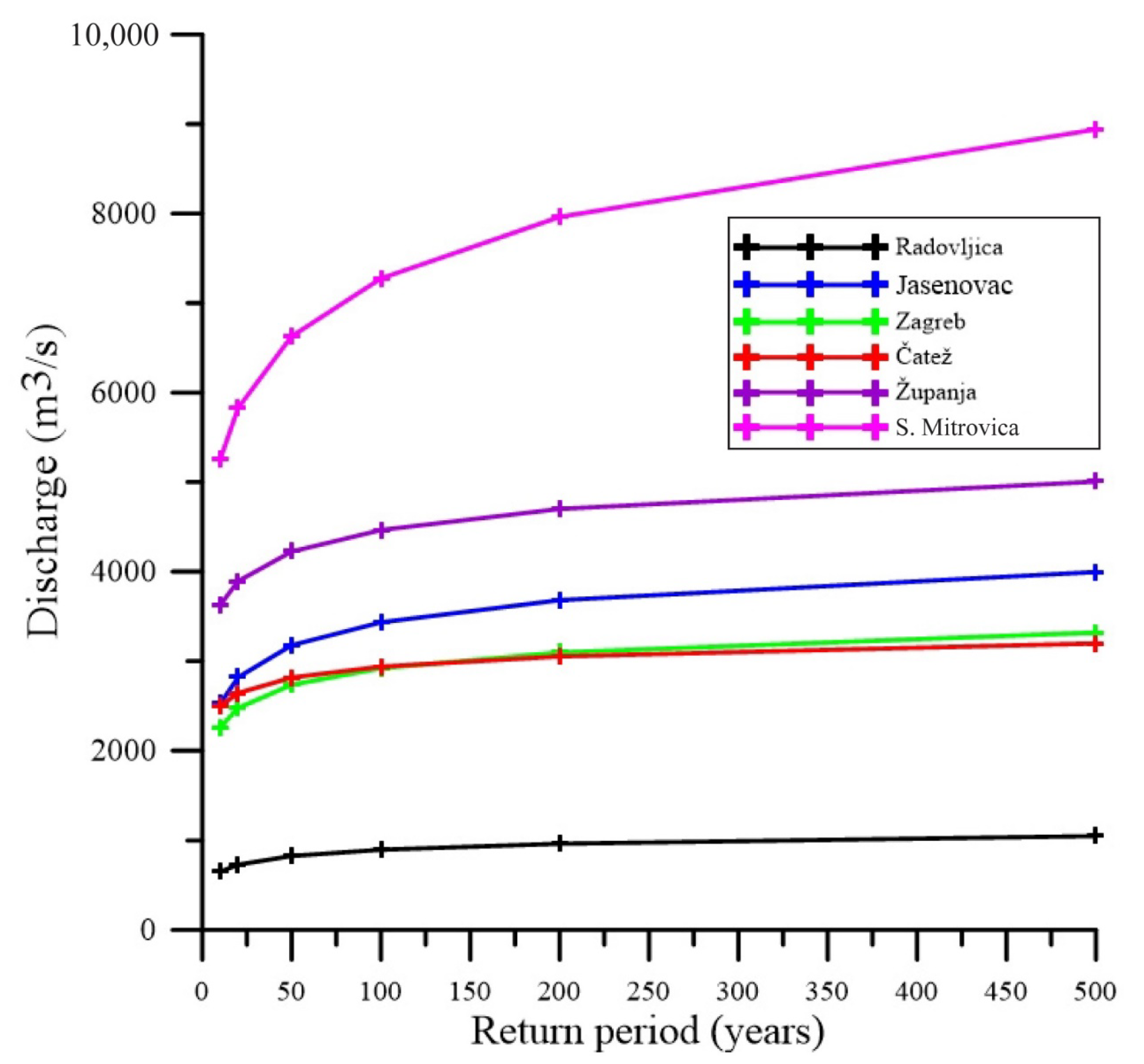
5.1. Regional Flood Frequency Analysis
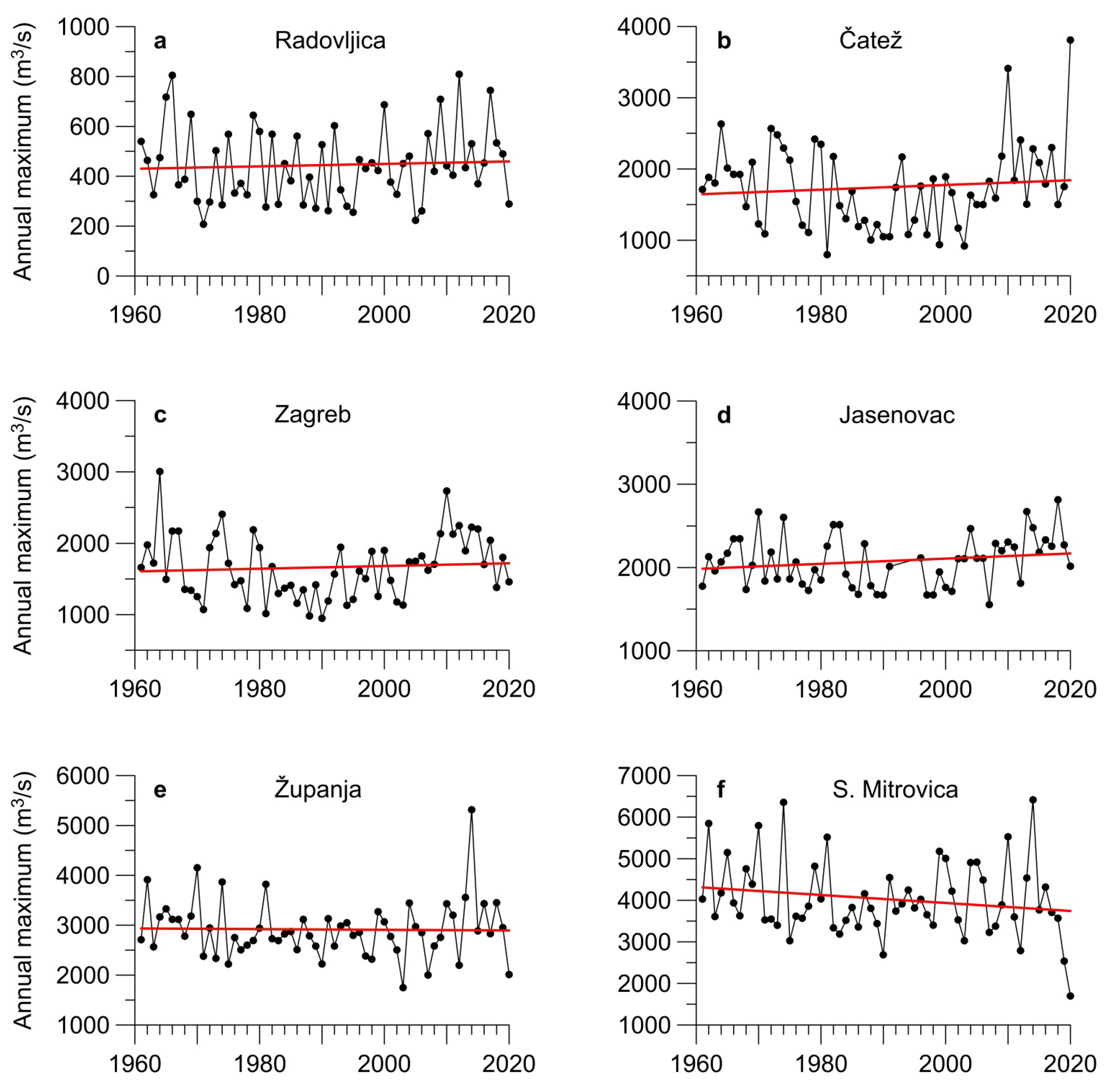
5.2. Trend Analysis
5.3. Homogeneity Assessment and Regional Flood Frequency Analysis
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Mathematical Formulas for the Distribution Functions
References
- Adikari, Y.; Yoshitani, J. Global Trends in Water-Related Disasters: An Insight for Policymakers; United Nations Educational, Scientific and Cultural Organization: Paris, France, 2009. [Google Scholar]
- Pandžić, K.; Trninić, D.; Likso, T.; Bošnjak, T. Long-term variations in water balance components for Croatia. Theor. Appl. Climatol. 2009, 95, 39–51. [Google Scholar] [CrossRef]
- Fischer, S.; Schumann, A.H. Multivariate flood frequency analysis in large river basins considering tributary impacts and flood types. Water Resour. Res. 2021, 57, e2020WR029029. [Google Scholar] [CrossRef]
- Kundzewicz, Z.W. (Ed.) Changes in Flood Risk in Europe; IAHS Press: Wallingford, UK, 2012. [Google Scholar]
- Mudelsee, M.; Börngen, M.; Tetzlaff, G.; Grünewald, U. Extreme floods in central Europe over the past 500 years: Role of cyclone pathway “Zugstrasse Vb.”. J. Geophys. Res. Atmos. 2004, 109, D23101. [Google Scholar] [CrossRef] [Green Version]
- Dottori, F.; Szewczyk, W.; Ciscar, J.-C.; Zhao, F.; Alfieri, L.; Hirabayashi, Y.; Bianchi, A.; Mongelli, I.; Frieler, K.; Betts, R.A.; et al. Increased human and economic losses from river flooding with anthropogenic warming. Nat. Clim. Change 2018, 8, 781–786. [Google Scholar] [CrossRef]
- Ward, P.J.; de Perez, E.C.; Dottori, F.; Jongman, B.; Luo, T.; Safaie, S.; Uhlemann-Elmer, S. The need for mapping, modeling, and predicting flood hazard and risk at the global scale. In Global Flood Hazard: Applications in Modeling, Mapping, and Forecasting; Schumann, G.J.-P., Bates, P.D., Apel, H., Aronica, G.T., Eds.; American Geophysical Union: Washington, DC, USA, 2018; pp. 1–15. [Google Scholar]
- Black, A.R. Major flooding and increased flood frequency in Scotland since 1988. Phys. Chem. Earth 1995, 20, 463–468. [Google Scholar] [CrossRef]
- Brázdil, R.; Kundzewicz, Z.W.; Benito, G.; Demarée, G.; Macdonald, N.; Roald, L.A. Historical floods in Europe in the past millennium. In Changes in Flood Risk in Europe; Kundzewicz, Z.W., Ed.; IAHS Press: Wallingford, UK, 2012; pp. 121–166. [Google Scholar]
- Disse, M.; Engel, H. Flood events in the Rhine basin: Genesis, influences and mitigation. Nat. Hazards 2001, 23, 271–290. [Google Scholar] [CrossRef]
- Jongman, B.; Hochrainer-Stigler, S.; Feyen, L.; Aerts, J.C.J.H.; Mechler, R.; Botzen, W.J.W.; Bouwer, L.M.; Pflug, G.; Rojas, R.; Ward, P.J. Increasing stress on disaster-risk finance due to large floods. Nat. Clim. Change 2014, 4, 264–268. [Google Scholar] [CrossRef]
- Mikhailova, M.V.; Mikhailov, V.N.; Morozov, V.N. Extreme hydrological events in the Danube river basin over the last decades. Water Resour. 2012, 39, 161–179. [Google Scholar] [CrossRef]
- Oblak, J.; Kobold, M.; Šraj, M. The influence of climate change on discharge fluctuations in Slovenian rivers. Acta Geogr. Slov. 2021, 61, 155–169. [Google Scholar] [CrossRef]
- Olsen, J.R.; Stedinger, J.R.; Matalas, N.C.; Stakhiv, E.Z. Climate variability and flood frequency estimation for the upper Mississippi and lower Missouri rivers. J. Am. Water Resour. Assoc. 1999, 35, 1509–1523. [Google Scholar] [CrossRef]
- Osterkamp, W.R.; Friedman, J.M. The disparity between extreme rainfall events and rare floods—with emphasis on the semi-arid American West. Hydrol. Process. 2000, 14, 2817–2829. [Google Scholar] [CrossRef]
- Paprotny, D.; Sebastian, A.; Morales-Nápoles, O.; Jonkman, S.N. Trends in flood losses in Europe over the past 150 years. Nat. Comm. 2018, 9, 1985. [Google Scholar] [CrossRef]
- Petrow, T.; Merz, B. Trends in flood magnitude, frequency and seasonality in Germany in the period 1951–2002. J. Hydrol. 2009, 371, 129–141. [Google Scholar] [CrossRef] [Green Version]
- Robson, A.J. Evidence for trends in UK flooding. Phil. Trans. R. Soc. Lond. A 2002, 360, 1327–1343. [Google Scholar] [CrossRef]
- de Roo, A.; Odijk, M.; Schmuck, G.; Koster, E.; Lucieer, A. Assessing the effects of land use changes on floods in the Meuse and Oder catchment. Phys. Chem. Earth Part B 2001, 26, 593–599. [Google Scholar] [CrossRef]
- Ulbrich, U.; Fink, A. The January 1995 flood in Germany: Meteorological versus hydrological causes. Phys. Chem. Earth 1995, 20, 439–444. [Google Scholar] [CrossRef]
- WMO. State of the Global Climate 2020; World Meteorological Organization: Geneva, Switzerland, 2021. [Google Scholar]
- Blöschl, G.; Hall, J.; Viglione, A.; Perdigão, R.A.P.; Parajka, J.; Merz, B.; Lun, D.; Arheimer, B.; Aronica, G.T.; Bilibashi, A.; et al. Changing climate both increases and decreases European river floods. Nature 2019, 573, 108–111. [Google Scholar] [CrossRef]
- Stocker, T.F.; Qin, D.; Plattner, G.-K.; Tignor, M.M.B.; Allen, S.K.; Boschung, J.; Nauels, A.; Xia, Y.; Bex, V.; Midgley, P.M. (Eds.) Climate Change 2013: The Physical Science Basis. Working Group I Contribution to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change; Cambridge University Press: Cambridge, UK, 2013. [Google Scholar]
- Tapoglou, E.; Vozinaki, A.E.; Tsanis, I. Climate change impact on the frequency of hydrometeorological extremes in the island of Crete. Water 2019, 11, 587. [Google Scholar] [CrossRef] [Green Version]
- Wilcox, C.; Vischel, T.; Panthou, G.; Bodian, A.; Blanchet, J.; Descroix, L.; Quantin, G.; Cassé, C.; Tanimoun, B.; Kone, S. Trends in hydrological extremes in the Senegal and Niger Rivers. J. Hydrol. 2018, 566, 531–545. [Google Scholar] [CrossRef]
- Christensen, J.H.; Christensen, O.B. Severe summertime flooding in Europe. Nature 2003, 421, 805–806. [Google Scholar] [CrossRef]
- Palmer, T.N.; Räisänen, J. Quantifying the risk of extreme seasonal precipitation events in a changing climate. Nature 2002, 415, 512–514. [Google Scholar] [CrossRef]
- Gavrilović, L.; Milanović Pešić, A.; Urošev, M. A hydrological analysis of the greatest floods in Serbia in the 1960-2010 period. Carpathian J. Earth Environ. Sci. 2012, 7, 107–116. [Google Scholar]
- Bezak, N.; Brilly, M.; Šraj, M. Flood frequency analyses, statistical trends and seasonality analyses of discharge data: A case study of the Litija station on the Sava River. J. Flood Risk Manag. 2016, 9, 154–168. [Google Scholar] [CrossRef]
- Ilnicki, P.; Farat, R.; Górecki, K.; Lewandowski, P. Impact of climatic change on river discharge in the driest region of Poland. Hydrol. Sci. J. 2014, 59, 1117–1134. [Google Scholar] [CrossRef] [Green Version]
- Leščešen, I.; Dolinaj, D. Regional flood frequency analysis of the Pannonian Basin. Water 2019, 11, 193. [Google Scholar] [CrossRef] [Green Version]
- Šraj, M.; Bezak, N. Comparison of time trend- and precipitation-informed models for assessing design discharges in variable climate. J. Hydrol. 2020, 589, 125374. [Google Scholar] [CrossRef]
- England, J.F., Jr.; Cohn, T.A.; Faber, B.A.; Stedinger, J.R.; Thomas, W.O., Jr.; Veilleux, A.G.; Kiang, J.E.; Mason, R.R., Jr. Guidelines for Determining Flood Flow Frequency—Bulletin 17C (ver. 1.1), Book 4, Chapter B5; U.S. Geological Survey: Reston, VA, USA, 2019.
- Thorarinsdottir, T.L.; Hellton, K.H.; Steinbakk, G.H.; Schlichting, L.; Engeland, K. Bayesian regional flood frequency analysis for large catchments. Water Resour. Res. 2018, 54, 6929–6947. [Google Scholar] [CrossRef] [Green Version]
- Cassalho, F.; Beskow, S.; de Mello, C.R.; de Moura, M.M. Regional flood frequency analysis using L-moments for geographically defined regions: An assessment in Brazil. J. Flood Risk Manag. 2019, 12, e12453. [Google Scholar] [CrossRef]
- Leščešen, I.; Šraj, M.; Pantelić, M.; Dolinaj, D. Assessing the impact of climate on annual and seasonal discharges at the Sremska Mitrovica station on the Sava River, Serbia. Water Supply 2022, 22, 195–207. [Google Scholar] [CrossRef]
- Šraj, M.; Bezak, N.; Brilly, M. Bivariate flood frequency analysis using the copula function: A case study of the Litija station on the Sava River. Hydrol. Process. 2014, 29, 225–238. [Google Scholar] [CrossRef]
- Bormann, H.; Pinter, N.; Elfert, S. Hydrological signatures of flood trends on German rivers: Flood frequencies, flood heights and specific stages. J. Hydrol. 2011, 404, 50–66. [Google Scholar] [CrossRef]
- Hailegeorgis, T.T.; Alfredsen, K. Regional flood frequency analysis and prediction in ungauged basins including estimation of major uncertainties for mid-Norway. J. Hydrol. Reg. Stud. 2017, 9, 104–126. [Google Scholar] [CrossRef]
- Rutkowska, A.; Żelazny, M.; Kohnová, S.; Łyp, M.; Banasik, K. Regional L-moment-based flood frequency analysis in the upper Vistula River basin, Poland. Pure Appl. Geophys. 2017, 174, 701–721. [Google Scholar] [CrossRef]
- Leščešen, I.; Urošev, M.; Dolinaj, D.; Pantelić, M.; Telbisz, T.; Varga, G.; Savić, S.; Milošević, D. Regional flood frequency analysis based on L-moment approach (case study Tisza River basin). Water Resour. 2019, 46, 853–860. [Google Scholar] [CrossRef]
- Morlot, M.; Brilly, M.; Šraj, M. Characterisation of the floods in the Danube River basin through flood frequency and seasonality analysis. Acta Hydrotech. 2019, 32, 73–89. [Google Scholar] [CrossRef]
- Hosking, J.R.M.; Wallis, J.R. Regional Frequency Analysis: An Approach Based on L-Moments; Cambridge University Press: Cambridge, UK, 1997. [Google Scholar]
- Kar, K.K.; Yang, S.-K.; Lee, J.-H.; Khadim, F.K. Regional frequency analysis for consecutive hour rainfall using L-moments approach in Jeju Island, Korea. Geoenviron. Disasters 2017, 4, 18. [Google Scholar] [CrossRef]
- Stadtherr, L.; Coumou, D.; Petoukhov, V.; Petri, S.; Rahmstorf, S. Record Balkan floods of 2014 linked to planetary wave resonance. Sci. Adv. 2016, 2, e1501428. [Google Scholar] [CrossRef] [Green Version]
- Vidmar, A.; Globevnik, L.; Koprivšek, M.; Sečnik, M.; Zabret, K.; Durović, B.; Anzeljc, D.; Kastelic, J.; Kobold, M.; Sušnik, M.; et al. The Bosna River floods in May 2014. Nat. Hazards Earth Syst. Sci. 2016, 16, 2235–2246. [Google Scholar] [CrossRef] [Green Version]
- Plavšić, J.; Vladiković, D.; Despotović, J. Floods in the Sava River basin in May 2014. In Monitoring, Modelling and Early Warning of Extreme Events Triggered by Heavy Rainfall; Ferrari, E., Versace, P., Eds.; University of Calabria: Cosenza, Italy, 2014; pp. 241–251. [Google Scholar]
- United Nations (UN); European Union (EU); World Bank (WB). Serbia Floods 2014; United Nations; European Union; World Bank: Belgrade, Serbia, 2014. [Google Scholar]
- Plavšić, J.; Vladiković, D.; Despotović, J. Hydrometeorological aspects of floods in May 2014 in the Sava River Basin and in Serbia. Voda Sanit. Teh. 2014, 44, 21–33. [Google Scholar]
- International Commission for the Protection of the Danube River (ICPDR); International Sava River Basin Commission (ISRBC). Floods in May 2014 in the Sava River Basin: Brief Overview of Key Events and Lessons Learned; International Commission for the Protection of the Danube River: Vienna, Austria, 2015. [Google Scholar]
- Ladan, T. Hrvatska Enciklopedija, Mrežno Izdanje; Sava; Leksikogr. Zavod Miroslav Krleža [Miroslav Krleža Institute of Lexicography]: Zagreb, Croatia, 2021. [Google Scholar]
- Dolšak, D.; Bezak, N.; Šraj, M. Temporal characteristics of rainfall events under three climate types in Slovenia. J. Hydrol. 2016, 541, 1395–1405. [Google Scholar] [CrossRef]
- Lavtar, K.; Bezak, N.; Šraj, M. Rainfall-runoff modeling of the nested non-homogeneous Sava River sub-catchments in Slovenia. Water 2020, 12, 128. [Google Scholar] [CrossRef] [Green Version]
- Ulaga, P.; Kobold, M.; Frantar, F. Trends of river discharges in Slovenia. IOP Conf. Ser. Earth Environ. Sci. 2008, 4, 012030. [Google Scholar] [CrossRef]
- Čanjevac, I.; Orešić, D. Changes in discharge regimes of rivers in Croatia. Acta Geogr. Slov. 2018, 58, 7–18. [Google Scholar] [CrossRef] [Green Version]
- Mudelsee, M. Statistical Analysis of Climate Extremes; Cambridge University Press: Cambridge, UK, 2020. [Google Scholar]
- Urošev, M.; Dolinaj, D.; Leščešen, I. Hydrological droughts in the Južna Morava River basin (Serbia). Geogr. Pannon. 2016, 20, 197–207. [Google Scholar] [CrossRef] [Green Version]
- Gumbel, E.J. Statistics of Extremes; Columbia University Press: New York, NY, USA, 1958. [Google Scholar]
- Bickel, P. Robust estimation. In Encyclopedia of Statistical Sciences; Kotz, S., Johnson, N.L., Read, C.B., Eds.; Wiley: New York, NY, USA, 1988; Volume 8, pp. 157–163. [Google Scholar]
- Bezak, N.; Brilly, M.; Šraj, M. Comparison between the peaks-over-threshold method and the annual maximum method for flood frequency analysis. Hydrol. Sci. J. 2014, 59, 959–977. [Google Scholar] [CrossRef] [Green Version]
- Faulkner, D.; Warren, S.; Spencer, P.; Sharkey, P. Can we still predict the future from the past? Implementing non-stationary flood frequency analysis in the UK. J. Flood Risk Manag. 2020, 13, e12582. [Google Scholar] [CrossRef] [Green Version]
- Kousar, S.; Khan, A.R.; Hassan, M.U.; Noreen, Z.; Bhatti, S.H. Some best-fit probability distributions for at-site flood frequency analysis of the Ume River. J. Flood Risk Manag. 2020, 13, e12640. [Google Scholar] [CrossRef]
- Mudelsee, M. Climate Time Series Analysis: Classical Statistical and Bootstrap Methods, 2nd ed.; Springer: Cham, Switzerland, 2014. [Google Scholar]
- Fisher, R.A.; Tippett, L.H.C. Limiting forms of the frequency distribution of the largest or smallest member of a sample. Math. Proc. Camb. Phil. Soc. 1928, 24, 180–190. [Google Scholar] [CrossRef]
- Fréchet, M. Sur la loi probabilité de l’écart maximum. Ann. Soc. Pol. Math. 1927, 6, 93–116. [Google Scholar]
- Karim, F.; Hasan, M.; Marvanek, S. Evaluating annual maximum and partial duration series for estimating frequency of small magnitude floods. Water 2017, 9, 481. [Google Scholar] [CrossRef] [Green Version]
- Zhang, Z.; Stadnyk, T.A. Investigation of attributes for identifying homogeneous flood regions for regional flood frequency analysis in Canada. Water 2020, 12, 2570. [Google Scholar] [CrossRef]
- Zalnezhad, A.; Rahman, A.; Vafakhah, M.; Samali, B.; Ahamed, F. Regional flood frequency analysis using the FCM-ANFIS algorithm: A case study in South-eastern Australia. Water 2022, 14, 1608. [Google Scholar] [CrossRef]
- St. George, S.; Mudelsee, M. The weight of the flood-of-record in flood frequency analysis. J. Flood Risk Manag. 2019, 12, e12512. [Google Scholar] [CrossRef] [Green Version]
- Robson, A.; Reed, D. Flood Estimation Handbook, Volume 3, Statistical Procedures for Flood Frequency Estimation; Centre for Ecology & Hydrology: Wallingford, UK, 1999. [Google Scholar]
- Bogdanowicz, E.; Kochanek, K.; Strupczewski, W.G. The weighted function method: A handy tool for flood frequency analysis or just a curiosity? J. Hydrol. 2018, 559, 209–221. [Google Scholar] [CrossRef]
- Rahman, A.S.; Rahman, A.; Zaman, M.A.; Haddad, K.; Ahsan, A.; Imteaz, M. A study on selection of probability distributions for at-site flood frequency analysis in Australia. Nat. Hazards 2013, 69, 1803–1813. [Google Scholar] [CrossRef]
- Hosking, J.R.M.; Wallis, J.R. Some statistics useful in regional frequency analysis. Water Resour. Res. 1993, 29, 271–281. [Google Scholar] [CrossRef]
- Peel, M.C.; Wang, Q.J.; Vogel, R.M.; McMahon, T.A. The utility of L-moment ratio diagrams for selecting a regional probability distribution. Hydrol. Sci. J. 2001, 46, 147–155. [Google Scholar] [CrossRef]
- Stephens, M.A. Kolmogorov–Smirnov-type tests of fit. In Encyclopedia of Statistical Sciences; Kotz, S., Johnson, N.L., Read, C.B., Eds.; Wiley: New York, NY, USA, 1983; Volume 4, pp. 398–402. [Google Scholar]
- Urošev, M.; Leščešen, I.; Štrbac, D.; Dolinaj, D. Extreme hydrological situations on Danube River—Case study Bezdan hydrological station (Serbia). In Sustainable Hydraulics in the Era of Global Change; Erpicum, S., Dewals, B., Archambeau, P., Pirotton, M., Eds.; Taylor & Francis: London, UK, 2016; p. 137. [Google Scholar]
- Bhat, M.S.; Alam, A.; Ahmad, B.; Kotlia, B.S.; Farooq, H.; Taloor, A.K.; Ahmad, S. Flood frequency analysis of river Jhelum in Kashmir basin. Quat. Int. 2019, 507, 288–294. [Google Scholar] [CrossRef]
- Kovacevic-Majkic, J.; Urosev, M. Trends of mean annual and seasonal discharges of rivers in Serbia. J. Geogr. Inst. Jovan Cvijic 2014, 64, 143–160. [Google Scholar] [CrossRef]
- Arnell, N.W.; Gosling, S.N. The impacts of climate change on river flow regimes at the global scale. J. Hydrol. 2013, 486, 351–364. [Google Scholar] [CrossRef]
- Schneider, C.; Laizé, C.L.R.; Acreman, M.C.; Flörke, M. How will climate change modify river flow regimes in Europe? Hydrol. Earth Syst. Sci. 2013, 17, 325–339. [Google Scholar] [CrossRef] [Green Version]
- Stagl, J.C.; Hattermann, F.F. Impacts of climate change on the hydrological regime of the Danube River and its tributaries using an ensemble of climate scenarios. Water 2015, 7, 6139–6172. [Google Scholar] [CrossRef]
- Ahmad, I.; Fawad, M.; Akbar, M.; Abbas, A.; Zafar, H. Regional frequency analysis of annual peak flows in Pakistan using linear combination of order statistics. Pol. J. Environ. Stud. 2016, 25, 2255–2264. [Google Scholar] [CrossRef]
- Zabret, K.; Brilly, M. Hydrological regionalisation of flood frequency analyses in Slovenia. Acta Hydrotech. 2014, 27, 139–156. [Google Scholar]
- Saf, B. Regional flood frequency analysis using L-moments for the West Mediterranean region of Turkey. Water Resour Manag. 2009, 23, 531–551. [Google Scholar] [CrossRef]
- Mosaffaie, J. Comparison of two methods of regional flood frequency analysis by using L-moments. Water Resour. 2015, 42, 313–321. [Google Scholar] [CrossRef]
- Čanjevac, I.; Orešić, D. Contemporary changes of mean annual and seasonal river discharges in Croatia. Hrvat. Geogr. Glas. 2015, 77, 7–27. [Google Scholar] [CrossRef] [Green Version]
- Steiger, R. The impact of snow scarcity on ski tourism: An analysis of the record warm season 2006/2007 in Tyrol (Austria). Tour. Rev. 2011, 66, 4–13. [Google Scholar] [CrossRef]
- Aziz, M.A.; Moniruzzaman, M.; Tripathi, A.; Hossain, M.I.; Ahmed, S.; Rahaman, K.R.; Rahman, F.; Ahmed, R. Delineating flood zones upon employing synthetic aperture data for the 2020 flood in Bangladesh. Earth Syst. Environ. 2022. [Google Scholar] [CrossRef]
- Farhadi, H.; Najafzadeh, M. Flood risk mapping by remote sensing data and random forest technique. Water 2021, 13, 3115. [Google Scholar] [CrossRef]
- Johnson, N.L.; Kotz, S.; Balakrishnan, N. Continuous Univariate Distributions, 2nd ed.; Wiley: New York, NY, USA, 1994; Volume 1. [Google Scholar]
- Johnson, N.L.; Kotz, S.; Balakrishnan, N. Continuous Univariate Distributions, 2nd ed.; Wiley: New York, NY, USA, 1995; Volume 2. [Google Scholar]
- Singh, V.P. Entropy-Based Parameter Estimation in Hydrology; Springer: Dordrecht, The Netherlands, 1998. [Google Scholar]

| Station | Country | Elevation (m a.s.l.) | Location (River-km) | Basin Area (km2) |
|---|---|---|---|---|
| Radovljica | Slovenia | 408 | 901 | 908 |
| Čatež | Slovenia | 137 | 737 | 10186 |
| Zagreb | Croatia | 112 | 664 | 12450 |
| Jasenovac | Croatia | 87 | 501 | 38953 |
| Županja | Croatia | 76 | 262 | 62891 |
| S. Mitrovica | Serbia | 72 | 139 | 87966 |
| Station | n | Mean (m3/s) | Median (m3/s) | Maximum * (m3/s) | STD (m3/s) | Skewness † | Kurtosis † |
|---|---|---|---|---|---|---|---|
| Radovljica | 60 | 445 | 433 | 809 | 149 | 0.60 | −0.39 |
| Čatež | 60 | 1744 | 1727 | 3811 | 588 | 0.95 | 1.49 |
| Zagreb | 60 | 1664 | 1643 | 3005 | 441 | 0.59 | 0.07 |
| Jasenovac ‡ | 56 | 2078 | 2089 | 2814 | 302 | 0.36 | −0.69 |
| Županja | 60 | 2915 | 2843 | 5317 | 573 | 1.26 | 3.66 |
| S. Mitrovica | 60 | 4027 | 3823 | 6420 | 910 | 0.56 | 0.49 |
| Station | * |
|---|---|
| Radovljica | 0.5 ± 1.1 |
| Čatež | 3.3 ± 4.6 |
| Zagreb | 1.9 ± 4.5 |
| Jasenovac | 3.1 ± 2.4 |
| Županja | −0.7 ± 4.2 |
| S. Mitrovica | −9.6 ± 6.4 |
| 0.14 | 0.13 | 0.14 | 0.04 | 0.07 | 0.077 |
| Distribution | Radovljica | Čatež | Zagreb | Jasenovac | Županja | S. Mitrovica |
|---|---|---|---|---|---|---|
| GEV | 0.3580 | 0.3516 | 0.3576 | 0.3280 | 0.3516 | 0.3575 |
| GLO | 0.3664 | 0.3607 | 0.3754 | 0.3674 | 0.3607 | 0.3785 |
| Gumbel | 0.3597 | 0.3611 | 0.3589 | 0.3399 | 0.3621 | 0.3612 |
| LNIII | 0.3575 | 0.3518 | 0.3578 | 0.3575 | 0.3515 | 0.3580 |
| LPIII | 0.3827 | 0.3598 | 0.3697 | 0.3798 | 0.3498 | 0.3666 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Leščešen, I.; Šraj, M.; Basarin, B.; Pavić, D.; Mesaroš, M.; Mudelsee, M. Regional Flood Frequency Analysis of the Sava River in South-Eastern Europe. Sustainability 2022, 14, 9282. https://doi.org/10.3390/su14159282
Leščešen I, Šraj M, Basarin B, Pavić D, Mesaroš M, Mudelsee M. Regional Flood Frequency Analysis of the Sava River in South-Eastern Europe. Sustainability. 2022; 14(15):9282. https://doi.org/10.3390/su14159282
Chicago/Turabian StyleLeščešen, Igor, Mojca Šraj, Biljana Basarin, Dragoslav Pavić, Minučer Mesaroš, and Manfred Mudelsee. 2022. "Regional Flood Frequency Analysis of the Sava River in South-Eastern Europe" Sustainability 14, no. 15: 9282. https://doi.org/10.3390/su14159282
APA StyleLeščešen, I., Šraj, M., Basarin, B., Pavić, D., Mesaroš, M., & Mudelsee, M. (2022). Regional Flood Frequency Analysis of the Sava River in South-Eastern Europe. Sustainability, 14(15), 9282. https://doi.org/10.3390/su14159282









