A Physical Model-Based Data-Driven Approach to Overcome Data Scarcity and Predict Building Energy Consumption
Abstract
:1. Introduction
2. Description of Target Building
3. Proposed Hybrid Model
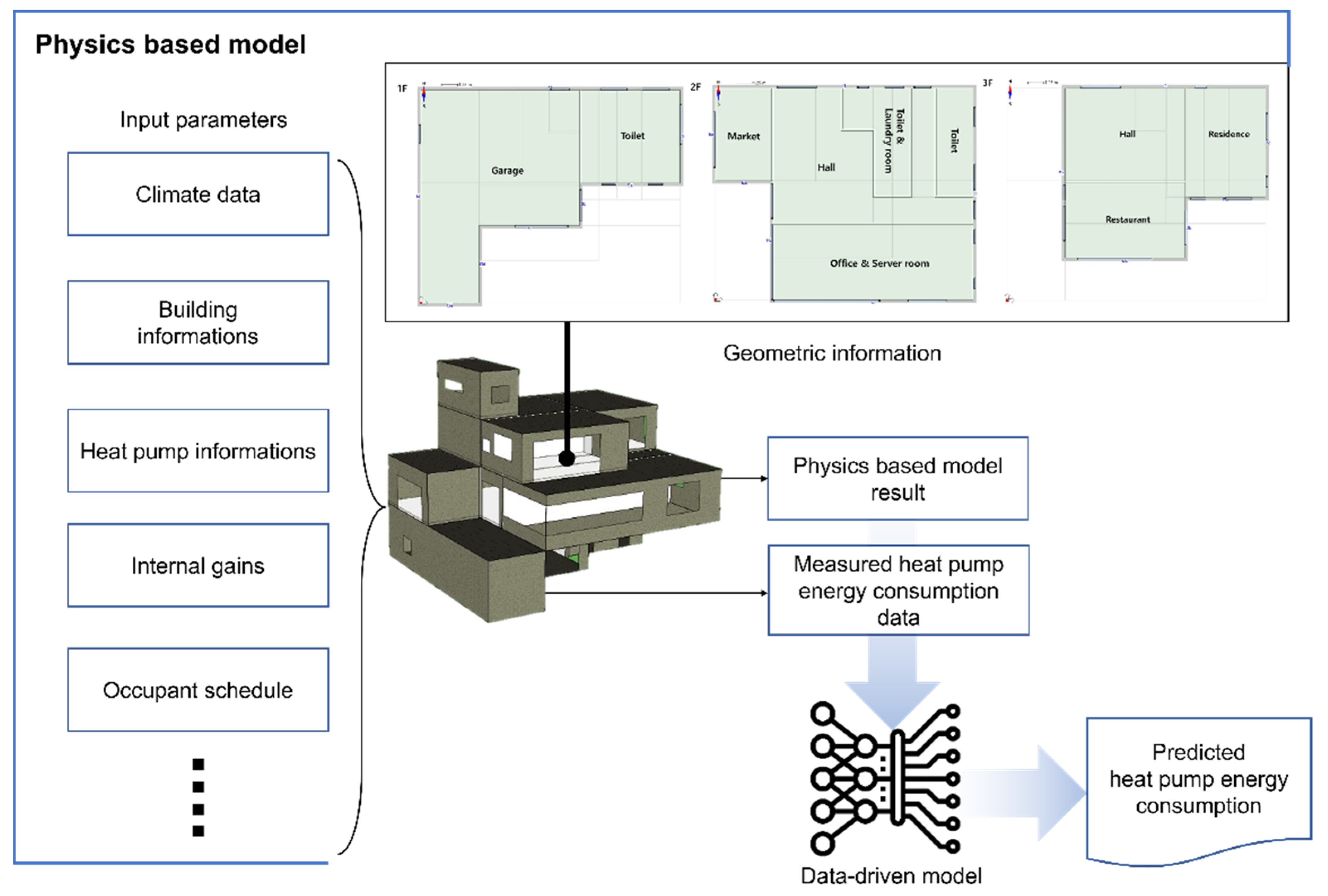
3.1. Development of Physical Model of Target Building
3.2. Reference Data-Driven Model
3.3. Hybrid Data-Driven Model Using Physical Model Results as Input Parameters
4. Results
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| SHGC | Solar heat gain coefficient |
| BEMS | Building energy management system |
| LSTM | Long short-term memory networks |
| RNN | Recurrent neural networks |
| MAE | Mean absolute error (%) |
| cvRMSE | Coefficient of variation of root mean square error (%) |
| cov | Covariance |
| E | Heat pump energy consumption (kWh) |
| T | Total actual period of use of the heat pump (hour) |
| P | Input variable |
| Subscript | |
| meas | Measured value |
| pred | Prediction value |
| Greek | |
| ρ | Correlation coefficient |
| σ | Standard deviation |
References
- IEA. Tracking Buildings 2021; IEA: Paris, France, 2021; Available online: https://www.iea.org/reports/tracking-buildings-2021 (accessed on 22 March 2022).
- González-Torres, M.; Pérez-Lombard, L.; Coronel, J.F.; Maestre, I.R.; Yan, D. A review on buildings energy information: Trends, end-uses, fuels and drivers. Energy Rep. 2022, 8, 626–637. [Google Scholar] [CrossRef]
- IEA. IEA World Energy Balances 2021; IEA: Paris, France, 2021; Available online: https://www.iea.org/data-and-statistics/data-product/world-energy-statistics-and-balances (accessed on 22 March 2022).
- Fumo, N. A review on the basics of building energy estimation. Renew. Sustain. Energy Rev. 2014, 31, 53–60. [Google Scholar] [CrossRef]
- Li, C.Z.; Zhang, L.; Liang, X.; Xiao, B.; Tam VW, Y.; Lai, X.; Chen, Z. Advances in the research of building energy saving. Energy Build. 2021, 254, 111556. [Google Scholar] [CrossRef]
- Liu, S.; Zou, Y.; Ji, W.; Zhang, Q.; Ahmed, A.; Han, X.; Shen, Y.; Zhang, S. Energy-saving potential prediction models for large-scale building: A state-of-the-art review. Renew. Sustain. Energy Rev. 2022, 156, 111992. [Google Scholar] [CrossRef]
- Bünning, F. Marrying Machine Learning and Model Predictive Control for efficient Building Energy Management. Ph.D. Thesis, ETH Zurich, 2021. Available online: https://www.research-collection.ethz.ch/handle/20.500.11850/526883 (accessed on 22 March 2022).
- Deb, C.; Dai, Z.; Schlueter, A. A machine learning-based framework for cost-optimal building retrofit. Appl. Energy 2021, 294, 116990. [Google Scholar] [CrossRef]
- Chen, Y.; Guo, M.; Chen, Z.; Chen, Z.; Ji, Y. Physical energy and data-driven models in building energy prediction: A review. Energy Rep. 2022, 8, 2656–2671. [Google Scholar] [CrossRef]
- Al-Hyari, L.; Kassai, M. Development of TRNSYS model for energy performance simulation of variable refrigerant flow air-conditioning system combined with energy recovery ventilation. Int. J. Green Energy 2021, 18, 390–401. [Google Scholar] [CrossRef]
- Im, P.; Joe, J.; Bae, Y.; New, J.R. Empirical validation of building energy modeling for multi-zones commercial buildings in cooling season. Appl. Energy 2020, 261, 114374. [Google Scholar] [CrossRef]
- Chen, Y.; Chen, Z.; Xu, P.; Li, W.; Sha, H.; Yang, Z.; Li, G.; Hu, C. Quantification of electricity flexibility in demand response: Office building case study. Energy 2019, 188, 116054. [Google Scholar] [CrossRef]
- Soleimani-Mohseni, M.; Nair, G.; Hasselrot, R. Energy simulation for a high-rise building using IDA ICE: Investigations in different climates. Build. Simul. 2016, 9, 629–640. [Google Scholar] [CrossRef]
- Sun, Y.; Haghighat, F.; Fung, B.C.M. A review of the-state-of-the-art in data-driven approaches for building energy prediction. Energy Build. 2020, 221, 110022. [Google Scholar] [CrossRef]
- An, D.; Kim, N.H.; Choi, J.H. Practical options for selecting data-driven or physics-based prognostics algorithms with reviews. Reliab. Eng. Syst. Saf. 2015, 133, 223–236. [Google Scholar] [CrossRef]
- Dong, B.; Li, Z.; Rahman, S.M.M.; Vega, R. A hybrid model approach for forecasting future residential electricity consumption. Energy Build. 2016, 117, 341–351. [Google Scholar] [CrossRef]
- Amasyali, K.; El-Gohary, N. Hybrid approach for energy consumption prediction: Coupling data-driven and physical approaches. Energy Build. 2022, 259, 111758. [Google Scholar] [CrossRef]
- Xu, X.; Taylor, J.E.; Pisello, A.L.; Culligan, P.J. The impact of place-based affiliation networks on energy conservation: An holistic model that integrates the influence of buildings, residents and the neighborhood context. Energy Build. 2012, 55, 637–646. [Google Scholar] [CrossRef]
- Li, A.; Xiao, F.; Fan, C.; Hu, M. Development of an ANN-based building energy model for information-poor buildings using transfer learning. Build. Simul. 2021, 14, 89–101. [Google Scholar] [CrossRef]
- Korea Meteorological Administration. Available online: https://www.weather.go.kr/ (accessed on 15 October 2021).
- Martin, M.; Berdahl, P. Characteristics of infrared sky radiation in the United States. Sol. Energy 1984, 33, 321–336. [Google Scholar] [CrossRef] [Green Version]
- Kasten, F.; Czeplak, G. Solar and terrestrial radiation dependent on the amount and type of cloud. Sol. Energy 1980, 24, 177–189. [Google Scholar] [CrossRef]
- ISO 13790; Energy Performance of Buildings-Calculation of Energy Use for Space Heating and Cooling. 2008. Available online: https://www.iso.org/obp/ui/#iso:std:iso:13790:ed-2:v1:en (accessed on 22 March 2022).
- Cortez, B.; Carrera, B.; Kim, Y.J.; Jung, J.Y. An architecture for emergency event prediction using LSTM recurrent neural networks. Expert Syst. Appl. 2018, 97, 315–324. [Google Scholar] [CrossRef]
- Wang, Z.; Hong, T.; Piette, M.A. Building thermal load prediction through shallow machine learning and deep learning. Appl. Energy 2020, 263, 114683. [Google Scholar] [CrossRef] [Green Version]
- Siami-Namini, S.; Tavakoli, N.; Namin, A.S. A comparison of ARIMA and LSTM in forecasting time series. In Proceedings of the 2018 17th IEEE International Conference on Machine Learning and Applications (ICMLA), Orlando, FL, USA, 17–20 December 2018; pp. 1394–1401. [Google Scholar] [CrossRef]
- Di Natale, L.; Svetozarevic, B.; Heer, P.; Jones, C.N. Physically Consistent Neural Networks for building thermal modeling: Theory and analysis. arXiv 2021, arXiv:2112.03212. [Google Scholar]
- Ramachandran, P.; Zoph, B.; Le, Q.V. Searching for activation functions. arXiv 2017, arXiv: 1710.05941. [Google Scholar] [CrossRef]
- Li, L.; Jamieson, K.; DeSalvo, G.; Rostamizadeh, A.; Talwalkar, A. Hyperband: A novel bandit-based approach to hyperparameter optimization. J. Mach. Learn. Res. 2017, 18, 6765–6816. [Google Scholar]
- Jeon, B.K.; Kim, E.J. Next-day prediction of hourly solar irradiance using local weather forecasts and LSTM trained with non-local data. Energies 2020, 13, 5258. [Google Scholar] [CrossRef]
- American Society of Heating, Ventilating, and Air Conditioning Engineers (ASHRAE). Errata Sheet for ASHRAE Guideline 14-2002, Measurement of Energy and Demand Savings; American Society of Heating, Ventilating, and Air Conditioning Engineers: Atlanta, GA, USA, 2008. [Google Scholar]
- Guyon, I.; Elisseeff, A. An introduction to variable and feature selection. J. Mach. Learn. Res. 2003, 3, 1157–1182. [Google Scholar]









| Type | Office | ||
|---|---|---|---|
| Construction year | 2020 | ||
| Building footprint (m2) | 413.35 | ||
| Gross floor area (m2) | 840.98 | ||
| Building-to-cover ratio | 10.33 | ||
| Floor area ratio | 17.18 | ||
| Height (m) | 15 | ||
| Structure | Reinforced concrete structure | ||
| Area and height of each floor | F1 | Floor area (m2) | 234.34 |
| Height (m) | 4.2 | ||
| F2 | Floor area (m2) | 285.81 | |
| Height (m) | 3.85 | ||
| F3 | Floor area (m2) | 166.90 | |
| Height (m) | 3.5 | ||
| Roof space | Floor area (m2) | 23.76 | |
| Height (m) | 3.45 | ||
| U-Value (W/m2K) | Solar Heat Gain Coefficient (-) | |
|---|---|---|
| External wall | 0.2733 | - |
| Internal wall | 0.2854 | - |
| Ceiling | 0.2511 | - |
| Floor | 0.2520 | - |
| Windows, curtain wall | 1.1000 | 0.620 |
| Windows at office | 0.9000 | 0.460 |
| Glass doors | 1.2600 | 0.212 |
| Type | Cooling Capacity (kW) | Cooling COP | Heating Capacity (kW) | Heating COP | Conditioning Area and Number of Units | ||
|---|---|---|---|---|---|---|---|
| Floor | Conditioning Area (m2) | Units | |||||
Wall-mounted type | 3.2 | 5.37 | 3.6 | 2.82 | F1 | - | - |
| F2 | 146.94 | 4 | |||||
| F3 | 52.53 | 2 | |||||
| Total | 199.47 | 6 | |||||
Multi type  | 6 | 5.7 | 7.2 | 3.1 | F1 | 55.11 | 2 |
| F2 | 123.27 | 4 | |||||
| F3 | - | - | |||||
| Total | 178.38 | 6 | |||||
High-capacity type | 11 | 5 | 13.2 | 3 | F1 | - | - |
| F2 | - | - | |||||
| F3 | 54.68 | 1 | |||||
| Total | 54.68 | 1 | |||||
| Days | Time | Conditioned Zone (W/m2) | Unconditioned Zone (W/m2) |
|---|---|---|---|
| Weekdays | 07:00–17:00 | 20 | 8 |
| 17:00–23:00 | 2 | 1 | |
| 23:00–07:00 | 2 | 1 | |
| Weekend | 07:00–17:00 | 2 | 1 |
| 17:00–23:00 | 2 | 1 | |
| 23:00–07:00 | 2 | 1 |
| Min | Max | Step | |
|---|---|---|---|
| Number of neurons | 16 | 512 | 16 |
| Learning rate | 1 × 10−6 | 1 × 10−3 | - |
| Batch size | 16 | 64 | 16 |
| Dropout | 0 | 0.5 | 0.01 |
| Case 1 | Case 2 | Case 3 | Case 4 | |
|---|---|---|---|---|
| Number of neurons | 284 | 492 | 325 | 256 |
| Learning rate | 4.1065 × 10−4 | 4.7858 × 10−3 | 9.6969 × 10−4 | 8.9327 × 10−4 |
| Batch size | 48 | 48 | 32 | 48 |
| Dropout | 0.05 | 0.05 | 0 | 0 |
| Reference (A1) | Reference with Feature Selection (A2) | Proposed Hybrid Model (A3) | ||||
|---|---|---|---|---|---|---|
| cvRMSE (%) | MAE (%) | cvRMSE (%) | MAE (%) | cvRMSE (%) | MAE (%) | |
| Case 1 | 62.2 | 29.0 | 41.6 | 9.9 | 21.5 | 3.2 |
| Case 2 | 19.3 | 3.1 | 13.2 | 3.3 | 17.9 | 4.0 |
| Case 3 | 43.9 | 19.5 | 35.4 | 21.4 | 26.1 | 10.0 |
| Case 4 | 96.1 | 20.8 | 35.1 | 11.3 | 25.6 | 7.1 |
| Parameter | ρ (−) |
|---|---|
| Outdoor temperature | 0.63 |
| Relative humidity | 0.23 |
| Wind velocity | 0.078 |
| Wind direction | 0.067 |
| Diffuse irradiance | 0.028 |
| Direct normal irradiance | 0.012 |
| Cloudiness | 0.0064 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Oh, K.; Kim, E.-J.; Park, C.-Y. A Physical Model-Based Data-Driven Approach to Overcome Data Scarcity and Predict Building Energy Consumption. Sustainability 2022, 14, 9464. https://doi.org/10.3390/su14159464
Oh K, Kim E-J, Park C-Y. A Physical Model-Based Data-Driven Approach to Overcome Data Scarcity and Predict Building Energy Consumption. Sustainability. 2022; 14(15):9464. https://doi.org/10.3390/su14159464
Chicago/Turabian StyleOh, Kyoungcheol, Eui-Jong Kim, and Chang-Young Park. 2022. "A Physical Model-Based Data-Driven Approach to Overcome Data Scarcity and Predict Building Energy Consumption" Sustainability 14, no. 15: 9464. https://doi.org/10.3390/su14159464
APA StyleOh, K., Kim, E.-J., & Park, C.-Y. (2022). A Physical Model-Based Data-Driven Approach to Overcome Data Scarcity and Predict Building Energy Consumption. Sustainability, 14(15), 9464. https://doi.org/10.3390/su14159464






