Heat Transfer Modeling on High-Temperature Charging and Discharging of Deep Borehole Heat Exchanger with Transient Strong Heat Flux
Abstract
:1. Introduction
2. Materials and Methods
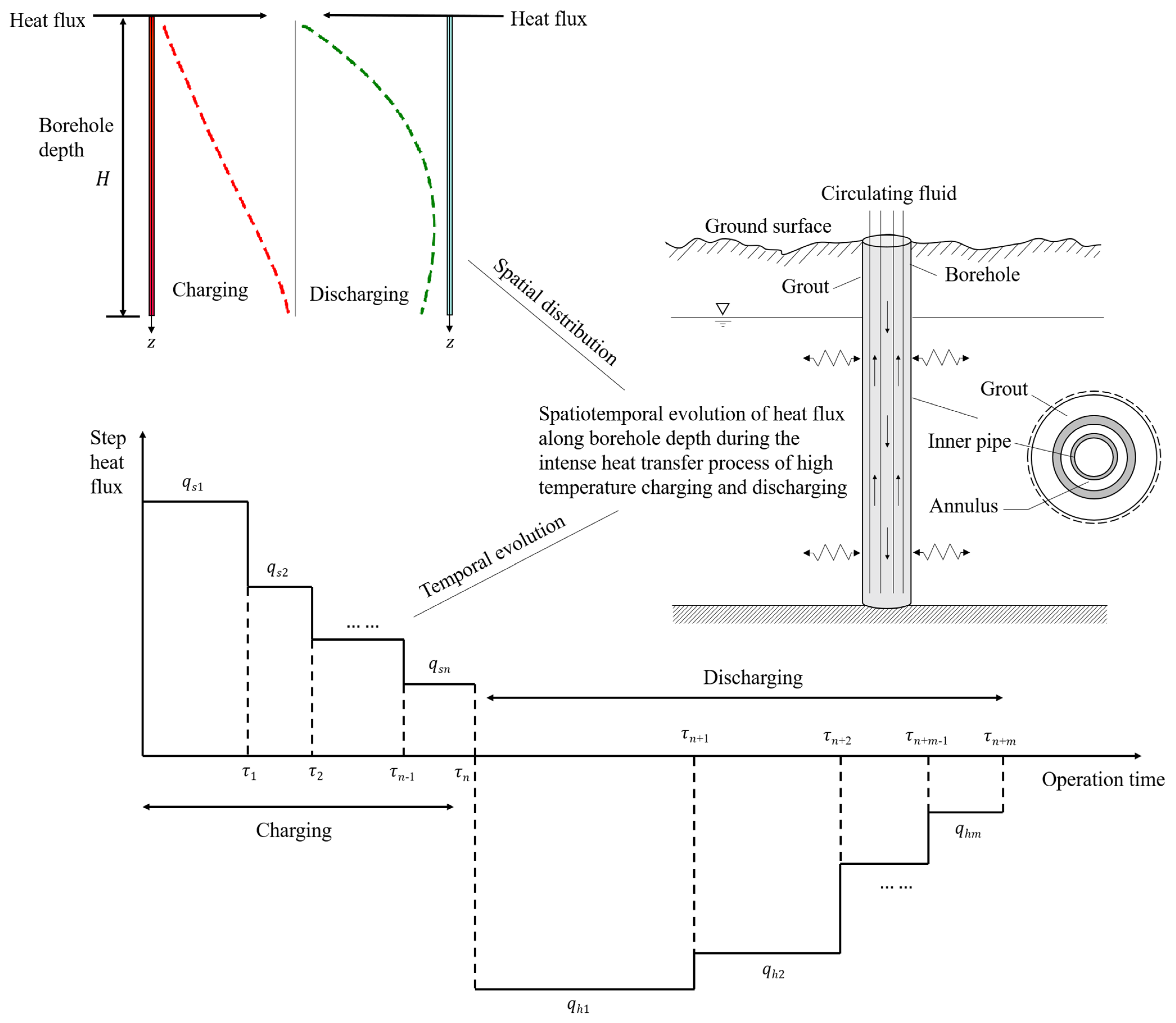
2.1. Transient Heat Transfer Model for DBHE
2.1.1. Model Assumptions
2.1.2. Unsteady Heat Transfer Outside the Borehole
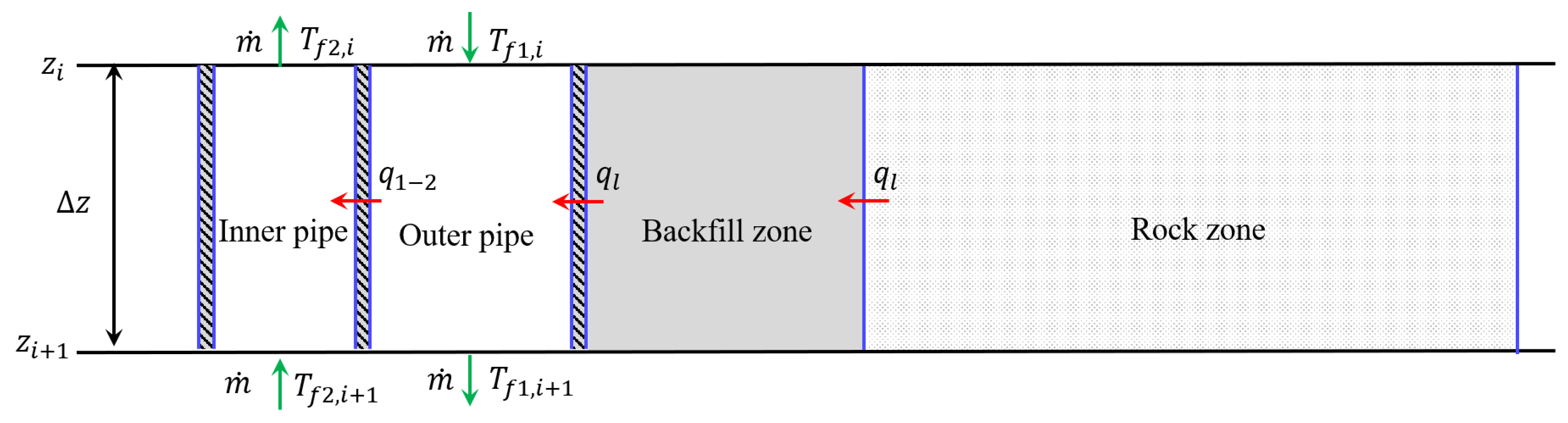
2.1.3. Quasi-Steady State Heat Transfer Inside the Borehole
- Heat storage mode for charging phase
- Heat extraction mode for discharging phase
2.2. High-Temperature Solar Collector Model
3. Results
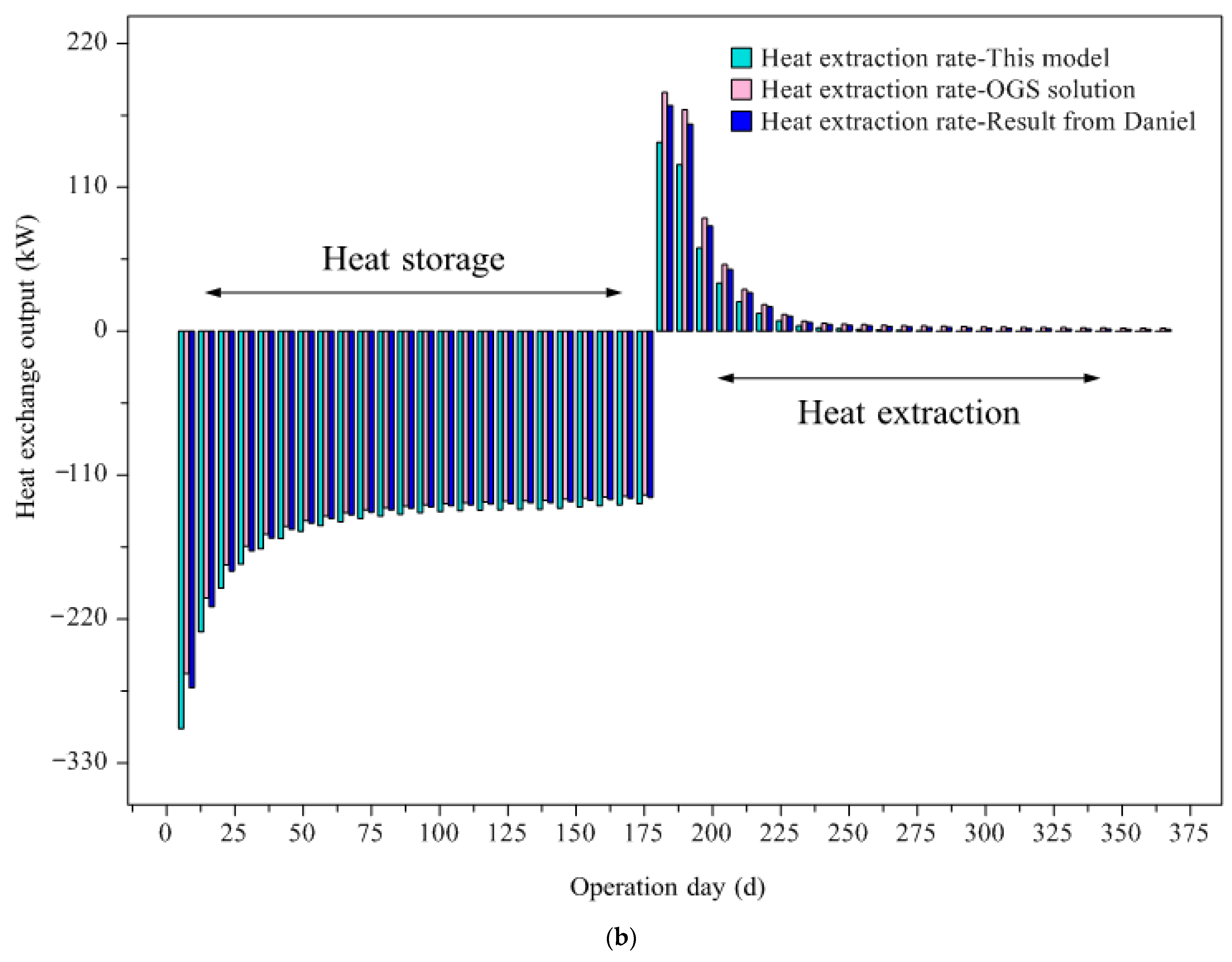
3.1. Model Validation Based on a Typical High-Temperature Heat Storage Case from the Literature
3.1.1. Simulation Accuracy of the Model
3.1.2. Simulation Efficiency of the Model
3.2. Model Validation against In Situ Field Test of a Demonstration Project
3.2.1. Project Overview
3.2.2. In Situ Field Test of the Project under Operation
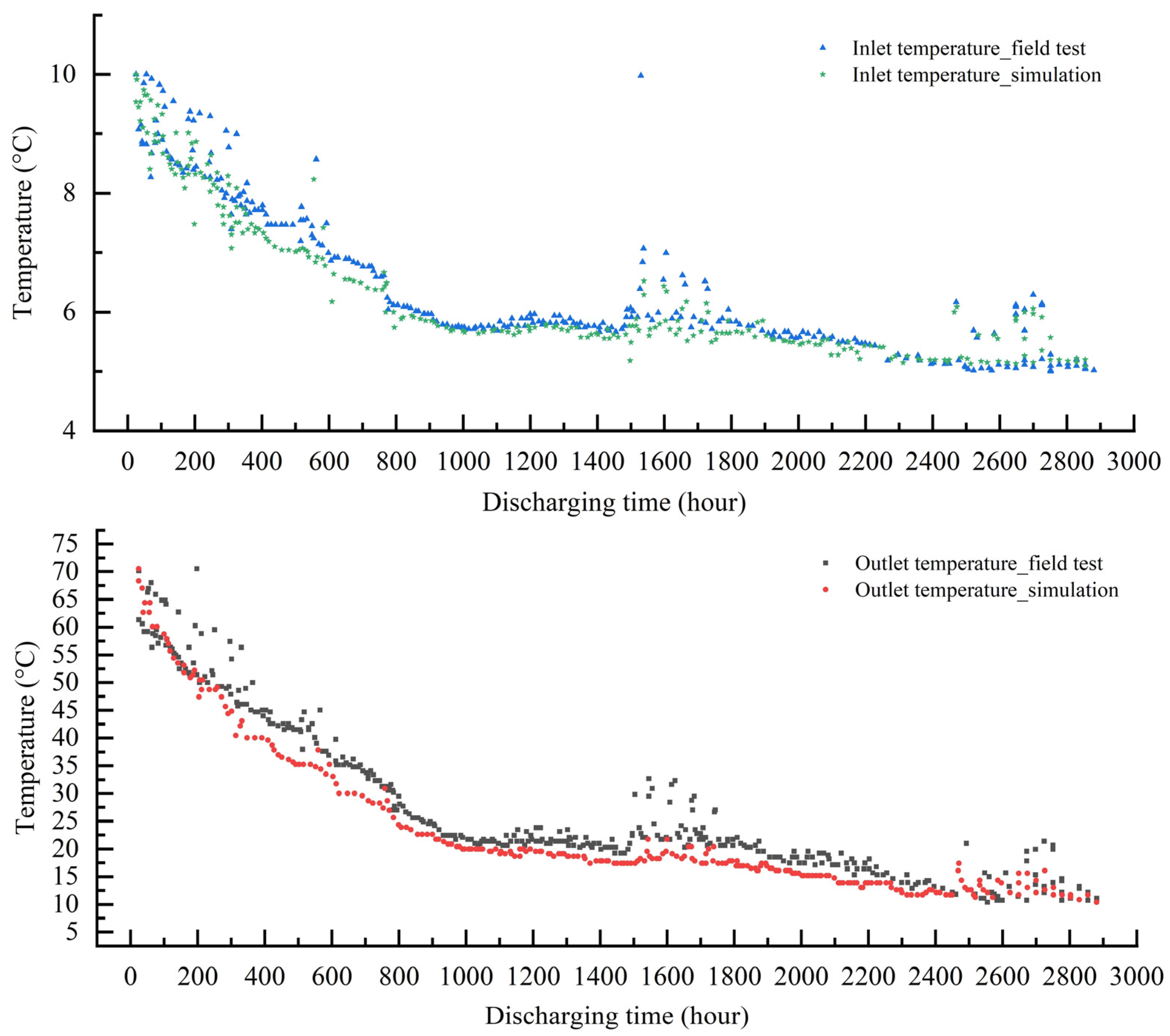
3.2.3. Model Validation during Charging
3.2.4. Model Validation during Discharging
3.2.5. Simulation Efficiency of the Model
4. Discussion
4.1. Advantages of the Heat Transfer Model for Deep BTES
- Generic applicability: The heat transfer model was developed to simulate both heat storage and heat extraction conditions of deep BTES. On one hand, this model couples unsteady heat conduction in the rock and quasi-steady heat transfer inside the deep borehole. The transient charging and discharging of DBHE could be simulated by minorly altering the flow circulation direction inside the borehole, as depicted in Figure 3, while heat conduction in the rock zone remains unchanged. Since the formulations including heat front propagation and heat flux density distribution along the depth are universal, therefore, they could be described in a generic way under charging or discharging of the deep BTES system. On the other hand, this modeling approach performs a heat transfer analysis of the DBHE underground and solar collector in Section 2.1 and Section 2.2 separately. The two major components represent storage and source in a typical energy system, and the corresponding mathematical formulations can be generalized for arbitrary deep BTES simulation with further improvement.
- Good accuracy: Through cross validation of the model in the typical high-temperature heat storage case, as well as the pilot demonstration project, large deviations are shown to mainly exist at the unsteady stage during the charging or discharging of DBHE, as shown in Table 3 and Table 10, while the simulation results are in excellent agreement with the OGS solution and field test data at the steady stage, according to Figure 8, Figure 9 and Figure 10. The prediction errors during both the charging and discharging phases are all around 5%, and they satisfy the accuracy requirement of engineering applications. Moreover, this model succeeded in depicting the dynamic evolution of extreme heat flux density and outlet water temperature in the pilot demonstration project, which was validated well against the OGS solution, as observed in Figure 11 and Figure 12. It could be seen that the large prediction error of the heat transfer model only existed in very short operation days during the initial unsteady stages of charging and discharging. Both relative errors under charging and discharging phases are within 5% during the steady state period. Hence, this model can simulate the challenging heat transfer problem with good accuracy.
- Easy implementation: No complex computations are involved in the overall simulation, as summarized in the flow chart of Figure 7. All the formulations are concise, without time-consuming iterations, which can be easily implemented by manual coding. In addition, this model could also be integrated into a HVAC system simulator such as TRNSYS or Energy-plus toolkits.
- High efficiency: Transient strong heat flux would appear during high-temperature charging and the subsequent discharging of DBHE. Extremely refined spatiotemporal resolution is required to capture the intense heat transfer, especially at the initial start-up. All the key physical laws of heat conduction in rock are formulated based on analytical solutions. Therefore, this model is featured with high computation efficiency in essence. Table 4 and Table 13 compare the simulation cost of both the charging and discharging phases of the deep BTES system, and demonstrate that our efficient heat transfer model achieves an acceleration ratio of 30 times, approximately relative to the fully numerical method.
4.2. Limitations of the Heat Transfer Model for Deep BTES
5. Conclusions
Author Contributions
Funding
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| Nomenclature | |
| BHE | Borehole heat exchanger |
| DBHE | Deep borehole heat exchanger |
| BTES | Borehole thermal energy storage |
| OGS | Open GeoSys |
| notation | |
| Depth of borehole | |
| Operation time of deep borehole heat exchanger | |
| Thermal diffusion coefficient | |
| Radius of borehole | |
| Drilling depth of borehole | |
| Thermal affecting radius | |
| Initial rock temperature distribution | |
| Rock temperature field | |
| Radial heat flux density along depth of borehole | |
| Cumulative heat released into or extracted from the rock segment | |
| Circulating flow rate | |
| Inlet temperature of circulating water | |
| Outlet temperature of circulating water | |
| Flow temperature distribution along annulus of deep borehole heat exchanger | |
| Flow temperature distribution along inner pipe of deep borehole heat exchanger | |
| Total heat storage amount during charging of deep borehole heat exchanger | |
| Total heat extraction output during discharging of deep borehole heat exchanger |
References
- Rybach, L.; Hopkirk, R. Shallow and deep borehole heat exchangers-achievements and prospects. In Proceedings of the 1st World Geothermal Congress (WGC1995), Florence, Italy, 18–31 May 1995; pp. 2133–2139. [Google Scholar]
- Sapinska, A.; Rosen, A.; Gonet, A.; Sliwa, T. Deep Borehole Heat Exchangers—A Conceptual and Comparative Review. Int. J. Air-Cond. Refrig. 2016, 24, 1630001. [Google Scholar] [CrossRef]
- Kohl, T.; Brenni, R.; Eugster, W. System performance of a deep borehole heat exchanger. Geothermics 2002, 31, 687–708. [Google Scholar] [CrossRef]
- Daniel, S. Simulation and Optimization of Medium Deep Borehole Thermal Energy Storage Systems. Ph.D. Thesis, Technische Universitat Darmstadt, Darmstadt, Germany, 2016. [Google Scholar]
- Deng, J.W.; Wei, Q.P.; Liang, M.; He, S.; Zhang, H. Field test on energy performance of medium-depth geothermal heat pump systems (MD-GHPs). Energy Build. 2019, 184, 289–299. [Google Scholar] [CrossRef]
- Bu, X.B.; Ran, Y.M.; Zhang, D.D. Experimental and simulation studies of geothermal single well for building heating. Renew. Energy 2019, 143, 1902–1909. [Google Scholar] [CrossRef]
- Cai, W.L.; Wang, F.H.; Chen, S.; Shao, H.B. Analysis of heat extraction performance and long-term sustainability for multiple deep borehole heat exchanger array: A project-based study. Appl. Energy 2021, 289, 116590. [Google Scholar] [CrossRef]
- Renaud, T.; Verdin, P.; Falcone, G. Numerical simulation of a deep borehole heat exchanger in the krafla geothermal system. Int. J. Heat Mass Transf. 2019, 143, 118496. [Google Scholar] [CrossRef]
- Kristian, B.; Wolfram, R.; Bastian, W.; Daniel, S.; Sebastian, H.; Ingo, S. Seasonal high temperature heat storage with medium deep borehole heat exchangers. Energy Procedia 2015, 76, 351–360. [Google Scholar]
- Bastian, W.; Wolfram, R.; Daniel, S. Characteristics of medium deep borehole thermal energy storage. Int. J. Energy Res. 2016, 40, 1855–1868. [Google Scholar]
- Fang, L.; Diao, N.R.; Shao, Z.K.; Zhu, K.; Fang, Z.H. A computationally efficient numerical model for heat transfer simulation of deep borehole heat exchangers. Energy Build. 2018, 167, 79–88. [Google Scholar] [CrossRef]
- Liu, J.; Wang, F.H.; Cai, W.L.; Wang, Z.H.; Wei, Q.P.; Deng, J.W. Numerical study on the effects of design parameters on the heat transfer performance of coaxial deep borehole heat exchanger. Int. J. Energy Res. 2019, 43, 6337–6352. [Google Scholar] [CrossRef]
- Luo, Y.Q.; Guo, H.S.; Meggers, F.; Zhang, L. Deep coaxial borehole heat exchanger: Analytical modeling and thermal analysis. Energy 2019, 185, 1298–1313. [Google Scholar] [CrossRef]
- Ma, L.; Zhao, Y.Z.; Yin, H.M.; Zhao, J.; Li, W.J.; Wang, H.Y. A coupled heat transfer model of medium-depth downhole coaxial heat exchanger based on the piecewise analytical solution. Energy Convers. Manag. 2019, 204, 112038. [Google Scholar] [CrossRef]
- Zhao, Y.Z.; Pang, Z.H.; Huang, Y.H.; Ma, Z.B. An efficient hybrid model for thermal analysis of deep borehole heat exchangers. Geotherm. Energy 2020, 8, 18. [Google Scholar] [CrossRef]
- Luo, Y.Q.; Yu, J.H.; Yan, T.; Zhang, L.; Liu, X. Improved analytical modeling and system performance evaluation of deep coaxial borehole heat exchanger with segmented finite cylinder source method. Energy Build. 2020, 212, 109829. [Google Scholar] [CrossRef]
- Luo, Y.Q.; Cheng, N.; Xu, G.Z. Analytical modeling and thermal analysis of deep coaxial borehole heat exchanger with stratified-seepage-segmented finite line source method (S3-FLS). Energy Build. 2021, 257, 111795. [Google Scholar] [CrossRef]
- Jordi, M. Large-Scale Underground Thermal Energy Storage Using Industrial Waste Heat to Supply District Heating. Bachelor’s Thesis, Universitat de Lleida, Lleida, Spain, 2014. [Google Scholar]
- Wang, H.J.; Qi, C.Y.; Wang, E.Y.; Zhao, J. A case study of underground thermal storage in a solar-ground coupled heat pump system for residential buildings. Renew. Energy 2009, 34, 307–314. [Google Scholar] [CrossRef]
- Diersch, H.; Bauer, D. Analysis, modeling and simulation of underground thermal energy storage (UTES) systems. In Woodhead Publishing Series in Energy, Advances in Thermal Energy Storage Systems; Woodhead Publishing: Sawston, UK, 2015; pp. 149–183. [Google Scholar]
- Farzin, R.; Alan, F. Solar community heating and cooling system with borehole thermal energy storage-Review of systems. Renew. Sustain. Energy Rev. 2016, 60, 1550–1561. [Google Scholar]
- Flynn, C.; Siren, K. Influence of location and design on the performance of a solar district heating system equipped with borehole seasonal storage. Renew. Energy 2015, 81, 377–388. [Google Scholar] [CrossRef]
- Emil, N.; Patrik, R. Performance evaluation of an industrial borehole thermal energy storage (BTES) project-Experiences from the first seven years of operation. Renew. Energy 2019, 143, 1022–1034. [Google Scholar]
- Xu, L.Y.; Torrens, I.; Guo, F.; Yang, X.D.; Hensen, J.L.M. Application of large underground seasonal thermal energy storage in district heating system: A model-based energy performance assessment of a pilot system in Chifeng, China. Appl. Therm. Eng. 2018, 137, 319–328. [Google Scholar] [CrossRef]
- Gao, L.H.; Zhao, J.; An, Q.S.; Liu, X.; Du, Y. Thermal performance of medium-to-high temperature aquifer thermal energy storage systems. Appl. Therm. Eng. 2019, 146, 898–909. [Google Scholar] [CrossRef]
- Gao, L.H.; Zhao, J.; An, Q.S.; Liu, X. A review on system performance studies of aquifer thermal energy storage. Energy Procedia 2017, 142, 3537–3545. [Google Scholar] [CrossRef]
- Hellstrom, G. Ground Heat Storage Thermal Analysis of Duct Storage Systems. Ph.D. Thesis, University of Lund, Lund, Sweden, 1991. [Google Scholar]
- Yang, H.; Cui, P.; Fang, Z.H. Vertical-borehole ground-coupled heat pumps: A review of models and systems. Appl. Energy 2010, 87, 16–27. [Google Scholar] [CrossRef]
- Zhang, F.F.; Fang, L.; Jia, L.R.; Man, Y.; Cui, P.; Zhang, W.K.; Fang, Z.H. A dimension reduction algorithm for numerical simulation of multi-borehole heat exchangers. Renew. Energy 2021, 179, 2235–2245. [Google Scholar] [CrossRef]
- Huang, Y.; Zhang, Y.; Xie, Y.; Zhang, Y.; Ma, J. Field test and numerical investigation on deep coaxial borehole heat exchanger based on distributed optical fiber temperature sensor. Energy 2020, 210, 118643. [Google Scholar] [CrossRef]
- Hu, X.C.; Banks, J.; Wu, L.P.; Liu, W.V. Numerical modeling of a coaxial borehole heat exchanger to exploit geothermal energy from abandoned petroleum wells in Hinton, Alberta. Renew. Energy 2020, 148, 1110–1123. [Google Scholar] [CrossRef]
- Wang, Z.H.; Wang, F.H.; Liu, J.; Ma, Z.J.; Han, E.S.; Song, M.J. Field test and numerical investigation on the heat transfer characteristics and optimal design of the heat exchangers of a deep borehole ground source heat pump system. Energy Convers. Manag. 2017, 153, 603–615. [Google Scholar] [CrossRef]
- Zhao, Y.Z.; Ma, Z.B.; Pang, Z.H. A fast simulation approach to the thermal recovery characteristics of deep borehole heat exchanger after heat extraction. Sustainability 2020, 12, 2021. [Google Scholar] [CrossRef] [Green Version]
- Duffie, J.A.; Deckman, W.A. Solar Engineering of Thermal Process; John Wiley and Sons: New York, NY, USA, 1980. [Google Scholar]







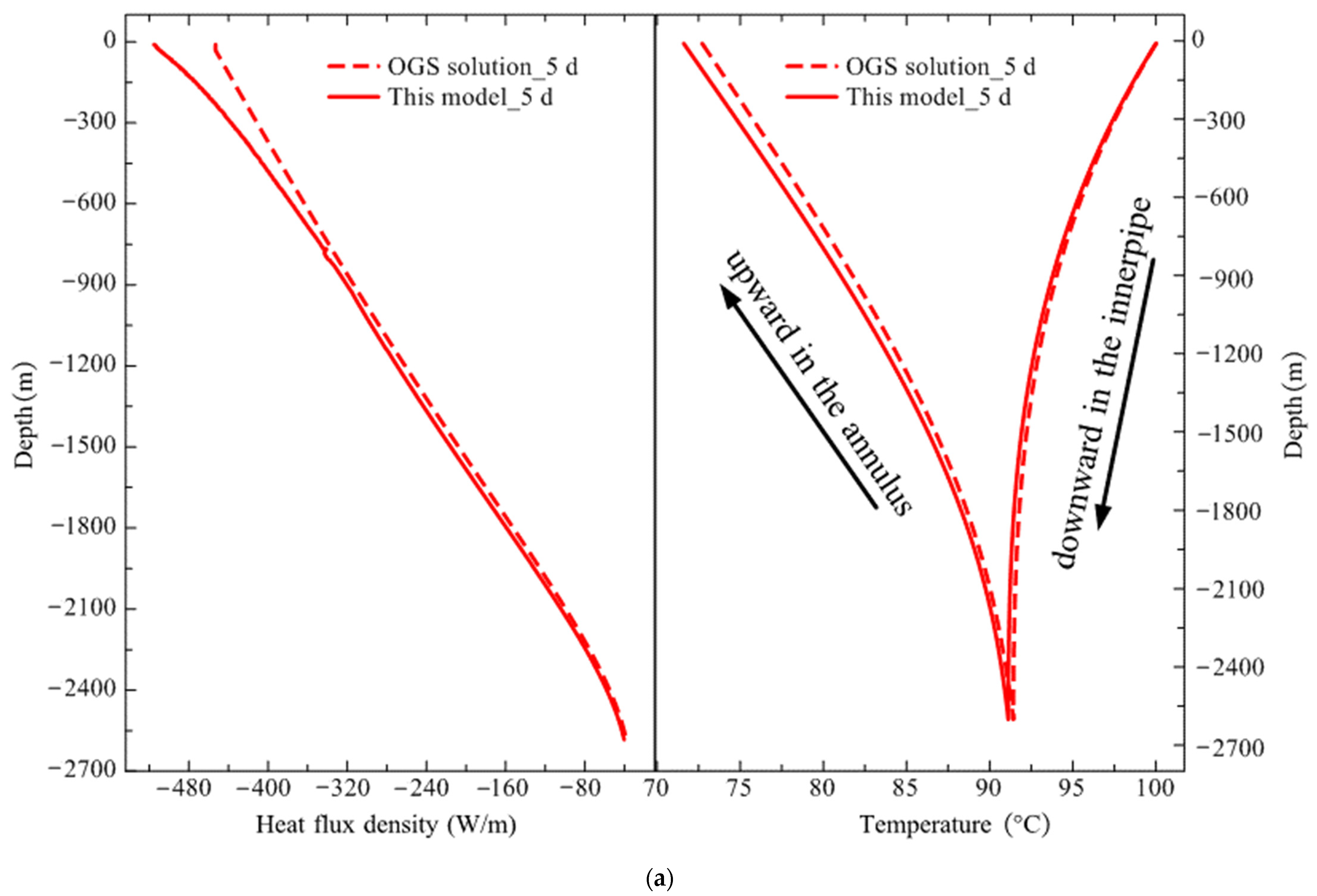

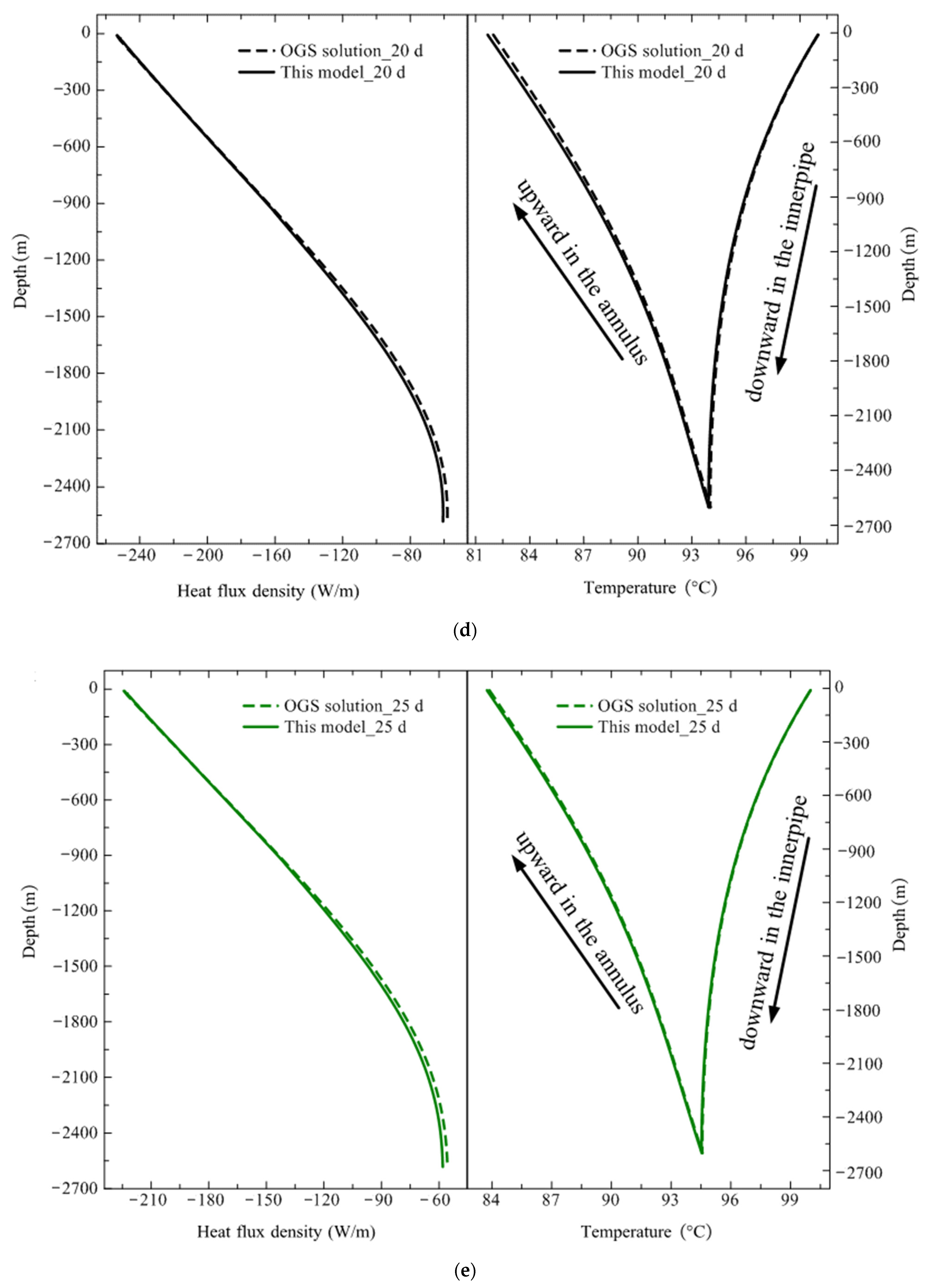


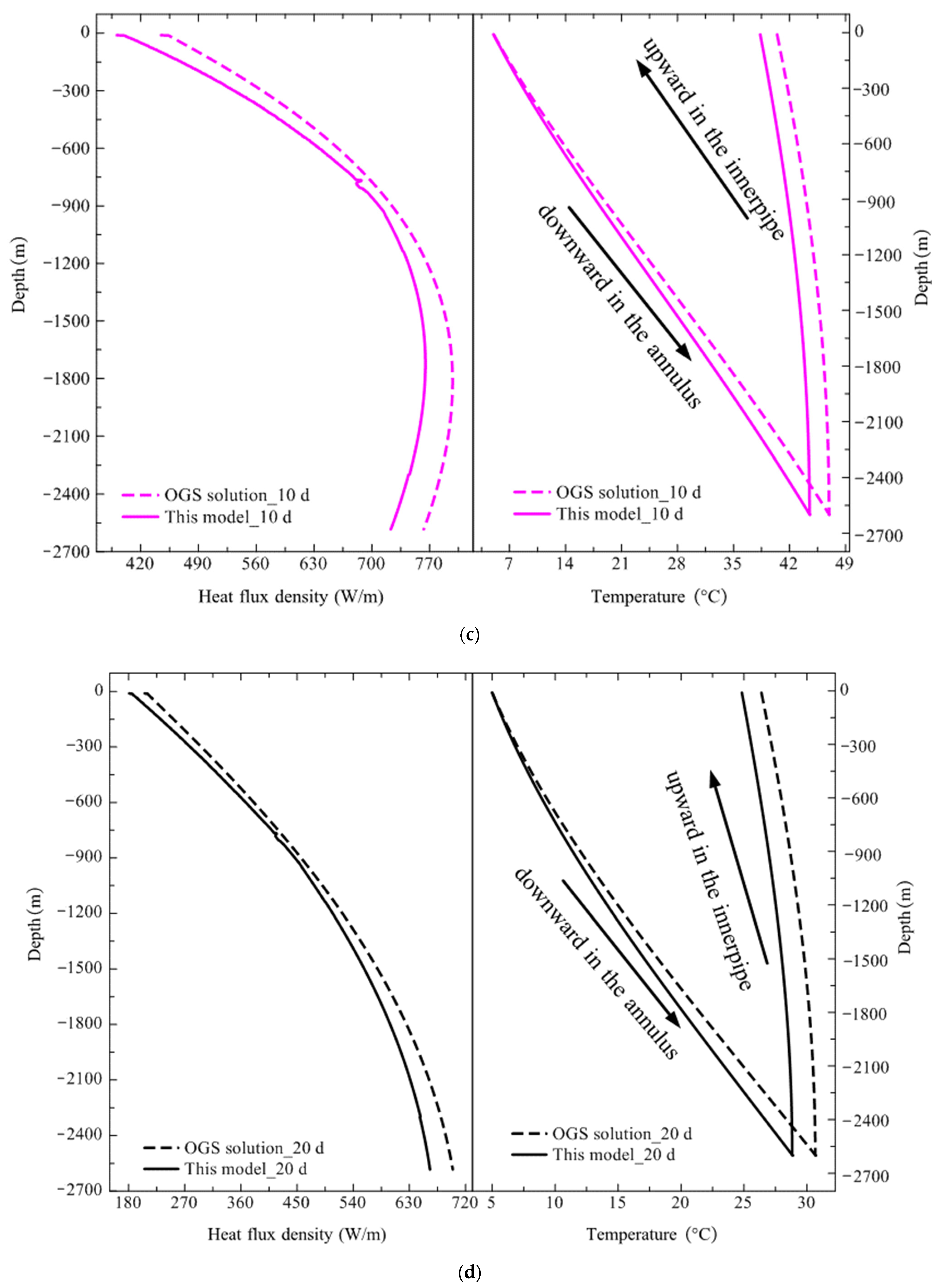


| Geological Parameters | Borehole Heat Exchanger Parameters | ||
|---|---|---|---|
| Parameter | Value | Parameter | Value |
| Thermal conductivity of rock | 2.6 W/m/K | Borehole radius | 152.2 mm |
| Bulk heat capacity of rock | 2.3 MJ/m3/K | Inner diameter of annulus | 127 mm |
| Thermal conductivity of geofluid | 0.65 W/m/K | Annulus wall thickness | 5.6 mm |
| Bulk heat capacity of geofluid | 4.2 MJ/m3/K | Inner diameter of inner pipe | 75 mm |
| Porosity of rock | 0.01 | Inner pipe wall thickness | 6.8 mm |
| Subsurface temperature | 10 °C | Thermal conductivity of annulus (steel pipe) | 54 W/m/K |
| Geothermal temperature gradient | 30 °C/km | Thermal conductivity of inner pipe (PE pipe) | 0.4 W/m/K |
| Permeability coefficient | 10−8 m/s | Thermal conductivity of backfill | 2 W/m/K |
| Hydraulic gradient in the rock | 0 | Bulk heat capacity of heat carrier (water) | 4.12 MJ/m3/K |
| Model length | 400 m | Thermal conductivity of heat carrier (water) | 0.65 W/m/K |
| Model width | 400 m | Dynamic viscosity coefficient of heat carrier (water) | 5.04 × 10−4 kg/m/s |
| Model depth | 2000 m | Density of heat carrier (water) | 977 kg/m3 |
| Literature Data | OGS Solution | Result of This Model | |
|---|---|---|---|
| Total heat storage (MWh) | 665.68 | 653.16 | 701.48 |
| Total heat extraction (MWh) | 103.33 | 112.88 | 78.17 |
| Average heat storage rate (kW) | 152.4 | 149.53 | 160.6 |
| Average heat extraction rate (kW) | 23.65 | 25.84 | 17.89 |
| Average heat flux density during charging (W/m) | 76.2 | 74.77 | 80.3 |
| Average heat flux density during discharging (W/m) | 11.83 | 12.92 | 8.95 |
| Heat storage efficiency | 15.52% | 17.28% | 11.14% |
| Literature Data | OGS Solution | Result of This Model | |
|---|---|---|---|
| Average outlet temperature during charging (°C) | 71.03 | 71.85 | 68.7 |
| Average outlet temperature during discharging (°C) | 44.45 | 45.31 | 41.99 |
| Relative error during charging | - | 1.15% | 3.28% |
| Relative error during discharging | - | 1.93% | 5.53% |
| Simulation Cost | OGS Software | This Model |
|---|---|---|
| Simulation for charging phase | 7.51 h | 0.25 h |
| Simulation for discharging phase | 7.7 h | 0.26 h |
| Parameter | Value |
|---|---|
| Surface temperature (°C) | 15 |
| Geothermal temperature gradient (°C/km) | 28 |
| Lithological stratifications | 5 |
| Groundwater conditions | Without ground water advection |
| Rock Layers | Rock Type | Depth (m) | Thermal Conductivity (W/m/K) | Specific Heat Capacity (J/kg/K) | Density (kg/m3) |
|---|---|---|---|---|---|
| Layer 1 | Soil | 0~100 | 1.16 | 840 | 1500 |
| Layer 2 | Basalt | 100~1985 | 2.78 | 925 | 2800 |
| Layer 3 | Sandstone | 1985~2410 | 2.8 | 920 | 2800 |
| Layer 4 | Limestone | 2410~2470 | 2.75 | 900 | 2780 |
| Layer 5 | Sandstone | 2470~2600 | 2.8 | 920 | 2800 |
| Design Parameters | Value |
|---|---|
| Drilling depth of DBHE (m) | 2600 |
| Inner pipe diameter of DBHE (mm) | 90/110 |
| Outer pipe diameter of DBHE (mm) | 159/178 |
| Borehole diameter of DBHE (mm) | 216 |
| Solar collector area (m2) | 25 |
| Operational Parameters | Value |
|---|---|
| Charging time (days) | 30 |
| Discharging time (days) | 120 |
| Flow rate during charging (m3/h) | 20 |
| Flow rate during discharging (m3/h) | 50 |
| Solar radiation intensity (W/m2) | 550~850 |
| Operation hours per day (hour) | 24 |
| Charging Time (day) | OGS Solution (W/m) | Result of This Model (W/m) | Relative Error | |
|---|---|---|---|---|
| Average Error | Maximum Error | |||
| 5 | 242.16 | 253.94 | 4.61% | 13.72% |
| 10 | 182.02 | 188.49 | 3.65% | 8.71% |
| 15 | 179.19 | 183.32 | 2.72% | 4.13% |
| 20 | 135.04 | 136.55 | 1.81% | 4.36% |
| 25 | 120.18 | 121.56 | 1.8% | 4.35% |
| 30 | 111.0 | 113.47 | 2.75% | 4.78% |
| Field Test | OGS Solution | Result of This Model | |
|---|---|---|---|
| Average outlet temperature during charging (°C) | 69.29 | 74.38 | 73.72 |
| Average outlet temperature during discharging (°C) | 48.35 | 41.35 | 39.64 |
| Relative error during charging | - | 7.34% | 6.39% |
| Relative error during discharging | - | 14.47% | 18.01% |
| Field Test | OGS Solution | Result of This Model | |
|---|---|---|---|
| Average outlet temperature during charging (°C) | 79.31 | 84.51 | 84.07 |
| Average outlet temperature during discharging (°C) | 10.75 | 10.77 | 10.70 |
| Relative error during charging | - | 6.55% | 6% |
| Relative error during discharging | - | 0.18% | 0.46% |
| Discharging Time (day) | OGS Solution (W/m) | Result of This Model (W/m) | Relative Error | |
|---|---|---|---|---|
| Average Error | Maximum Error | |||
| 1 | 1549.45 | 1476.25 | 4.38% | 12.07% |
| 5 | 1163.24 | 1115.03 | 4.13% | 12.06% |
| 10 | 720.26 | 689.81 | 4.38% | 12% |
| 20 | 511.98 | 490.5 | 4.38% | 12.02% |
| 30 | 226.34 | 217.08 | 4.05% | 9.78% |
| 40 | 169.73 | 162.89 | 3.73% | 7.68% |
| 50 | 149.46 | 142.63 | 4.21% | 8.23% |
| 120 | 116.55 | 118.36 | 1.88% | 3.52% |
| Simulation Cost | OGS Software | This Model |
|---|---|---|
| Simulation for charging phase | 1.25 h | 0.042 h |
| Simulation for discharging phase | 5.02 h | 0.17 h |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, Y.; Qin, X.; Shi, X. Heat Transfer Modeling on High-Temperature Charging and Discharging of Deep Borehole Heat Exchanger with Transient Strong Heat Flux. Sustainability 2022, 14, 9702. https://doi.org/10.3390/su14159702
Zhao Y, Qin X, Shi X. Heat Transfer Modeling on High-Temperature Charging and Discharging of Deep Borehole Heat Exchanger with Transient Strong Heat Flux. Sustainability. 2022; 14(15):9702. https://doi.org/10.3390/su14159702
Chicago/Turabian StyleZhao, Yazhou, Xiangxi Qin, and Xiangyu Shi. 2022. "Heat Transfer Modeling on High-Temperature Charging and Discharging of Deep Borehole Heat Exchanger with Transient Strong Heat Flux" Sustainability 14, no. 15: 9702. https://doi.org/10.3390/su14159702
APA StyleZhao, Y., Qin, X., & Shi, X. (2022). Heat Transfer Modeling on High-Temperature Charging and Discharging of Deep Borehole Heat Exchanger with Transient Strong Heat Flux. Sustainability, 14(15), 9702. https://doi.org/10.3390/su14159702







