Optimization Method of Temperature Measuring Point Layout for Steel-Concrete Composite Bridge Based on TLS-IPDP
Abstract
:1. Introduction
- (1)
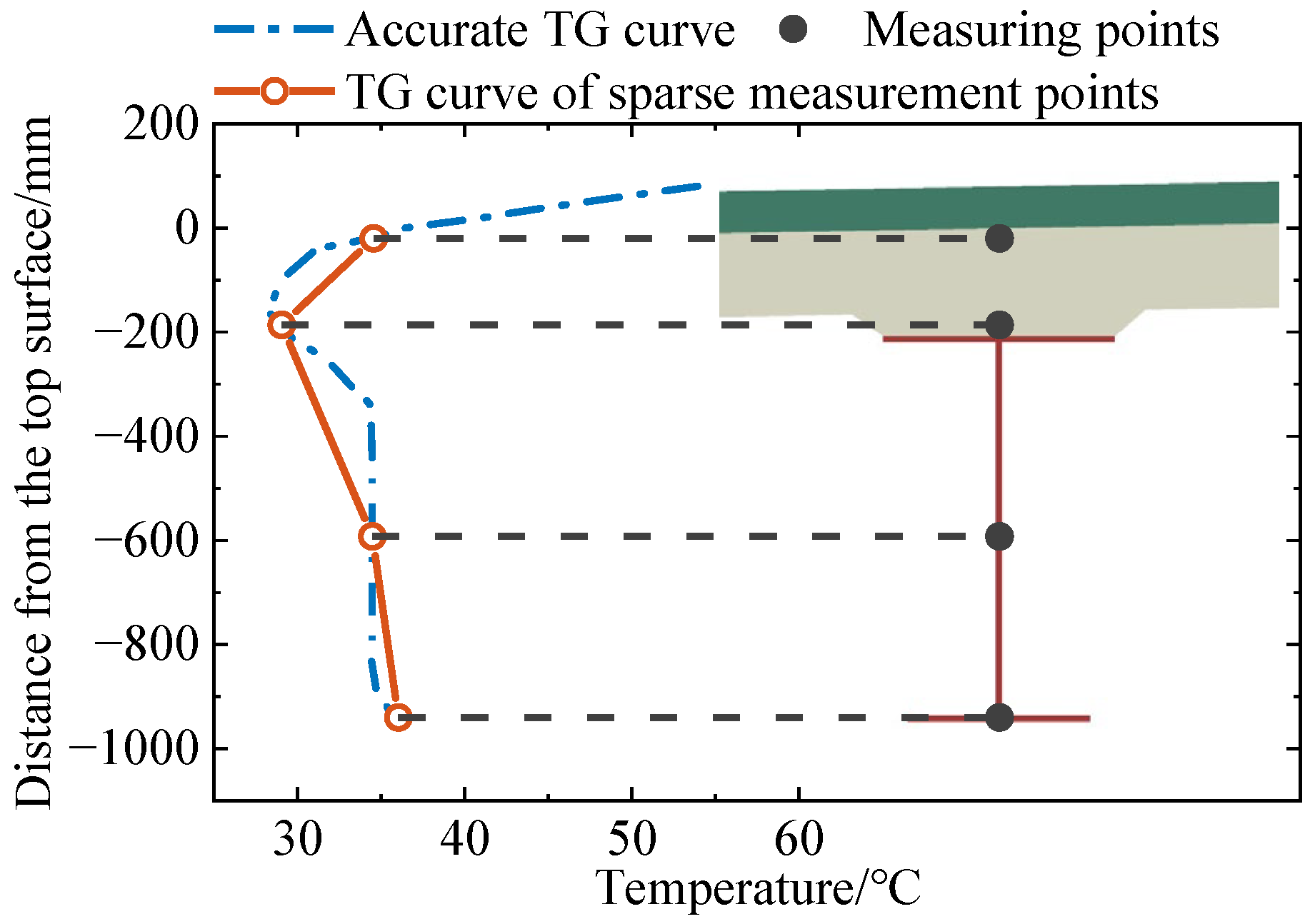
- The temperature measuring points’ number and distances are unreasonable in a large amount of actual bridge temperature experiments. In most studies, the measuring points are arranged at equal distances, whereas in a few studies, the measuring points are arranged with variable distance. However, the distance of the measuring points is relatively random, lacks theoretical support, and the location of the measuring points often cannot cover the local extreme temperature points of the structure. Consequently, capturing the maximum TG of the structure is difficult.
- (2)
- The distribution of measuring points on different paths is the same, and the difference in the distribution modes of TTG at different depths and VTG at different offset distances are not considered. Thus, the TG data collected in the test cannot truly reflect the actual TG at different positions of the structure.
- (3)
- The method of arranging measuring points according to the statistical rule of measured temperature data has the problems of the long measuring period, high cost, and sparse arrangement of measuring points. Moreover, after a more reasonable arrangement is obtained through long-term statistical analysis, no more temperature measuring points can be added inside the concrete or closed steel beam.
2. Basic Theory of TLS-IPDP Algorithm
2.1. Douglas–Peucker Algorithm
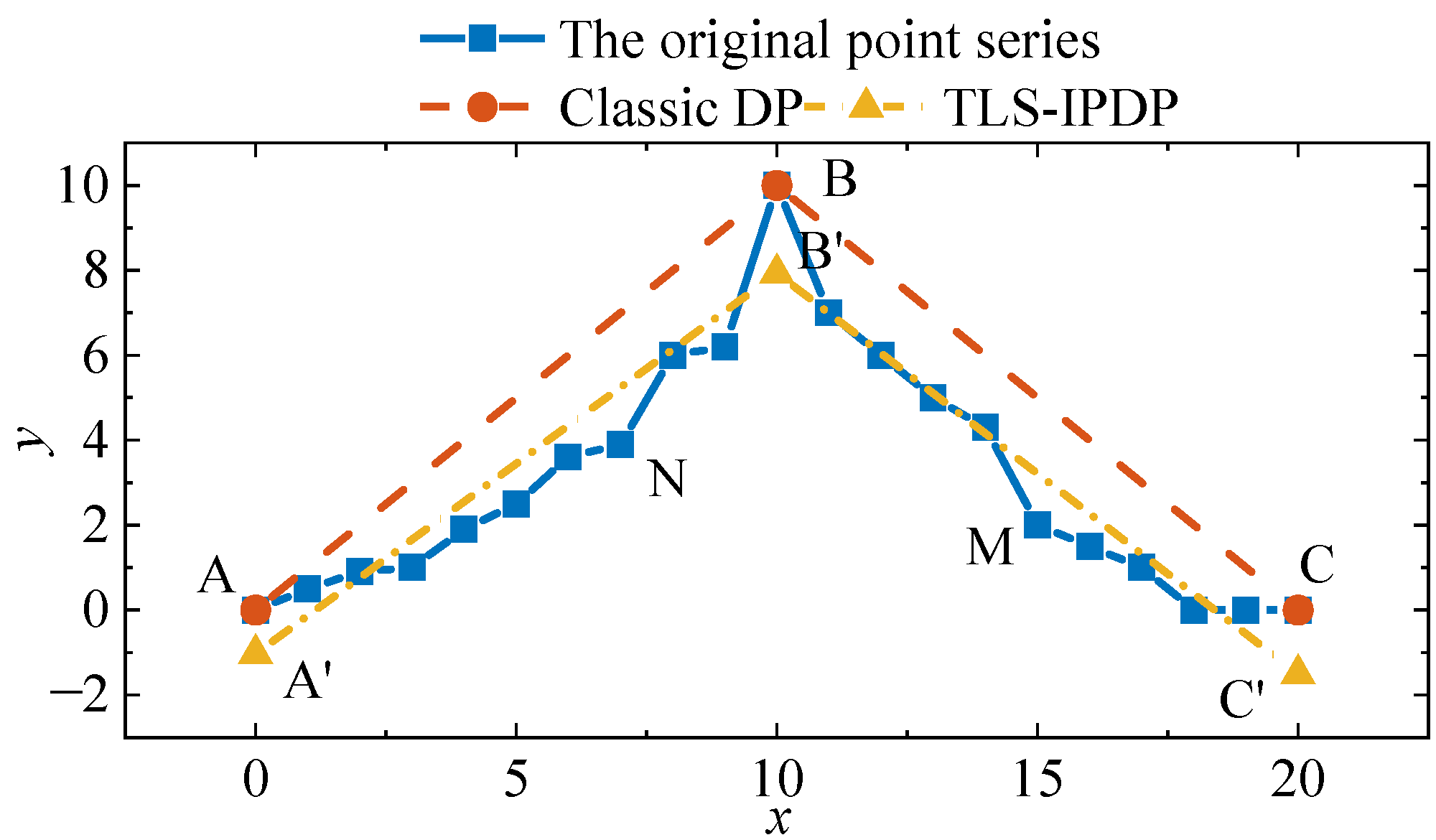
- (1)
- The loss of important feature points could easily occur in parts with large curvature; meanwhile, the retention of non-feature points could easily happen in parts with small curvature, thus affecting the compression effect.
- (2)
- Steel-concrete composite beams have a specific material boundary, and measuring points need to be arranged in specific locations as required; the feature points to be preserved cannot be specified artificially in the DP algorithm.
- (3)
- Considering the constraints of structural size and economic cost, the optimal number of sensors in steel-concrete composite beams should be calculated. However, in the DP algorithm, the number of feature points to be retained cannot be manually specified but can only be controlled by the threshold .
2.2. Design of TLS-IPDP Algorithm
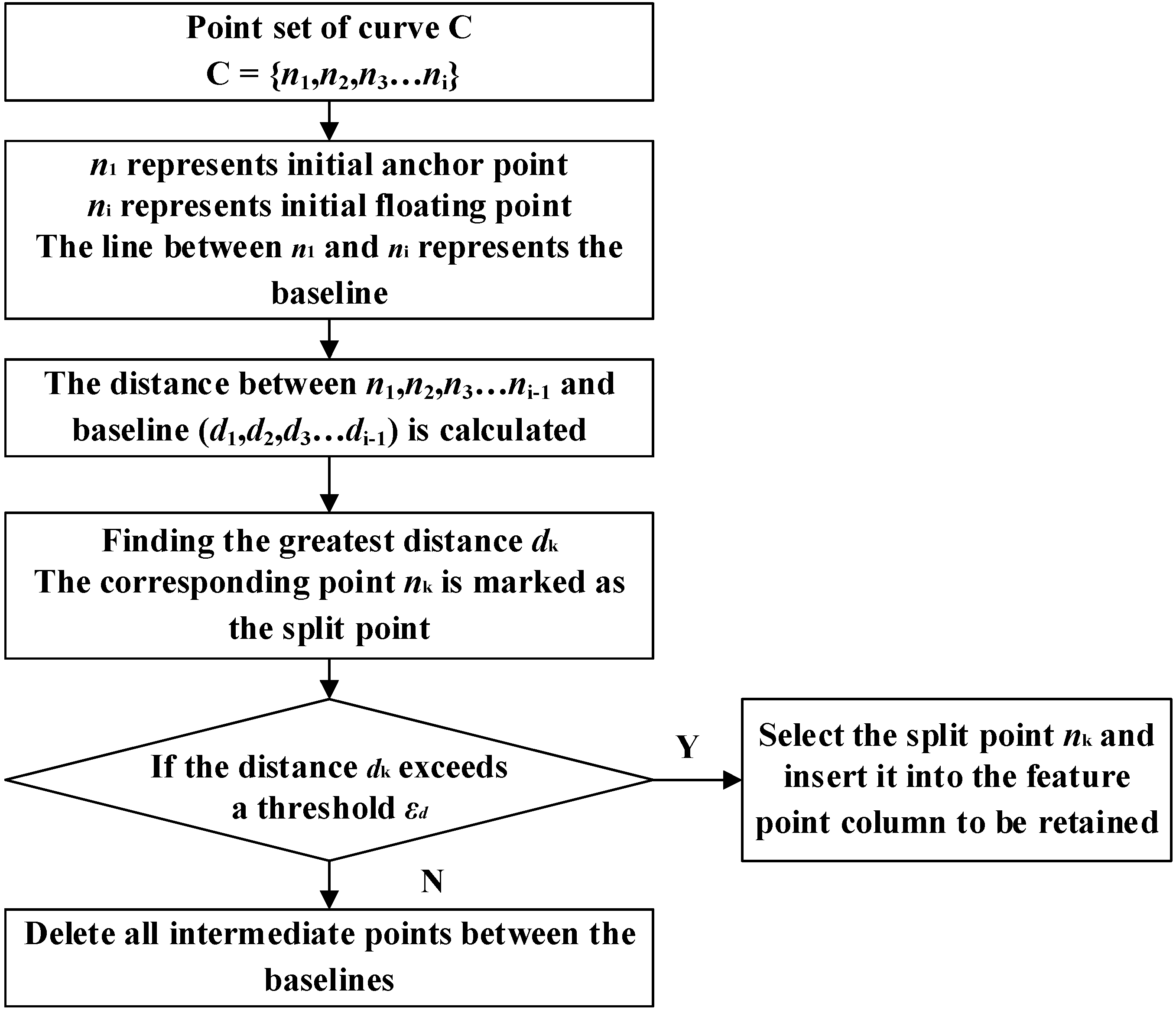
- (1)
- The total least square method is introduced. If , the total least square linear fitting is performed for all intermediate points between baselines. Otherwise, the split point is selected and inserted into the feature point series to be retained.
- (2)
- Before the search for the first split point, the retention points of the curve were manually specified according to the actual situation, and the feature point series was divided into multiple segments by the retention points. Then, the split points were searched for multi-segments.
- (3)
- The random search method is used to automatically search the appropriate threshold value according to the artificially specified retention feature point number n. The algorithm automatically updates the number of retention points to a value in the range of and recalculates until the threshold meets the requirements so that the original feature point series is thinned and the updated retention feature point number is closest to .
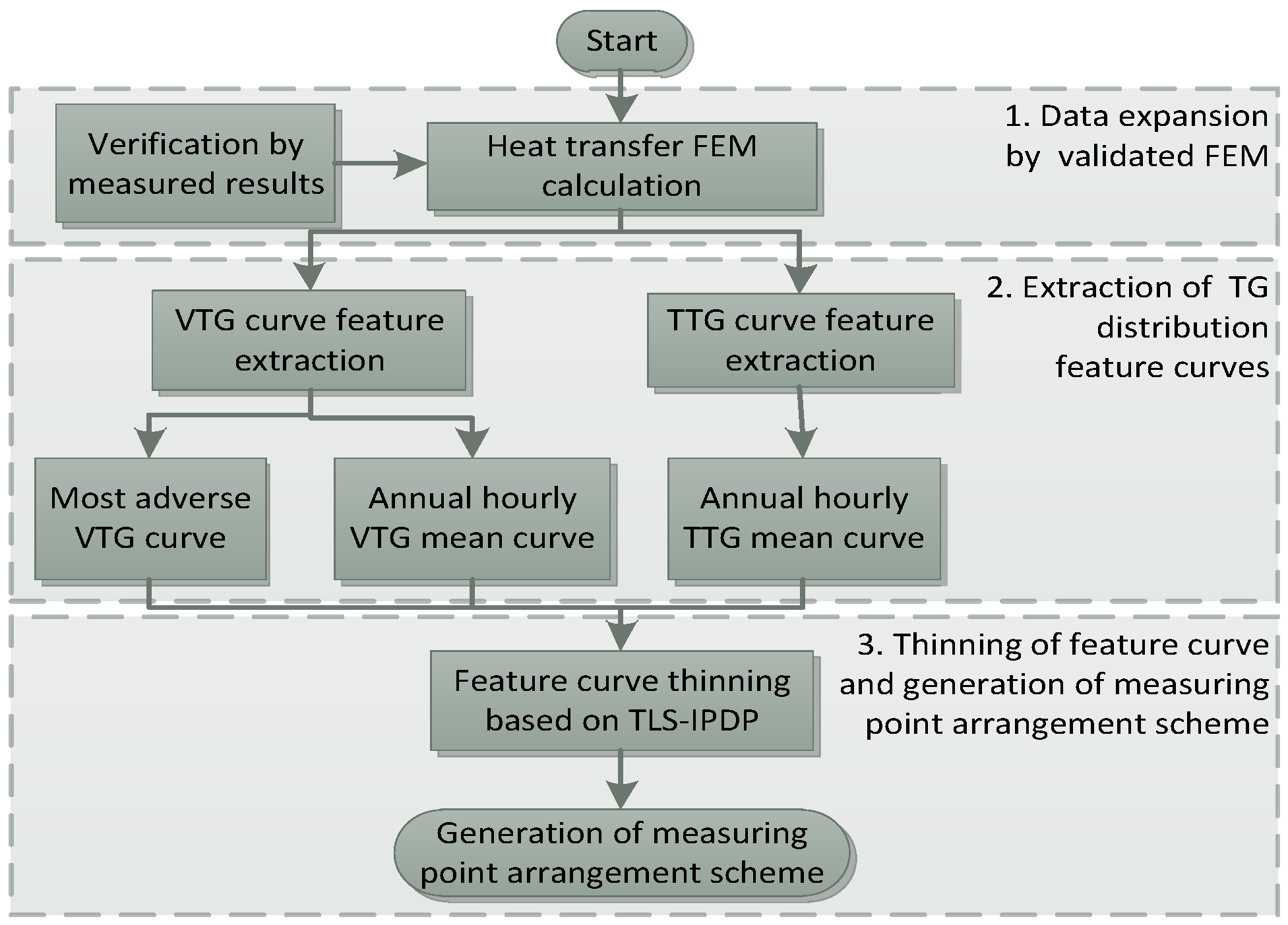
3. Optimization Method of Temperature Measuring Point Layout Based on TLS-IPDP
- (1)
- Owing to the influence of bridge orientation and geographical location, solar radiation and convective heat transfer with uneven time-varying characteristics lead to differences in TG distribution modes and temperature extremes between transverse paths with different depths and vertical paths with different offsets [12,24].
- (2)
- Owing to the difference in thermophysical parameters between steel and concrete, the vertical arrangement of temperature measuring points should be discussed separately for steel beam and concrete bridge slab.
- (3)
- Conventional steel-concrete composite beams have two typical structural forms: steel plate composite beam (Type I) and steel box composite beam (Type II). The temperature distributions of open and closed sections are different.
- (4)
- Statistical analysis of the long-term measured temperature data of the structure to obtain its distribution rule can reasonably guide the arrangement of temperature measuring points. However, for a real bridge that has been tested for a long time, adding extra temperature measuring points inside the concrete and closed steel beam is often impossible.
4. Case-Studies
4.1. Engineering Description
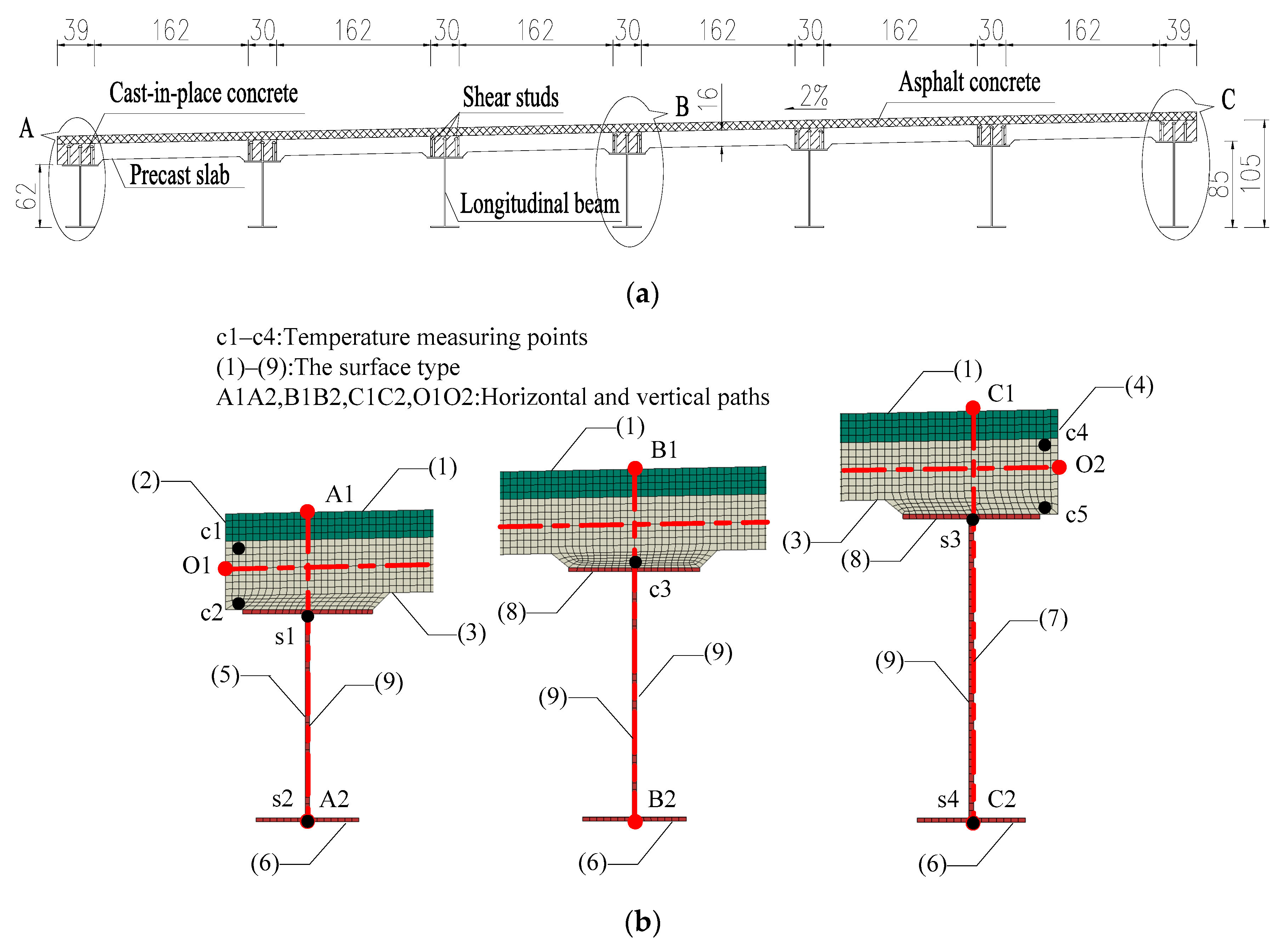
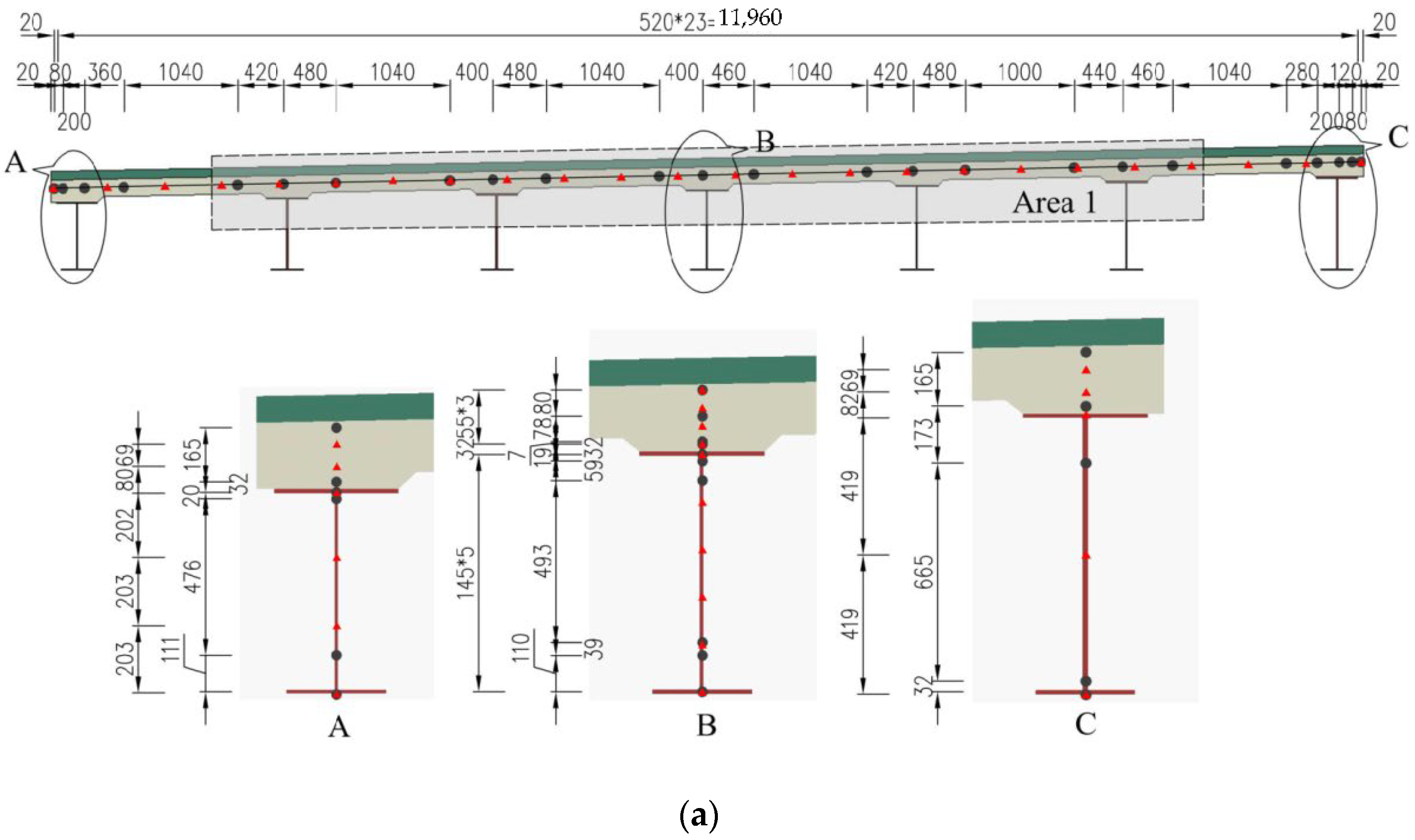
4.1.1. Type I: Steel Plate Composite Beam
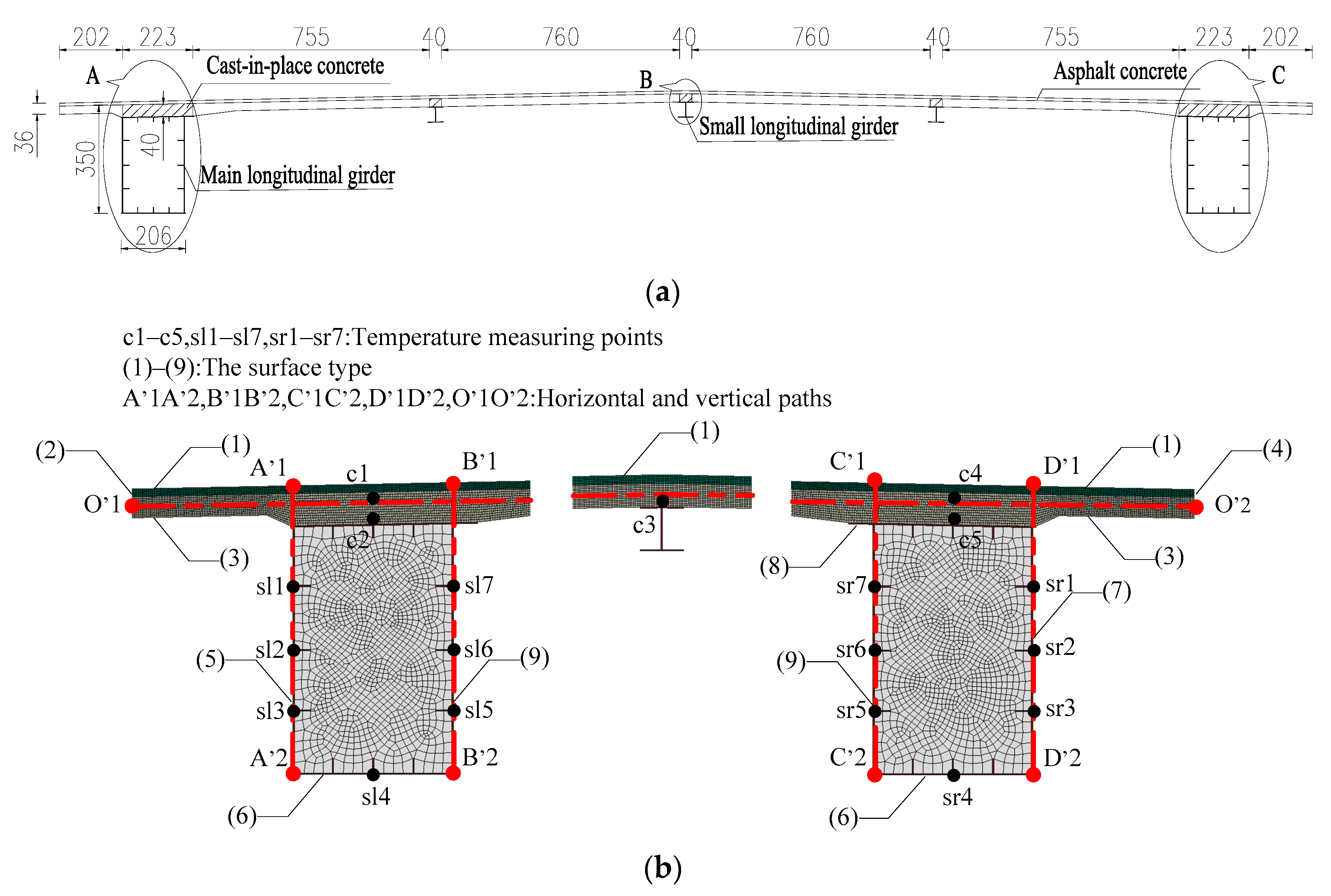
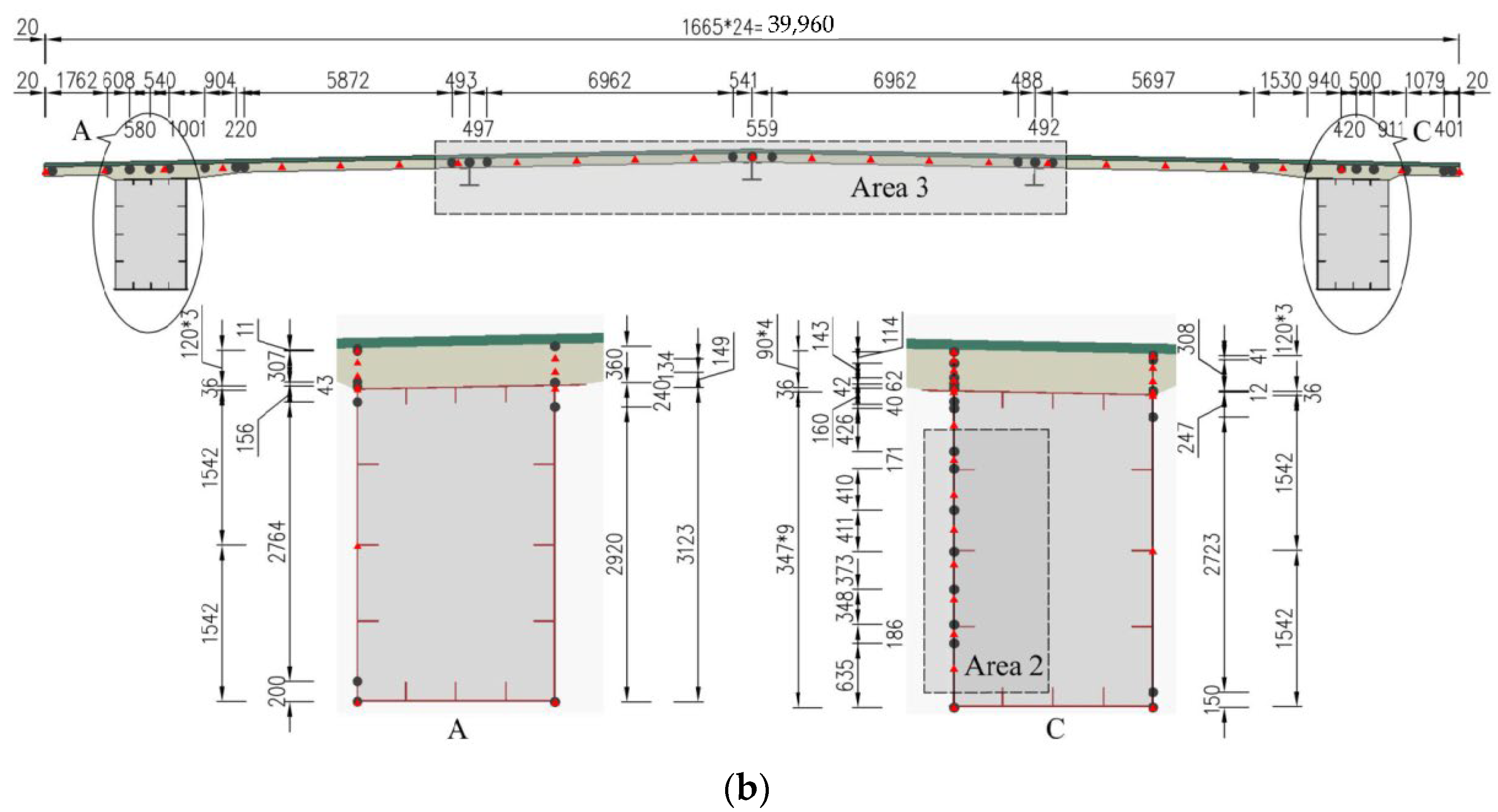
4.1.2. Type II: Steel Box Composite Beam
4.1.3. Selection and Arrangement of Temperature Sensors
4.2. Calculation of Structural Annual Periodic Hourly Temperature Field Considering the Geographical Location and Meteorological Condition Difference
4.2.1. FEM Modeling
4.2.2. Thermophysical Properties of Materials
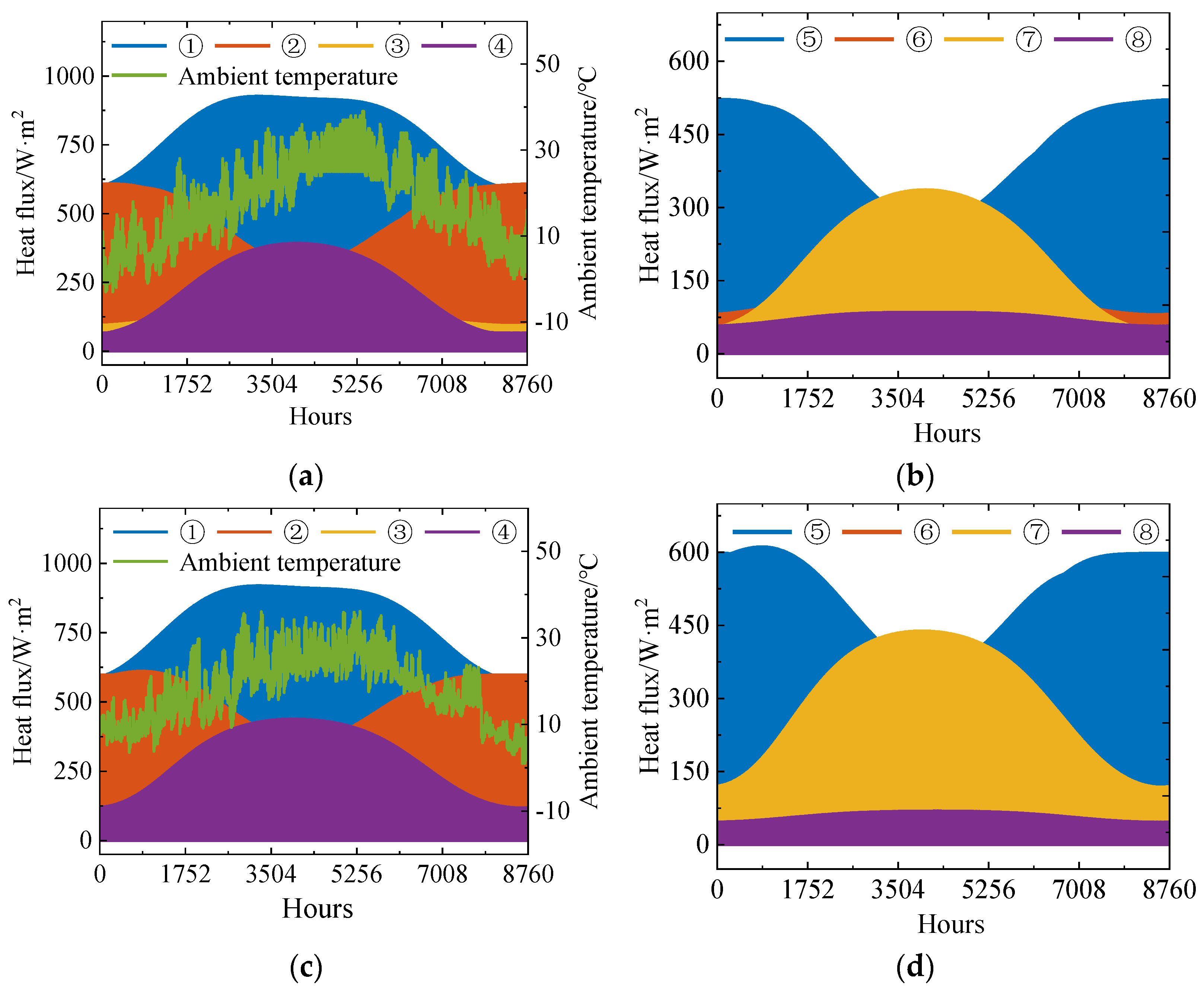
4.2.3. Boundary Conditions and Initial Temperature Field
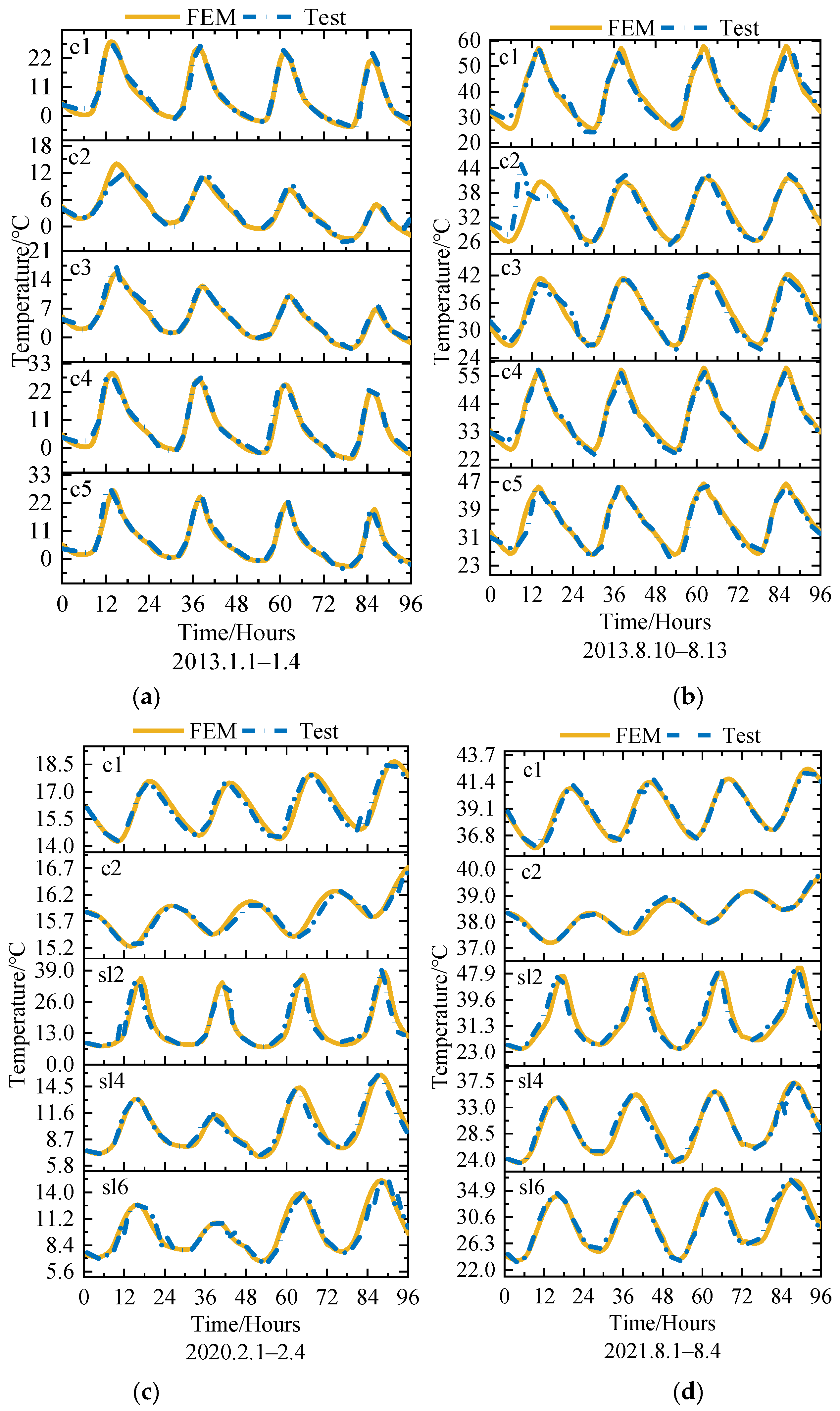
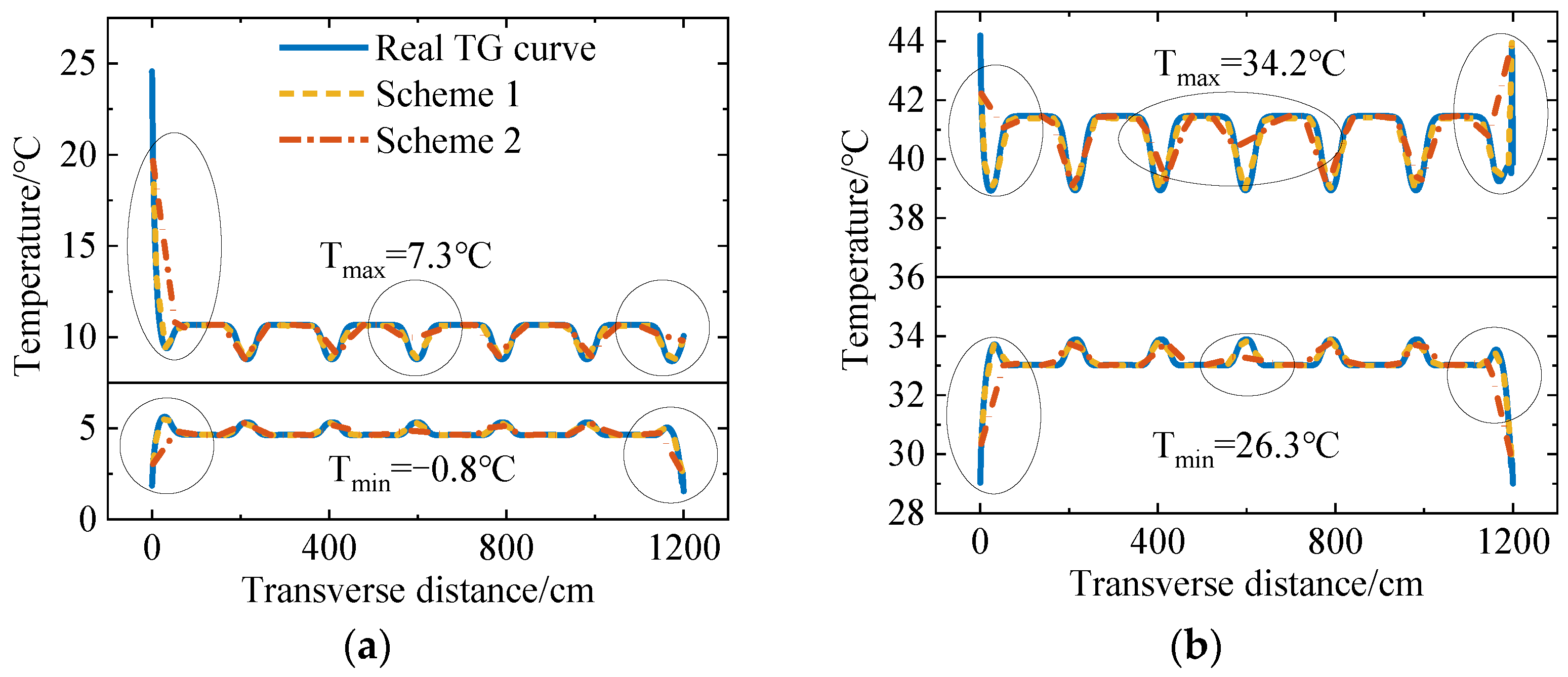
4.2.4. Verification of Calculation Results
4.3. Feature Extraction of TG Curve
4.3.1. VTG
4.3.2. TTG
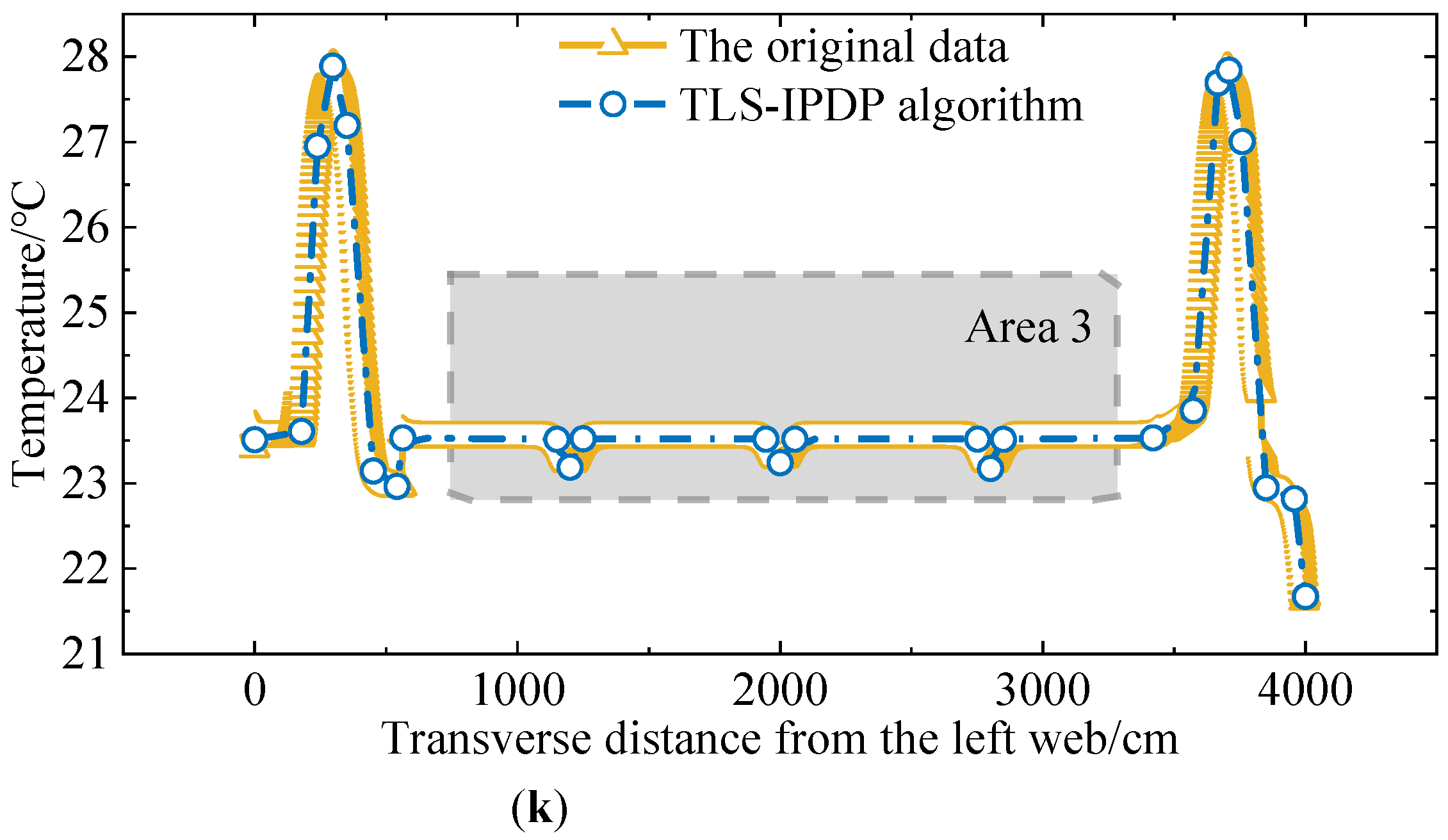
4.4. Generation of TG Curve Thinning and Measurement Point Layout Optimization Scheme Based on TLS-IPDP
4.5. Comparison with Traditional Measuring Point Arrangement Scheme
5. Conclusions
- (1)
- By improving the DP algorithm, the TLS-IPDP algorithm introduces the total least squares to enable a better approximation of the original data. Additionally, it has the function of artificially specifying the feature points to be retained and can automatically search the threshold according to the number of specified retained feature points.
- (2)
- The calculated results of FEM based on heat transfer theory are quite consistent with the measured results. In addition, a more accurate structure TG distribution can be obtained through FEM calculation, which overcomes the defects of real bridge measurement methods such as long periods, high cost, sparse measurement points, and inability to increase internal measurement points.
- (3)
- The TLS-IPDP algorithm proposed in this paper effectively realizes the thinning of original feature point columns under restricted conditions by manually specifying split points and automatically updating threshold values. The algorithm greatly simplifies the curve and compresses the redundant data. The maximum number of feature points after refining a single temperature curve for the vertical path is 10, and the maximum number of feature points after refining a single temperature curve for the horizontal path is 25. The effective optimization is achieved under the limitation of the number and accuracy of measuring points.
- (4)
- Using the TLS-IPDP algorithm combined with the results of FEM can generate a more reasonable temperature measuring point arrangement. Compared with the traditional equidistance temperature measuring point arrangement, the method in this paper considers the differences of TG modes under different paths and realizes the reasonable variable distance temperature measurement point arrangement of steel-concrete composite beams. The obtained TG curve is closer to the real TG distribution of the structure, and the error is smaller in the region with a larger gradient.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Liu, J.; Liu, Y.; Zhang, C.; Zhao, Q.; Lyu, Y.; Jiang, L. Temperature action and effect of concrete-filled steel tubular bridges: A review. J. Traffic. Transport. Eng. 2020, 7, 174–191. [Google Scholar] [CrossRef]
- Liu, Y.; Liu, J. Review on temperature action and effect of steel-concrete composite girder bridge. J. Traffic. Transport. Eng. 2020, 20, 42–59. [Google Scholar]
- Gottsäter, E.; Ivanov, O.L.; Molnár, M.; Crocetti, R.; Nilenius, F.; Plos, M. Simulation of thermal load distribution in portal frame bridges. Eng. Struct. 2017, 143, 219–231. [Google Scholar] [CrossRef]
- Abid, S.R.; Mussa, F.; Tayşi, N.; Özakça, M. Experimental and finite element investigation of temperature distributions in concrete-encased steel girders. Struct. Control Health Monit. 2018, 25, e2042. [Google Scholar] [CrossRef]
- Bao, Y.; Hoehler, M.S.; Smith, C.M.; Bundy, M.; Chen, G. Measuring three-dimensional temperature distributions in steel–concrete composite slabs subjected to fire using distributed fiber optic sensors. Sensors 2020, 20, 5518. [Google Scholar] [CrossRef]
- Wang, J.; Ding, F.; Dai, J. Monitoring and Numerical Analysis for Construction Phase of a Steel-concrete Composite Continuous Box Girder Bridge. J. Highw. Transp. Res. Dev. 2006, 23, 91–94. [Google Scholar]
- Zhou, G.; Yi, T. Thermal load in large-scale bridges: A state-of-the-art review. Int. J. Distrib. Sens. Netw. 2013, 9, 217983. [Google Scholar] [CrossRef]
- Wang, D.; Tan, B.; Xiang, S.; Wang, X. Fatigue Crack Propagation and Life Analysis of Stud Connectors in Steel-Concrete Composite Structures. Sustainability 2022, 14, 7253. [Google Scholar] [CrossRef]
- Huang, Y.; Zhang, Q.; Bao, Y.; Bu, Y. Fatigue assessment of longitudinal rib-to-crossbeam welded joints in orthotropic steel bridge decks. J. Constr. Steel Res. 2019, 159, 53–66. [Google Scholar] [CrossRef]
- Cheng, Z.; Zhang, Q.; Bao, Y.; Deng, P.; Wei, C.; Li, M. Flexural behavior of corrugated steel-UHPC composite bridge decks. Eng. Struct. 2021, 246, 113066. [Google Scholar] [CrossRef]
- Zhang, Q.; Ma, Y.; Cui, C.; Chai, X.; Han, S. Experimental investigation and numerical simulation on welding residual stress of innovative double-side welded rib-to-deck joints of orthotropic steel decks. J. Constr. Steel Res. 2021, 179, 106544. [Google Scholar] [CrossRef]
- Xiang, S.; Wang, D.; Yang, L.; Tan, B. Study on the life cycle simulation method of the temperature field and temperature effect of a steel–concrete composite bridge deck system. Meas. Control 2021, 54, 1068–1081. [Google Scholar] [CrossRef]
- Subramaniam, K.V.; Kunin, J.; Curtis, R.; Streeter, D. Influence of early temperature rise on movements and stress development in concrete decks. J. Bridge Eng. 2010, 15, 108–116. [Google Scholar] [CrossRef]
- Chang, S.; Im, C. Thermal behaviour of composite box-girder bridges. Proc. Inst. Civ. Eng. Struct. Build. 2000, 140, 117–126. [Google Scholar] [CrossRef]
- Wang, D.; Liu, Y.; Liu, Y. 3D temperature gradient effect on a steel-concrete composite deck in a suspension bridge with field monitoring data. Struct. Control Health Monit. 2018, 25, e2179. [Google Scholar]
- Liu, J.; Liu, Y.; Jiang, L.; Zhang, N. Long-term field test of temperature gradients on the composite girder of a long-span cable-stayed bridge. Adv. Struct. Eng. 2019, 22, 2785–2798. [Google Scholar] [CrossRef]
- Zhang, C.; Liu, Y.; Liu, J.; Yuan, Z.; Zhang, G.; Ma, Z. Validation of long-term temperature simulations in a steel-concrete composite girder. Structures 2020, 27, 1962–1976. [Google Scholar] [CrossRef]
- Sakiyama, F.I.H.; Lehmann, F.; Garrecht, H. Structural health monitoring of concrete structures using fibre-optic-based sensors: A review. Mag. Concr. Res. 2021, 73, 174–194. [Google Scholar] [CrossRef]
- Kim, J.-W.; Lee, C.; Park, S. Damage localization for CFRP-debonding defects using piezoelectric SHM techniques. Res. Nondestruct. Eval. 2012, 23, 183–196. [Google Scholar] [CrossRef]
- Jabir, S.A.; Gupta, N.K. Condition monitoring of the strength and stability of civil structures using thick film ceramic sensors. Measurement 2013, 46, 2223–2231. [Google Scholar] [CrossRef]
- Zhang, Q.; Zhang, D.; Cui, C.; Lao, W.; Qiu, S.; Miao, H.; Song, S. Fatigue Crack Detection Method Based on Ultrasonic-guided Waves for the Longitudinal Rib Butt Weld of Steel Decks. China J. Highw. Transp. 2022, 35, 101–112. [Google Scholar]
- Zhao, L.; Shi, G. A method for simplifying ship trajectory based on improved Douglas–Peucker algorithm. Ocean Eng. 2018, 166, 37–46. [Google Scholar] [CrossRef]
- Douglas, D.H.; Peucker, T.K. Algorithms for the reduction of the number of points required to represent a digitized line or its caricature. Cartogr. Int. J. Geogr. Inf. Geovis. 1973, 10, 112–122. [Google Scholar] [CrossRef] [Green Version]
- Lee, J.-H.; Kalkan, I. Analysis of thermal environmental effects on precast, prestressed concrete bridge girders: Temperature differentials and thermal deformations. Adv. Struct. Eng. 2012, 15, 447–459. [Google Scholar] [CrossRef]
- Tong, M.; Tham, L.; Au, F.; Lee, P. Numerical modelling for temperature distribution in steel bridges. Comput. Struct. 2001, 79, 583–593. [Google Scholar] [CrossRef]
- Fan, J.; Liu, Y.; Liu, C. Experiment study and refined modeling of temperature field of steel-concrete composite beam bridges. Eng. Struct. 2021, 240, 112350. [Google Scholar] [CrossRef]
- Wang, D.; Deng, Y.; Liu, Y.; Liu, Y. Numerical investigation of temperature gradient-induced thermal stress for steel–concrete composite bridge deck in suspension bridges. J. Cent. South Univ. 2018, 25, 185–195. [Google Scholar] [CrossRef]
- Qinghua, Z.; Ma, Y.; Wang, B. Analysis of Temperature Field and Thermal Stress Characteristics for a Novel Composite Bridge Tower Catering for Plateau Environment. Bridge Constr. 2020, 50, 30–36. [Google Scholar]
- Ma, Z.; Liu, J.; Liu, Y.; Lv, Y.; Zhang, G. Regional difference of value taking of effective temperature for steel-concrete composite girder bridges. J. Zhejiang Univ. 2022, 56, 909–919. [Google Scholar]
- Noumowé, A.; Siddique, R.; Ranc, G. Thermo-mechanical characteristics of concrete at elevated temperatures up to 310 C. Nucl. Eng. Des. 2009, 239, 470–476. [Google Scholar] [CrossRef]
- Adl-Zarrabi, B.; Boström, L.; Wickström, U. Using the TPS method for determining the thermal properties of concrete and wood at elevated temperature. Fire Mater. Int. J. 2006, 30, 359–369. [Google Scholar] [CrossRef]
- Branco, F.A.; Mendes, P.A. Thermal actions for concrete bridge design. J. Struct. Eng. 1993, 119, 2313–2331. [Google Scholar] [CrossRef]
- Krishnan, J.M.; Rajagopal, K. Triaxial testing and stress relaxation of asphalt concrete. Mech. Mater. 2004, 36, 849–864. [Google Scholar] [CrossRef]
- Zhao, R. Air Conditioning, 4th ed.; China Architecture & Building Press: Beijing, China, 2009. [Google Scholar]
- Wang, Y.; Zhan, Y.; Zhao, R. Analysis of thermal behavior on concrete box-girder arch bridges under convection and solar radiation. Adv. Struct. Eng. 2016, 19, 1043–1059. [Google Scholar] [CrossRef]
- Dilger, W.H.; Ghali, A.; Chan, M.; Cheung, M.S.; Maes, M.A. Temperature stresses in composite box girder bridges. J. Struct. Eng. 1983, 109, 1460–1478. [Google Scholar] [CrossRef]
- Tayşi, N.; Abid, S. Temperature distributions and variations in concrete box-girder bridges: Experimental and finite element parametric studies. Adv. Struct. Eng. 2015, 18, 469–486. [Google Scholar] [CrossRef]
- Kim, S.-H.; Cho, K.-I.; Won, J.-H.; Kim, J.-H. A study on thermal behaviour of curved steel box girder bridges considering solar radiation. Arch. Civ. Mech. Eng. 2009, 9, 59–76. [Google Scholar] [CrossRef]
- Wang, D.; Tan, B.; Wang, X.; Zhang, Z. Experimental study and numerical simulation of temperature gradient effect for steel-concrete composite bridge deck. Meas. Control 2021, 54, 681–691. [Google Scholar] [CrossRef]


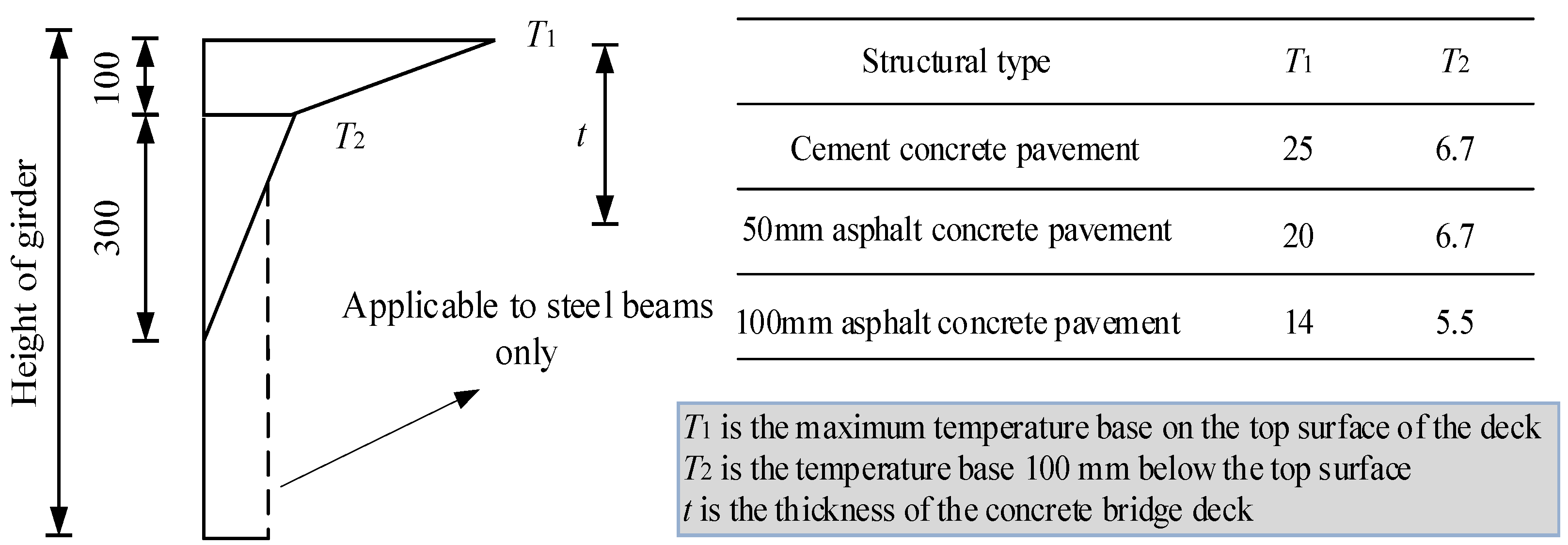
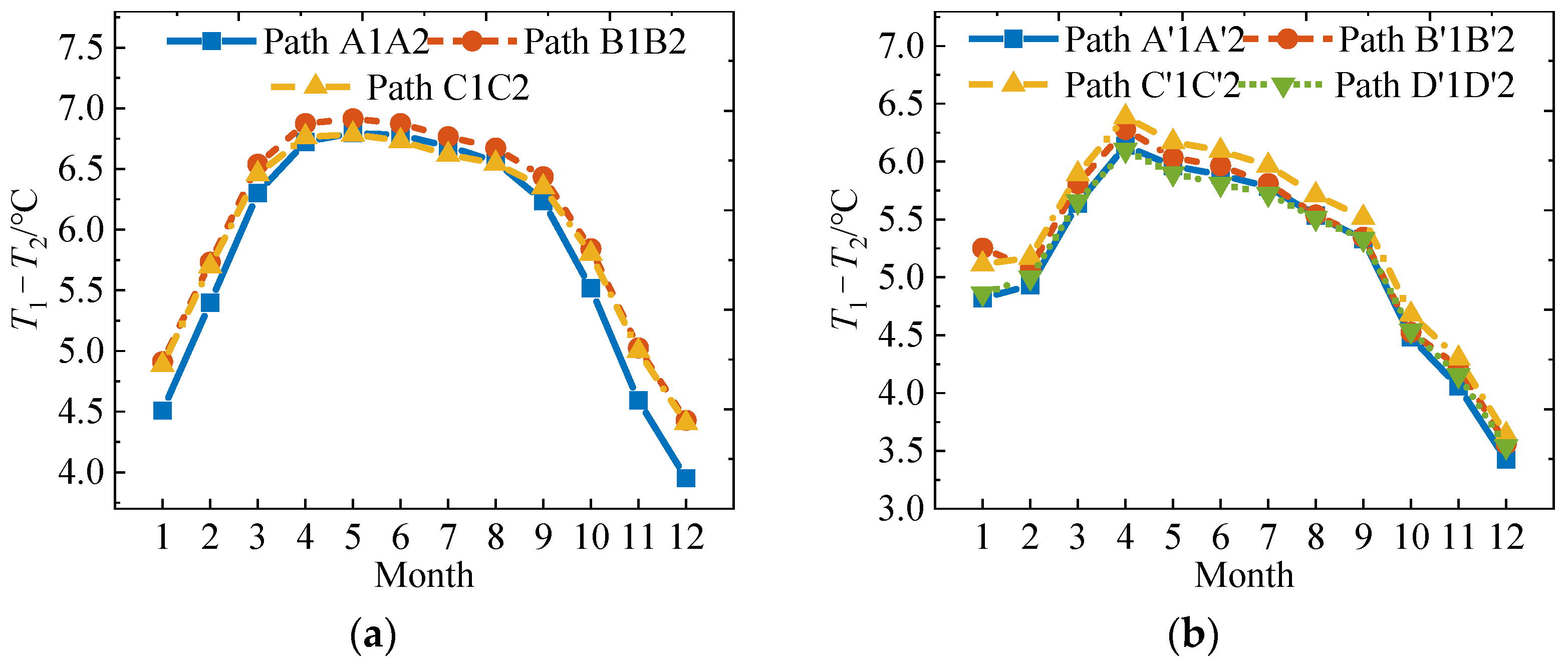
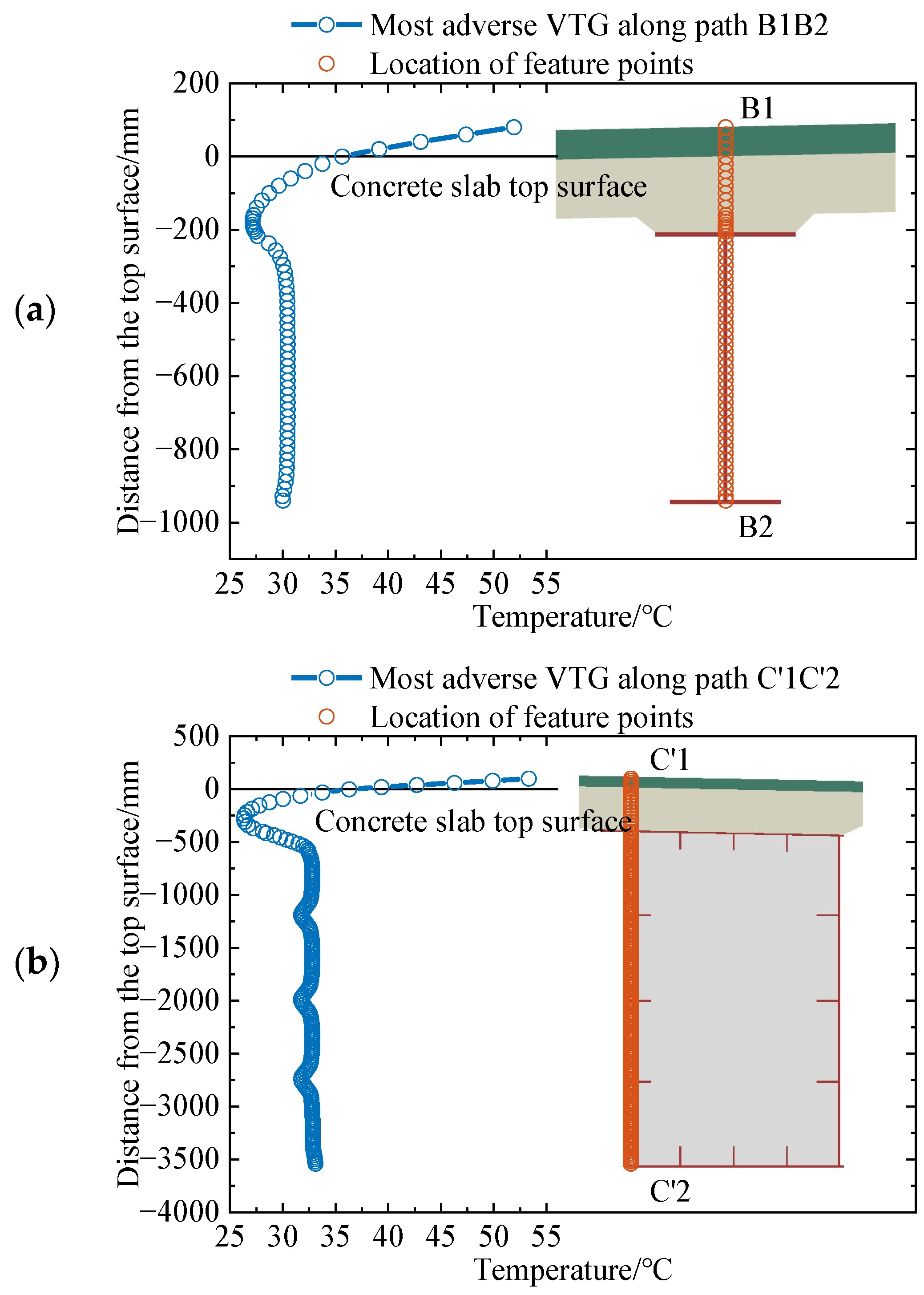
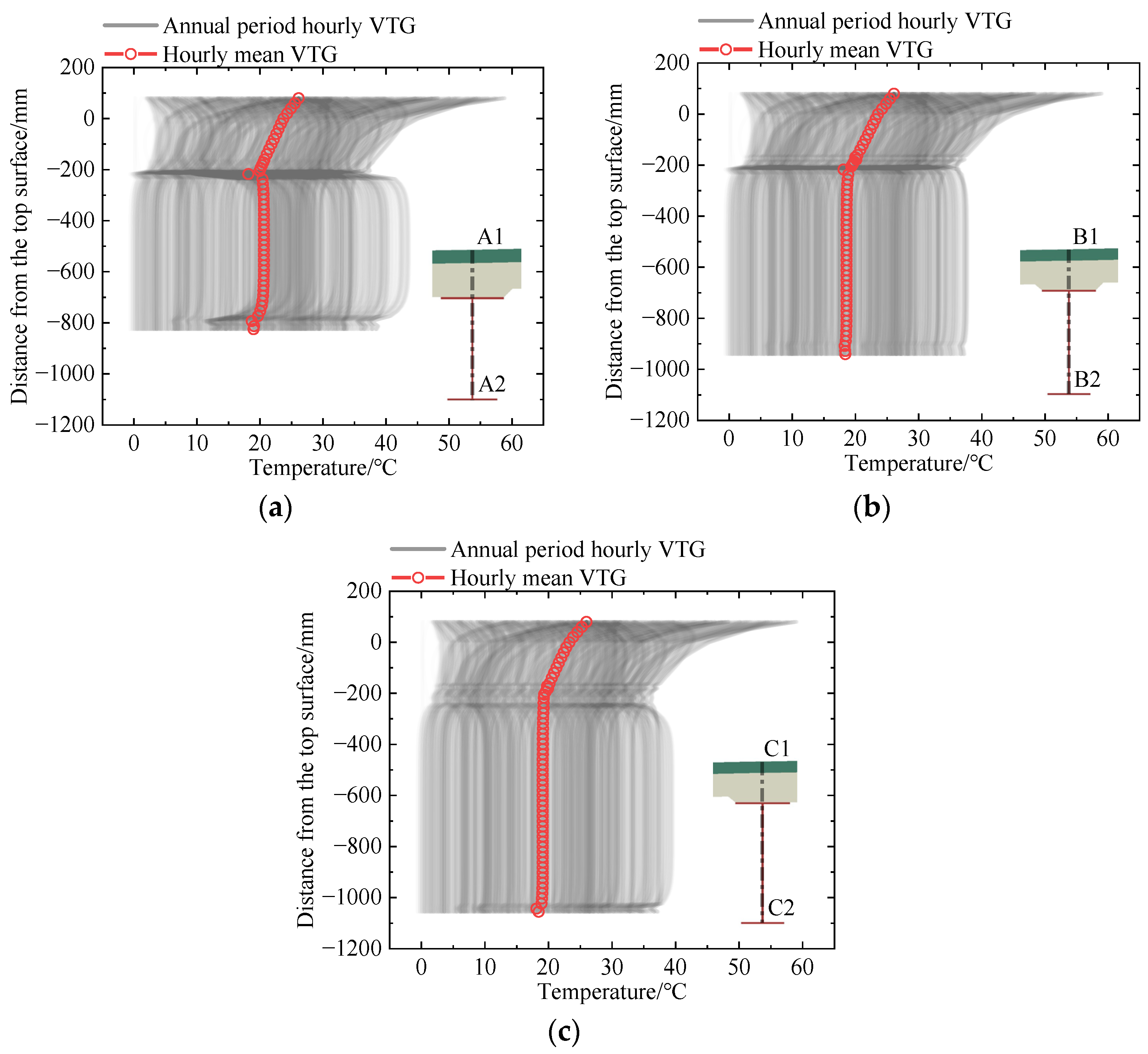
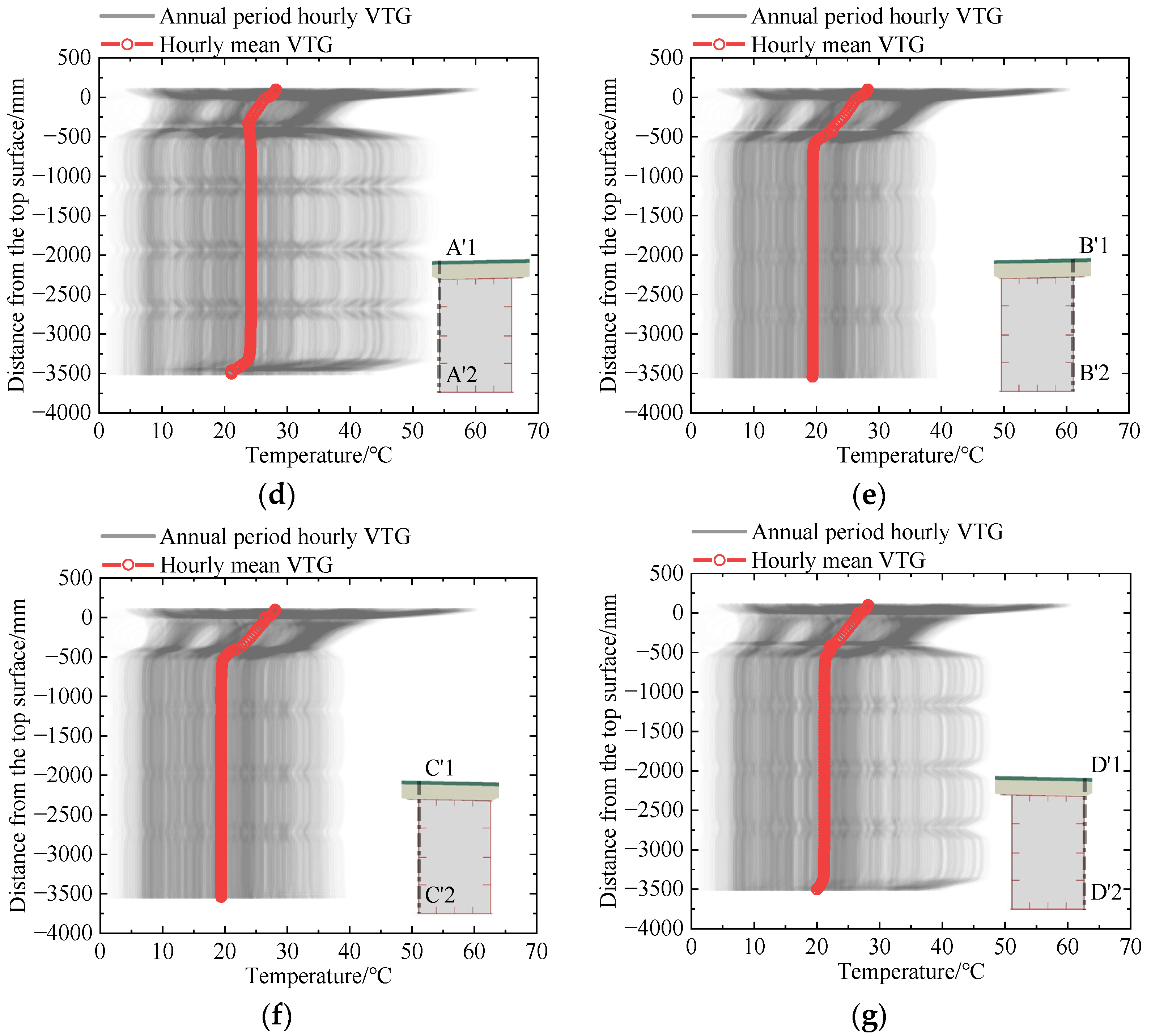
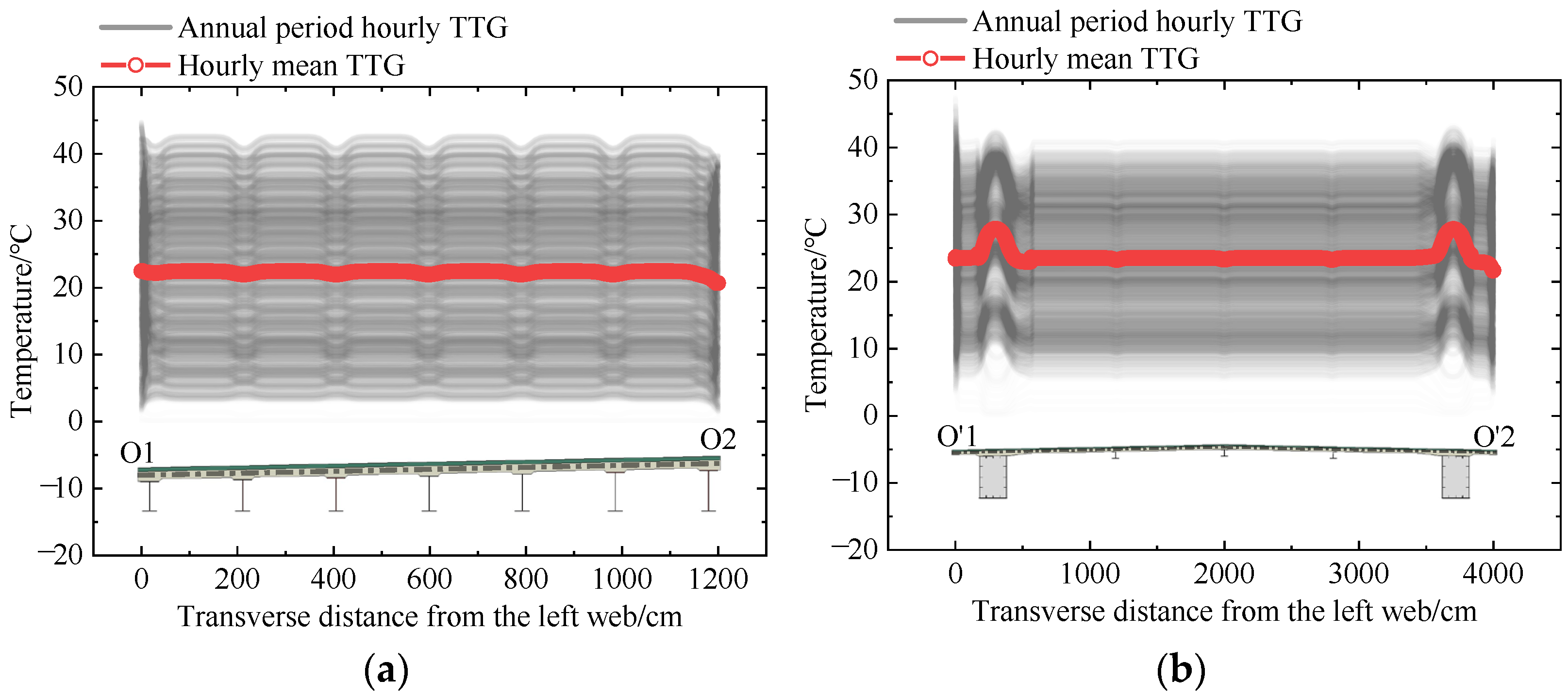
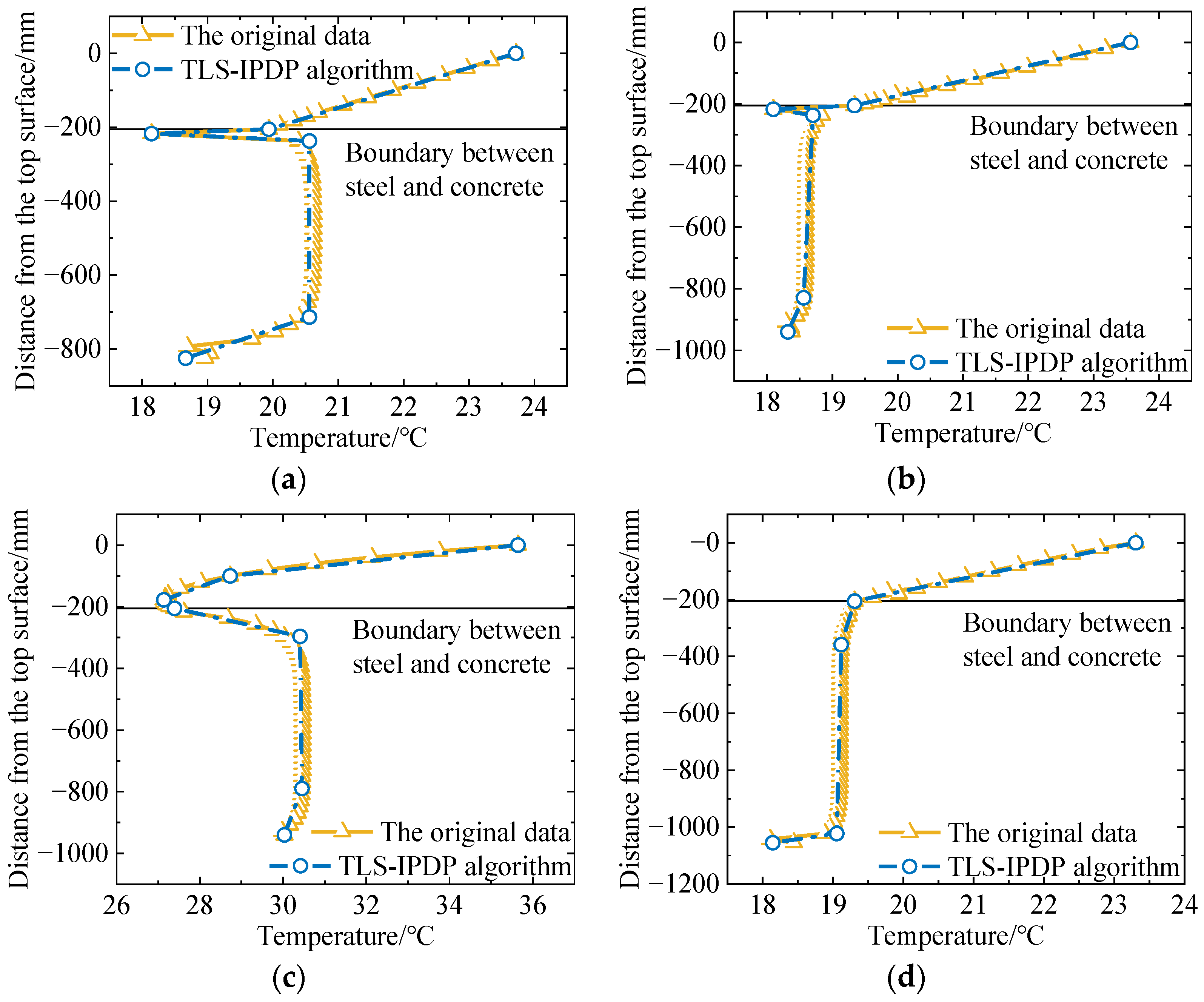
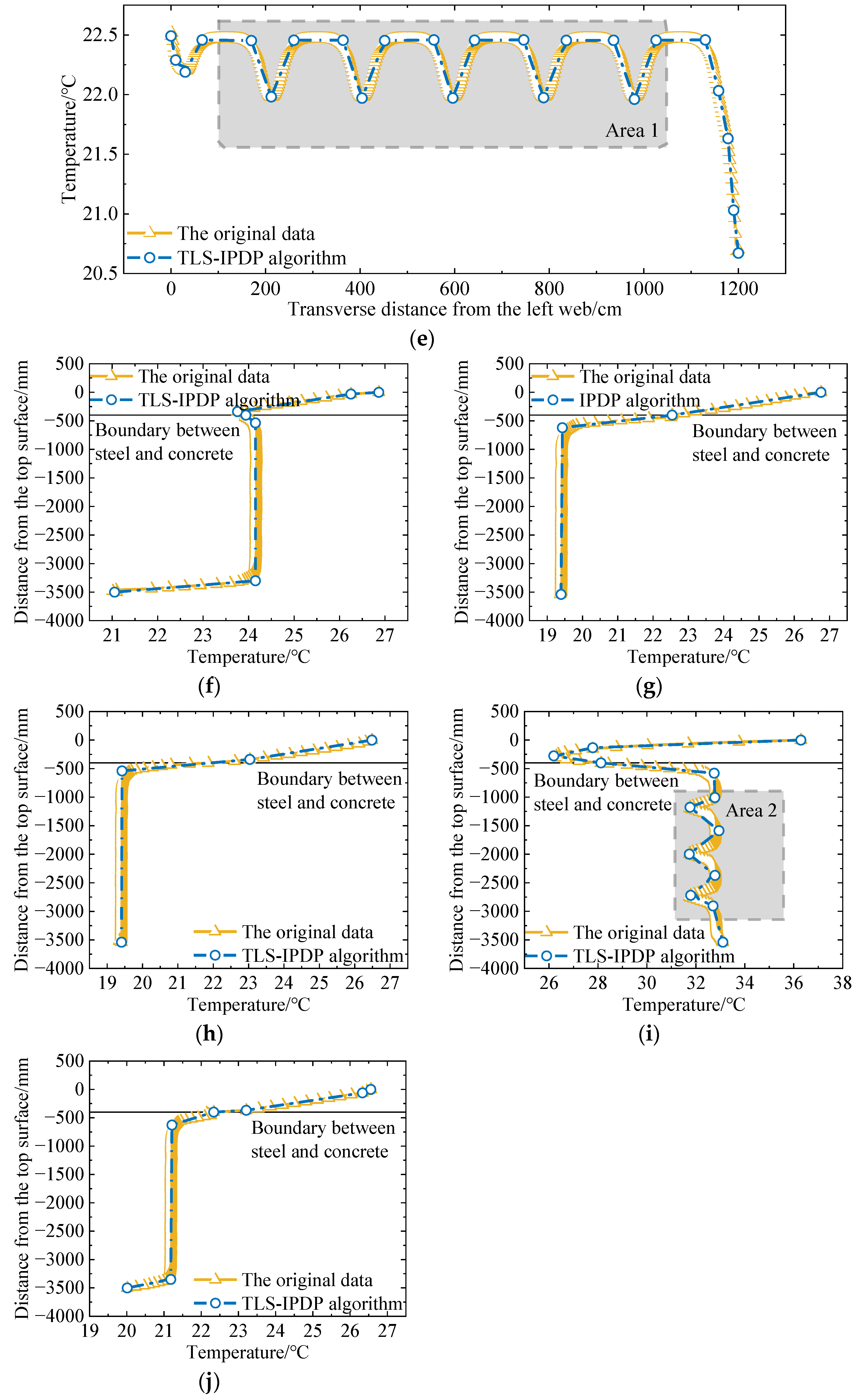
| Model Type | Material | ρ/kg·m−3 | Thermal Conductivity/W·m−1·K−1 | Specific Heat/J·kg−1·°C−1 |
|---|---|---|---|---|
| I | Concrete | 2549 | 1.70 | 920 |
| Asphalt concrete | 2100 | 1.05 | 1168 | |
| Steel | 7850 | 53.2 | 460 | |
| II | Concrete | 2549 | 1.70 | 960 |
| Asphalt concrete | 2360 | 1.05 | 1198 | |
| Steel | 7850 | 53.2 | 480 | |
| Air | See Table 2 | 0.023 | 1081 |
| t/°C | 0 | 10 | 20 | 30 | 40 | 50 | 60 | 70 | 80 |
|---|---|---|---|---|---|---|---|---|---|
| /kg·m−3 | 1.2928 | 1.2471 | 1.2046 | 1.1649 | 1.1277 | 1.0926 | 1.060 | 1.0291 | 1.000 |
| Parameters | Model | ||
|---|---|---|---|
| I | II | ||
| h/m·s−1 | Asphalt Concrete top surface (1) | 14.33 | 14.11 |
| Concrete lower surface (3) | 9.83 | 10.51 | |
| Concrete vertical surface (2)(4) | 11.33 | 11.54 | |
| Steel beam lower surface (6)(8) | 11.05 | 12.85 | |
| Steel beam vertical surface (5)(7)(9) | 13.29 | 13.17 | |
| Asphalt Concrete | 0.95 | 0.95 | |
| Concrete | 0.9 | 0.9 | |
| Steel | 0.6 | 0.6 | |
| C0/W·m−2·K−4 | 5.67 × 10−8 | ||
| Asphalt Concrete | 0.90 | 0.90 | |
| Concrete | 0.70 | 0.75 | |
| Steel | 0.60 | 0.75 | |
| Parts of the Structure | Number of Measuring Points | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| Type I Model | Type II Model | ||||||||
| A1A2 | B1B2 | C1C2 | O1O2 | A′1A′2 | B′1B′2 | C′1C′2 | D′1D′2 | O′1O′2 | |
| Concrete | 2 | 4 | 2 | 9 + 15 (Area 1) | 4 | 2 | 5 | 4 | 16 + 9 (Area 3) |
| Steel | 4 | 6 | 3 | / | 3 | 2 | 3 + 7 (Area 2) | 3 | / |
| Total | 6 | 10 | 5 | 24 | 7 | 4 | 15 | 7 | 25 |
| Model Type | Temperature | |
|---|---|---|
| Low | High | |
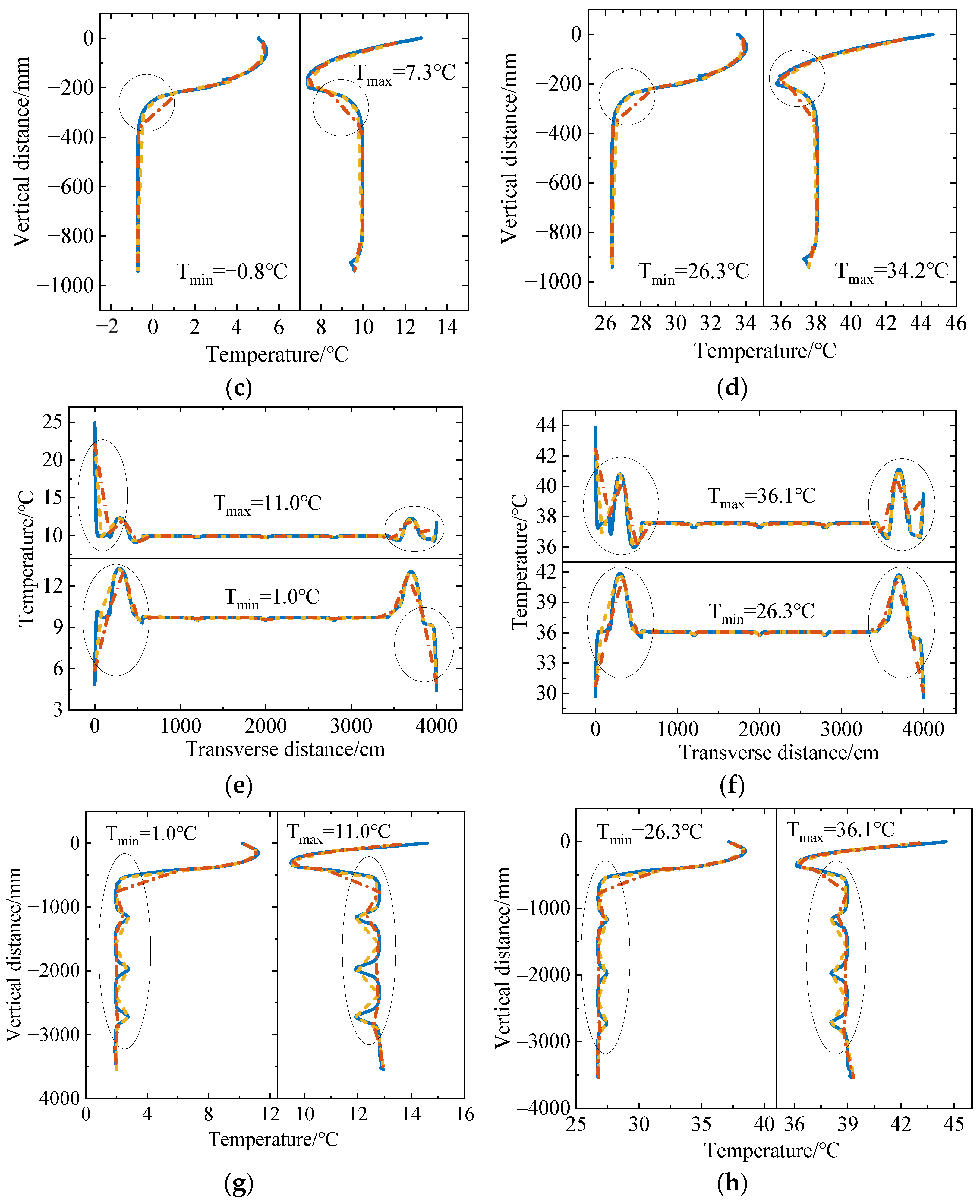
| I | 16 January (Tmin = −0.8 °C, Tmax = 7.3 °C) | 26 July (Tmin = 26.3 °C, Tmax = 34.2 °C) |
| II | 27 December (Tmin = 1.0 °C, Tmax = 11.0 °C) | 10 July (Tmin = 26.3 °C, Tmax = 36.1 °C) |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, J.; Wang, D.; Xiang, S.; Liu, Y.; Tan, B.; Yan, D. Optimization Method of Temperature Measuring Point Layout for Steel-Concrete Composite Bridge Based on TLS-IPDP. Sustainability 2022, 14, 9787. https://doi.org/10.3390/su14159787
Zhang J, Wang D, Xiang S, Liu Y, Tan B, Yan D. Optimization Method of Temperature Measuring Point Layout for Steel-Concrete Composite Bridge Based on TLS-IPDP. Sustainability. 2022; 14(15):9787. https://doi.org/10.3390/su14159787
Chicago/Turabian StyleZhang, Jun, Da Wang, Shengtao Xiang, Yang Liu, Benkun Tan, and Donghuang Yan. 2022. "Optimization Method of Temperature Measuring Point Layout for Steel-Concrete Composite Bridge Based on TLS-IPDP" Sustainability 14, no. 15: 9787. https://doi.org/10.3390/su14159787
APA StyleZhang, J., Wang, D., Xiang, S., Liu, Y., Tan, B., & Yan, D. (2022). Optimization Method of Temperature Measuring Point Layout for Steel-Concrete Composite Bridge Based on TLS-IPDP. Sustainability, 14(15), 9787. https://doi.org/10.3390/su14159787





