Scheduling Optimization of Offshore Oil Spill Cleaning Materials Considering Multiple Accident Sites and Multiple Oil Types
Abstract
:1. Introduction
- An optimization model for dispatching multilocation emergency supplies in response to small offshore oil spills that considers the total dispatching cost and oil spill recovery time is established.
- The interrelationships between the decision-making environment and the groundbreaking consideration of multisite cleanup of small oil spills are critical for an oil spill emergency response.
- Considering the timing of different types of oil spill recovery, this study uses the corresponding batch delivery time window to adjust the emergency operation and transportation of oil spill emergency supplementary resources.
- An improved genetic algorithm (IGA) is proposed to optimize the scheduling model of oil spills and sewage disposal materials in multiple offshore locations. This improves the efficiency and convergence speed of the calculation.
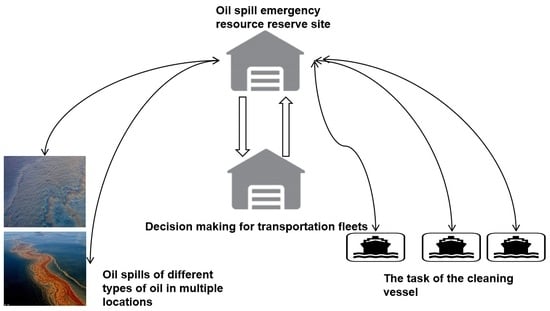
2. Background of the Problem
- (1)
- Materials for blocking oil spills, mainly for the containment boom, are used for containment, oil spill diversion, and potential oil spill prevention.
- (2)
- Materials for the recovery of oil spills, mainly for the oil collector, are used to recover water oil spills and oil and water mixtures.
- (3)
- Other items mainly include adsorption materials and chemical and biological treatment agents, which are used to reduce damage caused by oil spills and accelerate the recovery of damaged waters.
3. Model Building
3.1. Model Assumptions
- (1)
- In the case of general or small offshore oil spill accidents, the demand for emergency supplies is minimal, and the supply of shore-based points can meet the demand. In this case, emergency time is the most important factor. Various oil spill emergency materials, such as oil spill dispersants, oil booms, and oil absorption felt, are available in shore-based material storage. These materials are compatible in nature and can be loaded and transported together. In this study, the materials are packed and processed to form the decontamination-resource package when the demand for spilled oil materials is counted, and the quantity is measured in buckets during calculation. The total amount of shore-based storage completely meets the total demand.
- (2)
- The type and quantity of emergency supplies needed at each accident point should be determined by the actual emergency situation known by the ship–shore communication system and the Geographical Information System.
- (3)
- The loading and unloading times of materials account for a small proportion of the entire material scheduling process. The distance from the transport of materials from the emergency base to the cleaning vessel is extremely short, which has a limited impact on emergency efficiency. The cost and time of these factors are ignored to simplify the analysis.
- (4)
- The vessels from the emergency center to the accident spot transport goods bear the roles of wind and waves. However, the entire process of emergency response and the environment do not change. The differences can remain stable despite the different carriers in different emergency bases, with accident points back and forth between the speed rates. A specific rate calculation method can be referenced.
- (5)
- Territorial management is implemented between emergency bases. Loading between cleaning vessels is prohibited. The loading and unloading of supplies are not allowed to change vessels. Only one oil spill recovery vessel is needed for each accident point to complete the cleaning task. Cooperative operation of multiple vessels is unnecessary.
- (6)
- The loading capacity of the cleaning vessel and the demand for all types of oil spill materials can be arranged by a unified unit, and the materials at different accident points are forbidden from being mixed in the same transport ship.
- (7)
- The loading capacity of the cleaning vessel is sufficient, and the sum of the demands of each customer on each distribution path does not exceed the cargo capacity of the ship. The needs of each site must be met, and only one cleanup vessel can perform one mission.
- (8)
- All cleaning vessels must return to the dock for standby after completing cleaning tasks.
- (9)
- All the functions constructed in the model are continuously differentiable convex functions. Under the condition of effectively controlling oil spill pollution and related constraints, the total dispatching cost of emergency oil spill materials, considering the time window problem, is minimized as the emergency target [45,46].
3.2. Associated Symbols and Definitions
3.3. Establishment of Scheduling Model
4. Research Methods
4.1. Genetic Algorithm (GA)
4.2. Improved Genetic Algorithm (IGA)
4.2.1. Chromosome Coding
4.2.2. Fitness Function
4.2.3. Genetic Operators
- (1)
- Choice
- (2)
- Crossover and mutation operators
4.3. Algorithm Step
5. Implementation of Simulation Experiment and Analysis
5.1. Example Description
5.2. Experimental Results and Discussion
6. Conclusions and Future Research
- (1)
- In comparison to the SA and regular GA, the IGA produces superior results and arrives at the best answer faster in the evolutionary process.
- (2)
- The constructed multisite and multioil-type scheduling optimization model of oil spills and decontamination-related materials has universality. The designed hybrid GA has a high timeliness in solving the model, which can provide a scientific decision-making basis for solving small offshore multisite oil spill accidents.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Peres, L.C.; Trapido, E.; Rung, A.L.; Harrington, D.J.; Oral, E.; Fang, Z.; Fontham, E.; Peters, E.S. The deepwater horizon oil spill and physical health among adult women in southern Louisiana: The women and their children’s health (watch) study. Environ. Health Perspect. 2016, 124, 1208–1213. [Google Scholar] [CrossRef] [PubMed]
- Fan, A.Z.; Prescott, M.R.; Zhao, G.; Gotway, C.A.; Galea, S. Erratum to: Individual and community-level determinants of mental and physical health after the Deepwater horizon oil spill: Findings from two federal surveys. J. Behav. Health Serv. Res. 2015, 42, 123. [Google Scholar] [CrossRef]
- Chust, G.; Sagarminaga, Y. The multi-angle view of misr detects oil slicks under sun glitter conditions. Remote Sens. Environ. 2007, 107, 232–239. [Google Scholar] [CrossRef]
- Zhou, Y.; Wang, Q. CNOOC’s New Oil Spill in Bohai Bay. China Daily. 13 July 2011. Available online: https://www.chinadaily.com.cn/business/2011-07/13/content_12891346.htm (accessed on 30 March 2022).
- Liu, H.; He, W.; Guo, J.; Huang, Q. Risk propagation mechanism: Qingdao crude oil leaking and explosion case study. Eng. Fail. Anal. 2015, 56, 555–561. [Google Scholar] [CrossRef]
- Chen, J.; Di, Z.; Shi, J.; Shu, Y.; Zhang, W. Marine oil spill pollution causes and governance: A case study of sanchi tanker collision and explosion. J. Clean. Prod. 2020, 273, 122978. [Google Scholar] [CrossRef]
- Li, K.; Ouyang, J.; Yu, H.; Xu, Y.; Xu, J. Overview of Research on Monitoring of Marine Oil Spill. IOP Conf. Ser. Earth Environ. Sci. 2021, 787, 012078. [Google Scholar] [CrossRef]
- Idris, J.; Eyu, G.D.; Ahmad, Z.; Chukwuekezie, C.S. Oil Spills and Sustainable Cleanup Approach. Aust. J. Basic Appl. Sci. 2013, 7, 272–280. [Google Scholar]
- Dominguez-Péry, C.; Raju, L.N.; Corbett-Etchevers, I.; Tassabehji, R. World of Shipping Portugal. In Proceedings of the An International Research Conference on Maritime Affairs, Virtual Conference, 28–29 January 2021. [Google Scholar]
- Yang, Z.; Guo, L.; Yang, Z. Emergency logistics for wildfire suppression based on forecasted disaster evolution. Ann. Oper. Res. 2017, 283, 917–937. [Google Scholar] [CrossRef]
- Reuters. CHRONOLOGY-ConocoPhillips Oil Spill in China’s Bohai Bay. 2011. Available online: https://www.reuters.com/article/china-conoco-spill-idAFL3E7K60J320110919 (accessed on 19 September 2011).
- Ye, X.; Chen, B.; Li, P.; Jing, L.; Zeng, G. A simulation-based multi-agent particle swarm optimization approach for supporting dynamic decision making in marine oil spill responses. Ocean. Coast. Manag. 2019, 172, 128–136. [Google Scholar] [CrossRef]
- Xiong, W.; van Gelder, P.; Yang, K. A decision support method for design and operationalization of search and rescue in maritime emergency. Ocean. Eng. 2020, 207, 107399. [Google Scholar] [CrossRef]
- Lu, C.-C.; Ying, K.-C.; Chen, H.-J. Real-time relief distribution in the aftermath of disasters—A rolling horizon approach. Transp. Res. Part E Logist. Transp. Rev. 2016, 93, 1–20. [Google Scholar] [CrossRef]
- Song, X.; Wang, J.; Chang, C. Nonlinear continuous consumption emergency material dispatching problem. J. Syst. Eng. 2017, 32, 163–176. [Google Scholar]
- Chen, X.; Liu, L.; Huang, W. The detection and prediction for oil spill on the sea based on the infrared images. Infrared Phys. Technol. 2016, 77, 391–404. [Google Scholar] [CrossRef]
- Ju, G.; Liu, J.; Li, D.; Cheng, M.; Shi, F. Chemical and equipment-free strategy to fabricate water/oil separating materials for emergent oil-spill accidents. Langmuir ACS J. Surf. Colloids 2017, 33, 2664–2670. [Google Scholar] [CrossRef]
- Lu, J.; Yuan, F.; Mikkelsen, J.D.; Ohm, C.; Stange, E.; Holand, M. Modelling the transport of oil after a proposed oil spill accident in barents sea and its environmental impact on Alke species. IOP Conf. Ser. Earth Environ. Sci. 2017, 82, 012010. [Google Scholar] [CrossRef]
- Wu, Z.Y.; Li, C.; Liang, H.W.; Zhang, Y.N.; Wang, X.; Chen, J.F.; Yu, S.H. Carbon nanofiber aerogels for emergent cleanup of oil spillage and chemical leakage under harsh conditions. Sci. Rep. 2014, 4, 4079. [Google Scholar] [CrossRef] [PubMed]
- Moroni, D.; Pieri, G.; Tampucci, M. Environmental decision support systems for monitoring small scale oil spills: Existing solutions, best practices and current challenges. J. Mar. Sci. Eng. 2019, 7, 19. [Google Scholar] [CrossRef]
- Cai, M. Experience and thinking on emergency disposal of offshore oil spill accidents. Mod. Chem. Res. 2018. Available online: https://kns.cnki.net/kcms/detail/detail.aspx?dbcode=CJFD&dbname=CJFDLAST2018&filename=ZJTY201807063&uniplatform=NZKPT&v=vA7L_uTI5TImNjT_b_wmL-3tq9-XOucAEItpIL2zo6YjNhOCV-bjkLuTV8iSg07D (accessed on 20 March 2022).
- Alem, D.; Clark, A.; Moreno, A. Stochastic network models for logistics planning in disaster relief. Eur. J. Oper. Res. 2016, 255, 187–206. [Google Scholar] [CrossRef]
- Liu, K.; Li, Q.; Zhang, Z.-H. Distributionally robust optimization of an emergency medical service station location and sizing problem with joint chance constraints. Transp. Res. Part B Methodol. 2019, 119, 79–101. [Google Scholar] [CrossRef]
- Liu, C.S.; Kou, G.; Liu, D.B. Fuzzy dynamic LRP for post-earthquake multimodal relief delivery. J. Manag. Sci. China 2016, 19, 61–72. [Google Scholar]
- Zeng, J.; Yao, Q.G.; Zhang, Y.S.; Lu, J.T.; Wang, M. Optimal path selection for emergency relief supplies after mine disasters. Int. J. Simul. Model. 2019, 18, 476–487. [Google Scholar] [CrossRef]
- Li, P.; Cai, Q.; Lin, W.; Chen, B.; Zhang, B. Offshore oil spill response practices and emerging challenges. Mar. Pollut. Bull. 2016, 110, 6–27. [Google Scholar] [CrossRef] [PubMed]
- Wang, W.; Huang, L.; Zhang, X. Optimization of maritime emergency materials allocation based on network reliability. J. Coast. Res. 2018, 83 (Suppl. S1), 691–696. [Google Scholar] [CrossRef]
- Wang, H.; Du, L.; Ma, S. Multi-objective open location-routing model with split delivery for optimized relief distribution in post-earthquake. Transp. Res. Part E Logist. Transp. Rev. 2014, 69, 160–179. [Google Scholar] [CrossRef]
- Huang, X.; Ren, Y.; Zhang, J.; Wang, D.; Liu, J. Dynamic scheduling optimization of marine oil spill emergency resource. J. Coast. Res. 2020, 107 (Suppl. S1), 437. [Google Scholar] [CrossRef]
- Liu, J.; Guo, L.; Jiang, J.; Jiang, D.; Wang, P. Emergency material allocation with time-varying supply-demand based on dynamic optimization method for river chemical spills. Environ. Sci. Pollut. Res. 2018, 25, 17343–17353. [Google Scholar] [CrossRef]
- Hao, G.Z.; Huang, L.W.; Zhang, K.; Wang, Q.; Chen, L. On the dual-objective emergency material dispatching pattern of the marine oil spill accidents. J. Saf. Environ. 2020. [Google Scholar] [CrossRef]
- Garrett, R.A.; Sharkey, T.C.; Grabowski, M.; Wallace, W.A. Dynamic resource allocation to support oil spill response planning for energy exploration in the arctic. Eur. J. Oper. Res. 2017, 257, 272–286. [Google Scholar] [CrossRef]
- Choe, Y.; Kim, H.; Huh, C.; Kim, C.K.; Choi, H.J. Estimation of the mechanical recovery potential of spilled oil at sea considering the spatial thickness distribution. J. Mar. Sci. Eng. 2020, 8, 362. [Google Scholar] [CrossRef]
- Zhang, L.; Lu, J.; Yang, Z. Optimal scheduling of emergency resources for major maritime oil spills considering time-varying demand and transportation networks. Eur. J. Oper. Res. 2020, 293, 529–546. [Google Scholar] [CrossRef]
- Wu, W. A revised grey relational analysis method for multicriteria group decision-making with expected utility theory for oil spill emergency management. Math. Probl. Eng. 2021, 2021, 6682332. [Google Scholar] [CrossRef]
- Ye, X.; Chen, B.; Lee, K.; Storesund, R.; Kang, Q. An emergency response system by dynamic simulation and enhanced particle swarm optimization and application for a marine oil spill accident. J. Clean. Prod. 2021, 297, 126591. [Google Scholar] [CrossRef]
- Xuan, S.; Hu, S.; Li, Z.; Li, W.; Li, B. Dynamics simulation for process risk evolution on the bunker operation of an lng-fueled vessel with catastrophe mathematical models. J. Mar. Sci. Eng. 2019, 7, 299. [Google Scholar] [CrossRef]
- Li, S.; Grifoll, M.; Estrada, M.; Zheng, P.; Feng, H. Optimization on emergency materials dispatching considering the characteristics of integrated emergency response for large-scale marine oil spills. J. Mar. Sci. Eng. 2019, 7, 214. [Google Scholar] [CrossRef]
- Grubesic, T.H.; Wei, R.; Nelson, J. Optimizing oil spill cleanup efforts: A tactical approach and evaluation framework. Mar. Pollut. Bull. 2017, 125, 318–329. [Google Scholar] [CrossRef]
- Wu, B.; Yip, T.L.; Yan, X.; Mao, Z. A mutual information-based Bayesian network model for consequence estimation of navigational accidents in the Yangtze river. J. Navig. 2019, 73, 1–22. [Google Scholar] [CrossRef]
- Brussaard, C.P.D.; Peperzak, L.; Beggah, S.; Wick, L.Y.; Wuerz, B.; Weber, J.; Arey, J.S.; Van Der Burg, B.; Jonas, A.; Huisman, J.; et al. Immediate ecotoxicological effects of short-lived oil spills on marine biota. Nat. Commun. 2016, 7, 11206. [Google Scholar] [CrossRef]
- Zhang, Q.; An, W.; Zhao, J.; Liu, B.; Li, Q.; He, L. Influence of Weathering Process on Recovery Efficiency of Spilled Oil. Ship Ocean. Eng. 2020, 49, 75–79. [Google Scholar] [CrossRef]
- Zhang, Z.; Wang, Z.; Zhou, H. An Emergency Resource Allocation Method Based on Supernetwork for Urban Disaster. In International Conference on Applications and Techniques in Cyber Security and Intelligence; Springer: Cham, Switzerland, 2019. [Google Scholar]
- Yang, H.; Chen, L.; Liu, B.; Migdalas, A. Emergency decision-making model of suppliers with updating information in cases of sudden accidents. Comput. Ind. Eng. 2021, 162, 107740. [Google Scholar] [CrossRef]
- Manning, J.; Verfaillie, M.; Barker, C.; Berg, C.; Kinner, N. Responder needs addressed by arctic maritime oil spill modeling. J. Mar. Sci. Eng. 2021, 9, 201. [Google Scholar] [CrossRef]
- Yuan, D.; Lu, Z.; Zhang, J.; Li, X.; Ma, T. Integrative design of an emergency resource predicting-scheduling-repairing method for rail track faults. IEEE Access 2019, 7, 155686–155700. [Google Scholar] [CrossRef]
- Jiang, Y.; Li, L.; Liu, Z. A multi-objective robust optimization design for grid emergency goods distribution under mixed uncertainty. IEEE Access 2018, 6, 61117–61129. [Google Scholar] [CrossRef]
- Wang, F.; Pei, Z.; Dong, L.; Ma, J. Emergency resource allocation for multi-period post-disaster using multi-objective cellular genetic algorithm. IEEE Access 2020, 8, 82255–82265. [Google Scholar] [CrossRef]
- Yan, G.; Awa, B. Spatial scheduling for irregularly shaped blocks in shipbuilding. Comput. Ind. Eng. 2020, 152, 106985. [Google Scholar]
- Prentice, B.E.; Lau, Y.Y.; Ng, A. Transport airships for scheduled supply and emergency response in the arctic. Sustainability 2021, 13, 5301. [Google Scholar] [CrossRef]
- Zhang, C.Y.; Li, P.G.; Rao, Y.Q.; Guan, Z.L. A very fast TS/SA algorithm for the job shop scheduling problem. Comput. Oper. Res. 2008, 35, 282–294. [Google Scholar] [CrossRef]
- Sahoo, K.S.; Sahoo, B.; Dash, R.; Jena, N. Optimal controller selection in Software Defined Network using a Greedy-SA algorithm. In Proceedings of the International Conference on Computing for Sustainable Global Development, New Delhi, India, 16–18 March 2016; IEEE: Piscataway, NJ, USA, 2016. [Google Scholar]




| Oil Samples | Density (20 °C)/(Kg∙m−3) | Viscosity (20 °C)/(MPa∙s) |
|---|---|---|
| A | 933.4 | 437.7 |
| B | 926.9 | 581.2 |
| C | 934.0 | 1722.3 |
| Serial Number | X Coordinates | Y Coordinates | Required Materials /Drum | Amount of Dirty Oil Per Barrel | Occurrence Time of Oil Spills (AM) | Right Time Window (AM) | Cleaning Operation Time/Min | Oil Spill Species |
|---|---|---|---|---|---|---|---|---|
| 0 | 100 | 0 | 0 | 0 | 4:00 | 10:00 | 0 | 0 |
| 1 | 1 | 40 | 18 | 12 | 4:24 | 8:24 | 60 | A |
| 2 | 4 | 60 | 18 | 16 | 4:16 | 8:54 | 80 | B |
| 3 | 6 | 110 | 25 | 10 | 5:23 | 7:23 | 60 | C |
| 4 | 50 | 130 | 19 | 20 | 5:18 | 8:38 | 100 | A |
| 5 | 70 | 30 | 22 | 13 | 4:19 | 9:19 | 60 | B |
| 6 | 90 | 5 | 19 | 10 | 5:01 | 6:41 | 80 | C |
| 7 | 120 | 14 | 18 | 12 | 4:20 | 8:20 | 60 | A |
| 8 | 150 | 35 | 16 | 14 | 5:21 | 10:01 | 80 | B |
| 9 | 160 | 190 | 14 | 7 | 4:15 | 6:15 | 60 | C |
| 10 | 127 | 170 | 19 | 10 | 5:24 | 9:36 | 48 | A |
| 11 | 140 | 149 | 24 | 11 | 4:15 | 9:35 | 40 | B |
| 12 | 63 | 157 | 20 | 8 | 5:22 | 7:52 | 30 | C |
| Serial Number | Parameter | Value |
|---|---|---|
| 1 | Population size | 200 |
| 2 | Evolution algebra | 100 |
| 3 | Crossover probability | Pa = 0.8 Pb = 0.5 |
| 4 | Mutation probability | Pu = 0.1 Pv = 0.002 |
| 5 | Generation gap | 0.9 |
| 6 | Number of cleaning vessels on standby/vessel | 10 |
| 7 | Maximum carrying capacity of a cleaning vessel/barrel | 100 |
| 8 | Speed of the cleaning vessel/km/h | 50 |
| 9 | Use cost of cleaning vessel/10,000 yuan | 100 |
| 10 | Transport cost per unit distance of cleaning vessel/yuan∙Km−1 | 70 |
| 11 | Penalty cost for breach of loading capacity (10,000 yuan∙barrel−1) | 5 |
| 12 | Penalties for violating the time window constraints (10,000 yuan∙min−1) | 1 |
| Algorithm | Serial Number | Parameter | Value |
|---|---|---|---|
| GA | 1 | Population size | 200 |
| 2 | Evolution algebra | 100 | |
| 3 | Crossover probability | PC = 0.9 | |
| 4 | Mutation probability | Pm = 0.05 | |
| 5 | The generation gap | 0.9 | |
| SA | 1 | Initial temperature | 3000 |
| 2 | Final temperature | 0.01 | |
| 3 | Temperature attenuation factor | 0.98 | |
| 4 | Markov chain length | 100 | |
| 5 | Tolerance | 1 | |
| 6 | Step length factor | 0.3 | |
| 7 | A metropolis procedure always accepts points | 0 |
| Algorithm | Number of Cleaning Vessels Used | Total Cost of Clean-Up/Ten Thousand Yuan | Fuel Consumption /Ten Thousand Yuan | Penalty Cost for Breach of Loading Capacity/Ten Thousand Yuan | Penalty Costs for Time Window Violations/Ten Thousand Yuan | Scheduling Scheme for Cleaning Vessel Operation |
|---|---|---|---|---|---|---|
| IGA | 4 | 11,942,653 | 7,942,653 | 0 | 0 | The operation path of the NO. 1 cleaning vessel is: 0 ->1 -> 2 -> 5 -> 0 The operation path of the NO. 2 cleaning vessel is: 0 ->9 -> 10 -> 11 -> 8 -> 0 The operation path of the NO. 3 cleaning vessel is: 0 ->3 -> 12 -> 4 -> 0 The operation path of the NO. 4 cleaning vessel is: 0 ->6 -> 7 -> 0 |
| GA | 4 | 12,287,934 | 8,287,934 | 0 | 0 | The operation path of the NO. 1 cleaning vessel is: 0 ->1 -> 3 -> 2 -> 0 The operation path of the NO. 2 cleaning vessel is: 0 ->5 -> 12 -> 4 -> 0 The operation path of the NO. 3 cleaning vessel is: 0 ->6 -> 7 -> 0 The operation path of the NO. 4 cleaning vessel is: 0 ->9 -> 10 -> 11 -> 8 -> 0 |
| SA | 4 | 12,263,579 | 8,263,579 | 0 | 0 | The operation path of the NO. 1 cleaning vessel is: 0 ->3 -> 12 -> 4 -> 0 The operation path of the NO. 2 cleaning vessel is: 0 ->11 -> 9 -> 10 -> 0 The operation path of the NO. 3 cleaning vessel is: 0 ->6 -> 7 -> 8 -> 0 The operation path of the NO. 4 cleaning vessel is: 0 ->5 -> 2 -> 1 -> 0 |
| Algorithm | Average Value/Ten Thousand Yuan | Standard Deviation | Operation Time/s |
|---|---|---|---|
| GA | 12,301,256 | 19.33456 | 287.3153 |
| SA | 12,288,968 | 16.4226 | 1202.8636 |
| IGA | 11,902,352 | 5.3426 | 221.2729 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, K.; Yu, H.; Xu, Y.; Luo, X. Scheduling Optimization of Offshore Oil Spill Cleaning Materials Considering Multiple Accident Sites and Multiple Oil Types. Sustainability 2022, 14, 10047. https://doi.org/10.3390/su141610047
Li K, Yu H, Xu Y, Luo X. Scheduling Optimization of Offshore Oil Spill Cleaning Materials Considering Multiple Accident Sites and Multiple Oil Types. Sustainability. 2022; 14(16):10047. https://doi.org/10.3390/su141610047
Chicago/Turabian StyleLi, Kai, Hongliang Yu, Yiqun Xu, and Xiaoqing Luo. 2022. "Scheduling Optimization of Offshore Oil Spill Cleaning Materials Considering Multiple Accident Sites and Multiple Oil Types" Sustainability 14, no. 16: 10047. https://doi.org/10.3390/su141610047
APA StyleLi, K., Yu, H., Xu, Y., & Luo, X. (2022). Scheduling Optimization of Offshore Oil Spill Cleaning Materials Considering Multiple Accident Sites and Multiple Oil Types. Sustainability, 14(16), 10047. https://doi.org/10.3390/su141610047