Predictions of Geological Interface Using Relevant Vector Machine with Borehole Data
Abstract
:1. Introduction
2. Relevant Vector Machine
3. The Width Parameter Optimized by PSO
4. Results and Discussion
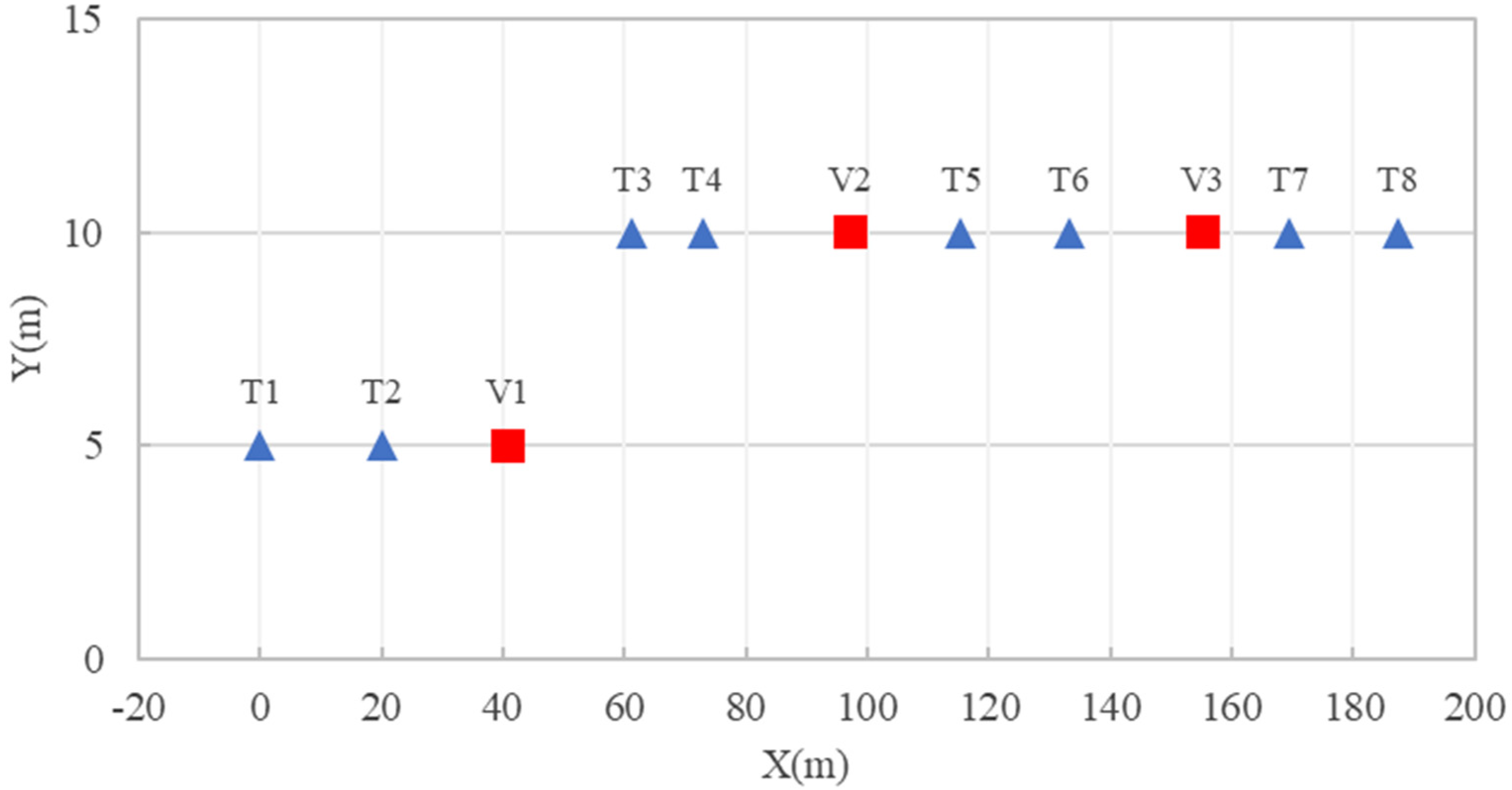
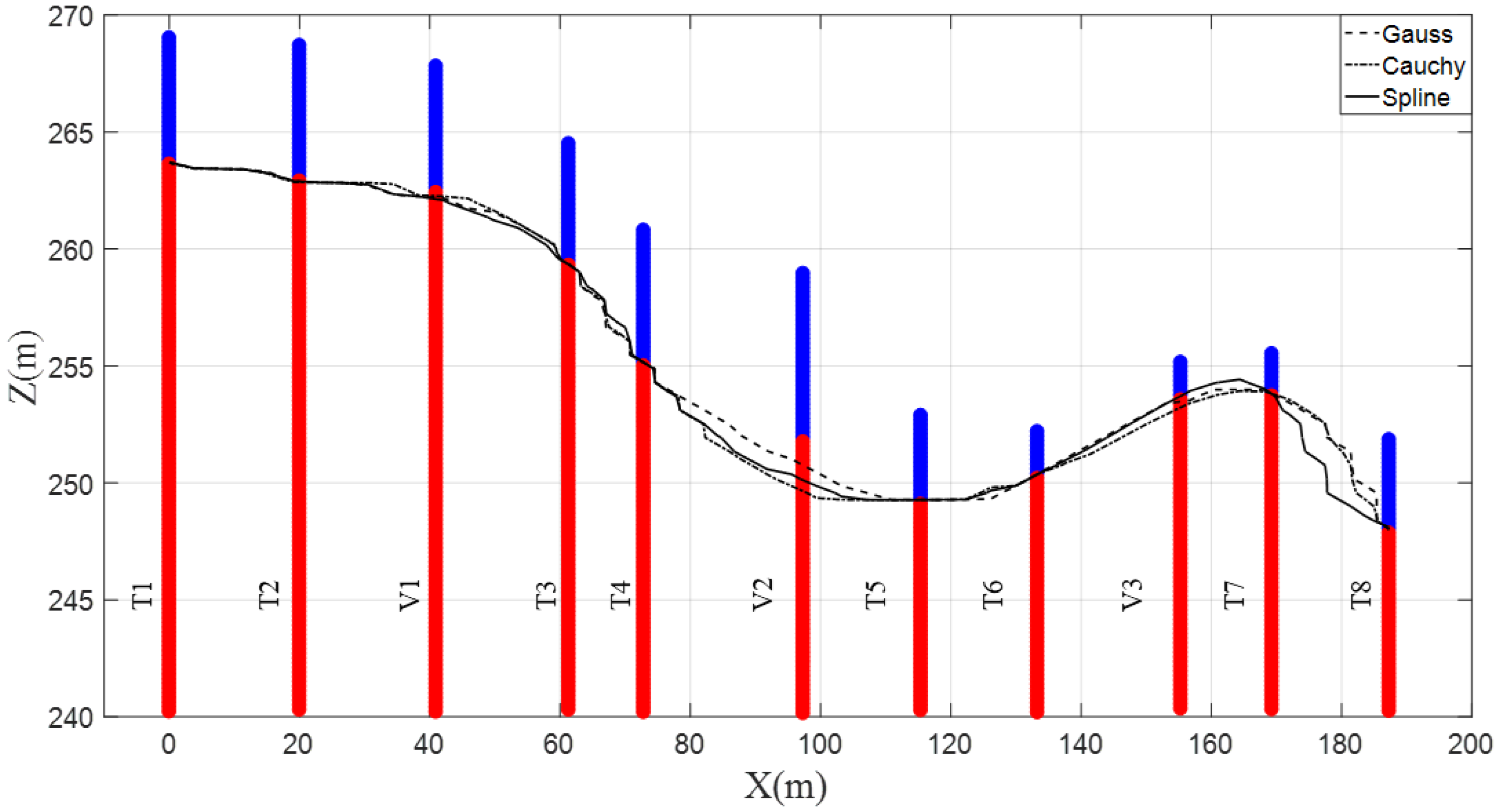
4.1. Two-Dimensional Analysis
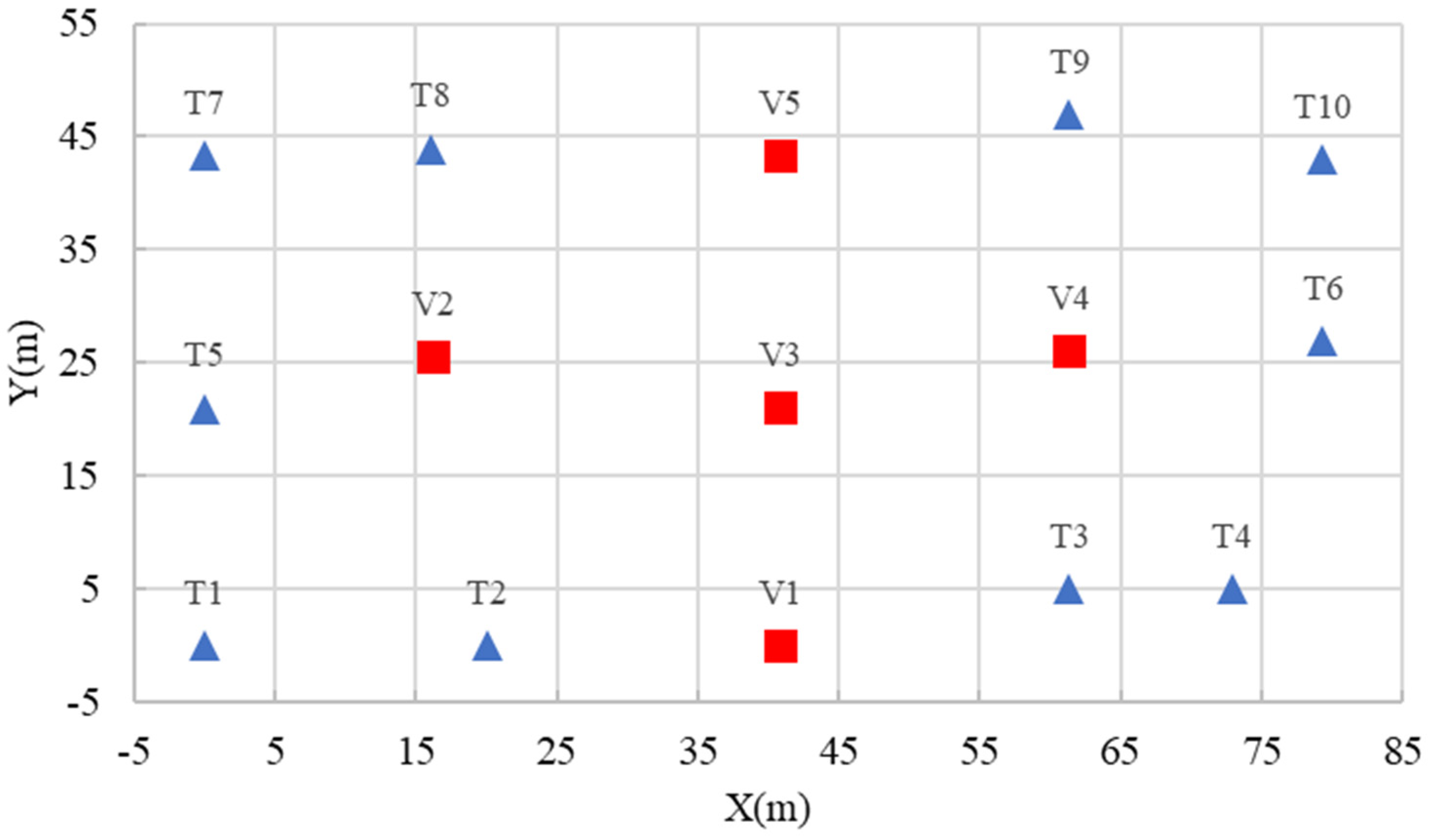
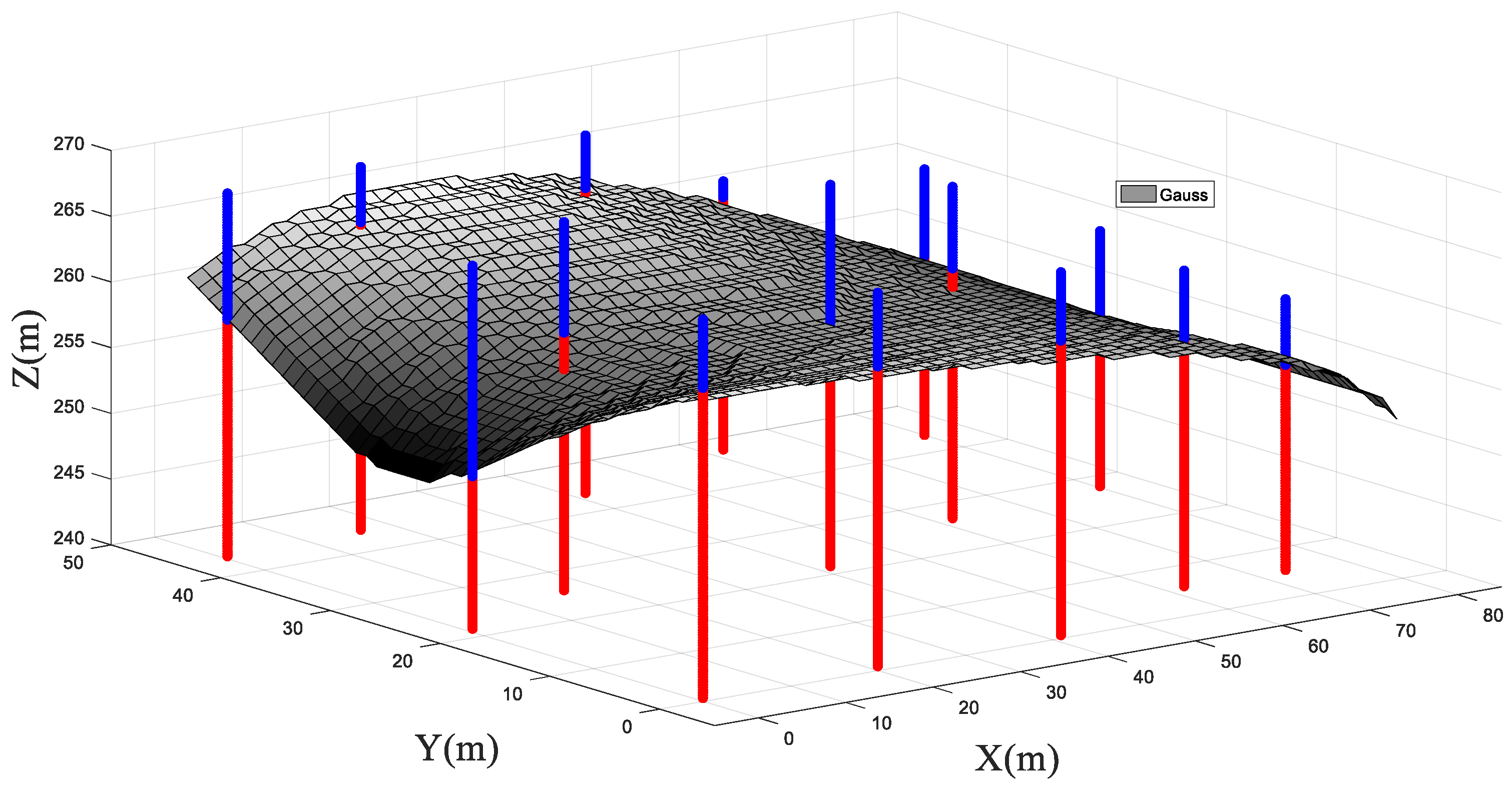
4.2. Three-Dimensional Analysis
5. Conclusions and Discussions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Source Codes of the Key Program in MATLAB
References
- Deng, Z.P.; Jiang, S.H.; Niu, J.T.; Pan, M.; Liu, L.L. Stratigraphic uncertainty characterization using generalized coupled Markov chain. Bull. Eng. Geol. Environ. 2020, 79, 5061–5078. [Google Scholar] [CrossRef]
- Phoon, K.K.; Ching, J.; Shuku, T. Challenges in data-driven site characterization. Georisk Assess. Manag. Risk Eng. Syst. Geohazards 2022, 16, 114–126. [Google Scholar] [CrossRef]
- Zhang, W.; Gu, X.; Tang, L.; Yin, Y.; Liu, D.; Zhang, Y. Application of machine learning, deep learning and optimization algorithms in geoengineering and geoscience: Comprehensive review and future challenge. Gondwana Res. 2022, 109, 1–17. [Google Scholar] [CrossRef]
- Liu, L.L.; Cheng, Y.M.; Pan, Q.J.; Dias, D. Incorporating stratigraphic boundary uncertainty into reliability analysis of slopes in spatially variable soils using one-dimensional conditional Markov chain model. Comput. Geotech. 2020, 118, 103321. [Google Scholar] [CrossRef]
- Liu, L.L.; Wang, Y. Quantification of stratigraphic boundary uncertainty from limited boreholes and its effect on slope stability analysis. Eng. Geol. 2022, 306, 106770. [Google Scholar] [CrossRef]
- Gong, W.; Tang, H.; Wang, H.; Wang, X.; Juang, C.H. Probabilistic analysis and design of stabilizing piles in slope considering stratigraphic uncertainty. Eng. Geol. 2019, 259, 105162. [Google Scholar] [CrossRef]
- Qi, X.; Wang, H.; Chu, J.; Chiam, K. Two-dimensional prediction of the interface of geological formations: A comparative study. Tunn. Undergr. Space Technol. 2022, 121, 104329. [Google Scholar] [CrossRef]
- Qi, X.; Wang, H.; Pan, X.; Chu, J.; Chiam, K. Prediction of interfaces of geological formations using the multivariate adaptive regression spline method. Undergr. Space 2021, 6, 252–266. [Google Scholar] [CrossRef]
- Li, Z.; Wang, X.; Wang, H.; Liang, R.Y. Quantifying stratigraphic uncertainties by stochastic simulation techniques based on Markov random field. Eng. Geol. 2016, 201, 106–122. [Google Scholar] [CrossRef]
- Li, X.Y.; Zhang, L.M.; Li, J.H. Using conditioned random field to characterize the variability of geologic profiles. J. Geotech. Geoenviron. Eng. 2016, 142, 04015096. [Google Scholar] [CrossRef]
- Han, L.; Wang, L.; Zhang, W.; Geng, B.; Li, S. Rockhead profile simulation using an improved generation method of conditional random field. J. Rock Mech. Geotech. Eng. 2022, 14, 896–908. [Google Scholar] [CrossRef]
- Zhang, J.Z.; Liu, Z.Q.; Zhang, D.M.; Huang, H.W.; Phoon, K.K.; Xue, Y.D. Improved coupled Markov chain method for simulating geological uncertainty. Eng. Geol. 2022, 298, 106539. [Google Scholar] [CrossRef]
- Shi, C.; Wang, Y. Data-driven construction of Three-dimensional subsurface geological models from limited Site-specific boreholes and prior geological knowledge for underground digital twin. Tunn. Undergr. Space Technol. 2022, 126, 104493. [Google Scholar] [CrossRef]
- Song, S.; Mukerji, T.; Hou, J. Geological facies modeling based on progressive growing of generative adversarial networks (GANs). Comput. Geosci. 2021, 25, 1251–1273. [Google Scholar] [CrossRef]
- Feng, R.; Grana, D.; Mukerji, T.; Mosegaard, K. Application of Bayesian Generative Adversarial Networks to Geological Facies Modeling. Math. Geosci. 2022, 54, 831–855. [Google Scholar] [CrossRef]
- Liu, Q.; Liu, W.; Yao, J.; Liu, Y.; Pan, M. An improved method of reservoir facies modeling based on generative adversarial networks. Energies 2021, 14, 3873. [Google Scholar] [CrossRef]
- Tipping, M.E. Sparse Bayesian learning and the relevance vector machine. J. Mach Learn. Res. 2001, 1, 211–244. [Google Scholar]
- Tipping, M. The relevance vector machine. Adv. Neural Inf. Process. Syst. 1999, 12, 652–658. [Google Scholar]
- Bishop, C.M.; Nasrabadi, N.M. Pattern Recognition and Machine Learning; Springer: New York, NY, USA, 2006; Volume 4, p. 738. [Google Scholar]
- Li, Y.; Chen, J.; Shang, Y. An RVM-based model for assessing the failure probability of slopes along the Jinsha River, close to the Wudongde dam site, China. Sustainability 2016, 9, 32. [Google Scholar] [CrossRef]
- Zhao, H.; Yin, S.; Ru, Z. Relevance vector machine applied to slope stability analysis. Int. J. Numer. Anal. Methods Geomech. 2012, 36, 643–652. [Google Scholar] [CrossRef]
- Pan, Q.J.; Leung, Y.F.; Hsu, S.C. Stochastic seismic slope stability assessment using polynomial chaos expansions combined with relevance vector machine. Geosci. Front. 2021, 12, 405–414. [Google Scholar] [CrossRef]
- Samui, P. Application of relevance vector machine for prediction of ultimate capacity of driven piles in cohesionless soils. Geotech. Geol. Eng. 2012, 30, 1261–1270. [Google Scholar] [CrossRef]
- Samui, P. Least square support vector machine and relevance vector machine for evaluating seismic liquefaction potential using SPT. Nat. Hazards 2011, 59, 811–822. [Google Scholar] [CrossRef]
- Abd-Elwahed, M.S. Drilling Process of GFRP Composites: Modeling and Optimization Using Hybrid ANN. Sustainability 2022, 14, 6599. [Google Scholar] [CrossRef]
- Esmaeili-Falak, M.; Katebi, H.; Vadiati, M.; Adamowski, J. Predicting triaxial compressive strength and Young’s modulus of frozen sand using artificial intelligence methods. J. Cold Reg. Eng. 2019, 33, 04019007. [Google Scholar] [CrossRef]
- Yuan, J.; Zhao, M.; Esmaeili-Falak, M. A comparative study on predicting the rapid chloride permeability of self-compacting concrete using meta-heuristic algorithm and artificial intelligence techniques. Struct. Concr. 2022, 23, 753–774. [Google Scholar] [CrossRef]
- Ge, D.M.; Zhao, L.C.; Esmaeili-Falak, M. Estimation of rapid chloride permeability of SCC using hyperparameters optimized random forest models. J. Sustain. Cem.-Based Mater. 2022, 5, 1–19. [Google Scholar] [CrossRef]
- Gong, Y.-L.; Hu, M.-J.; Yang, H.-F.; Han, B. Research on application of ReliefF and improved RVM in water quality grade evaluation. Water Sci. Technol. 2022, 83, 799–810. [Google Scholar] [CrossRef] [PubMed]
- Li, T.; Zhou, M.; Guo, C.; Luo, M.; Wu, J.; Pan, F.; Tao, Q.; He, T. Forecasting crude oil price using EEMD and RVM with adaptive PSO-based kernels. Energies 2016, 9, 1014. [Google Scholar] [CrossRef]
- Tao, H.; Al-Bedyry, N.K.; Khedher, K.M.; Luo, M. River water level prediction in coastal catchment using hybridized relevance vector machine model with improved grasshopper optimization. J. Hydrol. 2021, 598, 126477. [Google Scholar] [CrossRef]
- Poli, R.; Kennedy, J.; Blackwell, T. Particle swarm optimization. Swarm Intell. 2007, 1, 33–57. [Google Scholar] [CrossRef]
- Germin Nisha, M.; Pillai, G.N. Nonlinear model predictive control with relevance vector regression and particle swarm optimization. J. Control. Theory Appl. 2013, 11, 563–569. [Google Scholar] [CrossRef]
- Sengupta, S.; Basak, S.; Peters, R.A. Particle Swarm Optimization: A survey of historical and recent developments with hybridization perspectives. Mach. Learn. Knowl. Extr. 2018, 1, 10. [Google Scholar] [CrossRef]





| Kernel Function | for Training Data | for Validation Data | (m) for V2 |
|---|---|---|---|
| Spline | 1.0 | 0.8544 | 8.4 |
| Cauchy | 1.0 | 0.8576 | 12.4 |
| Gauss | 1.0 | 0.8479 | 9.4 |
| Kernel Function | V1 | V2 | V3 | ALL |
|---|---|---|---|---|
| Spline | 0.9712 | 0.9053 | 0.9733 | 0.9515 |
| Cauchy | 0.9712 | 0.7684 | 1.0 | 0.9159 |
| Gauss | 0.9640 | 0.5684 | 0.9867 | 0.8544 |
| Kernel Function | V1 | V2 | V3 | ALL |
|---|---|---|---|---|
| Spline | 0.8 | 1.8 | 0.4 | 1.0 |
| Cauchy | 0.8 | 4.4 | 0.2 | 1.8 |
| Gauss | 1.0 | 8.0 | 0.2 | 3.1 |
| Kernel Function | V1 | V2 | V3 | ALL | Execution Time [sec] |
|---|---|---|---|---|---|
| Spline | 0.9856 | 0.9053 | 1.0 | 0.9644 | 6910 |
| Cauchy | 0.9928 | 0.8842 | 0.9733 | 0.9547 | 7220 |
| Gauss | 0.9856 | 0.9368 | 0.9867 | 0.9709 | 7015 |
| Kernel Function | V1 | V2 | V3 | ALL |
|---|---|---|---|---|
| Spline | 0.4 | 1.7 | 0 | 0.7 |
| Cauchy | 0.2 | 2.0 | 0.4 | 0.9 |
| Gauss | 0.4 | 1.2 | 0.2 | 0.6 |
| Kernel Function | Spline | Cauchy | Gauss |
|---|---|---|---|
| V1 | 0.9784 | 0.9640 | 0.9712 |
| V2 | 0.9504 | 0.8582 | 0.9078 |
| V3 | 0.9589 | 0.8973 | 0.9110 |
| V4 | 0.9291 | 0.9764 | 0.9606 |
| V5 | 0.9927 | 0.9927 | 1.0000 |
| ALL | 0.9623 | 0.9362 | 0.9493 |
| Execution Time (sec) | 8012 | 9040 | 8520 |
| Kernel Function | Spline | Cauchy | Gauss |
|---|---|---|---|
| V1(m) | 0.4 | 1.0. | 0.8 |
| V2(m) | 1.4 | 4.0 | 2.6 |
| V3(m) | 1.0 | 3.8 | 2.4 |
| V4(m) | 1.8 | 0.6 | 1.0 |
| V5(m) | 0.4 | 0.0 | 0.0 |
| Mean(m) | 1.0 | 1.8 | 1.4 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ji, X.; Lu, X.; Guo, C.; Pei, W.; Xu, H. Predictions of Geological Interface Using Relevant Vector Machine with Borehole Data. Sustainability 2022, 14, 10122. https://doi.org/10.3390/su141610122
Ji X, Lu X, Guo C, Pei W, Xu H. Predictions of Geological Interface Using Relevant Vector Machine with Borehole Data. Sustainability. 2022; 14(16):10122. https://doi.org/10.3390/su141610122
Chicago/Turabian StyleJi, Xiaojia, Xuanyi Lu, Chunhong Guo, Weiwei Pei, and Hui Xu. 2022. "Predictions of Geological Interface Using Relevant Vector Machine with Borehole Data" Sustainability 14, no. 16: 10122. https://doi.org/10.3390/su141610122
APA StyleJi, X., Lu, X., Guo, C., Pei, W., & Xu, H. (2022). Predictions of Geological Interface Using Relevant Vector Machine with Borehole Data. Sustainability, 14(16), 10122. https://doi.org/10.3390/su141610122







