Deformation Characteristics and Damage Assessment of Prefabricated Frame Tunnels after Central and External Explosions

Abstract

The urban social environment is complex and changeable, and there are accidental and non-accidental explosion risks in tunnels. Performance analysis and assessment after tunnel explosions has become important work. In this study, a prefabricated frame structure (single-layer and double-layer) for urban road tunnels was designed. A three-dimensional refined dynamic response numerical model of a frame tunnel considering the joint effect was established, and the reliability of the modeling method was verified by a full-scale explosion test. Considering factors such as the explosion equivalent (100, 200, 300, and 400 kg), explosion distance (3, 6, 9, and 12 m), and central and external explosions, the deformation characteristics and damage evolution law of the prefabricated frame tunnel after the explosions were explored. The deformation failure mode of the prefabricated frame tunnel was analyzed. The study shows that the roof of a single-layer tunnel and the mid-partition of a double-layer tunnel are weak components of a prefabricated frame tunnel with steel column joints under a central explosion load. The deformation and damage at tunnel joints are greater than those at other positions. Under an external explosion load, the closer the explosion point is, the greater the damage and deformation of the prefabricated frame tunnel lining are. Furthermore, showing a high degree of locality. With the equal amplitude increase of the detonation distance (3–6 m, 6–9 m, 9–12 m), the lining displacement is relatively reduced by about 75.7%, 39.9%, and 10.0%, respectively, and the lining deformation is mainly represented by the overall bending deformation.

1. Introduction

Under the background of global warming and green low-carbon development, industrial construction methods are an important direction and path for tunnel engineering development. To date, industrial construction has been widely used in shield tunnels and underground utility tunnels. With accelerating urbanization and a rapidly increasing population, three-dimensional urban underground transportation has developed rapidly at a large scale. As a new industrialized construction method, prefabricated frame tunnels are favored in urban tunnel construction due to their high construction efficiency, less construction waste, reliable quality, and high space utilization [1,2].

Prefabricated assembly technology not only brings many advantages to tunnel construction but also has become an important research object. Many scholars have focused on the mechanical characteristics, bearing capacity [3], risk assessment [4], and waterproofness [5] of prefabricated tunnels. However, there have been few studies on the deformation failure mode and damage assessment of tunnels (especially prefabricated tunnels) under explosion loading. However, tunnel explosion accidents have occurred frequently in recent years. These include bomb attacks on the Moscow subway tunnel in Russia in 2010, tanker truck impact explosions in the Skatestraum tunnel in Norway in 2015 [1], and gas explosions in the Qishanyan tunnel in China in 2017 [6]. The serious consequences of these explosion accidents imply that the study of tunnel explosion damage characteristics and explosion resistance assessment is of great significance to improve the anti-explosion ability of tunnels.

To reduce the risk of tunnel operation and improve the anti-explosion ability of tunnel structures, scholars have carried out many valuable studies. Xue et al. [7] proposed a numerical model considering gas fluid properties and structural mechanical properties to simulate natural gas explosions in tunnels. The conditions of increasing explosion pressure, the propagation velocity of explosion clouds and the effective stress of the lining were determined. Lin et al. [8,9] proposed systematic and detailed approaches to simulate fracturing and failure behaviors of tunnel lining materials. Qian et al. [10] used a numerical method to simulate the effects of the explosion equivalent, lining reinforcement ratio, shear reinforcement arrangement, buried depth, and wall thickness on the explosion resistance of tunnels. These scholars believed that increasing the reinforcement ratio, lining thickness, and buried depth can improve the tunnel explosion resistance. Tiwari et al. [11] analyzed the explosion characteristics of tunnels under different weathered rock conditions and found that highly weathered rock has a large attenuation amplitude for shock waves. Mussa et al. [12] discussed the failure behavior of tunnels under different explosion equivalents. The propagation law of pressure waves in the form of hemispherical waves in soil was determined. The formula for calculating the peak pressure at a large distance was also derived. Ge et al. [13] carried out rock blasting model tests under the action of confining pressure to study the mechanism of in-situ stress blasting crack propagation and revealed the influence of in situ stress on the direction. Zhou et al. [14] determined the effects of basalt fiber reinforced polymer (BFRP) reinforcement on the explosion resistance of tunnels by test methods. Zhao et al. [15] analyzed and summarized the deformation and failure mode of traditional tunnel segments based on full-scale tunnel test results. According to the full-scale tunnel test, the setting of flexible damping pads can reduce the damage to the bolt contact area. Hanifehzadeh et al. [16] proposed a retrofit system consisting of an ultra-high-performance concrete (UHPC) layer surrounded by a thin steel sheath to provide higher lateral loads against blast loads. Williamson et al. [17] described in detail an experimental test procedure for evaluating the performance of highway bridge columns subjected to severe blast loads to investigate the response of key bridge components under blast loads. Huang et al. [18] combined fragility and restoration functions to propose practical resilience assessment framework for tunnels subjected to earthquakes. To date, researchers have studied the explosion characteristics of tunnels and obtained important conclusions. However, most studies have ignored the influence of the tunnel joint effect and simplified the calculation by setting the tunnel as a cylinder or square cylinder. This led to a certain deviation between the final calculation results and the actual project. In addition, current research on the influencing factors of tunnel explosion resistance has mostly focused on the influence of lining thickness, concrete strength, and tunnel section form. The explosion analysis of prefabricated tunnel structures with joints has not been considered. However, as a weak area of tunnels for mechanical performance, the joint structure is very important to the explosion resistance of the whole tunnel.

In this study, a prefabricated frame structure (single-layer and double-layer) for urban road tunnels was designed. The three-dimensional refined dynamic response models of fabricated and cast-in-situ frame tunnels were constructed by using ABAQUS software [19], and the reliability of the modeling methods was verified by full-scale explosion tests. This paper aims to explore the deformation characteristics and damage evolution law of a prefabricated frame tunnel under the load of a central explosion and external explosion (3, 6, 9, and 12 m away from the tunnel). The deformation and failure mode of prefabricated frame tunnels under central and external explosions were analyzed, and the deformation resistance of the prefabricated frame and cast-in-situ frame tunnels under explosion shock is discussed. Finally, the damage level of the prefabricated frame tunnel under an external explosion was assessed based on the deflection–span ratio damage criterion and assessment curves among different damage levels were determined.

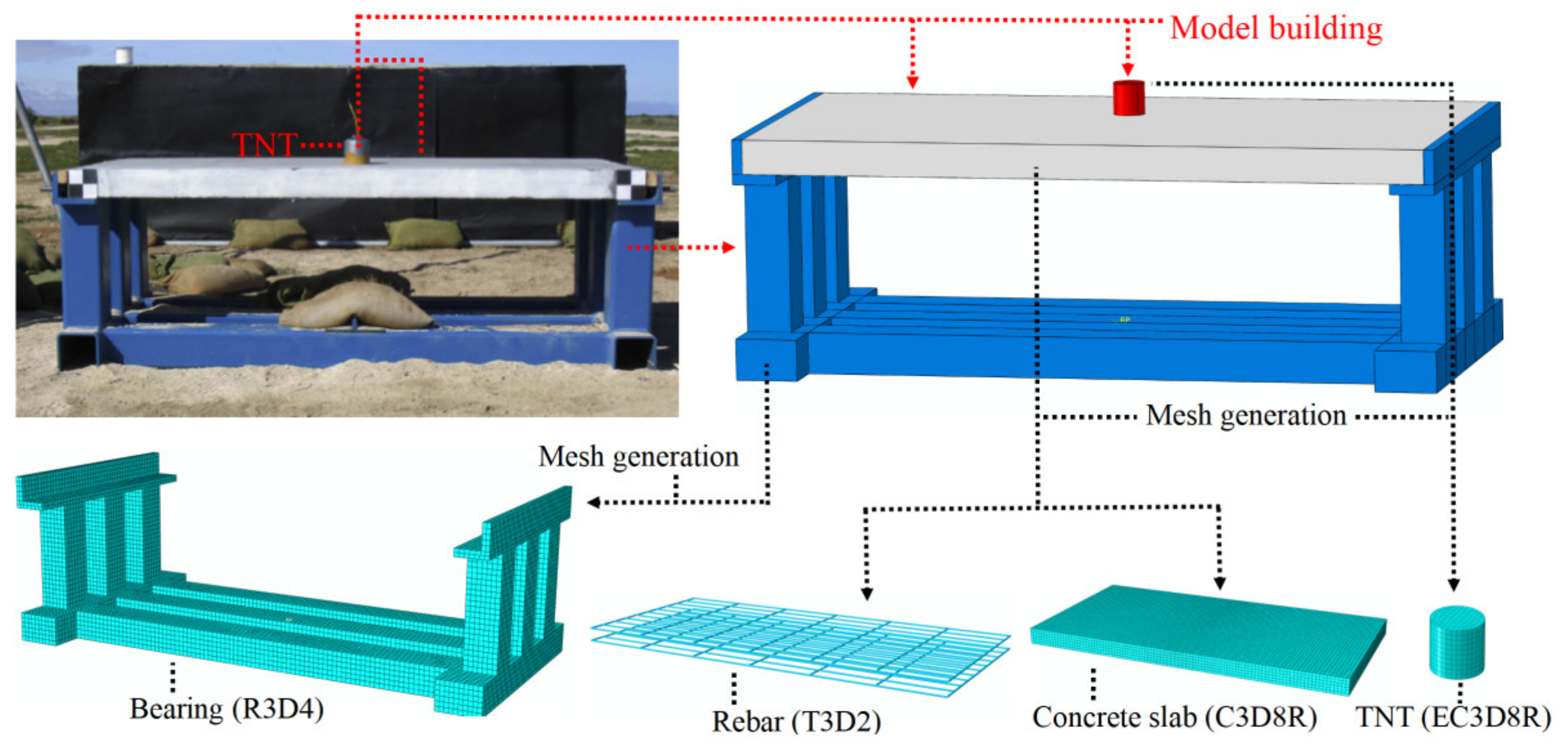
2. Structural Design and Numerical Model of a Prefabricated Frame Tunnel

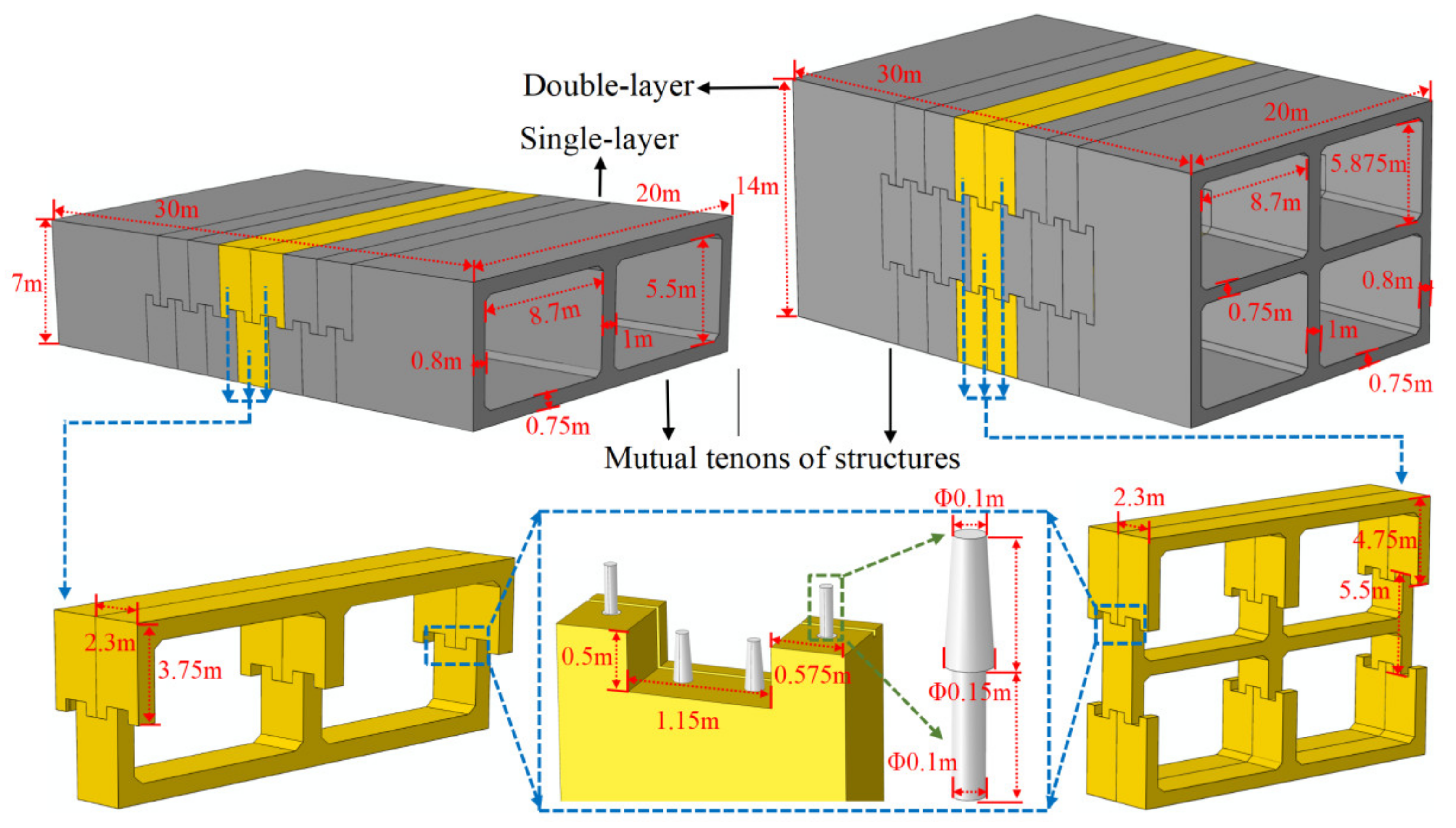
2.1. Structural Design of the Frame Tunnel

In this study, a prefabricated frame structure (single-layer and double-layer) for urban road tunnels was designed. The tunnel lining is connected by steel columns. The single ring of the tunnel lining is 2.3 m in width and 20 m in length. The tunnel structure form and detailed joint structure are shown in Figure 1. The characteristic of this prefabricated frame tunnel is that the lining block can be assembled by means of lifting equipment under the action of self-weight. The joint structure is provided with steel column components and the steel column is a circular platform structure with a small top and a large bottom. In this way, the assembly accuracy and the overall stiffness of the tunnel can be improved, and the horizontal shear capacity of the tunnel can be enhanced. To avoid the waste of calculation cost caused by a numerical model that is too complex, the area outside the middle six rings of the tunnel is simplified. The simplified method has been reasonably confirmed by the relevant research results of Shi et al. [20].

2.2. Constitutive Model

Abaqus software has the advantages of comprehensive material properties and a stable calculation ability for simulating explosion loads. Coupled Eulerian Lagrangian (CEL) technology effectively reduces grid distortion and other problems by considering the interaction between shock waves and structures when simulating tunnel explosions. Mandal et al. [21], Mussa et al. [12], and Tiwari et al. [11] all carried out research on tunnel explosions by using CEL technology. It was confirmed that CEL technology has excellent reliability and stability with regard to tunnel explosion simulations. In this study, CEL technology was used to simulate explosion loads.

2.2.1. Concrete and Steel Components

The materials involved in frame tunnels include a concrete lining, steel columns, reinforcements, and prestressed reinforcements. In the process of numerical simulation, the selection of the constitutive model should not only fully consider the nonlinear characteristics of the entire numerical model but also take into account the principle of computational efficiency and convergence of the model. In this study, the concrete damage plasticity (CDP) constitutive model was used to simulate tunnel lining materials [11]. The elastic-plastic constitutive model was used to simulate steel columns, reinforcements, and prestressed reinforcements.

The CDP model is based on the isotropic elastic damage and the plasticity theory of isotropic tension and compression to reflect the inelastic deformation of materials and includes the stiffness degradation caused by damage [22]. The stress–strain relationship of concrete in the CDP model is based on the following equations:

$${\sigma }_t=\left(1-d_t\right)D_0^{el}:\left(\epsilon -{\epsilon }_t^{pl}\right), {\sigma }_c=\left(1-d_c\right)D_0^{el}:\left(\epsilon -{\epsilon }_c^{pl}\right)$$

(1)

where t and c are respectively the tension and compression, ${\sigma }_t$ and ${\sigma }_c$ are respectively the tensile stress vector and compressive stress vector, $\epsilon$, ${\epsilon }_t^{pl}$, and ${\epsilon }_c^{pl}$ are plastic strains, $d_t$ and $d_c$ are damage variables of the plastic strain function, and $D_0^{el}$ is the initial elastic modulus.

The stress–strain curve of the reinforcement is given in the Code for design of concrete structures [23]. The corresponding stress–strain relationship is given as:

$${\sigma }_s=\left\{\begin{array}{l}{E}_s{\epsilon }_s\\ f_y^{\ast }\\ k_4{f}_y^{\ast }+\frac{E_s\left(1-k_4\right)}{{\epsilon }_y{(k_2-k_1)}^2}\cdot {\left({\epsilon }_s-k_2{\epsilon }_y\right)}^2\end{array}\right.\begin{array}{l}{\epsilon }_s\le {\epsilon }_y\\ {\epsilon }_y\le {\epsilon }_s\le k_1{\epsilon }_y\\ {\epsilon }_s>k_1{\epsilon }_y\end{array}$$

(2)

where ${\sigma }_s$ is the steel stress, $E_s$ is the steel elastic modulus, ${\epsilon }_s$ and ${\epsilon }_y$ represent respectively the steel strain and the yield steel strain, $f_y^{\ast }$ denotes the representative value of the yield strength of the steel, and $k_1$, $k_2$, $k_3$ and $k_4$ represent the ratios of the initial to yield strain, peak to yield strain, ultimate to yield strain, and peak stress to yield strength, respectively.

The strength grade of tunnel lining concrete is C60, and its material properties are shown in

Table 1. Material properties of C60 concrete.

Parameter	Value	Parameter	Value
Mass density	2440 kg/m3	Expansion angle-Ψ (°)	38
Elastic modulus	36 MPa	Eccentricity-ξ	0.1
Poisson’s ratio	0.2	σb0/σc0	1.16
Viscosity coefficient-µ (s−1)	1 × 10−5	Kc	2/3

[23,24,25,26,27]. The reinforcement and steel column have the same material properties [23]. The relevant material properties of prestressed reinforcement by Qian et al. [10] were used for reference. The corresponding material properties are shown in

Table 2. Material properties of steel columns and prestressing strand.

Steel columns and rebar	Parameter	Value	Prestressing strand	Parameter	Value
	Mass density	7850 kg/m3		Mass density	7850 kg/m3
	Elastic modulus	210 GPa		Elastic modulus	210 MPa
	Poisson’s ratio	0.28		Poisson’s ratio	0.3
	Yield stress	400 MPa		Yield stress	1860 MPa
				Thermal expansion coefficient	0.0001

. A prestress of 110 kN was applied to the prestressed reinforcement by the temperature method [2,28].

2.2.2. Air

Air material properties are defined by the equation of state (EOS). In addition, the gas pressure is defined as [10]:

$$p=C_0+C_{1}u+C_2{u}^2+C_3{u}^3+(C_4+C_{5}u+C_6{u}^2)E$$

(3)

where p is the gas pressure and $C_0-C_6$ are the gas constants. $u=\rho /{\rho }_0-1$, where $\rho$ is the current gas density, ${\rho }_0$ is the initial gas density, and E is the internal energy per unit volume. Air is commonly assumed to be an ideal gas. When air is set as the ideal gas, $C_0=C_1=C_2=C_3=C_6=0$, and $C_4=C_5=\gamma -1$. The EOS for an ideal gas is given by [10]:

$$p=\left(\gamma -1\right)\frac{\rho }{{\rho }_0}{E}_0$$

(4)

where γ is the adiabatic exponent. The material properties of the ideal gas are shown in

Table 3. Material properties of air.

Parameter	Value	Parameter	Value
Reference density	1.225 kg/m3	$\gamma$	1.4
Reference temperature	288.2 K	Specific heat	717.3 J/kg K

[29]:

2.2.3. TNT

The explosives in the tunnel explosion are mainly composed of high explosives such as trinitrotoluene (TNT) and flammable and explosive materials such as gas, while the explosion of high explosives such as TNT reacts violently, causing the tunnel lining structure to bear large instantaneous shear stress. The damage is more obvious. Therefore, it is more meaningful to study the dynamic response of the tunnel under the TNT explosion load. Tiwari et al. [11], Mussa et al. [12], and Luccioni et al. [29] used the Jones–Wilkins–Lee (JWL) EOS to simulate the pressure of TNT explosion when studying the dynamic response of tunnels under an explosion load. The JWL EOS has also been widely used in engineering calculations and can be easily calibrated. In this study, the JWL EOS was used to simulate TNT explosions, as follows [12]:

$$p=A\left[1-\frac{\omega }{R_{1}V}\right]e^{-R_{1}V}+B\left[1-\frac{\omega }{R_{2}V}\right]e^{-R_{2}V}+\omega \frac{e}{V}$$

(5)

where p is the pressure (N/m²), V is the relative volume, e is the initial volumetric energy (J/m³), and A, B, R₁, R₂ and ω are material constants. The material properties of TNT are shown in

Table 4. Material properties of TNT.

Parameter	Value	Parameter	Value
Reference density	1658 kg/m3	ω	0.35
A	3.7377 × 108 kPa	R1	4.15
B	3.73471 × 106 kPa	R2	0.9
Detonation velocity	6.93 × 103 m/s	Energy/unit volume	6 × 106 kJ/m3
Pressure	2.1 × 107 kPa	/	/

[29].

2.2.4. Soil

The nonlinear relationship between the principal stress and shear stress of a geotechnical material in the plastic yield state is described by the nonlinear Mohr–Coulomb criterion. This criterion has widely been used in the analysis of a series of geotechnical problems [30,31]. In this study, the nonlinear Mohr–Coulomb criterion is used to define the nonlinear behaviors of soil and can be expressed as the following equation [30]:

$${\tau }_n=C_0{\left(1+\frac{{\sigma }_n}{{\sigma }_t}\right)}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$m$}\right.}\leftarrow \left\{m\in \left(1,+\infty \right),{\sigma }_t\ge 0,C_0\ge 0\right\}$$

(6)

where ${\sigma }_n$ and ${\tau }_n$ are the normal stress and shear stress, respectively, $C_0$ is the initial cohesion, ${\sigma }_t$ is the axial tension, and m is the nonlinear coefficient. The material properties of the soil are shown in

Table 5. Material properties of soil.

Elastic		Mohr-Coulomb Plasticity
Young’s Modulus (kPa)	Passion’s Ratio	Friction Angle (°)	Dilation Angle	Cohesion Yield Stress (kPa)	Abs Plastic Strain	Density (kg/m3)
5.0 × 107	0.3	24	0	1.0 × 105	0.0	2200

[32].

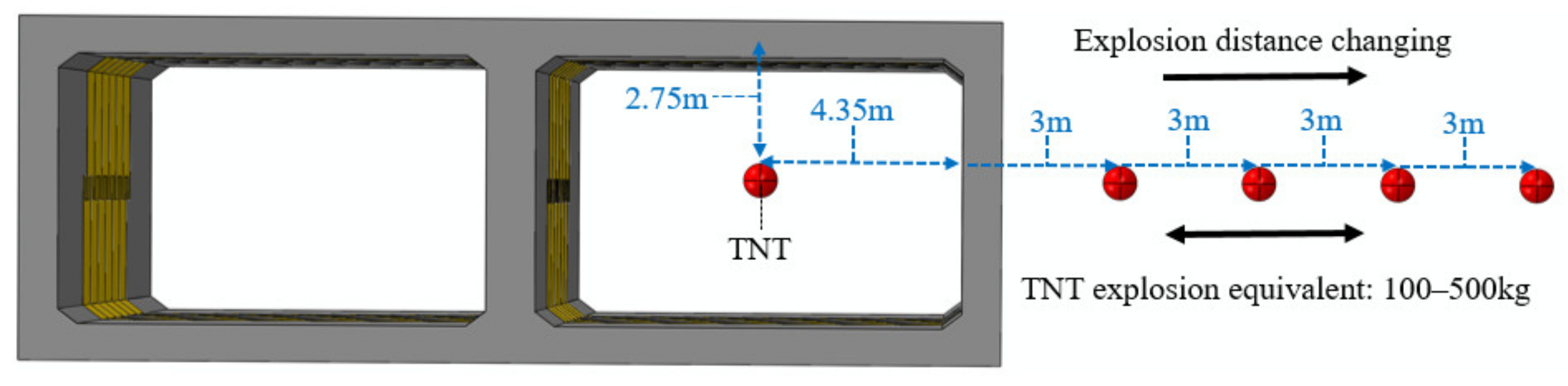
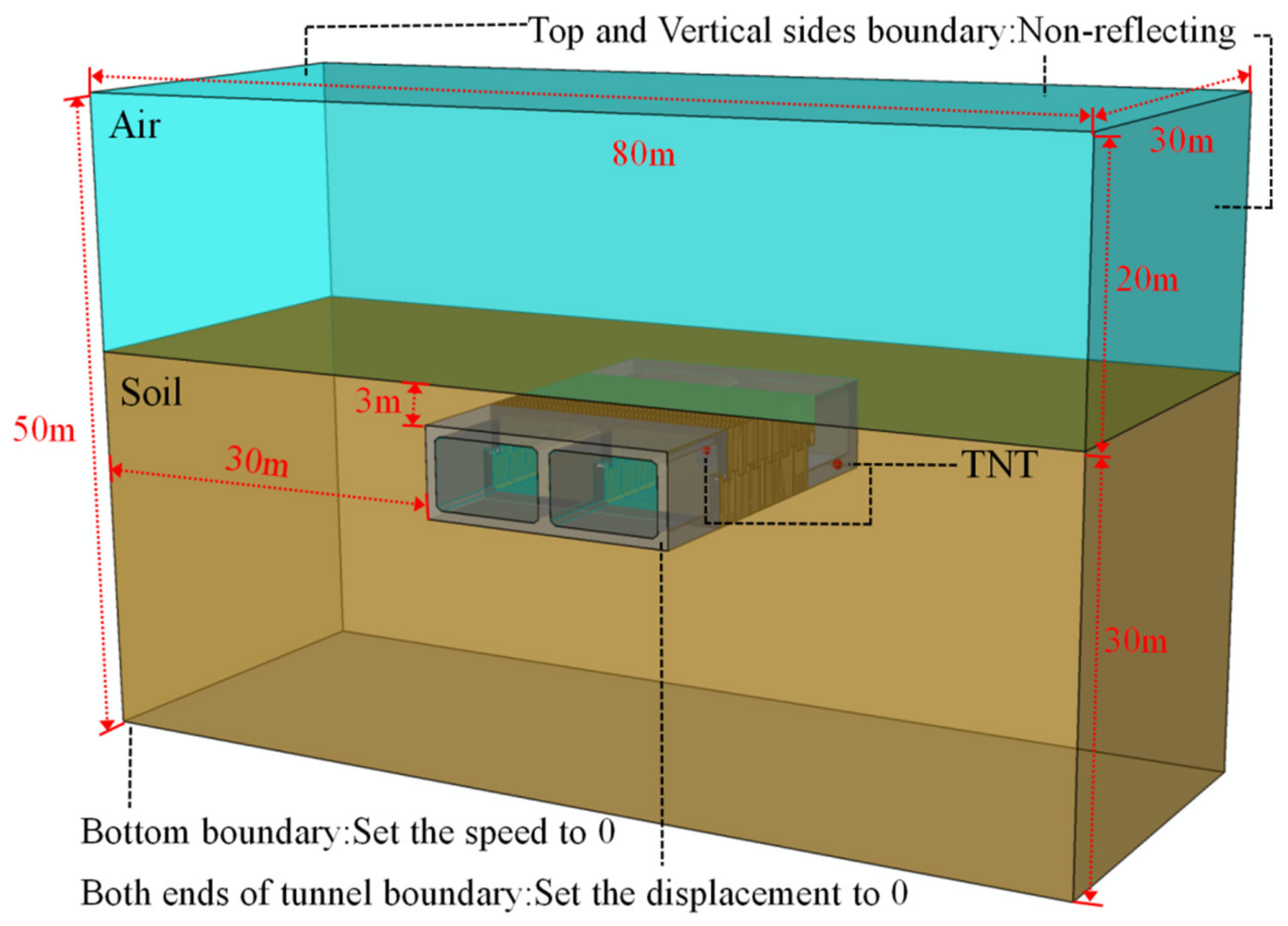
2.3. Boundary Conditions and Explosion Modes

The explosion position was set in the center of the frame tunnel and the soil outside the tunnel side wall to explore the damage to the tunnel lining caused by the shock wave after the TNT explosion, and the response process of the tunnel lining at different explosion distances was analyzed (Figure 2). The selection of TNT equivalent was calculated according to the volume of explosives that the vehicle can carry in the tunnel. The frame tunnel was an urban shallow buried tunnel, and the main vehicles were small and medium-sized vehicles such as sedans or SUVs, so the TNT equivalent should be 500 kg and below [12]. The explosion equivalent was taken as 100 kg, 200 kg, 300 kg, 400 kg, and 500 kg.

The Eulerian domain was used to simulate air, soil, and TNT in the numerical model. The overall dimension of the model was 80 m × 50 m × 30 m. The initial volume fraction was used to realize the material assignment in the Eulerian domain. This method is considered to be an improved method for the dynamic response of underground tunnels [12]. The top surface and the four symmetry planes of the Eulerian domain were set as non-reflective Eulerian boundaries to avoid the reflection of explosion waves [10]. The velocity at the bottom of the Eulerian domain was set to 0 to simulate the bedrock deep in the stratum. The displacement at the front and rear of the tunnel was set to 0. The spatial location and boundary conditions of the tunnel are shown in Figure 3.

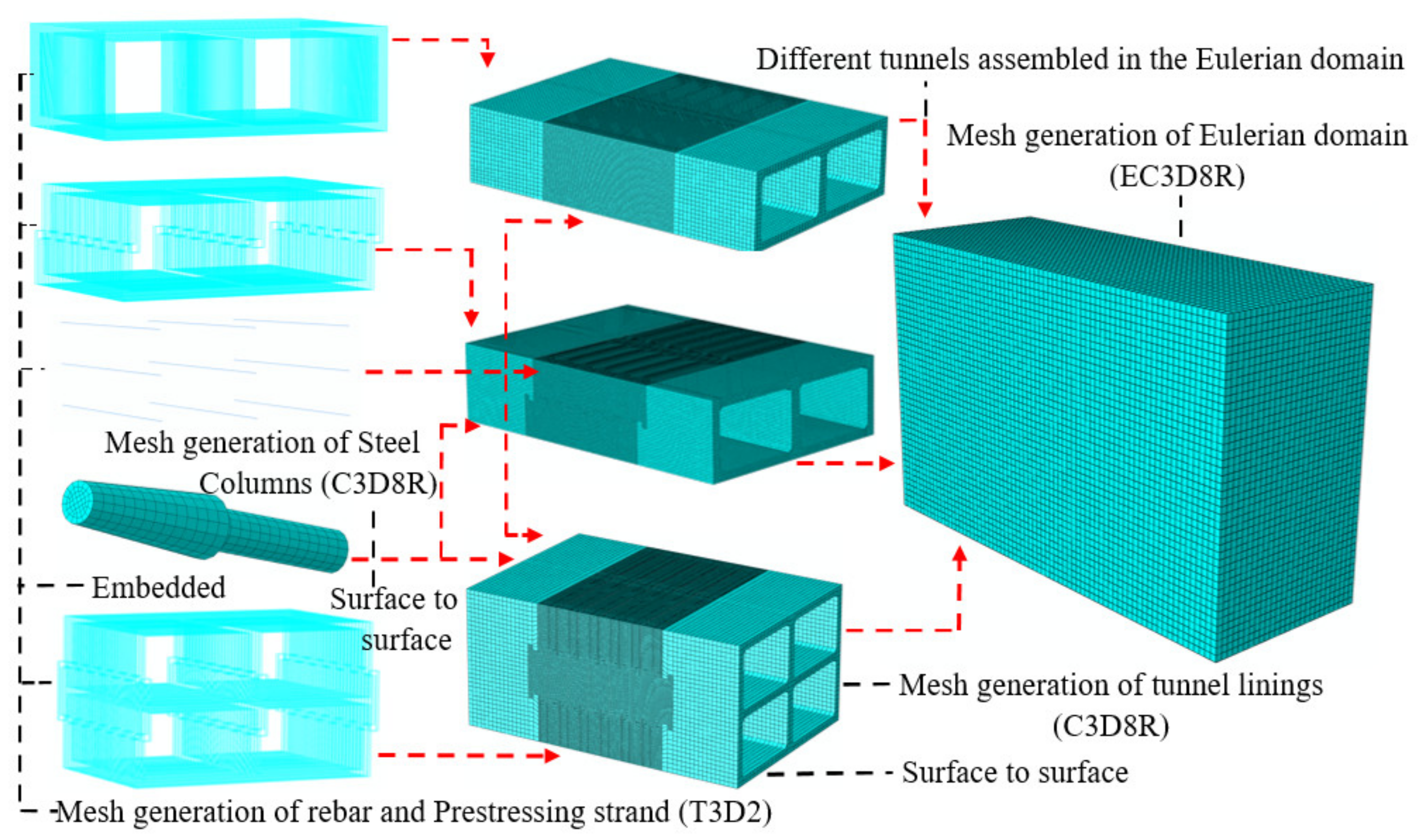
2.4. Contact Relationship and Mesh Generation

The contact property is an important factor affecting the interaction of tunnel components and the overall mechanical properties in the numerical model. In this study, the contact relationship between the tunnel linings and between steel columns and tunnel linings was set as a surface-to-surface contact considering tangential behavior and normal behavior. According to the existing literature research results, the friction coefficient between concrete and steel columns was set to 0.45 [33], and that between concrete was set to 0.55 [34]. The rebar and prestressed strand were connected to the tunnel lining by the embedded method. The contact relationship between the Eulerian domain and tunnel linings was general contact. The mechanical characteristics of the structure and the accuracy of the calculation results were considered when assembling the reinforcement cage. Combining calculation efficiency and convergence, only the main rebar was considered. Rebar with a diameter of 28 mm was selected as the main rebar and assembled at intervals of 100 mm. The thickness of the concrete cover was set to 5 cm. The reinforcement ratio satisfied the specification requirement of 0.6%, as defined in the Code for design of highway tunnel [35].

Combined with the geometric dimensions of the model, the numerical model was meshed by ABAQUS software. The eight-node hexahedral reduced integral element (C3D8R) was used to simulate the tunnel lining and steel column, the two-node linear truss element (T3D2) was used to simulate the rebar and prestressed stand, and the eight-node linear Eulerian hexahedral element (EC3D8R) was used to simulate the air, soil, and TNT. Due to the large size of the numerical model, the density of the lining mesh was increased only in the middle of the tunnel to avoid the low computational efficiency caused by too much mesh. The contact relationship and mesh generation of the model are shown in Figure 4.

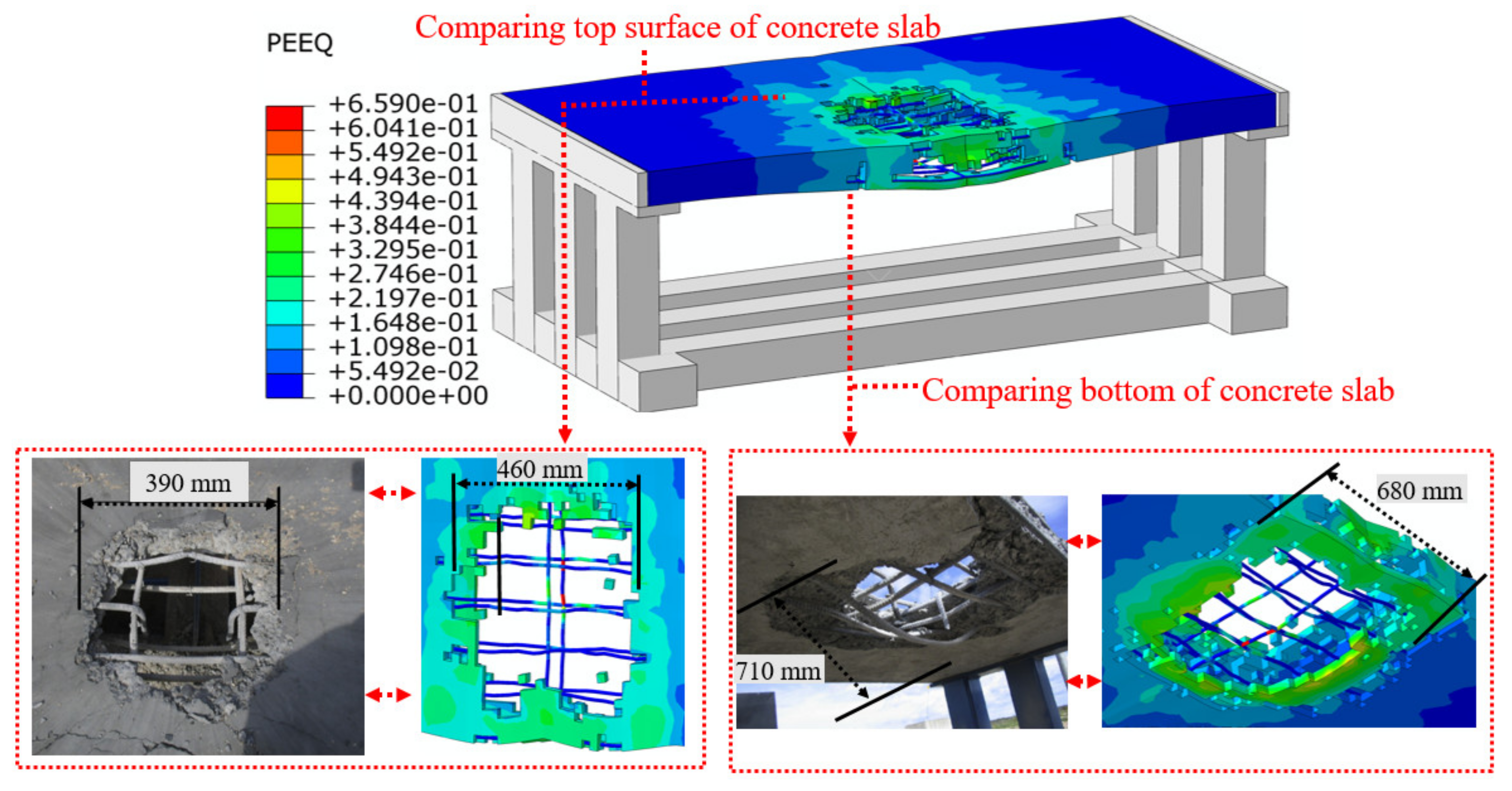
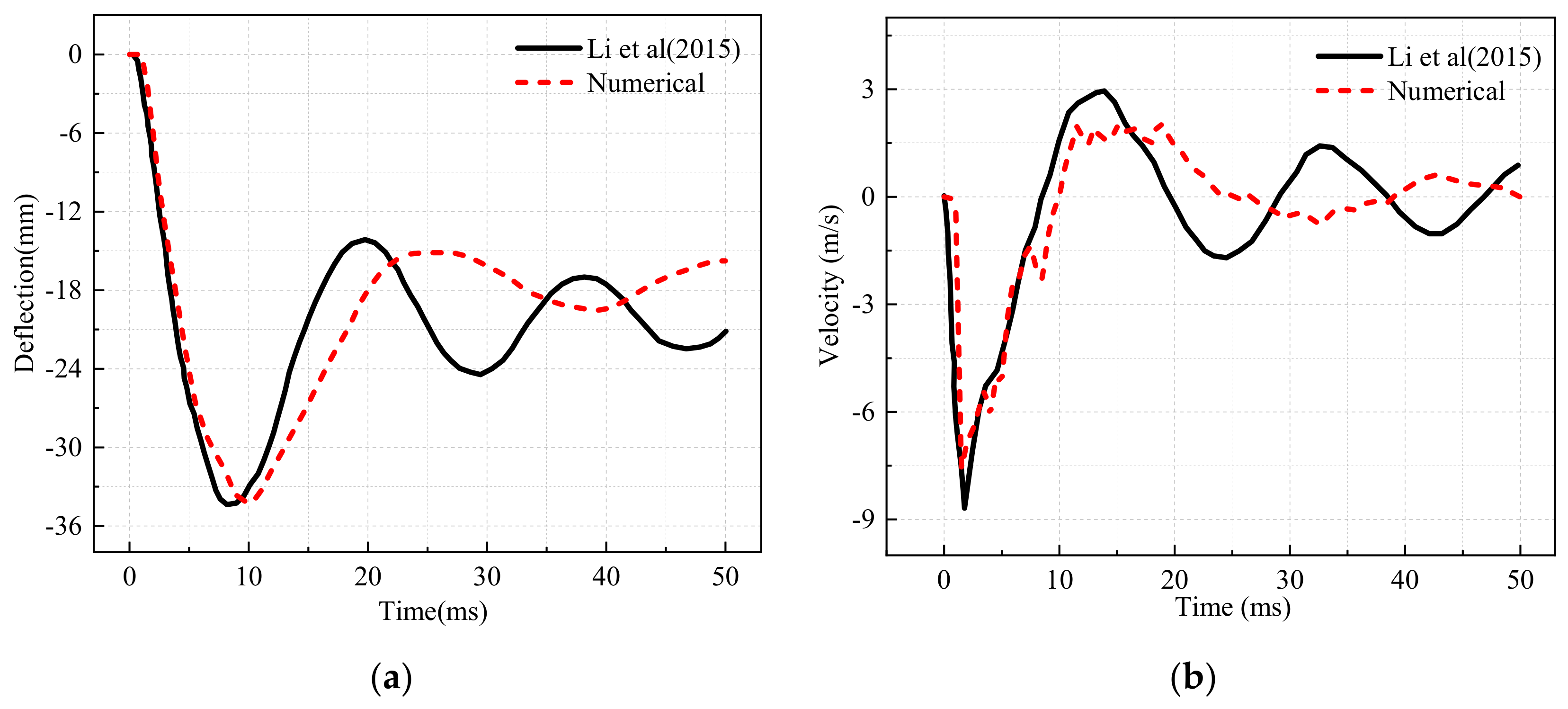
3. Model Validation

To compare the difference in explosion resistance between high-performance concrete and ordinary concrete, Li et al. [36] carried out a contact explosion test of concrete. In this study, based on the explosion test by Li et al. [36], the same model size and boundary conditions in the explosion test were used for numerical calculation. The rationality and reliability of the modeling process and the constitutive model were verified by comparing the failure mode and deformation characteristics of concrete slabs under explosion loading.

The two working conditions of contact explosion (1 kg TNT) of a conventional concrete slab and explosion (8.2 kg TNT) of a conventional concrete slab at an interval of 1.5 m were selected for comparative analysis from the explosion test of Li et al. [36]. The dimensions of the conventional concrete slab were 2 m × 1 m × 0.1 m, and the compressive strength and tensile strength of concrete were 39.5 MPa and 8.2 MPa, respectively. A total of 22 longitudinal stress-bearing reinforcements in the upper and lower layers were built in the concrete. The thickness of concrete cover was set to 10 mm. The reinforcement ratio was 1.2%. The yield strength of reinforcement was 600 MPa.

When validating the model, the modeling process is consistent with that of this study, and the component size and material properties were set according to the test. The CDP constitutive model and elastic-plastic constitutive were used to simulate concrete and rebar, respectively. Euler domain and equation of state were used to simulate TNT and air. The relevant material properties of TNT and air were consistent with the previous text. To avoid the influence of bearing deformation on the results under explosion loading, the bearing was set as a rigid body. The numerical model of the explosion test is shown in Figure 5.

The comparison of the failure modes between the experimental and numerical results of a conventional concrete slab under a contact explosion (1 kg TNT) is shown in Figure 6. To consider the failure states of both rebar and concrete, the equivalent plastic strain (PEEQ) was used to assess the damage of rebar and concrete. As shown in Figure 6, the difference in the failure zone between the experimental and numerical results on the top surface of the concrete slab was 17.9%, and that on the bottom of the concrete slab was 4.4%. The failure modes on the top and bottom surfaces of the concrete slab in the numerical model were basically consistent with the explosion test, which shows that the numerical model is reliable.

The comparison of the displacement and velocity in the middle of the concrete slab under the explosion of 8.2 kg TNT with an interval of 1.5 m is shown in Figure 7. As shown in the figures, the difference in the displacement amplitude and velocity amplitude between the numerical and experimental results was 1.6% and 12.6%, respectively. The displacement and velocity curves are close, which further illustrates the rationality of the numerical model. The deformation and failure characteristics of the concrete slab can be reflected well by the numerical model corresponding to the explosion test. This shows that the selection of model elements and constitutive relations in the numerical model is reasonable, and the numerical modeling method in this study is reliable.

4. Deformation Characteristics of a Prefabricated Frame Tunnel

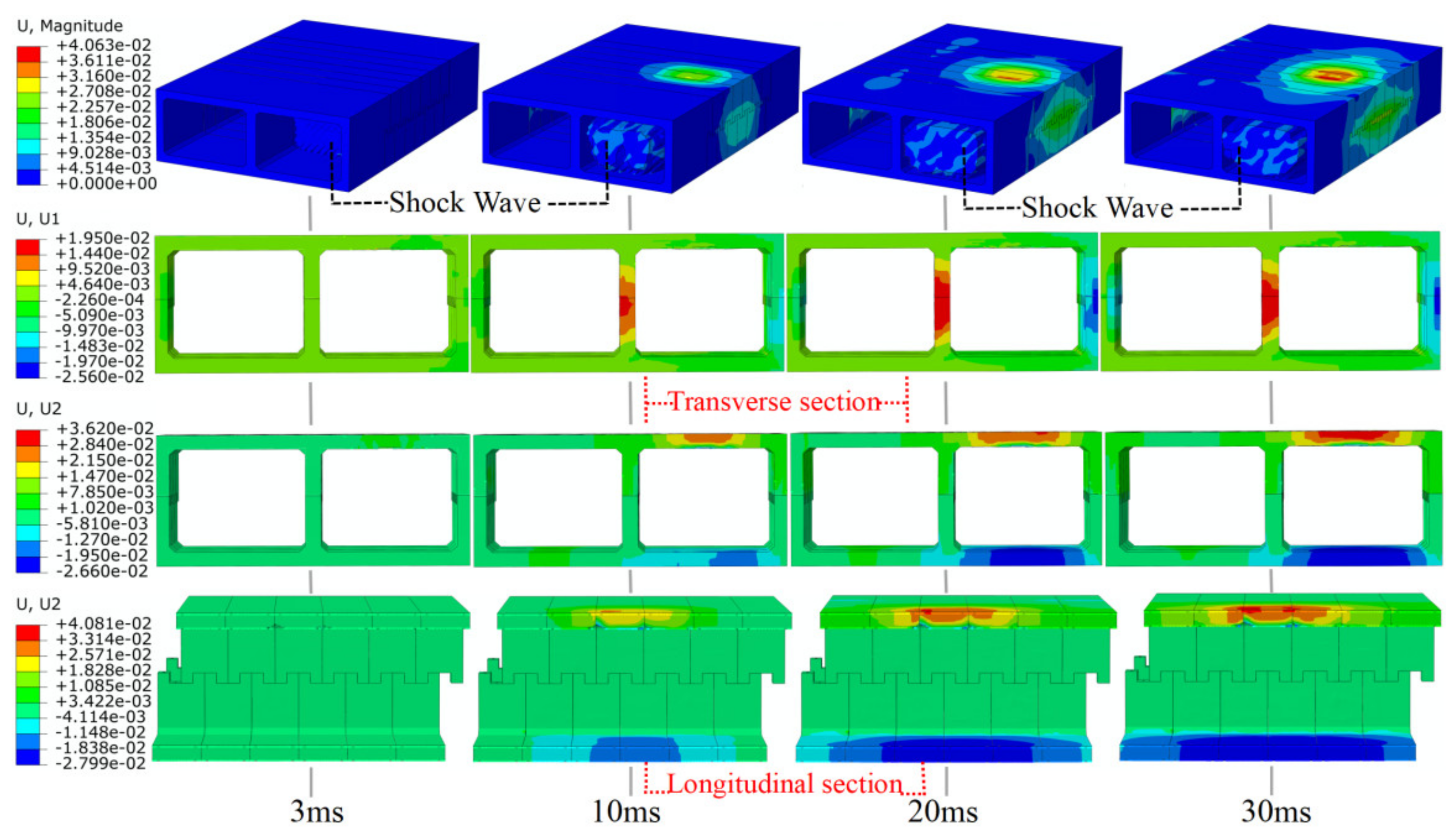
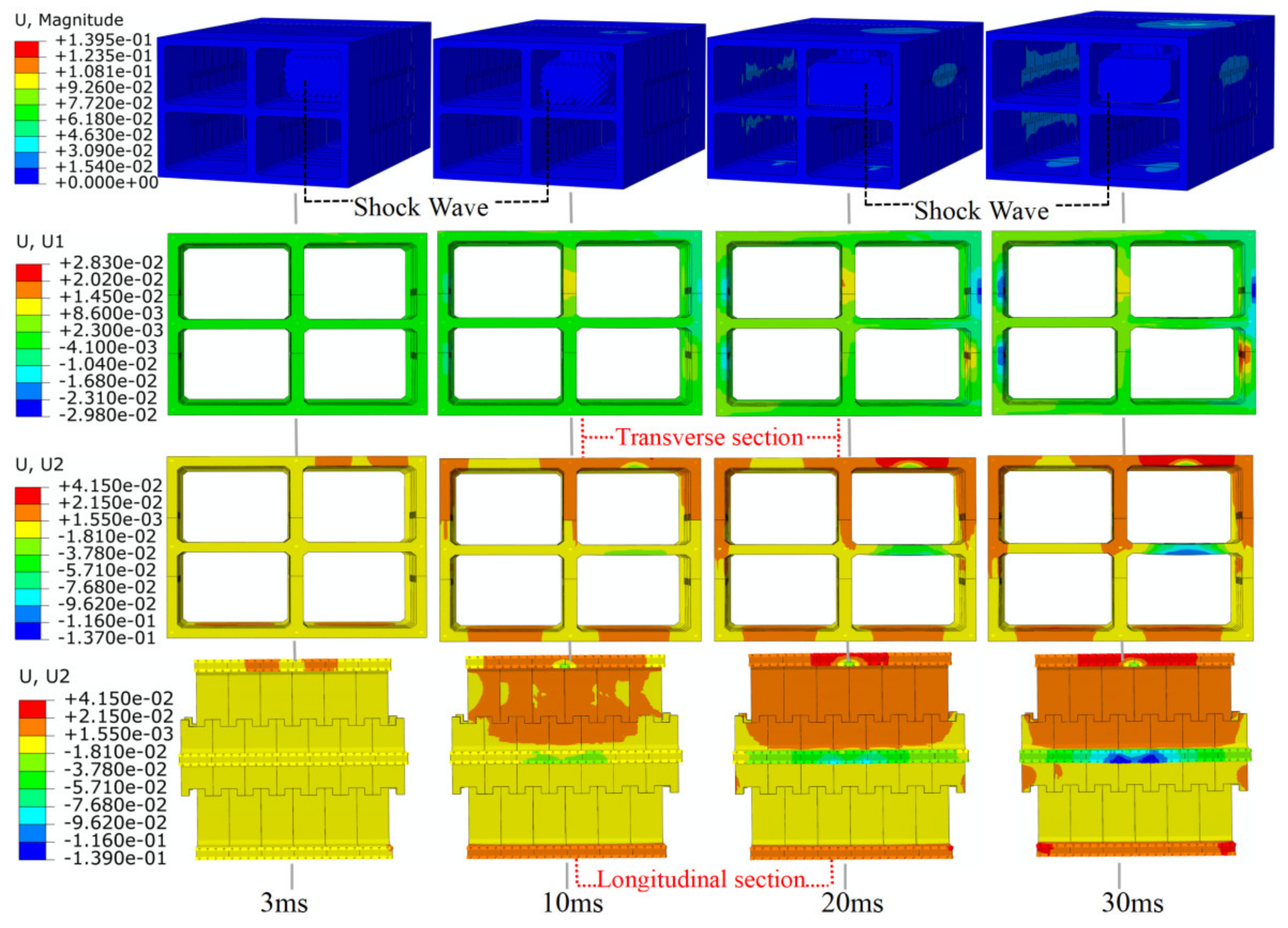
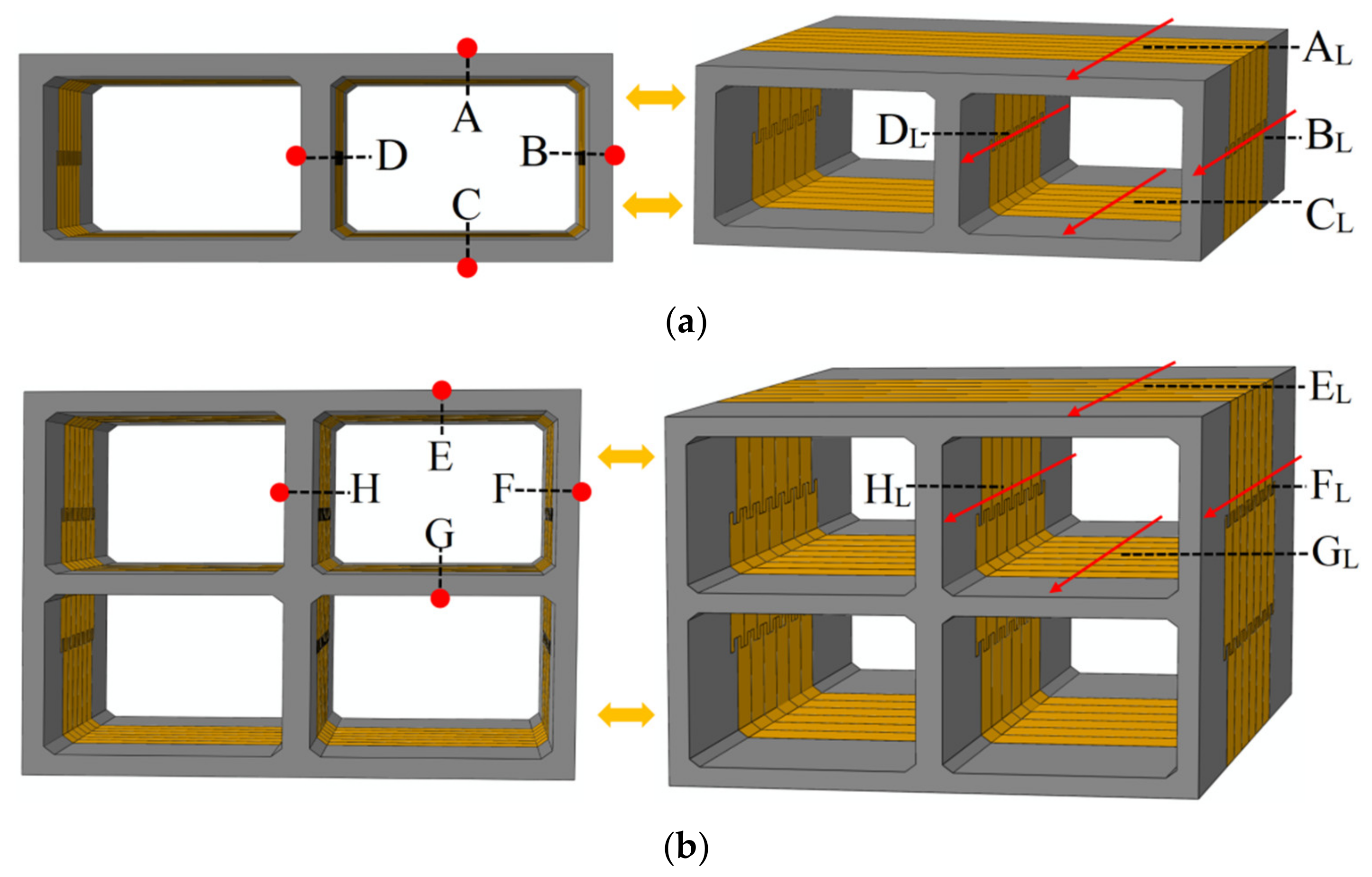
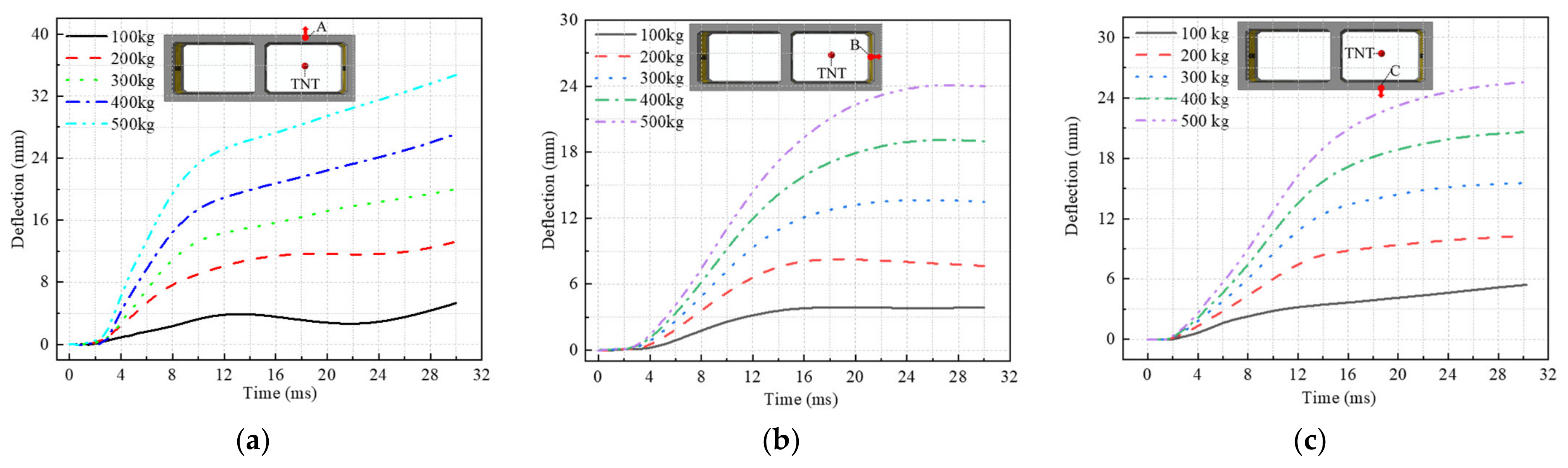
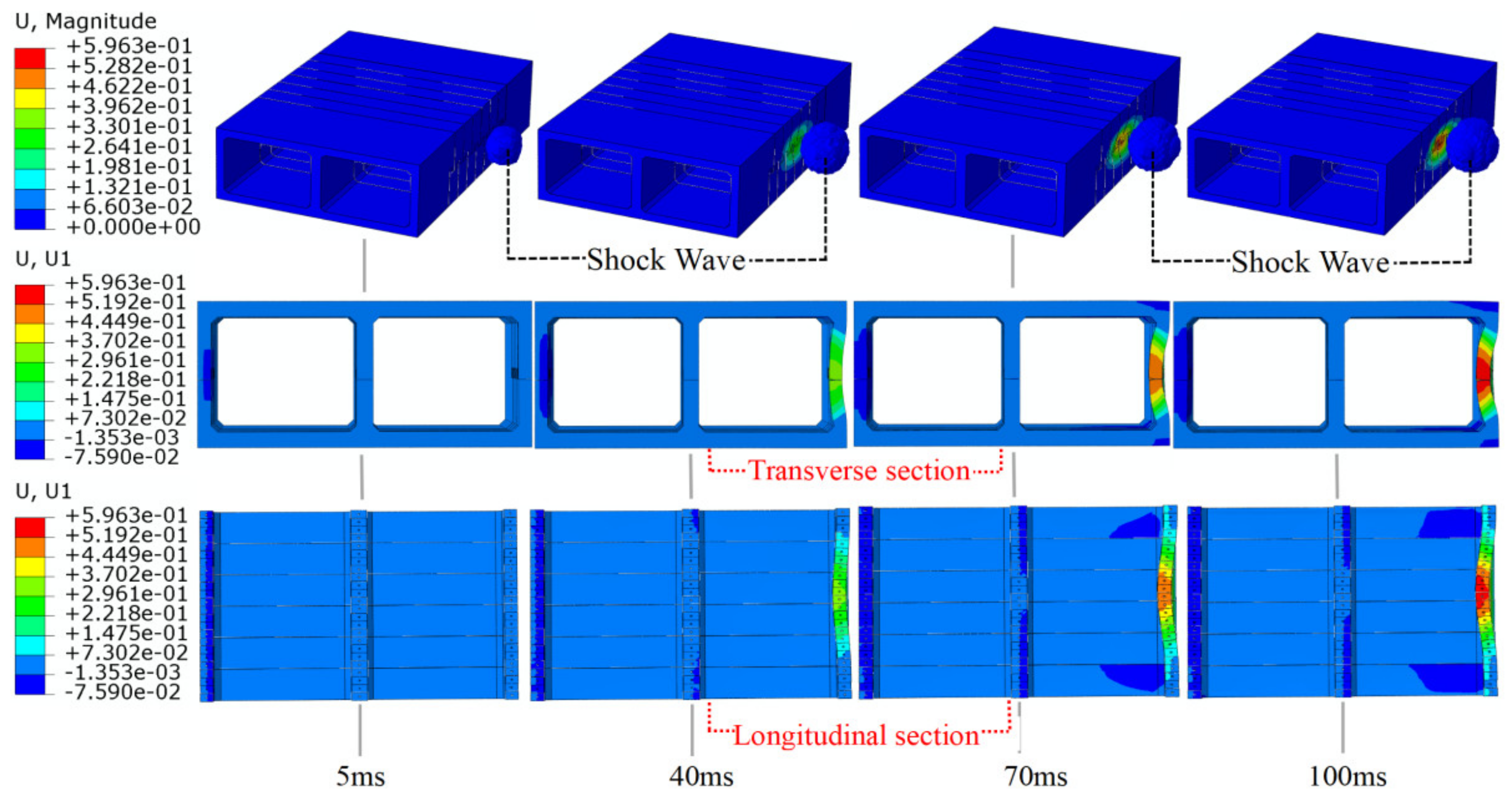
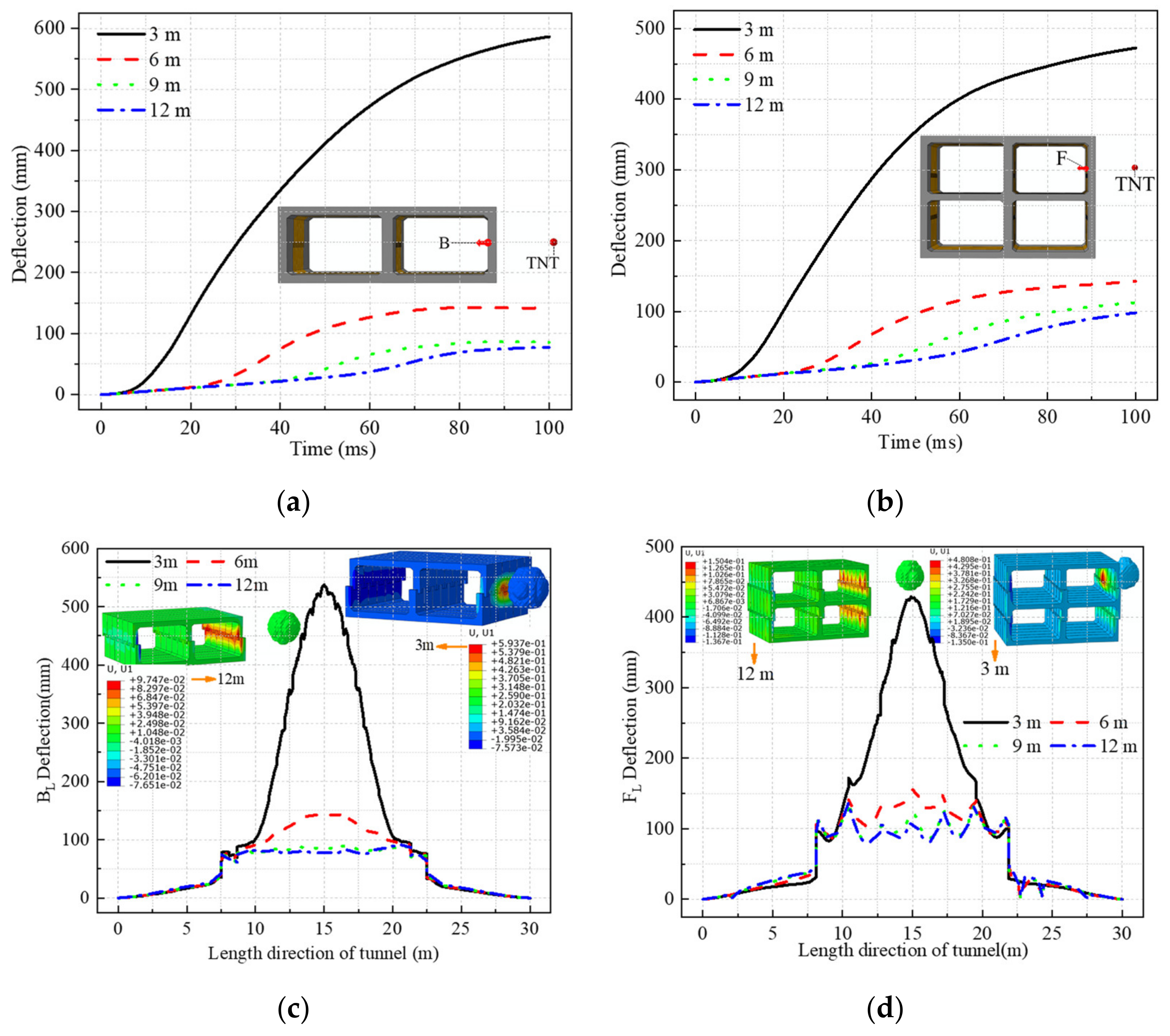
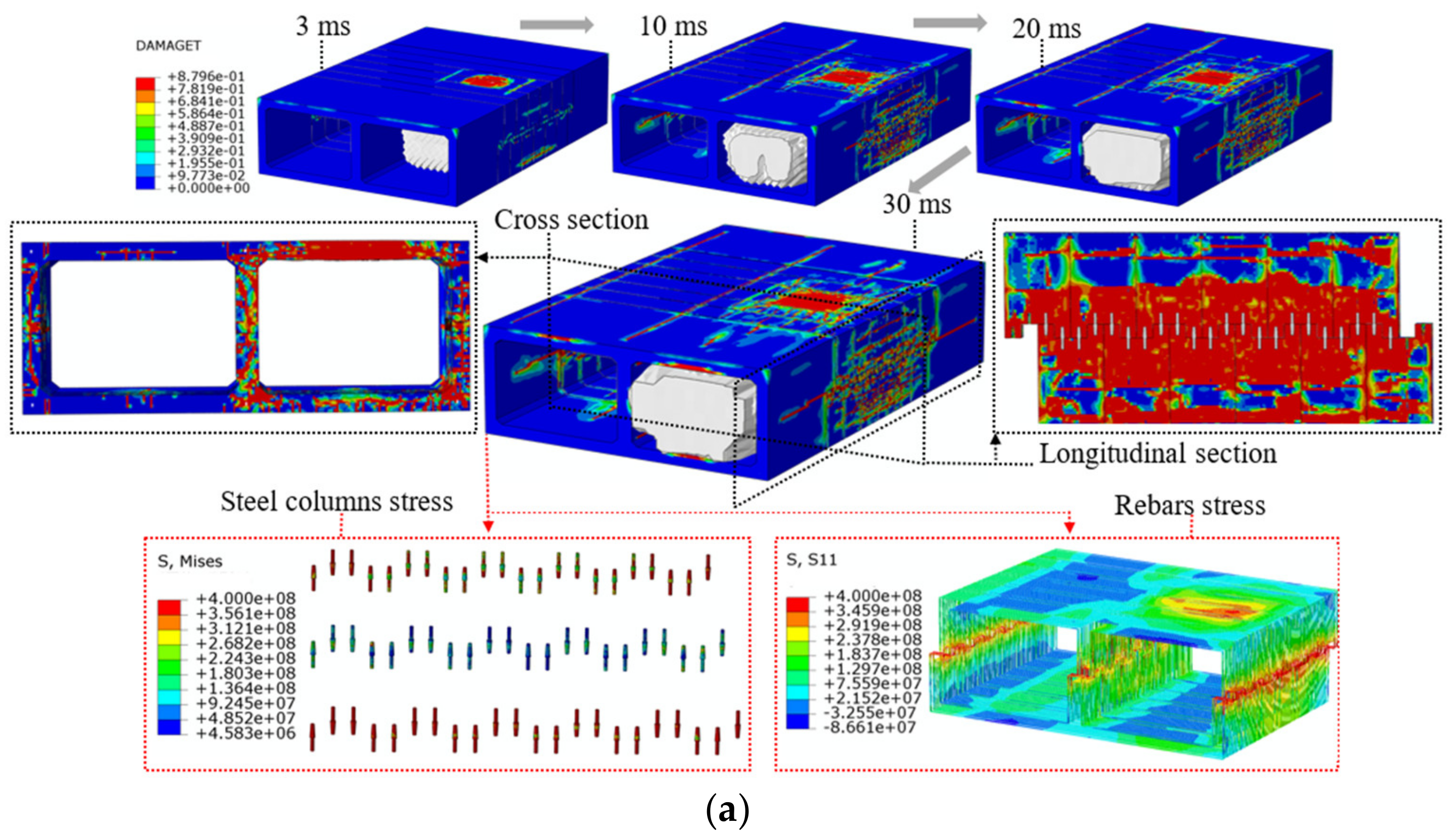
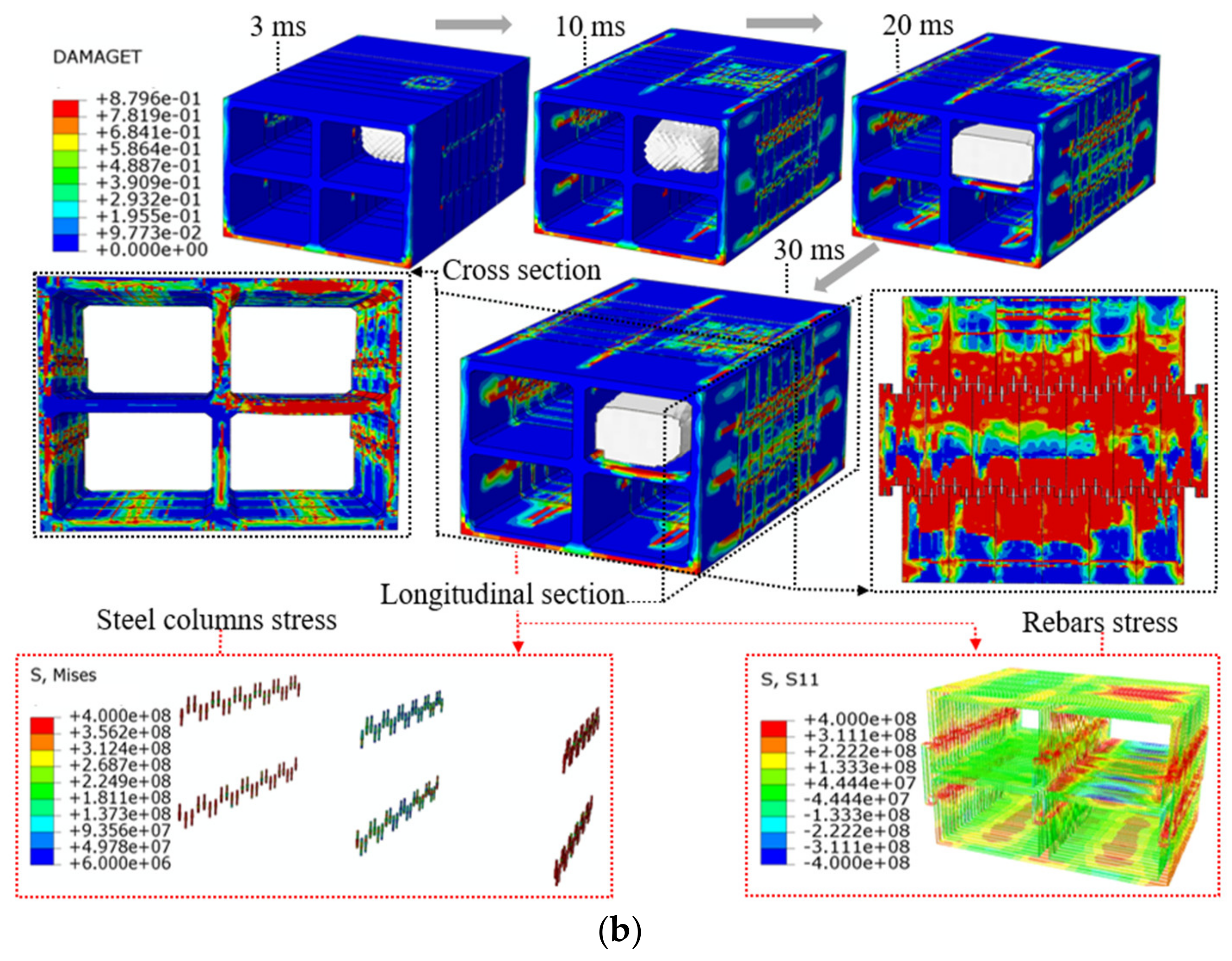
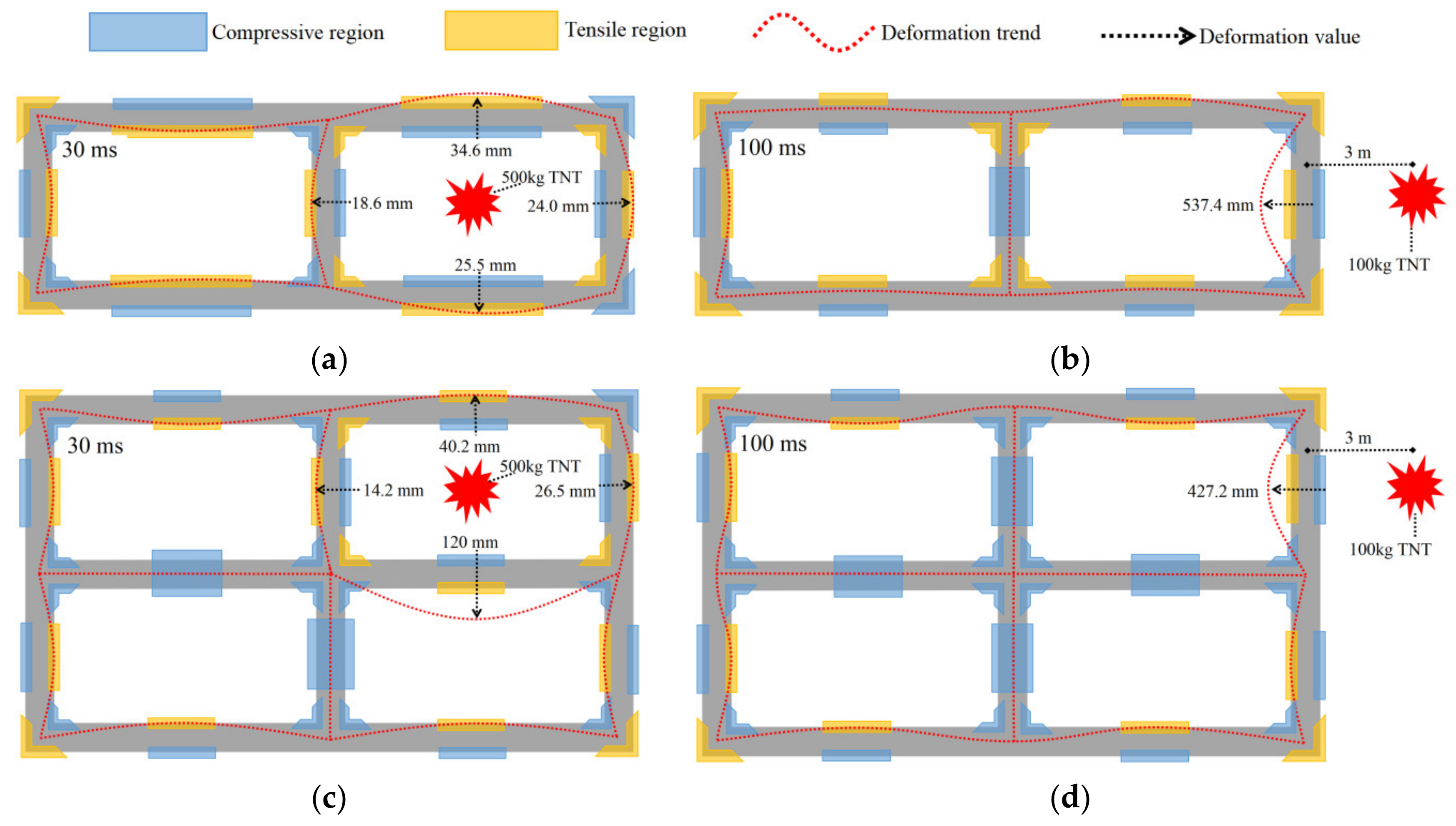
4.1. Central Explosion

To explore the deformation characteristics of a prefabricated frame tunnel under a central explosion, the dynamic responses of single-layer and double-layer prefabricated frame tunnels under central explosions with different TNT equivalents were simulated. The displacement graph of a single-layer prefabricated frame tunnel at different times after a central explosion (500 kg TNT) is shown in Figure 8. Spherical shock waves were generated rapidly at the explosion position after the central explosion. When the shock wave completely contacted the tunnel lining surface (t = 3 ms), a part of the shock wave was absorbed and propagated outward by the tunnel lining and surrounding soil, and the other part formed reflected waves through the surface of the tunnel lining. The initial kinetic energy of the shock waves began to be consumed by the tunnel and the surrounding soil, and the tunnel lining had not yet produced large deformation at this time. When the shock waves traveled longitudinally out of the tunnel (t = 10 ms), the initial kinetic energy of the shock waves was consumed by the deformation and absorption of the tunnel lining and surrounding soil, and the reflected waves were reflected again. The deformation of the tunnel roof, floor, mid-partition, and side wall expanded rapidly along the direction of the explosion wave. As time progressed (from t = 20 ms to t = 30 ms), with the continuous propagation of reflected waves in the tunnel, the kinetic energy of shock waves was also constantly consumed by the tunnel and surrounding soil. The lining deformation stopped gradually, and the maximum deformation occurred at the joint between the mid-partition and side wall of the tunnel.

The displacement graph of the double-layer prefabricated frame tunnel at different moments after central explosion (500 kg TNT) is shown in Figure 9. Due to the different structural forms of the tunnel, there were some differences in the deformation characteristics of the double-layer and single-layer tunnel linings, but the deformation trends were basically the same. The double-layer prefabricated frame tunnel lining structure absorbed and reflected the shock wave after the central explosion. The lining roof, floor, mid-partition, and side wall of the tunnel hole where the TNT was located all deformed along the propagation direction of the explosion wave. In the others, the deformation extremum of the roof and floor appeared in the middle of the slab, and the deformation extremum of the mid-partition and side wall appeared in the joint. The deformation degree of the tunnel hole where TNT was located in the double-layer fabricated frame tunnel was greater than that of the single-layer tunnel (t = 30 ms), especially the deformation in the lining floor. Because there was no soil to absorb and transmit energy and the deformation pressure could not be released by joint torsion, the deformation was much higher than that in other positions.

Eight data feature points (A, B, C, D, E, F, G, and H) were selected in the cross section of the tunnel where the central explosion is located (Figure 10). In addition, the eight data feature paths (A_L, B_L, C_L, D_L, E_L, F_L, G_L, and H_L) through the feature points and parallel to the tunnel longitudinal direction were selected. By extracting the deformation data of feature points and feature paths after explosion, the deformation response law of the prefabricated frame tunnel lining under explosion loading was further explored. It should be noted that the feature point was in the center of the roof, floor, side wall, and mid-partition where the explosion section was located, not the extreme point of the displacement. Considering the influence of lining reflected waves, the deformation data of the feature points and feature paths (within 30 ms of the explosion) were extracted.

The displacement of the feature points of the prefabricated frame tunnel lining changed with time after the central explosion with different TNT equivalent (Figure 11). The arrow direction of feature points in the figure expresses the deformation direction. As shown in Figure 11, except for the position of feature point G, the displacement of the others with time could be approximately divided into three stages. Stage A (from t = 0 to t = 3 ms): Blast waves generated and began to propagate in the air. At this stage, the blast waves completely contacted the tunnel lining surface, and the lining displacement was very small. Stage B (from t = 3 ms to t = 10 ms): Blast waves began to contact the tunnel lining and form reflected waves. Due to distance factors, the roof and floor contacted the blast wave and generated displacement earlier than the mid-partition and side wall. In this stage, the tunnel lining generated the displacement and developed rapidly. Stage C (from t = 10 ms to t = 30 ms): As the blast waves and reflected waves constantly contacted the tunnel lining, kinetic energy generated by explosion was largely absorbed by lining deformation and surrounding soil, and the increase in the lining displacement slowed down.

In addition, the TNT equivalent had a significant effect on the degree of lining displacement (Figure 11). With increasing TNT equivalent, the lining displacement increased faster. The growth of the lining displacement was basically the same for every 100 kg TNT equivalent increase under the same moment. The lining displacement at different tunnel positions was quite different with the same TNT equivalent. Taking the two feature points (A and C) as examples, due to the stratum soil factors, the displacement of the tunnel floor was limited, and the displacement of the roof was larger than that of the floor. Taking the two feature points (B and D) as examples, the displacement of the mid-partition and side wall was also quite different. Although there was soil around the side wall to help the lining absorb and transmit shock waves, the thickness of the mid-partition was more than 25% greater than that of the side wall, making the displacement of the side wall greater than that of the mid-partition. In the double-layer prefabricated frame tunnel, the displacement of the feature point G was significantly larger than that of other positions when the TNT equivalent reached 200 kg. This result shows that feature point G was the weakest part of the tunnel. When considering the explosion resistance of the tunnel in an actual project, measures such as increasing the thickness of the mid-partition can be taken to improve the explosion resistance of the tunnel.

The displacement curves of each feature path of the prefabricated frame tunnel at different times after the central explosion (500 kg TNT) are shown in Figure 12. As shown in the figure, the increased displacement of each feature path was not obvious (t = 2 ms or t = 3 ms). At t = 10 ms, there was obvious displacement on each feature path. At t = 20 ms and t = 30 ms, the increase in displacement of each feature path decreased.

In addition, the deformation of the tunnel lining showed a significant spatial effect after the central explosion (Figure 12). Clear deformation occurred near the tunnel area where the explosion was located. As the distance from the section of the explosion center increased, the displacement of each feature path decreased significantly. Furthermore, the deformation of the joint surface between the rings of the prefabricated frame tunnel was significantly higher than that of other locations, which showed a curve mutation in the figure. Therefore, measures, such as the use of flexible materials can be taken to avoid structural damage caused by large deformation.

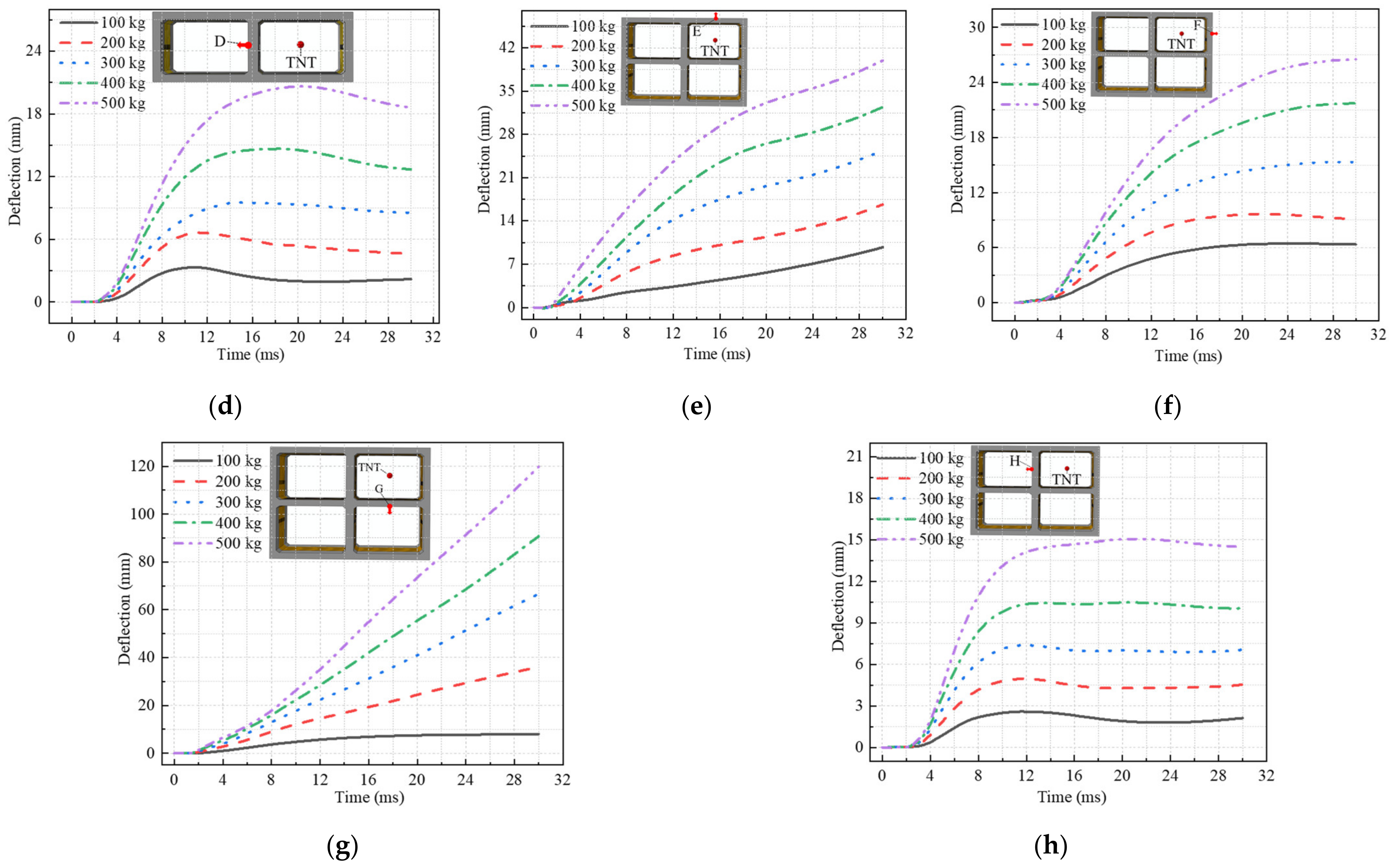
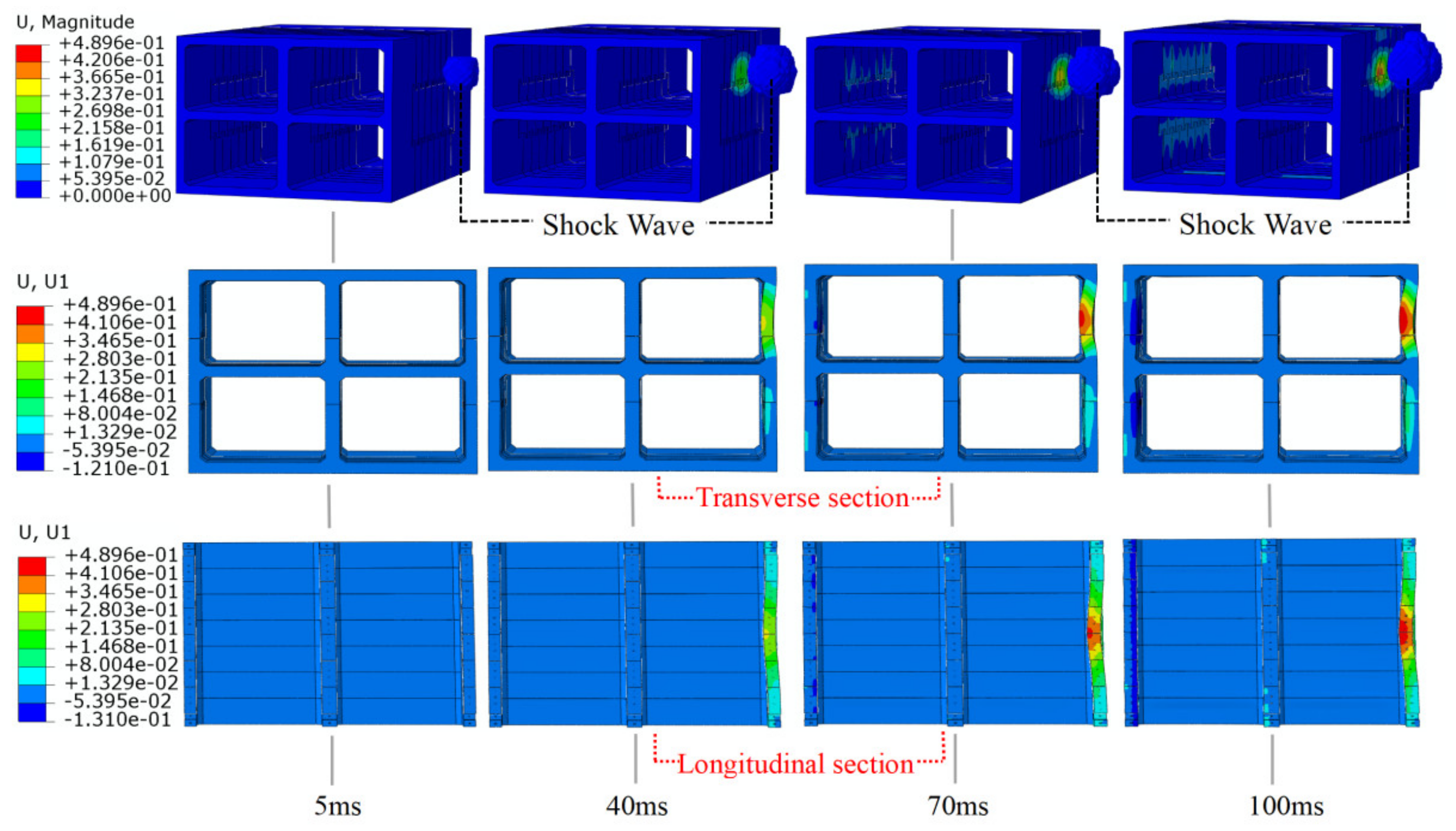
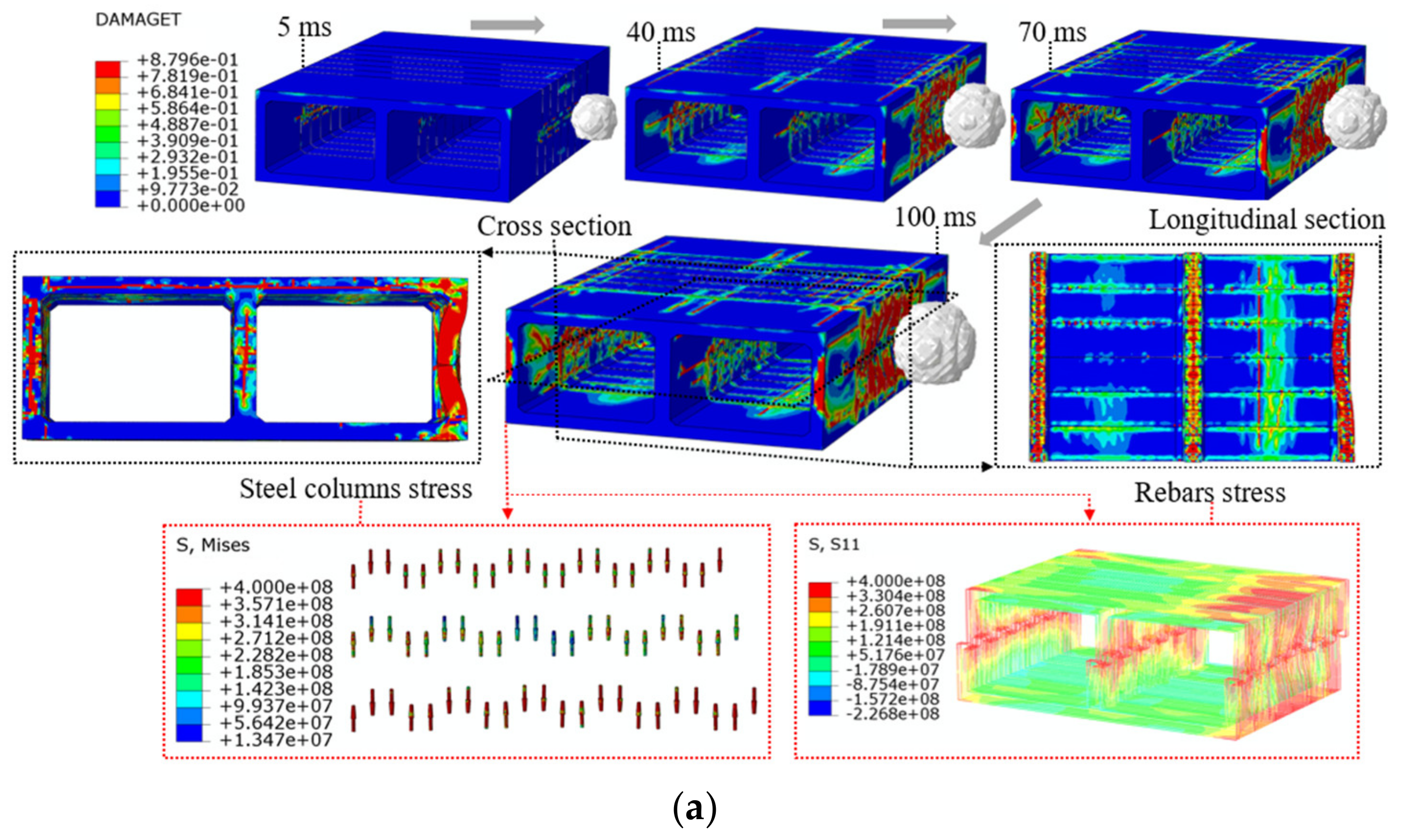
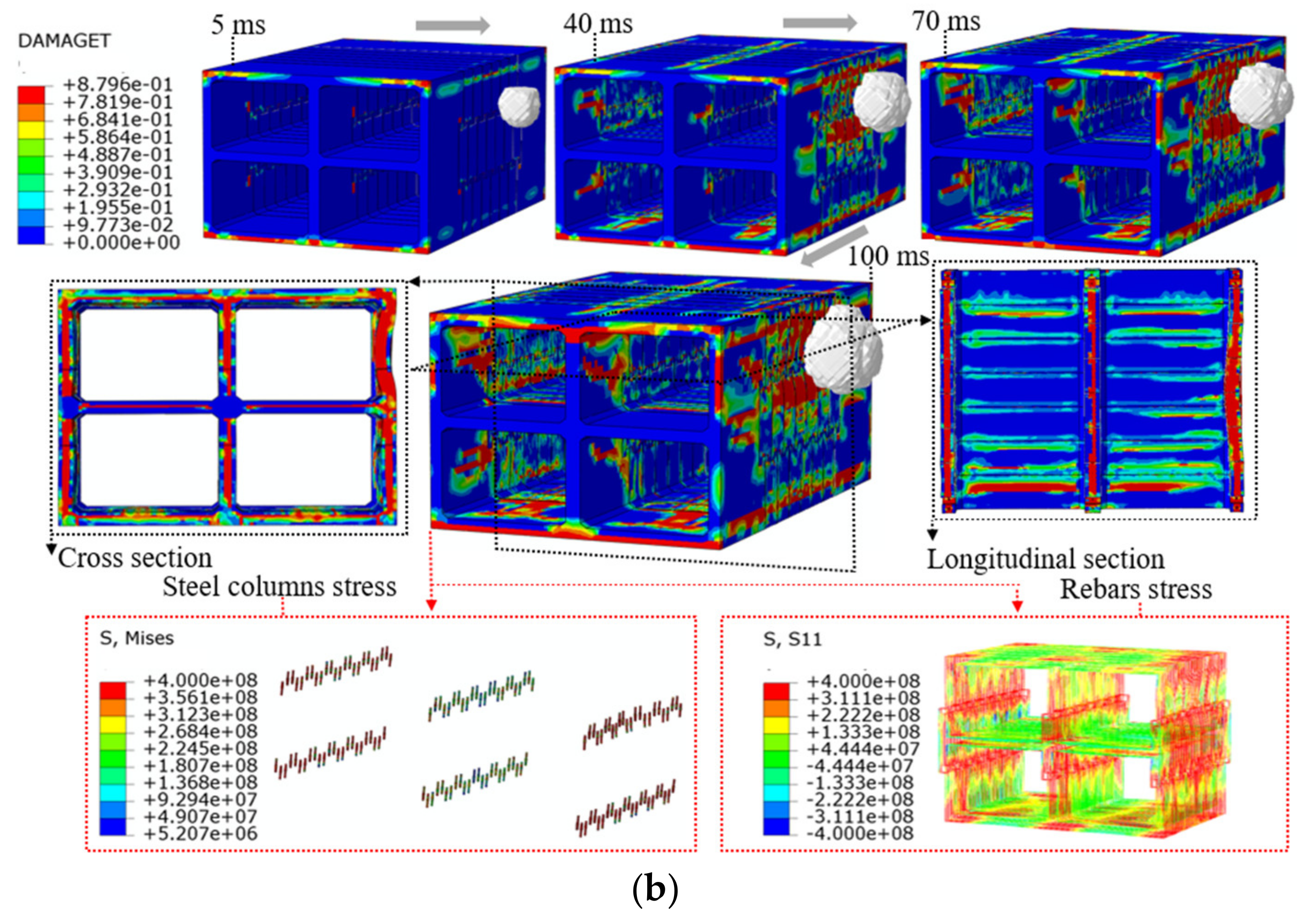
4.2. External Explosion

To explore the influence of an external explosion on the deformation characteristics of a prefabricated frame tunnel, the deformation response process of the fabricated frame tunnel under a 100 kg TNT external explosion (3 m, 6 m, 9 m, and 12 m from the center of the tunnel side wall) was simulated. The displacement chart at different times after the external explosion at the 3 m position of the single-layer frame tunnel is shown in Figure 13. Compared with air, the compressibility of soil is lower, the explosion power in soil is higher, and the attenuation of explosion waves is slower [37]. Therefore, in this study, the analysis time after explosion was extended, and the deformation data of each feature point and feature path were extracted within 100 ms after the external explosion.

After the external explosion of the tunnel, spherical shock waves were also generated in the soil and propagate outward rapidly. When the initial shock waves began to contact the outer surface of the tunnel lining side wall (t = 5 ms), some of the shock waves were absorbed by linings, and others were reflected by the tunnel lining, forming the reflected waves that were transmitted back into the soil. The tunnel lining had not yet produced large deformation at this time. As the subsequent shock waves constantly contacted the tunnel lining, the explosive pressure propagated in the soil. The explosion pressure on the outer surface of the tunnel lining decreased slowly after reaching the peak, and the deformation time of the tunnel lining extended. The deformation of the tunnel lining mainly occurred in the side wall near the TNT explosion, and the deformation degree was significantly higher than that in other parts of the tunnel.

The displacement chart at different times after the external explosion (100 kg TNT) at the 3 m position of the double-layer frame tunnel is shown in Figure 14. The deformation law of the double-layer tunnel lining was basically consistent with that of the single-layer tunnel lining. When the initial shock waves began to contact the outer surface of the tunnel lining side wall (t = 5 ms), the lining mainly deformed towards the inside of the tunnel along the direction of the explosion wave with the continuous action of the shock wave produced by the explosion. The deformation area was mainly concentrated in the lining side wall nearest to the explosion center, and the tunnel deformation presented locality.

As shown in Figure 13 and Figure 14, the deformation of the tunnel lining presented locality after an external explosion (100 kg TNT), and the displacement near feature points B and F closest to the explosion source was significantly higher than that at other parts of the lining. Therefore, the displacement data of feature points B and F and feature paths B_L and F_L under different distances of external explosion were extracted, and the displacement variation curves of feature points and feature paths were obtained (Figure 15).

As shown in Figure 15a,b, the displacement of feature points B and F under different distances of external explosion was very different. The displacement of the lining decreased by 75.7%, 39.9%, and 10.0% with increasing external explosion distance at equal distances (3–6 m, 6–9 m, and 9–12 m, respectively). The closer the explosion distance was, the greater the influence of the distance change on the lining deformation was. Similarly, the farther the explosion distance was, the smaller the influence of the distance change on the lining deformation was. Therefore, a safe distance should be limited when blasting around the prefabricated tunnel or when there are easily exploded pipelines.

The spatiality of lining deformation is reflected in Figure 15c,d. On feature path B_L, the maximum displacement of the lining at 15 m from the central position was 537.4 mm. It was 533.4% of the lining displacement at 10 m and 152.1% of the lining displacement at 12.5 m. On feature path F_L, the maximum displacement of the lining at 15 m from the central position was 427.2 mm. It was 329.6% of the lining displacement at 10 m and 169.5% of the lining displacement at 12.5 m. In view of the high locality of tunnel lining deformation under an external explosion, the lining near the explosion source should be locally strengthened when the prefabricated frame tunnel has the risk of an external explosion.

4.3. Damage Characteristics of the Prefabricated Frame Tunnel

In this section, the tensile damage DAMAGET parameters were used to assess the damage characteristics and failure modes of the prefabricated frame tunnel lining after an explosion. The damage evolution characteristics of single-layer and double-layer prefabricated frame tunnels after central and external explosions are shown in Figure 16 and Figure 17, respectively.

Due to the low acoustic impedance in air, compressive shock waves generated by the central explosion (500 kg TNT) were reflected by the lining surface to form tensile waves, and the resulting tensile stress was greater than the dynamic tensile strength of concrete, resulting in concrete damage and destruction [37]. Therefore, at t = 3 ms, the roof and floor of single-layer and double-layer prefabricated frame tunnels were damaged first (Figure 16). At t = 10 ms, the damage of the roof and floor of the prefabricated frame tunnel was enlarged, the lining structure was damaged by tension, and a large area of concrete spalling occurred. At the same time, many cracks appeared in the mid-partition and side walls far from the explosion point. At t = 20 ms, since the kinetic energy of the initial shock wave was severely consumed by the tunnel lining and the surrounding soil through deformation and absorption, the failure trend of the lining structure was slowed down. At t = 30 ms, the structural damage and concrete damage evolution almost stop.

After the central explosion of the tunnel, the failure modes of the roof and floor of the single-layer and double-layer prefabricated frame tunnels were different. The roof was the most fragile component in the single-layer tunnel, the mid-partition was the more fragile component in the double-layer tunnel, and these fragile parts showed more serious damage. The joint area of the lining structure also produced large area damage. The steel column and reinforcement cage at the joint bore a tremendous bending moment and shear force transmitted by the tunnel lining, and the stress of the steel column and reinforcement reached a peak.

The damage evolution characteristics of single-layer and double-layer prefabricated frame tunnels after external explosion (3 m, 100 kg TNT) are shown in Figure 17. Due to different explosion positions, the damage characteristics of the prefabricated frame tunnel after an external explosion were different from those of the central explosion. At t = 5 ms, the tunnel had obvious damage. At t = 40 ms, with the transmission of the explosion shock wave, the damage development of the concrete of the side wall near the explosion source was obvious. Additionally, the side wall along the direction of blasting wave propagation to the inside of the tunnel produced clear bending deformation. The lining structure was damaged by tension, and the concrete began to generate spalling in large areas. At t = 70 ms, due to the decrease in the kinetic energy of shock waves, the failure and damage development of the lining structure tended to be stable. At t = 100 ms, the structural damage and concrete damage evolution almost stopped. Compared with the central explosion, the damage and deformation caused by the external explosion mainly occurred in the side wall near the explosion source, and the damage development was also serious at the corner of the tunnel connected to the side wall.

4.4. Failure Mode of the Fabricated Frame Tunnel

To describe the failure mode of a prefabricated frame tunnel under explosion loading, the failure mode of a prefabricated frame tunnel after central and external explosions was obtained based on the deformation and damage characteristics of the tunnel (Figure 18).

As shown in Figure 18, the effects of central and external explosions on the structural deformation and mechanical characteristics of the prefabricated frame tunnel were different. The lining of the tunnel hole where the central explosion occurs deformed outward along the direction of the propagating explosion wave. The inner side region of the lining wall was compressed, and the outer side region exhibited tensile stress. The inner side region of the tunnel corner exhibited tensile stress, and the outer region was compressed. However, under the action of an external explosion, the side wall of the tunnel hole near the explosion source deformed towards the inside of the tunnel along the direction of the explosion wave. The outer side region of the side wall was compressed, and the inner side region exhibited tensile stress. The inner side region of the tunnel corner was compressed, and the outer region exhibited tensile stress.

5. Conclusions

In this study, a three-dimensional refined dynamic response numerical model considering the new fabricated frame tunnel joint effect and TNT explosion were established based on CEL technology and finite element coupling analysis. The deformation characteristics and damage evolution law of a prefabricated frame tunnel were analyzed. The analysis results of this study can be summarized as follows:

(1)

Under the central explosion load, the shock wave energy is continuously consumed by the tunnel and the surrounding soil, and the reflected wave continuously propagates inside the tunnel, causing large-area concrete spalling of the prefabricated frame tunnel lining. The lining deforms outward towards the tunnel in the direction of the explosion wave, the inner side of the tunnel is compressed, and the outer side is pulled. The deformation and damage at the structural joints of the single-layer and the double-layer frame are significantly higher than those at other parts, while the deformation and damage of the mid-partition in the double-layer frame are more serious. The mid-partition of the tunnel can be strengthened, and flexible damping material can be added at the joint to improve the explosion resistance of the prefabricated frame tunnel.

(2)

Under an external explosive load, part of the explosion shock wave is absorbed by the deformation of the tunnel lining, and the other part is reflected into the soil. External blasts are more damaging to the tunnel due to the low compressibility of the soil and the hollow interior of the frame. The close-range explosion not only causes local concrete collapse and spalling but also causes serious bending deformation of the tunnel lining. The tunnel deformation is localized. The tunnel side wall deforms inwardly towards the tunnel along the direction of the explosion wave, the outer side region of the tunnel is compressed, and the inner side region exhibits tensile stress. With increasing explosion distance, tunnel lining damage no longer shows a high degree of locality but is gradually dominated by bending deformation. Therefore, it is recommended to set a safe distance around the tunnel.

(3)

The disadvantage of this study is that the CEL algorithm can observe the process of air compression caused by the expansion of TNT, but the computational resource consumption is very large. Thus, the seed arrangement of the Euler grid needs to be carefully considered. At the same time, the M–C constitutive cannot reflect the yield caused by the compression characteristics during the simulation process, which may have an impact on the accuracy of the calculation results of the external explosion. Subsequent research can be aimed at the establishment of the soil constitutive model under the explosion load in terms of calculation accuracy and calculation efficiency.