Long-Term US Economic Growth and the Carbon Dioxide Emissions Nexus: A Wavelet-Based Approach
Abstract
:1. Introduction
2. Literature Review
3. Methodology
3.1. Continuous Wavelet Transform
3.2. Continuous Wavelet Transform-Based Causality
3.3. Data
4. Results
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- EPA. Inventory of U.S. Greenhouse Gas Emissions and Sinks: 1990-2018 United States Environmental Protection Agency; EPA 430-R-20-002; EPA: Washington, DC, USA, 2020.
- Olayeni, O.R. Causality in Continuous Wavelet Transform Without Spectral Matrix Factorization: Theory and Application. Comput. Econ. 2015, 47, 321–340. [Google Scholar] [CrossRef]
- Eichler, M. Granger causality and path diagrams for multivariate time series. J. Econ. 2007, 137, 334–353. [Google Scholar] [CrossRef]
- Diks, C.; Panchenko, V. A new statistic and practical guidelines for nonparametric Granger causality testing. J. Econ. Dyn. Control 2006, 30, 1647–1669. [Google Scholar] [CrossRef]
- In, F.; Kim, S. The Hedge Ratio and the Empirical Relationship between the Stock and Futures Markets: A New Approach Using Wavelet Analysis*. J. Bus. 2006, 79, 799–820. [Google Scholar] [CrossRef]
- Chou, C.C.; Show-lin, C. Integrated or segmented?A wavelet transform analysis on relationship between stock and real estate markets. Econ. Bull. 2011, 31, 3030–3040. [Google Scholar]
- Benhmad, F. Modeling nonlinear Granger causality between the oil price and U.S. dollar: A wavelet based approach. Econ. Model. 2012, 29, 1505–1514. [Google Scholar] [CrossRef]
- Andrieș, A.M.; Ihnatov, I.; Tiwari, A.K. Analyzing time–frequency relationship between interest rate, stock price and exchange rate through continuous wavelet. Econ. Model. 2014, 41, 227–238. [Google Scholar] [CrossRef]
- Andrieș, A.M.; Capraru, B.; Ihnatov, I.; Tiwari, A. The relationship between exchange rates and interest rates in a small open emerging economy: The case of Romania. Econ. Model. 2017, 67, 261–274. [Google Scholar] [CrossRef]
- Tiwari, A.K.; Mutascu, M.I.; Albulescu, C.T. The influence of the international oil prices on the real effective exchange rate in Romania in a wavelet transform framework. Energy Econ. 2013, 40, 714–733. [Google Scholar] [CrossRef]
- Albulescu, C.T.; Goyeau, D.; Tiwari, A.K. Contagion and Dynamic Correlation of the Main European Stock Index Futures Markets: A Time-frequency Approach. Procedia Econ. Financ. 2015, 20, 19–27. [Google Scholar] [CrossRef]
- Albulescu, C.T.; Goyeau, D.; Tiwari, A.K. Co-movements and contagion between international stock index futures markets. Empir. Econ. 2016, 52, 1529–1568. [Google Scholar] [CrossRef]
- Grinsted, A.; Moore, J.C.; Jevrejeva, S. Application of the cross wavelet transform and wavelet coherence to geophysical time series. Nonlinear Process. Geophys. 2004, 11, 561–566. [Google Scholar] [CrossRef]
- Rua, A. Measuring comovement in the time–frequency space. J. Macroecon. 2010, 32, 685–691. [Google Scholar] [CrossRef]
- Rua, A. Worldwide synchronization since the nineteenth century: A wavelet-based view. Appl. Econ. Lett. 2013, 20, 773–776. [Google Scholar] [CrossRef]
- Aguiar-Conraria, L.; Azevedo, N.; Soares, M.J. Using wavelets to decompose the time–frequency effects of monetary policy. Phys. A Stat. Mech. Its Appl. 2008, 387, 2863–2878. [Google Scholar] [CrossRef]
- Aguiar-Conraria, L.; Soares, M.J.; Sousa, R. California’s carbon market and energy prices: A wavelet analysis. Philos. Trans. R. Soc. London Ser. A Math. Phys. Eng. Sci. 2018, 376, 20170256. [Google Scholar] [CrossRef]
- Chen, Y.; Bressler, S.L.; Ding, M. Frequency decomposition of conditional Granger causality and application to multivariate neural field potential data. J. Neurosci. Methods 2006, 150, 228–237. [Google Scholar] [CrossRef]
- Dhamala, M.; Rangarajan, G.; Ding, M. Estimating Granger Causality from Fourier and Wavelet Transforms of Time Series Data. Phys. Rev. Lett. 2008, 100, 018701. [Google Scholar] [CrossRef]
- Dhamala, M.; Rangarajan, G.; Ding, M. Analyzing information flow in brain networks with nonparametric Granger causality. NeuroImage 2008, 41, 354–362. [Google Scholar] [CrossRef]
- Grossman, G.M.; Krueger, A.B. Environmental impacts of a North American Free Trade Agreement. Natl. Bur. Econ. Res. Work. Pap. 1991, 387, 1–57. [Google Scholar] [CrossRef]
- Kraft, J.; Kraft, A. On the relationship between energy and GNP. J. Energy Dev. 1978, 3, 401–403. [Google Scholar]
- Payne, J.E. Survey of the international evidence on the causal relationship between energy consumption and growth. J. Econ. Stud. 2010, 37, 53–95. [Google Scholar] [CrossRef]
- Ozturk, I. A literature survey on energy–growth nexus. Energy Policy 2010, 38, 340–349. [Google Scholar] [CrossRef]
- Akarca, A.T.; Long, T.V., II. Energy and employment: A time-series analysis of the causal relationship. Resour. Energy 1979, 2, 151–162. [Google Scholar] [CrossRef]
- Akarca, A.T.; Long, T.V., II. On the relationship between energy and GNP: A Reexamination. J. Energy Dev. 1980, 5, 326–331. [Google Scholar]
- Yu, E.S.; Hwang, B.-K. The relationship between energy and GNP: Further results. Energy Econ. 1984, 6, 186–190. [Google Scholar] [CrossRef]
- Abosedra, S.; Baghestani, H. New evidence on the causal relationship between United States energy consumption and gross national product. J. Energy Dev. 1988, 14, 285–292. [Google Scholar]
- Yu, E.S.; Jin, J.C. Cointegration tests of energy consumption, income, and employment. Resour. Energy 1992, 14, 259–266. [Google Scholar] [CrossRef]
- Stern, D.I. Energy and economic growth in the USA: A multivariate approach. Energy Econ. 1993, 15, 137–150. [Google Scholar] [CrossRef]
- Cheng, B.S. An investigation of cointegration and causality between energy consumption and economic growth. J. Energy Dev. 1995, 21, 73–84. [Google Scholar]
- Stern, D.I. A multivariate cointegration analysis of the role of energy in the US macroeconomy. Energy Econ. 2000, 22, 267–283. [Google Scholar] [CrossRef]
- Gang, L. A Causality Analysis on GDP and Air Emissions in Norway; Statistics Norway Research Department: Olso, Norway, 2006; Discussion Papers, No 447. [Google Scholar]
- Ang, J.B. CO2 emissions, energy consumption, and output in France. Energy Policy 2007, 35, 4772–4778. [Google Scholar] [CrossRef]
- Soytas, U.; Sari, R.; Ewing, B.T. Energy consumption, income, and carbon emissions in the United States. Ecol. Econ. 2007, 62, 482–489. [Google Scholar] [CrossRef]
- Ang, J.B. Economic development, pollutant emissions and energy consumption in Malaysia. J. Policy Model. 2008, 30, 271–278. [Google Scholar] [CrossRef]
- Payne, J.E. On the dynamics of energy consumption and output in the US. Appl. Energy 2009, 86, 575–577. [Google Scholar] [CrossRef]
- Halicioglu, F. An econometric study of CO2 emissions, energy consumption, income and foreign trade in Turkey. Energy Policy 2009, 37, 1156–1164. [Google Scholar] [CrossRef]
- Zhang, X.-P.; Cheng, X.-M. Energy consumption, carbon emissions, and economic growth in China. Ecol. Econ. 2009, 68, 2706–2712. [Google Scholar] [CrossRef]
- Jalil, A.; Mahmud, S.F. Environment Kuznets curve for CO2 emissions: A cointegration analysis for China. Energy Policy 2009, 37, 5167–5172. [Google Scholar] [CrossRef]
- Soytas, U.; Sari, R. Energy consumption, economic growth, and carbon emissions: Challenges faced by an EU candidate member. Ecol. Econ. 2009, 68, 1667–1675. [Google Scholar] [CrossRef]
- Menyah, K.; Wolde-Rufael, Y. CO2 emissions, nuclear energy, renewable energy and economic growth in the US. Energy Policy 2010, 38, 2911–2915. [Google Scholar] [CrossRef]
- Ghosh, S. Examining carbon emissions economic growth nexus for India: A multivariate cointegration approach. Energy Policy 2010, 38, 3008–3014. [Google Scholar] [CrossRef]
- Iwata, H.; Okada, K.; Samreth, S. Empirical study on the environmental Kuznets curve for CO2 in France: The role of nuclear energy. Energy Policy 2010, 38, 4057–4063. [Google Scholar] [CrossRef]
- Pao, H.-T.; Tsai, C.-M. Modeling and forecasting the CO2 emissions, energy consumption, and economic growth in Brazil. Energy 2011, 36, 2450–2458. [Google Scholar] [CrossRef]
- Wang, S.; Zhou, D.; Zhou, P.; Wang, Q. CO2 emissions, energy consumption and economic growth in China: A panel data analysis. Energy Policy 2011, 39, 4870–4875. [Google Scholar] [CrossRef]
- Saboori, B.; Sulaiman, J.; Mohd, S. Economic growth and CO2 emissions in Malaysia: A cointegration analysis of the Environmental Kuznets Curve. Energy Policy 2012, 51, 184–191. [Google Scholar] [CrossRef]
- Lim, K.-M.; Lim, S.-Y.; Yoo, S.-H. Oil Consumption, CO2 Emission, and Economic Growth: Evidence from the Philippines. Sustainability 2014, 6, 967–979. [Google Scholar] [CrossRef]
- Arora, V.; Shuping, S. Energy consumption and economic growth in the United States. Appl. Econ. 2016, 48, 3763–3773. [Google Scholar] [CrossRef]
- Ben Jebli, M.; Ben Youssef, S.; Apergis, N. The dynamic linkage between renewable energy, tourism, CO2 emissions, economic growth, foreign direct investment, and trade. Lat. Am. Econ. Rev. 2019, 28, 2. [Google Scholar] [CrossRef]
- Mushtaq, A.; Chen, Z.; Din, N.U.; Ahmad, B.; Zhang, X. Income inequality, innovation and carbon emission: Perspectives on sustainable growth. Econ. Res. 2020, 33, 769–787. [Google Scholar] [CrossRef]
- Abban, O.J.; Wu, J.; Mensah, I.A. Analysis on the nexus amid CO2 emissions, energy intensity, economic growth, and foreign direct investment in Belt and Road economies: Does the level of income matter? Environ. Sci. Pollut. Res. 2020, 27, 11387–11402. [Google Scholar] [CrossRef]
- Ben Jebli, M.; Kahia, M. The interdependence between CO2 emissions, economic growth, renewable and non-renewable energies, and service development: Evidence from 65 countries. Clim. Chang. 2020, 162, 193–212. [Google Scholar] [CrossRef]
- Hu, M.; Li, R.; You, W.; Liu, Y.; Lee, C.-C. Spatiotemporal evolution of decoupling and driving forces of CO2 emissions on economic growth along the Belt and Road. J. Clean. Prod. 2020, 277, 123272. [Google Scholar] [CrossRef]
- Adedoyin, F.F.; Gumede, M.I.; Bekun, F.V.; Etokakpan, M.U.; Balsalobre-Lorente, D. Modelling coal rent, economic growth and CO2 emissions: Does regulatory quality matter in BRICS economies? Sci. Total Environ. 2019, 710, 136284. [Google Scholar] [CrossRef]
- Adedoyin, F.F.; Zakari, A. Energy consumption, economic expansion, and CO2 emission in the UK: The role of economic policy uncertainty. Sci. Total Environ. 2020, 738, 140014. [Google Scholar] [CrossRef]
- Wasti, S.K.A.; Zaidi, S.W. An empirical investigation between CO2 emission, energy consumption, trade liberalization and economic growth: A case of Kuwait. J. Build. Eng. 2019, 28, 101104. [Google Scholar] [CrossRef]
- Alola, A.A.; Adebayo, T.S.; Onifade, S.T. Examining the dynamics of ecological footprint in China with spectral Granger causality and quantile-on-quantile approaches. Int. J. Sustain. Dev. World Ecol. 2021, 29, 263–276. [Google Scholar] [CrossRef]
- He, X.; Adebayo, T.S.; Kirikkaleli, D.; Umar, M. Consumption-based carbon emissions in Mexico: An analysis using the dual adjustment approach. Sustain. Prod. Consum. 2021, 27, 947–957. [Google Scholar] [CrossRef]
- Adebayo, T.S.; Abraham, A.A.; Jamiu, A.O.; Gbenga, D.A.; Wing-Keung, W.; Husam, R. Sustainability of energy-induced growth nexus in Brazil: Do carbon emissions and urbanization matter? Sustainability 2021, 13, 4371. [Google Scholar] [CrossRef]
- Adebayo, T.S.; Akinsola, G.D.; Kirikkaleli, D.; Bekun, F.V.; Umarbeyli, S.; Osemeahon, O.S. Economic performance of Indonesia amidst CO2 emissions and agriculture: A time series analysis. Environ. Sci. Pollut. Res. 2021, 28, 47942–47956. [Google Scholar] [CrossRef] [PubMed]
- Shabani, E.; Hayati, B.; Pishbahar, E.; Ghorbani, M.A.; Ghahremanzadeh, M. The relationship between CO2 emission, economic growth, energy consumption, and urbanization in the ECO member countries. Int. J. Environ. Sci. Technol. 2021, 19, 1861–1876. [Google Scholar] [CrossRef]
- Adebayo, T.S.; Oladipupo, S.D.; Adeshola, I.; Rjoub, H. Wavelet analysis of impact of renewable energy consumption and technological innovation on CO2 emissions: Evidence from Portugal. Environ. Sci. Pollut. Res. 2021, 29, 23887–23904. [Google Scholar] [CrossRef] [PubMed]
- Adebayo, T.S.; Rjoub, H.; Akinsola, G.D.; Oladipupo, S.D. The asymmetric effects of renewable energy consumption and trade openness on carbon emissions in Sweden: New evidence from quantile-on-quantile regression approach. Environ. Sci. Pollut. Res. 2021, 29, 1875–1886. [Google Scholar] [CrossRef]
- Cifter, A.; Ozun, A. Multi-scale causality between energy consumption and GNP in emerging markets: Evidence from Turkey. MPRA Pap. 2007, 2483, 1–14. [Google Scholar]
- Aslan, A.; Apergis, N.; Yildirim, S. Causality between energy consumption and GDP in the U.S.: Evidence from wavelet analysis. Front. Energy 2013, 8, 1–8. [Google Scholar] [CrossRef]
- Jammazi, R.; Aloui, C. Environment degradation, economic growth and energy consumption nexus: A wavelet-windowed cross correlation approach. Phys. A Stat. Mech. Its Appl. 2015, 436, 110–125. [Google Scholar] [CrossRef]
- Kristjanpoller, W.; Alejandro, S.; Javier, S. Dynamic co-movements between energy consumption and economic growth. A panel data and wavelet perspective. Energy Econ. 2018, 72, 640–649. [Google Scholar] [CrossRef]
- Fosten, J. CO2 emissions and economic activity: A short-to-medium run perspective. Energy Econ. 2019, 83, 415–429. [Google Scholar] [CrossRef]
- Bilgili, F. Business cycle co-movements between renewables consumption and industrial production: A continuous wavelet coherence approach. Renew. Sustain. Energy Rev. 2015, 52, 325–332. [Google Scholar] [CrossRef]
- Ben-Salha, O.; Hkiri, B.; Aloui, C. Sectoral energy consumption by source and output in the U.S.: New evidence from wavelet-based approach. Energy Econ. 2018, 72, 75–96. [Google Scholar] [CrossRef]
- Raza, S.A.; Shah, N.; Sharif, A. Time frequency relationship between energy consumption, economic growth and environmental degradation in the United States: Evidence from transportation sector. Energy 2019, 173, 706–720. [Google Scholar] [CrossRef]
- Bilgili, F.; Kuskaya, S.; Toguc, N.; Mugaloglu, E.; Koçak, E.; Bulut, Ü.; Bağlıtaş, H.H. A revisited renewable consumption-growth nexus: A continuous wavelet approach through disaggregated data. Renew. Sustain. Energy Rev. 2019, 107, 1–19. [Google Scholar] [CrossRef]
- Christopher, T.; Compo, G.P. A practical guide to wavelet analysis. Bull. Am. Mete-Orol. Soc. 1998, 79, 61–78. [Google Scholar] [CrossRef]
- Tiwari, A.K.; Oros, C.; Albulescu, C.T. Revisiting the inflation–output gap relationship for France using a wavelet transform approach. Econ. Model. 2014, 37, 464–475. [Google Scholar] [CrossRef]
- Salazar-Núñez, H.F.; Venegas-Martínez, F.; Tinoco-Zermeño, M. Impact of energy consumption and carbon dioxide emissions on economic growth: Cointegrated panel data in 79 countries grouped by income level. Int. J. Energy Econ. Policy 2020, 10, 218–226. [Google Scholar] [CrossRef]
- Li, K.; Hu, E.; Xu, C.; Musah, M.; Kong, Y.; Mensah, I.A.; Zu, J.; Jiang, W.; Su, Y. A heterogeneous analysis of the nexus between energy consumption, economic growth and carbon emissions: Evidence from the Group of Twenty (G20) countries. Energy Explor. Exploit. 2020, 39, 815–837. [Google Scholar] [CrossRef]
- Salari, M.; Javid, R.J.; Noghanibehambari, H. The nexus between CO2 emissions, energy consumption, and economic growth in the U.S. Econ. Anal. Policy 2020, 69, 182–194. [Google Scholar] [CrossRef]
- Nathaniel, S.P.; Alam, S.; Murshed, M.; Mahmood, H.; Ahmad, P. The roles of nuclear energy, renewable energy, and economic growth in the abatement of carbon dioxide emissions in the G7 countries. Environ. Sci. Pollut. Res. 2021, 28, 47957–47972. [Google Scholar] [CrossRef]
- Pata, U.K. Renewable and non-renewable energy consumption, economic complexity, CO2 emissions, and ecological footprint in the USA: Testing the EKC hypothesis with a structural break. Environ. Sci. Pollut. Res. 2020, 28, 846–861. [Google Scholar] [CrossRef]
- Liu, X.; Yuan, X. Novel research methods for energy use, carbon emissions, and economic growth: Evidence from the USA. Econ. Res.-Ekon. Istraživanja 2022, 387, 1–16. [Google Scholar] [CrossRef]
- Ortega-Ruiz, G.; Mena-Nieto, A.; Golpe, A.; García-Ramos, J. CO2 emissions and causal relationships in the six largest world emitters. Renew. Sustain. Energy Rev. 2022, 162, 112435. [Google Scholar] [CrossRef]
- Jiang, Y.; Zhou, Z.; Liu, C. Does economic policy uncertainty matter for carbon emission? Evidence from US sector level data. Environ. Sci. Pollut. Res. 2019, 26, 24380–24394. [Google Scholar] [CrossRef]
- Xue, C.; Shahbaz, M.; Ahmed, Z.; Ahmad, M.; Sinha, A. Clean energy consumption, economic growth, and environmental sustainability: What is the role of economic policy uncertainty? Renew. Energy 2021, 184, 899–907. [Google Scholar] [CrossRef]
- Zhang, W.; Huang, Y.; Wu, H. The symmetric and asymmetric effects of economic policy uncertainty and oil prices on carbon emissions in the USA and China: Evidence from the ARDL and non-linear ARDL approaches. Environ. Sci. Pollut. Res. 2021, 29, 26465–26482. [Google Scholar] [CrossRef] [PubMed]
- Niyonzima, P.; Yao, X.; Ofori, E.K. How Do Economic Growth and the Emissions of Carbon Dioxide Relate? OALib 2022, 9, 1–16. [Google Scholar] [CrossRef]
- Aguiar-Conraria, L.; Soares, M.J. The continuous wavelet transform: Moving beyond uni-and bivariate analysis. J. Econ. Surv. 2014, 28, 344–375. [Google Scholar] [CrossRef]
- Ramsey, J.B.; Lampart, C. Decompostition of Economic Relationships by Timescale Using Wavelets. Macroecon. Dyn. 1998, 2, 49–71. [Google Scholar] [CrossRef]
- Ramsey, J.B. Wavelets in Economics and Finance: Past and Future. Stud. Nonlinear Dyn. Econ. 2002, 6, 1–70. [Google Scholar] [CrossRef]
- Gençay, R.; Selçuk, F.; Whitcher, B. An Introduction to Wavelets and Other Filtering Methods in Finance and Economics; Elsevier: Amsterdam, The Netherlands; Academic Press: San Diego, CA, 2001; p. 12. [Google Scholar]
- Gençay, R.; Gradojevic, N.; Selçuk∥, F.; Whitcher, B. Asymmetry of information flow between volatilities across time scales. Quant. Financ. 2010, 10, 895–915. [Google Scholar] [CrossRef]
- Gallegati, M. Wavelet Variance Analysis of Output in G-7 Countries. Stud. Nonlinear Dyn. Econ. 2007, 11, 1435–1455. [Google Scholar] [CrossRef]
- Gallegati, M.; Ramsey, J.B.; Semmler, W.; Gallegati, M. The US Wage Phillips Curve across Frequencies and over Time*. Oxf. Bull. Econ. Stat. 2011, 73, 489–508. [Google Scholar] [CrossRef]
- Aguiar-Conraria, L.; Magalhães, P.C.; Soares, M.J. The nationalization of electoral cycles in the United States: A wavelet analysis. Public Choice 2013, 156, 387–408. [Google Scholar] [CrossRef]
- Aguiar-Conraria, L.; Soares, M.J. Oil and the macroeconomy: Using wavelets to analyze old issues. Empir. Econ. 2010, 40, 645–655. [Google Scholar] [CrossRef]
- Aguiar-Conraria, L.; Soares, M.J. The continuous wavelet transform: A primer. NIPE-Universidade do Minho 2011, 16, 1–43. [Google Scholar]
- Rua, A. Money Growth and Inflation in the Euro Area: A Time-Frequency View. Oxf. Bull. Econ. Stat. 2012, 74, 875–885. [Google Scholar] [CrossRef]
- Rua, A.; Nunes, L.C. A wavelet-based assessment of market risk: The emerging markets case. Q. Rev. Econ. Financ. 2012, 52, 84–92. [Google Scholar] [CrossRef]
- Sousa, R.; Aguiar-Conraria, L.; Soares, M.J. Carbon financial markets: A time–frequency analysis of CO2 prices. Phys. A Stat. Mech. Its Appl. 2014, 414, 118–127. [Google Scholar] [CrossRef]
- Tiwari, A.K.; Bhattacharyya, M.; Das, D.; Shahbaz, M. Output and stock prices: New evidence from the robust wavelet approach. Financ. Res. Lett. 2018, 27, 154–160. [Google Scholar] [CrossRef]
- Tiwari, A.K.; Adewuyi, A.O.; Awodumi, O.B.; Roubaud, D. Relationship between stock returns and inflation: New evidence from the US using wavelet and causality methods. Int. J. Financ. Econ. 2020, 387, 1–16. [Google Scholar] [CrossRef]
- Addo, P.M.; Billio, M.; Guegan, D. Alternative methodology for Turning-Point Detection in Business Cycle: A Wavelet Approach.⟨Halshs-00694420⟩. CES Working Papers 2012. Available online: https://halshs.archives-ouvertes.fr/halshs-00694420/ (accessed on 10 April 2016).
- Grossmann, A.; Morlet, J. Decomposition of Hardy Functions into Square Integrable Wavelets of Constant Shape. SIAM J. Math. Anal. 1984, 15, 723–736. [Google Scholar] [CrossRef]
- Aguiar-Conraria, L.; Martins, M.; Soares, M.J. The yield curve and the macro-economy across time and frequencies. J. Econ. Dyn. Control 2012, 36, 1950–1970. [Google Scholar] [CrossRef]
- Johnston, L.; Williamson, S.H. What Was the US GDP Then? Measuring Worth. 2019. Available online: http://www.measuringworth.org/usgdp/ (accessed on 10 April 2016).
- Boden, T.A.; Marland, G.; Andres, R.J. Global, Regional, and National Fossil-Fuel CO2 Emissions; Carbon Dioxide Information Analysis Center: Oak Ridge, TN, USA; Oak Ridge National Laboratory: Oak Ridge, TN, USA; US Department of Energy: Oak Ridge, TN, USA, 2017. [CrossRef]
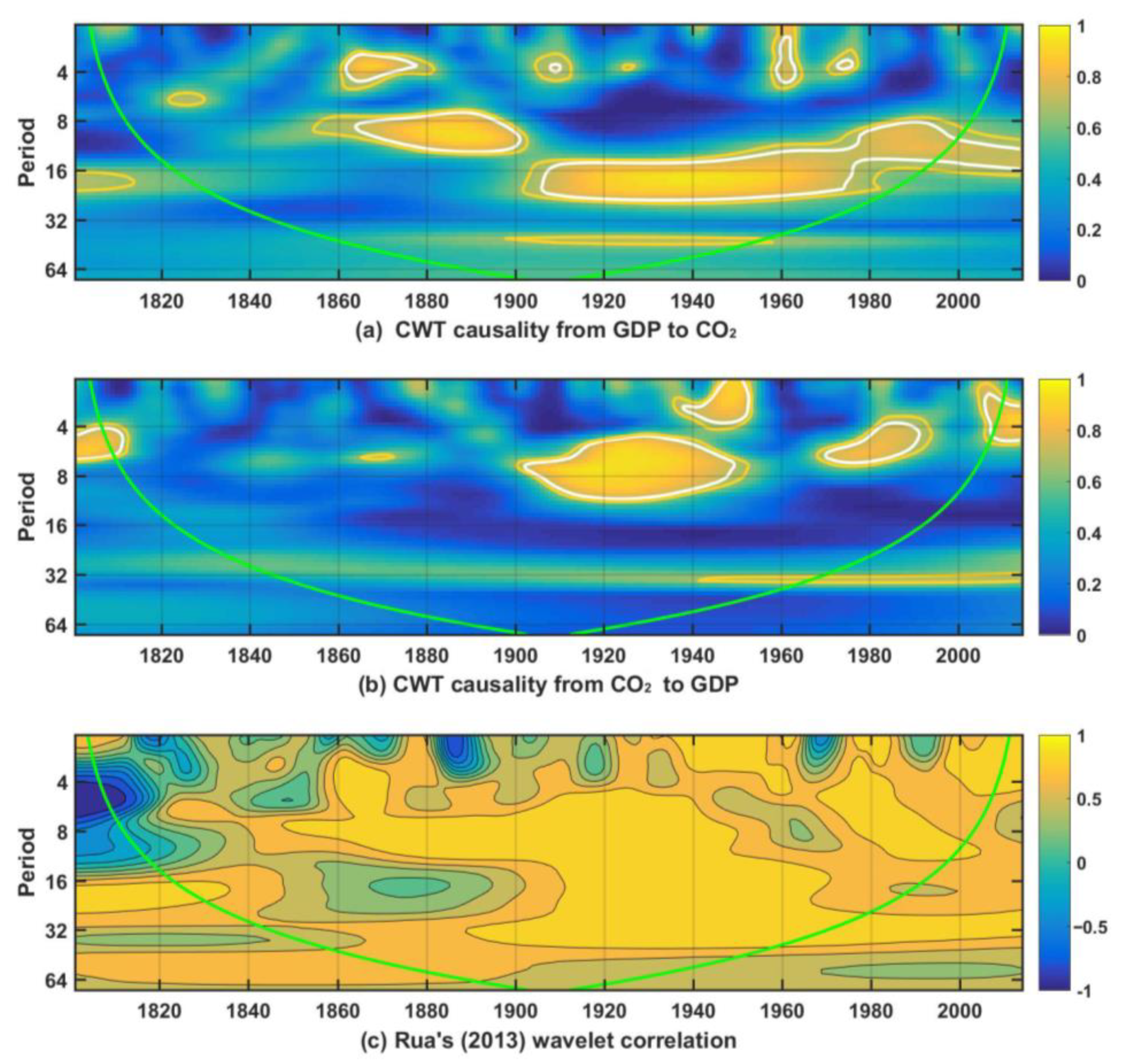
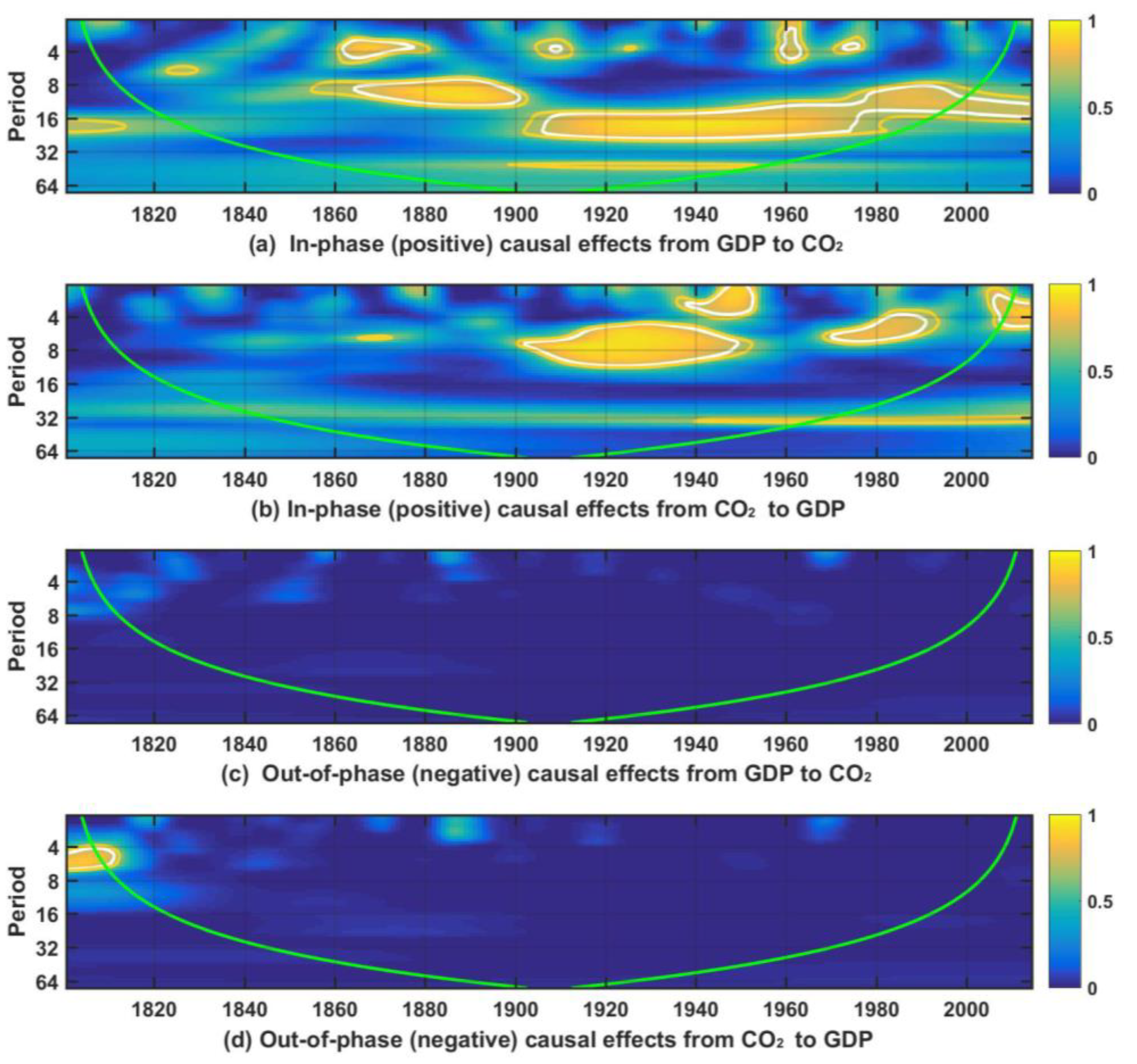
| Study | Country | Period | Methodology | Causality |
|---|---|---|---|---|
| [22] | US | 1947–1974 | GC | N→E |
| [25] | US | January 1973–March 1978 | GC | E→P |
| [26] | US | 1950–1970 | Sim’s GC | N---E |
| [27] | US | 1947–1979 | Sims’ GC | N---E |
| [28] | US | 1947–1987 | GC | N→E |
| [29] | US | 1974–1990 | GC | G---E |
| [30] | US | 1947–1990 | Multivariate VAR model | E→G |
| [31] | US | 1947–1990 | GC | G---E |
| [32] | US | 1948–1994 | GC | E→G |
| [33] | Norway | 1973–2003 | GC | G→C |
| [34] | France | 1960–2000 | ECM-based GC | G→C G→E |
| [35] | US | 1960–2004 | Toda and Yamamoto (1995) | E---G G---C E→C |
| [36] | Malaysia | 1971–1999 | ECM-based GC | C→G E↔G |
| [37] | US | 1949–2006 | Toda–Yamamoto (1995) | G---E |
| [38] | Turkey | 1960–2005 | VECM-based GC | C↔G C↔G2 C→E |
| [39] | China | 1960–2007 | Toda and Yamamoto (1995) | C---G G→E E→C |
| [40] | China | 1975–2005 | Pair-wise GC | G→C E→C |
| [41] | Turkey | 1960–2000 | Toda and Yamamoto (1995) | C---G C→E |
| [42] | US | 1960–2007 | Toda and Yamamoto (1995) | G↔C G→RE |
| [43] | India | 1971–2006 | VECM-based GC | C---G |
| [44] | France | 1960–2003 | GC | G→C |
| [45] | Brazil | 1980–2007 | ECM-based GC | G→C |
| [46] | China | 1995–2007 | VECM-based GC | G→C |
| [47] | Malaysia | 1980–2009 | VECM-based GC | C→G |
| [48] | Philippines | 1965−2010 | ECM-based GC | E↔G E↔C C→G |
| [49] | US | 1973Q1–2014Q1 | Time-varying GC | E↔G 1990s G→E 2000s |
| [50] | 22 Central and South American Countries | 1995–2010 | GC | G→E (short-run) G→C (long-run) |
| [51] | China | 1995–2015 | FE, PSCE, N-W, FGLS regression models | G→C |
| [52] | Belt and Road Initiative Countries | 1995–2015 | Panel causality and cointegration models | EI, G↔C |
| [53] | 65 countries | 1965–2019 | Panel causality and cointegration models | G↔ C |
| [54] | Belt and Road Initiative Countries | 1991–2016 | Tapio decoupling model, Kaya–LMDI model | G→C |
| [55] | BRICS countries | 1990–2014 | ARDL model, causality test | G→C |
| [56] | UK | 1985–2017 | ARDL model, causality test | G→C |
| [57] | Kuwait | 1971–2017 | ARDL, causality test | G→C |
| [58] | China | 1971–2016 | quantile-on-quantile regression, Granger causality | G→C |
| [59] | Mexico | 1990–2018 | ARDL, FMOLS models, and causality | G→C |
| [60] | Brazil | 1965–2019 | ARDL, DOLS, FMOLS, Maki cointegration, Wavelet coherence | E, C→G |
| [61] | Indonesia | 1965–2019 | ARDL, DOLS models | G↔C |
| [62] | ECO member countries | 1990–2014 | FMOLS model and causality test | G↔C |
| [63] | Portugal | 1980–2018 | FDC causality, Wavelet coherence | G→C |
| [64] | Sweden | 1965–2019 | quantile-on-quantile regression | G→C |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Torun, E.; Akdeniz, A.D.A.; Demireli, E.; Grima, S. Long-Term US Economic Growth and the Carbon Dioxide Emissions Nexus: A Wavelet-Based Approach. Sustainability 2022, 14, 10566. https://doi.org/10.3390/su141710566
Torun E, Akdeniz ADA, Demireli E, Grima S. Long-Term US Economic Growth and the Carbon Dioxide Emissions Nexus: A Wavelet-Based Approach. Sustainability. 2022; 14(17):10566. https://doi.org/10.3390/su141710566
Chicago/Turabian StyleTorun, Erdost, Afife Duygu Ayhan Akdeniz, Erhan Demireli, and Simon Grima. 2022. "Long-Term US Economic Growth and the Carbon Dioxide Emissions Nexus: A Wavelet-Based Approach" Sustainability 14, no. 17: 10566. https://doi.org/10.3390/su141710566
APA StyleTorun, E., Akdeniz, A. D. A., Demireli, E., & Grima, S. (2022). Long-Term US Economic Growth and the Carbon Dioxide Emissions Nexus: A Wavelet-Based Approach. Sustainability, 14(17), 10566. https://doi.org/10.3390/su141710566







