White-Tailed Eagle Algorithm for Global Optimization and Low-Cost and Low-CO2 Emission Design of Retaining Structures
Abstract
:1. Introduction
- Multiple potential solutions communicate information regarding the search space, resulting in unexpected leaps to the most promising area of the space;
- Several potential solutions collaborate to prevent finding the best solution locally;
- As opposed to single-solution algorithms, population-based metaheuristics allow for more exploration.
- An effective optimization approach, namely the white-tailed eagle algorithm (WEA) has been developed for global optimization problems;
- The performance of the WEA for numerical function optimization is evaluated on 13 frequently used benchmark functions and compared to other optimization algorithms;
- To verify the effectiveness of the proposed method for the solution of real-world problems, the new method is applied to retaining wall optimization under static and seismic loads;
- In the optimum design of the retaining walls, total construction cost as well as total CO2 emissions are considered objective functions;
- A sensitivity analysis is performed to determine the impact of the horizontal acceleration coefficient on the construction cost and CO2 emissions of the structure.
2. Related Works
2.1. Swarm Intelligence Algorithms
2.2. Evolutionary Algorithms
2.3. Physics-Based Algorithms (PhA)
2.4. Human-Based Algorithms
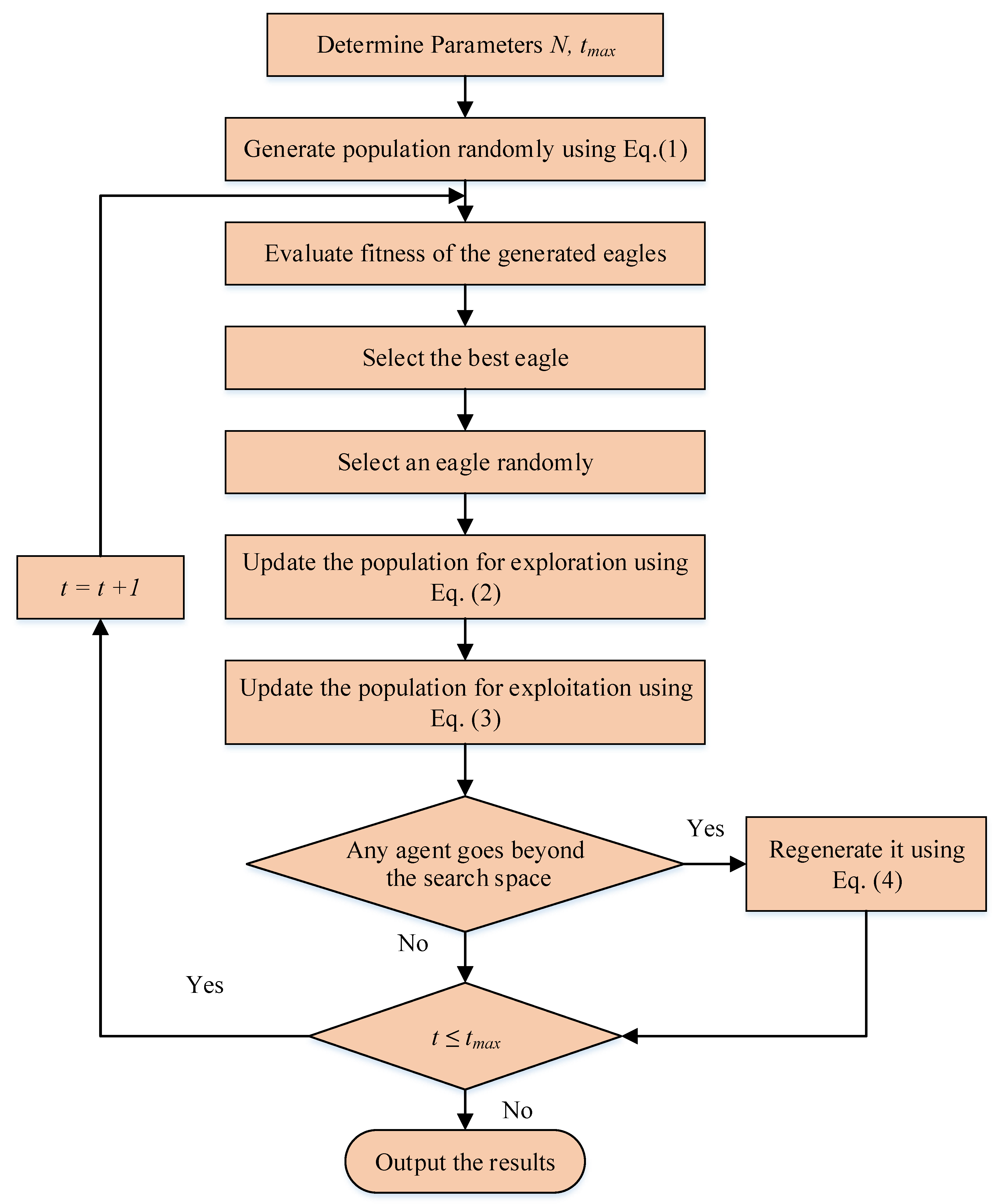
3. White-Tailed Eagle Algorithm (WEA)
3.1. Inspiration and Behavior of White-Tailed Eagles
3.2. Optimization Algorithm
| Algorithm 1. White-Tailed Eagle Algorithm (WEA) |
| Determine the parameters N, tMax Generate initial population of eagles using Equation (1) Evaluate eagles’ fitness Rank the eagles based on their fitness Consider the best eagle as t = 1 while t < tMax Update the position of each eagle based on Equation (2) Move each eagle toward the prey using Equation (3) Check if any eagle goes beyond the search space limit adjusts it Evaluate eagles’ fitness Rank the eagles based on their fitness Update t= t +1 end while Output the best solution |
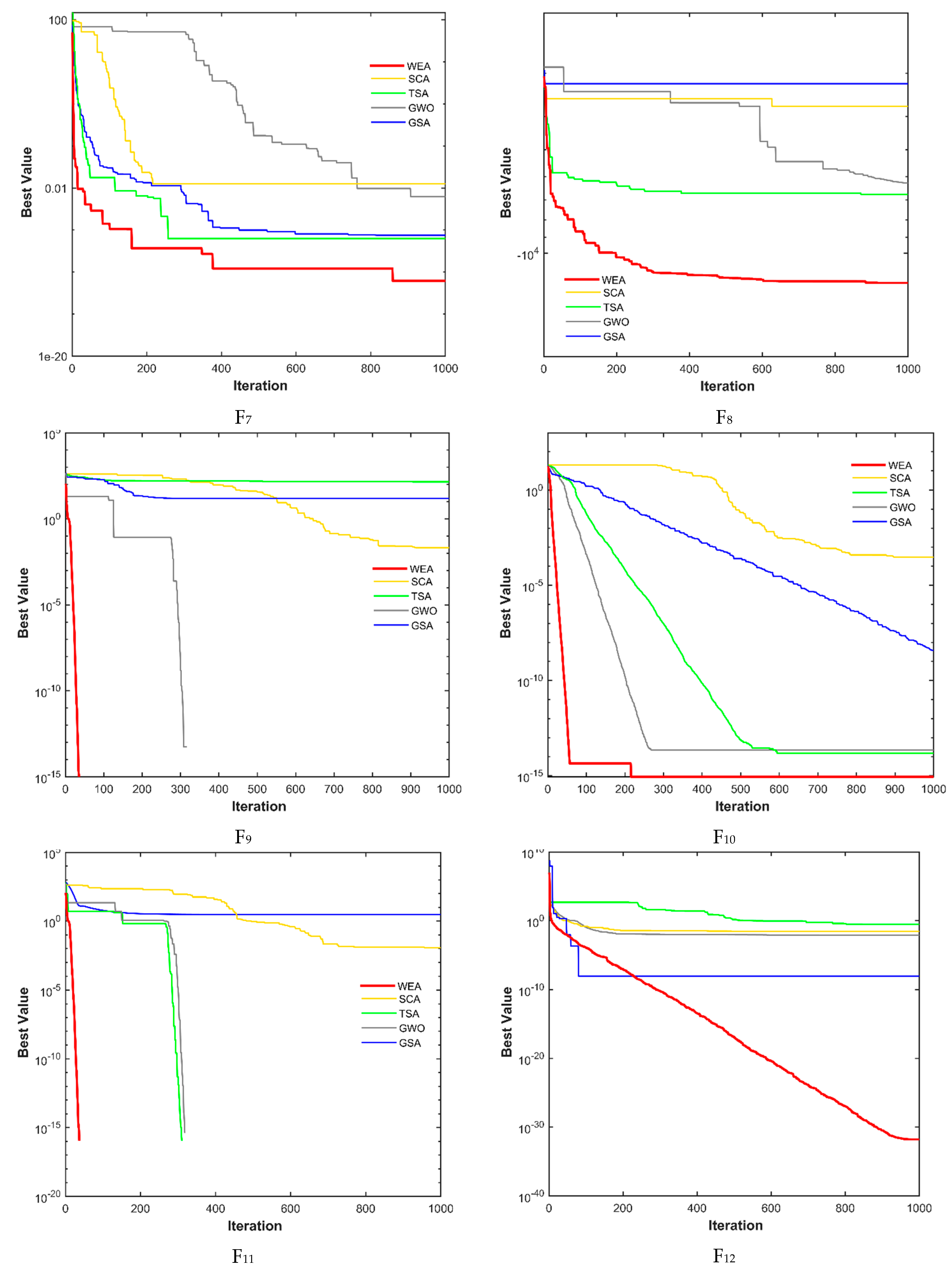
4. Comparative Analysis of the WEA
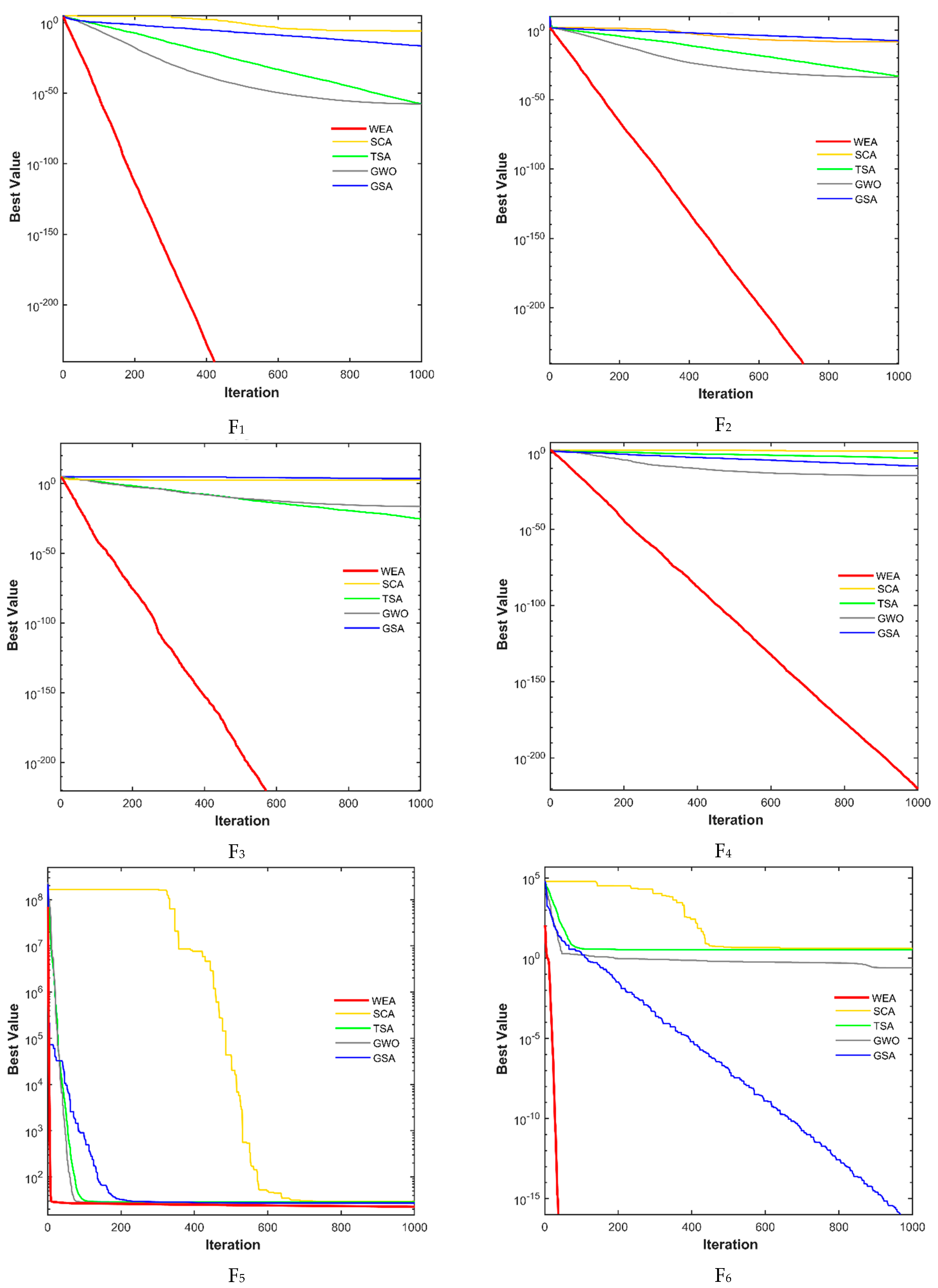
4.1. Exploitation Validation
4.2. Exploration Verification
4.3. Convergence Ability
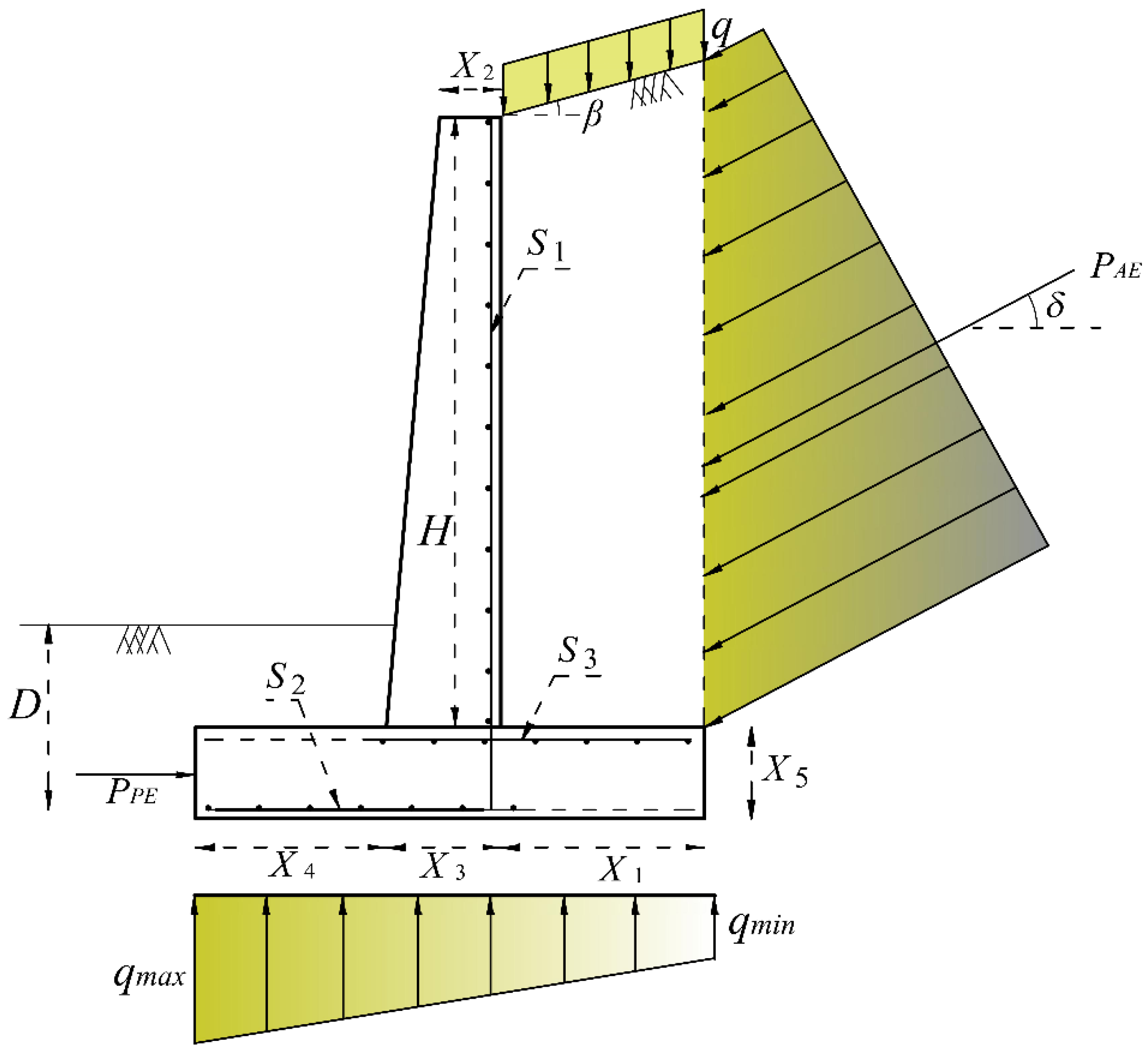
5. Retaining Structure Analysis
6. Optimization of Retaining Structure
6.1. Objective Function
6.2. Design Variables
6.3. Design Constraints
- Overturning Stability Constraint:where, FSOdesign is prescribed factors of safety against overturning.
- Sliding stability constraint:where, FSSdesign is prescribed factors of safety against sliding.
- Bearing capacity constraint:where, qu is the ultimate bearing capacity obtained by the Meyerhof Bearing Capacity Theory [90]; qmax is the maximum applied bearing stress. The maximum and minimum contact pressure are defined in the following equation:where, ∑V denotes the total vertical forces, B denotes the width of foundation, and e denotes the load’s eccentricity.
- No tension at the foundation:
- Moment capacity of toe, heel and bottom of stem:where, Mu is the ultimate bending moment, fc is the compressive concrete strength, and fy is the steel yield strength.
- Shear capacity of toe, heel, and stem:where, Vu is ultimate shearing force
- Limitation of flexural reinforcement:
7. Model Validation
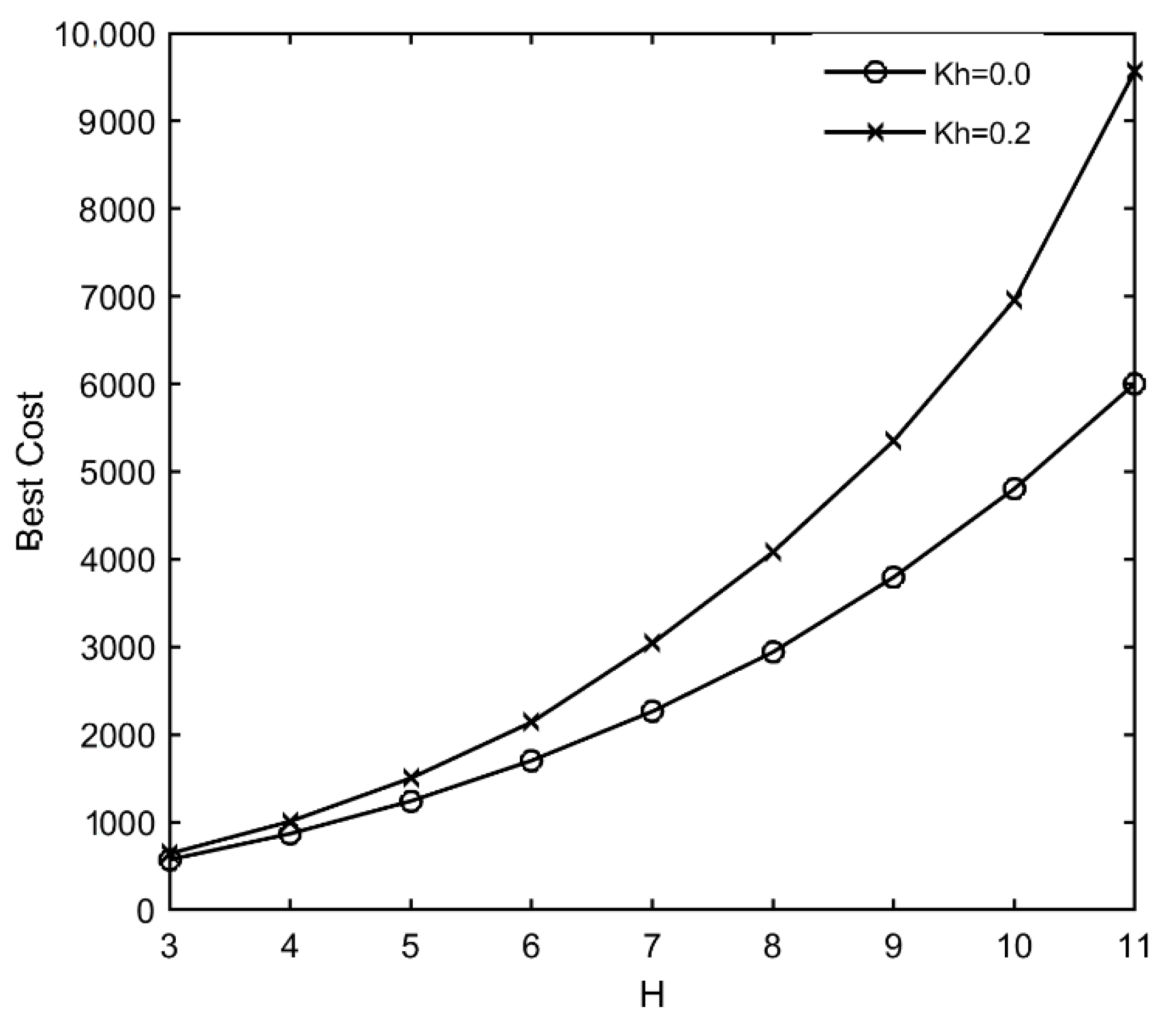
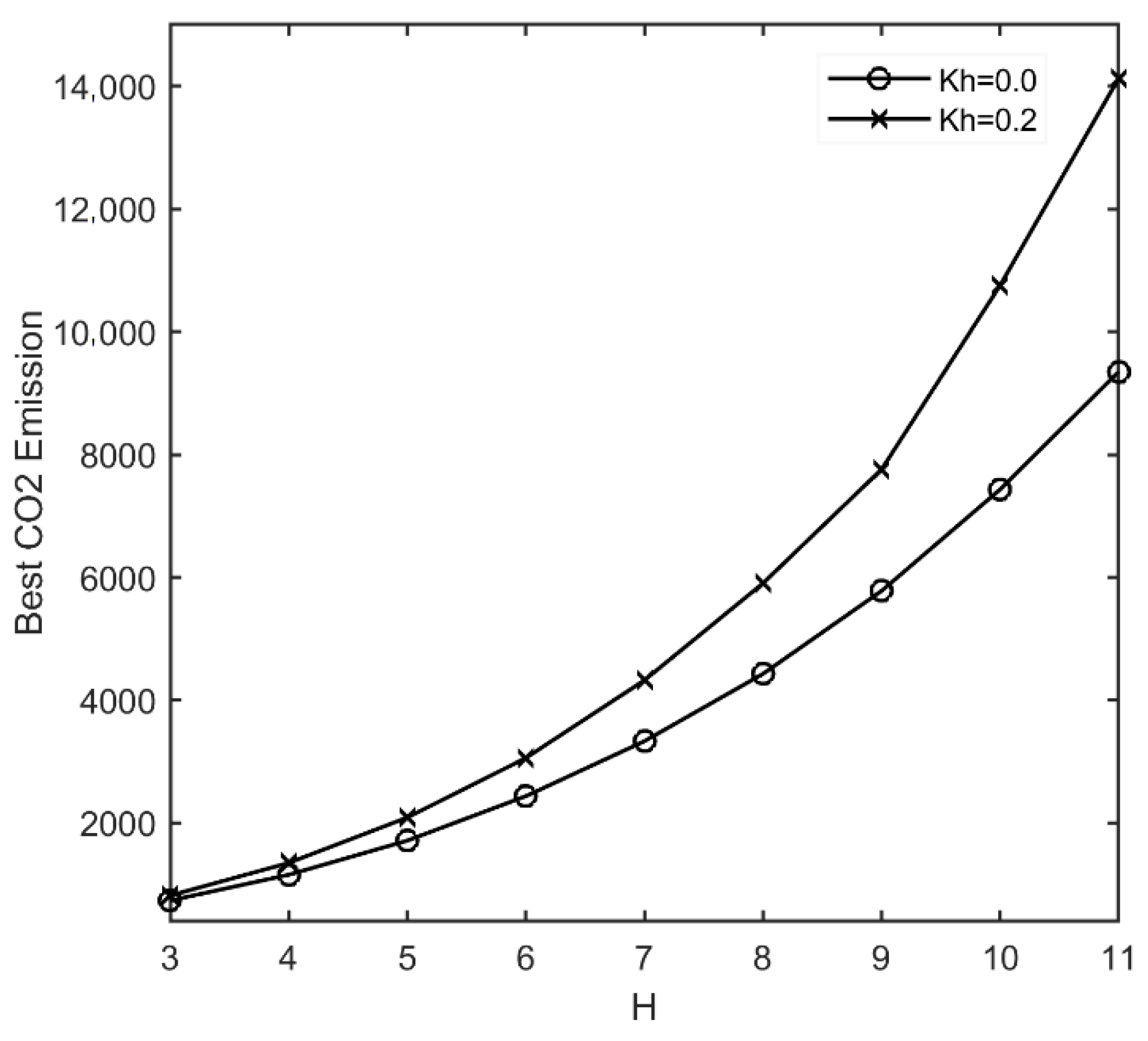
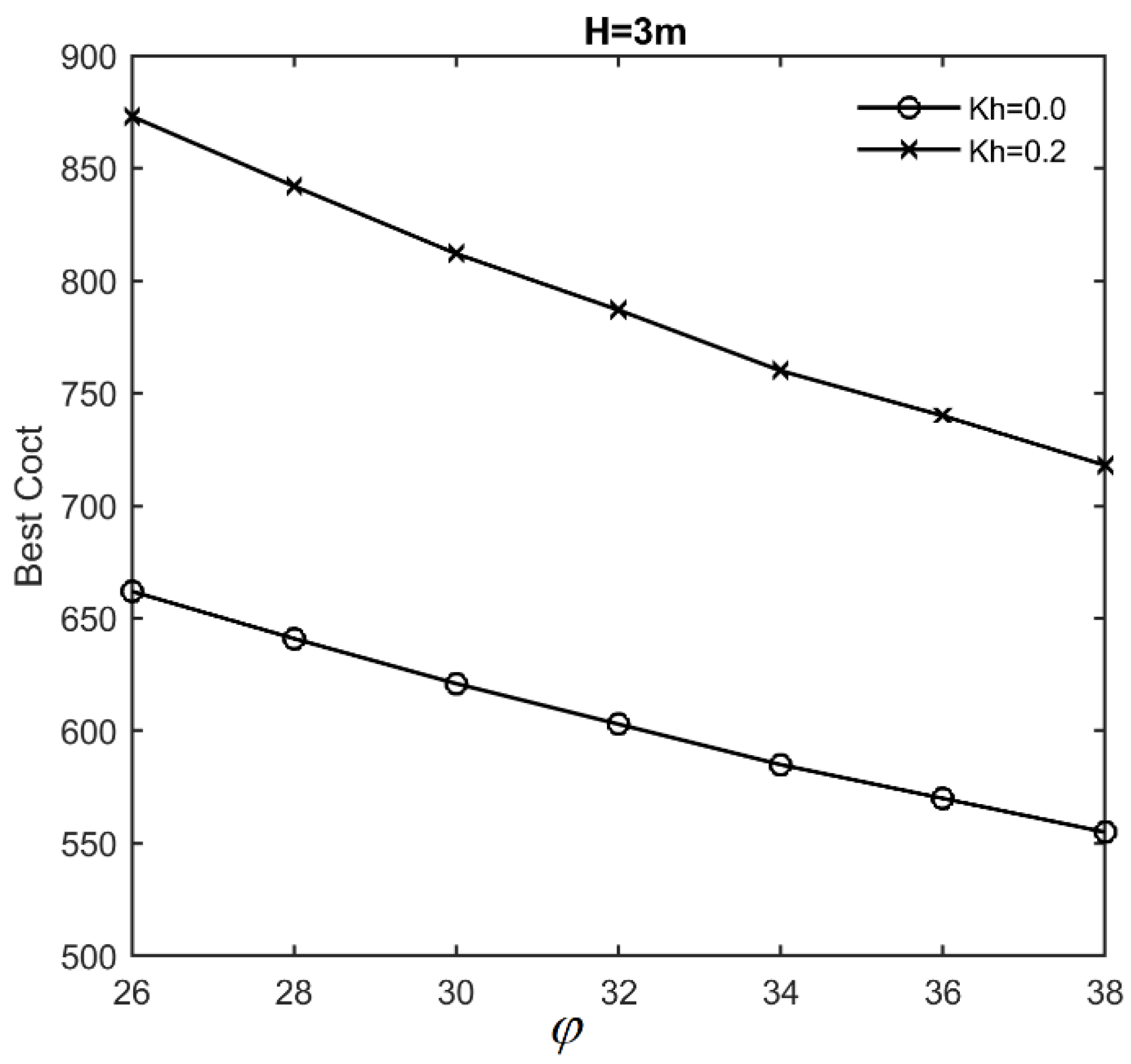
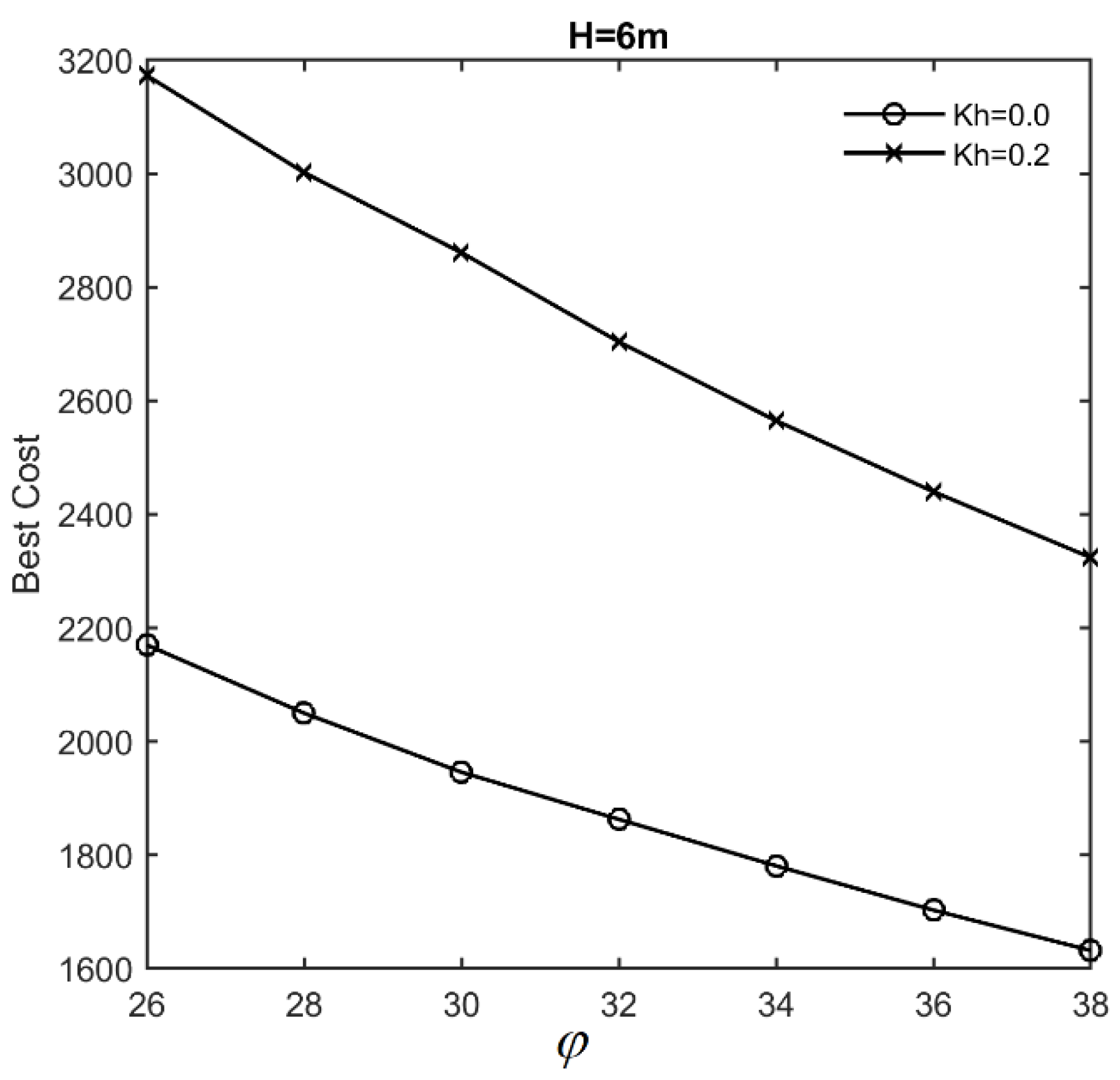
8. Model Application and Parametric Study
9. Conclusions and Further Research
- The major features of the WEA include its simplicity with just two main parameters, which are ease of coding and ease of implementation;
- Based on the statistical outcomes of the benchmark test problems, the WEA could produce either superior or relatively close results to other well-known competitors;
- Among thirteen considered benchmark problems, the new WEA reached the global optimum for six problems and in early iterations, indicating the robustness of the new method;
- The performance of the new algorithm for optimizing retaining structures subjected to both static and dynamic loading conditions indicates that the WEA design is nearly 5% less expensive than the previous approach;
- The numerical investigations show that, when compared to the other techniques, the newly proposed algorithm for the optimization of retaining structures is quite reliable and effective;
- Finally, seismic optimization results reveal that by increasing the horizontal acceleration coefficient to 0.2, the best cost and best CO2 emission designs will be increased by up to 12% and 11.1%, respectively.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Holland, J.H. Genetic algorithms. Sci. Am. 1992, 267, 66–73. [Google Scholar] [CrossRef]
- Dorigo, M.; Di Caro, G. Ant colony optimization: A new meta-heuristic. In Proceedings of the 1999 Congress on Evolutionary Computation—CEC99 (Cat. No. 99TH8406), Washington, DC, USA, 6–9 July 1999; pp. 1470–1477. [Google Scholar]
- Kennedy, J.; Eberhart, R. Particle swarm optimization. In Proceedings of the ICNN’95—International Conference on Neural Networks, Perth, WA, Australia, 27 November–1 December 1995; pp. 1942–1948. [Google Scholar]
- Cheng, Y.M.; Li, L.; Chi, S.-C.; Wei, W. Particle swarm optimization algorithm for the location of the critical non-circular failure surface in two-dimensional slope stability analysis. Comput. Geotech. 2007, 34, 92–103. [Google Scholar] [CrossRef]
- Zolfaghari, A.R.; Heath, A.C.; McCombie, P.F. Simple genetic algorithm search for critical non-circular failure surface in slope stability analysis. Comput. Geotech. 2005, 32, 139–152. [Google Scholar] [CrossRef]
- Angelo, J.S.; Bernardino, H.S.; Barbosa, H.J. Ant colony approaches for multiobjective structural optimization problems with a cardinality constraint. Adv. Eng. Softw. 2015, 80, 101–115. [Google Scholar] [CrossRef]
- Khajehzadeh, M.; Keawsawasvong, S.; Sarir, P.; Khailany, D.K. Seismic Analysis of Earth Slope Using a Novel Sequential Hybrid Optimization Algorithm. Period. Polytech. Civ. Eng. 2022, 66, 355–366. [Google Scholar] [CrossRef]
- Li, S.; Gong, W.; Gu, Q. A comprehensive survey on meta-heuristic algorithms for parameter extraction of photovoltaic models. Renew. Sustain. Energy Rev. 2021, 141, 110828. [Google Scholar] [CrossRef]
- Boussaïd, I.; Lepagnot, J.; Siarry, P. A survey on optimization metaheuristics. Inf. Sci. 2013, 237, 82–117. [Google Scholar] [CrossRef]
- Wolpert, D.H.; Macready, W.G. No free lunch theorems for optimization. IEEE Trans. Evol. Comput. 1997, 1, 67–82. [Google Scholar] [CrossRef]
- Catalonia Institute of Construction Technology. BEDEC PR/PCT ITEC Material Database; Catalonia Institute of Construction Technology: Barcelona, Spain, 2016. [Google Scholar]
- Yepes, V.; Gonzalez-Vidosa, F.; Alcala, J.; Villalba, P. CO2-optimization design of reinforced concrete retaining walls based on a VNS-threshold acceptance strategy. J. Comput. Civ. Eng. 2012, 26, 378–386. [Google Scholar] [CrossRef]
- Worrell, E.; Price, L.; Martin, N.; Hendriks, C.; Meida, L.O. Carbon dioxide emissions from the global cement industry. Annu. Rev. Energy Environ. 2001, 26, 303–329. [Google Scholar] [CrossRef]
- Paya-Zaforteza, I.; Yepes, V.; Hospitaler, A.; Gonzalez-Vidosa, F. CO2-optimization of reinforced concrete frames by simulated annealing. Eng. Struct. 2009, 31, 1501–1508. [Google Scholar] [CrossRef]
- Nelson, D.P. Cost and CO2 Optimization of Reinforced Concrete Beams using a Big Bang-Big Crunch Algorithm. Master’s Thesis, University of Memphis, Memphis, TN, USA, 2014. [Google Scholar]
- Camp, C.V.; Assadollahi, A. CO2and cost optimization of reinforced concrete footings using a hybrid big bang-big crunch algorithm. Struct. Multidiscip. Optim. 2013, 48, 411–426. [Google Scholar] [CrossRef]
- Yepes, V.; Martí, J.V.; García-Segura, T. Cost and CO2 emission optimization of precast–prestressed concrete U-beam road bridges by a hybrid glowworm swarm algorithm. Autom. Constr. 2015, 49, 123–134. [Google Scholar] [CrossRef]
- Beni, G.; Wang, J. Swarm intelligence in cellular robotic systems. In Robots and Biological Systems: Towards a New Bionics? Springer: Berlin/Heidelberg, Germany, 1993; pp. 703–712. [Google Scholar]
- Zhang, J.-R.; Zhang, J.; Lok, T.-M.; Lyu, M.R. A hybrid particle swarm optimization–back-propagation algorithm for feedforward neural network training. Appl. Math. Comput. 2007, 185, 1026–1037. [Google Scholar] [CrossRef]
- Khajehzadeh, M.; Taha, M.R.; El-Shafie, A.; Eslami, M. Modified particle swarm optimization for optimum design of spread footing and retaining wall. J. Zhejiang Univ.-Sci. A 2011, 12, 415–427. [Google Scholar] [CrossRef]
- Montalvo, I.; Izquierdo, J.; Pérez, R.; Tung, M.M. Particle swarm optimization applied to the design of water supply systems. Comput. Math. Appl. 2008, 56, 769–776. [Google Scholar] [CrossRef]
- Eslami, M.; Shareef, H.; Mohamed, A. Optimization and coordination of damping controls for optimal oscillations damping in multi-machine power system. Int. Rev. Electr. Eng. (IREE) 2011, 6, 1984–1993. [Google Scholar]
- Eslami, M.; Shareef, H.; Mohamed, A.; Khajehzadeh, M. Particle swarm optimization for simultaneous tuning of static var compensator and power system stabilizer. Przegląd Elektrotech. (Electr. Rev.) 2011, 87, 343–347. [Google Scholar]
- Liu, W.; Wang, Z.; Liu, X.; Zeng, N.; Bell, D. A novel particle swarm optimization approach for patient clustering from emergency departments. IEEE Trans. Evol. Comput. 2018, 23, 632–644. [Google Scholar] [CrossRef]
- Kahatadeniya, K.S.; Nanakorn, P.; Neaupane, K.M. Determination of the critical failure surface for slope stability analysis using ant colony optimization. Eng. Geol. 2009, 108, 133–141. [Google Scholar] [CrossRef]
- Xu, C.; Gordan, B.; Koopialipoor, M.; Armaghani, D.J.; Tahir, M.; Zhang, X. Improving performance of retaining walls under dynamic conditions developing an optimized ANN based on ant colony optimization technique. IEEE Access 2019, 7, 94692–94700. [Google Scholar] [CrossRef]
- Gao, W. Modified ant colony optimization with improved tour construction and pheromone updating strategies for traveling salesman problem. Soft Comput. 2021, 25, 3263–3289. [Google Scholar] [CrossRef]
- Karaboga, D.; Basturk, B. Artificial bee colony (ABC) optimization algorithm for solving constrained optimization problems. In Proceedings of the International Fuzzy Systems Association World Congress, Cancun, Mexico, 18–21 June 2007; pp. 789–798. [Google Scholar]
- Ozturk, H.T.; Durmus, A. Optimum cost design of RC columns using artificial bee colony algorithm. Struct. Eng. Mech. Int. J. 2013, 45, 643–654. [Google Scholar] [CrossRef]
- Akay, B.; Karaboga, D. Artificial bee colony algorithm for large-scale problems and engineering design optimization. J. Intell. Manuf. 2012, 23, 1001–1014. [Google Scholar] [CrossRef]
- Habib, H.U.R.; Subramaniam, U.; Waqar, A.; Farhan, B.S.; Kotb, K.M.; Wang, S. Energy cost optimization of hybrid renewables based V2G microgrid considering multi objective function by using artificial bee colony optimization. IEEE Access 2020, 8, 62076–62093. [Google Scholar] [CrossRef]
- Yang, X.S. Firefly algorithms for multimodal optimization. Lect. Notes Comput. Sci. 2009, 5792, 169–178. [Google Scholar]
- Khajehzadeh, M.; Taha, M.R.; Eslami, M. Opposition-based firefly algorithm for earth slope stability evaluation. China Ocean Eng. 2014, 28, 713–724. [Google Scholar] [CrossRef]
- Apostolopoulos, T.; Vlachos, A. Application of the firefly algorithm for solving the economic emissions load dispatch problem. Int. J. Comb. 2011, 2011, 523806. [Google Scholar] [CrossRef]
- Khurshaid, T.; Wadood, A.; Farkoush, S.G.; Kim, C.-H.; Yu, J.; Rhee, S.-B. Improved firefly algorithm for the optimal coordination of directional overcurrent relays. IEEE Access 2019, 7, 78503–78514. [Google Scholar] [CrossRef]
- Gandomi, A.H.; Alavi, A.H. Krill herd: A new bio-inspired optimization algorithm. Commun. Nonlinear Sci. Numer. Simul. 2012, 17, 4831–4845. [Google Scholar] [CrossRef]
- Askarzadeh, A. A novel metaheuristic method for solving constrained engineering optimization problems: Crow search algorithm. Comput. Struct. 2016, 169, 1–12. [Google Scholar] [CrossRef]
- Dhiman, G.; Garg, M.; Nagar, A.; Kumar, V.; Dehghani, M. A novel algorithm for global optimization: Rat swarm optimizer. J. Ambient Intell. Humaniz. Comput. 2020, 12, 8457–8482. [Google Scholar] [CrossRef]
- Khajehzadeh, M.; Keawsawasvong, S.; Nehdi, M.L. Effective hybrid soft computing approach for optimum design of shallow foundations. Sustainability 2022, 14, 1847. [Google Scholar] [CrossRef]
- Shehadeh, H.A.; Ahmedy, I.; Idris, M.Y.I. Sperm swarm optimization algorithm for optimizing wireless sensor network challenges. In Proceedings of the 6th International Conference on Communications and Broadband Networking, Singapore, 24–26 February 2018; pp. 53–59. [Google Scholar]
- Khajehzadeh, M.; Kalhor, A.; Tehrani, M.S.; Jebeli, M. Optimum design of retaining structures under seismic loading using adaptive sperm swarm optimization. Struct. Eng. Mech. 2022, 81, 93–102. [Google Scholar]
- Braik, M.S. Chameleon Swarm Algorithm: A bio-inspired optimizer for solving engineering design problems. Expert Syst. Appl. 2021, 174, 114685. [Google Scholar] [CrossRef]
- Fernandes, F.; Sousa, T.; Silva, M.; Morais, H.; Vale, Z.; Faria, P. Genetic algorithm methodology applied to intelligent house control. In Proceedings of the 2011 IEEE Symposium on Computational Intelligence Applications In Smart Grid (CIASG), Paris, France, 11–15 April 2011; pp. 1–8. [Google Scholar]
- Eslami, M.; Shareef, H.; Mohamed, A.; Khajehzadeh, M. Damping Controller Design for Power System Oscillations Using Hybrid GA-SQP. Int. Rev. Electr. Eng.-IREE 2011, 6, 888–896. [Google Scholar]
- Johnson, F.; Valderrama, A.; Valle, C.; Crawford, B.; Soto, R.; Ñanculef, R. Automating configuration of convolutional neural network hyperparameters using genetic algorithm. IEEE Access 2020, 8, 156139–156152. [Google Scholar] [CrossRef]
- Storn, R.; Price, K. Differential evolution a simple evolution strategy for fast optimization. Dr. Dobb’s J. 1997, 22, 18–24. [Google Scholar]
- Ilonen, J.; Kamarainen, J.-K.; Lampinen, J. Differential evolution training algorithm for feed-forward neural networks. Neural Process. Lett. 2003, 17, 93–105. [Google Scholar] [CrossRef]
- Goudos, S.K.; Siakavara, K.; Samaras, T.; Vafiadis, E.E.; Sahalos, J.N. Self-adaptive differential evolution applied to real-valued antenna and microwave design problems. IEEE Trans. Antennas Propag. 2011, 59, 1286–1298. [Google Scholar] [CrossRef]
- Maučec, M.S.; Brest, J.; Bošković, B. Improved differential evolution for large-scale black-box optimization. IEEE Access 2018, 6, 29516–29531. [Google Scholar] [CrossRef]
- Huang, X.; Xie, Y. Bidirectional evolutionary topology optimization for structures with geometrical and material nonlinearities. AIAA J. 2007, 45, 308–313. [Google Scholar] [CrossRef]
- Rad, M.M.; Ibrahim, S.K. Optimal plastic analysis and design of pile foundations under reliable conditions. Period. Polytech. Civ. Eng. 2021, 65, 761–767. [Google Scholar]
- Rad, M.M.; Habashneh, M.; Logo, J. Elasto-Plastic limit analysis of reliability based geometrically nonlinear bi-directional evolutionary topology optimization. In Structures; Elsevier: Amsterdam, The Netherlands, 2021; pp. 1720–1733. [Google Scholar]
- Habashneh, M.; Movahedi Rad, M. Reliability based geometrically nonlinear bi-directional evolutionary structural optimization of elasto-plastic material. Sci. Rep. 2022, 12, 5989. [Google Scholar] [CrossRef]
- Simon, D. Biogeography-based optimization. IEEE Trans. Evol. Comput. 2008, 12, 702–713. [Google Scholar] [CrossRef]
- Abd Elaziz, M.; Lu, S.; He, S. A multi-leader whale optimization algorithm for global optimization and image segmentation. Expert Syst. Appl. 2021, 175, 114841. [Google Scholar] [CrossRef]
- Jaderyan, M.; Khotanlou, H. Virulence optimization algorithm. Appl. Soft Comput. 2016, 43, 596–618. [Google Scholar] [CrossRef]
- Erol, O.K.; Eksin, I. A new optimization method: Big bang–big crunch. Adv. Eng. Softw. 2006, 37, 106–111. [Google Scholar] [CrossRef]
- Camp, C.V.; Akin, A. Design of retaining walls using big bang–big crunch optimization. J. Struct. Eng. 2012, 138, 438–448. [Google Scholar] [CrossRef]
- Sedighizadeh, M.; Esmaili, M.; Eisapour-Moarref, A. Voltage and frequency regulation in autonomous microgrids using Hybrid Big Bang-Big Crunch algorithm. Appl. Soft Comput. 2017, 52, 176–189. [Google Scholar] [CrossRef]
- Prayogo, D.; Cheng, M.-Y.; Wu, Y.-W.; Herdany, A.A.; Prayogo, H. Differential Big Bang-Big Crunch algorithm for construction-engineering design optimization. Autom. Constr. 2018, 85, 290–304. [Google Scholar] [CrossRef]
- Rashedi, E.; Nezamabadi-pour, H.; Saryazdi, S. GSA: A gravitational search algorithm. Inf. Sci. 2009, 179, 2232–2248. [Google Scholar] [CrossRef]
- Khajehzadeh, M.; Taha, M.R.; Eslami, M. Multi-objective optimization of foundation using global-local gravitational search algorithm. Struct. Eng. Mech.Int. J. 2014, 50, 257–273. [Google Scholar] [CrossRef]
- Khajehzadeh, M.; Taha, M.R.; Eslami, M. Multi-objective optimisation of retaining walls using hybrid adaptive gravitational search algorithm. Civ. Eng. Environ. Syst. 2014, 31, 229–242. [Google Scholar] [CrossRef]
- Rashedi, E.; Nezamabadi-Pour, H.; Saryazdi, S. Filter modeling using gravitational search algorithm. Eng. Appl. Artif. Intell. 2011, 24, 117–122. [Google Scholar] [CrossRef]
- Zhu, L.; He, S.; Wang, L.; Zeng, W.; Yang, J. Feature selection using an improved gravitational search algorithm. IEEE Access 2019, 7, 114440–114448. [Google Scholar] [CrossRef]
- Formato, R.A. Central force optimization: A new nature inspired computational framework for multidimensional search and optimization. In Nature Inspired Cooperative Strategies for Optimization (NICSO 2007); Springer: Berlin/Heidelberg, Germany, 2008; pp. 221–238. [Google Scholar]
- Hatamlou, A. Black hole: A new heuristic optimization approach for data clustering. Inf. Sci. 2013, 222, 175–184. [Google Scholar] [CrossRef]
- Moghaddam, F.F.; Moghaddam, R.F.; Cheriet, M. Curved space optimization: A random search based on general relativity theory. arXiv 2012, arXiv:1208.2214. [Google Scholar]
- Kaveh, A.; Khayatazad, M. A new meta-heuristic method: Ray optimization. Comput. Struct. 2012, 112, 283–294. [Google Scholar] [CrossRef]
- Mirjalili, S.; Mirjalili, S.M.; Hatamlou, A. Multi-verse optimizer: A nature-inspired algorithm for global optimization. Neural Comput. Appl. 2016, 27, 495–513. [Google Scholar] [CrossRef]
- Rao, R.V. Teaching-learning-based optimization algorithm. In Teaching Learning Based Optimization Algorithm; Springer: Berlin/Heidelberg, Germany, 2016; pp. 9–39. [Google Scholar]
- Rao, R.V.; Savsani, V.J.; Vakharia, D. Teaching–learning-based optimization: A novel method for constrained mechanical design optimization problems. Comput.-Aided Des. 2011, 43, 303–315. [Google Scholar] [CrossRef]
- Dede, T.; Togan, V. A teaching learning based optimization for truss structures with frequency constraints. Struct. Eng. Mech.Int. J. 2015, 53, 833–845. [Google Scholar] [CrossRef]
- Kumar, M.; Kulkarni, A.J.; Satapathy, S.C. Socio evolution & learning optimization algorithm: A socio-inspired optimization methodology. Future Gener. Comput. Syst. 2018, 81, 252–272. [Google Scholar]
- Atashpaz-Gargari, E.; Lucas, C. Imperialist competitive algorithm: An algorithm for optimization inspired by imperialistic competition. In Proceedings of the 2007 IEEE Congress on Evolutionary Computation, Singapore, 25–28 September 2007; pp. 4661–4667. [Google Scholar]
- Ghorbani, N.; Babaei, E. Exchange market algorithm. Appl. Soft Comput. 2014, 19, 177–187. [Google Scholar] [CrossRef]
- Moghdani, R.; Salimifard, K. Volleyball premier league algorithm. Appl. Soft Comput. 2018, 64, 161–185. [Google Scholar] [CrossRef]
- Uymaz, S.A.; Tezel, G.; Yel, E. Artificial algae algorithm (AAA) for nonlinear global optimization. Appl. Soft Comput. 2015, 31, 153–171. [Google Scholar] [CrossRef]
- Evans, R.J.; Wilson, J.D.; Amar, A.; Douse, A.; MacLennan, A.; Ratcliffe, N.; Whitfield, D.P. Growth and demography of a re-introduced population of White-tailed Eagles Haliaeetus albicilla. Ibis 2009, 151, 244–254. [Google Scholar] [CrossRef]
- Nadjafzadeh, M.; Hofer, H.; Krone, O. The link between feeding ecology and lead poisoning in white-tailed eagles. J. Wildl. Manag. 2013, 77, 48–57. [Google Scholar] [CrossRef]
- Nadjafzadeh, M.; Hofer, H.; Krone, O. Sit-and-wait for large prey: Foraging strategy and prey choice of White-tailed Eagles. J. Ornithol. 2016, 157, 165–178. [Google Scholar] [CrossRef]
- Olorunda, O.; Engelbrecht, A.P. Measuring exploration/exploitation in particle swarms using swarm diversity. In Proceedings of the 2008 IEEE congress on evolutionary computation (IEEE world congress on computational intelligence), Hong Kong, China, 1–6 June 2008; pp. 1128–1134. [Google Scholar]
- Patel, V.K.; Savsani, V.J. Heat transfer search (HTS): A novel optimization algorithm. Inf. Sci. 2015, 324, 217–246. [Google Scholar] [CrossRef]
- Digalakis, J.G.; Margaritis, K.G. On benchmarking functions for genetic algorithms. Int. J. Comput. Math. 2001, 77, 481–506. [Google Scholar] [CrossRef]
- Hussain, K.; Salleh, M.N.M.; Cheng, S.; Naseem, R. Common benchmark functions for metaheuristic evaluation: A review. JOIV Int. J. Inform. Vis. 2017, 1, 218–223. [Google Scholar] [CrossRef]
- Askari, Q.; Younas, I.; Saeed, M. Political Optimizer: A novel socio-inspired meta-heuristic for global optimization. Knowl. -Based Syst. 2020, 195, 105709. [Google Scholar] [CrossRef]
- Mirjalili, S.; Mirjalili, S.M.; Lewis, A. Grey wolf optimizer. Adv. Eng. Softw. 2014, 69, 46–61. [Google Scholar] [CrossRef]
- Das, B.M.; Luo, Z. Principles of Soil Dynamics; Cengage Learning: Boston, MA, USA, 2016. [Google Scholar]
- ACI Committee. Building Code Requirements for Structural Concrete (ACI 318-05); American Concrete Institute: Farmington Hills, MI, USA, 2005. [Google Scholar]
- Das, B.M.; Sobhan, K. Principles of Geotechnical Engineering, USA; Brooks/Cole-Thomson Learning Inc: Boston, MA, USA, 2002. [Google Scholar]
- Gandomi, A.; Kashani, A.; Zeighami, F. Retaining wall optimization using interior search algorithm with different bound constraint handling. Int. J. Numer. Anal. Methods Geomech. 2017, 41, 1304–1331. [Google Scholar] [CrossRef]
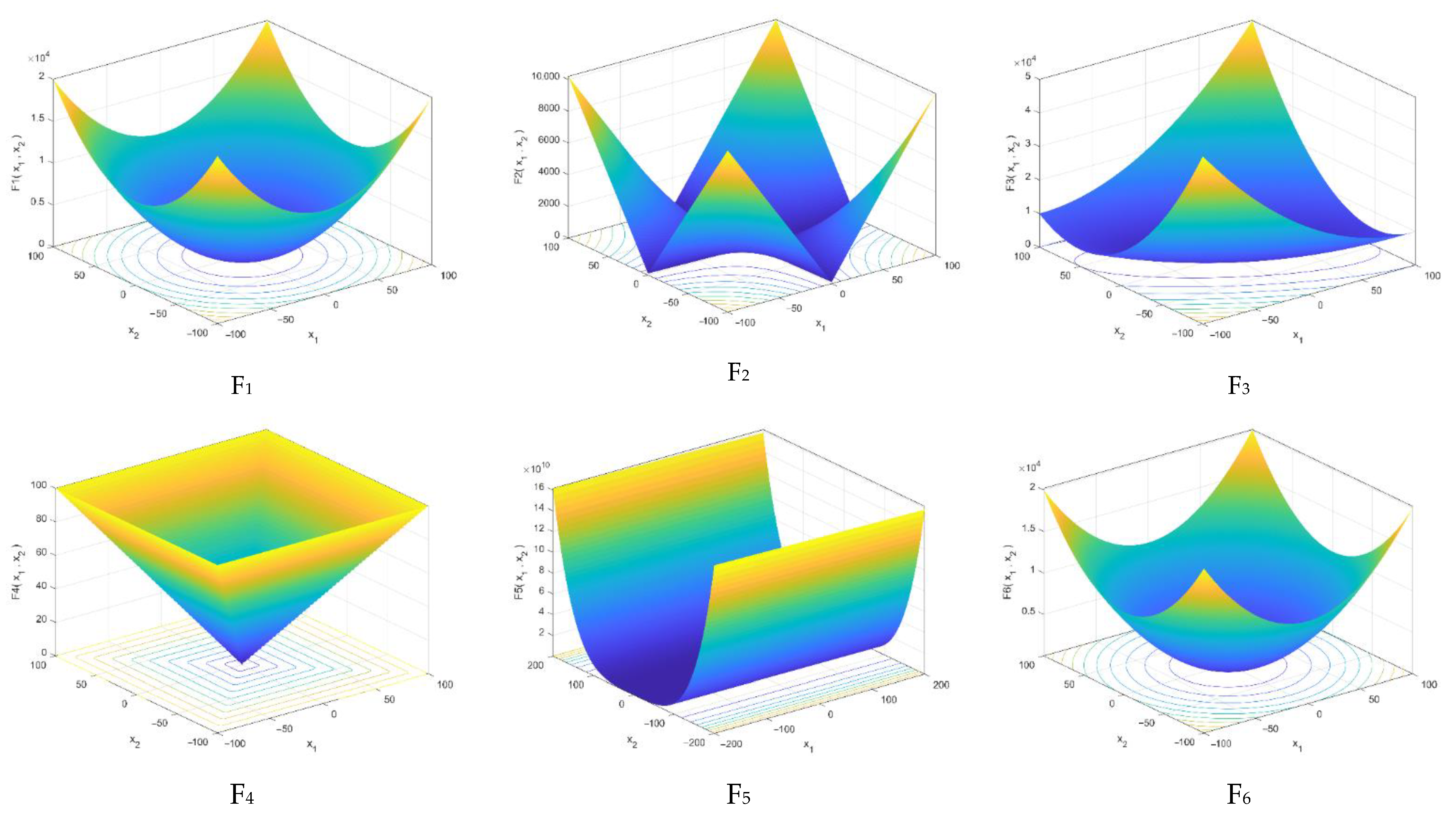





| Function | Range | n (Dim) | |
|---|---|---|---|
| 0 | 30 | ||
| 0 | 30 | ||
| 0 | 30 | ||
| 0 | 30 | ||
| 0 | 30 | ||
| 0 | 30 | ||
| 0 | 30 |
| Function | Range | n (Dim) | |
|---|---|---|---|
| 428.9829 × n | 30 | ||
| 0 | 30 | ||
| 0 | 30 | ||
| 0 | 30 | ||
| 0 | 30 | ||
| 0 | 30 |
| Algorithm (Year) | Parameter | Value |
|---|---|---|
| WEA (2022) | Number of eagles | 50 |
| Iterations’ Number | 1000 | |
| GSA (2009) | Agent’s Number | 50 |
| Gravitational constant | 100 | |
| Iterations’ Number | 1000 | |
| GWO (2014) | Agent’s Number | 50 |
| Control parameter | [2,0] | |
| Iterations’ Number | 1000 | |
| SCA (2016) | Agent’s Number | 50 |
| Number of elites | 2 | |
| Iterations’ Number | 1000 | |
| TSA (2020) | Agent’s Number | 50 |
| Iterations’ Number | 1000 |
| Fun. | Index | WEA | TSA | SCA | GSA | GWO |
|---|---|---|---|---|---|---|
| F1 | Min | 0.00 | 5.238 × 10−61 | 1.613 × 10−7 | 1.128 × 10−17 | 2.513 × 10−61 |
| Max | 0.00 | 1.218 × 10−54 | 2.931 × 10−3 | 3.243 × 10−17 | 3.754 × 10−58 | |
| Avg | 0.00 | 8.245 × 10−56 | 2.298 × 10−4 | 2.276 × 10−17 | 4.817 × 10−59 | |
| Med | 0.00 | 7.221 × 10−58 | 1.887 × 10−5 | 2.105 × 10−17 | 1.132 × 10−59 | |
| SD | 0.00 | 2.520 × 10−55 | 7.875 × 10−4 | 5.921 × 10−18 | 1.144 × 10−58 | |
| F2 | Min | 0.00 | 1.029 × 10−35 | 1.485 × 10−9 | 1.473 × 10−8 | 8.412 × 10−36 |
| Max | 0.00 | 3.321× 10−32 | 9.796 × 10−6 | 3.419 × 10−8 | 5.295 × 10−34 | |
| Avg | 0.00 | 2.233 × 10−33 | 1.732 × 10−6 | 2.465 × 10−8 | 8.421 × 10−35 | |
| Med | 0.00 | 3.224 × 10−34 | 5.342 × 10−7 | 2.497 × 10−8 | 5.891 × 10−35 | |
| SD | 0.00 | 6.133 × 10−33 | 2.316 × 10−6 | 3.898 × 10−9 | 9.789 × 10−35 | |
| F3 | Min | 0.00 | 2.575 × 10−32 | 70.8285 | 102.955 | 1.311 × 10−19 |
| Max | 0.00 | 2.452 × 10−17 | 267.0 | 468.616 | 3.499 × 10−13 | |
| Avg | 0.00 | 8.182 × 10−19 | 789.1620 | 245.469 | 1.488 × 10−14 | |
| Med | 0.00 | 1.871 × 10−24 | 619.4506 | 221.115 | 2.132 × 10−17 | |
| SD | 0.00 | 4.468 × 10−18 | 746.2287 | 100.102 | 6.612 × 10−14 | |
| F4 | Min | 6.02 × 10−224 | 3.318 × 10−8 | 1.2610 | 2.312 × 10−9 | 9.716 × 10−16 |
| Max | 3.82 × 10−218 | 6.419 × 10−5 | 35.6743 | 5.123 × 10−9 | 2.332 × 10−13 | |
| Avg | 6.27 × 10−219 | 1.222 × 10−5 | 9.3080 | 3.221 × 10−9 | 1.872 × 10−14 | |
| Med | 7.98 × 10−220 | 2.110 × 10−6 | 6.9806 | 3.191 × 10−9 | 6.412 × 10−15 | |
| SD | 0.00 | 1.717 × 10−5 | 8.0720 | 7.398 × 10−10 | 4.886 × 10−14 | |
| F5 | Min | 22.441 | 25.6273 | 27.3230 | 25.745 | 25.2273 |
| Max | 22.945 | 29.5430 | 49.5110 | 220.911 | 28.7294 | |
| Avg | 22.646 | 28.4422 | 29.9106 | 42.2647 | 26.9256 | |
| Med | 22.624 | 28.8115 | 29.0097 | 26.1443 | 27.1173 | |
| SD | 0.163 | 0.7616 | 4.1508 | 45.4674 | 0.8418 | |
| F6 | Min | 0.00 | 2.0585 | 3.4070 | 9.669 × 10−18 | 0.2466 |
| Max | 0.00 | 4.7791 | 4.4435 | 8.712 × 10−16 | 1.2619 | |
| Avg | 0.00 | 3.6724 | 4.0360 | 3.123 × 10−17 | 0.6376 | |
| Med | 0.00 | 3.5615 | 4.0572 | 2.889 × 10−17 | 0.7452 | |
| SD | 0.00 | 0.6918 | 0.2954 | 6.214 × 10−18 | 0.3353 | |
| F7 | Min | 9.764 × 10−6 | 6.711 × 10−4 | 0.0015 | 0.0061 | 1.492 × 10−4 |
| Max | 1.459 × 10−4 | 0.0036 | 0.0431 | 0.0462 | 2.132 × 10−3 | |
| Avg | 5.385 × 10−5 | 0.0018 | 0.0116 | 0.0237 | 7.885 × 10−4 | |
| Med | 5.271 × 10−5 | 0.0018 | 0.0078 | 0.0222 | 7.111 × 10−4 | |
| SD | 3.772 × 10−5 | 7.726 × 10−4 | 0.0101 | 0.0098 | 4.711 × 10−4 |
| Fun. | Index | WEA | TSA | SCA | GSA | GWO |
|---|---|---|---|---|---|---|
| F8 | Min | −1.242 × 104 | −7.776 × 103 | −5.341 × 103 | −3.713 × 103 | −8.964 × 103 |
| Max | −1.182 × 104 | −5.324 × 103 | −3.449 × 103 | −2.122 × 103 | −4.888 × 103 | |
| Avg | −1.204 × 104 | −6.598 × 103 | −4.143 × 103 | −2.654 × 103 | −6.161 × 103 | |
| Med | −1.193 × 104 | −6.599 × 103 | −3.886 × 103 | −2.854 × 103 | −6.155 × 103 | |
| SD | 88.432 | 600.1324 | 341.645 | 359.543 | 848.243 | |
| F9 | Min | 0.00 | 77.7761 | 1.0560 × 10−6 | 8.9546 | 0.00 |
| Max | 0.00 | 254.9883 | 51.4451 | 21.8891 | 10.0548 | |
| Avg | 0.00 | 151.4539 | 5.9694 | 15.6209 | 0.8853 | |
| Med | 0.00 | 149.6596 | 9.3391 × 10−4 | 15.9193 | 0.00 | |
| SD | 0.00 | 35.8717 | 12.2476 | 3.1043 | 2.4438 | |
| F10 | Min | 8.882 × 10−16 | 1.5099 × 10−14 | 1.5579 × 10−5 | 2.612 × 10−9 | 1.321 × 10−14 |
| Max | 4.441 × 10−15 | 4.3125 | 20.2198 | 4.325 × 10−9 | 2.314 × 10−14 | |
| Avg | 2.664 × 10−15 | 2.4095 | 14.3622 | 3.513 × 10−9 | 1.623 × 10−14 | |
| Med | 2.664 × 10−15 | 2.9381 | 20.1275 | 3.524 × 10−9 | 1.445 × 10−14 | |
| SD | 1.872 × 10−15 | 1.3920 | 8.9778 | 5.211 × 10−10 | 2.643 × 10−15 | |
| F11 | Min | 0.00 | 0.00 | 4.8381 × 10−7 | 1.6952 | 0.00 |
| Max | 0.00 | 0.0159 | 0.7703 | 10.6642 | 0.0140 | |
| Avg | 0.00 | 0.0077 | 0.1368 | 4.2510 | 0.0014 | |
| Med | 0.00 | 0.0082 | 0.0032 | 3.5667 | 0.00 | |
| SD | 0.00 | 0.0057 | 0.2218 | 2.0234 | 0.0041 | |
| F12 | Min | 1.571 × 10−32 | 0.2738 | 0.2631 | 8.203 × 10−2 | 0.0121 |
| Max | 1.909 × 10−32 | 13.8088 | 5.6300 | 0.1037 | 0.0920 | |
| Avg | 1.626 × 10−32 | 6.3735 | 0.9568 | 0.0198 | 0.0364 | |
| Med | 1.578 × 10−32 | 6.7411 | 0.4964 | 1.3512 | 0.0329 | |
| SD | 1.086 × 10−33 | 3.4586 | 1.1497 | 0.0400 | 0.0201 | |
| F13 | Min | 1.342 × 10−32 | 1.7796 | 1.8452 | 1.291 × 10−18 | 0.1006 |
| Max | 2.046 × 10−31 | 4.1077 | 22.5849 | 0.022 | 1.0416 | |
| Avg | 6.44 × 10−32 | 2.8976 | 3.4211 | 7.198 × 10−4 | 0.5280 | |
| Med | 3.075 × 10−32 | 2.8914 | 2.3552 | 2.034 × 10−18 | 0.5238 | |
| SD | 7.528 × 10−32 | 0.6436 | 3.9911 | 3.011 × 10−3 | 0.2359 |
| Item | Notaition | Unit | CO2 Emission | Unit Cost |
|---|---|---|---|---|
| Excavation | Ve | m3 | 13.16 Kg | 11.41 $ |
| Formwork | Af | m2 | 31.66 Kg | 37.08 $ |
| Reinforcement | Wst | kg | 2.82 Kg | 1.51 $ |
| Backfill | Vb | m3 | 27.20 Kg | 38.10 $ |
| Concrete | Vc | m3 | 224.34 Kg | 99.49 $ |
| Parameter | Unit | Symbol | Value |
|---|---|---|---|
| Height of stem | m | H | 3.0 |
| Internal friction angle of retained soil | degree | φ | 36 |
| Internal friction angle of base soil | degree | φ’ | 0.0 |
| Unit weight of retained soil | kN/m3 | γs | 17.5 |
| Unit weight of base soil | kN/m3 | γ’s | 18.5 |
| Unit weight of concrete | kN/m3 | γc | 23.5 |
| Unit weight of steel | kN/m3 | γsteel | 78.5 |
| Cohesion of base soil | kPa | c | 125 |
| Depth of soil in front of wall | m | D | 0.5 |
| Surcharge load | kPa | q | 20 |
| Backfill slop | degree | 𝛽 | 10 |
| Concrete cover | cm | dc | 7.0 |
| Yield strength of reinforcing steel | MPa | fy | 400 |
| Compressive strength of concrete | MPa | fc | 21 |
| Shrinkage and temporary reinforcement percent | - | ρst | 0.002 |
| Design load factor | - | LF | 1.7 |
| Factor of safety for overturning stability | - | FSO | 1.5 |
| Factor of safety against sliding | - | FSS | 1.5 |
| Factor of safety for bearing capacity | - | FSB | 3.0 |
| Design Variable | Unit | Optimum Values WEA (Current Study) | Optimum Values BB-BC [58] | Optimum Values ISA [91] |
|---|---|---|---|---|
| heel’s width (X1) | m | 0.65 | 0.8732 | 0.8023 |
| top stem thickness (X2) | m | 0.2 | 0.2 | 0.2 |
| bottom stem thickness (X3) | m | 0.272 | 0.2678 | 0.2875 |
| toe’s width (X4) | m | 0.68 | 0.6017 | 0.7536 |
| base slab’s thickness (X5) | m | 0.2722 | 0.2722 | 0.27 |
| stem’s vertical reinforcement (S1) | cm2/m | 12 | 12 | 13 |
| toe’s horizontal reinforcement (S2) | cm2/m | 8 | 8 | 7 |
| heel’s horizontal reinforcement (S3) | cm2/m | 8 | 8 | 7 |
| Best Cost | $/m | 68.76 | 70.96 | 73.05 |
| Case No. | Case 1 | Case 2 | Case 3 | Case 4 | Case 5 | Case 6 |
|---|---|---|---|---|---|---|
| Kh | 0.0 | 0.1 | 0.1 | 0.2 | 0.2 | 0.2 |
| KV | 0.0 | 0.0 | 0.1 | 0.0 | 0.1 | 0.2 |
| Design Variable | Unit | Optimum Values Case 1 | Optimum Values Case 2 | Optimum Values Case 3 | Optimum Values Case 4 | Optimum Values Case 5 | Optimum Values Case 6 |
|---|---|---|---|---|---|---|---|
| X1 | m | 0.5513 | 0.6539 | 0.613 | 0.7923 | 0.7887 | 0.7672 |
| X2 | m | 0.2 | 0.2 | 0.2 | 0.2 | 0.2 | 0.2 |
| X3 | m | 0.3567 | 0.0.3743 | 0.3686 | 0.3617 | 0.3364 | 0.3387 |
| X4 | m | 0.7778 | 0.7632 | 0.7778 | 0.7778 | 0.7778 | 0.7778 |
| X5 | m | 0.2727 | 0.2847 | 0.2821 | 0.2995 | 0.2997 | 0.2921 |
| S1 | cm2/m | 8 | 8 | 8 | 9 | 9 | 8 |
| S2 | cm2/m | 8 | 9 | 8 | 11 | 10 | 10 |
| S3 | cm2/m | 8 | 9 | 10 | 11 | 10 | 10 |
| Best Cost | $/m | 572.74 | 599.3 | 593.1 | 641.3 | 631.91 | 622.73 |
| Design Variable | Unit | Optimum Values Case 1 | Optimum Values Case 2 | Optimum Values Case 3 | Optimum Values Case 4 | Optimum Values Case 5 | Optimum Values Case 6 |
|---|---|---|---|---|---|---|---|
| X1 | m | 0.6074 | 0.7113 | 0.6835 | 0.862 | 0.7993 | 0.7825 |
| X2 | m | 0.2 | 0.2 | 0.2 | 0.2 | 0.2 | 0.2 |
| X3 | m | 0.2929 | 0.304 | 0.3064 | 0.2841 | 0.3251 | 0.32 |
| X4 | m | 0.7631 | 0.7635 | 0.75 | 0.7735 | 0.7777 | 0.7778 |
| X5 | m | 0.2728 | 0.2775 | 0.2734 | 0.2907 | 0.2928 | 0.2901 |
| S1 | cm2/m | 10 | 10 | 10 | 11 | 9 | 9 |
| S2 | cm2/m | 8 | 9 | 9 | 11 | 10 | 10 |
| S3 | cm2/m | 8 | 9 | 9 | 11 | 10 | 10 |
| Best CO2 | kg/m | 740.1 | 773.33 | 762.09 | 822.35 | 812.35 | 805.11 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Arandian, B.; Iraji, A.; Alaei, H.; Keawsawasvong, S.; Nehdi, M.L. White-Tailed Eagle Algorithm for Global Optimization and Low-Cost and Low-CO2 Emission Design of Retaining Structures. Sustainability 2022, 14, 10673. https://doi.org/10.3390/su141710673
Arandian B, Iraji A, Alaei H, Keawsawasvong S, Nehdi ML. White-Tailed Eagle Algorithm for Global Optimization and Low-Cost and Low-CO2 Emission Design of Retaining Structures. Sustainability. 2022; 14(17):10673. https://doi.org/10.3390/su141710673
Chicago/Turabian StyleArandian, Behdad, Amin Iraji, Hossein Alaei, Suraparb Keawsawasvong, and Moncef L. Nehdi. 2022. "White-Tailed Eagle Algorithm for Global Optimization and Low-Cost and Low-CO2 Emission Design of Retaining Structures" Sustainability 14, no. 17: 10673. https://doi.org/10.3390/su141710673
APA StyleArandian, B., Iraji, A., Alaei, H., Keawsawasvong, S., & Nehdi, M. L. (2022). White-Tailed Eagle Algorithm for Global Optimization and Low-Cost and Low-CO2 Emission Design of Retaining Structures. Sustainability, 14(17), 10673. https://doi.org/10.3390/su141710673









