A Modified SWAT Model to Simulate Soil Water Content and Soil Temperature in Cold Regions: A Case Study of the South Saskatchewan River Basin in Canada
Abstract
:1. Introduction
2. Materials and Methods
2.1. Study Area
2.2. Data Description
3. Methodology
4. Results
4.1. Model Sensitivity Analysis
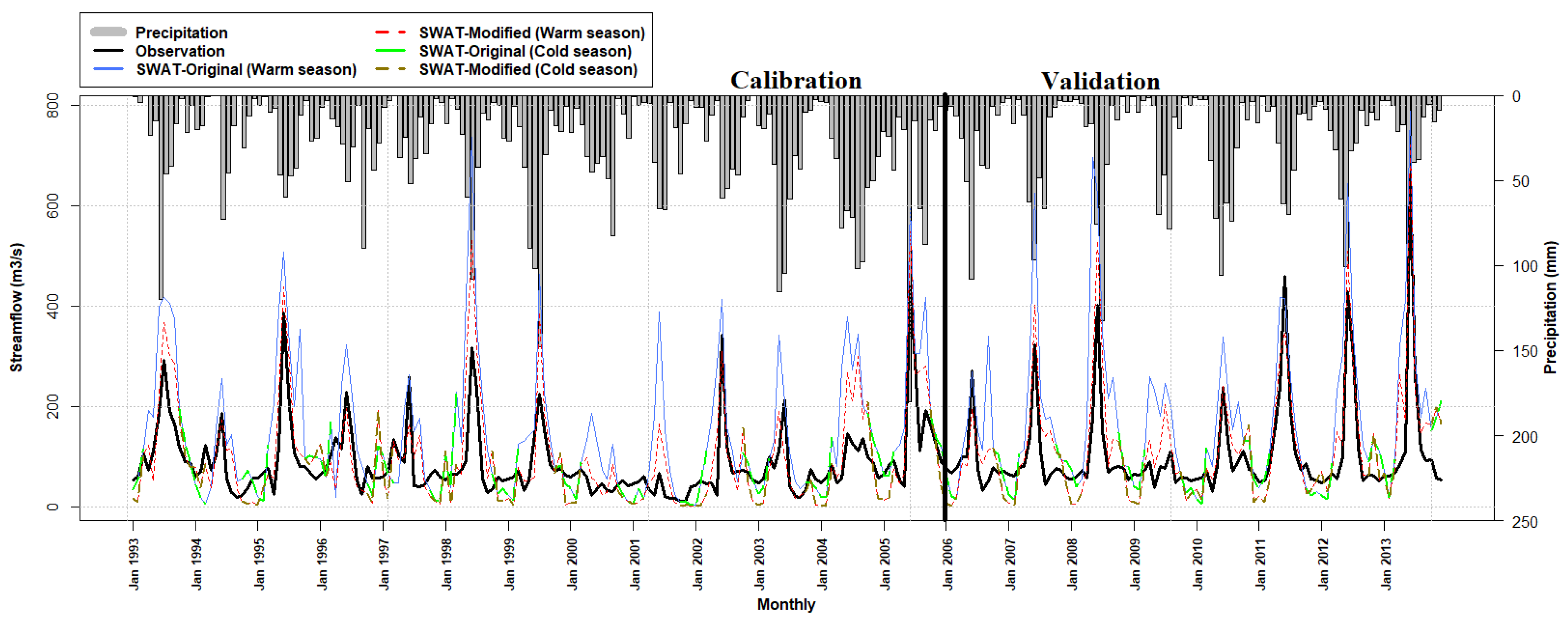
4.2. Calibration and Validation
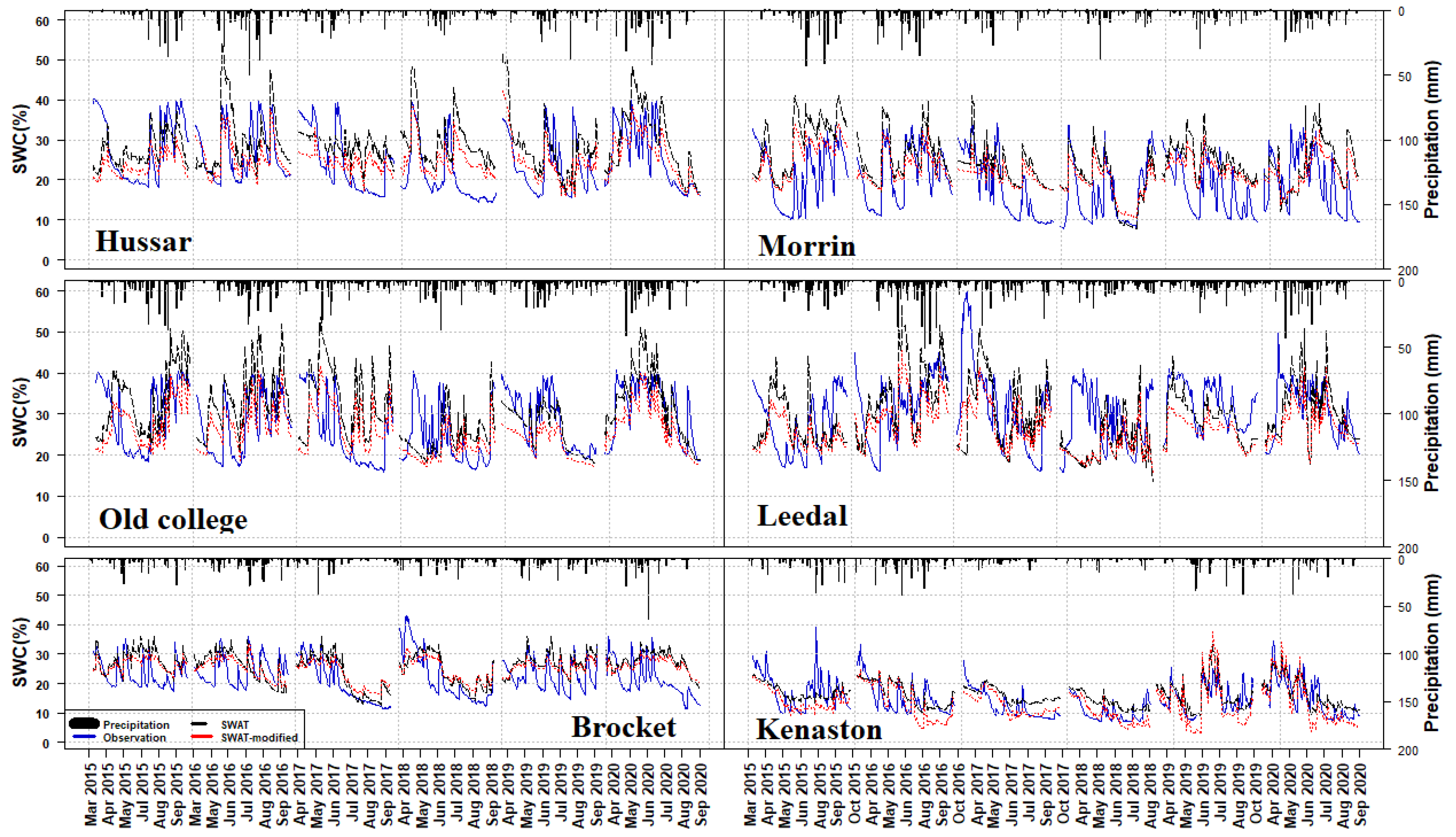
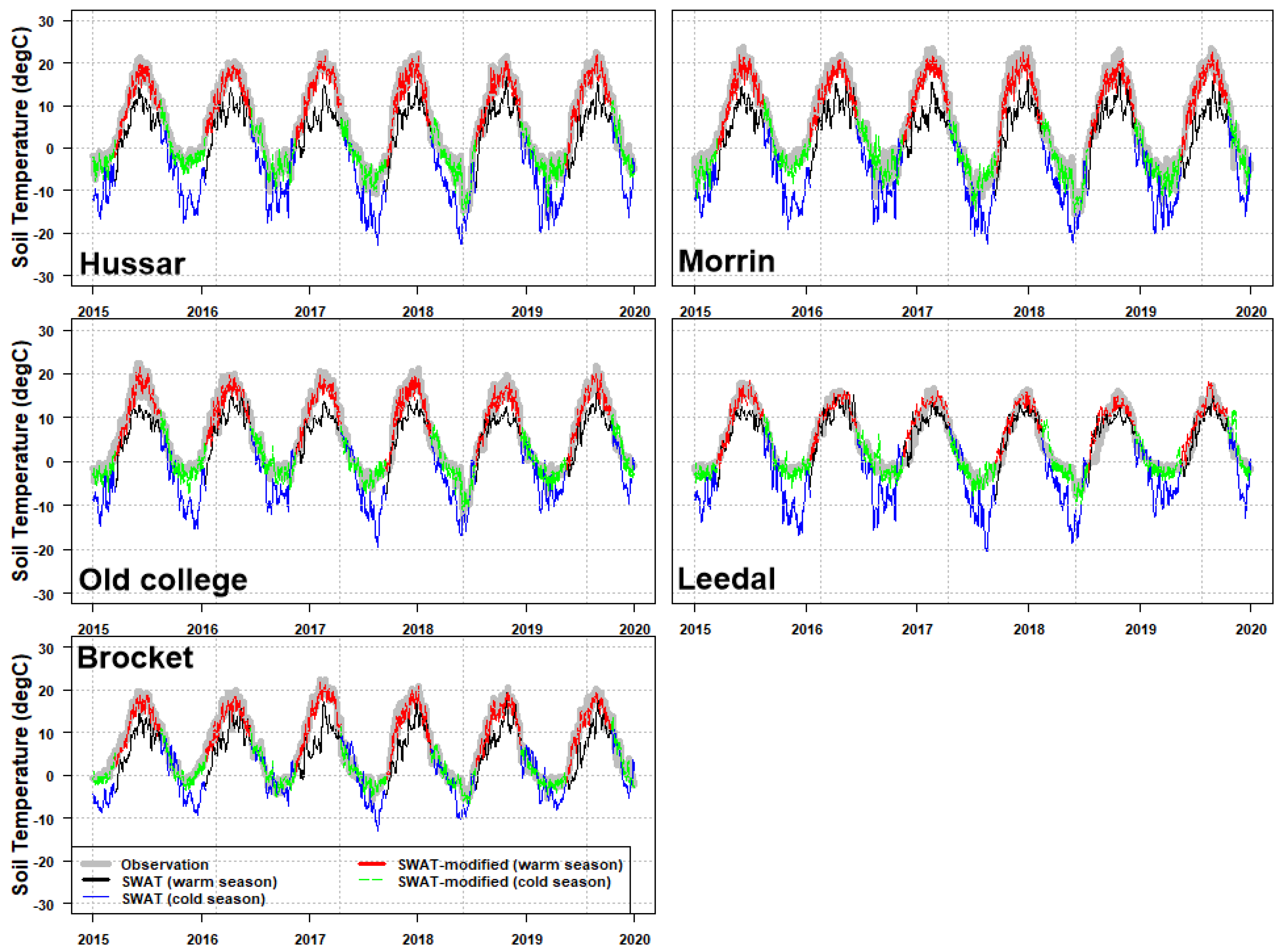
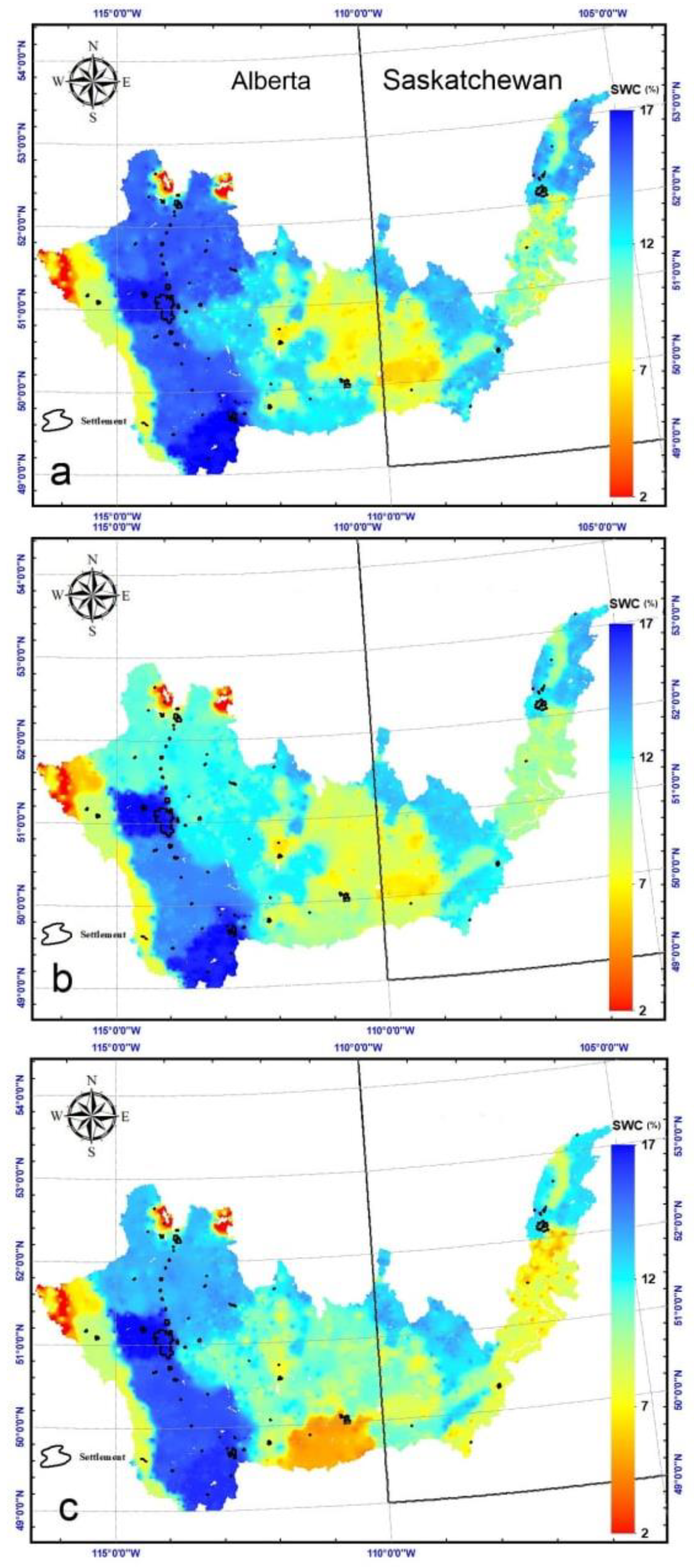
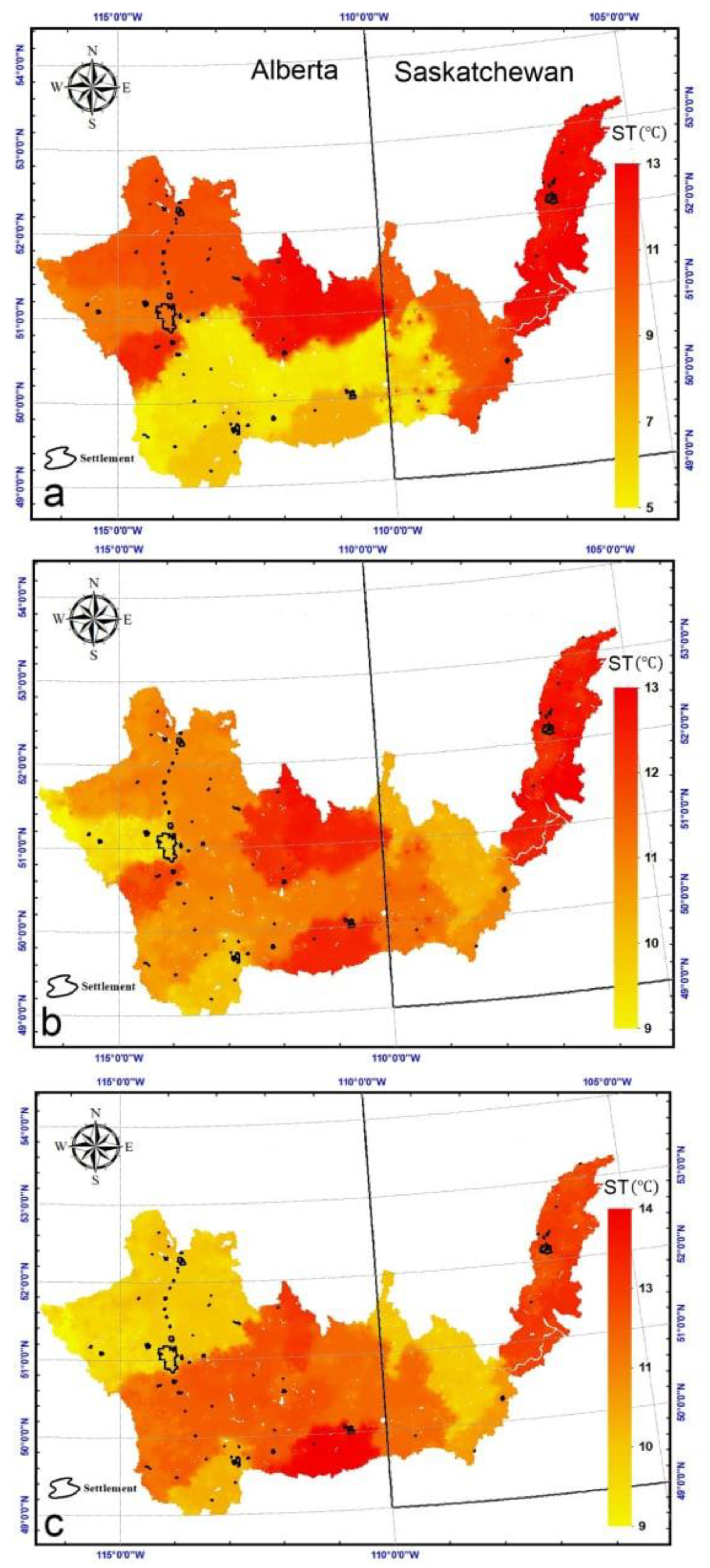
4.3. Spatial Pattern of SWC and Soil Temperature
5. Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Qi, J.; Zhang, X.; Cosh, M.H. Modeling soil temperature in a temperate region: A comparison between empirical and physically based methods in SWAT. Ecol. Eng. 2019, 129, 134–143. [Google Scholar] [CrossRef]
- Zare, M.; Azam, S.; Sauchyn, D. Evaluation of Soil Water Content Using SWAT for Southern Saskatchewan, Canada. Water 2022, 14, 249. [Google Scholar] [CrossRef]
- Park, J.Y.; Ahn, S.R.; Hwang, S.J.; Jang, C.H.; Park, G.A.; Kim, S.J. Evaluation of MODIS NDVI and LST for indicating soil moisture of forest areas based on SWAT modeling. Pad. Water Environ. Eng. 2014, 121, 77–88. [Google Scholar] [CrossRef]
- Yang, Y.T.; Roderick, M.L.; Zhang, S.L.; McVicar, T.R.; Donohue, R.J. Hydrologic implications of vegetation response to elevated CO2 in climate projections. Nat. Clim. Chang. 2019, 9, 44–49. [Google Scholar] [CrossRef]
- Koerselman, W.; Van Kerkhoven, M.B.; Verhoeven, J.T. Release of inorganic N, P and K in peat soils; effect of temperature, water chemistry and water level. Biogeochemistry 1993, 20, 63–81. [Google Scholar] [CrossRef]
- Stoller, E.W.; Wax, L.M. Temperature variations in the surface layers of an agricultural soil. Weed Res. 1973, 13, 273–282. [Google Scholar] [CrossRef]
- Wheater, H.S.; Gober, P.A. Water security in the Canadian Prairies: Science and management challenges. Philos. Trans. R. Soc. 2013, 371, 20120409. [Google Scholar] [CrossRef]
- Chipanshi, A.C.; Findlater, K.M.; Hadwen, T.; O’Brien, E.G. Analysis of consecutive droughts on the Canadian prairies. Clim. Res. 2006, 30, 175–187. [Google Scholar] [CrossRef]
- Bonsal, B.R.; Wheaton, E.E.; Chipanshi, A.C.; Lin, C.; Sauchyn, D.J.; Wen, L. Drought research in Canada: A review. Atmos. Ocean 2011, 49, 303–319. [Google Scholar] [CrossRef]
- Sauchyn, D.; Ilich, N. Nine Hundred Years of Weekly Streamflows: Stochastic Downscaling of Ensemble Tree-Ring Reconstructions. Water Resour. Res. 2017, 53, 9266–9283. [Google Scholar] [CrossRef] [Green Version]
- Bonsal, B.; Aider, R.; Gachon, P.; Lapp, S. An assessment of Canadian prairie drought: Past, present, and future. Clim. Dyn. 2013, 41, 501–516. [Google Scholar] [CrossRef]
- Masud, M.B.; Khaliq, M.N.; Wheater, H.S. Analysis of meteorological droughts for the Saskatchewan River basin using univariate and bivariate approaches. J. Hydrol. 2015, 522, 452–466. [Google Scholar] [CrossRef]
- Arnold, J.G.; Moriasi, D.N.; Gassman, P.W.; Abbaspour, K.C.; White, M.J.; Srinivasan, R.; Santhi, C.; Harmel, R.D.; Van Griensven, A.; Van Liew, M.W.; et al. SWAT: Model use, calibration, and validation, Trans. ASABE 2012, 55, 1491–1508. [Google Scholar] [CrossRef]
- Yang, X.; Liu, Q.; He, Y.; Luo, X.; Zhang, X. Comparison of daily and sub-daily SWAT models for daily streamflow simulation in the Upper Huai River Basin of China. Stoch. Environ. Res. Risk Assess. 2016, 30, 959–972. [Google Scholar] [CrossRef]
- Refsgaard, J.C.; Storm, B. MIKE-SHE. In Computer Models of Watershed Hydrology; Singh, V.J., Ed.; Water Resour Pub.: Englewood, CO, USA, 1995; pp. 809–846. [Google Scholar]
- Mapfumo, E.; Chanasyk, D.S.; Willms, W.D. Simulating daily soil water under foothills fescue grazing with the Soil and Water Assessment Tool model (Alberta, Canada). Hydrol. Process. 2004, 18, 2787–2800. [Google Scholar] [CrossRef]
- Narasimhan, B.; Srinivasan, R. Development and evaluation of Soil Moisture Deficit Index (SMDI) and Evapotranspiration Deficit Index (ETDI) for agricultural drought monitoring. Agric. For. Meteorol. 2005, 133, 69–88. [Google Scholar] [CrossRef]
- Havrylenko, S.B.; Bodoque, J.M.; Srinivasan, R.; Zucarelli, G.V.; Mercuri, P. Assessment of the soil water content in the Pampas region using SWAT. Catena 2016, 137, 298–309. [Google Scholar] [CrossRef]
- Lévesque, É.; Anctil, F.; Van Griensven, A.N.N.; Beauchamp, N. Evaluation of streamflow simulation by SWAT model for two small watersheds under snowmelt and rainfall. Hydrol. Sci. J. 2008, 53, 961–976. [Google Scholar] [CrossRef]
- Grusson, Y.; Sun, X.; Gascoin, S.; Sauvage, S.; Raghavan, S.; Anctil, F.; Sanchez Pérez, J.M. Assessing thevcapability of the SWAT model to simulate snow, snow melt and streamflow dynamics over an alpinevwatershed. J. Hydrol. 2015, 531, 574–588. [Google Scholar] [CrossRef]
- Masud, M.B.; McAllister, T.; Cordeiro, M.R.C.; Faramarzi, M. Modeling future water footprint of barley production in Alberta, Canada: Implications for water use and yields to 2064. Sci. Total Environ. 2018, 616, 208–222. [Google Scholar] [CrossRef]
- Liang, K.; Jiang, Y.; Qi, J.; Fuller, K.; Nyiraneza, J.; Meng, F.R. Characterizing the impacts of land use on nitrate load and water yield in an agricultural watershed in Atlantic Canada. Sci. Total Environ. 2020, 729, 138793. [Google Scholar] [CrossRef] [PubMed]
- Qi, J.; Li, S.; Li, Q.; Xing, Z.; Bourque, C.P.-A.; Meng, F.-R. A new soil-temperature module for swat application in regions with seasonal snow cover. J. Hydrol. 2016, 538, 863–877. [Google Scholar] [CrossRef]
- Myers, D.T.; Ficklin, D.L.; Robeson, S.M. Incorporating rain-on-snow into the SWAT model results in more accurate simulations of hydrologic extremes. J. Hydrol. 2021, 603, 126972. [Google Scholar] [CrossRef]
- Rücker, A.; Boss, S.; Kirchner, J.W.; von Freyberg, J. Monitoring snowpack outflow volumes and their isotopic composition to better understand streamflow generation during rain-on-snow events. Hydrol. Earth Syst. Sci. Discuss. 2019, 23, 2983–3005. [Google Scholar] [CrossRef]
- Morales-Martín, L.; Wheater, H.; Lindenschmidt, K.E. Potential changes of annual averaged nutrient export in the South Saskatchewan River Basin under climate and land use change scenarios. Water 2018, 10, 1438. [Google Scholar] [CrossRef]
- Tanzeeba, S.; Gan, T.Y. Potential impact of climate change on the water availability of South Saskatchewan River Basin. Clim. Chang. 2012, 112, 355–386. [Google Scholar] [CrossRef]
- Pomeroy, J.; Fang, X.; Williams, B. Impacts of Climate Change on Saskatchewan’s Water Resources; Centre for Hydrology, University of Saskatchewan: Saskatoon, SK, Canada, 2009. [Google Scholar]
- Lac, S. A Climate change adaptation study for the South Saskatchewan River Basin. In SSHRC MCRI-Institutional Adaptation to Climate Change Project; Canadian Plains Research Centre, University of Regina: Regina, SK, Canada, 2004. [Google Scholar]
- Agboma, C.; Itenfisu, D. Investigating the Spatio-Temporal dynamics in the soil water storage in Alberta’s Agricultural region. J. Hydrol. 2020, 588, 125104. [Google Scholar] [CrossRef]
- Neitsch, S.L.; Arnold, J.G.; Kiniry, J.R.; Williams, J.R. Soil and Water Assessment Tool–Theoretical Documentation Version 2009; Technical Report 406; Texas Water Resources Institute: Forney, TX, USA, 2011; 647p. [Google Scholar]
- Anderson, E.E.; Viskanta, R. Spectra1 and boundary effects on coupled conduction. Radiation heat transfer through semi-transparent solids. Wiirme StojZibertragung 1973, 1, 14–24. [Google Scholar] [CrossRef]
- Yin, X.; Arp, P.A. Predicting forest soil temperatures from monthly air temperature and precipitation records. Can. J. For. Res. 1993, 23, 2521–2536. [Google Scholar] [CrossRef]
- Qi, J.Y.; Li, S.; Yang, Q.; Xing, Z.S.; Meng, F.R. SWAT Setup with Long-Term Detailed Landuse and Management Records and Modification for a Micro-Watershed Influenced by Freeze-Thaw Cycles. Water Resour. Manag. 2017, 31, 3953–3974. [Google Scholar] [CrossRef]
- Wang, Q.; Qi, J.; Wu, H.; Zeng, Y.; Shui, W.; Zeng, J.; Zhang, X. Freeze-Thaw cycle representation alters response of watershed hydrology to future climate change. CATENA 2020, 195, 104767. [Google Scholar] [CrossRef]
- Qi, J.; Zhang, X.; Wang, Q. Improving hydrological simulation in the Upper Mississippi River Basin through enhanced freeze-thaw cycle representation. J. Hydrol. 2019, 571, 605–618. [Google Scholar] [CrossRef]
- Abbaspour, K.C.; Yang, J.; Maximov, I.; Siber, R.; Bogner, K.; Mieleitner, J.; Zobrist, J.; Srinivasan, R. Modelling hydrology and water quality in the pre-alpine/alpine Thur watershed using SWAT. J. Hydrol. 2007, 333, 413–430. [Google Scholar] [CrossRef]
- Van Griensven, A.; Meixner, T.; Grunwald, S.; Bishop, T.; Di Luzio, M.; Srinivasan, R. A global sensitivity analysis method for the parameters of multi-variable watershed models. J. Hydrol. 2006, 324, 10–23. [Google Scholar] [CrossRef]
- Nash, J.E.; Sutcliffe, J.V. River flow forecasting through conceptual models: Part I—A discussion of principles. J. Hydrol. 1970, 10, 282–290. [Google Scholar] [CrossRef]
- Moriasi, D.N.; Arnold, J.G.; Van Liew, M.W.; Binger, R.L.; Harmel, R.D.; Veith, T. Model evaluation guidelines for systematic quantification of accuracy in watershed simulations. Trans. ASABE 2007, 50, 885–900. [Google Scholar] [CrossRef]
- Legates, D.R.; McCabe, G.J. Evaluating the use of “goodness-of-fit” measures in hydrological and hydroclimatic model validation. Water Resour. Res. 1999, 35, 233–241. [Google Scholar] [CrossRef]
- Mamo, K.H.M.; Jain, M.K. Runoff and sediment modeling using SWAT in Gumera catchment, Ethiopia. Open J. Mod. Hydrol. 2013, 2013. [Google Scholar] [CrossRef]
- Gyamfi, C.; Ndambuki, J.M.; Salim, R.W. A historical analysis of rainfall trend in the Olifants Basin in South Africa. Earth Sci. Res. 2016, 5, 129–142. [Google Scholar] [CrossRef]
- Khalid, K.; Ali, M.F.; Rahman, N.F.A.; Mispan, M.R.; Haron, S.H.; Othman, Z.; Bachok, M.F. Sensitivity analysis in watershed model using SUFI-2 algorithm. Procedia Eng. 2016, 162, 441–447. [Google Scholar] [CrossRef] [Green Version]
- Thavhana, M.P.; Savage, M.J.; Moeletsi, M.E. SWAT model uncertainty analysis, calibration and validation for runo ff simulation in the Luvuvhu River catchment, South Africa. Phys. Chem. Earth 2018, 105, 115–124. [Google Scholar]
- Liu, Y.; Cui, G.; Li, H. Optimization and Application of Snow Melting Modules in SWAT Model for the Alpine Regions of Northern China. Water 2020, 12, 636. [Google Scholar] [CrossRef]
- Moriasi, D.N.; Gitau, M.W.; Pai, N.; Daggupati, P. Hydrologic and water quality models: Performance measures and evaluation criteria. Trans. ASABE 2015, 58, 1763–1785. [Google Scholar]
- Islam, Z.; Gan, T.Y. Potential combined hydrologic impacts of climate change and El Niño Southern Oscillation to South Saskatchewan River Basin. J. Hydrol. 2015, 523, 34–48. [Google Scholar] [CrossRef]
- Du, X.; Goss, G.; Faramarzi, M. Impacts of hydrological processes on stream temperature in a cold region watershed based on the SWAT Equilibrium Temperature model. Water 2020, 12, 1112. [Google Scholar] [CrossRef]
- Qi, J.; Zhang, X.; McCarty, G.W.; Sadeghi, A.M.; Cosh, M.H.; Zeng, X.; Gao, F.; Daughtry, C.S.; Huang, C.; Lang, M.W. Assessing the performance of a physically-based soil moisture module integrated within the Soil and Water Assessment Tool. Environ. Model. Softw. 2018, 109, 329–341. [Google Scholar] [CrossRef]
- Bristow, K.; Campbell, G.; Papendick, R.; Elliott, L. Simulation of heat and moisture transfer through a surface residue—Soil system. Agric. For. Meteorol. 1986, 36, 193–214. [Google Scholar] [CrossRef]
- Horton, R.; Bristow, K.L.; Kluitenberg, G.J.; Sauer, T.J. Crop residue effects on surface radiation and energy balance—Review. Theor. Appl. Clim. 1996, 54, 27–37. [Google Scholar] [CrossRef] [Green Version]
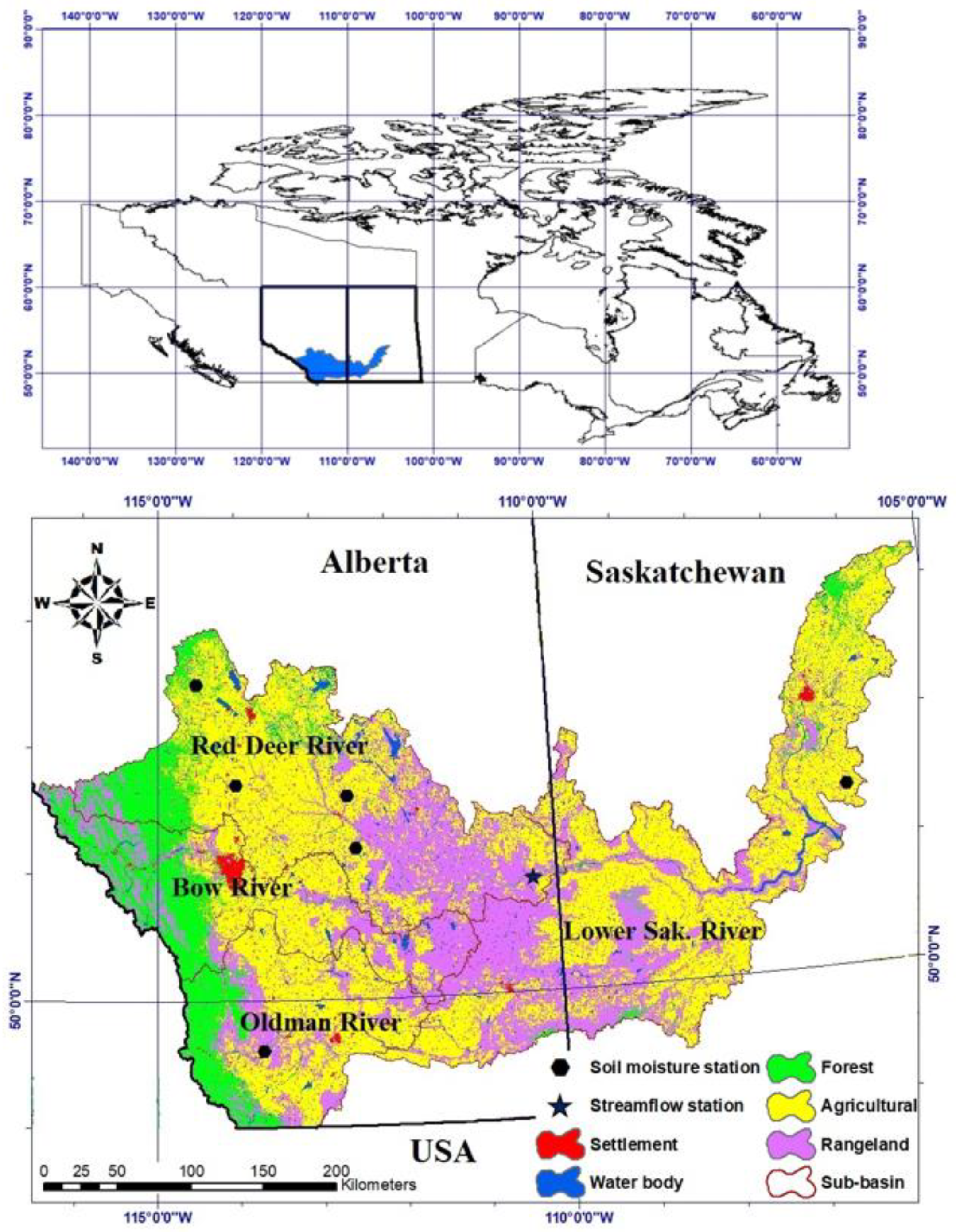
| Data Type | Description | Information | Source |
|---|---|---|---|
| Digital Elevation Model | Watershed delineation | Raster, 30 m-resolution | Digital Elevation Model |
| accessed on 24 August 2021 | |||
| Land use | Land-use classification | Raster, 30 m-resolution | http://geogratis.gc.ca |
| accessed on 30 August 2021 | |||
| Soil type | Soil properties | Vector | http://www.agr.gc.ca |
| accessed on 2 September 2021 | |||
| Weather | Precipitation and temperature | Daily | https://weather.gc.ca |
| accessed on 15 September 2021 | |||
| Streamflow measured | Calibration and validation | Monthly | https://wateroffice.ec.gc.ca |
| accessed on 4 December 2021 | |||
| Soil Moisture measured | Calibration model | Daily | https://acis.alberta.ca |
| accessed on 18 December 2021 | |||
| Soil temperature | Calibration model | Daily | https://acis.alberta.ca |
| accessed on 18 December 2021 |
| Parameter | Range | SWAT-M | SWAT-B | Fitted Value | |||||
|---|---|---|---|---|---|---|---|---|---|
| Rank | p-Value | t-State | Fitted Value | Rank | p-Value | t-State | |||
| CN2 | −0.2–0.2 | 1 | 0.00 | 7.96 | 0.15 | 1 | 0.00 | 8.32 | 0.18 |
| SOL_AWC | −0.1–1.0 | 2 | 0.00 | 5.3 | 0.35 | 9 | 0.61 | −0.5 | −0.075 |
| SFTMP | −5–5 | 3 | 0.01 | −2.33 | 3.52 | 3 | 0.24 | 1.17 | 2.68 |
| SMFMN | 0–10 | 4 | 0.03 | −2.09 | 7.42 | - | - | - | - |
| SOL_BD | −0.1–1.0 | 5 | 0.11 | −1.56 | 0.23 | 6 | 0.41 | 0.81 | 0.26 |
| SOL_K | −0.1–1.0 | 6 | 0.21 | 1.24 | 0.62 | 5 | 0.29 | 1.04 | 0.62 |
| SOL_Z | −0.1–1.0 | 7 | 0.21 | −1.23 | −0.05 | - | - | - | - |
| SMTMP | −5–5 | 8 | 0.38 | 0.87 | −4.22 | 12 | 0.84 | 0.19 | −2.49 |
| GWQMN | 0–2 | 9 | 0.56 | 0.58 | 0.24 | 7 | 0.5 | 0.66 | 0.23 |
| SMFMX | 0–10 | 10 | 0.58 | 0.54 | 0.52 | 2 | 0.1 | 1.64 | 1.83 |
| CH_K2 | 0–500 | 11 | 0.61 | 0.49 | 387 | 8 | 0.58 | 0.54 | 391 |
| SURLAG | 0–24 | 12 | 0.71 | −0.36 | 8.33 | - | - | - | - |
| CH_N2 | 0–0.3 | 13 | 0.71 | −0.36 | 0.03 | 13 | 0.88 | 0.14 | 0.017 |
| ESCO | 0.0–1.0 | 14 | 0.8 | −0.24 | 0.44 | 4 | 0.13 | 1.12 | 0.81 |
| ALPHA_BF | 0.0–1.0 | 15 | 0.84 | 0.2 | 0.55 | 10 | 0.71 | 0.36 | 0.52 |
| GW_DELAY | −0.2–0.2 | 16 | 0.89 | 0.13 | 0.18 | 11 | 0.78 | 0.22 | 0.17 |
| SUB_SMFMN | 0.0–10 | 17 | 0.9 | −0.12 | 0.63 | - | - | - | - |
| SOL_ALB | 0.0–0.25 | 18 | 0.92 | 0.09 | 0.07 | 14 | 0.96 | 0.04 | 0.07 |
| Statistics | Calibration (1993–2005) | Validation (2006–2013) | ||
|---|---|---|---|---|
| SWAT-B | SWAT-M | SWAT-B | SWAT-M | |
| 0.39 | 0.71 | 0.42 | 0.76 | |
| −18.3 | −9.3 | −19.2 | −8.4 | |
| 0.72 | 0.83 | 0.75 | 0.88 | |
| Statistical Indices | PBIAS | NSE | |||||
|---|---|---|---|---|---|---|---|
| Station | SWAT-B | SWAT-M | SWAT-B | SWAT-M | SWAT-B | SWAT-M | |
| SWC | Hussar | 0.48 | 0.55 | −13.6 | 9.5 | 0.61 | 0.72 |
| Morrin | 0.52 | 0.53 | −22 | −10.2 | 0.67 | 0.79 | |
| Olds College | 0.45 | 0.45 | 14 | −9.1 | 0.49 | 0.61 | |
| Leedale | 0.24 | 0.33 | 16.6 | 15.7 | 0.46 | 0.57 | |
| Brocket | 0.5 | 0.57 | −13.1 | −8.2 | 0.74 | 0.86 | |
| Kenaston | 0.6 | 0.65 | −11 | 7.1 | 0.64 | 0.78 | |
| Mean | 0.47 | 0.51 | 15.5 | 10 | 0.60 | 0.72 | |
| ST | Hussar | 0.92 | 0.9 | 6.5 | 2.8 | 0.32 | 0.6 |
| Morrin | 0.91 | 0.9 | 6.8 | 3.09 | 0.32 | 0.67 | |
| Olds College | 0.9 | 0.9 | 4.7 | 1.95 | 0.48 | 0.74 | |
| Leedale | 0.88 | 0.88 | 3.3 | 1.2 | 0.61 | 0.74 | |
| Brocket | 0.87 | 0.87 | 4 | 3.8 | 0.37 | 0.71 | |
| Mean | 0.90 | 0.9 | 5.06 | 2.57 | 0.42 | 0.69 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zare, M.; Azam, S.; Sauchyn, D. A Modified SWAT Model to Simulate Soil Water Content and Soil Temperature in Cold Regions: A Case Study of the South Saskatchewan River Basin in Canada. Sustainability 2022, 14, 10804. https://doi.org/10.3390/su141710804
Zare M, Azam S, Sauchyn D. A Modified SWAT Model to Simulate Soil Water Content and Soil Temperature in Cold Regions: A Case Study of the South Saskatchewan River Basin in Canada. Sustainability. 2022; 14(17):10804. https://doi.org/10.3390/su141710804
Chicago/Turabian StyleZare, Mohammad, Shahid Azam, and David Sauchyn. 2022. "A Modified SWAT Model to Simulate Soil Water Content and Soil Temperature in Cold Regions: A Case Study of the South Saskatchewan River Basin in Canada" Sustainability 14, no. 17: 10804. https://doi.org/10.3390/su141710804
APA StyleZare, M., Azam, S., & Sauchyn, D. (2022). A Modified SWAT Model to Simulate Soil Water Content and Soil Temperature in Cold Regions: A Case Study of the South Saskatchewan River Basin in Canada. Sustainability, 14(17), 10804. https://doi.org/10.3390/su141710804








