The Heterogeneous Effect of Economic Complexity and Export Quality on the Ecological Footprint: A Two-Step Club Convergence and Panel Quantile Regression Approach
Abstract
:1. Introduction
2. Literature Review
3. Data and Method
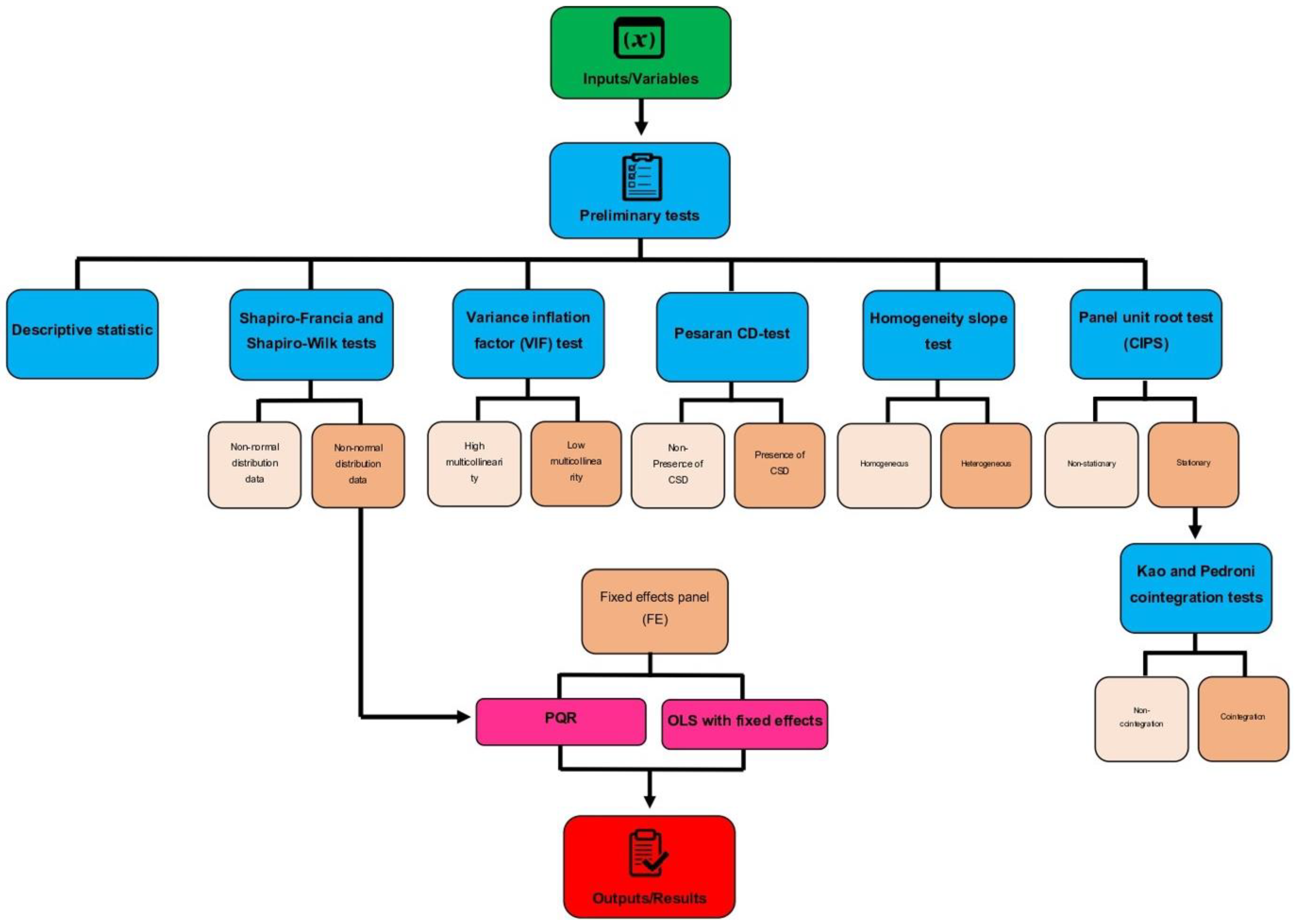
3.1. Data
3.2. Method Approach
3.2.1. The Club Convergence
- Sort countries based on their latest observations.
- Forming a Core Club, perform a statistical calculation of the tk convergence test for successive log(t) regressions based on the highest individuals k (2 ≤ k ≤ N) in the panel. Then, select the core size by maximizing tk with tb > −1.65.
- Add one country to the main group each time and estimate the log(t) regression in Equation (5). The decision on whether a country/territory should join the core group is based on the criteria.
- We repeat steps (b) and (c) for the remaining countries until we can no longer create a club, and each club has its convergence path. If the last group of the algorithm is not added, these countries form a divergent club.
3.2.2. The Panel Quantile Regression
4. Empirical Results and Discussion
4.1. Club Convergence Results
4.2. Panel Quantile Regression Results
4.2.1. Pre-Estimation Tests
4.2.2. Panel Quantile Regression Result and Discussion
4.2.3. Robustness Check
5. Conclusions and Policy Implications
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Bhattacharya, M.; Churchill, S.A.; Paramati, S.R. The dynamic impact of renewable energy and institutions on economic output and CO2 emissions across regions. Renew. Energy 2017, 111, 157–167. [Google Scholar] [CrossRef]
- Apergis, N.; Can, M.; Gozgor, G.; Lau, C.K.M. Effects of export concentration on CO2 emissions in developed countries: An empirical analysis. Environ. Sci. Pollut. Res. 2018, 25, 14106–14116. [Google Scholar] [CrossRef]
- Acheampong, A.O. Economic growth, CO2 emissions and energy consumption: What causes what and where? Energy Econ. 2018, 74, 677–692. [Google Scholar] [CrossRef]
- Al-Mulali, U.; Ozturk, I. The investigation of environmental Kuznets curve hypothesis in the advanced economies: The role of energy prices. Renew. Sustain. Energy Rev. 2016, 54, 1622–1631. [Google Scholar] [CrossRef]
- Ozcan, B.; Apergis, N.; Shahbaz, M. A revisit of the environmental Kuznets curve hypothesis for Turkey: New evidence from bootstrap rolling window causality. Environ. Sci. Pollut. Res. 2018, 25, 32381–32394. [Google Scholar] [CrossRef]
- Rahman, S.U.; Chen, S.; Saud, S.; Saleem, N.; Bari, M.W. Nexus between financial development, energy consumption, income level, and ecological footprint in CEE countries: Do human capital and biocapacity matter? Environ. Sci. Pollut. Res. 2019, 26, 31856–31872. [Google Scholar] [CrossRef]
- Germani, A.R.; Ker, A.P.; Castaldo, A. On the existence and shape of an environmental crime Kuznets Curve: A case study of Italian provinces. Ecol. Indic. 2020, 108, 105685. [Google Scholar] [CrossRef]
- Arango-Miranda, R.; Hausler, R.; Romero-López, R.; Glaus, M.; Pasillas-Díaz, J.R. Testing the Environmental Kuznets Curve Hypothesis in North America’s Free Trade Agreement (NAFTA) Countries. Energies 2020, 13, 3104. [Google Scholar] [CrossRef]
- Gozgor, G.; Can, M. Does export product quality matter for CO2 emissions? Evidence from China. Environ. Sci. Pollut. Res. 2017, 24, 2866–2875. [Google Scholar] [CrossRef]
- Chen, W.; Lei, Y. The impacts of renewable energy and technological innovation on environment-energy-growth nexus: New evidence from a panel quantile regression. Renew. Energy 2018, 123, 1–14. [Google Scholar] [CrossRef]
- Onafowora, O.A.; Owoye, O. Bound testing approach to analysis of the environment Kuznets curve hypothesis. Energy Econ. 2014, 44, 47–62. [Google Scholar] [CrossRef]
- Kasman, A.; Duman, Y.S. CO2 emissions, economic growth, energy consumption, trade and urbanization in new EU member and candidate countries: A panel data analysis. Econ. Model. 2015, 44, 97–103. [Google Scholar] [CrossRef]
- Wang, Z.; Liu, W. Determinants of CO2 emissions from household daily travel in Beijing. China: Individual Travel Characteristic Perspectives. Appl. Energy 2015, 158, 292–299. [Google Scholar] [CrossRef]
- Paramati, S.R.; Ummalla, M.; Apergis, N. The effect of foreign direct investment and stock market growth on clean energy use across a panel of emerging market economies. Energy Econ. 2016, 56, 29–34. [Google Scholar] [CrossRef]
- Doğan, E.; Turkekul, B. CO2 emissions, real output, energy consumption, trade, urbanization and financial development: Testing the EKC hypothesis for the USA. Environ. Sci. Pollut. Res. 2016, 23, 1203–1213. [Google Scholar] [CrossRef]
- Albulescu, C.; Tiwari, A.K.; Yoon, S.-M.; Kang, S.H. FDI, income, and environmental pollution in Latin America: Replication and extension using panel quantiles regression analysis. Energy Econ. 2019, 84, 104504. [Google Scholar] [CrossRef]
- Fang, J.; Gozgor, G.; Lu, Z.; Wu, W. Effects of the export product quality on carbon dioxide emissions: Evidence from developing economies. Environ. Sci. Pollut. Res. 2019, 26, 12181–12193. [Google Scholar] [CrossRef]
- Pata, U.K. Renewable and nonrenewable energy consumption, economic complexity, CO2 emissions, and ecological footprint in the USA: Testing the EKC hypothesis with a structural break. Environ. Sci. Pollut. Res. 2020, 28, 846–861. [Google Scholar] [CrossRef]
- Doğan, B.; Madaleno, M.; Tiwari, A.K.; Hammoudeh, S. Impacts of export quality on environmental degradation: Does income matter? Environ. Sci. Pollut. Res. 2020, 27, 13735–13772. [Google Scholar] [CrossRef]
- Murshed, M.; Dao, N.T.T. Revisiting the CO2 emission-induced EKC hypothesis in South Asia: The role of Export Quality Improvement. GeoJournal 2020, 87, 535–563. [Google Scholar] [CrossRef]
- Shahbaz, M.; Mahali, M.K.; Shah, S.H.; Sato, J.R. Time-varying analysis of CO2 emissions, energy consumption, and economic growth Nexus: Statistical experience in next 11 countries. Energy Policy 2016, 98, 33–48. [Google Scholar] [CrossRef]
- Neagu, O. Economic Complexity and Ecological Footprint: Evidence from the Most Complex Economies in the World. Sustainability 2020, 12, 31. [Google Scholar] [CrossRef]
- Lin, D.; Hanscom, L.; Martindill, J.; Borucke, M.; Cohen, L.; Galli, A.; Lazarus, E.; Zokai, G.; Iha, K.; Eaton, D. Working Guidebook to the National Footprint and Biocapacity Accounts; Global Footprint Network: Oakland, CA, USA, 2020; Available online: http://www.footprintnetwork.org (accessed on 1 August 2022).
- Nijkamp, P.; Rossi, E.; Vindigni, G. Ecological footprints in plural: A meta-analytic comparison of empirical results. Reg. Stud. 2004, 38, 747–765. [Google Scholar] [CrossRef]
- Al-Mulali, U.; Ozturk, I.; Lean, H.H. The influence of economic growth, urbanization, trade openness, financial development, and renewable energy on pollution in Europe. Nat. Hazards 2015, 79, 621–644. [Google Scholar] [CrossRef]
- Mrabet, Z.; Alsamara, M. Testing the Kuznets curve hypothesis for Qatar: A comparison between carbon dioxide and ecological footprint. Energy Rev. 2017, 70, 1366–1375. [Google Scholar] [CrossRef]
- Destek, M.A.; Ulucak, R.; Doğan, E. Analyzing the environmental Kuznets curve for the EU countries: The role of ecological footprint. Environ. Sci. Pollut. Res. 2018, 25, 29387–29396. [Google Scholar] [CrossRef]
- Gómez, M.; Rodríguez, J.C. Analysis of the environmental Kuznets curve in the NAFTA Countries. EconoQuantum 2020, 17, 57–79. [Google Scholar] [CrossRef]
- Gómez, M.; Rodríguez, J.C. The Ecological Footprint and Kuznets Environmental Curve in the USMCA Countries: A Method of Moments Quantile Regression Analysis. Moments Quantile Regression Analysis. Energies 2020, 13, 6650. [Google Scholar] [CrossRef]
- Charfeddine, L.; Mrabet, Z. The impact of economic development and social-political factors on ecological footprint: A panel data analysis for 15 MENA countries. Renew. Sustain. Energy Rev. 2017, 76, 138–154. [Google Scholar] [CrossRef]
- Alola, A.A.; Bekun, F.V.; Sarkodie, S.A. Dynamic impact of trade policy, economic growth, fertility rate, renewable and nonrenewable energy consumption on ecological footprint in Europe. Sci. Total. Environ. 2019, 685, 702–709. [Google Scholar] [CrossRef]
- Chen, Y.; Wang, Z.; Zhong, Z. CO2 emissions, economic growth, renewable and nonrenewable energy production and foreign trade in China. Renew. Energy 2019, 131, 208–216. [Google Scholar] [CrossRef]
- Danish Hassan, S.T.; Baloch, M.A.; Mahmood, N.; Zhang, J.W. Linking economic growth and ecological footprint through human capital and biocapacity. Sustain. Cities Soc. 2019, 47, 101516. [Google Scholar] [CrossRef]
- Yilanci, V.; Pata, U.K. Investigating the EKC hypothesis for China: The role of economic complexity on ecological footprint. Environ. Sci. Pollut. Res. 2020, 27, 32683–32694. [Google Scholar] [CrossRef]
- Kazemzadeh, E.; Fuinhas, J.A.; Koengkan, M. The impact of income inequality and economic complexity on ecological footprint: An analysis covering a long-time span. J. Environ. Econ. Policy 2021, 11, 133–153. [Google Scholar] [CrossRef]
- World Bank Data (WBD). Available online: https://databank.worldbank.org/home (accessed on 23 July 2022).
- Raza, S.A.; Shah, N. Testing environmental Kuznets curve hypothesis in G7 countries: The role of renewable energy consumption and trade. Environ. Sci. Pollut. Res. 2018, 25, 26965–26977. [Google Scholar] [CrossRef]
- Zhang, S.; Liu, X.; Bae, J. Does trade openness affect CO2 emissions: Evidence from ten newly industrialized countries? Environ. Sci. Pollut. Res. 2017, 24, 17616–17625. [Google Scholar] [CrossRef]
- Shahbaz, M.; Shafiullah, M.; Mahalik, M.K. The dynamics of financial development, globalisation, economic growth, and life expectancy in sub-Saharan Africa. Aust. Econ. Pap. 2019, 58, 444–479. [Google Scholar] [CrossRef]
- Can, M.; Gozgor, G. Effects of export product diversification on quality upgrading: An empirical study. J. Int. Trade Econ. Dev. 2018, 27, 293–313. [Google Scholar] [CrossRef]
- Rafindadi, A.A. Does the need for economic growth influence energy consumption and CO2 emissions in Nigeria? Evidence from the innovation accounting test. Renew. Sustain. Energy Rev. 2016, 62, 1209–1225. [Google Scholar] [CrossRef]
- Gozgor, G.; Can, M. Export product diversification and the environmental Kuznets curve: Evidence from Turkey. Environ. Sci. Pollut. Res. 2016, 23, 21594–21603. [Google Scholar] [CrossRef]
- Moghadam, H.E.; Dehbashi, V. The impact of financial development and trade on environmental quality in Iran. Empir. Econ. 2018, 54, 1777–1799. [Google Scholar] [CrossRef]
- Neagu, O. The Link between Economic Complexity and Carbon Emissions in the European Union Countries: A Model Based on the Environmental Kuznets Curve (EKC) Approach. Sustainability 2019, 11, 4753. Available online: https://www.mdpi.com/2071-1050/11/17/4753/htm (accessed on 23 July 2022). [CrossRef]
- Lapatinas, A.; Garas, A.; Boleti, E.; Kyriakou, A. Economic Complexity and Environmental Performance: Evidence from A World Sample. 2019. Available online: https://mpra.ub.uni-muenchen.de/92833/1/MPRA_paper_92833.pdf (accessed on 1 August 2022).
- Doğan, B.; Driha, O.M.; Balsalobre-Lorente, D.; Shahzad, U. The mitigating effects of economic complexity and renewable energy on carbon emissions in developed countries. Sustain. Dev. 2021, 29, 1–12. [Google Scholar] [CrossRef]
- Hausmann, R.; Hidalgo, C.A.; Bustos, S.; Coscia, M.; Simoes, A.; Yildirim, M.A. The Atlas of Economic Complexity: Mapping Paths to Prosperity; MIT Press: Cambridge, MA, USA, 2014. [Google Scholar]
- Wang, Z.; Jebli, M.B.; Madaleno, M.; Doğan, B.; Shahzad, U. Does export product quality and renewable energy induce carbon dioxide emissions: Evidence from leading complex and renewable energy economies. Renewable Energy 2021, 171, 360–370. [Google Scholar] [CrossRef]
- Kazemzadeh, E.; Fuinhas, J.A.; Koengkan, M.; Osmani, F.; Silva, N. Do energy efficiency and export quality affect the ecological footprint in emerging countries? A two-step approach using the SBM–DEA model and panel quantile regression. In Environment Systems and Decisions; Springer: Cham, Switzerland, 2022; pp. 1–18. [Google Scholar] [CrossRef]
- Li, M.; Ahmad, M.; Fareed, Z.; Hassan, T.; Kirikkaleli, D. Role of trade openness, export diversification, and renewable electricity output in realizing carbon neutrality dream of China. J. Environ. Manag. 2021, 297, 113419. [Google Scholar] [CrossRef]
- Can, M.; Gozgor, G. The impact of economic complexity on carbon emissions: Evidence from France. Environ. Sci. Pollut. Res. 2017, 24, 16364–16370. [Google Scholar] [CrossRef] [PubMed]
- Rafei, M.; Esmaeili, P.; Balsalobre-Lorente, D. A step towards environmental mitigation: How do economic complexity and natural resources matter? Focusing on different institutional quality level countries. Resour. Policy 2022, 78, 102848. [Google Scholar] [CrossRef]
- Shahzad, U.; Fareed, Z.; Shahzad, F.; Shahzad, K. Investigating the nexus between economic complexity, energy consumption and ecological footprint for the United States: New insights from quantile methods. J. Clean. Prod. 2021, 279, 123806. [Google Scholar] [CrossRef]
- Kazemzadeh, E.; Fuinhas, J.A.; Salehnia, N.; Osmani, F. The effect of economic complexity, fertility rate, and information and communication technology on ecological footprint in the emerging economies: A two-step stirpat model and panel quantile regression. In Quality & Quantity; Springer: Cham, Switzerland, 2022; pp. 1–27. [Google Scholar] [CrossRef]
- Global Footprint Network (GFN). Available online: https://www.footprintnetwork.org/resources/data (accessed on 23 July 2022).
- British Petroleum (BP). Available online: https://www.bp.com/content/dam/bp/business-sites/en/global/corporate/xlsx/energy-economics/statistical-review/bp-stats-review-2020-all-data.xlsx (accessed on 23 July 2022).
- International Monetary Fund (IMF). Available online: https://data.imf.org/?sk=3567E911-4282-4427-98F9-2B8A6F83C3B6 (accessed on 23 July 2022).
- Phillips, P.C.; Sul, D. Transition modeling and econometric convergence tests. Econometrica 2007, 75, 1771–1855. [Google Scholar] [CrossRef]
- Panopoulou, E.; Pantelidis, T. Club convergence in carbon dioxide emissions. Environ. Resour. Econ. 2009, 44, 47–70. [Google Scholar] [CrossRef]
- Koenker, R.; Bassett, G., Jr. Regression quantiles. Econom. J. Econom. Soc. 1978, 46, 33–50. [Google Scholar] [CrossRef]
- Koenker, R. Quantile regression for longitudinal data. J. Multivar. Anal. 2004, 91, 74–89. [Google Scholar] [CrossRef]
- Buchinsky, M. Recent Advances in Quantile Regression Models: A Practical Guideline for Empirical Research. J. Hum. Resour. 1998, 33, 88–126. Available online: http://www.jstor.org/stable/pdfplus/146316 (accessed on 23 July 2022). [CrossRef]
- Koengkan, M. The positive influence of urbanization on energy consumption in Latin American countries. Rev. De Estud. Sociais 2018, 20, 4. Available online: https://dialnet.unirioja.es/servlet/articulo?codigo=6637808 (accessed on 30 August 2022).
- Fuinhas, J.A.; Koengkan, M.; Santiago, R. The capacity of energy transition to decrease deaths from air pollution: Empirical evidence from Latin America and the Caribbean countries. In Physical Capital Development and Energy Transition in Latin America and the Caribbean; Elsevier: Amsterdam, The Netherlands, 2021; pp. 185–205. [Google Scholar] [CrossRef]
- Steers, R.J.; Funk, J.L.; Allen, E.B. Can resource-use traits predict native vs. exotic plant success in carbon amended soils? Ecol. Appl. 2011, 21, 1211–1224. [Google Scholar] [CrossRef]
- Zhu, H.; Duan, L.; Guo, Y.; Yu, K. The effects of FDI, economic growth and energy consumption on carbon emissions in ASEAN-5: Evidence from panel quantile regression. Econ. Model. 2016, 58, 237–248. [Google Scholar] [CrossRef]
- Xu, R.; Xu, L.; Xu, B. Assessing CO2 emissions in China’s iron and steel industry: Evidence from quantile regression approach. J. Clean. Prod. 2017, 152, 259–270. [Google Scholar] [CrossRef]
- Paltasingh, K.R.; Goyari, P. Statistical Modeling of Crop-Weather Relationship in India: A Survey on Evolutionary Trend of Methodologies. Asian J. Agric. Dev. 2018, 15, 43. Available online: http://ageconsearch.umn.edu/record/275688/files/AJAD%272015_275681_Paper%275203.pdf (accessed on 23 July 2022).
- Buhari, D.O.; Lorente, D.B.; Nasir, M.A. European commitment to COP21 and the role of energy consumption, FDI, trade and economic complexity in sustaining economic growth. J. Environ. Manag. 2020, 273, 111146. [Google Scholar] [CrossRef]
- Xu, B.; Lin, B. What cause large regional differences in PM2. 5 pollutions in China? Evidence from quantile regression model. J. Clean. Prod. 2018, 174, 447–461. [Google Scholar] [CrossRef]
- Royston, J. A Simple Method for Evaluating the Shapiro–Francia W′ Test of Non-Normality. J. R. Stat. Soc. Ser. D 1983, 32, 297–300. [Google Scholar] [CrossRef]
- Royston, P. Approximating the Shapiro-Wilk W-test for non-normality. Stat. Comput. 1992, 2, 117–119. [Google Scholar] [CrossRef]
- Belsley, D.A.; Kuh, E.; Welsch, R.E. Regression Diagnostics: Identifying Influential Data and Sources of Collinearity; John Wiley & Sons: Hoboken, NJ, USA, 2005. [Google Scholar] [CrossRef]
- Pesaran, H. General diagnostic tests for cross-sectional dependence in panels. University of Cambridge, Cambridge Working Papers in Economics. 2004. Available online: https://www.econstor.eu/bitstream/10419/18868/1/cesifo1_wp1229.pdf (accessed on 23 July 2022).
- Pesaran, M.H. A simple panel unit root test in the presence of cross-section dependence. J. Appl. Econom. 2007, 22, 265–312. [Google Scholar] [CrossRef]
- Kao, C. Spurious regression and residual-based tests for cointegration in panel data. J. Econom. 1999, 90, 1–44. [Google Scholar] [CrossRef]
- Pedroni, P. Critical values for cointegration tests in heterogeneous panels with multiple regressors. Oxf. Bull. Econ. Stat. 1990, 61, 653–670. [Google Scholar] [CrossRef]
- Fuinhas, J.A.; Koengkan, M.; Santiago, R. The role of public, private, and public-private partnership capital stock on the expansion of renewable energy investment in Latin America and the Caribbean region. In Physical Capital Development and Energy Transition in Latin America and the Caribbean; Elsevier: Amsterdam, The Netherlands, 2021; pp. 117–137. [Google Scholar] [CrossRef]
- Koengkan, M. O Nexo entre o Consumo de Energia Primária e o Crescimento Económico nos Países da América da Sul: Uma Análise de Longo Prazo. Cad. UniFOA 2017, 12, 63–74. [Google Scholar] [CrossRef]
- Pesaran, M.H.; Yamagata, T. Testing slope homogeneity in large panels. J. Econom. 2008, 142, 50–93. [Google Scholar] [CrossRef] [Green Version]
- Wang, S.; Li, G.; Fang, C. Urbanization, economic growth, energy consumption, and CO2 emissions: Empirical evidence from countries with different income levels. Renew. Sustain. Energy Rev. 2018, 81, 2144–2159. [Google Scholar] [CrossRef]
- Westerlund, J. Testing for error correction in panel data. Oxf. Bull. Econ. Stat. 2007, 69, 709–748. [Google Scholar] [CrossRef]
- Santiago, R.; Fuinhas, J.A.; Marques, A.C.; Koengkan, M. What effect does public and private capital have on income inequality? The case of the Latin America and Caribbean region. Lat. Am. Econ. Rev. 2022, 31, 1–30. [Google Scholar] [CrossRef]
- Shah, N. Impact of Working capital management on firms profitability in different business cycles: Evidence from Pakistan. J. Financ. Econ. Res. 2016, 1, 58–70. [Google Scholar] [CrossRef]
- Azam, M.; Raza, S.A. Do workers’ remittances boost human capital development? Pak. Dev. Rev. 2016, 55, 123–149. Available online: https://www.jstor.org/stable/44986034 (accessed on 23 July 2022). [CrossRef]
- Raza, S.A.; Karim, M. Do liquidity and financial leverage constrain the impact of firm size and dividend payouts on share price in emerging economy. J. Financ. Econ. Res. 2016, 1, 73–88. [Google Scholar] [CrossRef]
- Sbia, R.; Shahbaz, M.; Hamdi, H. A contribution of foreign direct investment, clean energy, trade openness, carbon emissions and economic growth to energy demand in UAE. Econ. Model. 2014, 36, 191–197. [Google Scholar] [CrossRef]
- Ahmed, K.; Shahbaz, M.; Kyophilavong, P. Revisiting the emissions-energy-trade nexus: Evidence from the newly industrializing countries. Environ. Sci. Pollut. Res. 2016, 23, 7676–7691. [Google Scholar] [CrossRef]
- Aşıcı, A.A.; Acar, S. Does income growth relocate ecological footprint? Ecol. Indic. 2016, 61, 707–714. [Google Scholar] [CrossRef]
- Baek, J.; Cho, Y.; Koo, W.W. The environmental consequences of globalization: A country-specific time-series analysis. Ecol. Econ. 2009, 68, 2255–2264. [Google Scholar] [CrossRef] [Green Version]
- Frankel, J.A.; Rose, A.K. Is trade good or bad for the environment? Sorting out the causality. Rev. Econ. Stat. 2005, 87, 85–91. [Google Scholar] [CrossRef]
- Ali, S.; Yusop, Z.; Kaliappan, S.R.; Chin, L. Dynamic common correlated effects of trade openness, FDI, and institutional performance on environmental quality: Evidence from OIC countries. Environ. Sci. Pollut. Res. 2020, 27, 11671–11682. [Google Scholar] [CrossRef]
- Al-Mulali, U.; Solarin, S.A.; Sheau-Ting, L.; Ozturk, I. Does moving towards renewable energy cause water and land inefficiency? An empirical investigation. Energy Policy 2016, 93, 303–314. [Google Scholar] [CrossRef]
- Le, T.-H.; Chang, Y.; Park, D. Trade openness and environmental quality: International evidence. Energy Policy 2016, 92, 45–55. [Google Scholar] [CrossRef]
- Can, M.; Ahmad, M.; Khan, Z. The impact of export composition on environment and energy demand: Evidence from newly industrialized countries. Environ. Sci. Pollut. Res. 2021, 128, 33599–33612. [Google Scholar] [CrossRef]
- Shahzad, U.; Ferraz, D.; Doğan, B.; do Nascimento Rebelatto, D.A. Export product diversification and CO2 emissions: Contextual evidences from developing and developed economies. J. Clean. Prod. 2020, 276, 124146. [Google Scholar] [CrossRef]
- Hu, G.; Can, M.; Paramati, S.R.; Doğan, B.; Fang, J. The effect of import product diversification on carbon emissions: New evidence for sustainable economic policies. Econ. Anal. Policy 2020, 65, 198–210. [Google Scholar] [CrossRef]
- Balsalobre-Lorente, D.; Shahbaz, M.; Roubaud, D.; Farhani, S. How economic growth, renewable electricity and natural resources contribute to CO2 emissions? Energy Policy 2018, 113, 356–367. [Google Scholar] [CrossRef]
- Saud, S.; Chen, S.; Haseeb, A. Impact of financial development and economic growth on environmental quality: An empirical analysis from Belt and Road Initiative (BRI) countries. Environ. Sci. Pollut. Res. 2019, 26, 2253–2269. [Google Scholar] [CrossRef]
- Banday, U.J.; Aneja, R. Energy consumption, economic growth and CO2 emissions: Evidence from G7 countries. World J. Sci. Technol. Sustain. Dev. 2019, 16, 22–39. [Google Scholar] [CrossRef]
- Hanif, I. Impact of economic growth, nonrenewable and renewable energy consumption, and urbanization on carbon emissions in Sub-Saharan Africa. Environ. Sci. Pollut. Res. 2018, 25, 15057–15067. [Google Scholar] [CrossRef]
- Sarkodie, S.A. The invisible hand and EKC hypothesis: What are the drivers of environmental degradation and pollution in Africa? Environ. Sci. Pollut. Res. 2018, 25, 21993–22022. [Google Scholar] [CrossRef]
- Haseeb, A.; Xia, E.; Baloch, M.A.; Abbas, K. Financial development, globalization, and CO2 emission in the presence of EKC: Evidence from BRICS countries. Environ. Sci. Pollut. Res. 2018, 25, 31283–31296. [Google Scholar] [CrossRef]
- Alam, M.M.; Murad, M.W.; Noman, A.H.M.; Ozturk, I. Relationships among carbon emissions, economic growth, energy consumption and population growth: Testing Environmental Kuznets Curve hypothesis for Brazil, China, India and Indonesia. Ecol. Indic. 2016, 70, 466–479. [Google Scholar] [CrossRef]
- Ahmed, Z.; Adebayo, T.S.; Udemba, E.N.; Murshed, M.; Kirikkaleli, D. Effects of economic complexity, economic growth, and renewable energy technology budgets on ecological footprint: The role of democratic accountability. Environ. Sci. Pollut. Res. 2022, 29, 24925–24940. Available online: https://link.springer.com/article/10.1007/s11356-021-17673-2 (accessed on 1 August 2022). [CrossRef] [PubMed]
- Doğan, B.; Saboori, B.; Can, M. Does economic complexity matter for environmental degradation? An empirical analysis for different stages of development. Environ. Sci. Pollut. Res. 2019, 26, 31900–31912. [Google Scholar] [CrossRef] [PubMed]
- Lv, Z.; Xu, T. Trade openness, urbanization and CO2 emissions: Dynamic panel data analysis of middle-income countries. J. Int. Trade Econ. Dev. 2019, 28, 317–330. [Google Scholar] [CrossRef]
- Saidi, K.; Mbarek, M.B. The impact of income, trade, urbanization, and financial development on CO2 emissions in 19 emerging economies. Environ. Sci. Pollut. Res. 2017, 24, 12748–12757. [Google Scholar] [CrossRef] [PubMed]
- Sharma, S.S. Determinants of carbon dioxide emissions: Empirical evidence from 69 countries. Appl. Energy 2011, 88, 376–382. [Google Scholar] [CrossRef]
- Parikh, J.; Shukla, V. Urbanization, energy use and greenhouse effects in economic development: Results from a cross-national study of developing countries. Glob. Environ. Chang. 1995, 5, 87–103. [Google Scholar] [CrossRef]
- Wang, Y.; Chen, L.; Kubota, J. The relationship between urbanization, energy use and carbon emissions: Evidence from a panel of Association of Southeast Asian Nations (ASEAN) countries. J. Clean. Prod. 2016, 112, 1368–1374. [Google Scholar] [CrossRef]
- Wang, J.; Dong, K. What drives environmental degradation? Evidence from 14 Sub-Saharan African countries. Sci. Total. Environ. 2019, 656, 165–173. [Google Scholar] [CrossRef]
- Koengkan, M.; Santiago, R.; Fuinhas, J.A. The impact of public capital stock on energy consumption: Empirical evidence from Latin America and the Caribbean region. Int. Econ. 2019, 160, 43–55. [Google Scholar] [CrossRef]



| Abbreviation | Variables | Sources | QR Codes |
|---|---|---|---|
| EFPG | Ecological footprint (in global hectares) | Global Footprint Network (GFN) [55] |  |
| ECI | Economic Complexity Index | Observatory of Economic Complexity (OEC) [55] |  |
| GDP | Gross domestic product (GDP) (constant = USD 2010) | World Bank Data (WBD) [36] |  |
| NONREC | Consumption of fossil fuels (e.g., oil, gas, and coal) in a million tonnes of oil equivalent | British Petroleum (BP) [56] |  |
| EQ | Export Quality Index | International Monetary Fund (IMF) [57] |  |
| URB | Urban population (% of the total population) | World Bank Data (WBD) [36] |  |
| POP | Total Population | World Bank Data (WBD) [36] |  |
| TO | Total economic openness = Import + Export (constant = USD 2010) | World Bank Data (WBD) [36] |  |
| Panel A: Club convergence tests | coef. | ||
| Full sample convergence | Countries | −0.4848 | −34.5298 ** |
| 1st club | India, the United States of America, Brazil, and Canada | 0.230 | 4.281 |
| 2nd club | Argentina, Australia, Italy, Egypt, Malaysia, France, Germany, Ghana, Indonesia, Japan, Mexico, South Africa, the United Kingdom, and South Korea | 0.245 | 5.327 |
| 3rd club | Austria, Belgium, Bolivia, Cambodia, Cameroon, Chile, Colombia, Denmark, Ecuador, Finland, Gabon, Greece, Guatemala, Tanzania, Guinea, Israel, Singapore, Jordan, Kenya, Lebanon, Morocco, Portugal, Mozambique, the Netherlands, Oman, Peru, Poland, Qatar, Romania, Sri Lanka, Sweden, Switzerland, Spain, Tunisia, Venezuela, and Zambia | 0.180 | 4.116 |
| 4th club | Costa Rica, Cuba, Djibouti, El Salvador, Haiti, Honduras, Hungary, Ireland, Paraguay, Liberia, Niger, Madagascar, Mauritania, New Zealand, Norway, Panama, Senegal, Sierra Leone, Philippines, and Somalia | 0.227 | 6.310 |
| 5th club | Albania, Bhutan, Bulgaria, Burundi, Fiji, Gambia, Jamaica, Luxembourg, Myanmar, Nicaragua, North Korea, and Zimbabwe | 0.123 | 5.140 |
| 6th club | Barbados, Malta, and Tonga | 0.039 | 0.750 |
| 7th club | China and Cyprus | −0.878 | −59.077 *** |
| Panel B: Club merging analysis | coef. | ||
| New club I | Merging Club 1 + 2 | 0.0554 | 1.3645 |
| New club II | Merging Club 2 + 3 | −0.1523 | −4.7723 ** |
| New club III | Merging Club 3 + 4 | −0.0168 | −0.5046 |
| New club IV | Merging Club 4 + 5 | 0.0458 | 1.6717 |
| New club V | Merging Club 5 + 6 | −0.1970 | −15.015 *** |
| New club VI | Merging Club 6 + 7 | −0.7617 | −291.984 *** |
| Panel C: Final club classifications | coef. | ||
| Club 1 | Argentina, Brazil, Australia, Egypt, Canada, France, India, Indonesia, South Korea, Italy, Japan, Malaysia, Mexico, Germany, the United States, South Africa, and the United Kingdom | 0.055 | 1.365 |
| Club 2 | Austria, Norway, Bolivia, Costa Rica, Cambodia, Belgium, Cameroon, Colombia, New Zealand, Denmark, Ecuador, Tanzania, El Salvador, Finland, Chile, Spain, Gabon, Greece, Guatemala, Guinea, Honduras, Ireland, Israel, Jordan, Kenya, Lebanon, Mauritania, Morocco, Mozambique, the Netherlands, Hungary, Oman, Panama, Romania, Paraguay, Peru, Poland, Portugal, Sri Lanka, Qatar, Senegal, Sweden, Singapore, Switzerland, Tunisia, Venezuela, and Zambia | −0.017 | −0.505 |
| Club 3 | Albania, Bhutan, Bulgaria, Burundi, Fiji, Gambia, Jamaica, Luxembourg, Nicaragua, Niger, North Korea, Zimbabwe, Cuba, Sierra Leone, Haiti, and Liberia | 0.123 | 5.140 |
| Club 4 | Barbados, Djibouti, Malta, Madagascar, Myanmar, Philippines, Somalia, and Tonga | 0.039 | 0.750 |
| Not convergent Group 5 | China and Cyprus | −0.878 | −59.077 ** |
| Variables | Descriptive Statistics | ||||
|---|---|---|---|---|---|
| Obs. | Mean | Std.-Dev. | Min. | Max. | |
| EFPG | 1200 | 3.94 × 107 | 3.92 × 107 | 1216662 | 2.67 × 108 |
| TO | 1200 | 82.313 | 50.7916 | 23.98087 | 437.3267 |
| EQ | 1200 | 0.8165417 | 0.1739464 | 0.2 | 1.07 |
| GDP | 1200 | 1.59 × 1011 | 2.25 × 1011 | 2.06 × 109 | 1.47 × 1012 |
| ECI | 1200 | 3.053186 | 1.019706 | 0.8217199 | 5.32899 |
| NONREC | 1200 | 1.83 × 107 | 2.56 × 107 | 25313.77 | 1.44 × 108 |
| POP | 1200 | 1.31 × 107 | 1.10 × 107 | 476278 | 5.00 × 107 |
| URB | 1200 | 62.74421 | 22.13819 | 15.546 | 100 |
| Variables | Skewness | Kurtosis | Shapiro–Wilk Test | Shapiro–Francia Test | Obs | ||
|---|---|---|---|---|---|---|---|
| Statistic | Statistic | ||||||
| LEFPG | −0.2046549 | 3.554171 | 0.98945 | *** | 0.98966 | *** | 1200 |
| LTO | 0.8929333 | 4.984875 | 0.95518 | *** | 0.95518 | *** | 1200 |
| LEQ | −1.535696 | 6.753622 | 0.86400 | *** | 0.86422 | *** | 1200 |
| LGDP | −0.35884 | 2.747878 | 0.96742 | *** | 0.96836 | *** | 1200 |
| LECI | −0.331808 | 2.672438 | 0.97726 | *** | 0.97778 | *** | 1200 |
| LNONREC | −0.581245 | 2.368702 | 0.94329 | *** | 0.94420 | *** | 1200 |
| LPOP | −0.377437 | 3.302496 | 0.97973 | *** | 0.98030 | *** | 1200 |
| LURB | −1.152019 | 3.569148 | 0.88414 | *** | 0.88518 | *** | 1200 |
| Variables | VIF-Test | Cross-Sectional Dependence (CSD-Test) | |||
|---|---|---|---|---|---|
| VIF | Mean VIF | CD Test | Corr | Abs (Corr) | |
| EFPG | n.a. | 2.31 | 79.34 *** | 0.472 | 0.581 |
| TO | 1.54 | 58.91 *** | 0.351 | 0.493 | |
| EQ | 2.57 | 23.30 *** | 0.139 | 0.387 | |
| GDP | 3.26 | 155.50 *** | 0.926 | 0.926 | |
| ECI | 2.23 | 7.61 *** | 0.045 | 0.393 | |
| NONREC | 3.11 | 56.00 *** | 0.339 | 0.649 | |
| POP | 1.46 | 125.64 *** | 0.748 | 0.957 | |
| URB | 1.97 | 100.58 *** | 0.634 | 0.825 | |
| Homogeneity Slope test | |||||
| Models | Delta | Adjusted Delta | |||
| Model I | 26.075 *** | 28.305 *** | |||
| CIPS | CIPS | ||||
|---|---|---|---|---|---|
| Variables | Lags | (Zt-Bar) | Variables | Lags | (Zt-Bar) |
| EFPG | 0 | −1.165 | LEFPG | 0 | −3.483 *** |
| 1 | 1.093 | 1 | −0.537 | ||
| TO | 0 | −1.218 | LTO | 0 | −1.874 ** |
| 1 | −2.462 | 1 | −3.257 *** | ||
| EQ | 0 | −5.871 *** | LEQ | 0 | −5.020 *** |
| 1 | −3.855 ** | 1 | −2.824 *** | ||
| GDP | 0 | 7.423 | LGDP | 0 | −1.161 |
| 1 | 4.503 | 1 | −2.349 *** | ||
| ECI | 0 | 2.807 | LECI | 0 | −1.119 |
| 1 | 4.079 | 1 | −2.469 *** | ||
| NONREC | 0 | 4.158 | LNONREC | 0 | −2.041 *** |
| 1 | 4.055 | 1 | −2.483 *** | ||
| POP | 0 | 5.117 | LPOP | 0 | −1.408 ** |
| 1 | −8.005 *** | 1 | −7.868 *** | ||
| URB | 0 | −3.110 *** | LURB | 0 | −6.790 *** |
| 1 | −2.113 ** | 1 | −6.002 *** | ||
| Kao Cointegration Test | Pedroni Cointegration Test | ||||
|---|---|---|---|---|---|
| Estimators | t-Statistic | Prob. | Estimators | t-Statistic | Prob. |
| ADF | −5.3062 | 0.0000 *** | Modified Phillips–Perron t | 7.0314 | 0.0000 *** |
| Residual variance | 0.00164 | Phillips–Perron t | −11.9530 | 0.0000 *** | |
| HAC variance | 0.00135 | Augmented Dickey-Fuller t | −10.6734 | 0.0000 *** | |
| Westerlund panel cointegration test | |||||
| Statistic | Value | Z-value | Robust p−value | ||
| Gt | −2.426 | 0.139 | 0.002 | *** | |
| Ga | −6.664 | 5.690 | 0.041 | ** | |
| Pt | −14.757 | 1.557 | 0.080 | * | |
| Pa | −4.228 | 5.892 | 0.140 | ||
| Quantile | Country |
|---|---|
| Gabon, Mauritania, Panama, and Costa Rica | |
| Zambia, El Salvador, Jordan, Honduras, Guinea, Cambodia, Senegal, and Lebanon | |
| Mozambique, Cameroon, Tunisia, Madagascar, Paraguay, Guatemala, Sri Lanka, New Zealand, Bolivia, Ireland, Ecuador, and Singapore | |
| Oman, Norway, Finland, Israel, Kenya, Hungary, Qatar, Switzerland, Morocco, Denmark, Portugal, and Tanzania | |
| Austria, Peru, Sweden, Chile, Greece, Romania, Belgium, and Venezuela | |
| Colombia, the Netherlands, Poland, and Spain |
| Variables | Quantiles | OLS | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 10th | 25th | 50th | 75th | 90th | Fixed Effects | |||||||
| LTO | −0.0790 | *** | −0.0950 | *** | −0.066 | ** | −0.0872 | ** | −0.0356 | −0.1775 | *** | |
| LEQ | 0.0700 | 0.1074 | −0.154 | *** | −1.0933 | *** | −1.6452 | *** | −0.4141 | *** | ||
| LGDP | 0.2603 | *** | 0.2875 | *** | 0.2646 | *** | 0.3675 | *** | 0.3897 | *** | 0.2619 | *** |
| LECI | 0.2243 | *** | −0.005 | −0.245 | *** | −0.1779 | ** | −0.1949 | ** | −0.1476 | *** | |
| LNONREC | 0.1306 | *** | 0.1617 | *** | 0.2441 | *** | 0.2095 | *** | 0.3059 | *** | 0.2774 | *** |
| LPOP | 0.5836 | *** | 0.4787 | *** | 0.3750 | *** | 0.2670 | *** | 0.1575 | *** | 0.2899 | *** |
| LURB | −0.5802 | * | −0.207 | *** | −0.342 | *** | −0.4041 | *** | −0.8012 | *** | −0.4779 | ** |
| Constant | −0.3712 | −0.207 | *** | 1.6245 | *** | 1.6225 | *** | 1.8114 | *** | 1.4410 | *** | |
| Pseudo R2 | 0.9312 | 0.8831 | 0.8802 | 0.8519 | 0.8689 | 0.8661 | ||||||
| Variables | DOLS | FMOLS | MM-Estimation |
|---|---|---|---|
| LTO | −0.0344 ** | −0.0221 ** | −0.0627 *** |
| LEQ | −0.0163 *** | −0.0102 *** | −0.0265 ** |
| LGDP | 0.3548 *** | 0.3278 *** | 0.2796 *** |
| LECI | −0.2338 *** | −0.2660 *** | −0.1336 ** |
| LNONREC | 0.2264 *** | 0.2406 *** | 0.1341 *** |
| LPOP | 0.2498 *** | 0.1877 *** | 0.5035 *** |
| LURB | −0.4917 *** | −0.4164 *** | −0.1509 *** |
| Constant | 2.4329 *** | ||
| R2 | 0.9250 | 0.9198 | 0.9384 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kazemzadeh, E.; Fuinhas, J.A.; Koengkan, M.; Osmani, F. The Heterogeneous Effect of Economic Complexity and Export Quality on the Ecological Footprint: A Two-Step Club Convergence and Panel Quantile Regression Approach. Sustainability 2022, 14, 11153. https://doi.org/10.3390/su141811153
Kazemzadeh E, Fuinhas JA, Koengkan M, Osmani F. The Heterogeneous Effect of Economic Complexity and Export Quality on the Ecological Footprint: A Two-Step Club Convergence and Panel Quantile Regression Approach. Sustainability. 2022; 14(18):11153. https://doi.org/10.3390/su141811153
Chicago/Turabian StyleKazemzadeh, Emad, José Alberto Fuinhas, Matheus Koengkan, and Fariba Osmani. 2022. "The Heterogeneous Effect of Economic Complexity and Export Quality on the Ecological Footprint: A Two-Step Club Convergence and Panel Quantile Regression Approach" Sustainability 14, no. 18: 11153. https://doi.org/10.3390/su141811153
APA StyleKazemzadeh, E., Fuinhas, J. A., Koengkan, M., & Osmani, F. (2022). The Heterogeneous Effect of Economic Complexity and Export Quality on the Ecological Footprint: A Two-Step Club Convergence and Panel Quantile Regression Approach. Sustainability, 14(18), 11153. https://doi.org/10.3390/su141811153








