Wind Tunnel Tests of an Aeroelastic Model of a Long-Span Transmission Tower
Abstract
:1. Introduction
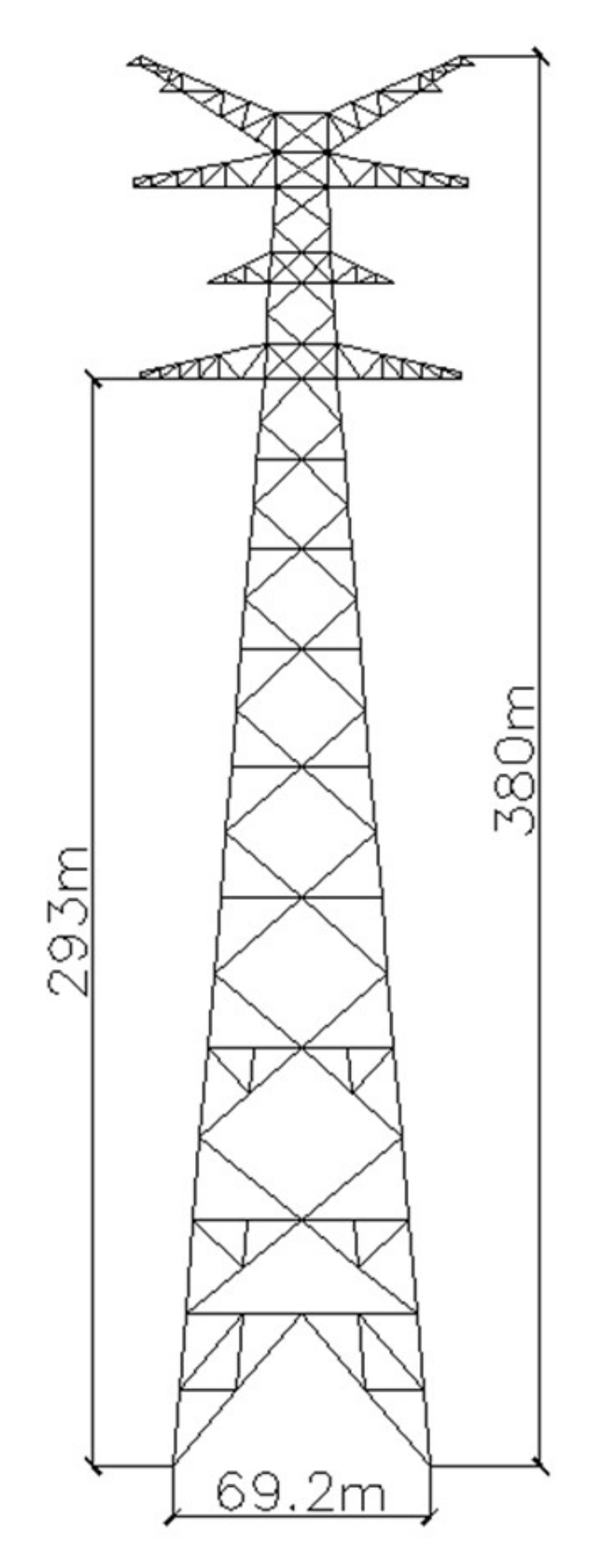
2. Finite Element Modeling of a Transmission Tower
3. Aeroelastic Model Test
3.1. Aeroelastic Model
3.2. Measuring Points and Test Methods
3.3. Natural Frequency and Damping
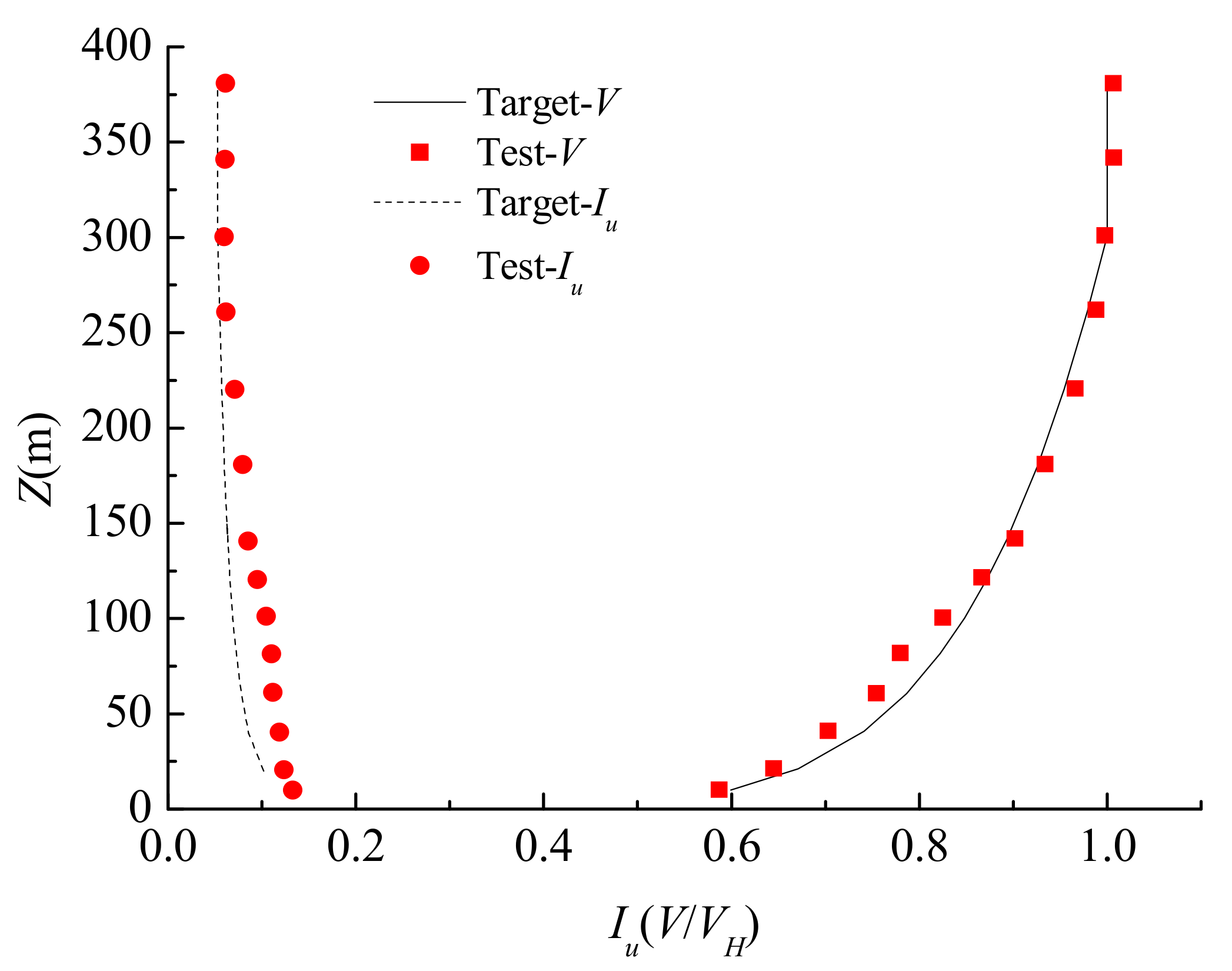
3.4. Wind Field and Test Conditions
4. Results of Wind-Induced Response
4.1. Verification of Test Results
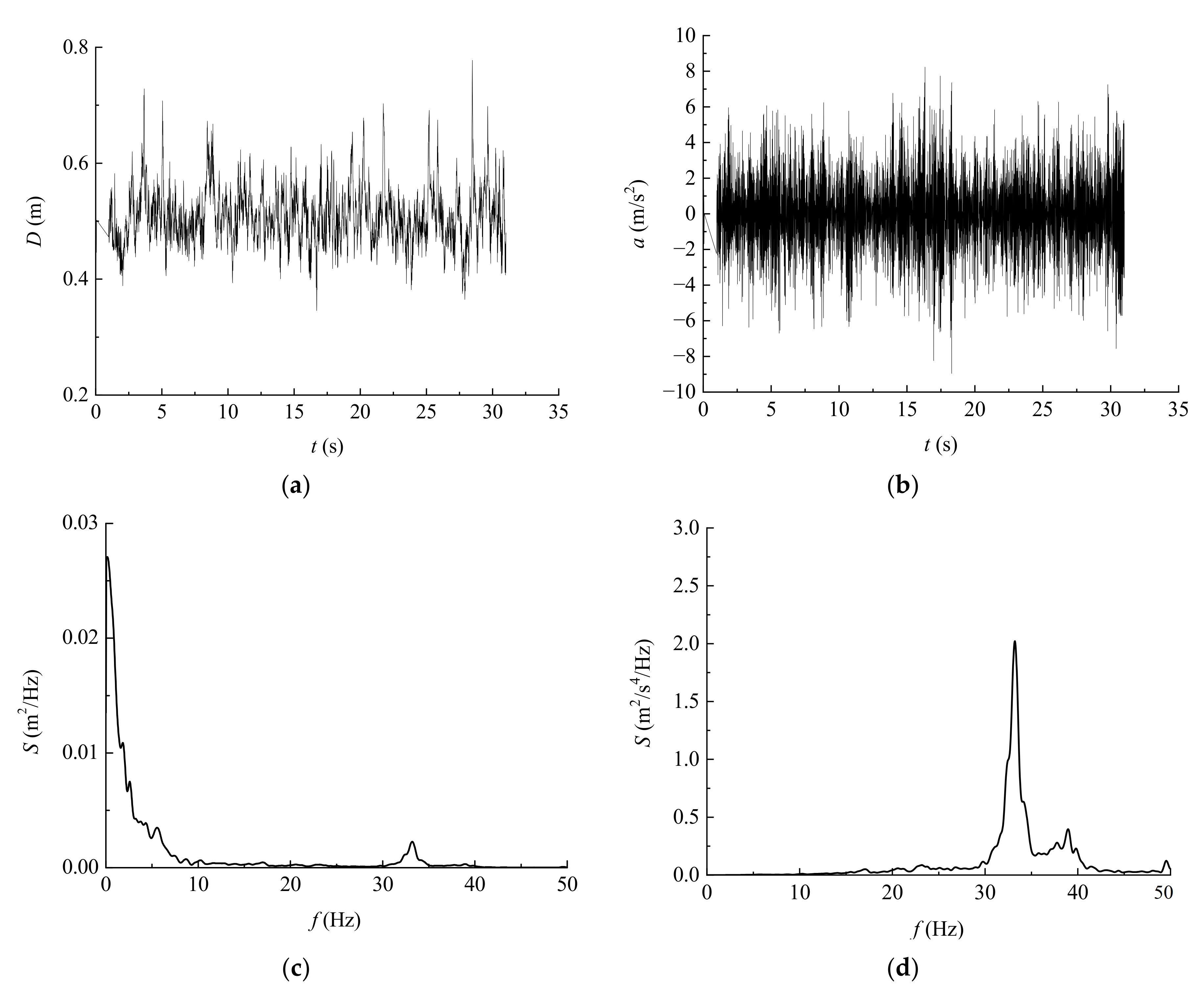
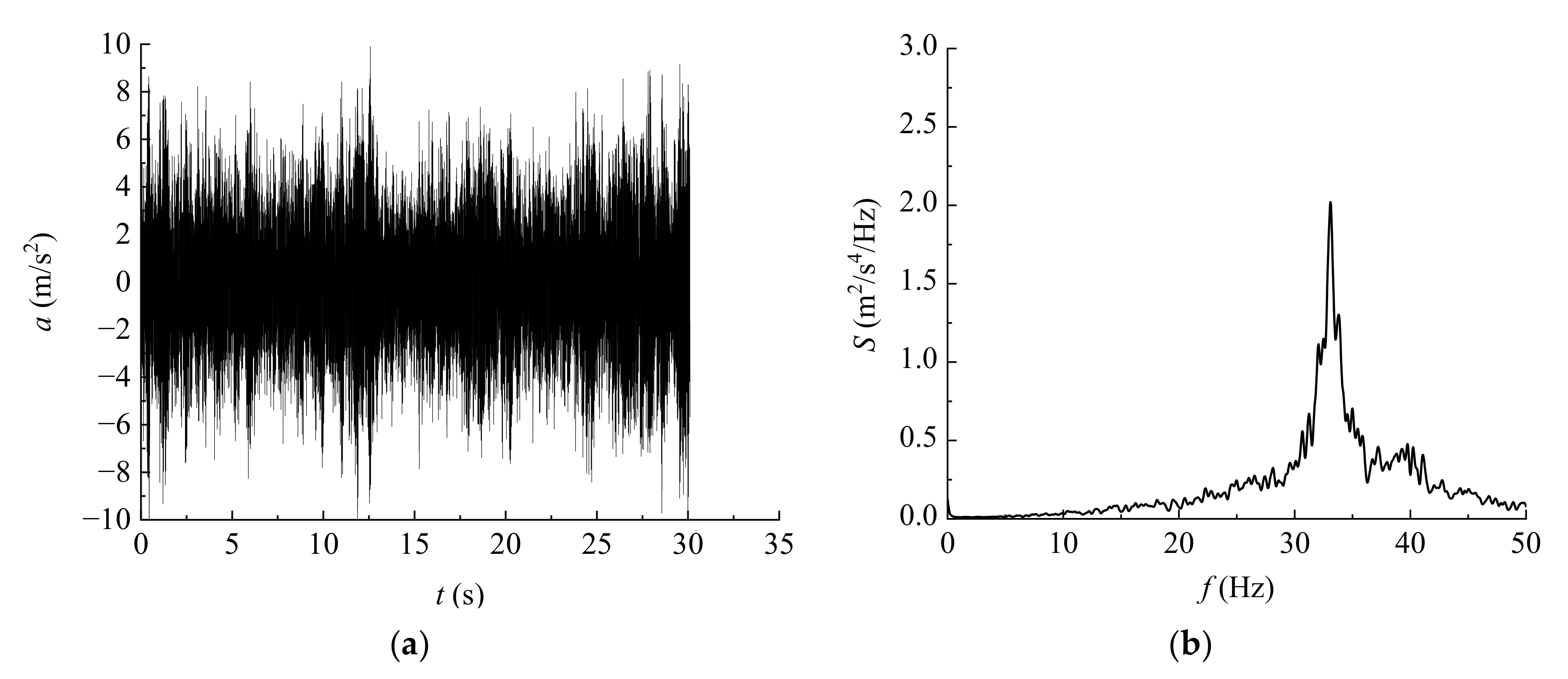
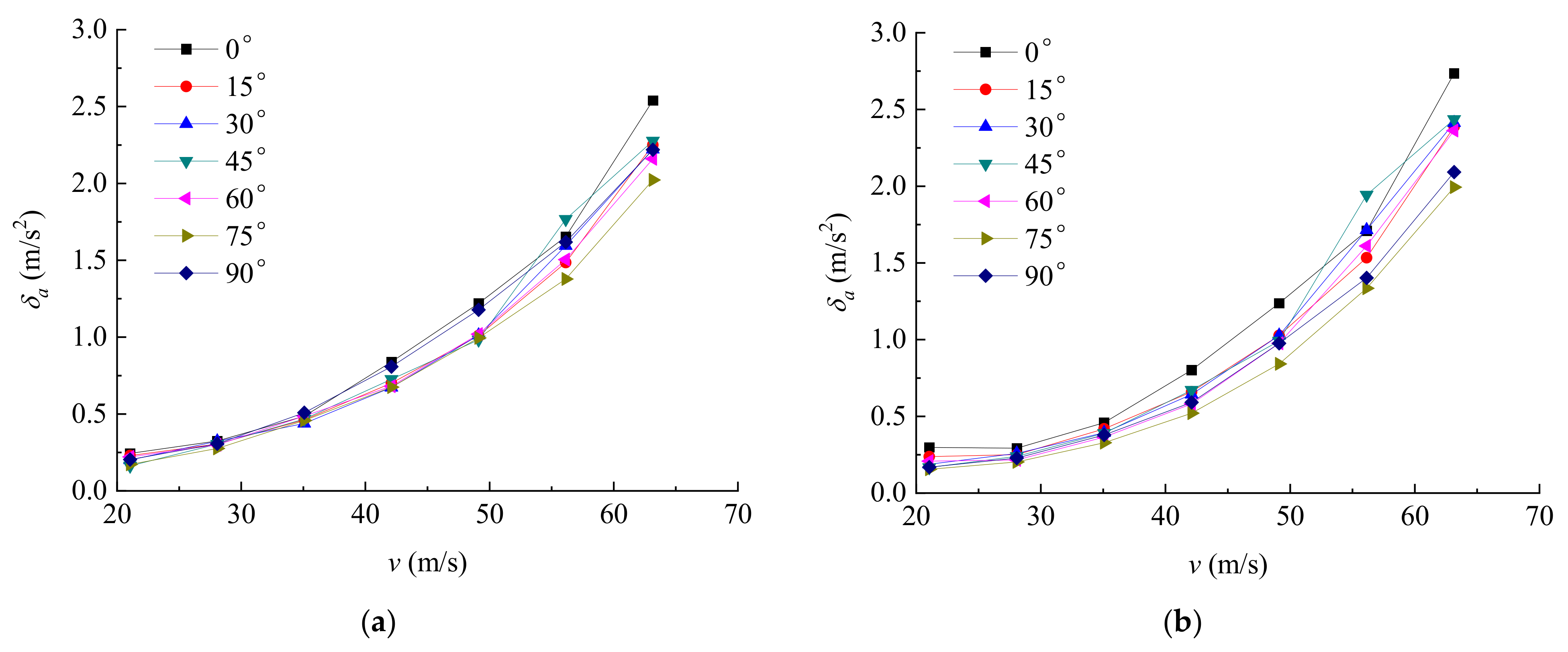
4.2. Acceleration Response
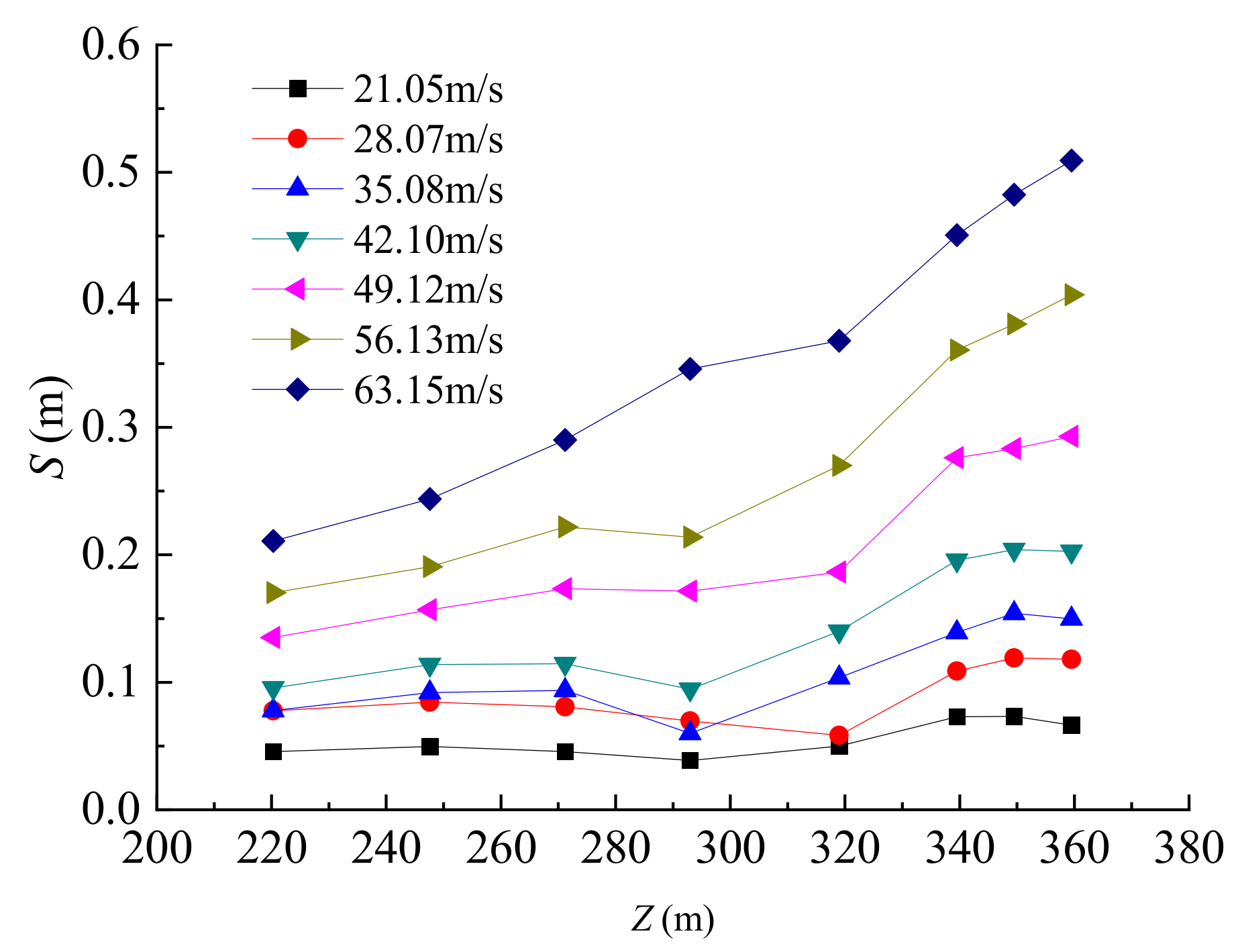
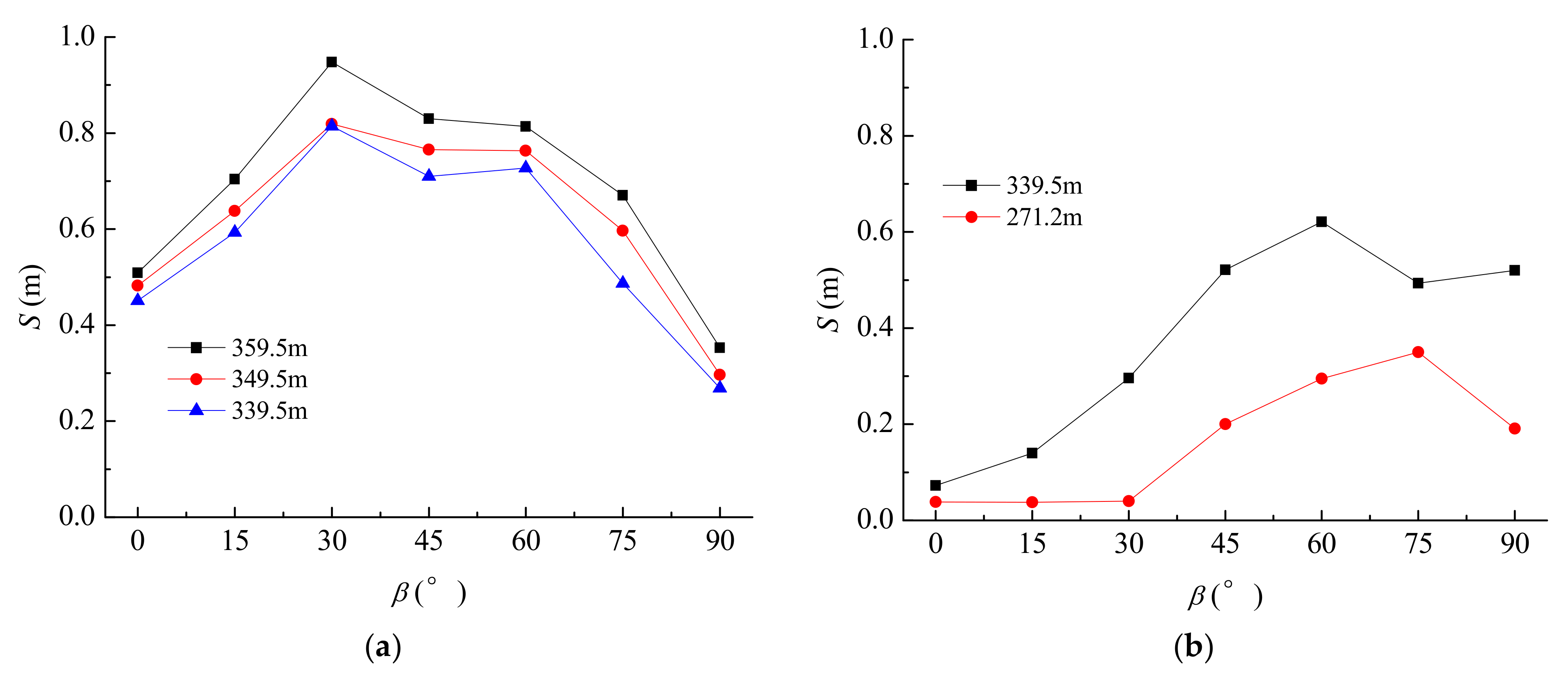
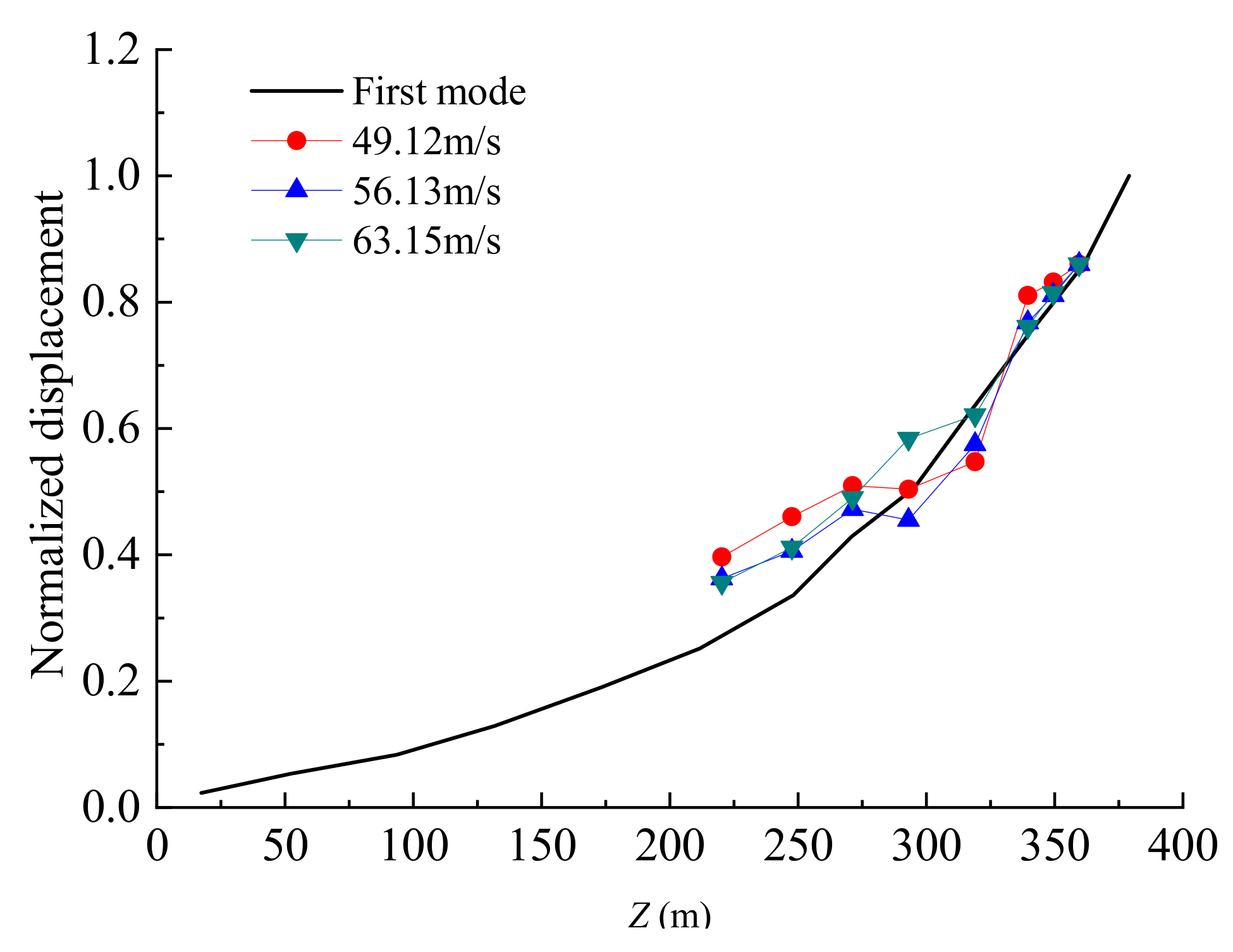
4.3. Displacement Response
5. Gust Response Factor
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Xie, Q.; Zhang, Y.; Li, J. Investigation on Tower Collapses of 500 kV Ren-Shang 5237 Transmission Line Caused by Downburst. Power Syst. Technol. 2006, 30, 59–63. [Google Scholar]
- Yin, H.J. Wind-Induced Response and Vibration Control of Long-Span Transmission System. Master’s Thesis, Wuhan University of Technology, Wuhan, China, 2003. [Google Scholar]
- Guo, Y. Study on Wind-Induced Dynamic Response and Vibration Control of Long Span Transmission Line System. Master’s Thesis, Zhejiang University, Hangzhou, China, 2006. [Google Scholar]
- Jung, S.H.; Huh, J.H. A novel on transmission line tower big data analysis model using altered K-means and ADQL. Sustainability 2019, 11, 3499. [Google Scholar] [CrossRef]
- Ballio, G.; Maberini, F.; Solari, G. A 60 Year Old, 100 m High Steel Tower: Limit States under Wind Actions. J. Wind Eng. Ind. Aerod. 1992, 43, 2089–2100. [Google Scholar] [CrossRef]
- Liu, Q.; Yang, J.C.; Zhou, L.B. Research of coupling viberation between stel-tower Frame and Conductor for HV overhead lines. Electr. Power China 1997, 30, 9–49. [Google Scholar]
- He, M.J.; Yang, B.F. Site Vibration Experiment of Jiang Yin 500kV Guyed Transmission Tower. Struct. Eng. 2003, 4, 74–79. [Google Scholar]
- Yasui, H.; Marukawa, H.; Momomura, Y.; Ohkuma, T. Analytical study on wind-induced vibration of power transmission towers. J. Wind Eng. Ind. Aerod. 1999, 83, 431–441. [Google Scholar] [CrossRef]
- Loredo-Souza, A.M.; Davenport, A.G. The Influence of The Design Methodology in The Response of Transmission Towers to Wind Loading. J. Wind Eng. Ind. Aerod. 2003, 91, 995–1005. [Google Scholar] [CrossRef]
- Yao, D.; Shen, G.H.; Pan, F.; Xing, Y.; Guo, Y. Wind-Induced Dynamic Response of Transmission Tower Using Vector-Form Intrinsic Finite Element Method. Eng. Mech. 2015, 32, 63–70. [Google Scholar]
- Zhu, N.; Sparling, B.F.; King, J.P.C. Comparison of aeroelastic wind tunnel tests and frequency domain analyses of guyed mast dynamics response. Can. J. Civil. Eng 2011, 38, 984–997. [Google Scholar]
- Yang, F.L.; Deng, H.Z.; Niu, H.W.; Zhang, H.; Zhu, B. Wind Tunnel Tests on Wind Loads Acting on an Angled Steel Triangular Transmission Tower. J. Wind Eng. Ind. Aerodyn. 2016, 156, 93–103. [Google Scholar] [CrossRef]
- Carril, C.F., Jr.; Isyumov, N.; Brasil, R.M. Experimental study of the wind forces on rectangular latticed communication towers with antennas. J. Wind Eng. Ind. Aerod. 2003, 91, 1007–1022. [Google Scholar] [CrossRef]
- Wang, S.C.; Sun, B.N.; Lou, W.J.; Ye, Y. Wind Tunnel Test and Theoretical Analysis on Aeroelastic Model of Single-Rod Transmission Tower. J. Zhejiang Univ. Eng. Sci. 2005, 39, 88–92. [Google Scholar]
- Deng, H.Z.; Zhu, S.Y.; Chen, X.M.; Wang, Z.M. Wind Tunnel Investigation on Model of Long Span Transmission Line System. J. Tongji Univ. 2003, 31, 132–137. [Google Scholar]
- Cheng, Z.J.; Fu, G.H.; Lou, W.J.; Sun, B.N. Research for the Wind Force on High-Rise Latticed Tower. J. Exp. Mech. 2000, 15, 51–55. [Google Scholar]
- Fu, G.H.; Cheng, Z.J.; Sun, B.N.; Tang, J.C. Research for the Wind-Induced Vibration of the Overhead Power Transmission Line System. Exp. Meas. Fluid Mech. 2001, 15, 16–22. [Google Scholar]
- Li, Z.L.; Xiao, Z.Z.; Han, F.; Yan, Z.T. Aeroelastic Model Design and Wind Tunnel Tests of 1000 kV Hanjiang Long Span Transmission Line System. Power Syst. Technol. 2008, 32, 5–9. [Google Scholar]
- Guo, Y.; Sun, B.N.; Ye, Y.; Shen, G.H.; Lou, W.J. Wind Tunnel Test on Aeroelastic Model of Long Span Transmission Line System. J. Zhejiang Univ. Eng. Sci. 2007, 41, 1482–1486. [Google Scholar]
- Xiong, T.H.; Liang, S.G.; Zou, L.H. Wind Loading Identification of Transmission Towers Based on Wind Tunnel Tests of Full Aero-Elastic Model. J. Build. Struct. 2010, 31, 48–54. [Google Scholar]
- Zhao, G.F.; Xie, Q.; Liang, S.G.; Li, J. Wind Tunnel Test on Wind-induced Nonlinear Vibrations of High-voltage Transmission Tower-line Coupling System. J. Tongji Univ. Nat. Sci. 2009, 37, 1157–1164. [Google Scholar]
- Song, J.; Liang, S.G.; Mei, X.H.; Zou, L. Wind-induced tension and deflection of multi-span bundled transmission conductors using aeroelastic model wind tunnel test. Eng. Struct. 2022, 256, 114011. [Google Scholar] [CrossRef]
- Li, Z.L.; Ren, K.; Xiao, Z.Z.; Wang, Z.S.; Yu, K. Aeroelastic Model Design and Wind Tunnel Tests of UHV Transmission Line System. Acta Aerodyn. Sin. 2011, 29, 102–106. [Google Scholar]
- Liang, Z.P.; Li, Z.L. An Aeroelastic Model Design of Ultra-High Voltage Power Transmission Line Systems. J. Chongqing Univ. 2009, 32, 131–136. [Google Scholar]
- Xiao, Z.Z.; Li, Z.L.; Wang, Z.S.; Yan, Z.T.; Ren, K. Wind-induced Vibration Analysis of UHV Transmission Tower Based on the HFFB Tests. Eng. Mech. 2010, 27, 218–225. [Google Scholar]
- Nyquist, H. Certain topics in telegraph transmission theory. Trans. Am. Inst. Electr. Eng. 1928, 47, 617–644. [Google Scholar] [CrossRef]
- GB50009-2012; Load Code for the Design of Building Structures. China Architecture and Building Press: Beijing, China, 2012.
- Xu, J.P. Key Technology of Design and Construction of 500 Kv Overhead Long Span Transmission Tower-Line; China Electric Power Press: Beijing, China, 2022. [Google Scholar]
- GB 50135-2006; Code for Design of High-Rising Structures. China Planning Publishing House: Beijing, China, 2006.
- Zhao, S.; Yan, Z.T.; Li, Z.L.; Dong, J.Y.; Wang, L.Z. Investigation on wind-induced vibration coefficients of Sutong long span transmission tower based on wind tunnel tests. J. Build. Struct. 2019, 40, 35–44. [Google Scholar]
- Yang, F.L.; Chen, B.; Xu, Z.Y.; Xu, Q.; Shao, S. Study on Wind-induced Vibration Coefficients of the Transmission Tower in 500 kV Long Span Line Crossing the Yangtze River. Proc. CSEE 2022, 42, 2542–2556. [Google Scholar]
- Yang, J.B.; Niu, H.W.; Hua, X.G.; Wu, J.; Chen, Z.Q. Study on Wind-induced Vibration Coefficient of Steel Tubular Transmission Truss Tower. J. Build. Struct. 2010, 31 (Suppl. S2), 182–186. [Google Scholar]
- Deng, H.Z.; Zhang, Y.F.; Chen, Q.; Wu, Y. Study on Wind Vibration Response of Transmission Tower. Spec. Struct. 2008, 2008, 9–13. [Google Scholar]
- Zheng, J.S.; Wen, L.X.; Zheng, N.M.; Tang, Z.Q.; Wu, F.Q.; Cai, Q.R.; Chen, F.B. Comparison Study of Wind Effects on Transmission Tower under Typhoon Wind Field and Terrain B Wind Field. J. Hunan Univ. Nat. Sci. 2020, 47, 99–106. [Google Scholar]
- Nie, J.B.; Pan, F.; Shen, J.G.; Zheng, J.W. Study on Wind Vibration Characteristics of ±800 kV T-long Cross Transmission Tower. Spec. Struct. 2013, 30, 48–52. [Google Scholar]





| Mode | Frequency (Hz) | Axial Direction |
|---|---|---|
| 1 | 0.595 | x-axial direction |
| 2 | 0.598 | y-axial direction |
| 3 | 0.836 | Torsional direction (z-axial) |
| 4 | 0.860 | x-axial direction |
| 5 | 0.870 | y-axial direction |
| 6 | 1.172 | Torsional direction (z-axial) |
| Parameter | Scaling Ratio |
|---|---|
| Length CL | CL = 1/n |
| Density Cρs | L |
| Mass Cm | L/n3 |
| Axial rigidity CEA | 1/n2 m2 |
| Frequency Cf | Cf |
| Acceleration Ca | Cf2 CL/L |
| Velocity Cv | CfCL |
| Mode | Prototype Calculated Value (Hz) | Model Target Value (Hz) | Model Measured Value (Hz) | Model Damping Ratio |
|---|---|---|---|---|
| 1 | 0.595 | 34.51 | 33.93 | 0.011 |
| 2 | 0.598 | 34.68 | 34.23 | 0.011 |
| GB 50009-2012 | GB 50135-2006 | Wind Tunnel Test | Numerical Simulation | |
|---|---|---|---|---|
| y-direction | 1.53 | 1.40 | 1.38 | 1.37 |
| x-direction | 1.53 | 1.41 | 1.35 | 1.33 |
| βz | Height/m | Type | Method | |
|---|---|---|---|---|
| Present study | 1.38 | 380 | tube | test |
| Yang et al. [32] | 1.46 | 96.3 | tube | simulation |
| Deng et al. [33] | 1.27 | 81.3 | tube & angle | simulation |
| Yang et al. [31] | 1.38 | 385 | tube | simulation |
| Zheng et al. [34] | 1.59 | 60 | angle | test |
| Nie et al. [35] | 1.74 | 81.05 | angle | simulation |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yao, J.; Shen, G.; Tu, Z.; Chen, Y.; Lou, W. Wind Tunnel Tests of an Aeroelastic Model of a Long-Span Transmission Tower. Sustainability 2022, 14, 11613. https://doi.org/10.3390/su141811613
Yao J, Shen G, Tu Z, Chen Y, Lou W. Wind Tunnel Tests of an Aeroelastic Model of a Long-Span Transmission Tower. Sustainability. 2022; 14(18):11613. https://doi.org/10.3390/su141811613
Chicago/Turabian StyleYao, Jianfeng, Guohui Shen, Zhibin Tu, Yong Chen, and Wenjuan Lou. 2022. "Wind Tunnel Tests of an Aeroelastic Model of a Long-Span Transmission Tower" Sustainability 14, no. 18: 11613. https://doi.org/10.3390/su141811613





