A Comprehensive Literature Review on Sustainable Horizontal Collaboration
Abstract
:1. Introduction
- What are the current directions of studies dealing with HC?
- Has HC been implemented in the industrial field?
- What is the role that HC plays to ensure sustainability?
- What are the challenges and success factors of implementing HC?
- How can the performance of HC be improved?
2. Selection Procedure and Classification of Articles
- Formulation of questions: This step consists in clearly identifying the research questions answered in the present study and defining the current directions taken in horizontal collaboration by citing these practices and their performance in terms of sustainability indicators. This paper also specifies the challenges and success factors of implementing horizontal collaboration. In addition, it shows the factors responsible for enhancing the performance of collaboration.
- Inclusion criteria: This step consists in using inclusion criteria to select the main papers to be analyzed. The used criteria are:
- -
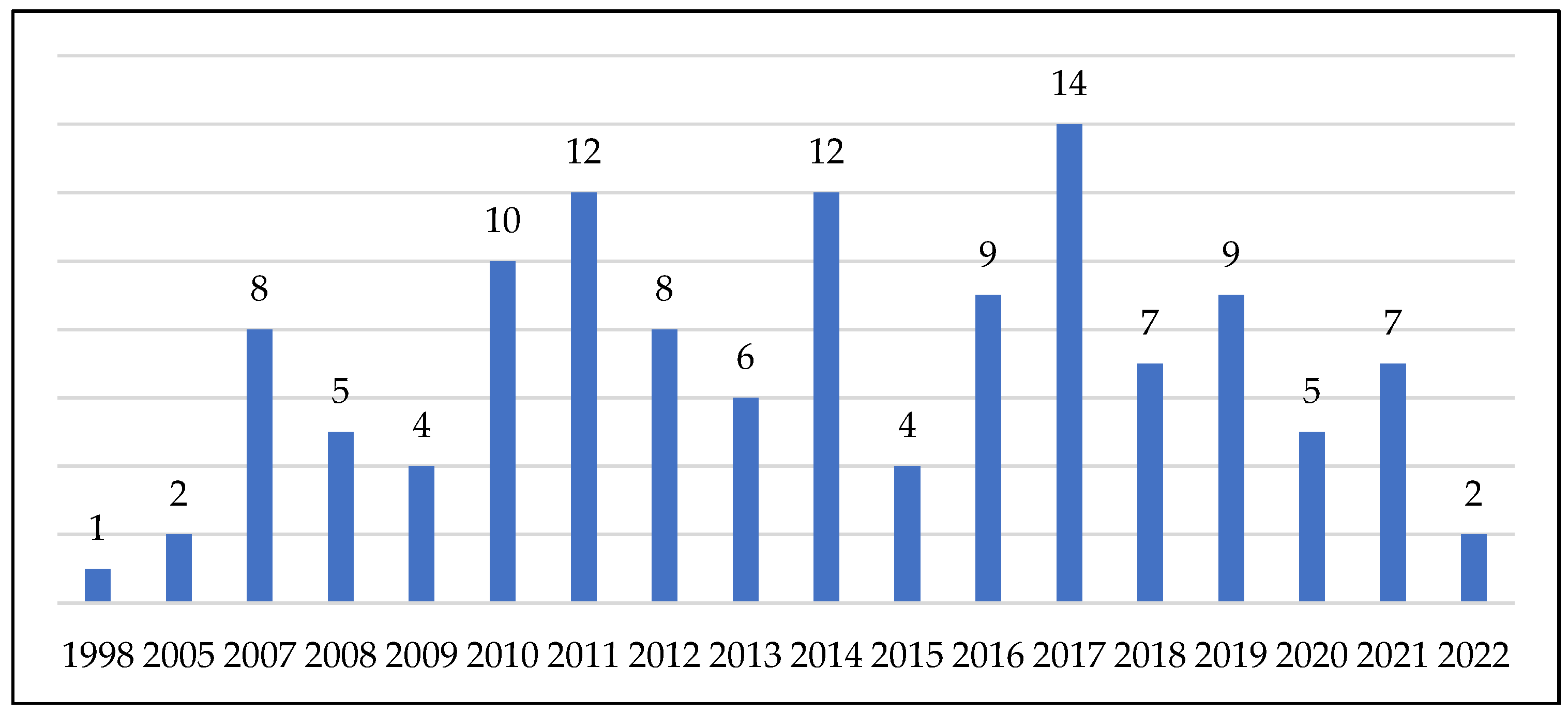
- Papers published between 1998 and 2022,
- -
- Papers published in peer-reviewed academic journals focusing on logistics,
- -
- Papers written in English,
- -
- Papers dealing with problems related to logistics and transportation in horizontal collaboration.
- Data search: In this step, data sources were chosen. The following databases were utilized: ScienceDirect, Google Scholar, Wiley Online Library, Taylor and Francis, Emerald and Springer. Then, the research was conducted by combining keywords from the two categories defined in the first step.
3. Results
3.1. Practices Used in the Collaboration
- CCC: the establishment of collaborative consolidation centers is a key development factor because it promotes goods consolidation, which guarantees economies of scale in terms of transport. It also facilitates the shared distribution of goods by grouping many suppliers on the same site to consolidate their orders [24]. Indeed, consolidation centers reduce not only transportation costs but also GHG emissions [134].
- PPM: this strategy corresponds to the placing of orders jointly for part or all of a process by one of these entities or by a third party. Successful procurement depends on the technical capacity, the financial resources of the company, the type of information systems used, and the effectiveness of the management.
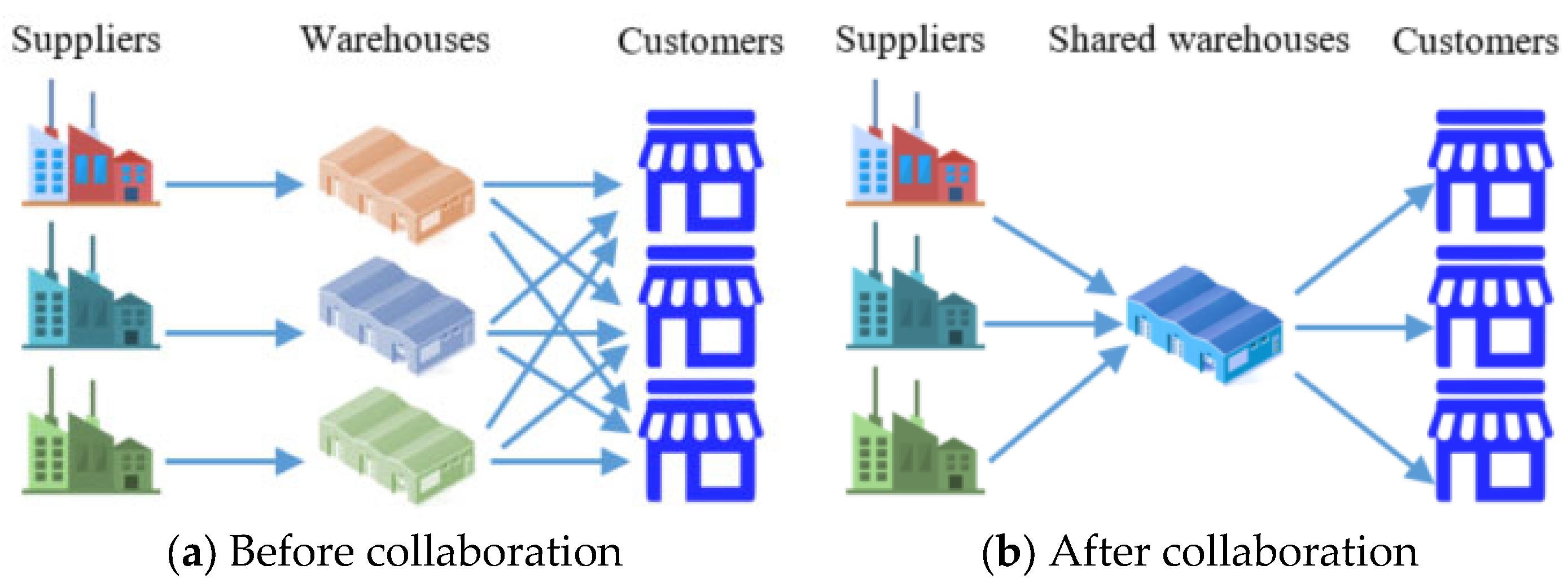
- CTM: it constitutes specific forms of logistics infrastructure such as shared distribution centers that are generally supported by the public authorities. Generally, these centers are installed in the city or on its outskirts to ensure freight distribution and improve transportation performance.
3.1.1. Transportation Collaboration
3.1.2. Collaboration in Transport and Storage
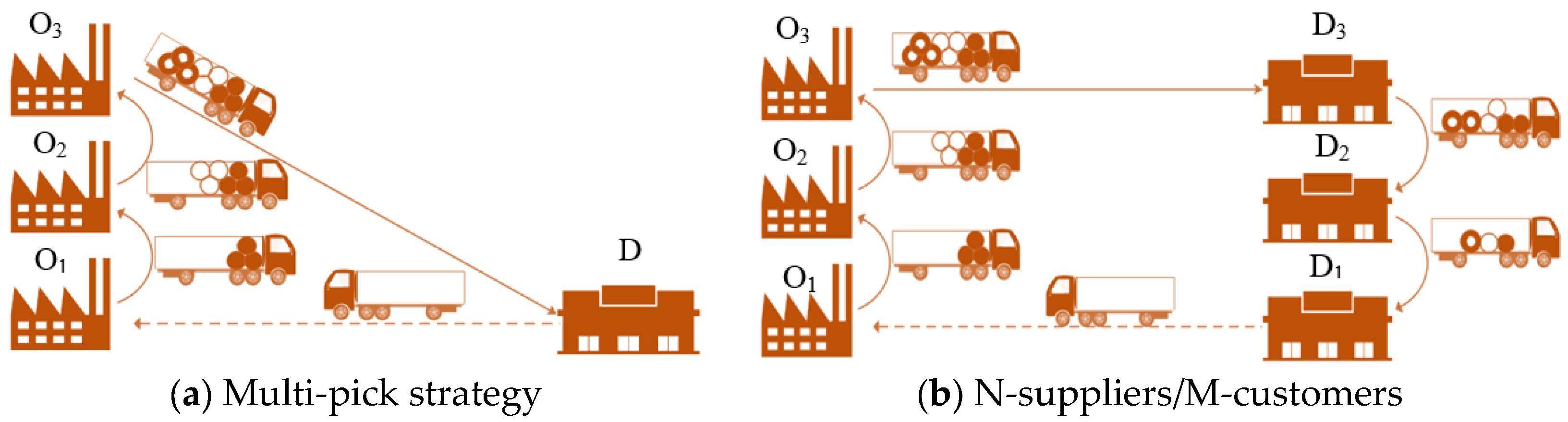
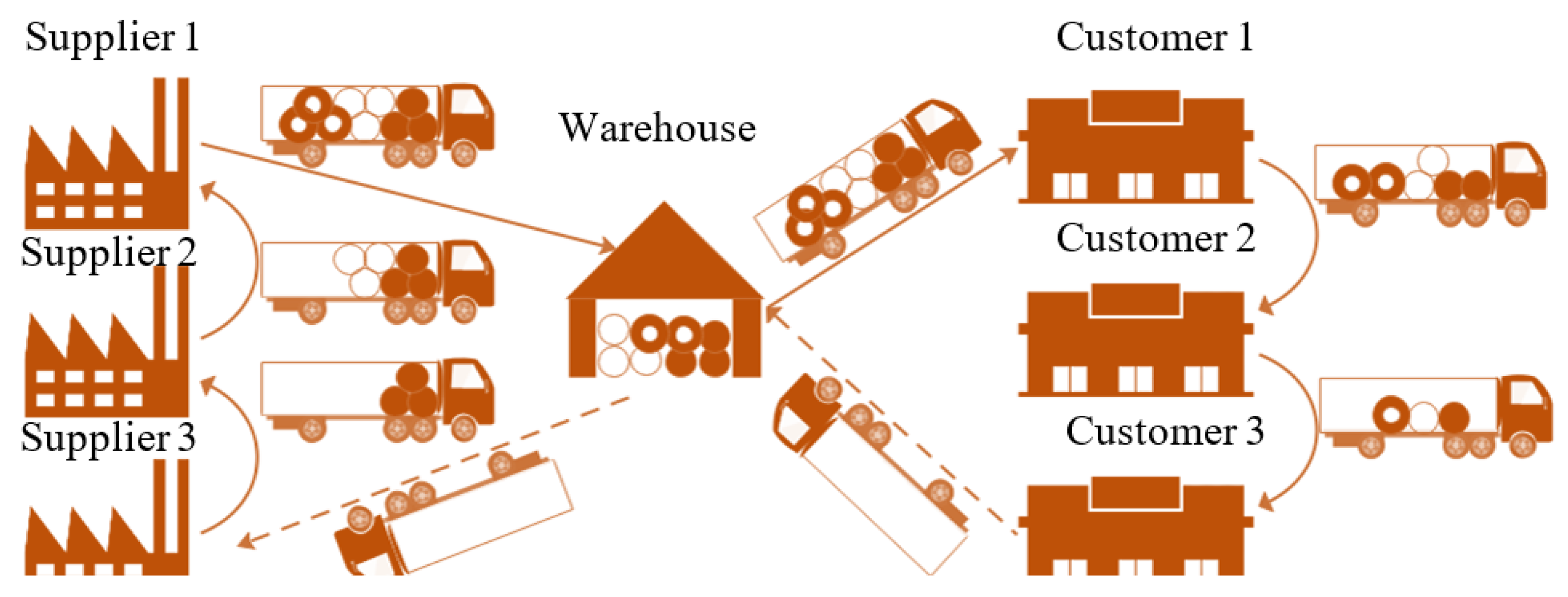
- Collaborative distribution network without vehicle rounds
- Hub-and-spoke
- The combination of multi-pick, multi-drop, and warehouse pooling
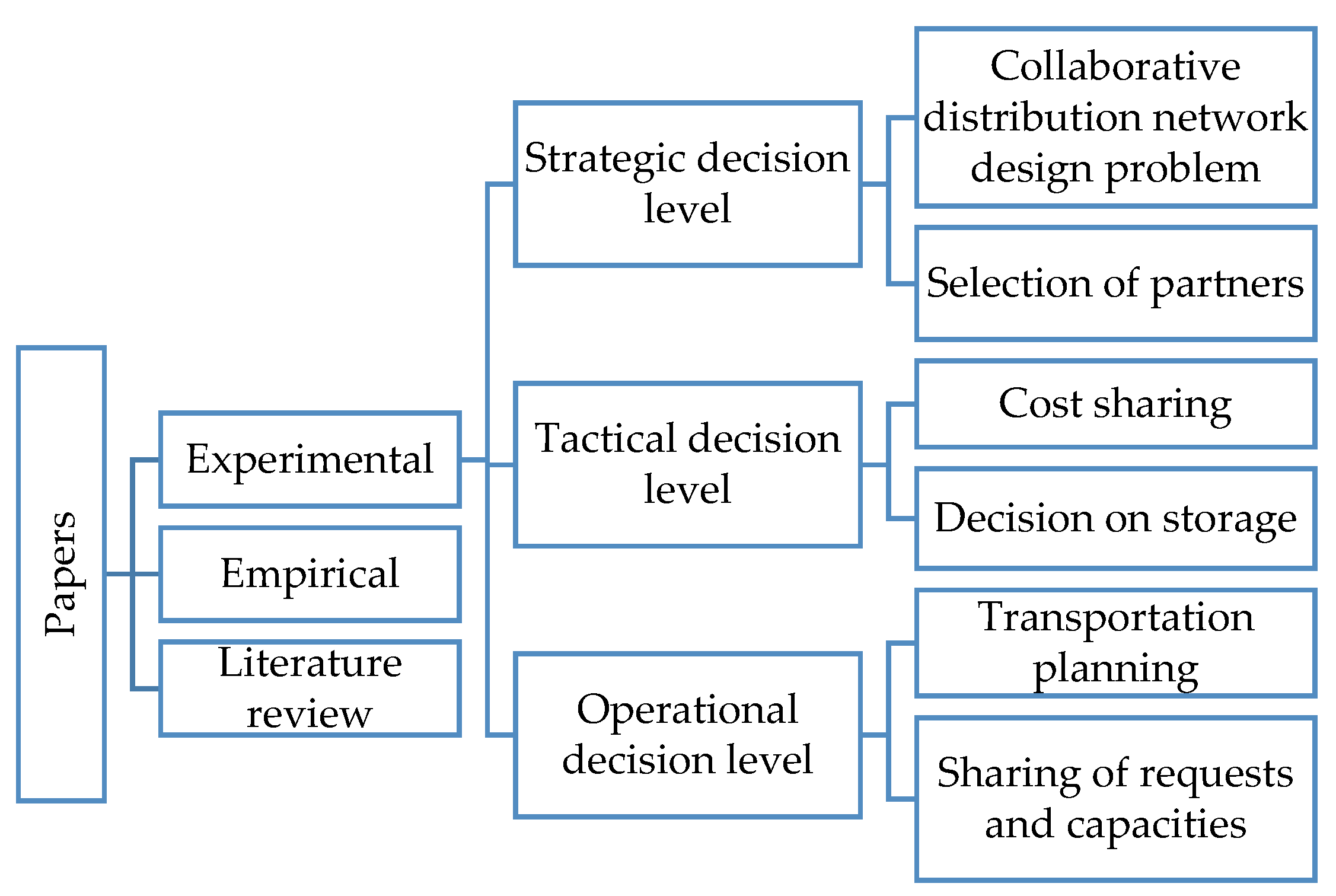
3.2. Experimental Studies
3.2.1. Strategic Decision Level
- Collaborative distribution network design problem
- Selection of partners
3.2.2. Tactical Decision Level
- Sharing the costs of collaboration
- Storage decisions
3.2.3. Operational Decision Level
- Collaborative transportation planning
- Mechanism used to exchange requests
3.3. Empirical Studies
3.4. Literature Reviews
3.5. Sustainability Indicators
- Classification according to the Triple-P
- -
- Profit impacts: inefficiency and waste of resources, low route reliability, and on-time delivery, potentially resulting in deteriorating the quality of service, reduced economic development, and congestion, as well as low accessibility to the city.
- -
- Impacts on the planet: polluting emissions, use of non-renewable natural resources, waste, and loss of wildlife habitat.
- -
- Impacts on people: physical consequences of pollutant emissions on public health, injuries, and deaths resulting from traffic accidents, increased nuisance, reduced air quality, and damaged buildings and infrastructure.
- Classification according to dimensions
- -
- Economic impacts: logistical costs, increased traffic congestion, lost time and inefficiencies for person or company doing the transport, unreliable delivery, inadequate use of resources.
- -
- Environmental impacts: emissions of pollutants that contribute to global climate change (e.g., carbon dioxide (CO2)), use of non-renewable resources (fossil fuels, aggregates, soil, etc.), waste materials such as tires, oil, and other materials, loss of wildlife habitat, and threats to wildlife.
- -
- Social impacts: health impacts (local air pollution, traffic accidents, and noise pollution), traffic congestion, damaging the buildings and infrastructure (vibration, traffic accidents, degradation of pavement due to the weight of commercial vehicles), deteriorating quality-of-life issues (loss of sites, visual intrusion, physical barrier, stench, vibration).
4. Success and Failure Factors
4.1. Success Conditions
- Partner selection: the first step that should be made is to choose the appropriate partners [18] based on several criteria (size of the partner, financial status, number of joint customers, reputation, visions, etc.).
- Product compatibility: this condition is essential in order to group products in the same trucks and in the same warehouses under the same storage conditions (temperature, humidity, etc.) [130].
- Common objectives: the partners participating in pooling must have the same objectives and the same visions [5].
- Common customers: collaboration with partners who have common customers ensure the massification of flows by grouping goods from several origins and transporting them to the same destination [131].
- Information sharing: pooling refers to collaboration with partners who may be in competition, which makes information sharing a critical factor for all partners [52]. This problem can be overcome by entrusting the coordination and management of pooling to a neutral organizer such as the logistics providers. In addition, a minimum of trust is necessary to improve the performance of pooling [123].
- A fair system of gain sharing: this factor can prevent the success and continuity of pooling. Therefore, before collaboration, it is essential to find an approach that ensures the equitable sharing of gains [124].
4.2. Collaboration Performance Enhancers
- The relaxation of delivery conditions
- The use of a heterogeneous fleet of vehicles
- The size of the collaboration
- The degree of collaboration
- The multi-modal transport
- The increase in the number of warehouses
- The resilience and uncertainty
5. Research Insights
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Scarpin, M.R.S.; Scarpin, J.E.; Musial, N.T.K.; Nakamura, W.T. The implications of COVID-19: Bullwhip and ripple effects in global supply chains. Int. J. Prod. Econ. 2022, 251, 108523. [Google Scholar] [CrossRef]
- Handfield, R.B.; Graham, G.; Burns, L. Corona virus, tariffs, trade wars and supply chain evolutionary design. Int. J. Oper. Prod. Manag. 2020, 40, 1649–1660. [Google Scholar] [CrossRef]
- Moosavi, J.; Fathollahi-Fard, A.M.; Dulebenets, M.A. Supply chain disruption during the COVID-19 pandemic: Recognizing potential disruption management strategies. Int. J. Disaster Risk Reduct. 2022, 75, 102983. [Google Scholar] [CrossRef] [PubMed]
- Camarinha-Matos, L.M. Collaborative Networks: A Mechanism for Enterprise Agility and Resilience. In Enterprise Interoperability VI; Springer: Cham, Switzerland, 2014; pp. 3–11. [Google Scholar]
- Ouhader, H.; Kyal, M.E. Assessing the economic and environmental benefits of horizontal cooperation in delivery: Performance and scenario analysis. Uncertain Supply Chain Manag. 2020, 8, 303–320. [Google Scholar] [CrossRef]
- Pan, S.; Trentesaux, D.; Ballot, E.; Huang, G.Q. Horizontal collaborative transport: Survey of solutions and practical implementation issues. Int. J. Prod. Res. 2019, 57, 5340–5361. [Google Scholar] [CrossRef]
- Aloui, A.; Hamani, N.; Derrouiche, R.; Delahoche, L. Systematic literature review on collaborative sustainable transportation: Overview, analysis and perspectives. Transp. Res. Interdiscip. Perspect. 2021, 9, 100291. [Google Scholar] [CrossRef]
- Moutaoukil, A.; Neubert, G.; Derrouiche, R. Urban Freight Distribution: The impact of delivery time on sustainability. IFAC-PapersOnLine 2015, 48, 2368–2373. [Google Scholar] [CrossRef]
- Pan, S.; Ballot, E.; Fontane, F.; Hakimi, D. Environmental and economic issues arising from the pooling of SMEs’ supply chains: Case study of the food industry in western France. Flex Serv. Manuf. J. 2014, 26, 92–118. [Google Scholar] [CrossRef]
- Vanovermeire, C.; Sörensen, K. Measuring and rewarding flexibility in collaborative distribution, including two-partner coalitions. Eur. J. Oper. Res. 2014, 239, 157–165. [Google Scholar] [CrossRef]
- Aloui, A.; Hamani, N.; Delahoche, L. An integrated optimization approach using a collaborative strategy for sustainable cities freight transportation: A Case study. Sustain. Cities Soc. 2021, 75, 103331. [Google Scholar] [CrossRef]
- Gonzalez-Feliu, J.; Malhéné, N. Logistics Pooling for City Supply. Supply Chain Forum Int. J. 2014, 15, 2–4. [Google Scholar] [CrossRef]
- Pomponi, F.; Fratocchi, L.; Tafuri, S.R.; Palumbo, M. Horizontal Collaboration in Logistics: A Comprehensive Framework. Res. Logist. Prod. 2013, 3, 13. [Google Scholar]
- Ferrell, W.; Ellis, K.; Kaminsky, P.; Rainwater, C. Horizontal collaboration: Opportunities for improved logistics planning. Int. J. Prod. Res. 2019, 58, 4267–4284. [Google Scholar] [CrossRef]
- Senkel, M.-P.; Durand, B.; Vo, T.l. La mutualisation logistique: Entre théories et pratiques. Logistique Manag. 2013, 21, 19–30. [Google Scholar] [CrossRef]
- Verdonck, L.; Caris, A.; Ramaekers, K.; Janssens, G.K. Collaborative Logistics from the Perspective of Road Transportation Companies. Transp. Rev. 2013, 33, 700–719. [Google Scholar] [CrossRef]
- Gansterer, M.; Hartl, R.F. Collaborative vehicle routing: A survey. Eur. J. Oper. Res. 2018, 268, 1–12. [Google Scholar] [CrossRef]
- Cruijssen, F.; Cools, M.; Dullaert, W. Horizontal cooperation in logistics: Opportunities and impediments. Transp. Res. Part E Logist. Transp. Rev. 2007, 43, 129–142. [Google Scholar] [CrossRef]
- Nagarajan, M.; Sošić, G. Game-theoretic analysis of cooperation among supply chain agents: Review and extensions. Eur. J. Oper. Res. 2008, 187, 719–745. [Google Scholar] [CrossRef]
- Guajardo, M.; Rönnqvist, M. A review on cost allocation methods in collaborative transportation: M. Guajardo and M. Rönnqvist. Intl. Trans. Op. Res. 2016, 23, 371–392. [Google Scholar] [CrossRef]
- Karam, A.; Reinau, K.H.; Østergaard, C.R. Horizontal collaboration in the freight transport sector: Barrier and decision-making frameworks. Eur. Transp. Res. Rev. 2021, 13, 2021. [Google Scholar] [CrossRef]
- Chen, L.; Zhao, X.; Tang, O.; Price, L.; Zhang, S.; Zhu, W. Supply chain collaboration for sustainability: A literature review and future research agenda. Int. J. Prod. Econ. 2017, 194, 73–87. [Google Scholar] [CrossRef]
- Durach, C.F.; Kembro, J.; Wieland, A. A New Paradigm for Systematic Literature Reviews in Supply Chain Management. J. Supply Chain Manag. 2017, 53, 67–85. [Google Scholar] [CrossRef]
- Nataraj, S.; Ferone, D.; Quintero-Araujo, C.; Juan, A.A.; Festa, P. Consolidation centers in city logistics: A cooperative approach based on the location routing problem. Int. J. Ind. Eng. Comput. 2019, 10, 393–404. [Google Scholar] [CrossRef]
- Ballot, E.; Fontane, F. Reducing transportation CO2 emissions through pooling of supply networks: Perspectives from a case study in French retail chains. Prod. Plan. Control 2010, 21, 640–650. [Google Scholar] [CrossRef]
- Pan, S.; Ballot, E.; Fontane, F. The reduction of greenhouse gas emissions from freight transport by pooling supply chains. Int. J. Prod. Econ. 2013, 143, 86–94. [Google Scholar] [CrossRef]
- Groothedde, B.; Ruijgrok, C.; Tavasszy, L. Towards collaborative, intermodal hub networks. Transp. Res. Part E Logist. Transp. Rev. 2005, 41, 567–583. [Google Scholar] [CrossRef]
- Cheong, M.L.F.; Bhatnagar, R.; Graves, S.C.; Singapore-MIT Alliance, Nanyang Technological University. Logistics network design with supplier consolidation hubs and multiple shipment options. J. Ind. Manag. Optim. 2007, 3, 51–69. [Google Scholar] [CrossRef]
- Verdonck, L.; Beullens, P.; Caris, A.; Ramaekers, K.; Janssens, G.K. Analysis of collaborative savings and cost allocation techniques for the cooperative carrier facility location problem. J. Oper. Res. Soc. 2016, 67, 853–871. [Google Scholar] [CrossRef]
- Fernández, E.; Sgalambro, A. On carriers collaboration in hub location problems. Eur. J. Oper. Res. 2020, 283, 476–490. [Google Scholar] [CrossRef]
- Tuzkaya, U.R.; Önüt, S. A holonic approach based integration methodology for transportation and warehousing functions of the supply network. Comput. Ind. Eng. 2009, 56, 708–723. [Google Scholar] [CrossRef]
- Leitner, R.; Meizer, F.; Prochazka, M.; Sihn, W. Structural concepts for horizontal cooperation to increase efficiency in logistics. CIRP J. Manuf. Sci. Technol. 2011, 4, 332–337. [Google Scholar] [CrossRef]
- Wang, H.; Unnikrishnan, A.; Hernández, S.; Cheu, R.K. Capacitated Centralized Carrier Collaboration Multihub Location Problem: Tabu Search Approach. Transp. Res. Rec. 2014, 2466, 22–30. [Google Scholar] [CrossRef]
- Quintero-Araujo, C.L.; Gruler, A.; Juan, A.A.; Faulin, J. Using horizontal cooperation concepts in integrated routing and facility-location decisions. Intl. Trans. Op. Res. 2019, 26, 551–576. [Google Scholar] [CrossRef]
- Habibi, M.K.K.; Allaoui, H.; Goncalves, G. Collaborative hub location problem under cost uncertainty. Comput. Ind. Eng. 2018, 124, 393–410. [Google Scholar] [CrossRef]
- Tang, X.; Lehuédé, F.; Péton, O.; Pan, L. Network design of a multi-period collaborative distribution system. Int. J. Mach. Learn. Cyber. 2019, 10, 279–290. [Google Scholar] [CrossRef]
- Allaoui, H.; Guo, Y.; Sarkis, J. Decision support for collaboration planning in sustainable supply chains. J. Clean. Prod. 2019, 229, 761–774. [Google Scholar] [CrossRef]
- Hacardiaux, T.; Tancrez, J.-S. Assessing the environmental benefits of horizontal cooperation using a location-inventory model. Cent. Eur. J. Oper. Res. 2019, 28, 1363–1387. [Google Scholar] [CrossRef]
- Mrabti, N.; Hamani, N.; Delahoche, L. The pooling of sustainable freight transport. J. Oper. Res. Soc. 2020, 72, 2180–2195. [Google Scholar] [CrossRef]
- Aloui, A.; Hamani, N.; Derrouiche, R.; Delahoche, L. Assessing the benefits of horizontal collaboration using an integrated planning model for two-echelon energy efficiency-oriented logistics networks design. Int. J. Syst. Sci. Oper. Logist. 2021, 9, 302–323. [Google Scholar] [CrossRef]
- Aloui, A.; Hamani, N.; Delahoche, L. Designing a Resilient and Sustainable Logistics Network under Epidemic Disruptions and Demand Uncertainty. Sustainability 2021, 13, 14053. [Google Scholar] [CrossRef]
- Gargouri, M.A.; Hamani, N.; Mrabti, N.; Kermad, L. Optimization of the Collaborative Hub Location Problem with Metaheuristics. Mathematics 2021, 9, 2759. [Google Scholar] [CrossRef]
- Snoussi, I.; Hamani, N.; Mrabti, N.; Kermad, L. A Robust Mixed-Integer Linear Programming Model for Sustainable Collaborative Distribution. Mathematics 2021, 9, 2318. [Google Scholar] [CrossRef]
- Mrabti, N.; Hamani, N.; Delahoche, L. A sustainable collaborative approach to the distribution network design problem with CO2 emissions allocation. Int. J. Shipp. Transp. Logist. 2022, 14, 114–140. [Google Scholar] [CrossRef]
- Ding, J.-F.; Liang, G.-S. The choices of employing seafarers for the national shipowners in Taiwan: An empirical study. Marit. Policy Manag. 2005, 32, 123–137. [Google Scholar] [CrossRef]
- Büyüközkan, G.; Feyzioğlu, O.; Nebol, E. Selection of the strategic alliance partner in logistics value chain. Int. J. Prod. Econ. 2008, 113, 148–158. [Google Scholar] [CrossRef]
- Bahinipati, B.K.; Kanda, A.; Deshmukh, S.G. Horizontal collaboration in semiconductor manufacturing industry supply chain: An evaluation of collaboration intensity index. Comput. Ind. Eng. 2009, 57, 880–895. [Google Scholar] [CrossRef]
- Feng, B.; Fan, Z.-P.; Ma, J. A method for partner selection of codevelopment alliances using individual and collaborative utilities. Int. J. Prod. Econ. 2010, 124, 159–170. [Google Scholar] [CrossRef]
- Chen, S.H.; Wang, P.W.; Chen, C.M.; Lee, H.T. An analytic hierarchy process approach with linguistic variables for selection of an R&D strategic alliance partner. Comput. Ind. Eng. 2010, 58, 278–287. [Google Scholar] [CrossRef]
- Creemers, S.; Woumans, G.; Boute, R.; Beliën, J. Tri-Vizor Uses an Efficient Algorithm to Identify Collaborative Shipping Opportunities. Interfaces 2017, 47, 244–259. [Google Scholar] [CrossRef]
- Jouida, S.B.; Krichen, S.; Klibi, W. Coalition-formation problem for sourcing contract design in supply networks. Eur. J. Oper. Res. 2017, 257, 539–558. [Google Scholar] [CrossRef]
- Chen, W.; Goh, M. Mechanism for cooperative partner selection: Dual-factor theory perspective. Comput. Ind. Eng. 2019, 128, 254–263. [Google Scholar] [CrossRef]
- Algaba, E.; Fragnelli, V.; Llorca, N.; Sánchez-Soriano, J. Horizontal cooperation in a multimodal public transport system: The profit allocation problem. Eur. J. Oper. Res. 2019, 275, 659–665. [Google Scholar] [CrossRef]
- Audy, J.-F.; D’Amours, S.; Rousseau, L.-M. Cost allocation in the establishment of a collaborative transportation agreement—An application in the furniture industry. J. Oper. Res. Soc. 2011, 62, 960–970. [Google Scholar] [CrossRef]
- Dahlberg, J.; Göthe-Lundgren, M.; Engevall, S. A note on the nonuniqueness of the Equal Profit Method. Appl. Math. Comput. 2017, 308, 84–89. [Google Scholar] [CrossRef]
- Dai, B.; Chen, H. Profit allocation mechanisms for carrier collaboration in pickup and delivery service. Comput. Ind. Eng. 2012, 62, 633–643. [Google Scholar] [CrossRef]
- Vos, B.D.; Raa, B. Stability Analysis of Cost Allocation Methods for Inventory Routing. IFAC-PapersOnLine 2018, 51, 1682–1688. [Google Scholar] [CrossRef]
- Defryn, C.; Sörensen, K.; Dullaert, W. Integrating partner objectives in horizontal logistics optimisation models. Omega 2019, 82, 1–12. [Google Scholar] [CrossRef]
- Engevall, S.; Göthe-Lundgren, M.; Värbrand, P. The traveling salesman game: An application of cost allocation in a gas and oil company. Ann. Oper. Res. 1998, 82, 203–218. [Google Scholar] [CrossRef]
- Frisk, M.; Göthe-Lundgren, M.; Jörnsten, K.; Rönnqvist, M. Cost allocation in collaborative forest transportation. Eur. J. Oper. Res. 2010, 205, 448–458. [Google Scholar] [CrossRef]
- Kellner, F.; Otto, A. Allocating CO2 emissions to shipments in road freight transportation. J. Manag. Control 2012, 22, 451–479. [Google Scholar] [CrossRef]
- Krajewska, M.A.; Kopfer, H.; Laporte, G.; Ropke, S.; Zaccour, G. Horizontal cooperation among freight carriers: Request allocation and profit sharing. J. Oper. Res. Soc. 2008, 59, 1483–1491. [Google Scholar] [CrossRef]
- Leenders, B.P.J.; Velázquez-Martínez, J.C.; Fransoo, J.C. Emissions allocation in transportation routes. Transp. Res. Part D Transp. Environ. 2017, 57, 39–51. [Google Scholar] [CrossRef]
- Liu, K.; Zhou, Y.; Zhang, Z. Capacitated location model with online demand pooling in a multi-channel supply chain. Eur. J. Oper. Res. 2010, 207, 218–231. [Google Scholar] [CrossRef]
- Lozano, S.; Moreno, P.; Adenso-Díaz, B.; Algaba, E. Cooperative game theory approach to allocating benefits of horizontal cooperation. Eur. J. Oper. Res. 2013, 229, 444–452. [Google Scholar] [CrossRef]
- Massol, O.; Tchung-Ming, S. Cooperation among liquefied natural gas suppliers: Is rationalization the sole objective? Energy Econ. 2010, 32, 933–947. [Google Scholar] [CrossRef]
- Özener, O.Ö.; Ergun, Ö. Allocating Costs in a Collaborative Transportation Procurement Network. Transp. Sci. 2008, 42, 146–165. [Google Scholar] [CrossRef]
- Ramaekers, K.; Verdonck, L.; Caris, A.; Meers, D.; Macharis, C. Allocating collaborative costs in multimodal barge networks for freight bundling. J. Transp. Geogr. 2017, 65, 56–69. [Google Scholar] [CrossRef]
- Sanchez, M.; Pradenas, L.; Deschamps, J.-C.; Parada, V. Reducing the carbon footprint in a vehicle routing problem by pooling resources from different companies. NETNOMICS Econ. Res. Electron. Netw. 2016, 17, 29–45. [Google Scholar] [CrossRef]
- Vanovermeire, C.; Sörensen, K. Integration of the cost allocation in the optimization of collaborative bundling. Transp. Res. Part E Logist. Transp. Rev. 2014, 72, 125–143. [Google Scholar] [CrossRef]
- Wick, C.; Klumpp, M.; Kandel, C. Shapley value simulation for allocating ghg emission savings due to logistics pooling within ecr cooperations. In Proceedings of the European Simulation and Modelling Conference, Krakow, Poland, 7–10 June 2011; p. 6. [Google Scholar]
- Wong, H.; Oudheusden, D.V.; Cattrysse, D. Cost allocation in spare parts inventory pooling. Transp. Res. Part E Logist. Transp. Rev. 2007, 43, 370–386. [Google Scholar] [CrossRef]
- Xu, X.; Pan, S.; Ballot, E. A sharing mechanism for superadditive and non-superadditive logistics cooperation. In Proceedings of the 2013 International Conference on Industrial Engineering and Systems Management (IESM), Agdal, Morocco, 28–30 October 2013; p. 12. [Google Scholar]
- Mrabti, N.; Hamani, N.; Delahoche, L. A new metric for gain sharing assessment in collaborative distribution: The sustainability and flexibility rate. Int. J. Syst. Sci. Oper. Logist. 2022, 1–16. [Google Scholar] [CrossRef]
- Özen, U.; Sošić, G.; Slikker, M. A collaborative decentralized distribution system with demand forecast updates. Eur. J. Oper. Res. 2012, 216, 573–583. [Google Scholar] [CrossRef]
- Stellingwerf, H.M.; Laporte, G.; Cruijssen, F.C.A.M.; Kanellopoulos, A.; Bloemhof, J.M. Quantifying the environmental and economic benefits of cooperation: A case study in temperature-controlled food logistics. Transp. Res. Part D Transp. Environ. 2018, 65, 178–193. [Google Scholar] [CrossRef]
- Soysal, M.; Bloemhof-Ruwaard, J.M.; Haijema, R.; van der Vorst, J.G.A.J. Modeling a green inventory routing problem for perishable products with horizontal collaboration. Comput. Oper. Res. 2018, 89, 168–182. [Google Scholar] [CrossRef]
- Ergun, O.; Kuyzu, G.; Savelsbergh, M. Reducing Truckload Transportation Costs Through Collaboration. Transp. Sci. 2007, 41, 206–221. [Google Scholar] [CrossRef]
- Agarwal, R.; Ergun, Ö. Network Design and Allocation Mechanisms for Carrier Alliances in Liner Shipping. Oper. Res. 2010, 58, 1726–1742. [Google Scholar] [CrossRef]
- Hernández, S.; Peeta, S.; Kalafatas, G. A less-than-truckload carrier collaboration planning problem under dynamic capacities. Transp. Res. Part E Logist. Transp. Rev. 2011, 47, 933–946. [Google Scholar] [CrossRef]
- Dai, B.; Chen, H. Mathematical model and solution approach for carriers’ collaborative transportation planning in less than truckload transportation. Int. J. Adv. Oper. Manag. 2012, 4, 62–84. [Google Scholar] [CrossRef]
- Wang, X.; Kopfer, H.; Gendreau, M. Operational transportation planning of freight forwarding companies in horizontal coalitions. Eur. J. Oper. Res. 2014, 237, 1133–1141. [Google Scholar] [CrossRef]
- Montoya-Torres, J.R.; Muñoz-Villamizar, A.; Vega-Mejía, C.A. On the impact of collaborative strategies for goods delivery in city logistics. Prod. Plan. Control 2016, 27, 443–455. [Google Scholar] [CrossRef]
- Chabot, T.; Bouchard, F.; Legault-Michaud, A.; Renaud, J.; Coelho, L.C. Service level, cost and environmental optimization of collaborative transportation. Transp. Res. Part E Logist. Transp. Rev. 2018, 110, 1–14. [Google Scholar] [CrossRef]
- Adenso-Díaz, B.; Lozano, S.; Garcia-Carbajal, S.; Smith-Miles, K. Assessing partnership savings in horizontal cooperation by planning linked deliveries. Transp. Res. Part A Policy Pract. 2014, 66, 268–279. [Google Scholar] [CrossRef]
- Pérez-Bernabeu, E.; Juan, A.A.; Faulin, J.; Barrios, B.B. Horizontal cooperation in road transportation: A case illustrating savings in distances and greenhouse gas emissions. Int. Trans. Oper. Res. 2015, 22, 585–606. [Google Scholar] [CrossRef]
- Fernández, E.; Fontana, D.; Speranza, M.G. On the Collaboration Uncapacitated Arc Routing Problem. Comput. Oper. Res. 2016, 67, 120–131. [Google Scholar] [CrossRef]
- Hernández, S.; Peeta, S. Centralized Time-Dependent Multiple-Carrier Collaboration Problem for Less-Than-Truckload Carriers. Transp. Res. Rec. 2011, 2263, 26–34. [Google Scholar] [CrossRef]
- Fernández, E.; Roca-Riu, M.; Speranza, M.G. The Shared Customer Collaboration Vehicle Routing Problem. Eur. J. Oper. Res. 2018, 265, 1078–1093. [Google Scholar] [CrossRef]
- Caballini, C.; Sacone, S.; Saeednia, M. Cooperation among truck carriers in seaport containerized transportation. Transp. Res. Part E Logist. Transp. Rev. 2016, 93, 38–56. [Google Scholar] [CrossRef]
- Molenbruch, Y.; Braekers, K.; Caris, A. Benefits of horizontal cooperation in dial-a-ride services. Transp. Res. Part E Logist. Transp. Rev. 2017, 107, 97–119. [Google Scholar] [CrossRef]
- Wang, X.; Kopfer, H. Collaborative transportation planning of less-than-truckload freight. OR Spectr. 2014, 36, 357–380. [Google Scholar] [CrossRef]
- Hernández, S.; Peeta, S. A carrier collaboration problem for less-than-truckload carriers: Characteristics and carrier collaboration model. Transp. A Transp. Sci. 2014, 10, 327–349. [Google Scholar] [CrossRef]
- Wang, X.; Kopfer, H. Rolling horizon planning for a dynamic collaborative routing problem with full-truckload pickup and delivery requests. Flex. Serv. Manuf. J. 2015, 27, 509–533. [Google Scholar] [CrossRef]
- Zhang, M.; Pratap, S.; Huang, G.Q.; Zhao, Z. Optimal collaborative transportation service trading in B2B e-commerce logistics. Int. J. Prod. Res. 2017, 55, 5485–5501. [Google Scholar] [CrossRef]
- Muñoz-Villamizar, A.; Montoya-Torres, J.R.; Faulin, J. Impact of the use of electric vehicles in collaborative urban transport networks: A case study. Transp. Res. Part D Transp. Environ. 2017, 50, 40–54. [Google Scholar] [CrossRef]
- Kuyzu, G. Lane covering with partner bounds in collaborative truckload transportation procurement. Comput. Oper. Res. 2017, 77, 32–43. [Google Scholar] [CrossRef]
- Ergun, Ö.; Kuyzu, G.; Savelsbergh, M. Shipper collaboration. Comput. Oper. Res. 2007, 34, 1551–1560. [Google Scholar] [CrossRef]
- Houghtalen, L.; Ergun, Ö.; Sokol, J. Designing Mechanisms for the Management of Carrier Alliances. Transp. Sci. 2011, 45, 465–482. [Google Scholar] [CrossRef]
- Özener, O.Ö.; Ergun, Ö.; Savelsbergh, M. Lane-Exchange Mechanisms for Truckload Carrier Collaboration. Transp. Sci. 2011, 45, 1–145. [Google Scholar] [CrossRef]
- Agarwal, R.; Ergun, Ö. Mechanism design for a multicommodity flow game in service network alliances. Oper. Res. Lett. 2008, 36, 520–524. [Google Scholar] [CrossRef]
- Zhou, G.; Hui, Y.V.; Liang, L. Strategic alliance in freight consolidation. Transp. Res. Part E Logist. Transp. Rev. 2011, 47, 18–29. [Google Scholar] [CrossRef]
- Van Lier, T.; Caris, A.; Macharis, C. Sustainability SI: Bundling of Outbound Freight Flows: Analyzing the Potential of Internal Horizontal Collaboration to Improve Sustainability. Netw. Spat. Econ. 2016, 16, 277–302. [Google Scholar] [CrossRef]
- Xu, S.X.; Huang, G.Q. Efficient auctions for distributed transportation procurement. Transp. Res. Part B Methodol. 2014, 65, 47–64. [Google Scholar] [CrossRef]
- Berger, S.; Bierwirth, C. Solutions to the request reassignment problem in collaborative carrier networks. Transp. Res. Part E Logist. Transp. Rev. 2010, 46, 627–638. [Google Scholar] [CrossRef]
- Huang, G.Q.; Xu, S.X. Truthful multi-unit transportation procurement auctions for logistics e-marketplaces. Transp. Res. Part B Methodol. 2013, 47, 127–148. [Google Scholar] [CrossRef]
- Xu, S.X.; Huang, G.Q.; Cheng, M. Truthful, Budget-Balanced Bundle Double Auctions for Carrier Collaboration. Transp. Sci. 2017, 51, 1365–1386. [Google Scholar] [CrossRef]
- Xu, S.X.; Huang, G.Q. Transportation service procurement in periodic sealed double auctions with stochastic demand and supply. Transp. Res. Part B Methodol. 2013, 56, 136–160. [Google Scholar] [CrossRef]
- Dai, B.; Chen, H. A multi-agent and auction-based framework and approach for carrier collaboration. Logist. Res. 2011, 3, 101–120. [Google Scholar] [CrossRef]
- Chen, H. Combinatorial clock-proxy exchange for carrier collaboration in less than truck load transportation. Transp. Res. Part E Logist. Transp. Rev. 2016, 91, 152–172. [Google Scholar] [CrossRef]
- Kuo, A.; Miller-Hooks, E. Developing Responsive Rail Services through collaboration. Transp. Res. Part B Methodol. 2012, 46, 424–439. [Google Scholar] [CrossRef]
- Lai, M.; Cai, X.; Hu, Q. An iterative auction for carrier collaboration in truckload pickup and delivery. Transp. Res. Part E Logist. Transp. Rev. 2017, 107, 60–80. [Google Scholar] [CrossRef]
- Sandberg, E. Logistics collaboration in supply chains: Practice vs. theory. Int. J. Logist. Manag. 2007, 18, 274–293. [Google Scholar] [CrossRef]
- Mason, R.; Lalwani, C.; Boughton, R. Combining vertical and horizontal collaboration for transport optimisation. Supply Chain Manag. Int. J. 2007, 12, 187–199. [Google Scholar] [CrossRef]
- Verstrepen, S.; Cools, M.; Cruijssen, F.; Dullaert, W. A dynamic framework for managing horizontal cooperation in logistics. Int. J. Logist. Syst. Manag. 2009, 5, 228–248. [Google Scholar] [CrossRef]
- Klaas-Wissing, T.; Albers, S. Cooperative versus corporate governance of LTL networks. Int. J. Logist. Res. Appl. 2010, 13, 493–506. [Google Scholar] [CrossRef]
- Wallenburg, C.M.; Raue, J.S. Conflict and its governance in horizontal cooperations of logistics service providers. Int. J. Phys. Distrib. Logist. Manag. 2011, 41, 385–400. [Google Scholar] [CrossRef]
- Hingley, M.; Lindgreen, A.; Grant, D.B.; Kane, C. Using fourth-party logistics management to improve horizontal collaboration among grocery retailers. Supply Chain Manag. Int. J. 2011, 16, 316–327. [Google Scholar] [CrossRef]
- Schmoltzi, C.; Wallenburg, C.M. Operational Governance in Horizontal Cooperations of Logistics Service Providers: Performance Effects and the Moderating Role of Cooperation Complexity. J. Supply Chain Manag. 2012, 48, 53–74. [Google Scholar] [CrossRef]
- Albers, S.; Klaas-Wissing, T. Organisation of multilateral LTL alliances. Int. J. Logist. Res. Appl. 2012, 15, 181–198. [Google Scholar] [CrossRef]
- Buijs, P.; Wortmann, J.C.H. Joint operational decision-making in collaborative transportation networks: The role of IT. Supply Chain Manag. Int. J. 2014, 19, 200–210. [Google Scholar] [CrossRef]
- Wang, Y.; Rodrigues, V.S.; Evans, L. The use of ICT in road freight transport for CO2 reduction—An exploratory study of UK’s grocery retail industry. Int. J. Logist. Manag. 2015, 26, 2–29. [Google Scholar] [CrossRef]
- Rodrigues, V.S.; Harris, I.; Mason, R. Horizontal logistics collaboration for enhanced supply chain performance: An international retail perspective. Supply Chain Manag. Int. J. 2015, 20, 631–647. [Google Scholar] [CrossRef]
- Allen, J.; Bektaş, T.; Cherrett, T.; Friday, A.; McLeod, F.; Piecyk, M.; Piotrowska, M.; Austwick, M.Z. Enabling a Freight Traffic Controller for Collaborative Multidrop Urban Logistics: Practical and Theoretical Challenges. Transp. Res. Rec. 2017, 2609, 77–84. [Google Scholar] [CrossRef]
- Agrell, P.J.; Lundin, J.; Norrman, A. Supply Chain Management: Horizontal carrier coordination through cooperative governance structures. Int. J. Prod. Econ. 2017, 194, 59–72. [Google Scholar] [CrossRef]
- Wilhelm, M.M. Managing coopetition through horizontal supply chain relations: Linking dyadic and network levels of analysis. J. Oper. Manag. 2011, 29, 663–676. [Google Scholar] [CrossRef]
- Naesens, K.; Gelders, L.; Pintelon, L. A swift response framework for measuring the strategic fit for a horizontal collaborative initiative. Int. J. Prod. Econ. 2009, 121, 550–561. [Google Scholar] [CrossRef]
- Schulz, S.F.; Blecken, A. Horizontal cooperation in disaster relief logistics: Benefits and impediments. Int. Jnl. Phys. Dist. Log. Manag. 2010, 40, 636–656. [Google Scholar] [CrossRef]
- Dahl, S.; Derigs, U. Cooperative planning in express carrier networks—An empirical study on the effectiveness of a real-time Decision Support System. Decis. Support Syst. 2011, 51, 620–626. [Google Scholar] [CrossRef]
- Badraoui, I.; van der Vorst, J.G.A.J.; Boulaksil, Y. Horizontal logistics collaboration: An exploratory study in Morocco’s agri-food supply chains. Int. J. Logist. Res. Appl. 2020, 23, 85–102. [Google Scholar] [CrossRef]
- Cruijssen, F.; Dullaert, W.; Fleuren, H. Horizontal Cooperation in Transport and Logistics: A Literature Review. Transp. J. 2007, 46, 22–39. [Google Scholar] [CrossRef]
- Pomponi, F.; Fratocchi, L.; Tafuri, S.R. Trust development and horizontal collaboration in logistics: A theory based evolutionary framework. Supply Chain Manag. Int. J. 2015, 20, 83–97. [Google Scholar] [CrossRef]
- Juan, A.A.; Faulin, J.; Pérez-Bernabeu, E.; Jozefowiez, N. Horizontal Cooperation in Vehicle Routing Problems with Backhauling and Environmental Criteria. Procedia-Soc. Behav. Sci. 2014, 111, 1133–1141. [Google Scholar] [CrossRef]
- Ülkü, S.; Schmidt, G.M. Matching Product Architecture and Supply Chain Configuration. Prod. Oper. Manag. 2011, 20, 16–31. [Google Scholar] [CrossRef]
- Pels, E. Optimality of the hub-spoke system: A review of the literature, and directions for future research. Transp. Policy 2021, 104, A1–A10. [Google Scholar] [CrossRef]
- Campbell, J.F.; Ernst, A.T.; Krishnamoorthy, M. Hub Arc Location Problems: Part I—Introduction and Results. Manag. Sci. 2005, 51, 1540–1555. [Google Scholar] [CrossRef]
- Ebery, J.; Krishnamoorthy, M.; Ernst, A.; Boland, N. The capacitated multiple allocation hub location problem: Formulations and algorithms. Eur. J. Oper. Res. 2000, 120, 614–631. [Google Scholar] [CrossRef]
- Zineldin, M.; Bredenlöw, T. Strategic alliance: Synergies and challenges. Int. J. Phys. Distrib. Logist. Manag. 2003, 33, 449–464. [Google Scholar] [CrossRef]
- Defryn, C.; Vanovermeire, C.; Sörensen, K.; van Breedam, A.; Vannieuwenhuyse, B.; Verstrepen, S. Gain Sharing in Horizontal Logistic Collaboration. A Case Study in the Fresh Fruit and Vegetables Sector. 2014. Working Papers 2014004, University of Antwerp, Faculty of Business and Economics. Available online: https://ideas.repec.org/p/ant/wpaper/2014004.html (accessed on 5 September 2022).
- Amer, L.E.; Eltawil, A.B. Analysis of quantitative models of horizontal collaboration in supply chain network design: Towards “green collaborative” strategies. In Proceedings of the 2015 International Conference on Industrial Engineering and Operations Management (IEOM), Dubai, United Arab Emirates, 3–5 March 2015; pp. 1–10. [Google Scholar] [CrossRef]
- Soubbotina, T.P. Beyond Economic Growth an Introduction to Sustainable Development, 2nd ed.; World Bank: Washington, DC, USA, 2004; Available online: https://openknowledge.worldbank.org/handle/10986/14865 (accessed on 5 September 2022).
- Anderson, S.; Allen, J.; Browne, M. Urban logistics—How can it meet policy makers’ sustainability objectives? J. Transp. Geogr. 2005, 13, 71–81. [Google Scholar] [CrossRef]
- Quak, H.J. Sustainability of Urban Freight Transport: Retail Distribution and Local Regulations in Cities (No. EPS-2008-124-LIS). 2008. ERIM Ph.D. Series Research in Management. Erasmus Research Institute of Management. Available online: http://hdl.handle.net/1765/11990 (accessed on 5 September 2022).
- Khalifehzadeh, S.; Seifbarghy, M.; Naderi, B. A four-echelon supply chain network design with shortage: Mathematical modeling and solution methods. J. Manuf. Syst. 2015, 35, 164–175. [Google Scholar] [CrossRef]
- Meier, J.F. An improved mixed integer program for single allocation hub location problems with stepwise cost function: Xxx. Intl. Trans. Op. Res. 2017, 24, 983–991. [Google Scholar] [CrossRef]
- Rostami, B.; Buchheim, C. The Uncapacitated Single Allocation p-Hub Median Problem with Stepwise Cost Function. Optimization Online. 2015, p. 18. Available online: https://optimization-online.org/?p=13555 (accessed on 5 September 2022).
- Serper, E.Z.; Alumur, S.A. The design of capacitated intermodal hub networks with different vehicle types. Transp. Res. Part B Methodol. 2016, 86, 51–65. [Google Scholar] [CrossRef]
- Hu, L.; Zhu, J.X.; Wang, Y.; Lee, L.H. Joint design of fleet size, hub locations, and hub capacities for third-party logistics networks with road congestion constraints. Transp. Res. Part E Logist. Transp. Rev. 2018, 118, 568–588. [Google Scholar] [CrossRef]
- Varriale, V.; Cammarano, A.; Michelino, F.; Caputo, M. The Unknown Potential of Blockchain for Sustainable Supply Chains. Sustainability 2020, 12, 9400. [Google Scholar] [CrossRef]



| Journal | No. of Articles |
|---|---|
| Transportation Research Part E: Logistics and Transportation Review | 12 |
| European Journal of Operational Research | 10 |
| Computers & Industrial Engineering | 5 |
| International Journal of Production Economics | 6 |
| Transportation Science | 5 |
| Computers & Operations Research | 4 |
| Journal of the Operational Research Society | 4 |
| Transportation Research Part B: Methodology | 4 |
| International Journal of Logistics Research and Applications | 3 |
| International Journal of Production Research | 3 |
| International Transactions in Operational Research | 3 |
| Supply Chain Management: An International Journal | 3 |
| Transportation Research Part D: Transportation and Environment | 3 |
| Transportation Research Record: Journal of the Transportation Research Board | 3 |
| Flexible Services and Manufacturing Journal | 2 |
| International Journal of Physical Distribution & Logistics Management | 2 |
| International Journal of Systems Science: Operations & Logistics | 2 |
| Mathematics | 2 |
| GOLD Spectrum | 2 |
| Production Planning & Control: The Management of Operations | 2 |
| supply chain management | 2 |
| The International Journal of Logistics Management | 2 |
| Annals of Operations Research | 1 |
| Applied Mathematics and Computation | 1 |
| CIRP Journal of Manufacturing Science and Technology | 1 |
| Decision Support Systems | 1 |
| Energy Economics | 1 |
| IFAC Proceedings Volumes | 1 |
| PapersOnLine | 1 |
| Industrial Engineering | 1 |
| INFORMS Journal on Applied Analytics | 1 |
| International Journal of Advanced Operations Management | 1 |
| International Journal of Industrial Engineering Computations | 1 |
| International Journal of Logistics Systems and Management | 1 |
| International Journal of Machine Learning and Cybernetics | 1 |
| International Journal of Shipping and Transport Logistics | 1 |
| Journal of Cleaner Production | 1 |
| Journal of industrial and management optimization | 1 |
| Journal of Management Control | 1 |
| Journal of Operations Research | 1 |
| Journal of Operations Management | 1 |
| Journal of Service Science and Management | 1 |
| Journal of Supply Chain Management | 1 |
| Journal of Transport Geography | 1 |
| Logistics Research | 1 |
| European Transport Research Review | 1 |
| Maritime Policy & Management | 1 |
| NETNOMICS: Economic Research and Electronic Networking | 1 |
| Networks and Spatial Economics | 1 |
| Omega | 1 |
| Operations Research | 1 |
| Operations Research letters | 1 |
| Research in Logistics and Production | 1 |
| Sustainability | 1 |
| Sustainable Cities and Society | 1 |
| Transportation Reviews | 1 |
| Transportation Journal | 1 |
| Transportation Research Interdisciplinary Perspectives | 1 |
| Transportation Research Part A: Policy and Practice | 1 |
| Transportmetrica A: Transport Science | 1 |
| Some supply chain management | 1 |
| Working Papers | 1 |
| Types | Decision Level | References |
|---|---|---|
| Strategic Level | ||
| Experimental studies |
| [5,11,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44] |
| [45,46,47,48,49,50,51,52] | |
| Tactical level | ||
| [5,10,35,38,53,54,55,56,57,58,59,60,61,62,63,64,65,66,67,68,69,70,71,72,73,74] | |
| [75,76,77] | |
| Operational level | ||
| [62,78,79,80,81,82,83,84,85,86,87,88,89,90,91,92,93,94,95,96,97,98] | |
| [99,100,101,102,103,104,105,106,107,108,109,110,111,112] | |
| Empirical studies | [13,18,113,114,115,116,117,118,119,120,121,122,123,124,125,126,127,128,129,130] | |
| Literature review | [6,7,14,16,17,19,20,21,22,131,132] | |
| Reference | Approach | Economic Costs of: | Environmental CO2 Emissions Due to the: | Social |
|---|---|---|---|---|
| [27] | Heuristic | Transport | ||
| Storage | ||||
| Order picking | ||||
| Handling | ||||
| [28] | ILP | Transport | ||
| Storage | ||||
| Warehouse operations | ||||
| [31] | LP | Transport | ||
| Handling | ||||
| Storage | ||||
| Delayed delivery | ||||
| [25] | MILP | Transport | ||
| [32] | Simulation | Transport | Transport | |
| [26] | MILP | Transport | ||
| [9] | MILP | Transport | Transport | |
| Storage (post-evaluation) | ||||
| [33] | ILP | Transport | ||
| Opening of the hubs | ||||
| [29] | MILP | Transport | ||
| Warehouse operations | ||||
| [34] | Heuristic | Transport Opening of the hubs | Transport | |
| [35] | MILP | Transport | ||
| Opening of the hubs | ||||
| [36] | MILP | Transport | ||
| Handling | ||||
| [24] | Heuristic | Transport | Transport | |
| Opening of the hubs | ||||
| [37] | MILP and meta-heuristics | Logistics cost | Transport Water and energy consumption | Created job opportunities Accident risk |
| [38] | MICQP | Transport | Transport | |
| Storage | ||||
| Opening of the hubs | ||||
| Placement of orders | ||||
| [30] | MILP | Transport | ||
| [5] | MILP | Transport | Transport | |
| [39,42] | MILP and meta-heuristic | Transport Opening of hubs Storage Delayed delivery | Transport | |
| [11,40,41] | MILP | Transport Storage Handling Opening of hubs | Transport Warehouse operations | |
| [43] | Transport Storage Handling Opening of hubs Delayed delivery | Transport Depreciation of vehicles Operations of hubs Construction of hubs |
| Reference | Approach | Type of Criteria | Criteria |
|---|---|---|---|
| [45] | FMCDM | Individual criteria | Additional capabilities |
| Similarities in correspondence | |||
| Financial health | |||
| Physical facilities | |||
| Availability of the adequate equipment | |||
| Intangible assets | |||
| Access to the market knowledge | |||
| [46] | FAHP | Criteria on the strategic aspect | Objectives of each partner |
| Partner size | |||
| Financial stability | |||
| Culture of each partner | |||
| Successful track record | |||
| Ability to develop a lasting relationship | |||
| Evaluation criteria | Technical expertise | ||
| Performance | |||
| Quality of partners | |||
| Management experience | |||
| [47] | AHP–FLM | Characteristic of the industry | Industry Structure |
| Financial stability | |||
| Global Reputation | |||
| Competitive advantages | Product orientation | ||
| Overall competitive advantage | |||
| Internal parameters | Operational parameters | ||
| Tactical parameters | |||
| Strategic parameters | |||
| External parameters | Product characteristics | ||
| Industry focus | |||
| [48] | FMADM | Individual criteria | Technological capability |
| Financial strength | |||
| Management knowledge and experience | |||
| Ability to access new markets | |||
| Collaborative criteria | Complementarity of resources | ||
| Overlapping knowledge bases | |||
| Matching objectives | |||
| Cultural compatibility | |||
| [49] | AHP | Organizational compatibility | Compatibility of the business strategies |
| Symmetry of scale and scope | |||
| Management and organizational culture | |||
| Mutual trust and commitment | |||
| Technological capacity | Manufacturing the technological capability | ||
| Product development and improvement | |||
| Capacity for innovation and invention | |||
| Potential breadth of the application of skills | |||
| Resources for R&D | Intensity of R&D investment | ||
| Extent of the additional resources | |||
| Number of R&D personnel | |||
| Quality of R&D personnel | |||
| Financial conditions | Return on investment over the last five years | ||
| Future profitability | |||
| Growth potential | |||
| [50] | BBaRT | Individual criteria | Geographical compatibility and volume of the delivered goods |
| [51] | CRA | Financial conditions | Expected profitability of each partner |
| [52] | TFSS TODIM | Individual criteria | Operations and financial health |
| Management knowledge and previous experience | |||
| Geographic distance | |||
| Technological capacity | |||
| Collaborative criteria | Cultural compatibility | ||
| Trust and commitment | |||
| Willingness to share information | |||
| Additional benefits |
| Type of Approach | Approach | Reference |
|---|---|---|
| Classical approaches | ABC | [10] |
| EA | [35,61] | |
| PA | [56,61,64,68] | |
| Volume | [10,35,38,58,139] | |
| CenA;ToKmA | [61] | |
| KTA;DDA | [61] | |
| SDA | [38,61] | |
| Approaches based on cooperative game theory | ACAM | [54,60,61,139] |
| CCPS | [53] | |
| Core-centre | [65] | |
| Demand Nucleolus | [59] | |
| ECM | [10,60] | |
| EPM | [54,60] | |
| ES | [53] | |
| LEPM | [55] | |
| Minmax core | [65] | |
| Nucleolus | [10,57,59,61,64,66,67] | |
| Shapley value | [5,10,35,57,59,60,61,62,64,65,66,67,69,72] | |
| WRSA | [61,64] | |
| τ-Value | [59,60,61,63,65] |
| Reference | Approach | Economic Cost of: | Environmental CO2 Emissions Due to: |
|---|---|---|---|
| [75] | Cooperative game theory | Transport | |
| Storage | |||
| [76] | LP | Transport | Transport |
| Storage | |||
| [77] | LP | Vehicle routing | Transport |
| Penalty for wasted products | |||
| Storage |
| Reference | Approach | Economic Costs of: | Environmental CO2 Emissions Due to: | |
|---|---|---|---|---|
| VRP | [62] | Local Research | Transport | |
| [79] | MILP | Transport | ||
| [80] | ILP | Transport | ||
| [81] | MILP | Transport | ||
| [88] | ILP | Transport | ||
| Handling | ||||
| 3PL Service | ||||
| [92] | ILP | Use of vehicles | ||
| Transport | ||||
| Subcontracting | ||||
| [85] | QIP | Transport | ||
| [92] | LP | Transport | ||
| Planning | ||||
| [88] | Binary (0–1) | Transport | ||
| [94] | LP | Transport | ||
| [83] | Mathematical modeling | Transport | Transport | |
| [87] | MILP | Transport | ||
| [90] | BLP | Transport | ||
| [91] | MBLP | Transport | ||
| Driver’s salary | ||||
| [95] | Algorithm Stochastic | Transport | ||
| [96] | MILP | Transport | Transport | |
| [84] | ILP | Transport | Transport | |
| [89] | MILP | Transport | ||
| [86] | Heuristic | Transport | Transport | |
| CLCP | [97] | MILP | Transport | |
| [98] | ILP | Transport | ||
| [78] | ILP | Transport |
| Problem | Reference | Approach |
|---|---|---|
| Exchange of requests with lateral payment | [101] | Inverse optimization |
| [99] | LP | |
| [100] | ILP | |
| [102] | Simulation | |
| [103] | Simulation | |
| Exchange of requests with an auction mechanism | [105] | LP |
| [107] | LP | |
| [109] | LP | |
| [104] | LP | |
| [106] | LP | |
| [102] | LP | |
| [105] | LP | |
| [108] | LP | |
| [110] | LP |
| References | Tools | Sector | Country | Conclusion |
|---|---|---|---|---|
| [18] | Investigations | LSP | Belgium | - Importance of partner selection |
| - Importance of equitable distribution of benefits | ||||
| - Importance of finding a reliable party to drive collaboration | ||||
| [113] | Investigations | Manufacturing companies | Sweden | - Top management is an important factor for the success of collaboration |
| [114] | Interviews with experienced experts and scholars | LSP | UK | - The combination of vertical and horizontal collaboration can further optimize transport efficiency |
| [115] | Data gathering | LSP | Belgium and the Netherlands | - Collaboration faces competition and fluctuating demands |
| - Collaboration makes it possible to serve new geographic regions | ||||
| - Collaboration improves the level of service | ||||
| - Collaboration makes efficient use of resources | ||||
| - Collaboration saves costs | ||||
| - Importance of partner selection and gain sharing | ||||
| - Importance of ICT systems for better coordination | ||||
| - Importance of finding a reliable party to ensure the success of collaboration | ||||
| [127] | Synthetic approaches | General | General | - Importance of strategic alignment between partners |
| - Importance of equitable distribution of benefits | ||||
| - Importance of information sharing | ||||
| [128] | Synthetic approaches | General | General | - Importance of trust between partners |
| [116] | Interviews | LSP | Germany | - Importance of partner selection |
| - Importance of profit distribution | ||||
| [126] | Interviews | Japanese and German automotive industries | Japan and Germany | - Importance of trust between partners |
| [117] | Investigations | LSP | Germany | - Relational governance reduces the scope of conflict |
| - Formal governance increases the scope of conflict | ||||
| - Conflicts decrease the efficiency of collaboration | ||||
| [118] | Interviews | LSP | UK | - Large LSPs agree to implement 4PL management |
| - Setting up a 4PL generates a high investment cost | ||||
| - Retailers promote 4PL implementation | ||||
| [129] | Analysis of simulation results | Carriers | General | - Importance of equitable distribution of benefits |
| [120] | Interviews | Small and medium-sized LSPs | Germany | - Importance of partner selection |
| - Importance of strategic decisions such as network design | ||||
| [119] | Interviews with logistics practitioners and researchers | LSP | Germany | - Collaboration between LSPs is more stable than that between manufacturing industries |
| [13] | Synthetic approaches | General | General | - Importance of trust between partners |
| [121] | Interviews | Carriers | UK and Netherlands | - Importance of partner selection |
| - Importance of profit distribution | ||||
| - Importance of information sharing | ||||
| [122] | Interviews | Retailers | UK | - Importance of ICT in reducing CO2 emissions |
| [123] | Interviews | LSP | UK | - Importance of synergies and enablers (legislation, trust, 3PL and equitable benefit sharing) |
| [124] | Interviews | Carriers | UK | - Importance of a trusted third party |
| [125] | Exploratory | Carriers | Sweden | - Importance of coordination |
| - Importance of trust between partners | ||||
| [130] | Exploratory | Food companies | Morocco | - Product compatibility - Selection of partners Technical equipment Trust between partners |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mrabti, N.; Hamani, N.; Delahoche, L. A Comprehensive Literature Review on Sustainable Horizontal Collaboration. Sustainability 2022, 14, 11644. https://doi.org/10.3390/su141811644
Mrabti N, Hamani N, Delahoche L. A Comprehensive Literature Review on Sustainable Horizontal Collaboration. Sustainability. 2022; 14(18):11644. https://doi.org/10.3390/su141811644
Chicago/Turabian StyleMrabti, Nassim, Nadia Hamani, and Laurent Delahoche. 2022. "A Comprehensive Literature Review on Sustainable Horizontal Collaboration" Sustainability 14, no. 18: 11644. https://doi.org/10.3390/su141811644
APA StyleMrabti, N., Hamani, N., & Delahoche, L. (2022). A Comprehensive Literature Review on Sustainable Horizontal Collaboration. Sustainability, 14(18), 11644. https://doi.org/10.3390/su141811644






