Tab2vox: CNN-Based Multivariate Multilevel Demand Forecasting Framework by Tabular-To-Voxel Image Conversion
Abstract
:1. Introduction
1.1. Backgroud and Purpose
1.2. Related Work
1.2.1. Previous Studies on Demand Forecasting
1.2.2. Studies on Converting Tabular Data into Images
1.2.3. Research Gaps
- Although demand forecasting methodology has become increasingly sophisticated, studies applying the CNN architecture using image data have not yet been conducted.
- Recently, there have been attempts to express tabular data as images in some studies in the field of biotechnology, but image transformation and an evaluation of predictive models were performed independently. That is, it was not a method in which optimal image conversion was performed by linking with the loss function (predictive measurement accuracy).
- In addition, previous studies converting tabular features into images have extracted features using 2D CNNs in the form of integrated demand sources; however, a high-dimensional CNN that integrates and reflects multi-dimensional information between subdivided levels is required.
1.3. Organization of This Paper
2. Materials and Methods
2.1. Neural Architecture Search (NAS)
2.2. Proposed Method: Tab2vox
3. Case Study of MND (Ministry of National Defense, Republic of Korea) Spare Parts Dataset by Tab2vox
3.1. Datasets
3.1.1. Data Collection
3.1.2. Feature Generation
3.1.3. Data Preparation
3.1.4. Data Representation & Prediction
3.2. Evaluation with Comparisons
3.2.1. Overview
3.2.2. Tab2vox Architecture for the MND Dataset
3.2.3. Machine Learning Methods
- Machine Learning: the PyCaret Python package was used with the tuned parameters.
- IGTD: the public IGTD source code was used, which is available at https://github.com/zhuyitan/IGTD (accessed on 1 January 2022).
4. Results
4.1. Evaluation Metrics
4.2. Prediction Accuracy by a Single Model
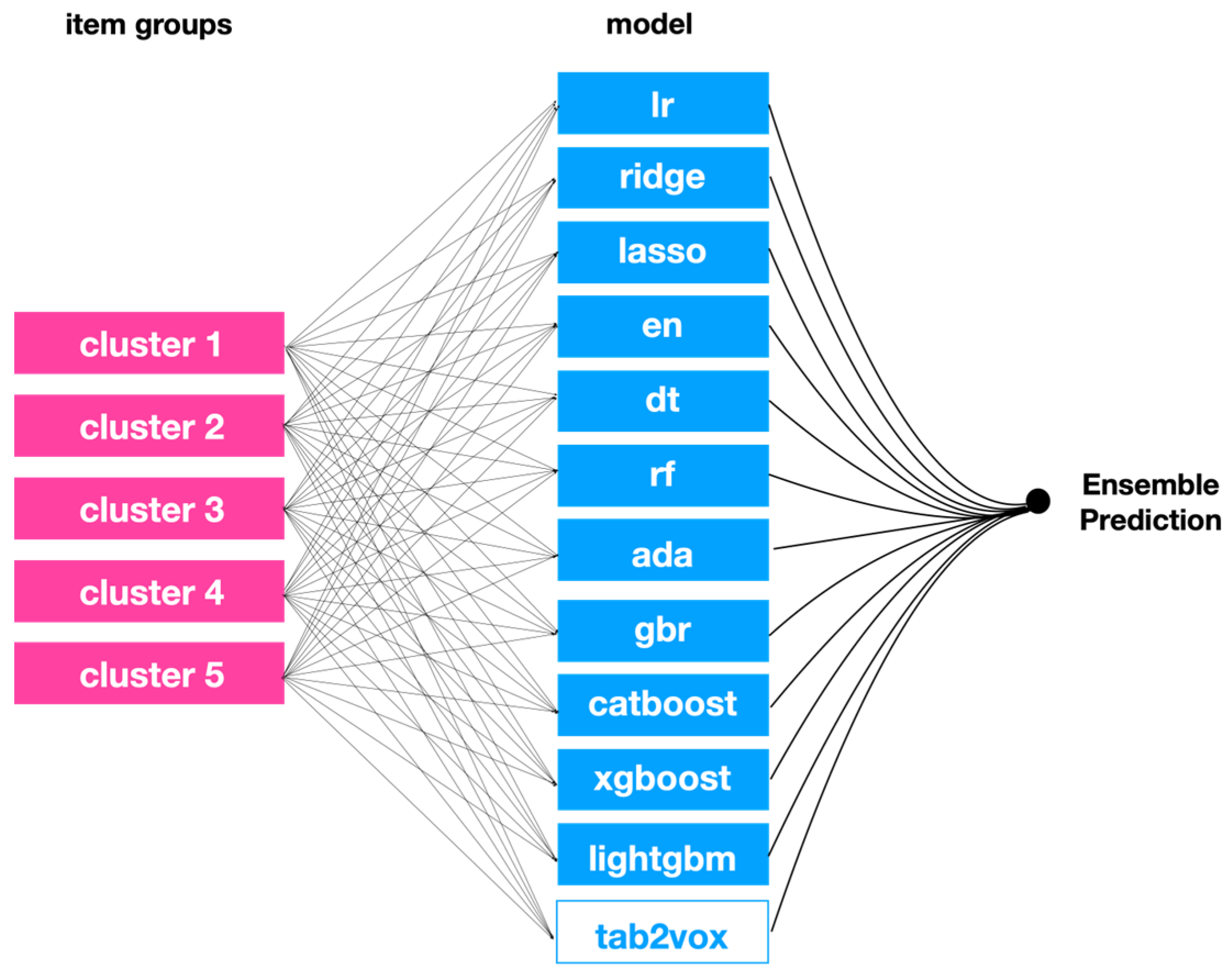
4.3. Ensemble Approach
4.3.1. Model Selection Problem
4.3.2. Optimal Model Combination Considering the Number of Item Group Clusters
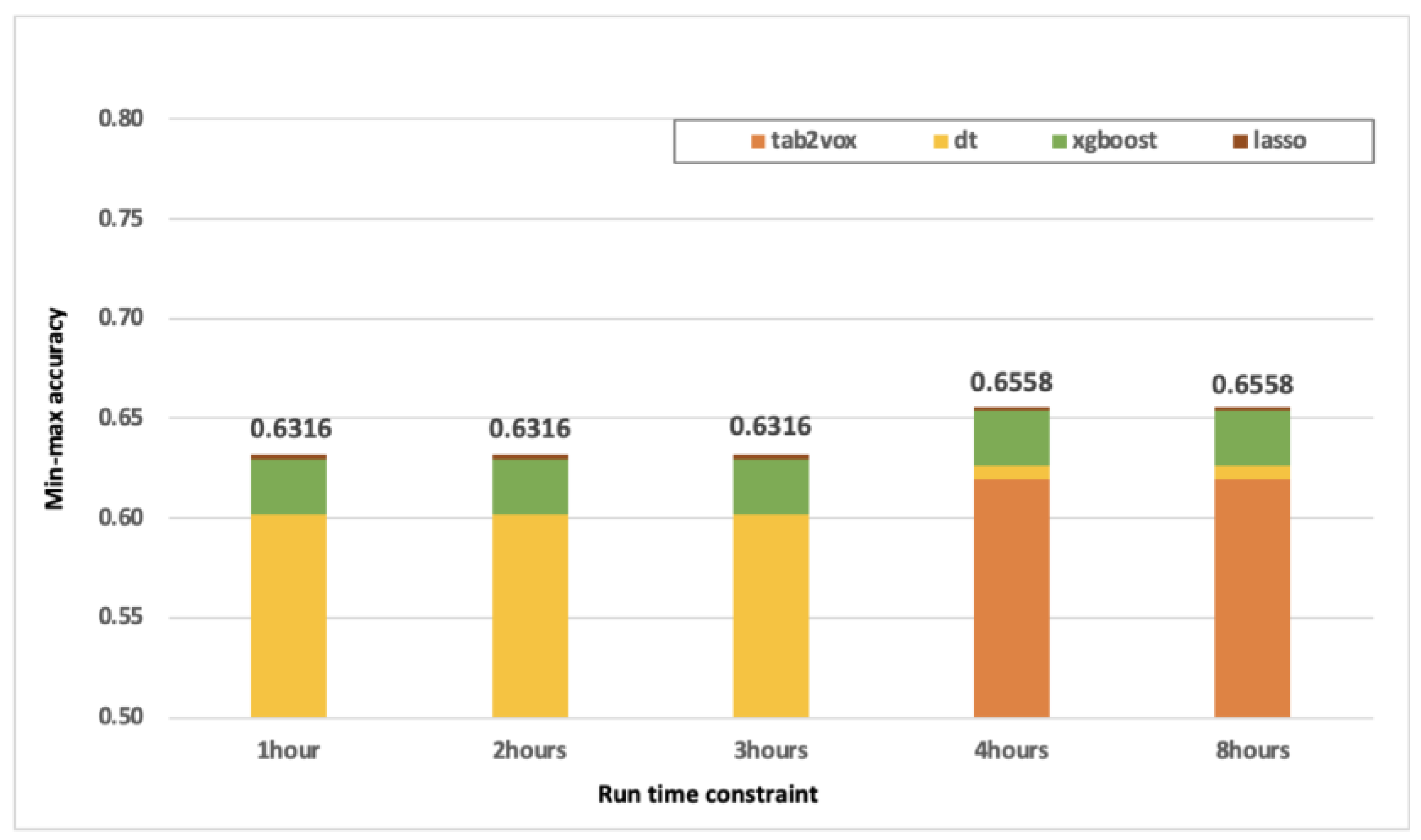
4.3.3. Optimal Model Combination According to Run Time Constraints
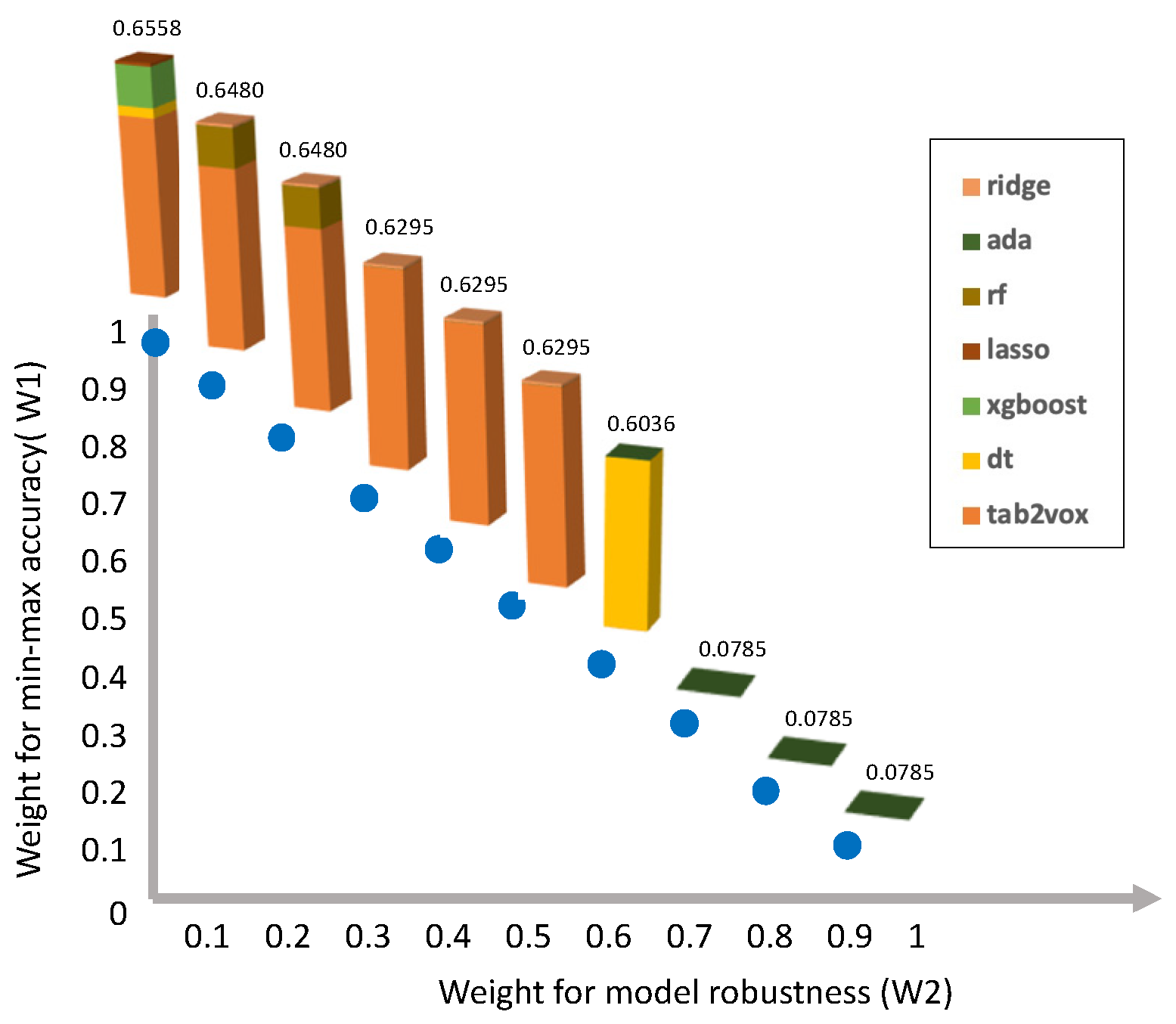
4.3.4. Optimal Model Combination Considering Robustness
5. Discussion
6. Conclusions
6.1. Implications
6.2. Limitations and Further Research
- 1.
- It is only recently that researchers have begun to gather big data. We wanted to verify the Tab2vox framework in datasets from various industries, but it was difficult to acquire benchmark datasets segmented to a multi-level format. Additional verification by datasets from various domains is required.
- 2.
- After DARTS was first introduced, many NAS models with differentiable concepts appeared. With a more recent and advanced NAS model, the Tab2vox input embedding method could be further advanced.
- 3.
- Unlike previous studies using dimensionality reduction methodology, Tab2vox maps the features of each level to each dimension of the voxel image while preserving the dimension of the feature set. By applying the explainable artificial intelligence (XAI) technique, it is possible to add explainability to the model by performing actions such as displaying a heat map showing features on which the model focuses, and generating demand. Intuitive interpretation is possible because a single voxel itself has an explicit meaning.
- 4.
- Because of the intermittent demand characteristics, we had no choice but to use yearly data. In addition, despite using all datasets after 2010, when the Defense Logistics Integrated Information System (DELIIS) was developed, the time series period was not sufficient. Therefore, the target year was set to 1 year for analysis. The effect on mid- to long-term forecasting can also be reviewed with industrial data, such as production line data and electricity demand data, where demand occurs continuously rather than intermittently and the time series is sufficient.
- 5.
- In this work, the average effective image-embedding architecture and CNN architecture were searched for entire items by applying the Tab2vox framework to entire items. However, if the Tab2vox framework is applied to each item group, it will be possible to find a network that fits the characteristics of the item group. This is possible when sufficient samples for each item group are secured.
- Tab2vox is a NAS model that embeds tabular data into optimal voxel images and finds the optimal CNN architecture for the images.
- We demonstrated better performance, compared to previous time series and machine learning techniques, using tabular data and the latest tabular to image conversion studies.
- Tab2vox is particularly meaningful because it is a general-purpose model that provides a framework that can be applied to demand forecasting in all sectors, rather than proposing a fixed architecture verified only in a specific dataset and domain.
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Syntetos, A.A.; Boylan, J.E. Intermittent Demand Forecasting: Context, Methods and Applications; John Wiley & Sons: Hoboken, NJ, USA, 2021. [Google Scholar]
- Gonçalves, J.N.C.; Cortez, P.; Carvalho, M.S.; Frazão, N.M. A multivariate approach for multi-step demand forecasting in assembly industries: Empirical evidence from an automotive supply chain. Decis. Support Syst. 2021, 142, 113452. [Google Scholar] [CrossRef]
- Garcia, C.; Delakis, M. Convolutional face finder: A neural architecture for fast and robust face detection. IEEE Trans. Pattern Anal. Mach. Intell. 2004, 26, 1408–1423. [Google Scholar] [CrossRef] [PubMed]
- Hadsell, R.; Sermanet, P.; Ben, J.; Erkan, A.; Scoffier, M.; Kavukcuoglu, K.; Muller, U.; LeCun, Y. Learning Long-Range Vision for Autonomous Off-Road Driving. J. Field. Robot. 2009, 26, 120–144. [Google Scholar] [CrossRef]
- Tompson, J.; Goroshin, R.; Jain, A.; LeCun, Y.; Bregler, C. Efficient object localization using Convolutional Networks. In Proceedings of the IEEE Computer Society Conference on Computer Vision and Pattern Recognition, Boston, MA, USA, 7–12 June 2015; pp. 648–656. [Google Scholar] [CrossRef]
- Sermanet, P.; Kavukcuoglu, K.; Chintala, S.; Lecun, Y. Pedestrian detection with unsupervised multi-stage feature learning. In Proceedings of the IEEE Computer Society Conference on Computer Vision and Pattern Recognition, Portland, OR, USA, 23–28 June 2013; pp. 3626–3633. [Google Scholar] [CrossRef]
- Kather, J.N.; Pearson, A.T.; Halama, N.; Jäger, D.; Krause, J.; Loosen, S.H.; Marx, A.; Boor, P.; Tacke, F.; Neumann, U.P.; et al. Deep learning can predict microsatellite instability directly from histology in gastrointestinal cancer. Nat. Med. 2019, 25, 1054–1056. [Google Scholar] [CrossRef]
- Schmauch, B.; Romagnoni, A.; Pronier, E.; Saillard, C.; Maillé, P.; Calderaro, J.; Kamoun, A.; Sefta, M.; Toldo, S.; Zaslavskiy, M.; et al. A deep learning model to predict RNA-Seq expression of tumours from whole slide images. Nat Commun. 2020, 11, 3877. [Google Scholar] [CrossRef]
- Collobert, R.; Weston, J.; Bottou, L.; Karlen, M.; Kavukcuoglu, K.; Kuksa, P. Natural Language Processing (almost) from Scratch. J. Mach. Learn. Res. 2011, 12, 2493–2537. Available online: http://arxiv.org/abs/1103.0398 (accessed on 1 January 2022).
- Sainath, T.N.; Kingsbury, B.; Mohamed, A.-R.; Dahl, G.E.; Saon, G.; Soltau, H.; Beran, T.; Aravkin, A.Y.; Ramabhadran, B. Improvements to deep convolutional neural networks for LVCSR. arXiv 2013, arXiv:1309.1501. Available online: http://arxiv.org/abs/1309.1501 (accessed on 1 January 2022).
- Liu, H.; Deepmind, K.S.; Yang, Y. Darts: Differentiable architecture search. arXiv Prepr. 2018, arXiv:1806.09055. Available online: https://github.com/quark0/darts (accessed on 1 January 2022).
- Syntetos, A.A.; Boylan, J.E. The accuracy of intermittent demand estimates. Int. J. Forecast. 2005, 21, 303–314. [Google Scholar] [CrossRef]
- Bzdok, D.; Altman, N.; Krzywinski, M. Statistics versus machine learning. Nat. Methods 2018, 15, 233. [Google Scholar] [CrossRef]
- Romeijnders, W.; Teunter, R.; van Jaarsveld, W. A two-step method for forecasting spare parts demand using information on component repairs. Eur. J. Oper. Res. 2012, 220, 386–393. [Google Scholar] [CrossRef]
- Dekker, R.; Pinçe, Ç.; Zuidwijk, R.; Jalil, M.N. On the use of installed base information for spare parts logistics: A review of ideas and industry practice. Int. J. Prod. Econ. 2013, 143, 536–545. [Google Scholar] [CrossRef]
- Suh, J.H. Generating future-oriented energy policies and technologies from the multidisciplinary group discussions by text-mining-based identification of topics and experts. Sustainability 2018, 10, 3709. [Google Scholar] [CrossRef]
- Chen, T.; Guestrin, C. XGBoost: A Scalable Tree Boosting System. In Proceedings of the 22nd ACM Sigkdd International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 13–17 August 2016. [Google Scholar] [CrossRef]
- Freund, Y.; Schapire, R.E. A decision-theoretic generalization of on-line learning and an application to boosting. In Lecture Notes in Computer Science (Including Subseries Lecture Notes in Artificial Intelligence and Lecture Notes in Bioinformatics); Springer: Berlin/Heidelberg, Germany, 1995; Volume 904, pp. 23–37. [Google Scholar] [CrossRef]
- Breiman, L. Random Forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Sherstinsky, A. Fundamentals of Recurrent Neural Network (RNN) and Long Short-Term Memory (LSTM) Network. Phys. D Nonlinear Phenom. 2018, 404, 132306. [Google Scholar] [CrossRef]
- Sak, H.H.; Senior, A.; Google, B. Long Short-Term Memory Recurrent Neural Network Architectures for Large Scale Acoustic Modeling. In Proceedings of the Annual Conference of the International Speech Communication Association, INTERSPEECH, Singapore, 14–18 September 2014; pp. 338–342. [Google Scholar]
- Salinas, D.; Flunkert, V.; Gasthaus, J. DeepAR: Probabilistic Forecasting with Autoregressive Recurrent Networks. arXiv 2017, arXiv:1704.04110. Available online: http://arxiv.org/abs/1704.04110 (accessed on 1 January 2022). [CrossRef]
- Arik, S.O.; Pfister, T. TabNet: Attentive Interpretable Tabular Learning. arXiv 2019, arXiv:1908.07442. Available online: http://arxiv.org/abs/1908.07442 (accessed on 1 January 2022). [CrossRef]
- Huang, X.; Khetan, A.; Cvitkovic, M.; Karnin, Z. TabTransformer: Tabular Data Modeling Using Contextual Embeddings. arXiv 2020, arXiv:2012.06678. Available online: http://arxiv.org/abs/2012.06678 (accessed on 1 January 2022).
- Rosienkiewicz, M.; Chlebus, E.; Detyna, J. A hybrid spares demand forecasting method dedicated to mining industry. Appl. Math. Model. 2017, 49, 87–107. [Google Scholar] [CrossRef]
- Soltani, M.; Farahmand, M.; Pourghaderi, A.R. Machine learning-based demand forecasting in cancer palliative care home hospitalization. J. Biomed. Inform. 2022, 130, 104075. [Google Scholar] [CrossRef]
- Hussain, A.; Alam Memon, J.; Murshed, M.; Alam, S.; Mehmood, U.; Alam, M.N.; Rahman, M.; Hayat, U. A time series forecasting analysis of overall and sector-based natural gas demand: A developing South Asian economy case. Environ. Sci. Pollut. Res. 2022. [Google Scholar] [CrossRef]
- Shorfuzzaman, M.; Hossain, M.S. Predictive Analytics of Energy Usage by IoT-Based Smart Home Appliances for Green Urban Development. ACM Trans. Internet Technol. 2022, 22, 1–26. [Google Scholar] [CrossRef]
- Sheikhoushaghi, A.; Gharaei, N.Y.; Nikoofard, A. Application of Rough Neural Network to forecast oil production rate of an oil field in a comparative study. J. Pet. Sci. Eng. 2022, 209, 109935. [Google Scholar] [CrossRef]
- Fan, G.-F.; Yu, M.; Dong, S.-Q.; Yeh, Y.-H.; Hong, W.-C. Forecasting short-term electricity load using hybrid support vector regression with grey catastrophe and random forest modeling. Util. Policy 2021, 73, 101294. [Google Scholar] [CrossRef]
- Tschora, L.; Pierre, E.; Plantevit, M.; Robardet, C. Electricity price forecasting on the day-ahead market using machine learning. Appl. Energy 2022, 313, 118752. [Google Scholar] [CrossRef]
- Choi, B.; Suh, J.H. Forecasting spare parts demand of military aircraft: Comparisons of data mining techniques and managerial features from the case of South Korea. Sustainability 2020, 12, 6045. [Google Scholar] [CrossRef]
- Ma, S.; Zhang, Z. OmicsMapNet: Transforming omics data to take advantage of Deep Convolutional Neural Network for discovery. Available online: http://www.kegg.jp/ (accessed on 1 January 2022).
- Sharma, A.; Vans, E.; Shigemizu, D.; Boroevich, K.A.; Tsunoda, T. DeepInsight: A methodology to transform a non-image data to an image for convolution neural network architecture. Sci. Rep. 2019, 9, 11399. [Google Scholar] [CrossRef]
- Bazgir, O.; Zhang, R.; Dhruba, S.R.; Rahman, R.; Ghosh, S.; Pal, R. Representation of features as images with neighborhood dependencies for compatibility with convolutional neural networks. Nat. Commun. 2020, 11, 4391. [Google Scholar] [CrossRef]
- Tang, H.; Yu, X.; Liu, R.; Zeng, T. Vec2image: An explainable artificial intelligence model for the feature representation and classification of high-dimensional biological data by vector-to-image conversion. Brief Bioinform. 2022, 23, bbab584. [Google Scholar] [CrossRef]
- Box, P.O.; van der Maaten, L.; Postma, E.; van den Herik, J. Tilburg Centre for Creative Computing Dimensionality Reduction: A Comparative Review Dimensionality Reduction: A Comparative Review. 2009. Available online: http://www.uvt.nl/ticc (accessed on 1 January 2022).
- Zhu, Y.; Brettin, T.; Xia, F.; Partin, A.; Shukla, M.; Yoo, H.; Evrard, Y.A.; Doroshow, J.H.; Stevens, R.L. Converting tabular data into images for deep learning with convolutional neural networks. Sci. Rep. 2021, 11, 11325. [Google Scholar] [CrossRef]
- He, X.; Zhao, K.; Chu, X. AutoML: A Survey of the State-of-the-Art. Available online: https://www.datasearch.elsevier.com/ (accessed on 1 January 2022).
- Mannor, S.; Jin, X.; Han, J.; Zhang, X. K-Means Clustering. In Encyclopedia of Machine Learning; Springer: Boston, MA, USA, 2011; pp. 563–564. [Google Scholar] [CrossRef]
- Altman, N.S. An Introduction to Kernel and Nearest-Neighbor Nonparametric Regression. Am. Stat. 1992, 46, 175–185. [Google Scholar] [CrossRef]
- Nielsen, F. Hierarchical clustering. In Introduction to HPC with MPI for Data Science; Springer: Cham, Switzerland, 2016; pp. 195–211. [Google Scholar] [CrossRef]
- Yu, Q.; Yang, D.; Roth, H.; Bai, Y.; Zhang, Y.; Yuille, A.L.; Xu, D. C2FNAS: Coarse-to-Fine Neural Architecture Search for 3D Medical Image Segmentation. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 13–19 June 2020. [Google Scholar]
- Zhou, B.; Li, Y.; Wan, J. Regional Attention with Architecture-Rebuilt 3D Network for RGB-D Gesture Recognition. arXiv 2021, arXiv:2102.05348. Available online: http://arxiv.org/abs/2102.05348 (accessed on 1 January 2022). [CrossRef]
- Carreira, J.; Zisserman, A. Quo Vadis, Action Recognition? A New Model and the Kinetics Dataset. arXiv 2017, arXiv:1705.07750. Available online: http://arxiv.org/abs/1705.07750 (accessed on 1 January 2022).
- Simonyan, K.; Zisserman, A. Very Deep Convolutional Networks for Large-Scale Image Recognition. arXiv 2014, arXiv:1409.1556. Available online: http://arxiv.org/abs/1409.1556 (accessed on 1 January 2022).
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep Residual Learning for Image Recognition. Available online: http://image-net.org/challenges/LSVRC/2015/ (accessed on 1 January 2022).
- Bergstra, J.; Ca, J.B.; Ca, Y.B. Random Search for Hyper-Parameter Optimization Yoshua Bengio. 2012. Available online: http://scikit-learn.sourceforge.net (accessed on 1 January 2022).
- Carrera, B.; Kim, K. Comparison analysis of machine learning techniques for photovoltaic prediction using weather sensor data. Sensors 2020, 20, 3129. [Google Scholar] [CrossRef]
- Box, G.E.P. Science and Statistics. J. Am. Stat. Assoc. 1976, 71, 791–799. [Google Scholar] [CrossRef]
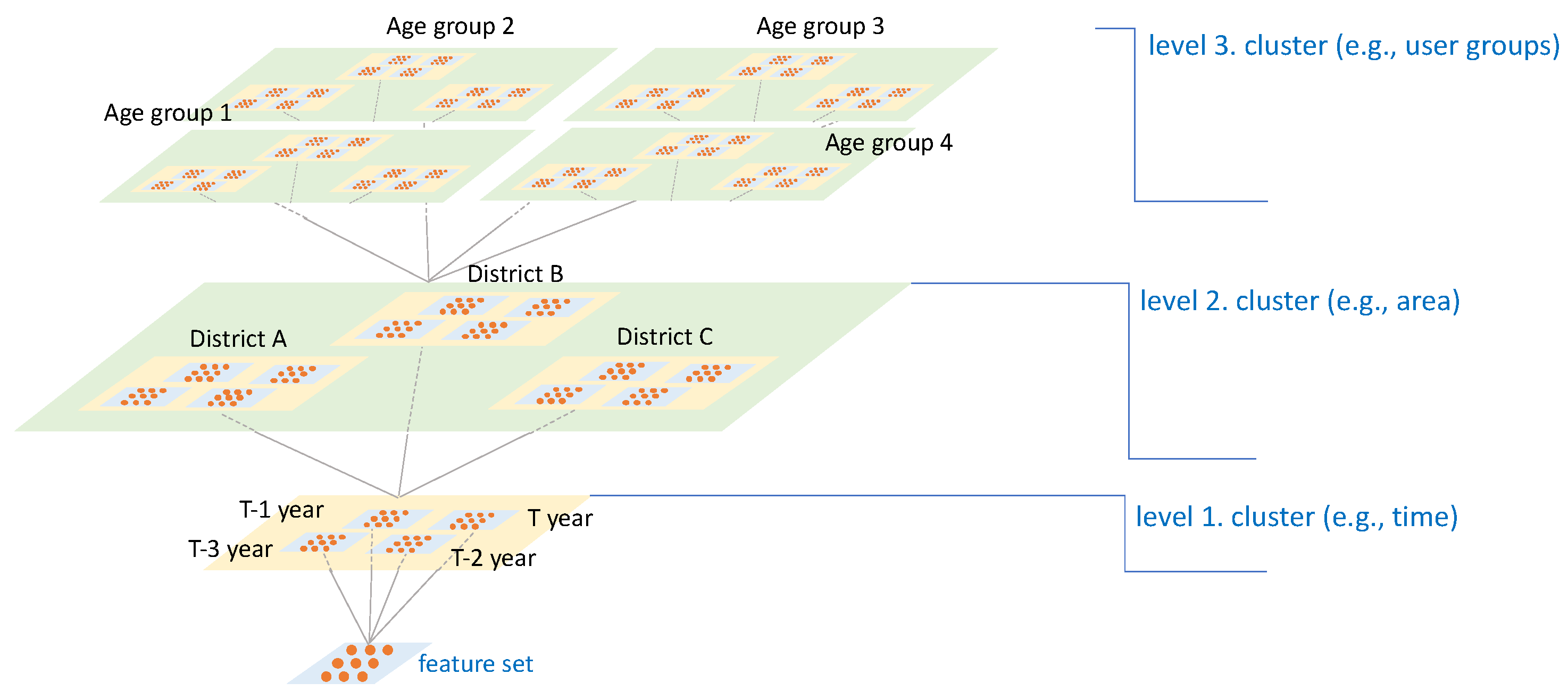



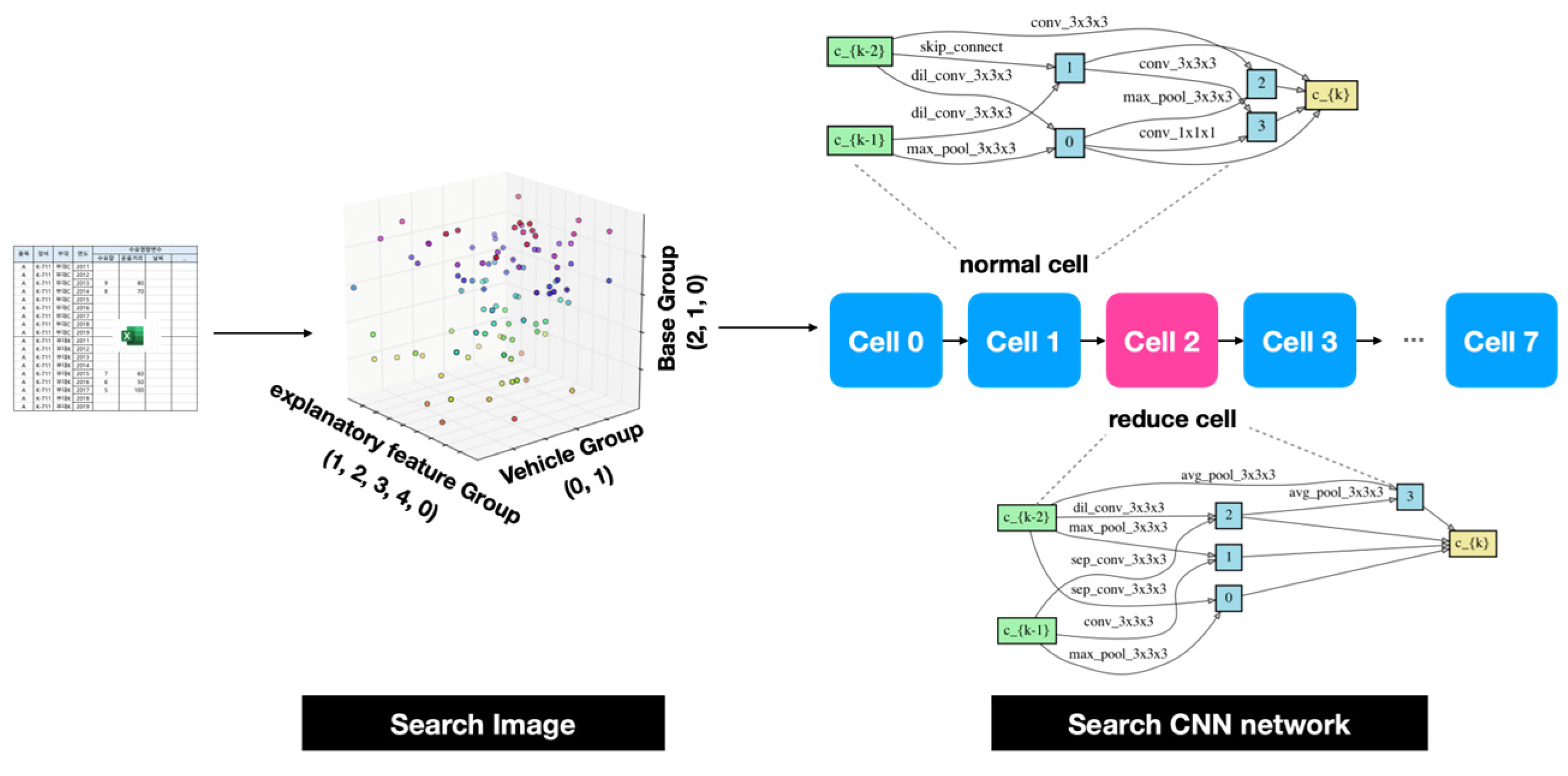


| DARTS | Tab2vox | ||
|---|---|---|---|
| Input Embedding Architecture Search | none |  |  |
 | |||
| CNN Architecture Search |  |  | |
 |  | ||
| Task | Classification | Regression | |
| Category | Feature | Definition | Type | Range | Level 1 | ||
|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | |||||
| Spare parts specifications | X1 | Unit price of spare parts (KRW) | numerical | [3, 13,519,541] | |||
| X2 | Length of spare parts (cm) | numerical | [0, 350] | ||||
| X3 | Width of spare parts (cm) | numerical | [0, 520] | ||||
| X4 | Height of spare parts (cm) | numerical | [0, 138] | ||||
| X5 | Weight of spare parts (kg) | numerical | [0, 1800] | ||||
| X6 | Volume of spare parts (m3) | numerical | [0, 3] | ||||
| X7 | Quantity Per Application (QPA): Number of spare parts installed per weapon system | numerical | [1, 168] | ✓ | |||
| X8 | Base Repair Percent (BRP): Average percentage of spare parts repaired at bases out of maintenance requests | numerical | [0, 1] | ||||
| X9 | Depot Repair Percent (DRP): Average percentage of spare parts repaired at depot out of maintenance requests from bases | numerical | [0, 1] | ||||
| X10 | Condemnation Percentage (ConPct): Average percentage of spare parts discarded as non-repairable by depot | numerical | [0, 1] | ||||
| X11 | Average repair cost of spare parts at depot base level | numerical | [2, 13,699,405] | ✓ | |||
| X12 | Average repair cost of spare parts at depot maintenance level | numerical | [0.9, 7,229,964] | ✓ | |||
| X13 | Procurement Lead Time (PROLT): Lead time, which is the period time (in days) from the purchase request to the receipt completion for spare parts | numerical | [18, 999] | ||||
| Consumption history | X14 | Monthly spare parts demand average in year t | numerical | [0, 243] | ✓ | ✓ | ✓ |
| X15 | Monthly spare parts demand median in year t | numerical | [0, 115] | ✓ | ✓ | ✓ | |
| X16 | Monthly spare parts demand deviation in year t | numerical | [0, 182,992] | ✓ | ✓ | ✓ | |
| X17 | Daily spare parts demand average in year t | numerical | [0, 8] | ✓ | ✓ | ✓ | |
| X18 | Daily spare parts demand median in year t | numerical | [0, 1] | ✓ | ✓ | ✓ | |
| X19 | Daily spare parts demand deviation in year t | numerical | [0, 4749] | ✓ | ✓ | ✓ | |
| X20 | The amount of spare parts consumption in January in year t | numerical | [0, 1] | ✓ | ✓ | ✓ | |
| X21 | The amount of spare parts consumption in February from 2010 to year t | numerical | [0, 1] | ✓ | ✓ | ✓ | |
| X22 | The amount of spare parts consumption in March from 2010 to year t | numerical | [0, 1] | ✓ | ✓ | ✓ | |
| X23 | The amount of spare parts consumption in April from 2010 to year t | numerical | [0, 1] | ✓ | ✓ | ✓ | |
| X24 | The amount of spare parts consumption in May from 2010 to year t | numerical | [0, 1] | ✓ | ✓ | ✓ | |
| X25 | The amount of spare parts consumption in June from 2010 to year t | numerical | [0, 1] | ✓ | ✓ | ✓ | |
| X26 | The amount of spare parts consumption in July from 2010 to year t | numerical | [0, 1] | ✓ | ✓ | ✓ | |
| X27 | The amount of spare parts consumption in August from 2010 to year t | numerical | [0, 1] | ✓ | ✓ | ✓ | |
| X28 | The amount of spare parts consumption in September from 2010 to year t | numerical | [0, 1] | ✓ | ✓ | ✓ | |
| X29 | The amount of spare parts consumption in October from 2010 to year t | numerical | [0, 1] | ✓ | ✓ | ✓ | |
| X30 | The amount of spare parts consumption in November from 2010 to year t | numerical | [0, 1] | ✓ | ✓ | ✓ | |
| X31 | The amount of spare parts consumption in December from 2010 to year t | numerical | [0, 1] | ✓ | ✓ | ✓ | |
| X32 | Average monthly spare parts inventory quantity in year t | numerical | [0, 9150] | ✓ | ✓ | ||
| X33 | Spare parts consumption in year t | numerical | [0, 2919] | ✓ | ✓ | ✓ | |
| X34 | Squared coefficient of variation (CV2): Standard deviation of the demand divided by the average demand for non-zero demand periods. | numerical | [0, 63] | ✓ | ✓ | ||
| X35 | Average inter-demand interval (ADI): Average interval time between two demand occurrences. | numerical | [0, 9] | ✓ | ✓ | ||
| X36 | Mean time between failures (MTBF): | numerical | [1, 9] | ✓ | ✓ | ||
| Operating environment | X37 | Operating distance (in hours) of the weapon system, related to a spare part, in year t | numerical | [0, 3,229,201] | ✓ | ||
| X38 | Operating time (in hours) of the weapon system, related to a spare part, in year t | numerical | [0, 7,854,334] | ✓ | |||
| X39 | Oil consumption in year t | numerical | [0, 406,682] | ✓ | |||
| X40 | Average equipment age in year t | numerical | [2.85, 35] | ✓ | ✓ | ||
| X41 | Number of weapon systems operated in year t | numerical | [0, 3584] | ✓ | ✓ | ✓ | |
| X42 | Average temperature up to year t in the weapon system operating bases | numerical | [21.2, 25] | ✓ | |||
| X43 | Maximum temperature up to year t in the weapon system operating bases | numerical | [25.3, 30] | ✓ | |||
| X44 | Minimum temperature up to year t in the weapon system operating bases | numerical | [15.9, 22] | ✓ | |||
| X45 | Average amount of precipitation up to year t in the weapon system operating bases | numerical | [1.2, 17] | ✓ | |||
| X46 | Average humidity up to year t in the weapon system operating bases | numerical | [61.4, 86] | ✓ | |||
| X47 | Weapon system utilization rate in year t | numerical | [0.98, 1] | ✓ | |||
| X48 | Forest ratio to total area (%) | numerical | [23.76, 97] | ✓ | |||
| X49 | Road pavement ratio to total area (%) | numerical | [3.72, 100] | ✓ | |||
| X50 | Land ratio to total area (%) | numerical | [0.79, 1] | ✓ | |||
| X51 | Sea ratio to total area (%) | numerical | [0, 0] | ✓ | |||
| X52 | Urban ratio to total area (%) | numerical | [0.53, 100] | ✓ | |||
| Time Series | Regression | Ensemble |
|---|---|---|
| Arithmetic Mean (am) | Linear Regression (lr) | Random Forest (rf) |
| Simple Exponential Smoothing (ses) | Decision Tree (dt) | AdaBoost (ada) |
| Weighted Moving Average (wma) | Ridge Regression (ridge) | Gradient Boosting Regressor (gbr) |
| Bayesian Ridge (br) | Extreme Gradient Boosting (xgboost) | |
| Lasso Regression (lasso) | Light Gradient Boosting Machine (lightgbm) | |
| ElasticNet (en) | CatBoost Regressor (catboost) |
| Data Representation | Prediction Model | Min-Max | RMSE | MAE | ||||
|---|---|---|---|---|---|---|---|---|
| Mean | Std | Mean | Std | Mean | Std | |||
| Tabular data | Time Series | Arithmetic Mean | 0.343 | 0.015 | 486.92 | 84.67 | 110.98 | 10.05 |
| Simple Exponential Smoothing | 0.486 | 0.010 | 249.15 | 63.51 | 56.47 | 9.36 | ||
| Weighted Moving Average | 0.449 | 0.012 | 389.38 | 77.37 | 83.57 | 9.39 | ||
| Regression | LinearRegression | 0.333 | 0.043 | 140.57 | 24,799.10 | 41.16 | 1371.85 | |
| DecisionTree | 0.629 | 0.024 | 166.41 | 40.27 | 36.40 | 5.97 | ||
| Ridge | 0.332 | 0.044 | 140.62 | 52.31 | 41.25 | 6.76 | ||
| BayesianRidge | 0.334 | 0.044 | 140.62 | 26.69 | 41.09 | 4.70 | ||
| Lasso | 0.230 | 0.022 | 179.27 | 28.70 | 47.59 | 4.37 | ||
| ElasticNet | 0.295 | 0.024 | 213.86 | 39.06 | 52.70 | 6.17 | ||
| Ensemble | RandomForest | 0.545 | 0.021 | 148.61 | 37.62 | 34.58 | 6.09 | |
| AdaBoost | 0.094 | 0.031 | 305.53 | 1622.54 | 182.08 | 898.37 | ||
| GradientBoosting | 0.388 | 0.025 | 154.79 | 29.27 | 34.17 | 4.10 | ||
| XGBoost | 0.506 | 0.016 | 133.17 | 33.40 | 31.42 | 5.36 | ||
| LGBM | 0.468 | 0.019 | 150.36 | 30.80 | 32.42 | 4.89 | ||
| CatBoost | 0.493 | 0.006 | 156.24 | 37.63 | 33.51 | 5.47 | ||
| Images | IGTD (2D images) | 2D-CNN | 0.171 | 0.006 | 485.45 | 157.85 | 112.58 | 28.71 |
| Tab2Vox (3D images) | 3D-CNN | 0.631 | 0.014 | 518.81 | 160.65 | 92.28 | 22.86 | |
| Item Group | Clustering Rules | Number of Items | |
|---|---|---|---|
| Item Cost (IC) | Annual Demand (AD) | ||
| Item group 1 | <8M KRW | <1.3 | 433 |
| Item group 2 | 1.3 | 19 | |
| Item group 3 | 4 | 4 | |
| Item group 4 | 8M KRW | - | 2 |
| Symbol | Description |
|---|---|
| Sets | |
| Set of item groups = {0, 1, …, n} | |
| Set of prediction models = {0, 1, …, 12} | |
| Parameters | |
| Number of items in item group | |
| Prediction accuracy of model j in item group | |
| Standard deviation between the prediction accuracies of 5-fold test sets in model j in item group | |
| Run time of model | |
| Total number of test items | |
| Total run time | |
| Decision variables | |
| Binary decision variable, equal to 1 if the item group selects the prediction model . | |
| Cluster | Number of Items | ada | br | catboost | dt | en | gbr | lasso | lightgbm | lr | rf | ridge | xgboost | Tab2vox |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 433 | 0.074 | 0.322 | 0.488 | 0.630 | 0.283 | 0.377 | 0.212 | 0.460 | 0.322 | 0.541 | 0.319 | 0.498 | 0.655 |
| 2 | 19 | 0.575 | 0.631 | 0.641 | 0.606 | 0.564 | 0.628 | 0.593 | 0.638 | 0.631 | 0.634 | 0.630 | 0.659 | 0.189 |
| 3 | 4 | 0.028 | 0.275 | 0.366 | 0.767 | 0.218 | 0.485 | 0.385 | 0.556 | 0.222 | 0.644 | 0.259 | 0.671 | 0.435 |
| 4 | 2 | 0.037 | 0.271 | 0.482 | 0.386 | 0.299 | 0.336 | 0.497 | 0.415 | 0.225 | 0.333 | 0.425 | 0.422 | 0.041 |
| Model Combinations | Number of Item Groups (A) | Number of Models (B) | Workload | Min–Max Accuracy |
|---|---|---|---|---|
| tab2vox + dt | 2 | 2 | 4 | 0.6358 |
| tab2vox + dt + xgboost | 3 | 3 | 9 | 0.6553 |
| tab2vox + dt + xgboost + lasso | 4 (optimal) | 4 | 16 | 0.6558 |
| tab2vox + dt + xgboost + lasso + br | 5 | 5 | 25 | 0.6560 |
| tab2vox + dt + xgboost + lasso + br | 6 | 5 | 30 | 0.6680 |
| tab2vox + dt + xgboost + lasso + br | 7 | 5 | 35 | 0.6683 |
| tab2vox + dt + xgboost + lasso + br | 8 | 5 | 40 | 0.6685 |
| tab2vox + dt + xgboost + lasso + br | 9 | 5 | 45 | 0.6685 |
| tab2vox + dt + xgboost + lasso + br | 10 | 5 | 50 | 0.6685 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lee, E.; Nam, M.; Lee, H. Tab2vox: CNN-Based Multivariate Multilevel Demand Forecasting Framework by Tabular-To-Voxel Image Conversion. Sustainability 2022, 14, 11745. https://doi.org/10.3390/su141811745
Lee E, Nam M, Lee H. Tab2vox: CNN-Based Multivariate Multilevel Demand Forecasting Framework by Tabular-To-Voxel Image Conversion. Sustainability. 2022; 14(18):11745. https://doi.org/10.3390/su141811745
Chicago/Turabian StyleLee, Euna, Myungwoo Nam, and Hongchul Lee. 2022. "Tab2vox: CNN-Based Multivariate Multilevel Demand Forecasting Framework by Tabular-To-Voxel Image Conversion" Sustainability 14, no. 18: 11745. https://doi.org/10.3390/su141811745
APA StyleLee, E., Nam, M., & Lee, H. (2022). Tab2vox: CNN-Based Multivariate Multilevel Demand Forecasting Framework by Tabular-To-Voxel Image Conversion. Sustainability, 14(18), 11745. https://doi.org/10.3390/su141811745






