An Adaptive Switching Control Strategy under Heavy–Light Load for the Bidirectional LLC Considering Parasitic Capacitance
Abstract
1. Introduction
- (1)
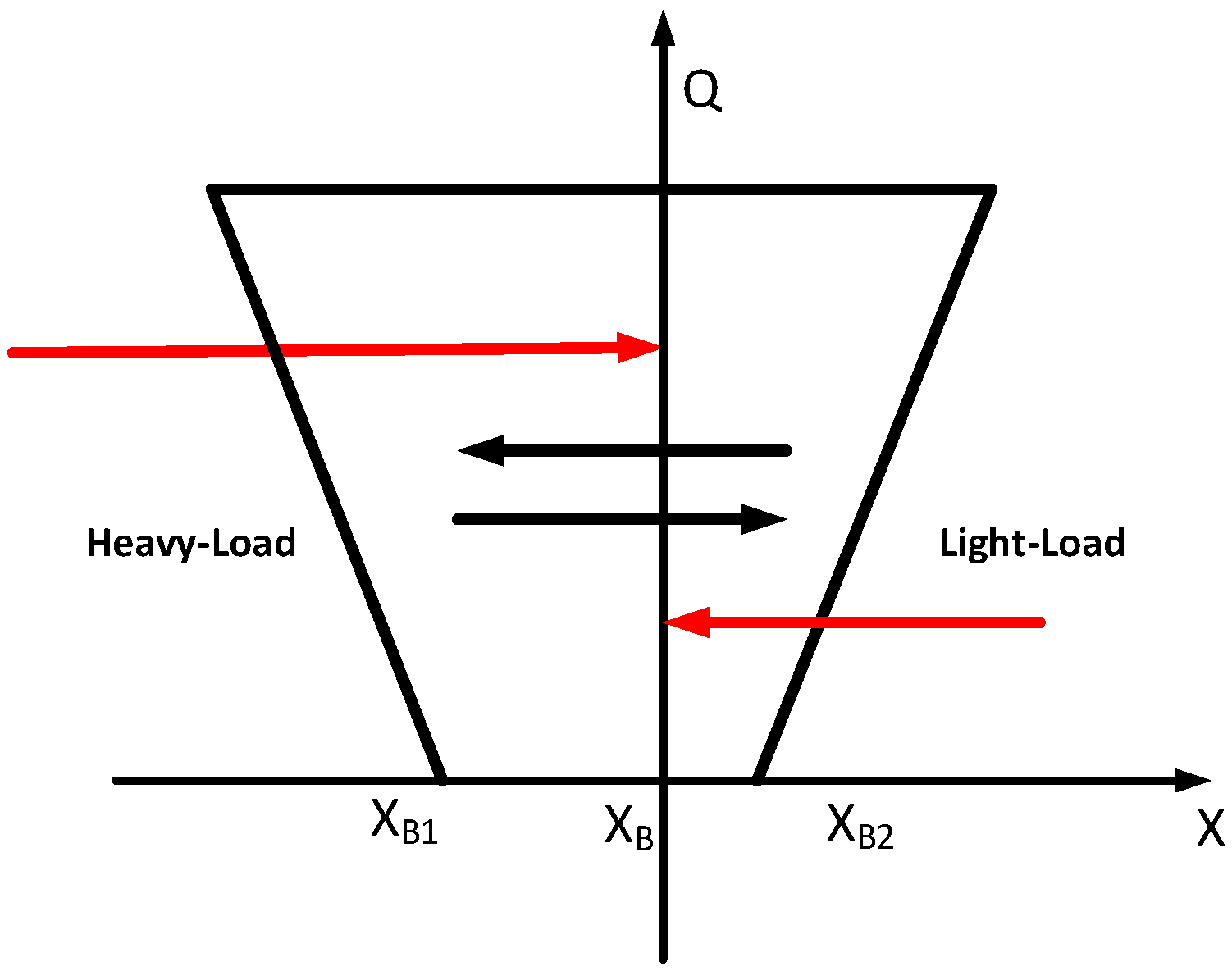
- An adaptive switching control strategy is provided for the LLC, which can adjust the hysteresis loop boundary range according to the load. It solves the problem of higher output voltage than the reference and ensures the control continuity.
- (2)
- A bidirectional model considering parasitic capacitance is established, which compensates for accuracy in the light-load condition. It accurately describes the voltage gain curve under light load, which is more realistic than the previous model.
- (3)
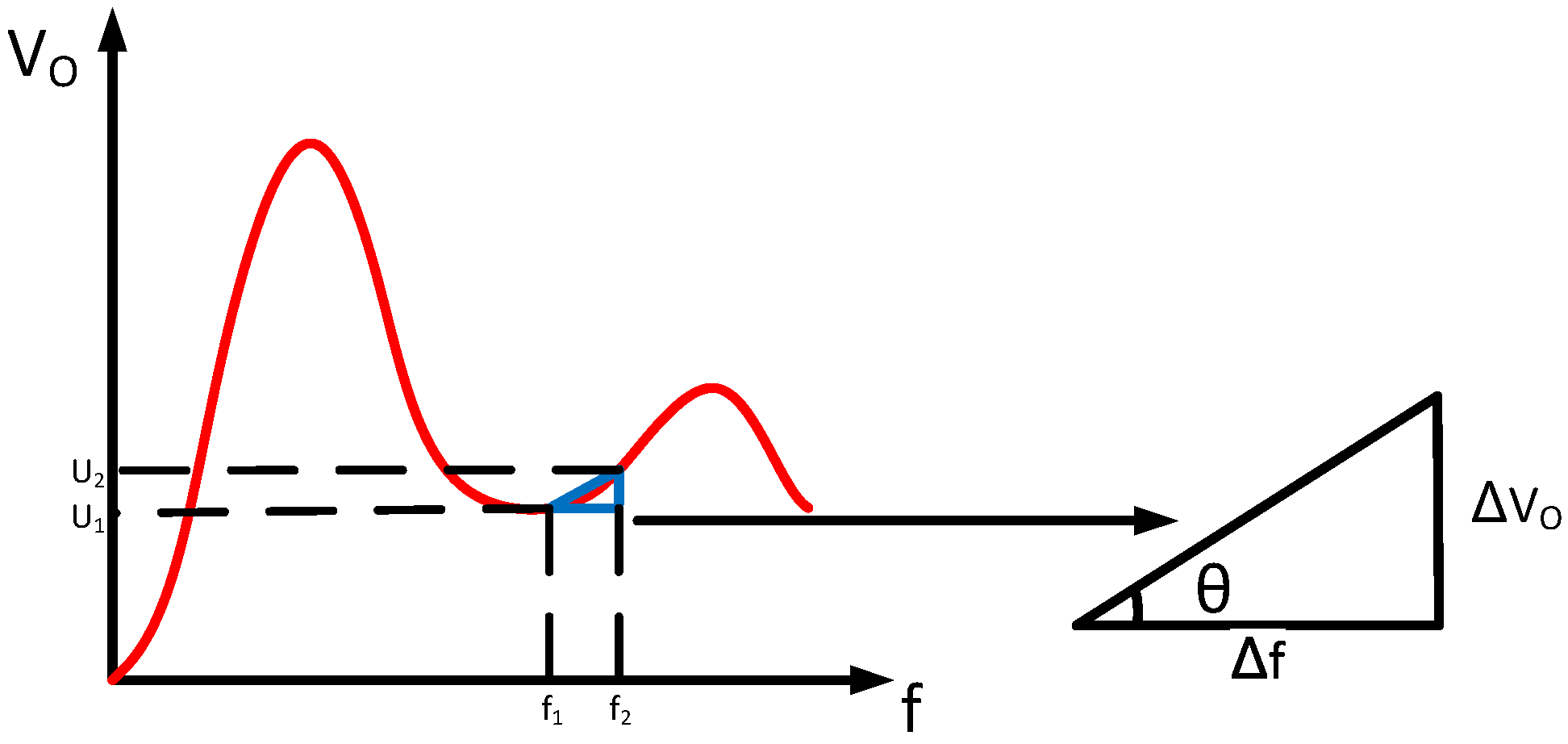
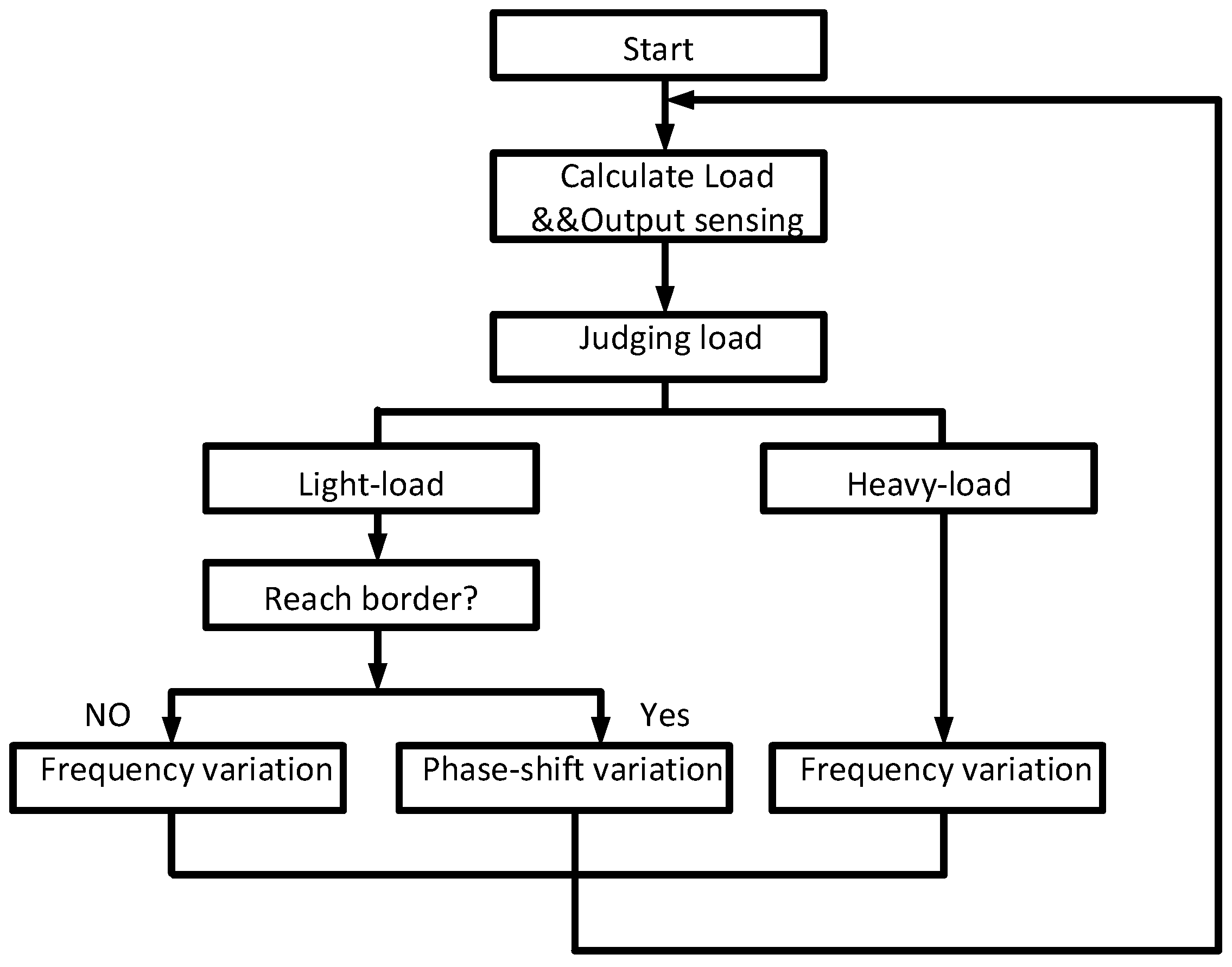
- The mentioned switching points are determined according to the rate of change of the output voltage and frequency, which ensures smooth switching. In addition, the energy hysteresis strategy is adopted near the switching point, in which the length of the hysteresis adapts to load changes. It plays an important role in improving the stability near the switching point under slight disturbance.
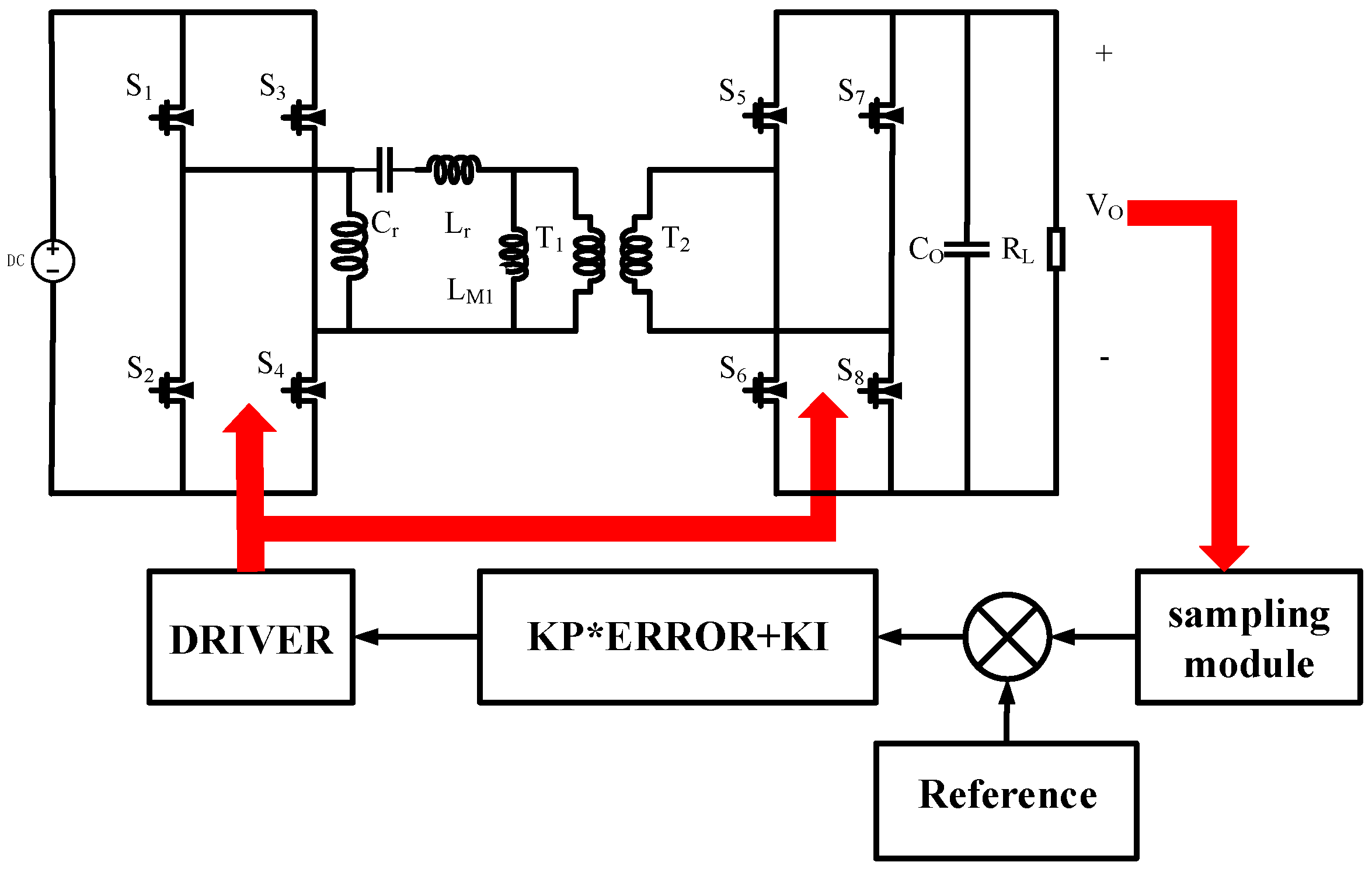
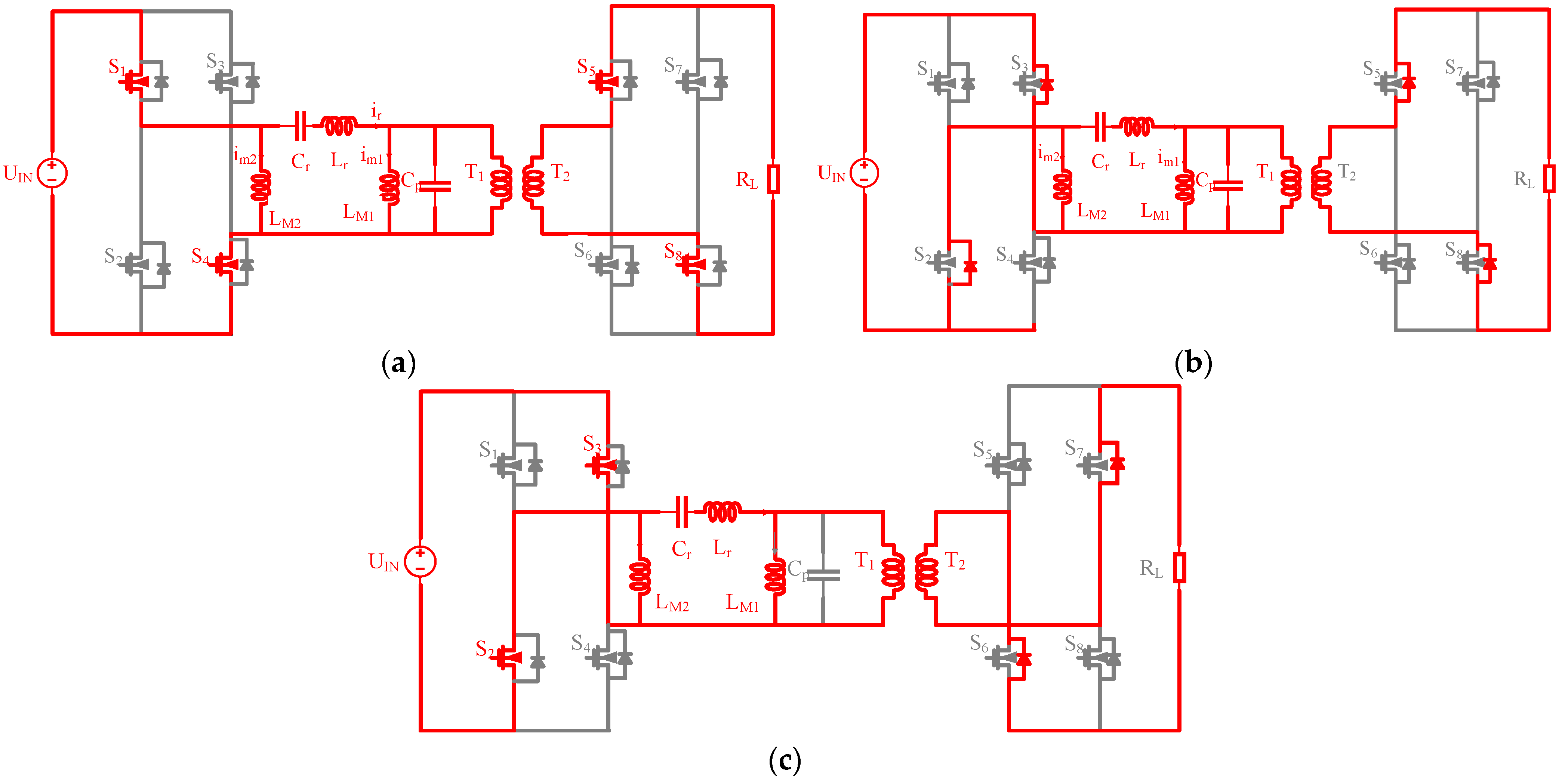
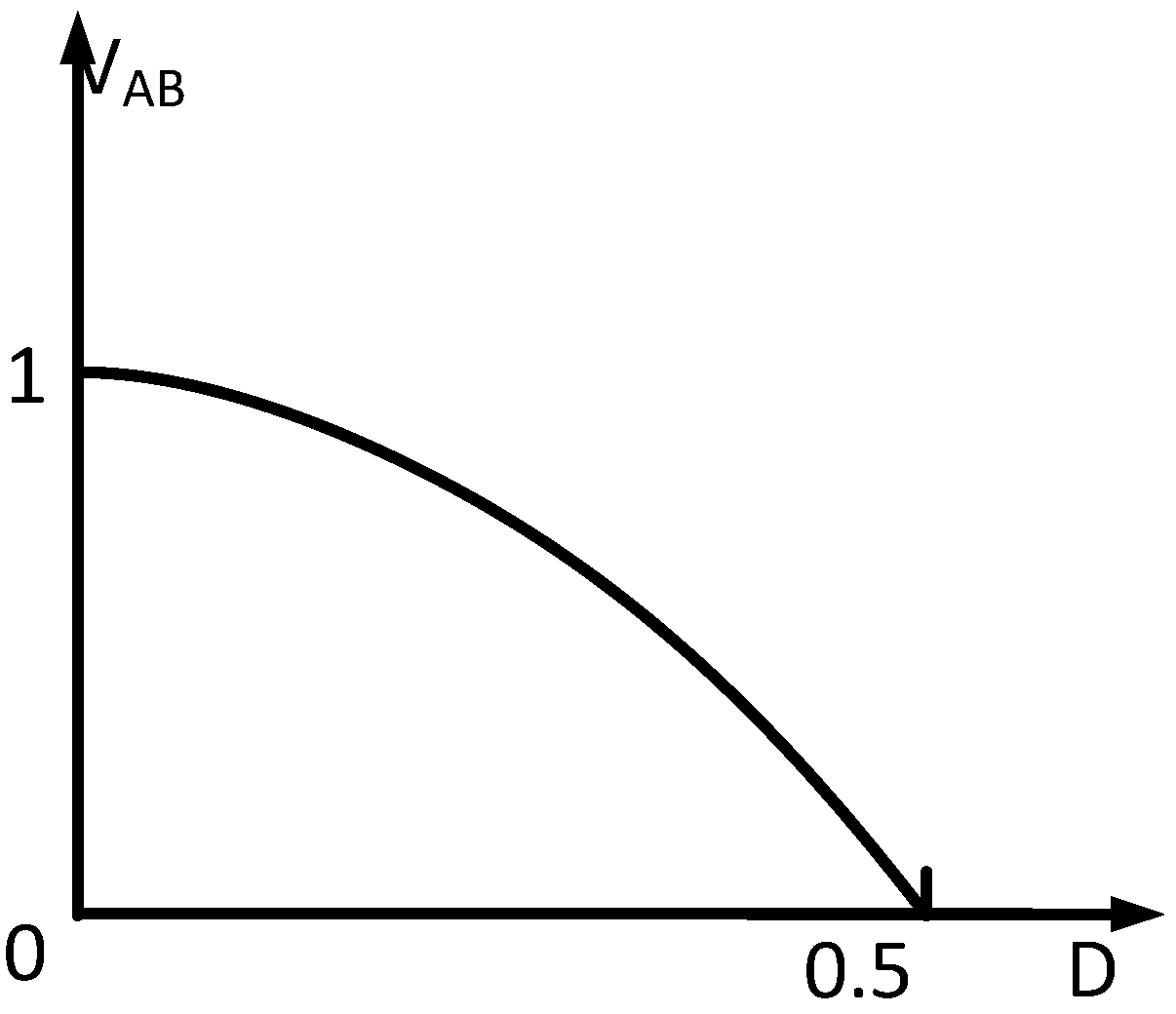
2. Conventional Topology and Control Method
3. The Proposed Model and Conventional Method
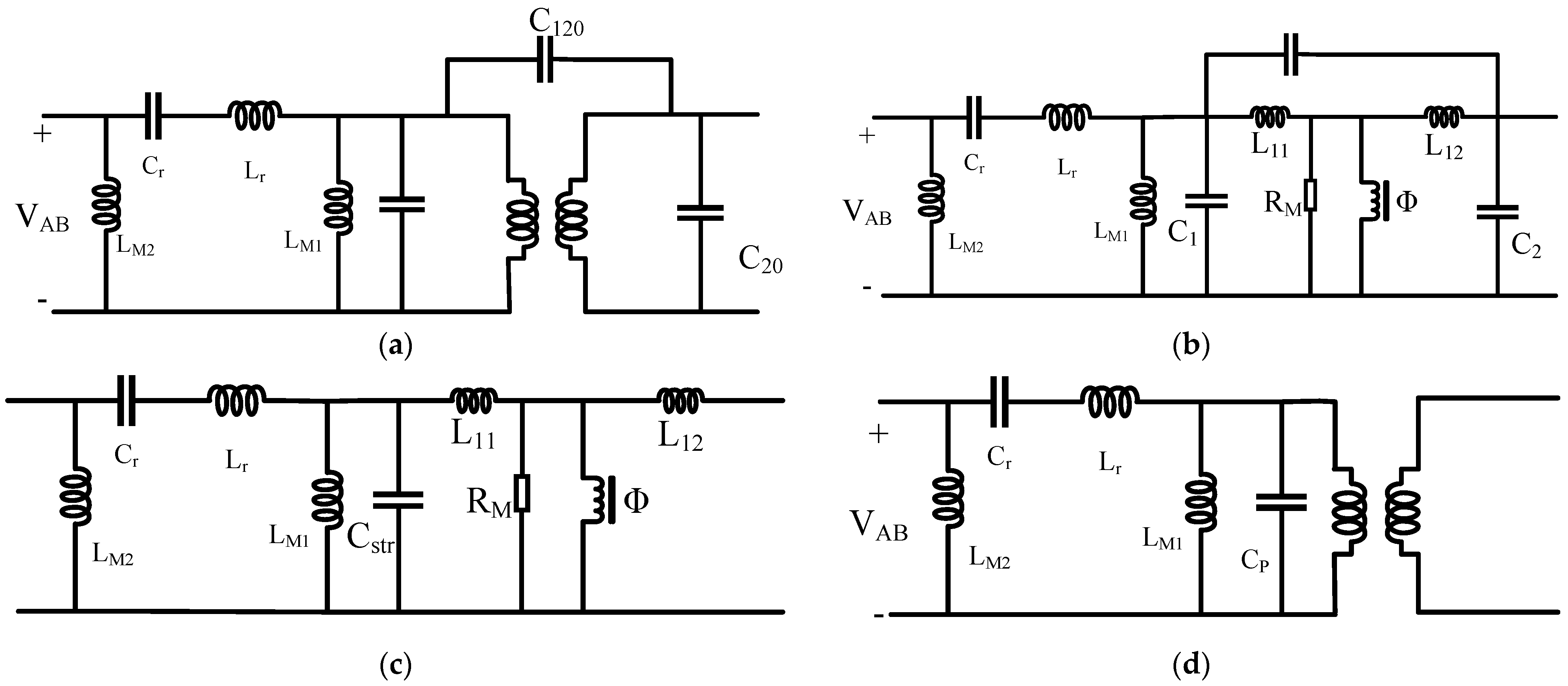
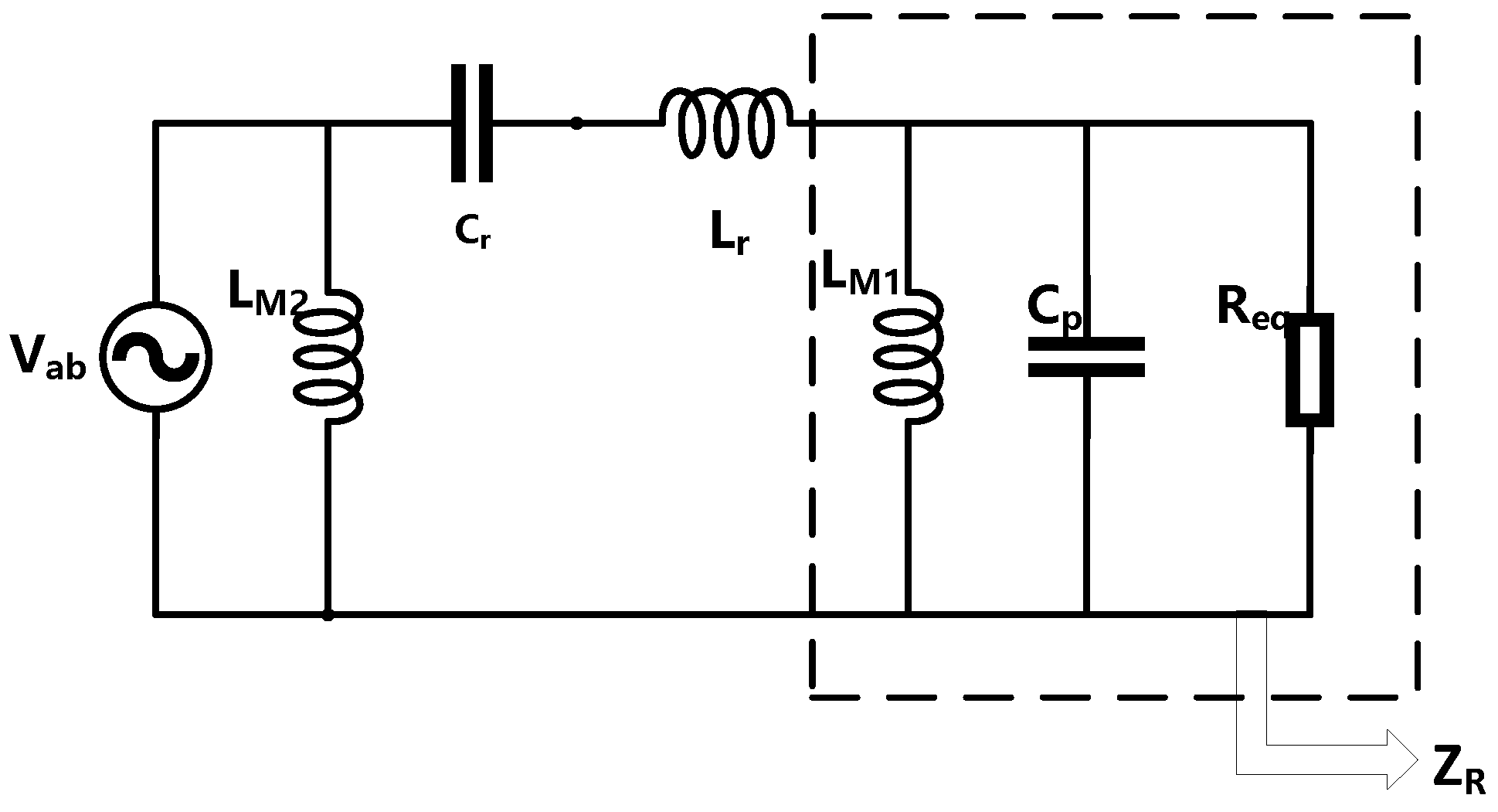
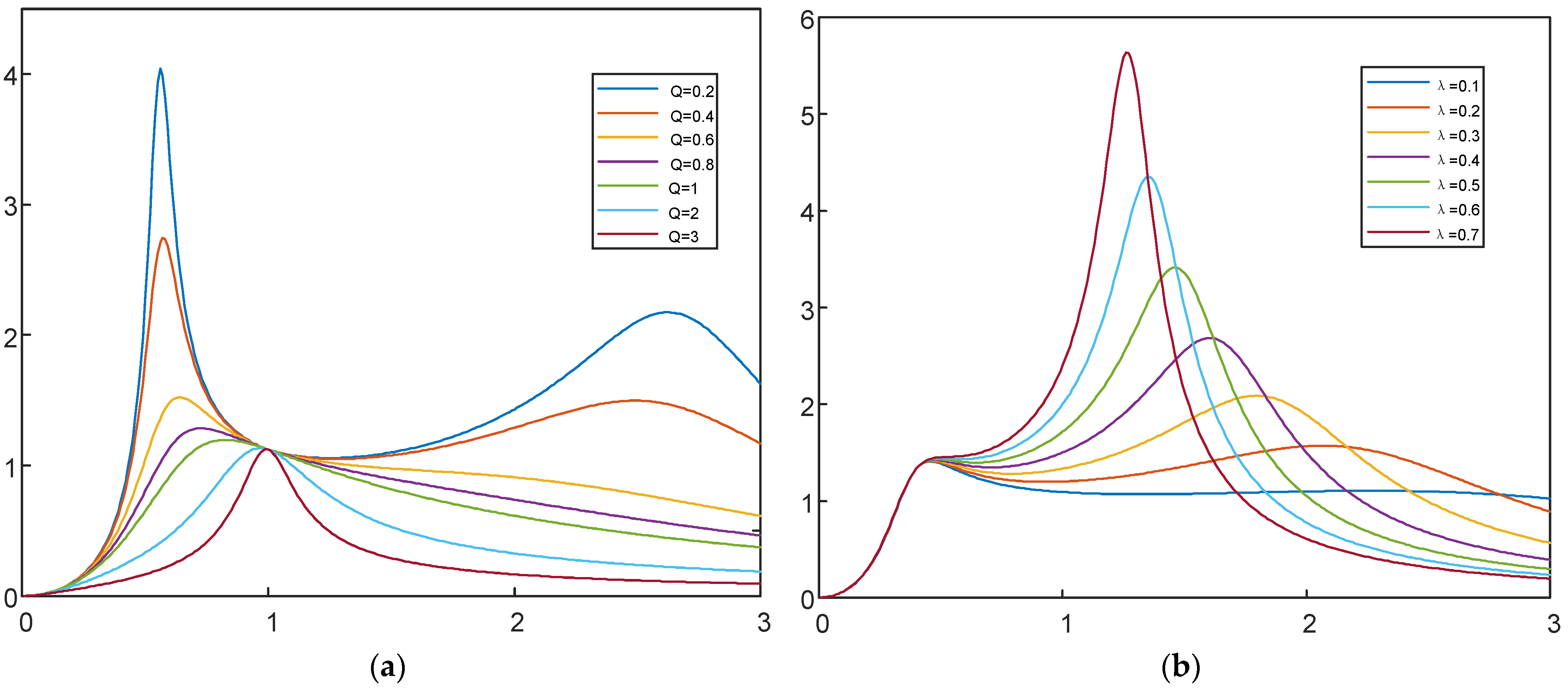
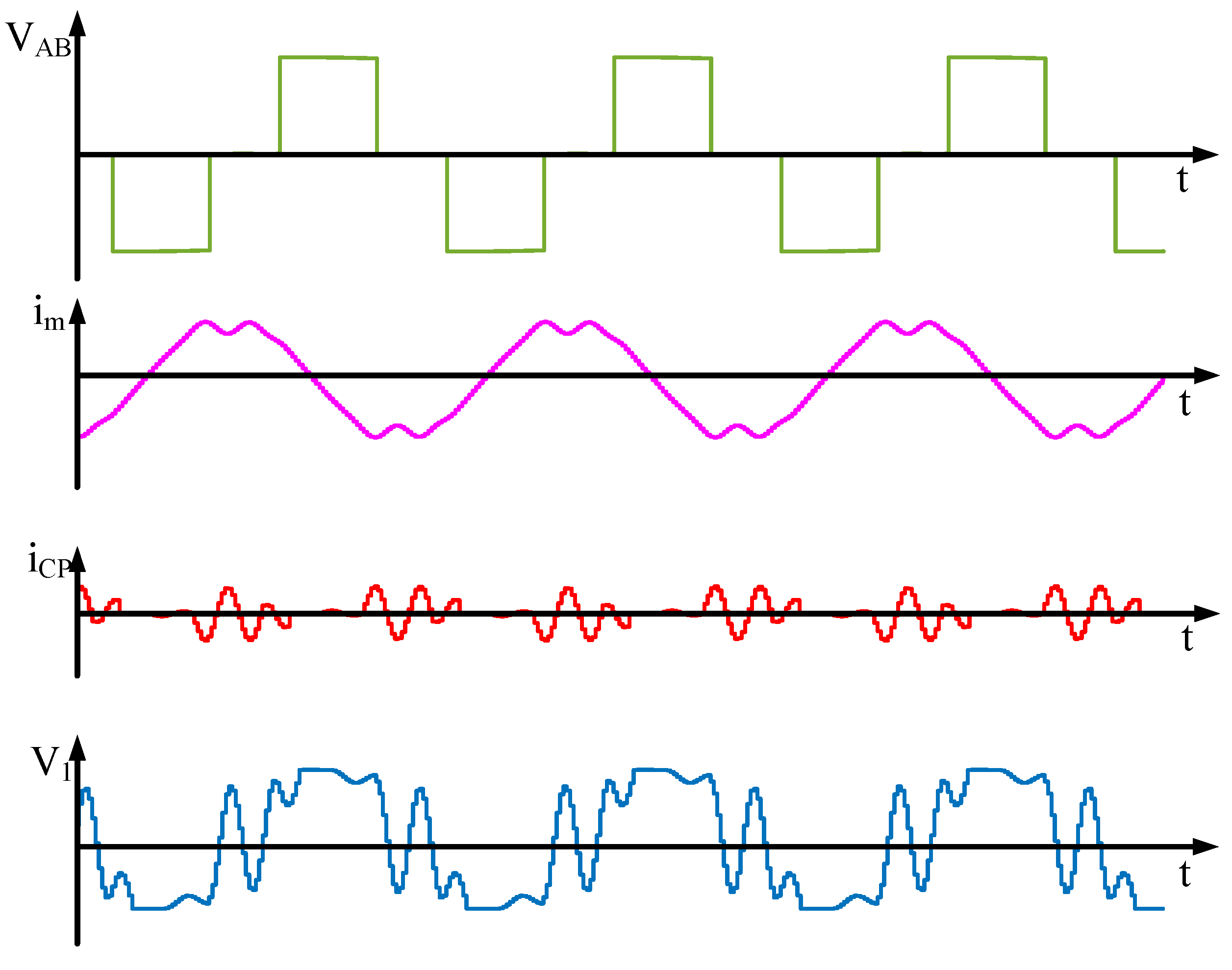
3.1. The LLC Model Considering Parasitic Capacitance
3.2. An Adopting Switching Control Method
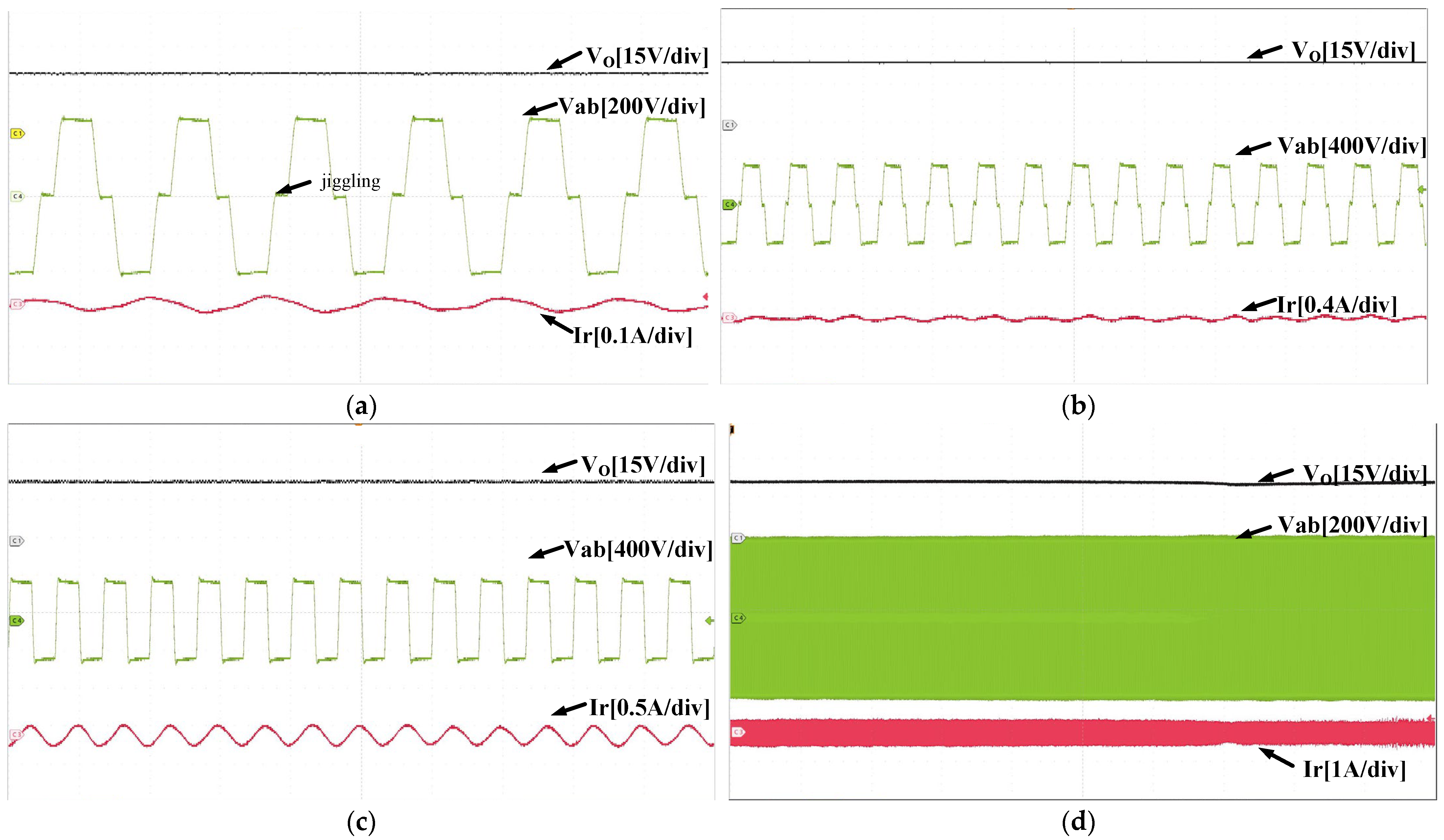
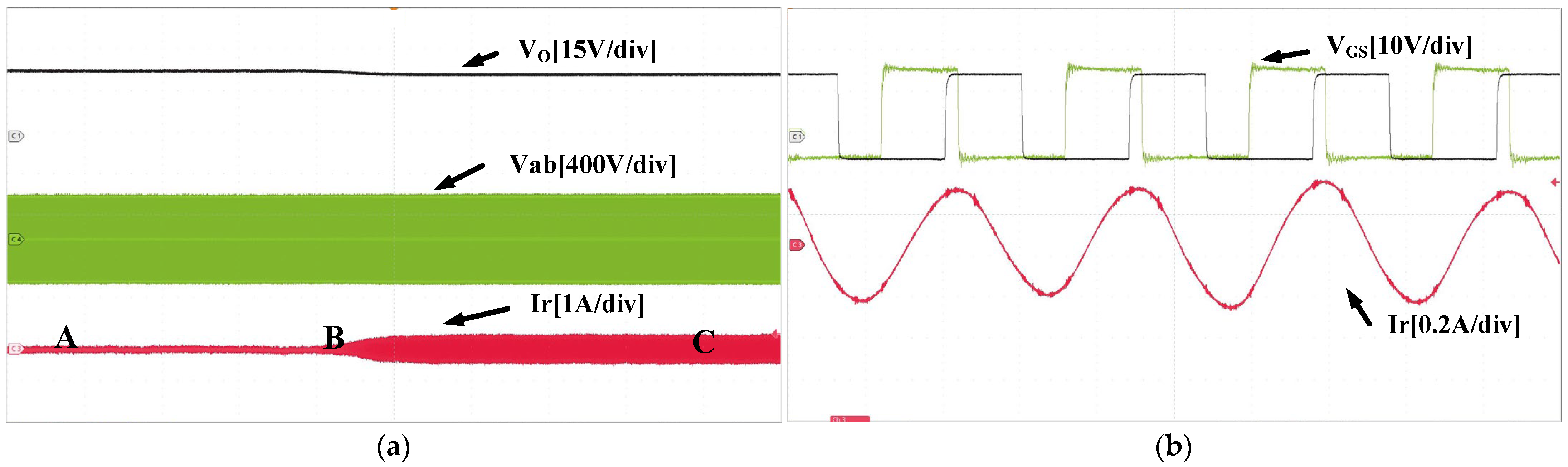
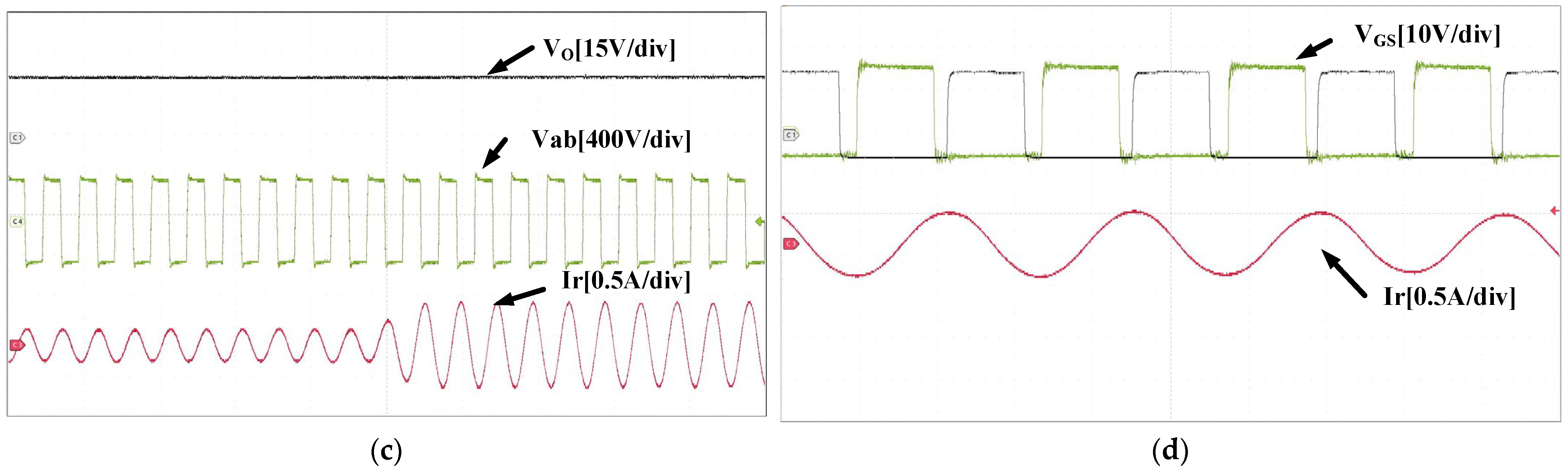
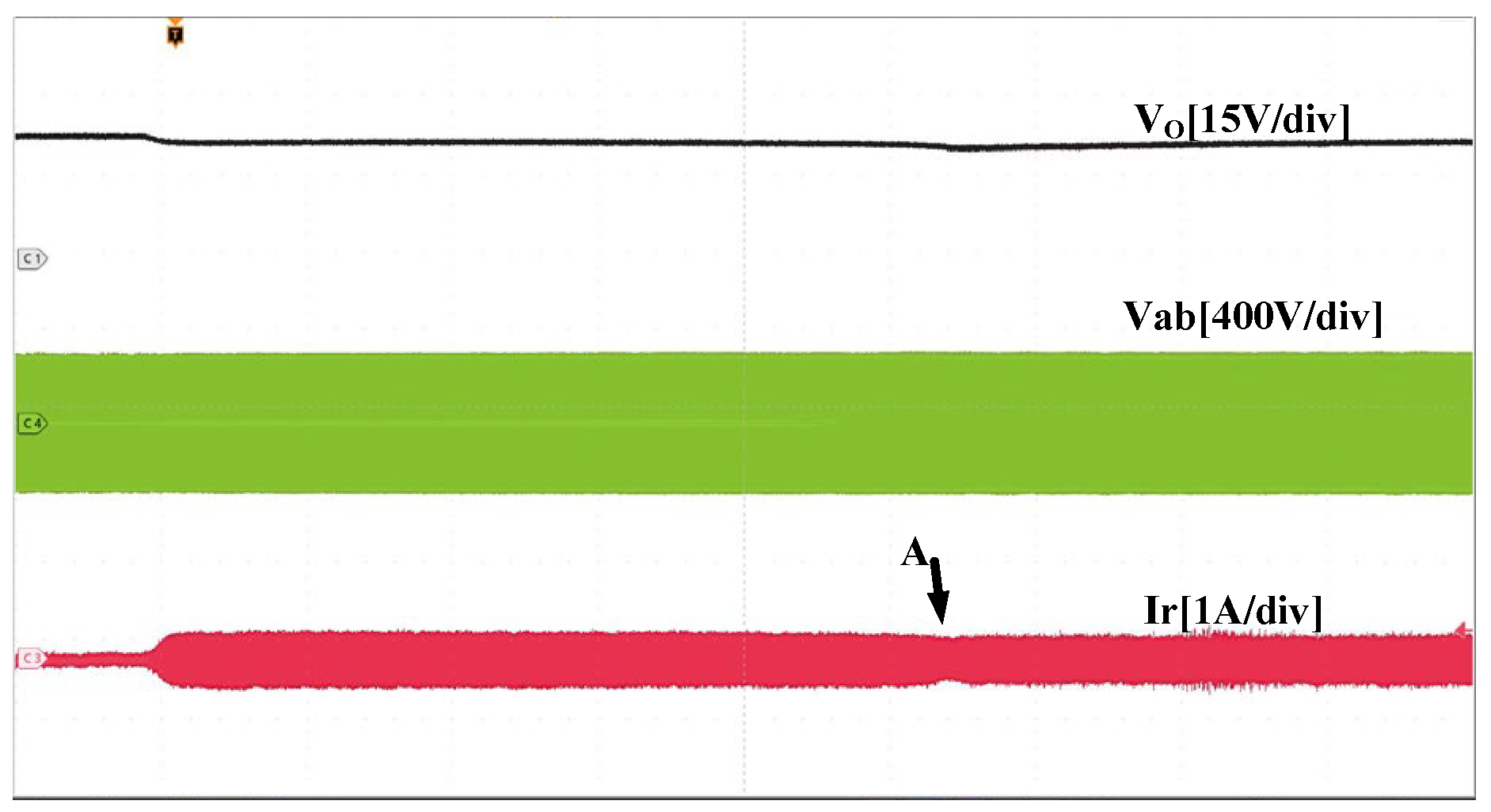
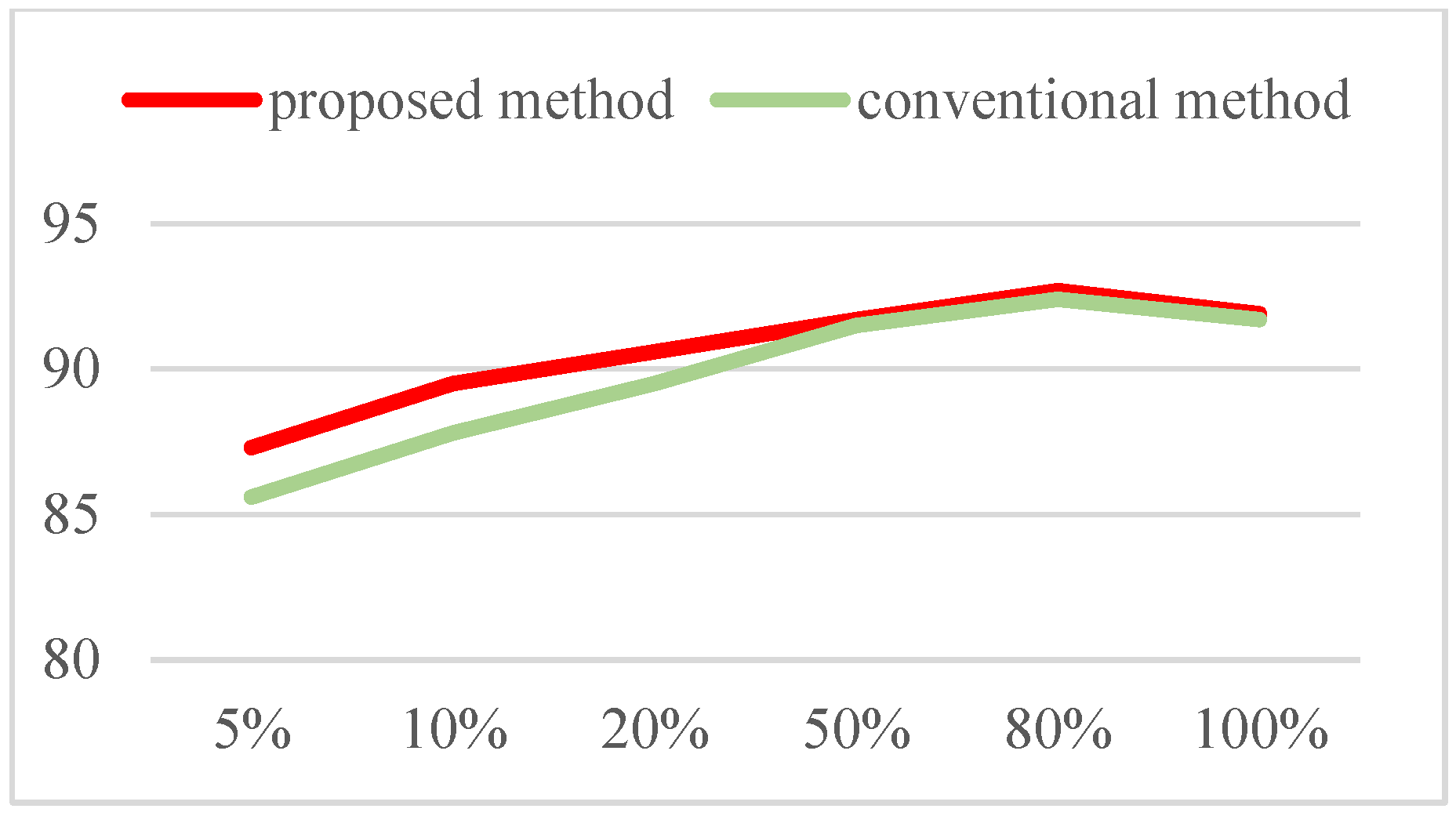
4. Experimental Results
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Conflicts of Interest
References
- Gao, S.; Zhao, H.; Gui, Y.; Luo, J.; Blaabjerg, F. Impedance Analysis of Voltage Source Converter Using Direct Power Control. IEEE Trans. Energy Convers. 2020, 36, 831–840. [Google Scholar] [CrossRef]
- Gao, S.; Zhao, H.; Wang, P.; Gui, Y.; Terzija, V.; Blaabjerg, F. Comparative Study of Symmetrical Controlled Grid-Connected Inverters. IEEE Trans. Power Electron. 2021, 37, 3954–3968. [Google Scholar] [CrossRef]
- Xie, F.; McEntee, C.; Zhang, M.; Mather, B.; Lu, N. Development of an Encoding Method on a Co-Simulation Platform for Mitigating the Impact of Unreliable Communication. IEEE Trans. Smart Grid 2020, 12, 2496–2507. [Google Scholar] [CrossRef]
- Alawieh, H.; Riachy, L.; Arab Tehrani, K.; Azzouz, Y.; Dakyo, B. A new dead-time effect elimination method for H-bridge inverters. In Proceedings of the IECON 2016—42nd Annual Conference of the IEEE Industrial Electronics Society, Florence, Italy, 23–26 October 2016; pp. 3153–3159. [Google Scholar]
- Zhao, H.; Wu, Q.; Wang, J.; Liu, Z.; Shahidehpour, M.; Xue, Y. Combined Active and Reactive Power Control of Wind Farms Based on Model Predictive Control. IEEE Trans. Energy Convers. 2017, 32, 1177–1187. [Google Scholar] [CrossRef]
- Montero-Cassinello, J.; Cheah-Mane, M.; Prieto-Araujo, E.; Gomis-Bellmunt, O. Small-signal analysis of a fast central control for large scale PV power plants. Int. J. Electr. Power Energy Syst. 2022, 141, 108157. [Google Scholar] [CrossRef]
- Gao, S.; Zhao, H.; Gui, Y.; Zhou, D.; Terzija, V.; Blaabjerg, F. A Novel Direct Power Control for DFIG with Parallel Compensator Under Unbalanced Grid Condition. IEEE Trans. Ind. Electron. 2020, 68, 9607–9618. [Google Scholar] [CrossRef]
- Faraji, R.; Adib, E.; Farzanehfard, H. Soft-switched non-isolated high step-up multi-port DC-DC converter for hybrid energy system with minimum number of switches. Int. J. Electr. Power Energy Syst. 2018, 106, 511–519. [Google Scholar] [CrossRef]
- Li, H.; Zhao, L.; Xu, C.; Zheng, X. A Dual Half-Bridge Phase-Shifted Converter with Wide ZVZCS Switching Range. IEEE Trans. Power Electron. 2017, 33, 2976–2985. [Google Scholar] [CrossRef]
- Chen, Z.; Liu, S.; Shi, L. A Soft Switching Full Bridge Converter with Reduced Parasitic Oscillation in a Wide Load Range. IEEE Trans. Power Electron. 2014, 29, 801–811. [Google Scholar] [CrossRef]
- Chan, Y.P.; Loo, K.H.; Yaqoob, M.; Lai, Y.M. A Structurally Reconfigurable Resonant Dual-Active-Bridge Converter and Modulation Method to Achieve Full-Range Soft-Switching and Enhanced Light-Load Efficiency. IEEE Trans. Power Electron. 2018, 34, 4195–4207. [Google Scholar] [CrossRef]
- Shi, H.; Wen, H.; Chen, J.; Hu, Y.; Jiang, L.; Chen, G.; Ma, J. Minimum-Backflow-Power Scheme of DAB-Based Solid-State Transformer with Extended-Phase-Shift Control. IEEE Trans. Ind. Appl. 2018, 54, 3483–3496. [Google Scholar] [CrossRef]
- Wang, K.; Wei, G.; Wei, J.; Wu, J.; Wang, L.; Yang, X. Current Detection and Control of Synchronous Rectifier in High-Frequency LLC Resonant Converter. IEEE Trans. Power Electron. 2022, 37, 3691–3696. [Google Scholar] [CrossRef]
- Wu, X.; Hua, G.; Zhang, J.; Qian, Z. A New Current-Driven Synchronous Rectifier for Series–Parallel Resonant (LLC) DC–DC Converter. IEEE Trans. Ind. Electron. 2010, 58, 289–297. [Google Scholar] [CrossRef]
- Feng, W.; Mattavelli, P.; Lee, F.C. Pulsewidth Locked Loop (PWLL) for Automatic Resonant Frequency Tracking in LLC DC–DC Transformer (LLC-DCX). IEEE Trans. Power Electron. 2012, 28, 1862–1869. [Google Scholar] [CrossRef]
- Li, H.; Wang, S.; Zhang, Z.; Zhang, J.; Zhu, W.; Ren, X.; Hu, C. A Bidirectional Synchronous/Asynchronous Rectifier Control for Wide Battery Voltage Range in SiC Bidirectional LLC Chargers. IEEE Trans. Power Electron. 2021, 37, 6090–6101. [Google Scholar] [CrossRef]
- Li, H.; Zhang, Z.; Wang, S.; Tang, J.; Ren, X.; Chen, Q. A 300-kHz 6.6-kW SiC Bidirectional LLC Onboard Charger. IEEE Trans. Ind. Electron. 2020, 67, 1435–1445. [Google Scholar] [CrossRef]
- Fei, C.; Li, Q.; Lee, F.C. Digital Implementation of Adaptive Synchronous Rectifier (SR) Driving Scheme for High-Frequency LLC Converters with Microcontroller. IEEE Trans. Power Electron. 2017, 33, 5351–5361. [Google Scholar] [CrossRef]
- Xue, B.; Wang, H.; Liang, J.; Cao, Q.; Li, Z. Phase-Shift Modulated Interleaved LLC Converter with Ultrawide Output Voltage Range. IEEE Trans. Power Electron. 2020, 36, 493–503. [Google Scholar] [CrossRef]
- Jovanovic, M.M.; Irving, B.T. On-the-Fly Topology-Morphing Control—Efficiency Optimization Method for LLC Resonant Converters Operating in Wide Input- and/or Output-Voltage Range. IEEE Trans. Power Electron. 2016, 31, 2596–2608. [Google Scholar] [CrossRef]
- Buccella, C.; Cecati, C.; Latafat, H.; Pepe, P.; Razi, K. Observer-Based Control of LLC DC/DC Resonant Converter Using Extended Describing Functions. IEEE Trans. Power Electron. 2015, 30, 5881–5891. [Google Scholar] [CrossRef]
- Li, H.; Wang, S.; Zhang, Z.; Zhang, J.; Li, M.; Gu, Z.; Ren, X.; Chen, Q. Bidirectional Synchronous Rectification on-Line Calculation Control for High Voltage Applications in SiC Bidirectional LLC Portable Chargers. IEEE Trans. Power Electron. 2020, 36, 5557–5568. [Google Scholar] [CrossRef]
- Kirshenboim, O.; Peretz, M.M. Combined Multilevel and Two-Phase Interleaved LLC Converter with Enhanced Power Processing Characteristics and Natural Current Sharing. IEEE Trans. Power Electron. 2017, 33, 5613–5620. [Google Scholar] [CrossRef]
- Jung, J.H.; Kim, H.S.; Ryu, M.H.; Baek, J.W. Design Methodology of Bidirectional CLLC Resonant Converter for High-Frequency Isolation of DC Distribution Systems. IEEE Trans. Power Electron. 2013, 28, 1741–1755. [Google Scholar] [CrossRef]
- Jiang, T.; Zhang, J.; Wu, X.; Sheng, K.; Wang, Y. A Bidirectional LLC Resonant Converter with Automatic Forward and Backward Mode Transition. IEEE Trans. Power Electron. 2014, 30, 757–770. [Google Scholar] [CrossRef]
- Jiang, T.; Zhang, J.; Wu, X.; Sheng, K.; Wang, Y. A Bidirectional Three-Level LLC Resonant Converter with PWAM Control. IEEE Trans. Power Electron. 2016, 31, 2213–2225. [Google Scholar] [CrossRef]
- Awasthi, A.; Bagawade, S.; Jain, P.K. Analysis of a Hybrid Variable-Frequency-Duty-Cycle-Modulated Low-Q LLC Resonant Converter for Improving the Light-Load Efficiency for a Wide Input Voltage Range. IEEE Trans. Power Electron. 2020, 36, 8476–8493. [Google Scholar] [CrossRef]
- Hu, Z.; Qiu, Y.; Wang, L.; Liu, Y.-F. An Interleaved LLC Resonant Converter Operating at Constant Switching Frequency. IEEE Trans. Power Electron. 2013, 29, 2931–2943. [Google Scholar] [CrossRef]
- Yoon, H.; Lee, H.; Ham, S.; Choe, H.; Kang, B. Off-Time Control of LLC Resonant Half-Bridge Converter to Prevent Audible Noise Generation Under a Light-Load Condition. IEEE Trans. Power Electron. 2018, 33, 8808–8817. [Google Scholar] [CrossRef]
- Fei, C.; Gadelrab, R.; Li, Q.; Lee, F.C. High-Frequency Three-Phase Interleaved LLC Resonant Converter with GaN Devices and Integrated Planar Magnetics. IEEE J. Emerg. Sel. Top. Power Electron. 2019, 7, 653–663. [Google Scholar] [CrossRef]
- Tehrani, K.; Capitaine, T.; Barrandon, L.; Hamzaoui, M.; Rafiei, S.M.R.; Lebrun, A. Current control design with a fractional-order PID for a three-level inverter. In Proceedings of the 2011 14th European Conference on Power Electronics and Applications, Birmingham, UK, 30 August 2011–1 September 2011; pp. 1–7. [Google Scholar]
- Priya, M.; Ponnambalam, P. Circulating Current Control of Phase-Shifted Carrier-Based Modular Multilevel Converter Fed by Fuel Cell Employing Fuzzy Logic Control Technique. Energies 2022, 15, 6008. [Google Scholar] [CrossRef]
- Lu, H.Y.; Zhu, J.G.; Hui, S. Experimental determination of stray capacitances in high frequency transformers. IEEE Trans. Power Electron. 2003, 18, 1105–1112. [Google Scholar] [CrossRef]




| Parameters | Value |
|---|---|
| Resonance inductor | Lr = 101 μH |
| Resonance capacitance | Cr = 24.6 μH |
| Magnetic inductance | LM1 = LM2 = 606 μH |
| Ratio of transformer | n = 12 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Han, Y.; Wang, R.; Zhang, Y.; Ma, D.; Jiang, S.; Wen, L. An Adaptive Switching Control Strategy under Heavy–Light Load for the Bidirectional LLC Considering Parasitic Capacitance. Sustainability 2022, 14, 11832. https://doi.org/10.3390/su141911832
Han Y, Wang R, Zhang Y, Ma D, Jiang S, Wen L. An Adaptive Switching Control Strategy under Heavy–Light Load for the Bidirectional LLC Considering Parasitic Capacitance. Sustainability. 2022; 14(19):11832. https://doi.org/10.3390/su141911832
Chicago/Turabian StyleHan, Yetong, Rui Wang, Yi Zhang, Dazhong Ma, Shaoxv Jiang, and Liangwu Wen. 2022. "An Adaptive Switching Control Strategy under Heavy–Light Load for the Bidirectional LLC Considering Parasitic Capacitance" Sustainability 14, no. 19: 11832. https://doi.org/10.3390/su141911832
APA StyleHan, Y., Wang, R., Zhang, Y., Ma, D., Jiang, S., & Wen, L. (2022). An Adaptive Switching Control Strategy under Heavy–Light Load for the Bidirectional LLC Considering Parasitic Capacitance. Sustainability, 14(19), 11832. https://doi.org/10.3390/su141911832







