Model for Determining Noise Level Depending on Traffic Volume at Intersections
Abstract
:1. Introduction
2. Materials and Methods
- High intensity of traffic load (more than 3000 veh/h);
- Presence of trucks and buses;
- Intersection with signalization;
- Street fronts and buildings near the intersection.
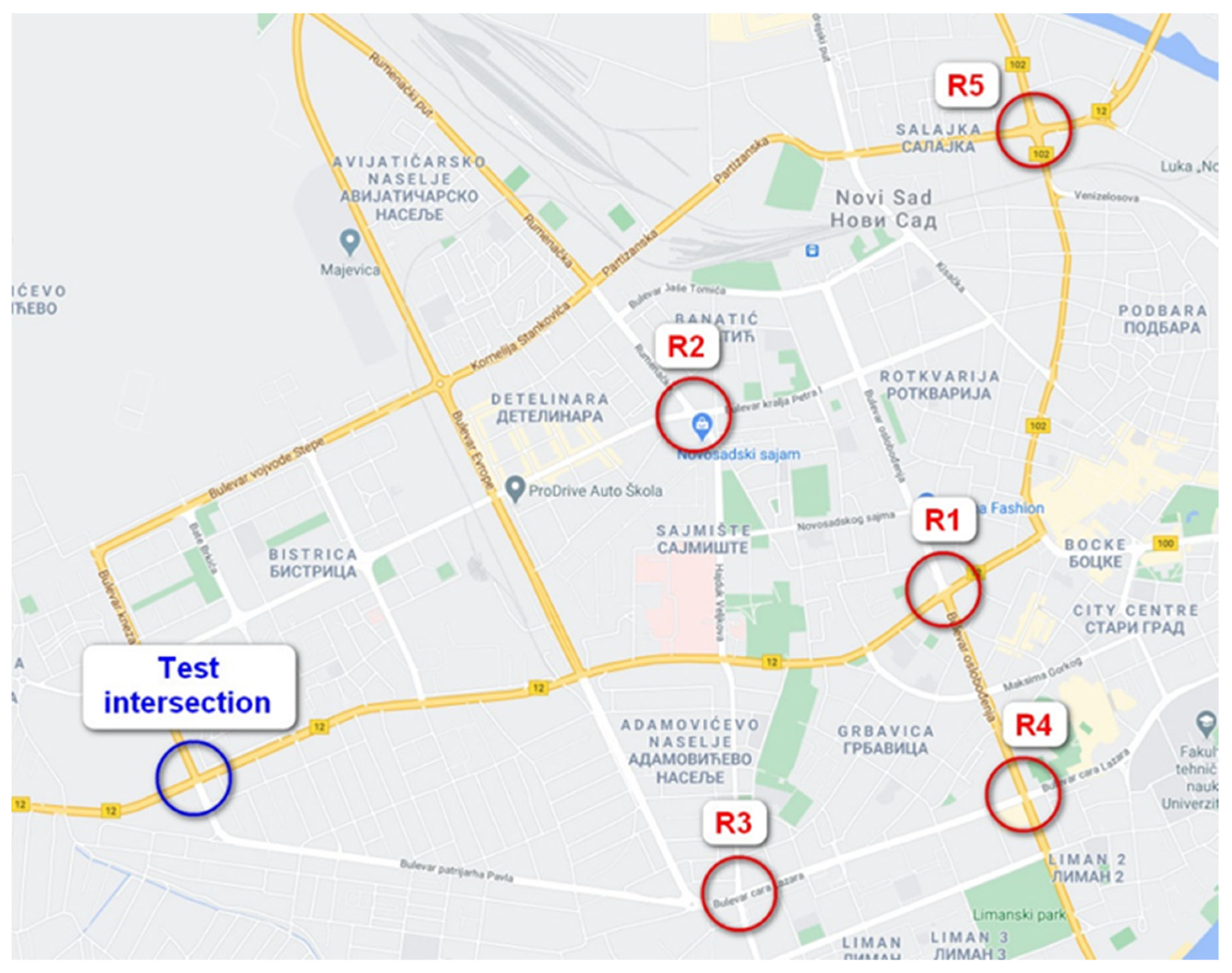
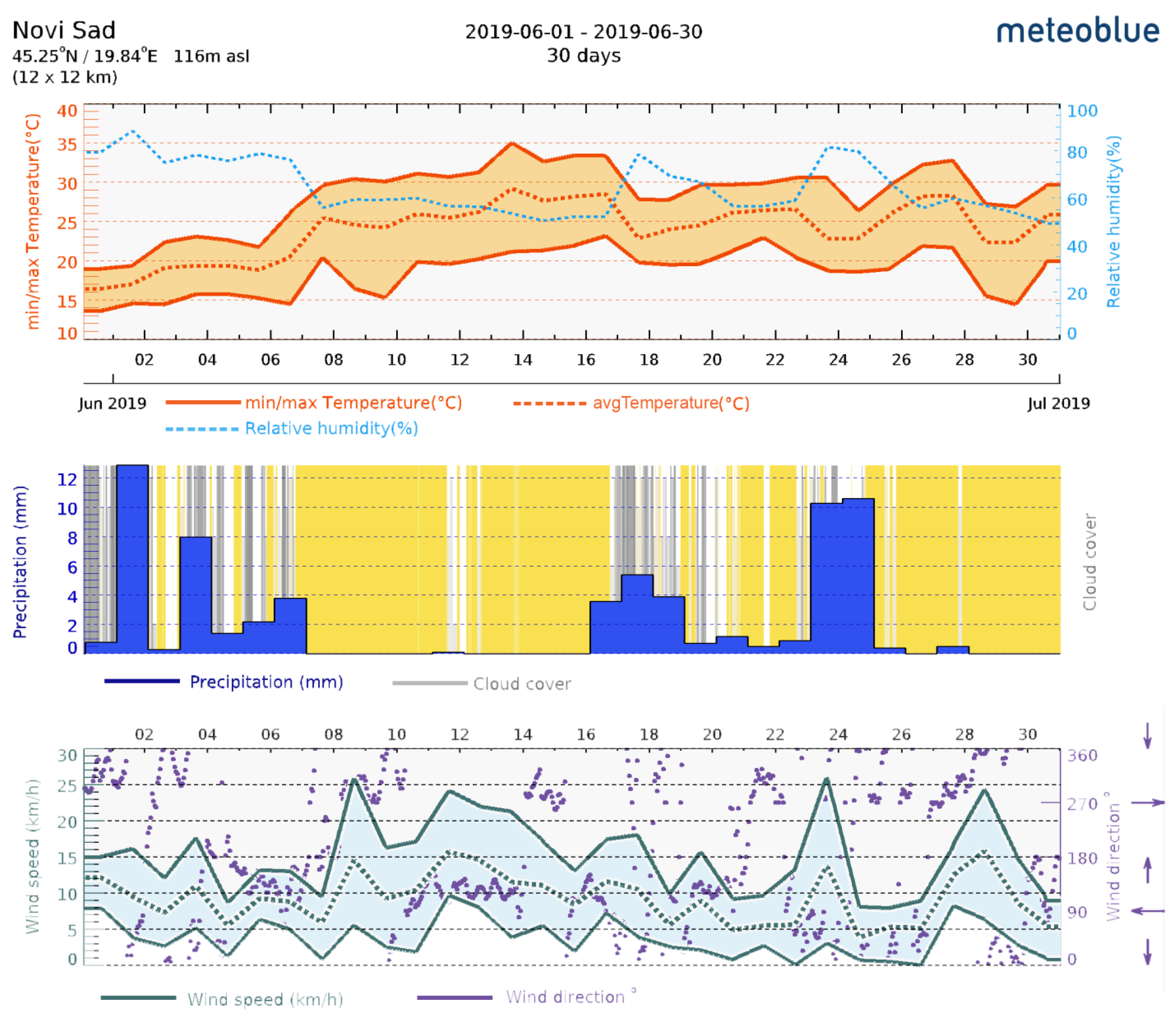
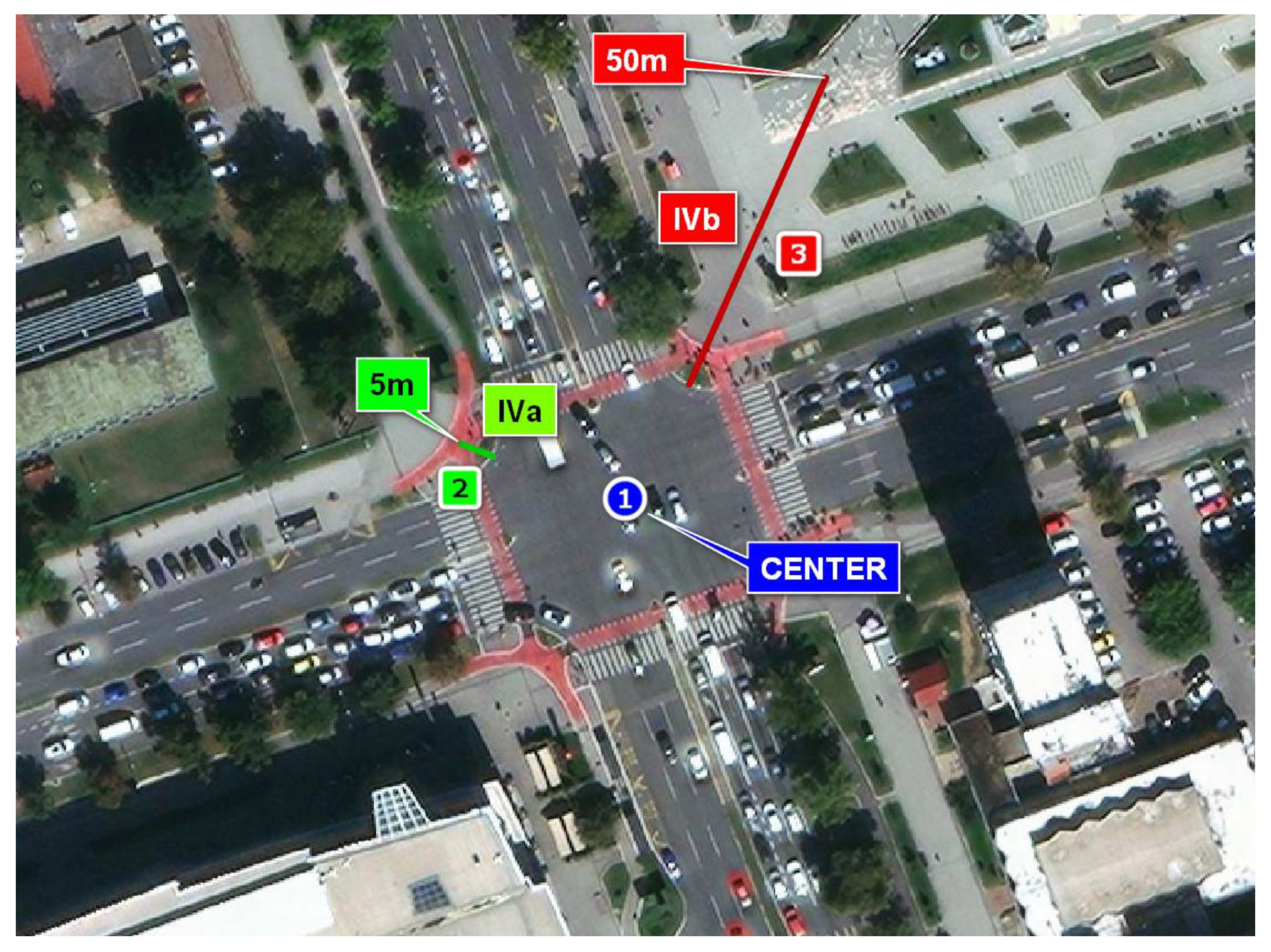
2.1. Noise Measurement Methodology
2.2. Traffic Counting Methodology
- -
- PA—Passenger car,
- -
- BUS *—Bus,
- -
- HV *—Heavy vehicles,
- -
- BUS + HV *—Bus and heavy vehicles.
2.3. Non-Linear Regression Models
2.3.1. ANN Modeling
Global Sensitivity Analysis
2.3.2. RFR Modeling
2.4. The Accuracy of the Model
3. Results
3.1. Mathematical Models
3.1.1. ANN1 Model
3.1.2. ANN2 Model
3.1.3. RFR Model
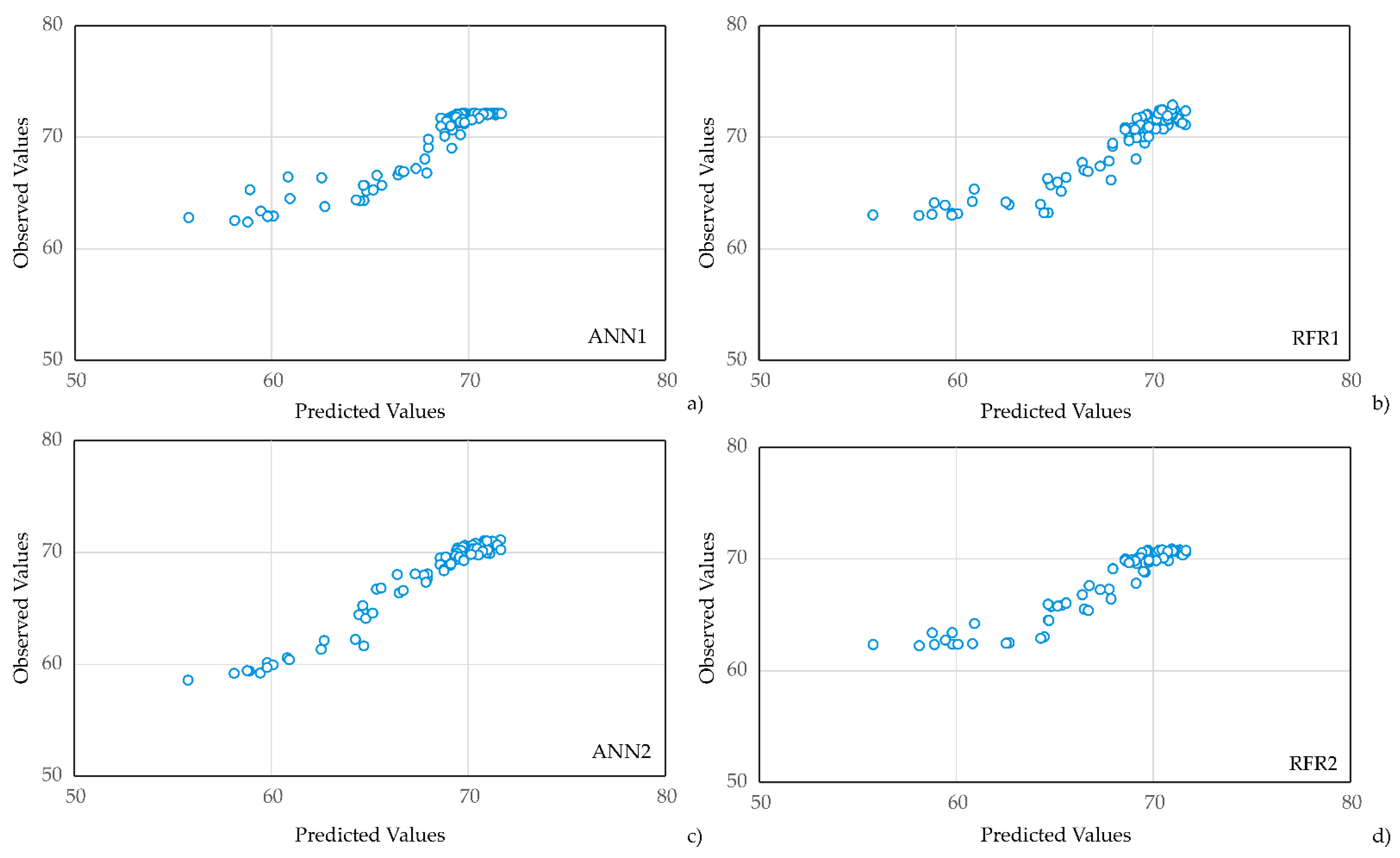
3.1.4. Model Testing
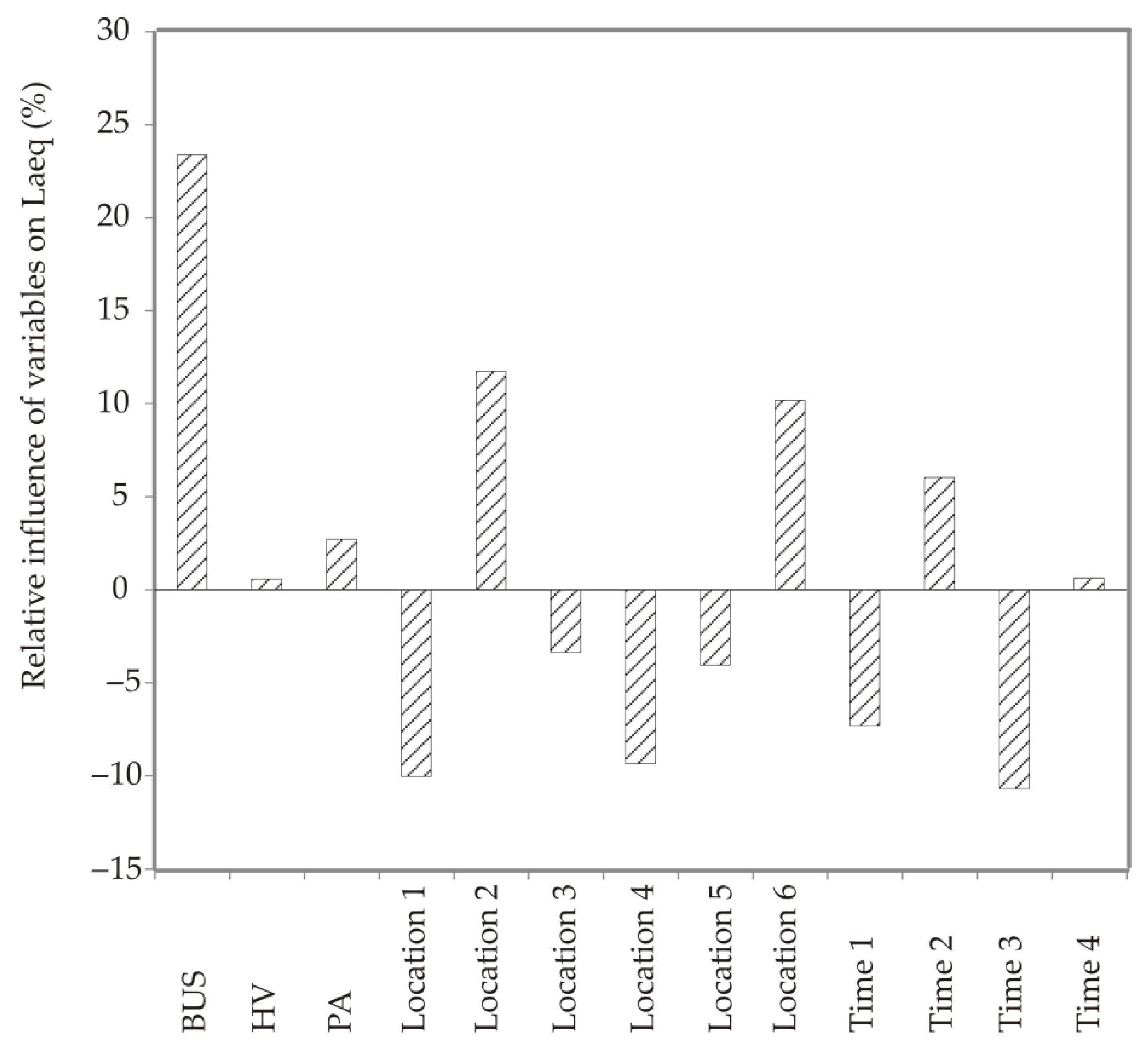
3.1.5. Global Sensitivity Analysis—Yoon’s Interpretation Method
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- World Health Organization; Regional Office for Europe. Environmental Noise Guidelines for the European Region. 2018. Available online: https://www.euro.who.int/en/publications/abstracts/environmental-noise-guidelines-for-the-european-region-2018 (accessed on 20 January 2021).
- Boryaev, A.; Malygin, I.; Marusin, A. Areas of focus in ensuring the environmental safety of motor transport. Transp. Res. Procedia 2020, 50, 68–76. [Google Scholar] [CrossRef]
- Wong, C.K.; Lee, Y.Y. The Effects of Signal System and Traffic Flow on the Sound Level. Appl. Sci. 2020, 10, 4454. [Google Scholar] [CrossRef]
- Van Kempen, E.; Casas, M.; Pershagen, G.; Foraster, M. WHO environmental noise guidelines for the European region: A systematic review on environmental noise and cardiovascular and metabolic effects: A summary. Int. J. Environ. Res. Public Health 2018, 15, 379. [Google Scholar] [CrossRef] [PubMed]
- Brink, M.; Stahel, W.A.; Basner, M. Determination of awakening probabilities in night time noise effects research. Somnol. Schlafforschung Schlafmed. 2009, 31, 236. [Google Scholar] [CrossRef]
- Pirrera, S.; De Valck, E.; Cluydts, R. Nocturnal road traffic noise: A review on its assessment and consequences on sleep and health. Environ. Int. 2010, 36, 492–498. [Google Scholar] [CrossRef]
- Münzel, T.; Schmidt, F.P.; Steven, S.; Herzog, J.; Daiber, A.; Sørensen, M. Environmental noise and the cardiovascular system. J. Am. Coll. Cardiol. 2018, 71, 688–697. [Google Scholar] [CrossRef]
- Dutilleux, G.; Paviotti, M.; Backman, A.; Gergely, B.; McManus, B.; Bento Coelho, L.; Hinton, J.; Kephalopoulos, S.; Licitra, G.; Rasmussen, S.; et al. Good practice guide on noise exposure and potential health effects. In European Environmental Agency Technical Report, 1st ed.; Babisch, W., van den Berg, M., Eds.; Official Publications of the European Union: Luxembourg, 2010; pp. 1–40. [Google Scholar]
- Ozdenerol, E.; Huang, Y.; Javadnejad, F.; Antipova, A. The impact of traffic noise on housing values. J. Real Estate Pract. Educ. 2015, 18, 35–53. [Google Scholar] [CrossRef]
- Szopińska, K.; Krajewska, M.; Kwiecień, J. The Impact of Road Traffic Noise on Housing Prices-Case Study in Poland. Real Estate Manag. Valuat. 2020, 28, 21–36. [Google Scholar] [CrossRef]
- Theebe, M.A. Planes, trains, and automobiles: The impact of traffic noise on house prices. J. Real Estate Finance Econ. 2004, 28, 209–234. [Google Scholar] [CrossRef]
- UN Environment Programme. Noise, Blazes and Mismatches; UN Environment Programme: Nairobi, Kenya, 2022. [Google Scholar]
- Khomenko, S.; Cirach, M.; Barrera-Gómez, J.; Pereira-Barboza, E.; Iungman, T.; Mueller, N.; Foraster, M.; Tonne, C.; Thondoo, M.; Jephcote, C.; et al. Impact of road traffic noise on annoyance and preventable mortality in European cities: A health impact assessment. Environ. Int. 2022, 162, 107160. [Google Scholar] [CrossRef]
- Schomer, P.D. Criteria for assessment of noise annoyance. Noise Control Eng. J. 2005, 53, 125–137. [Google Scholar] [CrossRef]
- Hood, R.A. Calculation of Road Traffic Noise. Appl. Acoust. 1987, 21, 139–146. [Google Scholar] [CrossRef]
- Mishra, R.K.; Mishra, A.R.; Singh, A. Traffic noise analysis using RLS-90 model in urban city. In Proceedings of the INTER-NOISE and NOISE-CON Congress and Conference Proceedings, Madrid, Spain, 16–19 June 2019. [Google Scholar]
- Noise, T. Nord 2000. New Nordic Prediction Method for Road Traffic Noise; SP Rapport 2001:10; DiVA: Uppsala, Sweden, 2001. [Google Scholar]
- Tomic, J.Z. Application of Soft Computing Techniques in Traffic Noise Prediction. Ph.D. Thesis, University of Belgrade, Belgrade, Serbia, 2017. [Google Scholar]
- Jandacka, D.; Decky, M.; Durcanska, D. Traffic Related Pollutants and Noise Emissions in the Vicinity of Different Types of Urban Crossroads. IOP Conf. Ser. Mater. Sci. Eng. 2019, 661, 012152. [Google Scholar] [CrossRef]
- Van Blockland, G.J.; De Graff, D.F. Measures on Road Traffic Noise in the EU; Interest Group on Traffic Noise Abatement: Springfield, KY, USA, 2012; pp. 1–48. [Google Scholar]
- Bühlmann, E.; Egger, S. Assessing the noise reduction potential of speed limit 30 km/h. In Proceedings of the INTER-NOISE 2017—46th International Congress on Noise Control Engineering, Hong Kong, China, 27–30 August 2017. [Google Scholar]
- Institut za Bezbednosti i Sigurnost na Radu Doo. Monitoring buke u Životnoj Sredini (Environmental Noise Monitoring).pdf. 2018. Available online: http://www.ekourbapv.vojvodina.gov.rs/wp-content/uploads/2018/08/monitoring-buke-APV-SU2018-2.pdf (accessed on 1 September 2020).
- “Urbanizam”, Public Enterprise, Saobraćajna Studija Grada Novog Sada sa Dinamikom Uređenja Saobraćaja (Traffic Study of the City of Novi Sad with the Dynamics of Traffic Organization); Нoстрам: Novi Sad, Serbia, 2009.
- Dangel, U.; McDonagh, P.; Murphy, L. Traffic-condition Analysis using Publicly-Available Data Sets. 12th Inf. Technol. &Telecommunications Conf. 2013. Available online: http://hdl.handle.net/10344/3353 (accessed on 1 September 2020).
- Official Journal of the European Communities. Directive 2002/49/EC of the European Parlament and of the Council. 2002. Available online: https://eur-lex.europa.eu/LexUriServ/LexUriServ.do?uri=OJ:L:2002:189:0012:0025:EN:PDF (accessed on 1 September 2020).
- Official Journal of the European Communities. Recommendation 2003/613/EC concerning the Guidelines on the Revised Interim Computation Methods for Industrial Noise, Aircraft Noise, Road Traffic Noise and Railway Noise, and Related Emission Data. Available online: https://leap.unep.org/countries/eu/national-legislation/commission-recommendation-2003613ec-concerning-guidelines-revised (accessed on 20 January 2021).
- ISO 1996-1:2016; Acoustics—Description, Measurement and Assessment of Environmental Noise—Part 1: Basic Quantities and Assessment Procedures. International Organization for Standardization: Geneva, Switzerland, 2016. Available online: https://www.iso.org/standard/59765.html (accessed on 1 September 2020).
- Genaro, N.; Torija, A.; Ramos-Ridao, A.; Requena, I.; Ruiz, D.P.; Zamorano, M. A neural network based model for urban noise prediction. J. Acous. Soc. Am. 2010, 128, 1738–1746. [Google Scholar] [CrossRef] [PubMed]
- Garg, N.; Mangal, S.K.; Saini, P.K.; Dhiman, P.; Maji, S. Comparison of ANN and Analytical Models in Traffic Noise Modeling and Predictions. Acoust. Aust. 2015, 43, 179–189. [Google Scholar] [CrossRef]
- Tiwari, G.; Fazio, J.; Gaurav, S. Traffic planning for nonhomogeneous traffic. Sadhana 2007, 32, 309–328. [Google Scholar] [CrossRef]
- Givargis, S.; Karimi, H. A basic neural traffic noise prediction model for Tehran’s roads. J. Environ. Manag. 2010, 91, 2529–2534. [Google Scholar] [CrossRef]
- Parabat, K.; Nagarnaik, P.B. Assessment and ANN modeling of noise levels at major road intersections in an Indian intermediate city. J. Res. Sci. Comput. Eng. 2007, 4, 39–49. Available online: http://www.ejournals.ph/form/cite.php?id=2168 (accessed on 10 May 2022). [CrossRef]
- Torija, A.J.; Rúiz, D.P.; Ramos-Ridao, A.F. Use of backpropagation neural networks to predict both level and temporal spectral composition of sound pressure in urban sound environments. Build. Environ. 2012, 52, 45–56. [Google Scholar] [CrossRef]
- Mansourkhaki, A.; Berangi, M.; Haghiri, M.; Haghani, M. A neural network noise prediction model for Tehran urban roads. J. Environ. Eng. Landsc. 2018, 26, 88–97. [Google Scholar] [CrossRef]
- Liu, Y.; Oiamo, T.; Rainham, D.; Chen, H.; Hatzopoulou, M.; Brook, J.R.; Davies, H.; Goudreau, S.; Smargiassi, A. Integrating random forests and propagation models for high-resolution noise mapping. Environ. Res. 2021, 195, 110905. [Google Scholar] [CrossRef] [PubMed]
- Staab, J.; Schady, A.; Weigand, M.; Lakes, T.; Taubenböck, H. Predicting traffic noise using land-use regression—A scalable approach. J. Expo. Sci. Environ. Epidemiol. 2022, 32, 232–243. [Google Scholar] [CrossRef] [PubMed]
- Adulaimi, A.A.A.; Pradhan, B.; Chakraborty, S.; Alamri, A. Traffic Noise Modelling Using Land Use Regression Model Based on Machine Learning, Statistical Regression and GIS. Energies 2021, 14, 5095. [Google Scholar] [CrossRef]
- The Ministry of Environmental Protection, Government of Serbia. Rulebook on Noise Measurement Methods, Content and Scope of the Noise Measurement Report. Official Gazette of the Republic of Serbia, No. 72/10. Available online: https://rspdf.info/%D0%B4%D0%BE%D0%BA%D1%83%D0%BC%D0%B5%D0%BD%D1%82/2e2ddc6/pravilnik-o-metodama-meren%D1%98a-buke-sadr%C5%BEini-i-obimu--putevi-srbije (accessed on 1 September 2020).
- The Ministry of Environmental Protection, Government of Serbia. Regulation on Noise Indicators, Limit Values, Methods for Evaluation of Noise Indicators, Harassment and Harmful Effects of Environmental Noise. 2010. Available online: https://www.putevi-srbije.rs/images/pdf/regulativa/uredba_o_indikatorima_buke_GV_metodama_za_ocenjivanje_indikatora_buke.pdf (accessed on 1 September 2020).
- Saad Ahmad Abo-Qudais, A.A. Effect of distance from road intersection on developed traffic noise levels. Can. J. Civ. Eng. 2011, 31, 533–538. [Google Scholar] [CrossRef]
- European Parliament, Council of the European Union. Regulation (EU) No 540/2014. 2014. Available online: https://eur-lex.europa.eu/eli/reg/2014/540/oj (accessed on 1 September 2020).
- Aguilera, I.; Foraster, M.; Basagaña, X.; Corradi, E.; Deltell, A.; Morelli, X.; Phuleria, H.C.; Ragettli, M.S.; Rivera, M.; Thomasson, A.; et al. Application of land use regression modelling to assess the spatial distribution of road traffic noise in three European cities. J. Expo. Sci. Environ. Epidemiol. 2015, 25, 97–105. [Google Scholar] [CrossRef]
- Ryan, P.H.; LeMasters, G.K. A review of land-use regression models for characterizing intraurban air pollution exposure. Inhal. Toxicol. 2007, 19, 127–133. [Google Scholar] [CrossRef]
- Kollo, T.; von Rosen, D. Advanced Multivariate Statistics with Matrices. In Mathematics and Its Applications, 1st ed.; Hazewinkel, M., Ed.; Springer: Dordrecht, The Netherlands, 2005; Volume 579, pp. 1–485. [Google Scholar]
- Pezo, L.; Ćurčić, B.L.; Filipović, V.S.; Nićetin, M.R.; Koprivica, G.B.; Mišljenović, N.M.; Lević, L.B. Artificial neural network model of pork meat cubes osmotic dehydration. Hem. Ind. 2013, 67, 465–475. [Google Scholar] [CrossRef]
- Hosseini, A.S.; Hajikarimi, P.; Gandomi, M.; Nejad, F.M.; Gandomi, A.H. Optimized machine learning approaches for the prediction of viscoelastic behavior of modified asphalt binders. Constr. Build. Mater. 2021, 299, 124264. [Google Scholar] [CrossRef]
- Shukla, V.; Khandekar, P.; Khaparde, A. Noise estimation in 2D MRI using DWT coefficients and optimized neural network. Biomed. Signal Process. Control 2022, 71, 103225. [Google Scholar] [CrossRef]
- Seshia, S.A.; Sadigh, D.; Sastry, S.S. Toward verified artificial intelligence. Commun. ACM 2022, 65, 46–55. [Google Scholar] [CrossRef]
- Yoon, Y.; Swales, G.; Margavio, T.M. Comparison of Discriminant Analysis versus Artificial Neural Networks. J. Oper. Res. Soc. 2017, 44, 51–60. [Google Scholar] [CrossRef]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Liu, Y.; Goudreau, S.; Oiamo, T.; Rainham, D.; Hatzopoulou, M.; Chen, H.; Davies, H.; Tremblay, M.; Johnson, J.; Bockstael, A.; et al. Comparison of land use regression and random forests models on estimating noise levels in five Canadian cities. Environ. Pollut. 2020, 256, 113367. [Google Scholar] [CrossRef]
- Rajković, D.; Marjanović Jeromela, A.; Pezo, L.; Lončar, B.; Zanetti, F.; Monti, A.; Kondić Špika, A. Yield and Quality Prediction of Winter Rapeseed—Artificial Neural Network and Random Forest Models. Agronomy 2022, 12, 58. [Google Scholar] [CrossRef]
- Montgomery, D.C. Design and Analysis of Experiments, 2nd ed.; John Wiley and Sons: Hoboken, NJ, USA, 1984; pp. 1–556. [Google Scholar]
- Debnath, A.; Singh, P.K.; Banerjee, S. Vehicular traffic noise modelling of urban area—A contouring and artificial neural network based approach. Environ. Sci. Pollut. Res. 2022, 29, 39948–39972. [Google Scholar] [CrossRef]
- Kumar, P.; Nigam, S.P.; Kumar, N. Vehicular traffic noise modeling using artificial neural network approach. Transp. Res. C Emerg. Technol. 2014, 40, 111–122. [Google Scholar] [CrossRef]
- Nourani, V.; Gökçekuş, H.; Umar, I.K.; Najafi, H. An emotional artificial neural network for prediction of vehicular traffic noise. Sci. Total Environ. 2020, 707, 136134. [Google Scholar] [CrossRef]
- Cammarata, G.; Cavalier, S.; Fichera, A. A neural network architecture for noise prediction. Neural Netw. 1995, 8, 963–973. [Google Scholar] [CrossRef]
- Hamoda, M.F. Modeling of construction noise for environmental impact assessment. J. Construct. Dev. Ctries. 2008, 13, 79–89. [Google Scholar]
- Erbay, Z.; Icier, F. Optimization of hot air drying of olive leaves using response surface methodology. J. Food Eng. 2009, 91, 533–541. [Google Scholar] [CrossRef]
- Turanyi, T.; Tomlin, A.S. Analysis of Kinetics Reaction Mechanisms, 1st ed.; Springer: Berlin/Heidelberg, Germany, 2014; pp. 1–363. [Google Scholar]
- Jiménez-Uribe, D.A.; Daniels, D.; Fleming, Z.L.; Vélez-Pereira, A.M. Road Traffic Noise on the Santa Marta City Tourist Route. Appl. Sci. 2021, 11, 7196. [Google Scholar] [CrossRef]



| Location | Parameter | BUS | HV | BUS + HV | PA | Laeq |
|---|---|---|---|---|---|---|
| R1 | Mean | 7.792 | 27.729 | 35.521 | 632.521 | 72.206 |
| St.Dev. | 3.744 | 22.480 | 24.736 | 378.003 | 2.943 | |
| Min. | 0 | 0 | 0 | 30 | 64.910 | |
| Max. | 16 | 70 | 81 | 1100 | 75.790 | |
| R2 | Mean | 13.156 | 47.219 | 60.375 | 584.333 | 69.942 |
| St.Dev. | 6.758 | 36.836 | 41.527 | 332.679 | 4.149 | |
| Min. | 1 | 3 | 4 | 78 | 59.130 | |
| Max. | 33 | 118 | 142 | 1103 | 73.350 | |
| R3 | Mean | 22.021 | 29.635 | 51.656 | 689.719 | 70.305 |
| St.Dev. | 11.635 | 24.512 | 32.992 | 389.268 | 3.695 | |
| Min. | 0 | 1 | 1 | 46 | 61.090 | |
| Max. | 43 | 82 | 109 | 1131 | 77.210 | |
| R4 | Mean | 12.042 | 27.573 | 39.615 | 783.000 | 68.719 |
| St.Dev. | 6.961 | 20.728 | 25.663 | 409.785 | 3.903 | |
| Min. | 0 | 1 | 2 | 109 | 56.970 | |
| Max. | 31 | 73 | 88 | 1322 | 72.650 | |
| R5 | Mean | 7.417 | 22.115 | 29.531 | 548.240 | 70.233 |
| St.Dev. | 3.873 | 17.965 | 21.104 | 323.031 | 2.093 | |
| Min. | 0 | 0 | 0 | 29 | 64.870 | |
| Max. | 14 | 61 | 75 | 997 | 72.590 | |
| R6 | Mean | 8.865 | 29.083 | 37.948 | 551.667 | 68.096 |
| St.Dev. | 4.990 | 24.346 | 26.318 | 319.610 | 3.672 | |
| Min. | 0 | 0 | 1 | 21 | 55.790 | |
| Max. | 24 | 80 | 87 | 1009 | 71.660 |
| Network | Performance | Error | Train. Algorithm | Error Funct. | Hidden Activation | Output Activation | ||||
|---|---|---|---|---|---|---|---|---|---|---|
| Train. | Test. | Valid. | Train. | Test. | Valid. | |||||
| MLP 2-5-1 | 0.681 | 0.692 | 0.757 | 2.238 | 1.852 | 1.728 | BFGS 84 | SOS | Tanh | Logistic |
| Model | χ2 | RMSE | MBE | MPE | SSE | AARD | R2 | Skew | Kurt | Mean | StDev | Var |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| ANN1 | 4.160 | 2.038 | −0.080 | 2.236 | 2367.430 | 1937.642 | 0.697 | 0.070 | 1.303 | −0.080 | 2.038 | 4.153 |
| RFR1 | 4.073 | 2.016 | 0.076 | 2.198 | 2318.340 | 1602.760 | 0.703 | −0.056 | 1.391 | 0.076 | 2.017 | 4.067 |
| ANN2 | 0.559 | 0.747 | −0.049 | 0.807 | 320.196 | 652.730 | 0.959 | 0.224 | 2.503 | −0.049 | 0.746 | 0.557 |
| RFR2 | 1.837 | 1.354 | 0.016 | 1.357 | 1056.331 | 895.384 | 0.882 | −0.704 | 3.678 | 0.016 | 1.355 | 1.837 |
| Model | χ2 | RMSE | MBE | MPE | SSE | AARD | R2 | Skew | Kurt | Mean | StDev | Var |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| ANN1 | 4.736 | 2.165 | −1.729 | 2.668 | 163.033 | 107.967 | 0.877 | −1.342 | 3.689 | −1.729 | 1.310 | 1.716 |
| RFR1 | 3.698 | 1.913 | −1.346 | 2.273 | 177.343 | 112.211 | 0.872 | −1.262 | 3.898 | −1.346 | 1.366 | 1.867 |
| ANN2 | 0.446 | 0.664 | −0.038 | 0.762 | 42.234 | 48.705 | 0.968 | −0.412 | 2.170 | −0.038 | 0.667 | 0.445 |
| RFR2 | 1.918 | 1.378 | −0.426 | 1.377 | 166.464 | 88.218 | 0.898 | −1.929 | 5.493 | −0.426 | 1.317 | 1.734 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ruškić, N.; Mirović, V.; Marić, M.; Pezo, L.; Lončar, B.; Nićetin, M.; Ćurčić, L. Model for Determining Noise Level Depending on Traffic Volume at Intersections. Sustainability 2022, 14, 12443. https://doi.org/10.3390/su141912443
Ruškić N, Mirović V, Marić M, Pezo L, Lončar B, Nićetin M, Ćurčić L. Model for Determining Noise Level Depending on Traffic Volume at Intersections. Sustainability. 2022; 14(19):12443. https://doi.org/10.3390/su141912443
Chicago/Turabian StyleRuškić, Nenad, Valentina Mirović, Milovan Marić, Lato Pezo, Biljana Lončar, Milica Nićetin, and Ljiljana Ćurčić. 2022. "Model for Determining Noise Level Depending on Traffic Volume at Intersections" Sustainability 14, no. 19: 12443. https://doi.org/10.3390/su141912443
APA StyleRuškić, N., Mirović, V., Marić, M., Pezo, L., Lončar, B., Nićetin, M., & Ćurčić, L. (2022). Model for Determining Noise Level Depending on Traffic Volume at Intersections. Sustainability, 14(19), 12443. https://doi.org/10.3390/su141912443








