An Improved Overmodulation Strategy for a Three-Level NPC Inverter Considering Neutral-Point Voltage Balance and Common-Mode Voltage Suppression
Abstract
:1. Introduction
- An overmodulation strategy based on minimum amplitude error method is proposed to improve the utilization of DC-bus voltage;
- A VSVPWM strategy is adopted to balance the NP voltage and suppress the CMV, and the leakage current has also been effectively suppressed;
- The difficulty of obtaining key variables in the overmodulation strategy is simplified by fitting.
2. Model of 3L-NPC-VSI
3. Proposed Overmodulation Strategy
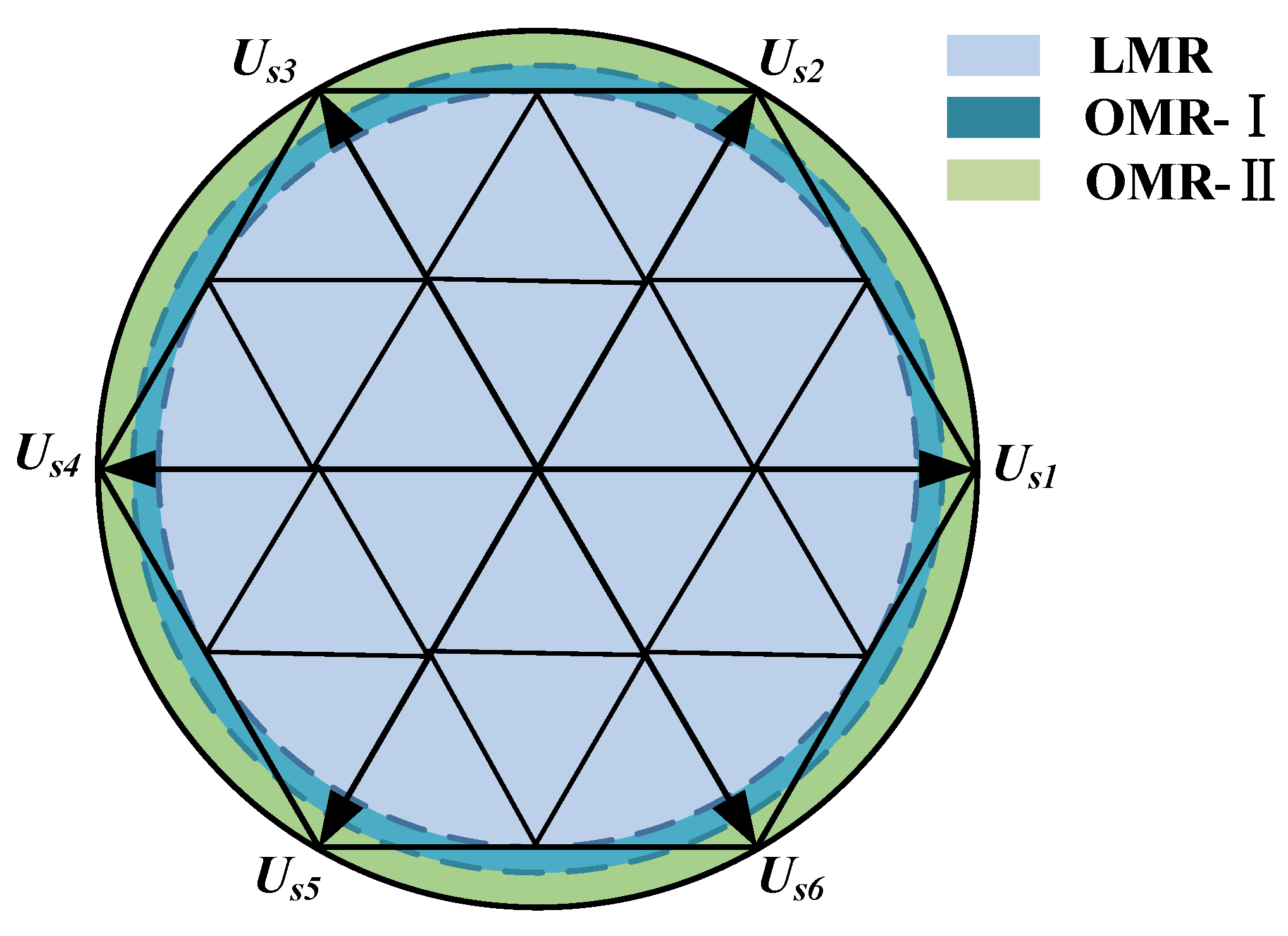
3.1. LMR
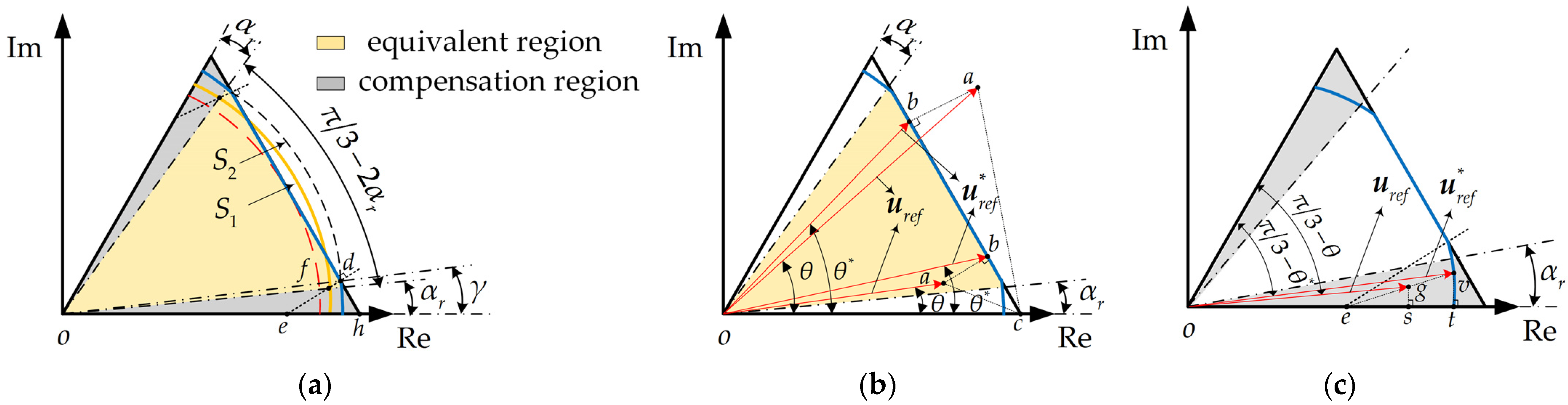
3.2. OMR-I
3.2.1. Vector Correction of Equivalent Region
3.2.2. Vector Correction of Compensation Region
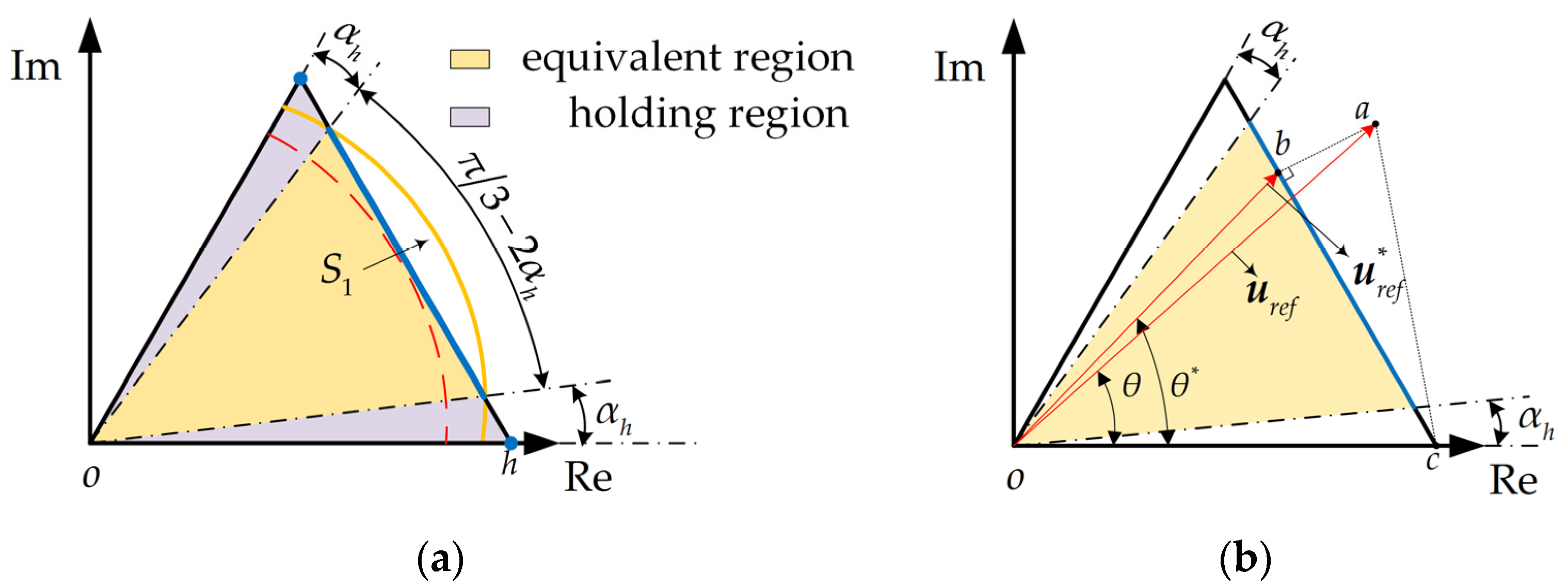
3.3. OMR-II
3.3.1. Vector Correction of Equivalent Region
3.3.2. Vector Correction of Holding Region
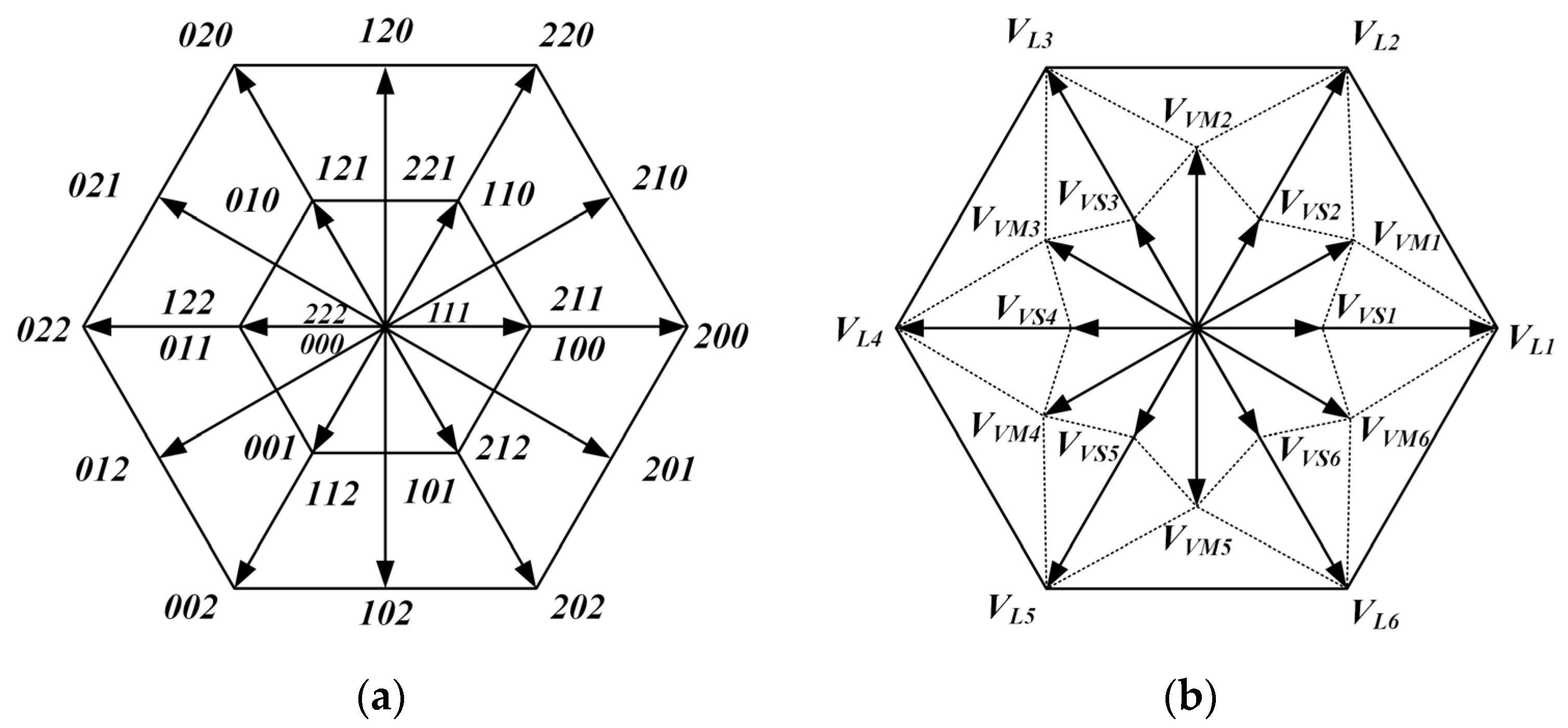
4. NP Voltage Balance and CMV Suppression
5. Simulation and Experimental Results
5.1. Simulation Results
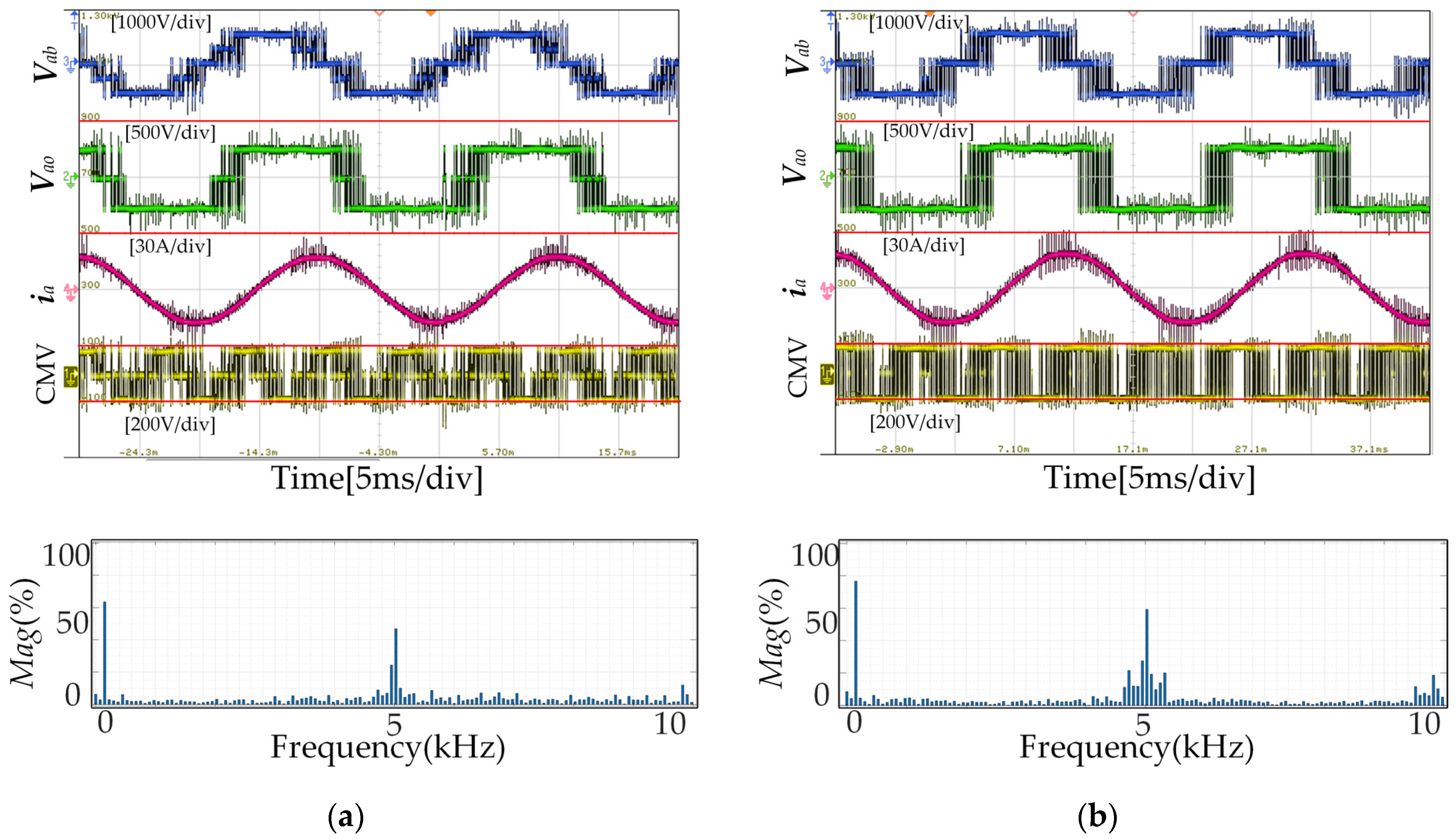
5.1.1. NP Voltage Balance and CMV Suppression
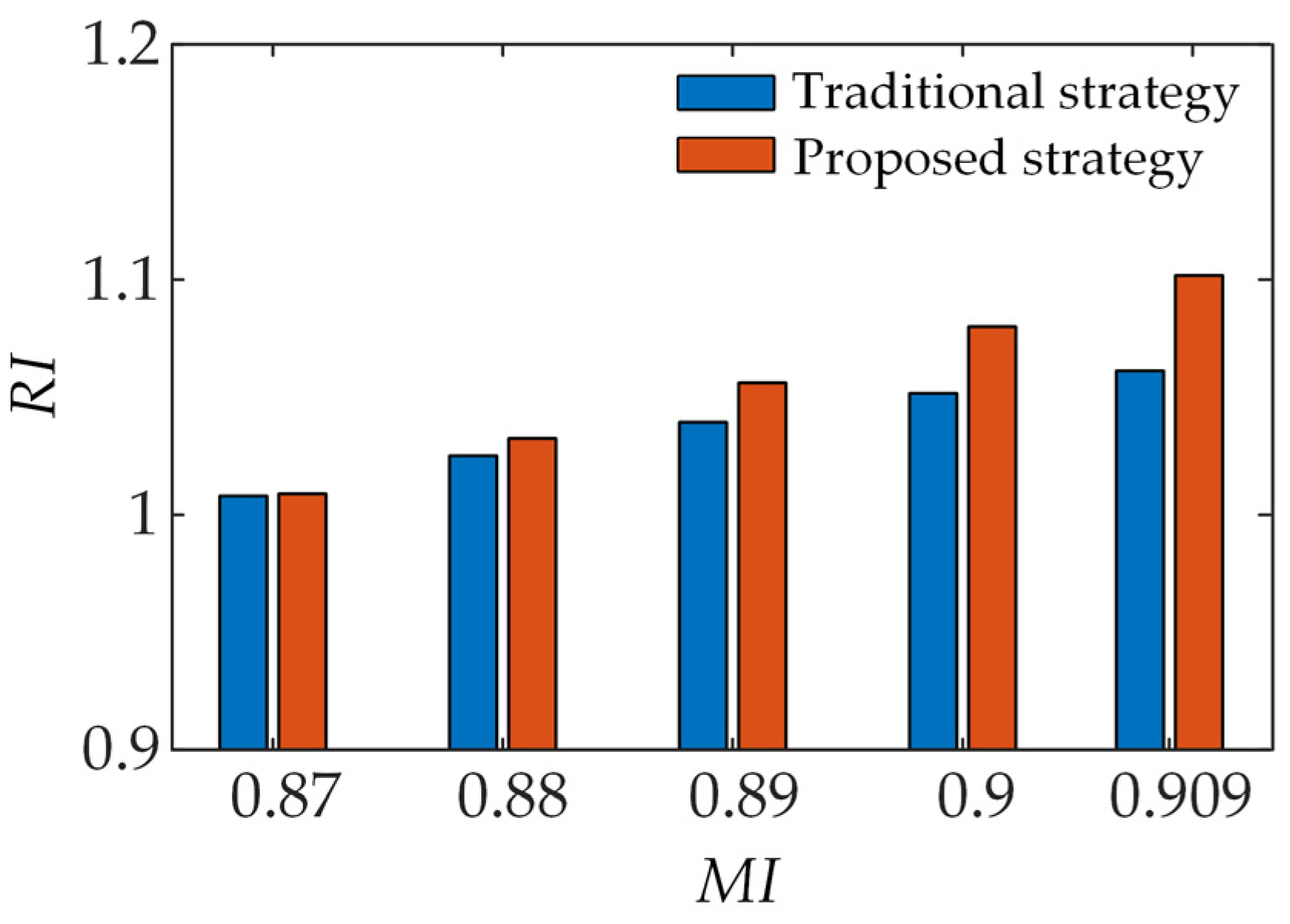
5.1.2. Improvement of DC-Bus Voltage Utilization
5.2. Experimental Results
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Zhang, B.; Yang, P.; Ge, Q.; Wang, X.; Li, Y. A New High Output Frequency Multilevel Inverter Topology of Traction Converter for Superspeed Maglev Train. In Proceedings of the 2021 13th International Symposium on Linear Drives for Industry Applications (LDIA), Wuhan, China, 1–3 July 2021; pp. 1–5. [Google Scholar]
- Lee, J.; Jo, J.; Han, Y.; Lee, C. Development of LSM Control System for Super Speed Maglev. In Proceedings of the 2013 13th International Conference on Control, Automation and Systems (ICCAS 2013), Gwangju, Korea, 20–23 October 2013; pp. 466–469. [Google Scholar]
- Ma, Z.; Sun, Y.; Zhao, Y.; Zhang, Z.; Lin, G. Dichotomy Solution Based Model Predictive Control for Permanent Magnet Linear Synchronous Motors. In Proceedings of the 2019 22nd International Conference on Electrical Machines and Systems (ICEMS), Harbin, China, 11–14 August 2019; pp. 1–5. [Google Scholar]
- Nabae, A.; Takahashi, I.; Akagi, H. A New Neutral-Point-Clamped PWM Inverter. IEEE Trans. Ind. Appl. 1981, IA-17, 518–523. [Google Scholar]
- Teichmann, R.; Bernet, S. A comparison of three-level converters versus two-level converters for low-voltage drives, traction, and utility applications. IEEE Trans. Ind. Appl. 2005, 41, 855–865. [Google Scholar]
- Jiang, H.; Deng, F.; Wang, Z.; Zou, Z.; Li, B.; Blaabjerg, F. Harmonic Optimization Strategy for CPS-PWM Based MMCs Under Submodule Capacitor Voltage Reduction Control. IEEE Trans. Power Electron. 2022, 37, 4288–4300. [Google Scholar]
- Kwon, Y.; Kim, S.; Sul, S. Six-step operation of PMSM with instantaneous current control. IEEE Trans. Ind. Electron. 2014, 50, 2614–2625. [Google Scholar]
- Stumpf, P.; Halàsz, S. Optimization of PWM for the overmodulation region of two-level inverters. IEEE Trans. Ind. Appl. 2018, 54, 3393–3404. [Google Scholar]
- Nasiri, M.; Mobayen, S.; Arzani, A. PID-type Terminal Sliding Mode Control for Permanent Magnet Synchronous Generator-based Enhanced Wind Energy Conversion Systems. CSEE J. Power Energy Syst. 2022, 8, 993–1003. [Google Scholar]
- Pujol-Vazquez, G.; Acho, L.; Mobayen, S.; Nápoles, A.; Pérez, V. Rotary inverted pendulum with magnetically external perturbations as a source of the pendulum’s base navigation commands. J. Frankl. Inst. 2018, 355, 4077–4096. [Google Scholar]
- Alsofyani, I.M.; Lee, K. Improved transient-based overmodulation method for increased torque capability of direct torque control with constant torque-switching regulator of induction machines. IEEE Trans. Power Electron. 2020, 35, 3928–3938. [Google Scholar]
- Yun, J.; Son, Y.-K.; Sul, S.-K. Parallel Operation of Permanent Magnet Synchronous Generators under Six-Step Operation Mode. In Proceedings of the 2022 IEEE Transportation Electrification Conference & Expo (ITEC), Anaheim, CA, USA, 15–17 June 2022; pp. 635–639. [Google Scholar]
- Holtz, J.; Lotzkat, W.; Khambadkone, A.M. On continuous control of PWM inverters in the overmodulation range including the six-step mode. IEEE Trans. Power Electron. 1993, 8, 546–553. [Google Scholar]
- Narayanan, G.; Ranganathan, V.T. Extension of operation of space vector PWM strategies with low switching frequencies using different overmodulation algorithms. IEEE Trans. Power Electron. 2002, 17, 788–798. [Google Scholar]
- Narayanan, G. Synchronised Pulse width Modulation Strategies Based on Space Vector approach for Induction Motor Drives; etd AT Indian Institute of Science: Bengaluru, India, 1999. [Google Scholar]
- Modi, M.K.; Narayanan, G. Improved Single-Zone Overmodulation Algorithm for Space Vector Modulated Inverters. 2014 IEEE International Conference on Power Electronics, Drives and Energy Systems (PEDES), Mumbai, India, 16–19 December 2014; pp. 1–6. [Google Scholar]
- Jing, R.; Zhang, G.; Wang, G.; Bi, G.; Ding, D.; Xu, D. An Overmodulation Strategy Based on Voltage Vector Space Division for High-Speed Surface- Mounted PMSM Drives. IEEE Trans. Power Electron. 2022, 37, 15370–15381. [Google Scholar]
- Sarajian, A.; Garcia, C.F.; Guan, Q.; Wheeler, P.; Khaburi, D.A.; Kennel, R.; Rodriguez, J.; Abdelrahem, M. Overmodulation Methods for Modulated Model Predictive Control and Space Vector Modulation. IEEE Trans. Power Electron. 2021, 36, 4549–4559. [Google Scholar]
- Busquets-Monge, S.; Bordonau, J.; Boroyevich, D.; Somavilla, S. The nearest three virtual space vector PWM—A modulation for the comprehensive neutral-point balancing in the three-level NPC inverter. IEEE Power Electron. Lett. 2004, 2, 11–15. [Google Scholar]
- Choudhury, A.; Pillay, P.; Williamson, S.S. DC-bus Voltage Balancing Algorithm for Three-Level Neutral-Point-Clamped (NPC) Traction Inverter Drive With Modified Virtual Space Vector. IEEE Trans. Ind. Appl. 2016, 52, 3958–3967. [Google Scholar]
- Li, C.; Yang, T.; Kulsangcharoen, P.; Calzo, G.L.; Bozhko, S.; Gerada, C.; Wheeler, P. A Modified Neutral Point Balancing Space Vector Modulation for Three-Level Neutral Point Clamped Converters in High-Speed Drives. IEEE Trans. Ind. Electron. 2019, 66, 910–921. [Google Scholar]
- Jiang, D.; Shen, Z.; Wang, F. Common-Mode Voltage Reduction for Paralleled Inverters. IEEE Trans. Power Electron. 2018, 33, 3961–3974. [Google Scholar]
- Xia, S.; Wu, X.; Zheng, J.; Li, X.; Wang, K. A Virtual Space Vector PWM With Active Neutral Point Voltage Control and Common Mode Voltage Suppression for Three-Level NPC Converters. IEEE Trans. Ind. Electron. 2021, 68, 11761–11771. [Google Scholar]
- Morris, C.T.; Han, D.; Sarlioglu, B. Reduction of common mode voltage and conducted EMI through three-phase inverter topology. IEEE Trans. Power Electron. 2016, 32, 1720–1724. [Google Scholar]
- Palanisamy, R.; Vijayakumar, K. Minimization of Common Mode Voltage and Capacitor Voltage Unbalance of 3-Phase 4-Wire 3-Level NPC inverter using 4D-SVM. IEEE Trans. Power Electron. 2022. [Google Scholar]
- Wu, X.; Tan, G.; Ye, Z.; Yao, G.; Liu, Z.; Liu, G. Virtual-Space-Vector PWM for a Three-Level Neutral-Point-Clamped Inverter With Unbalanced DC-buss. IEEE Trans. Power Electron. 2018, 33, 2630–2642. [Google Scholar]
- Niu, H.; Ma, Z.; Han, Y.; Chen, G.; Liao, Z.; Lin, G. Model Predictive Control with Common-Mode Voltage Minimization for a Three-level NPC Inverter PMLSM Drive System. In Proceedings of the 2021 13th International Symposium on Linear Drives for Industry Applications (LDIA), Wuhan, China, 1–3 July 2021; pp. 1–5. [Google Scholar]
- Jiang, W.; Wang, P.; Ma, M.; Wang, J.; Li, J.; Li, L.; Chen, K. A Novel Virtual Space Vector Modulation With Reduced Common-Mode Voltage and Eliminated Neutral Point Voltage Oscillation for Neutral Point Clamped Three-Level Inverter. IEEE Trans. Ind. Electron. 2020, 67, 884–894. [Google Scholar]
- Khoun Jahan, H.; Eskandari, R.; Rahimi, T.; Shalchi Alishah, R.; Ding, L.; Bertilsson, K.; Sabahi, M.; Blaabjerg, F. A Limited Common-Mode Current Switched-Capacitor Multilevel Inverter Topology and Its Performance and Lifetime Evaluation in Grid-Connected Photovoltaic Applications. Energies 2021, 14, 1915. [Google Scholar]
- Kakosimos, P.; Abu-Rub, H. Predictive control of a grid-tied cascaded full-bridge NPC inverter for reducing high-frequency common-mode voltage components. IEEE Trans. Ind. Inform. 2017, 14, 2385–2394. [Google Scholar]
- Xie, L.; Yao, J. Common-Mode Voltage Reduction and Neutral Point Voltage Balance Modulation Technology of Quasi-Z-Source T-Type Three-Level Inverter. Electronics 2022, 11, 2203. [Google Scholar]
- Xing, X.; Li, X.; Gao, F.; Qin, C.; Zhang, C. Improved Space Vector Modulation Technique for Neutral-Point Voltage Oscillation and Common-Mode Voltage Reduction in Three-Level Inverter. IEEE Trans. Power Electron. 2019, 34, 8697–8714. [Google Scholar]
- Li, X.; Xing, X.; Zhang, C.; Chen, A.; Qin, C.; Zhang, G. Simultaneous Common-Mode Resonance Circulating Current and Leakage Current Suppression for Transformerless Three-Level T-Type PV Inverter System. IEEE Trans. Ind. Electron. 2019, 66, 4457–4467. [Google Scholar]

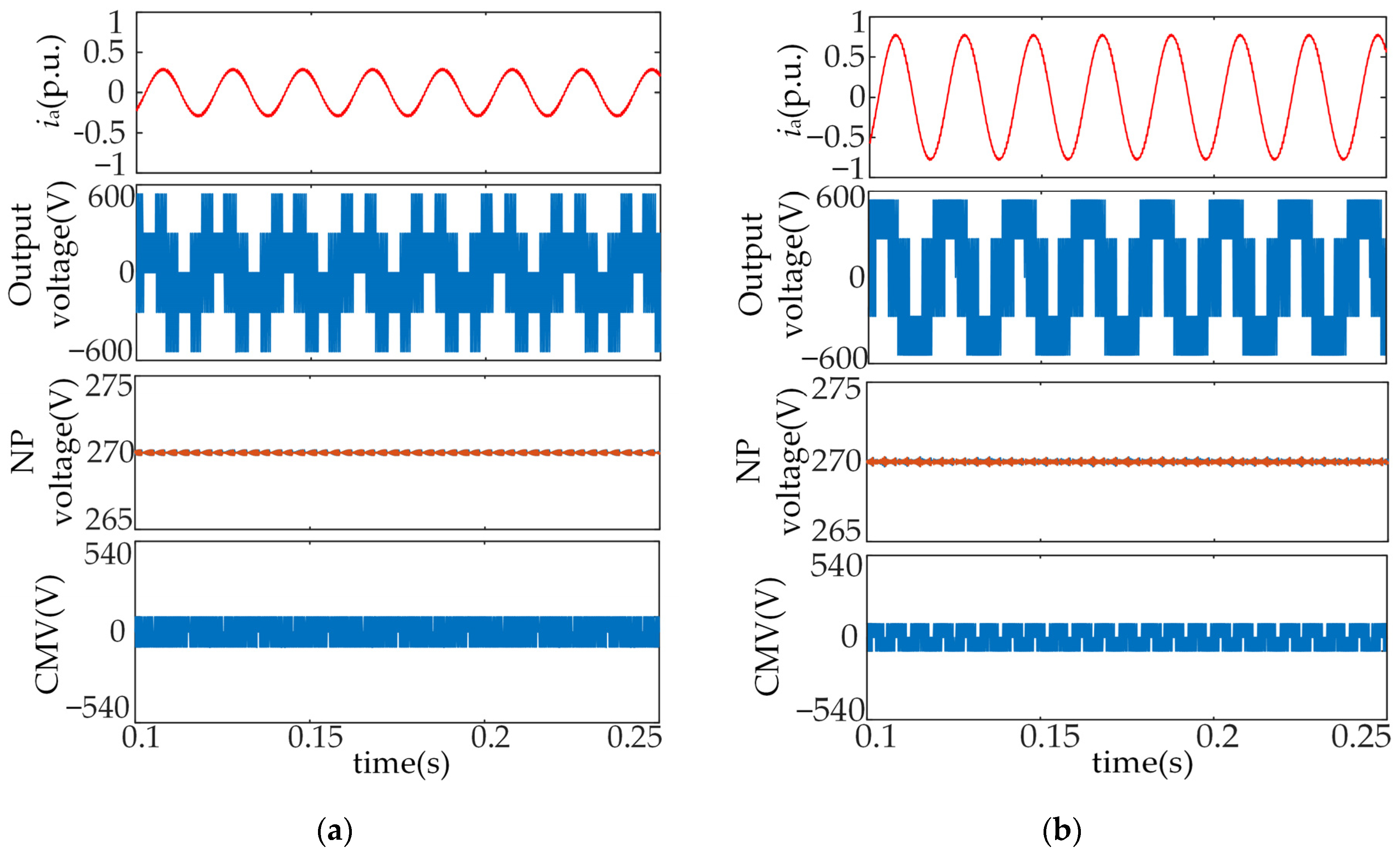
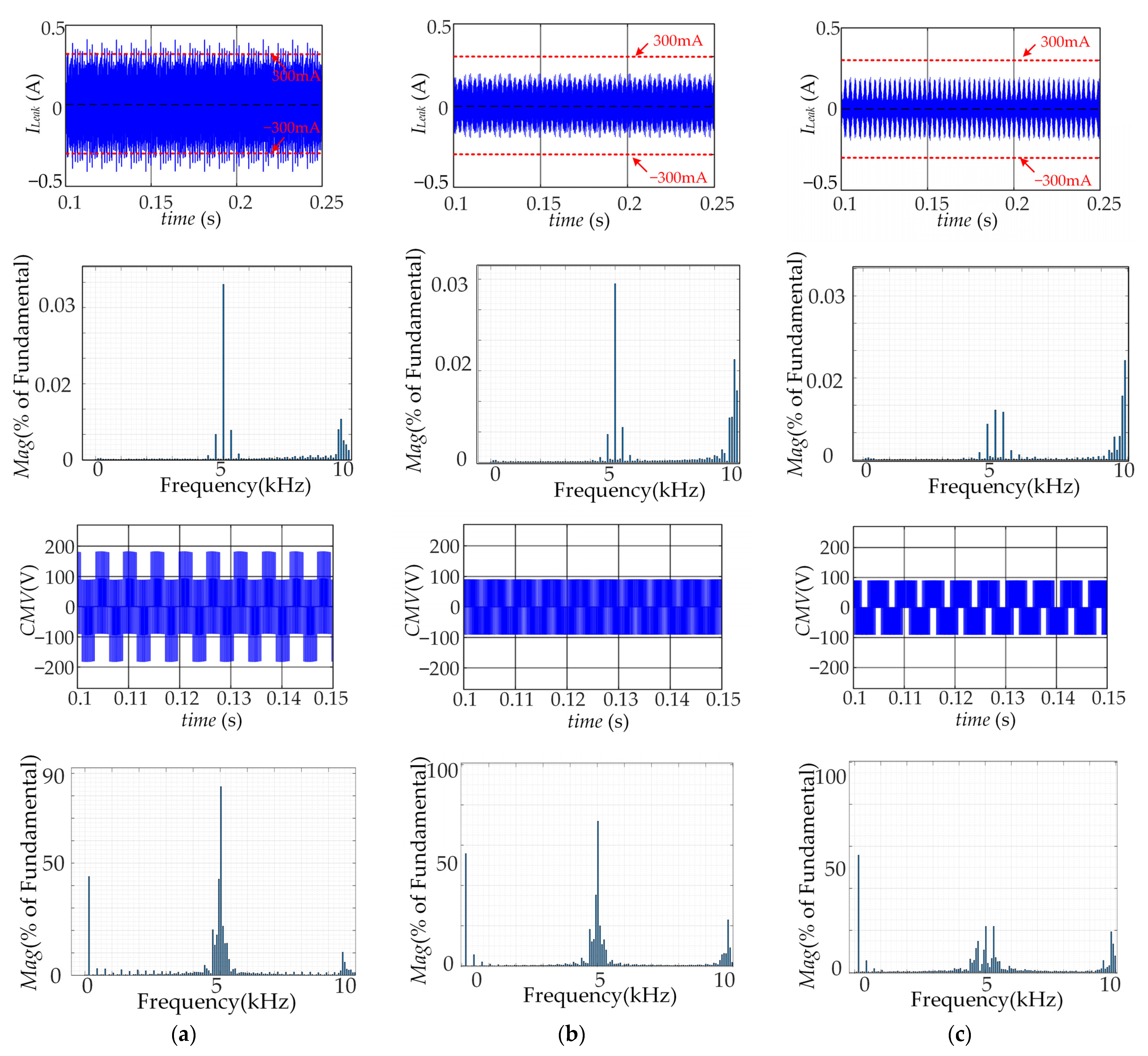
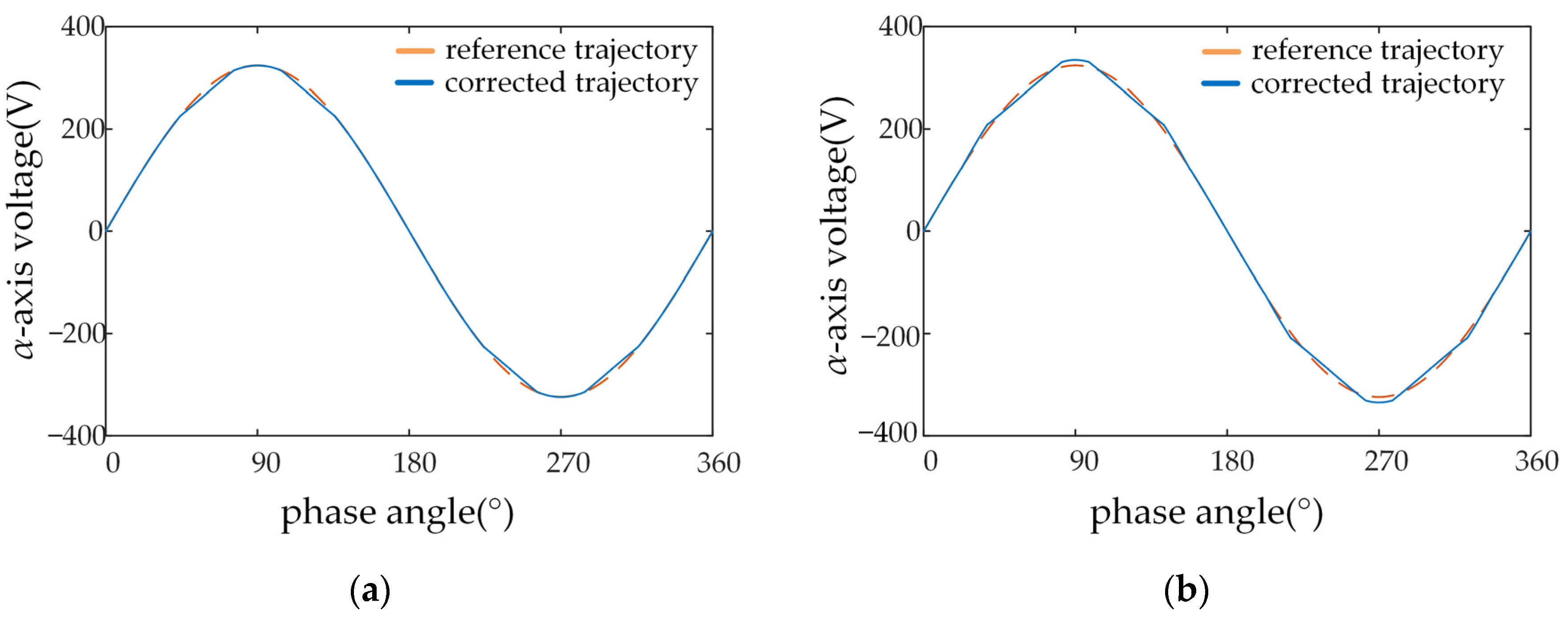
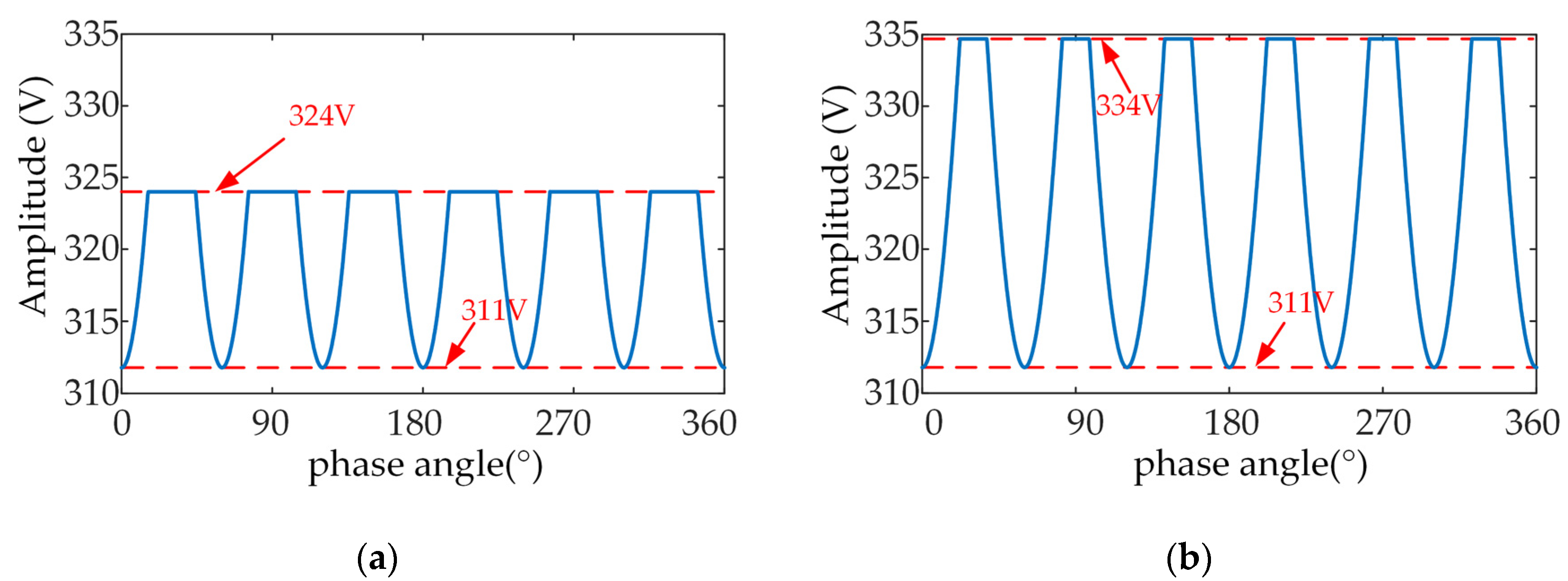


| Parameters | Values |
|---|---|
| DC-bus voltage Vdc | 540 V |
| DC-bus capacitors Lc1, Lc2 | 2100 × 10−6 F |
| Output resistance R | 8 Ω |
| Output inductance L | 23 mH |
| Switching frequency fs | 5 kHz |
| Parasitic capacitance | 10 nF |
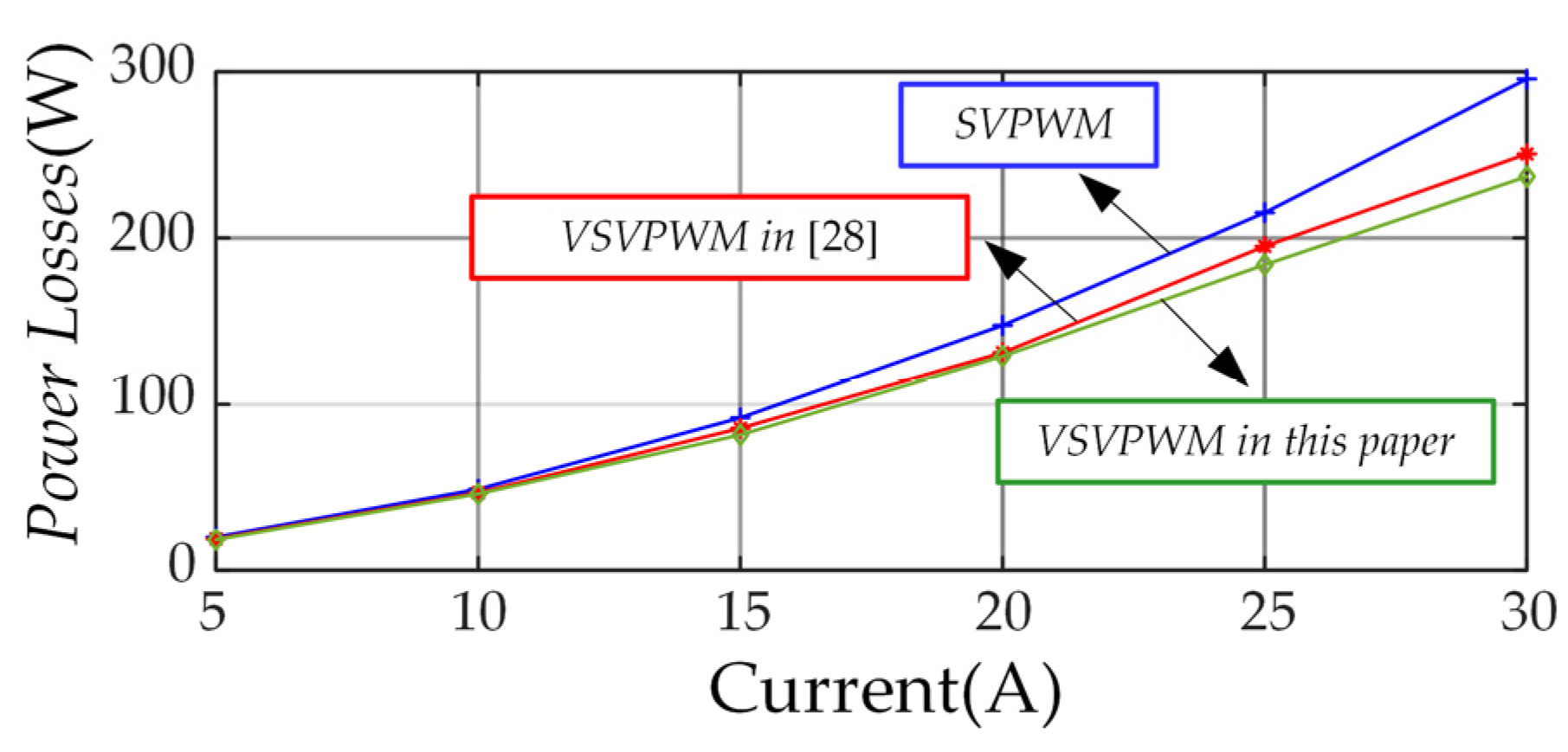
| Method | CMV Suppression | Ileak | High-Component around 5 kHz | Power Losses |
|---|---|---|---|---|
| SVPWM | No | 410 mA | high | high |
| VSVPWM in [28] | Yes | 199 mA | medium | medium |
| VSVPWM in this paper | Yes | 200 mA | low | low |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ma, Z.; Niu, H.; Wu, X.; Zhang, X.; Lin, G. An Improved Overmodulation Strategy for a Three-Level NPC Inverter Considering Neutral-Point Voltage Balance and Common-Mode Voltage Suppression. Sustainability 2022, 14, 12558. https://doi.org/10.3390/su141912558
Ma Z, Niu H, Wu X, Zhang X, Lin G. An Improved Overmodulation Strategy for a Three-Level NPC Inverter Considering Neutral-Point Voltage Balance and Common-Mode Voltage Suppression. Sustainability. 2022; 14(19):12558. https://doi.org/10.3390/su141912558
Chicago/Turabian StyleMa, Zhixun, Haichuan Niu, Xiang Wu, Xu Zhang, and Guobin Lin. 2022. "An Improved Overmodulation Strategy for a Three-Level NPC Inverter Considering Neutral-Point Voltage Balance and Common-Mode Voltage Suppression" Sustainability 14, no. 19: 12558. https://doi.org/10.3390/su141912558
APA StyleMa, Z., Niu, H., Wu, X., Zhang, X., & Lin, G. (2022). An Improved Overmodulation Strategy for a Three-Level NPC Inverter Considering Neutral-Point Voltage Balance and Common-Mode Voltage Suppression. Sustainability, 14(19), 12558. https://doi.org/10.3390/su141912558










