Numerical Simulation of Thermal Storage Performance of Different Concrete Floors
Abstract
:1. Introduction
2. Materials and Methods
2.1. Governing Equation
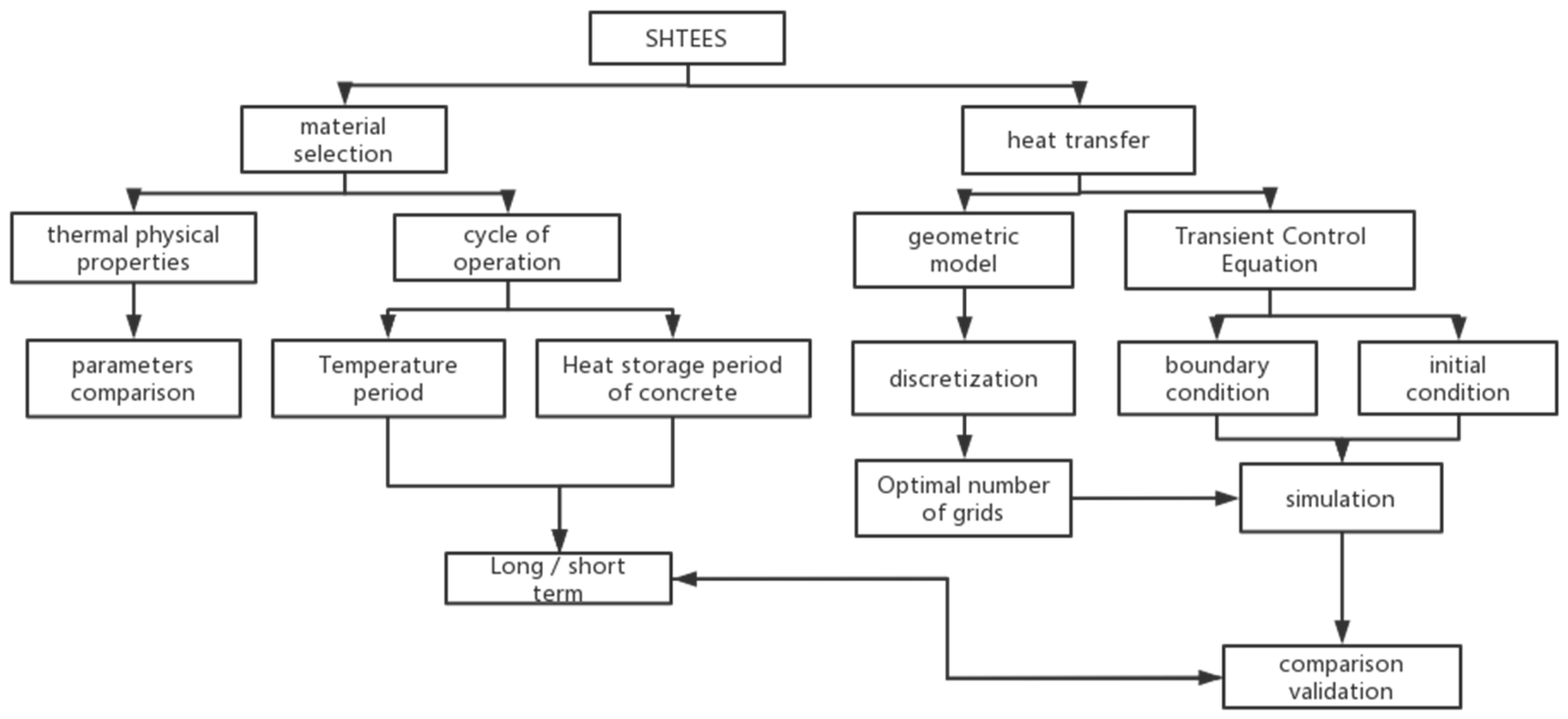
2.2. Design and Simulation Method Used for the SHTES Floor
- The coil material used here is high-temperature resistant polyethylene (PE-RT) with good thermal conductivity; it can ignore the heat transfer effect of the coil on the filling layer. Accordingly, the temperature of the contact surface between the filling layer and the tube wall can be similar to the temperature of the outer surface of the tube wall;
- The material of each layer is uniform and isotropic;
- The water flow rate in the coils is high, and the temperature drop along the flow direction of the pipeline can be ignored. Since it is a two-dimensional heat conduction model, the heat is transferred along the thickness of the floor in a direction between the adjacent coils.
- When designing a floor structure, the interlayer formed between the coil and insulation layer is generally set using a reflection film; this leads to excellent prevention of heat loss because the bottom of the coil and floor surface function as the adiabatic boundary and heat dissipation boundary, respectively.
2.3. Screening Concrete SHTES Materials
- Heat transfer within a concrete material mainly occurs via heat conduction, and the factors affecting thermal conductivity are aggregate type, water-cement ratio, and moisture content. In addition, the influence of thermal conductivity on thermal performance is also related to temperature. When the concrete temperature rises, its thermal conductivity is significantly reduced; however, this effect is only observed when the temperature exceeds 500 °C [55].
- Volumetric heat capacity is an important factor affecting the temperature distribution inside concrete. It decreases rapidly with a decrease in water content at the initial stage. Therefore, compared with the ideal situation of a constant volumetric heat capacity, the volumetric heat capacity is altered with environmental changes [56].
- The selection of concrete as a heat storage material should be based on the selection of materials with high thermal performance. It should be ensured that the SHTES module maximizes heat storage benefits.
- The thermal diffusion coefficient should be appropriately increased, since the concrete mix design can significantly affect the thermal characteristics [57].
3. Results
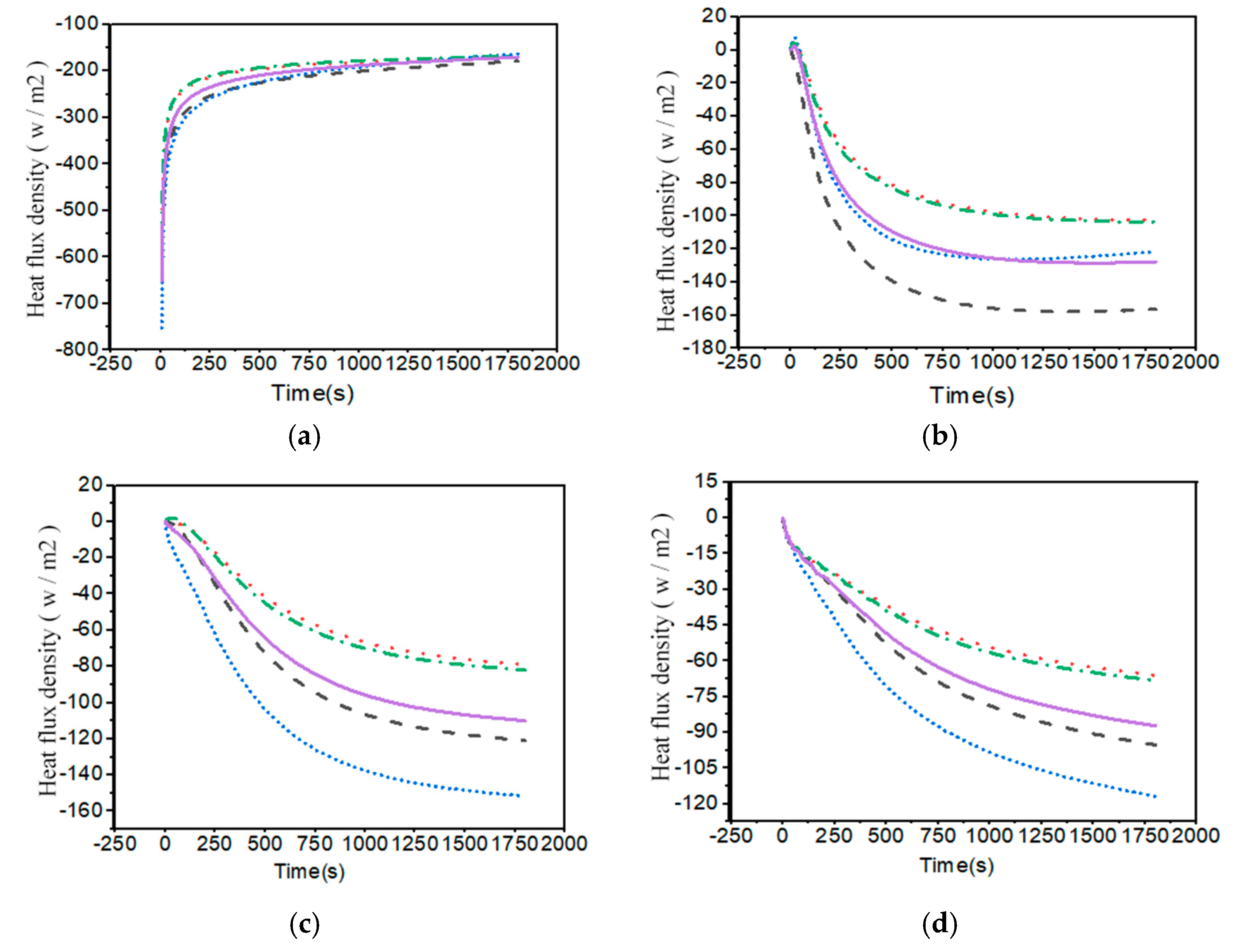
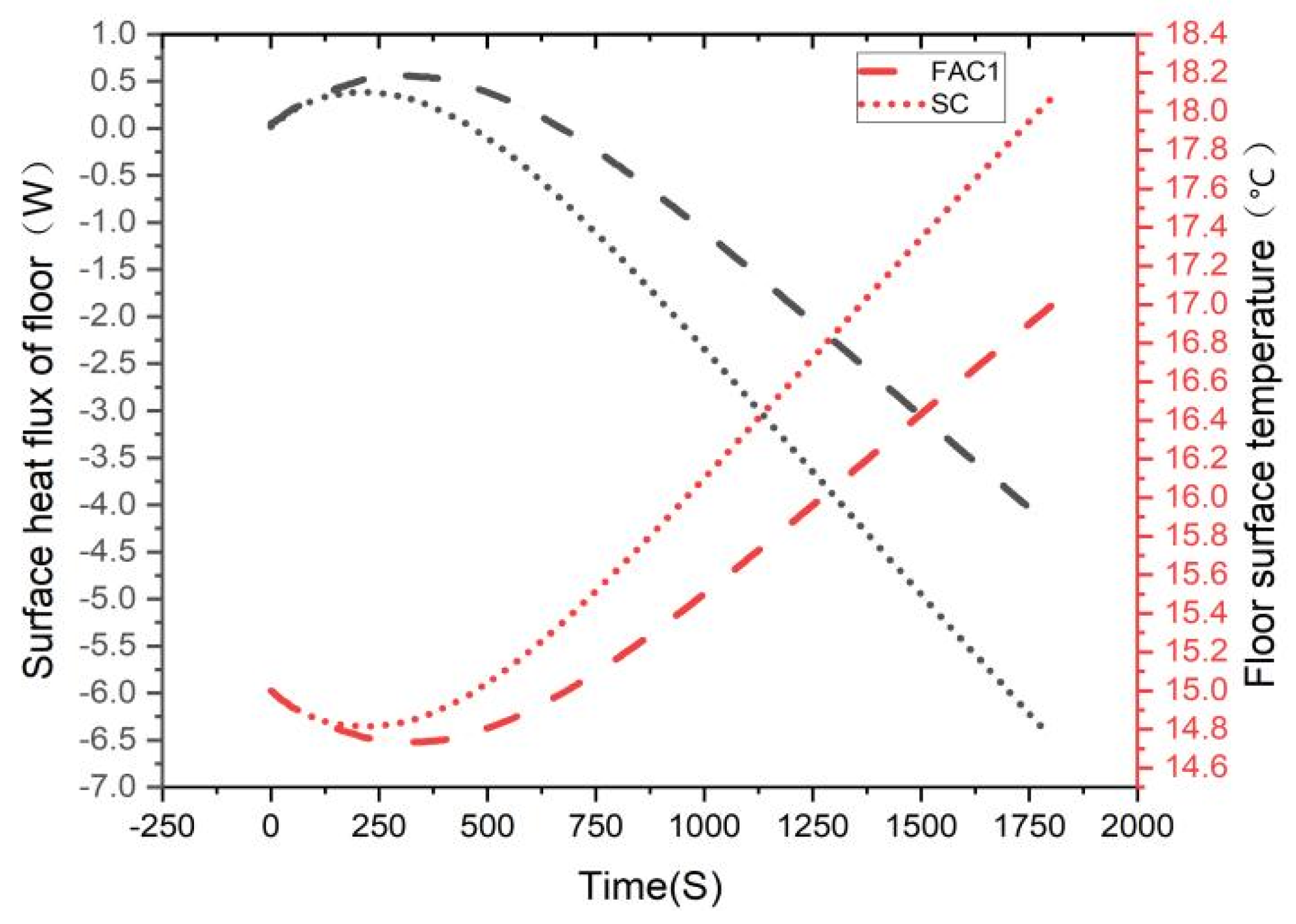
3.1. Changes in Floor Temperature and Heat Flux
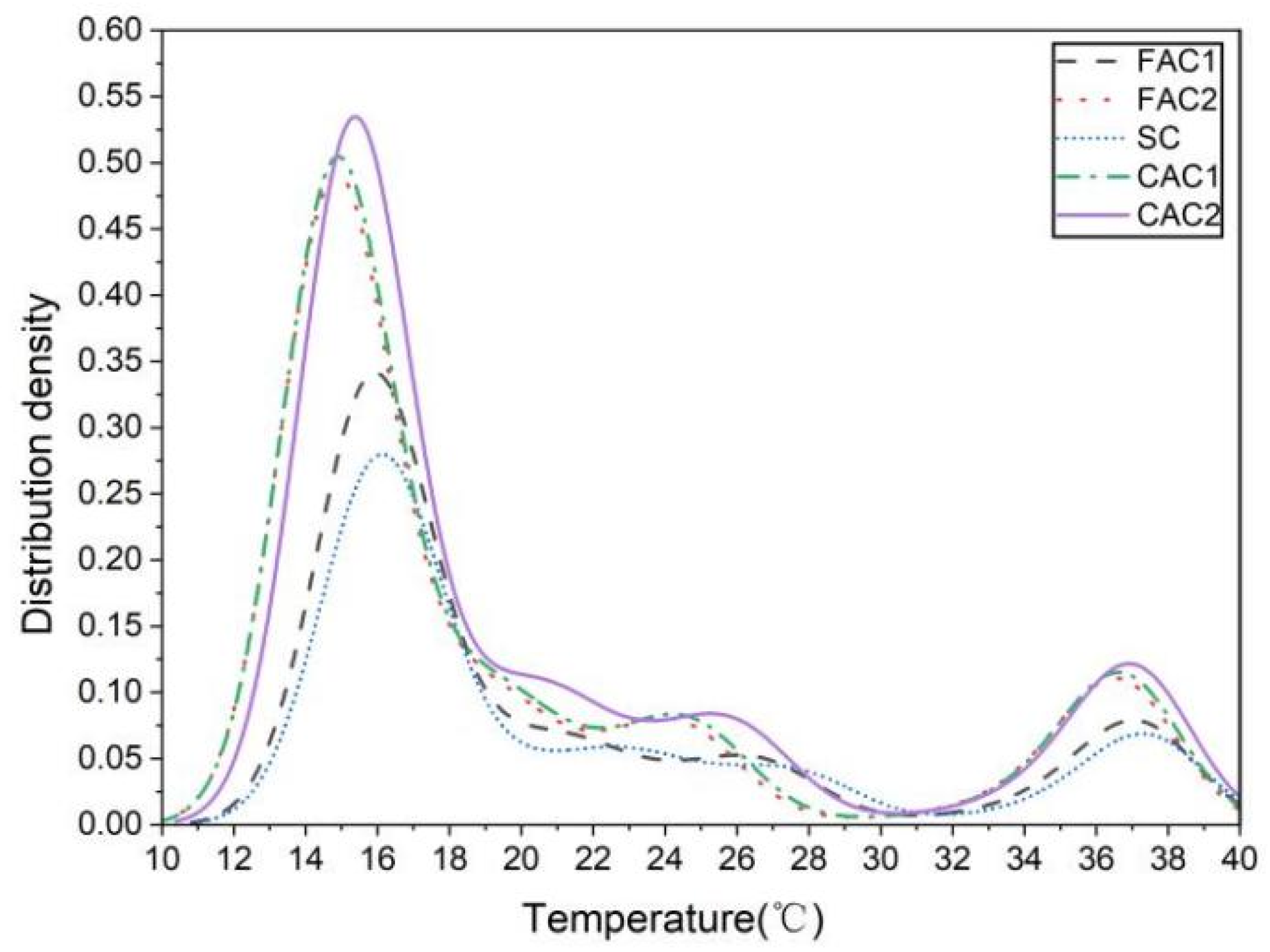
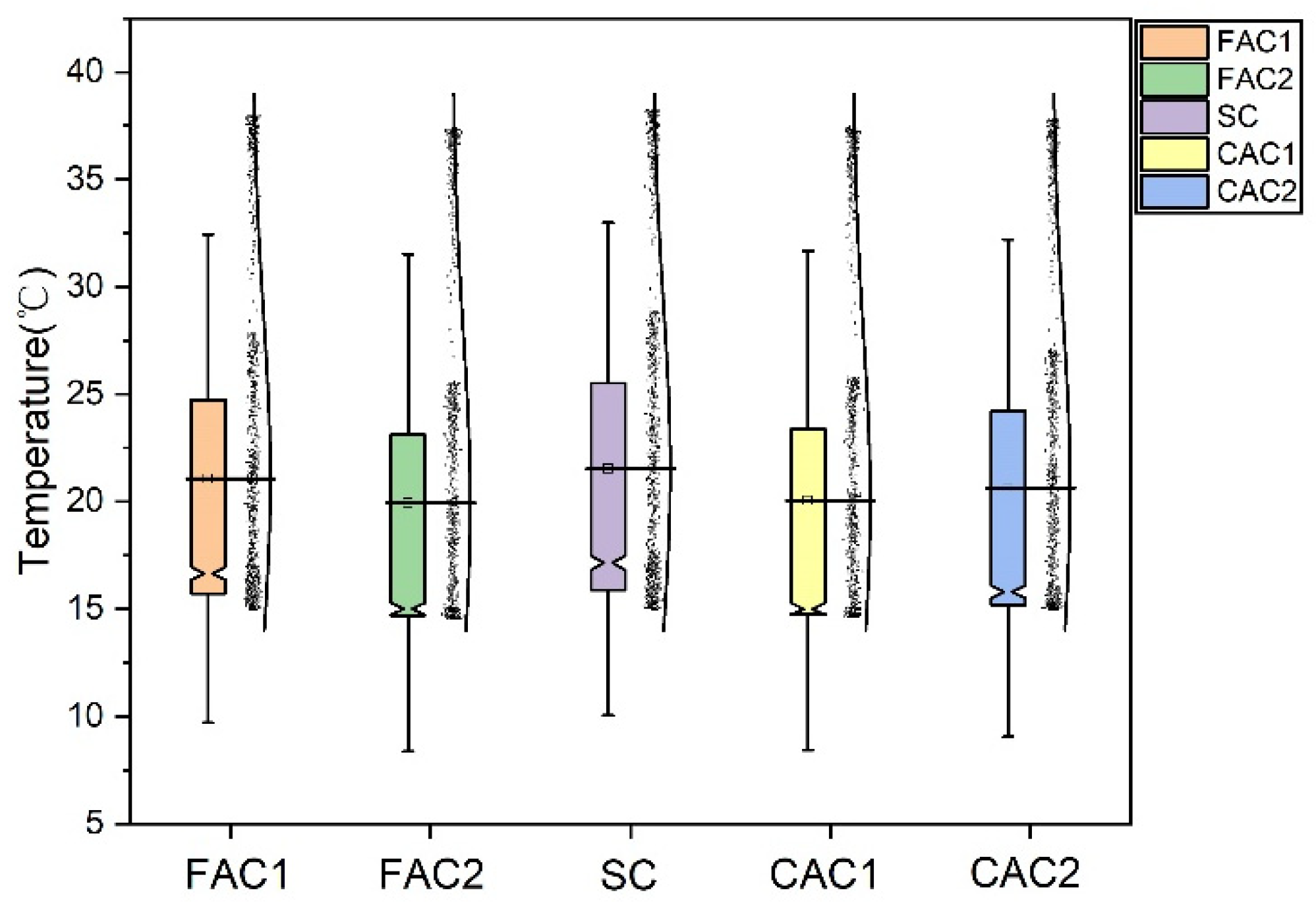
3.2. Influence of Concrete Thermal Properties on Heat Storage Process
4. Discussion
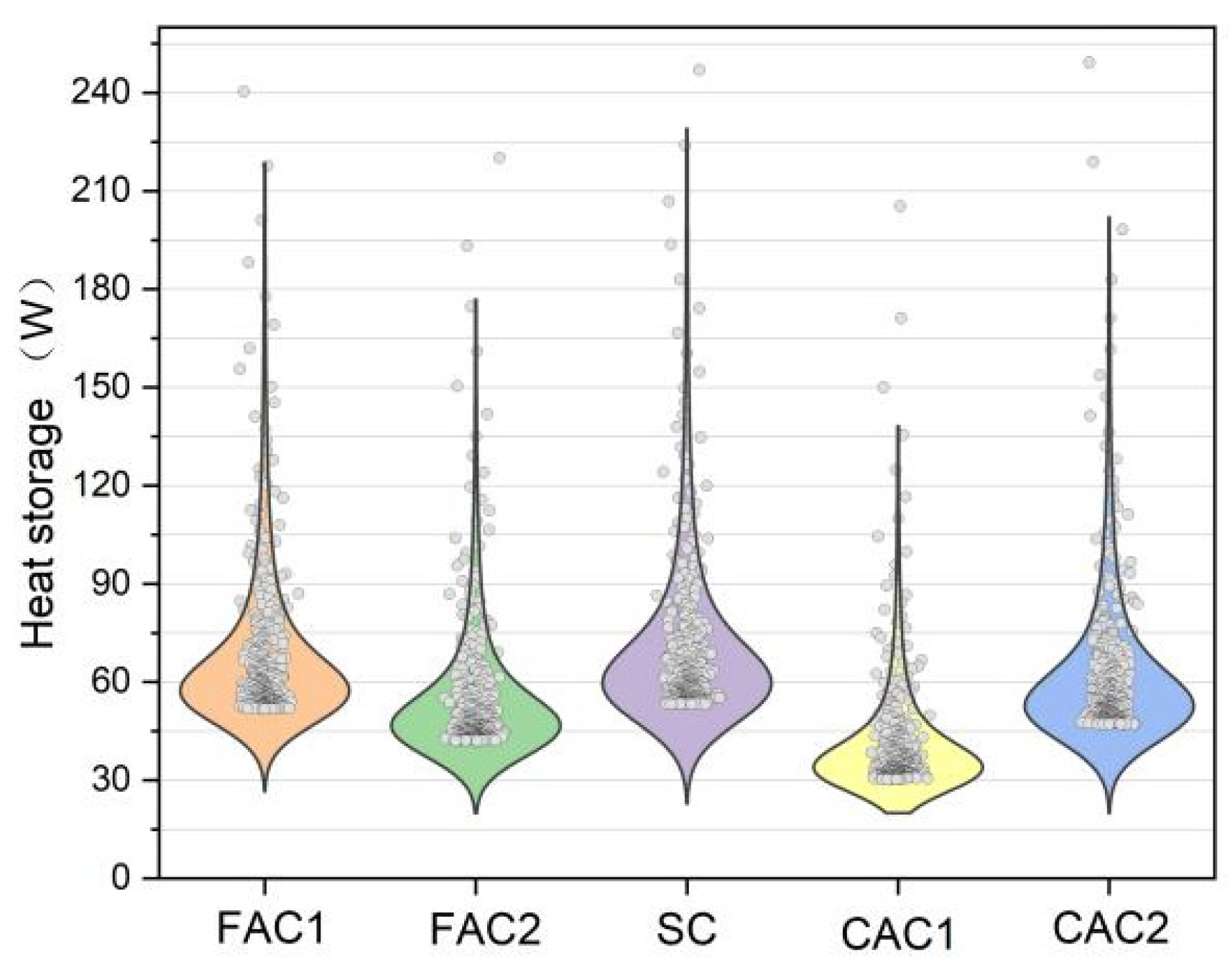
4.1. Floor Heat Storage
4.2. Instantaneous Heat Storage Rate inside the Floor
4.3. Correlation Analysis of Influencing Factors of Heat Storage
5. Conclusions
- After the simulation of floor heating within half an hour, the analysis of the floor surface temperature and internal heat flux density shows that the results of different concrete types under the same conditions are quite different, among which SC is more suitable for floor heat storage.
- Analysis of the thermal physical properties of concrete revealed that volume density and heat capacity exhibit same trends; the coefficient of thermal conductivity of floors comprising different concrete types had a greater influence on the heat accumulation; however, it is important to note that the heat storage material cannot be chosen based on a single thermal physical property, and that the heat transfer characteristics and thermal physical properties must be comprehensively considered.
- The total heat storage capacity in slag concrete for 0.5 and 7 h has been determined via fitting and verification analysis (61.0277 and 848.512 J, respectively). Meanwhile, the heat storage rate in the floor is strongly correlated with the heat flow on the coil surface and the floor heat storage.
Author Contributions
Funding
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Baek, S.; Kim, S. Determination of Optimum Hot-Water Temperatures for PCM Radiant Floor-Heating Systems Based on the Wet Construction Method. Sustainability 2018, 10, 4004. [Google Scholar] [CrossRef] [Green Version]
- Yeom, G.; Jung, D.E.; Do, S.L. Improving a Heating Supply Water Temperature Control for Radiant Floor Heating Systems in Korean High-Rise Residential Buildings. Sustainability 2019, 11, 3926. [Google Scholar] [CrossRef] [Green Version]
- Ying, X.; Li, W. Effect of Floor Shape Optimization on Energy Consumption for U-Shaped Office Buildings in the Hot-Summer and Cold-Winter Area of China. Sustainability 2020, 12, 2079. [Google Scholar] [CrossRef] [Green Version]
- Li, Y.; Wang, D.; Li, S.; Gao, W. Impact Analysis of Urban Morphology on Residential District Heat Energy Demand and Microclimate Based on Field Measurement Data. Sustainability 2021, 13, 2070. [Google Scholar] [CrossRef]
- Loibl, W.; Stollnberger, R.; Österreicher, D. Residential Heat Supply by Waste-Heat Re-Use: Sources, Supply Potential and Demand Coverage—A Case Study. Sustainability 2017, 9, 250. [Google Scholar] [CrossRef] [Green Version]
- Kalder, J.; Annuk, A.; Allik, A.; Kokin, E. Increasing Solar Energy Usage for Dwelling Heating, Using Solar Collectors and Medium Sized Vacuum Insulated Storage Tank. Energies 2018, 11, 1832. [Google Scholar] [CrossRef] [Green Version]
- Liu, Z.; Wu, D.; Jiang, M.; Yu, H.; Ma, W. Field Measurement and Evaluation of the Passive and Active Solar Heating Systems for Residential Building Based on the Qinghai-Tibetan Plateau Case. Energies 2017, 10, 1706. [Google Scholar] [CrossRef] [Green Version]
- Wang, J.; Tang, C.Y.; Brambley, M.R.; Song, L. Predicting home thermal dynamics using a reduced-order model and automated real-time parameter estimation. Energy Build. 2019, 198, 305–317. [Google Scholar] [CrossRef]
- Wang, Z.; Chen, Y.; Li, Y. Development of State space model for thermal dynamic analysis of buildings through model structure simplification. Energy Build. 2019, 195, 51–67. [Google Scholar] [CrossRef]
- Chen, T. Application of adaptive predictive control to a floor heating system with a large thermal lag. Energy Build. 2002, 34, 45–51. [Google Scholar] [CrossRef]
- Rawlings, J.B.; Patel, N.R.; Risbeck, M.J.; Maravelias, C.T.; Wenzel, M.J.; Turney, R.D. Economic MPC and real-time decision making with application to large-scale HVAC energy systems. Comput. Chem. Eng. 2018, 114, 89–98. [Google Scholar] [CrossRef]
- Hu, M.; Xiao, F.; Jørgensen, J.B.; Li, R. Price-responsive model predictive control of floor heating systems for demand response using building thermal mass. Appl. Therm. Eng. 2019, 153, 316–329. [Google Scholar] [CrossRef]
- Guo, J.; Jiang, Y.; Wang, Y.; Zou, B. Thermal storage and thermal management properties of a novel ventilated mortar block integrated with phase change material for floor heating: An experimental study. Energy Convers. Manag. 2020, 205, 112288. [Google Scholar] [CrossRef]
- Guo, J.; Dong, J.; Wang, H.; Jiang, Y.; Tao, J. On-site measurement of the thermal performance of a novel ventilated thermal storage heating floor in a nearly zero energy building. Build. Environ. 2021, 201, 107993. [Google Scholar] [CrossRef]
- Sun, W.; Zhang, Y.; Ling, Z.; Fang, X.; Zhang, Z. Experimental investigation on the thermal performance of double-layer PCM radiant floor system containing two types of inorganic composite PCMs. Energy Build. 2020, 211, 109806. [Google Scholar] [CrossRef]
- Prieto, C.; Cabeza, L.F. Thermal energy storage (TES) with phase change materials (PCM) in solar power plants (CSP). Concept andplant performance. Appl. Energy 2019, 254, 113646. [Google Scholar] [CrossRef]
- Jiang, Z.Y.; Qu, Z.G. Lithium–ion battery thermal management using heat pipe and phase change material during discharge–charge cycle: A comprehensive numerical study. Appl. Energy 2019, 242, 378–392. [Google Scholar] [CrossRef]
- Oravec, J.; Šikula, O.; Krajčík, M.; Arıcı, M.; Mohapl, M. A comparative study on the applicability of six radiant floor, wall, and ceiling heating systems based on thermal performance analysis. J. Build. Eng. 2021, 36, 102133. [Google Scholar] [CrossRef]
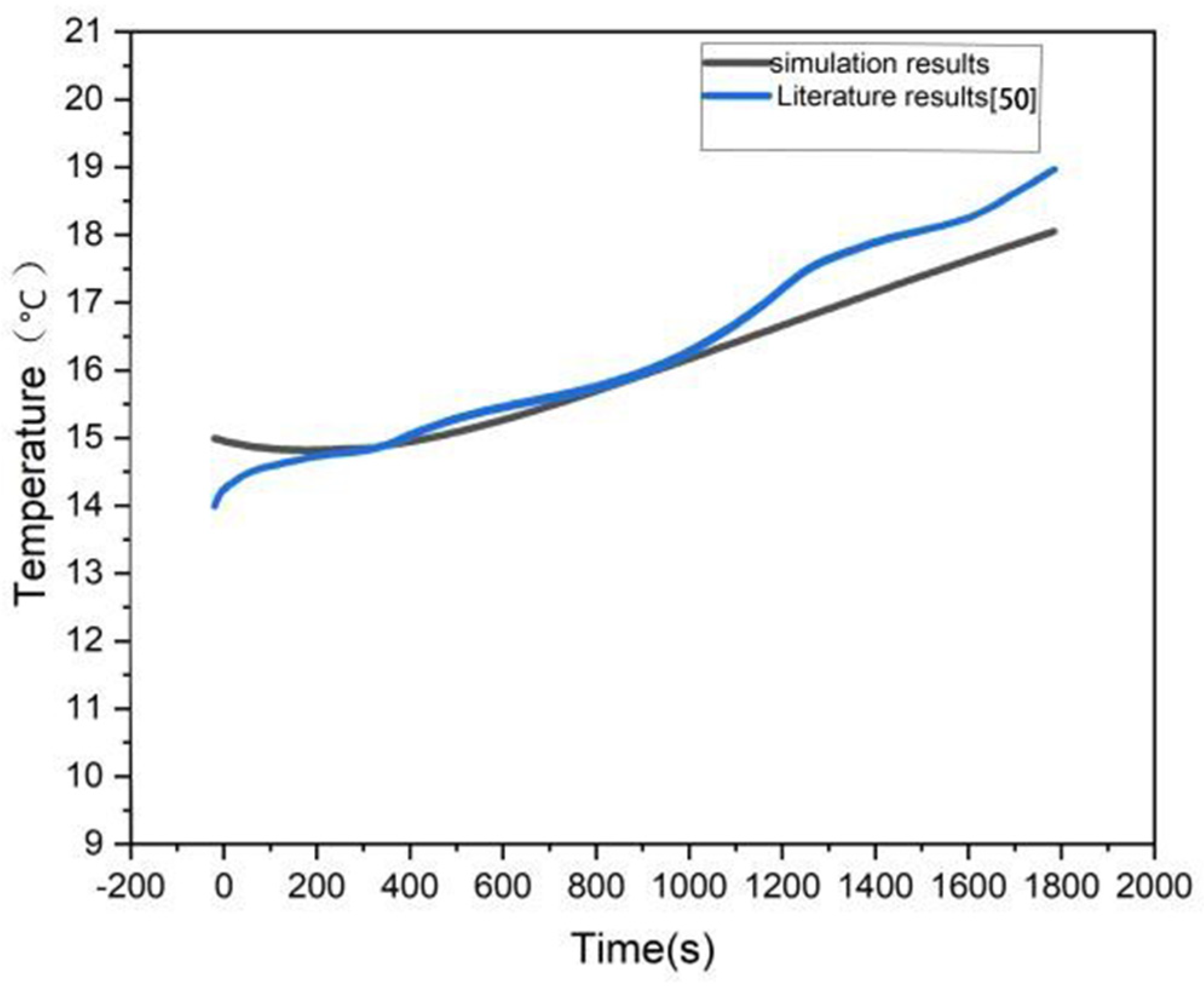
- Jara, E.R.; Ruiz-Pardo, Á.; García, M.C.; Ríos, J.A.T. Effect of Wood Properties and Building Construction on Thermal Performance of Radiant Floor Heating Worldwide. Appl. Sci. 2022, 12, 5427. [Google Scholar] [CrossRef]
- Tota-Maharaj, K.; Adeleke, B.O. Thermal performance of radiant floor heating systems concrete slabs. Proc. Inst. Civ. Eng. Energy 2022, 1–12. [Google Scholar] [CrossRef]
- Abbas, N.; Shatanawi, W. Heat and Mass Transfer of Micropolar-Casson Nanofluid over Vertical Variable Stretching Riga Sheet. Energies 2022, 15, 4945. [Google Scholar] [CrossRef]
- Abbas, N.; Shatanawi, W.; Abodayeh, K. Computational Analysis of MHD Nonlinear Radiation Casson Hybrid Nanofluid Flow at Vertical Stretching Sheet. Symmetry 2022, 14, 1494. [Google Scholar] [CrossRef]
- Sarbu, I.; Sebarchievici, C. A Comprehensive Review of Thermal Energy Storage. Sustainability 2018, 10, 191. [Google Scholar] [CrossRef] [Green Version]
- Fengwu, B.; Chao, X. Performance analysis of a two-stage thermal energy storage system using concrete and steam accumulator. Appl. Therm. Eng. 2011, 31, 2764–2771. [Google Scholar]
- David, B.; George, C. The Heat Equation, 1st ed.; Chapman and Hall/CRC: Boca Raton, FL, USA, 1995. [Google Scholar]
- Ferone, C.; Colangelo, F.; Frattini, D.; Roviello, G.; Cioffi, R.; Di Maggio, R. Finite element method modeling of sensible heat thermal energy storage with innovative concretes and comparative analysis with literature benchmarks. Energies 2014, 7, 5291–5316. [Google Scholar] [CrossRef] [Green Version]
- Park, M.; Min, J.; Bae, J.; Ju, Y. Thermal Contact Conductance-Based Thermal Behavior Analytical Model for a Hybrid Floor at Elevated Temperatures. Materials 2014, 13, 4257. [Google Scholar] [CrossRef] [PubMed]
- Wang, W.; Zeng, X.; Niyonzima, E.; Gao, Y.; Yang, Q.; Chen, S. Size Effect of Shear Strength of Recycled Concrete Beam without Web Reinforcement: Testing and Explicit Finite Element Simulation. Sustainability 2021, 13, 4294. [Google Scholar] [CrossRef]
- Yu, B.; Hu, P.; Saputra, A.; Gu, Y. The scaled boundary finite element method based on the hybrid quadtree mesh for solving transient heat conduction problems. Appl. Math. Model. 2021, 89, 541–571. [Google Scholar] [CrossRef]
- Lim, M.; Lee, C. A Study on the Heat and Stress Evaluation of Reinforced Concrete through High-Frequency Induction Heating System Using Finite Element Techniques. Sustainability 2021, 13, 6061. [Google Scholar] [CrossRef]
- Hasan, A.; Al-Sallal, K.; Alnoman, H.; Rashid, Y.; Abdelbaqi, S. Effect of Phase Change Materials (PCMs) Integrated into a Concrete Block on Heat Gain Prevention in a Hot Climate. Sustainability 2016, 8, 1009. [Google Scholar] [CrossRef] [Green Version]
- Selvam, R.; Castro, M. 3D FEM model to improve the heat transfer in concrete for thermal energy storage in solar power generation. Energy Sustain. 2010, 43956, 699–707. [Google Scholar]
- Oti, J.; Kinuthia, J.; Adeleke, B. The Strength Characterisation of Concrete Made with Alumina Waste Filler. Sustainability 2020, 12, 10235. [Google Scholar] [CrossRef]
- Del Rey Castillo, E.; Almesfer, N.; Saggi, O.; Ingham, J.M. Light-weight concrete with artificial aggregate manufactured from plastic waste. Constr. Build. Mater. 2020, 265, 120199. [Google Scholar] [CrossRef]
- Chinnu, S.; Minnu, S.; Bahurudeen, A.; Senthilkumar, R. Recycling of industrial and agricultural wastes as alternative coarse aggregates: A step towards cleaner production of concrete. Constr. Build. Mater. 2021, 287, 123056. [Google Scholar] [CrossRef]
- Ashour, T.; Morsy, M.; Korjenic, A.; Fischer, H.; Khalil, M.; Sesto, E.; Orabi, M.; Yehia, I. Engineering Parameters of Rice Straw Concrete with Granulated Blast Furnace Slag. Energies 2021, 14, 343. [Google Scholar] [CrossRef]
- Hamad, M.A.; Nasr, M.; Shubbar, A.; Al-Khafaji, Z.; Al Masoodi, Z.; Al-Hashimi, O.; Kot, P.; Alkhaddar, R.; Hashim, K. Production of Ultra-High-Performance Concrete with Low Energy Consumption and Carbon Footprint Using Supplementary Cementitious Materials Instead of Silica Fume: A Review. Energies 2021, 14, 8291. [Google Scholar] [CrossRef]
- Ozdenefe, M.; Dewsbury, J. Thermal performance of a typical residential Cyprus building with phase change materials. Build. Serv. Eng. Res. Technol. 2015, 37, 0143624415603004. [Google Scholar] [CrossRef] [Green Version]
- Vijayan, P.K.; Nayak, A.K.; Kumar, N. Steady-state and transient analysis of supercritical natural circulation systems. In Single-Phase, Two-Phase and Supercritical Natural Circulation Systems; Woodhead Publishing: Sawston, UK, 2019; pp. 237–272. [Google Scholar]
- Wang, D.; Liu, Y.; Wang, Y.; Liu, J. Numerical and experimental analysis of floor heat storage and release during an intermittent in-slab floor heating process. J. Appl. Therm. Eng. 2014, 62, 398–406. [Google Scholar] [CrossRef]
- Yuanyuan, Z.; Mei, H.; Jiyuan, H.; Hou, R. CFD investigation for a 7-pin wire-wrapped fuel assembly with different shapes of fuel duct wall. Ann. Nucl. Energy 2020, 141, 107272. [Google Scholar]
- Cho, J.; Park, B.; Lim, T. Experimental and numerical study on the application of low-temperature radiant floor heating system with capillary tube: Thermal performance analysis. Appl. Therm. Eng. 2019, 163, 114360. [Google Scholar] [CrossRef]
- Weitzmann, P.; Kragh, J.; Roots, P.; Svendsen, S. Modelling floor heating systems using a validated two-dimensional ground-coupled numerical model. J. Build. Environ. 2005, 40, 153–163. [Google Scholar] [CrossRef]
- Nering, K.; Stypula, K. Evaluation of Floating Floor System with Steady State Dynamics Simulation in the Context of Impact Sound Level. IOP Conf. Ser. Mater. Sci. Eng. 2019, 471, 062017. [Google Scholar] [CrossRef]
- Dincer, I. Heat Transfer Aspects of Energy. In Comprehensive Energy Systems; Elsevier: Amsterdam, The Netherlands, 2018; pp. 422–477. [Google Scholar]
- Erasmo, C.; Fiorenzo, A. Solution of Sample Problems in Classical Thermoelasticity; Academic Press: Cambridge, MA, USA, 2017; Chapter 2; pp. 25–80. [Google Scholar]
- Wang, Y.; Zheng, T.; Zheng, X.; Liu, Y.; Darkwa, J.; Zhou, G. Thermo-mechanical and moisture absorption properties of fly ash-based lightweight geopolymer concrete reinforced by polypropylene fibers. Constr. Build. Mater. 2020, 251, 118960. [Google Scholar] [CrossRef]
- Mizobuchi, T.; Ishizeki, K.; Sagawa, T.; Kanda, T. Study on the Influence of Minor Constituents in Blast Furnace Slag Rich Cement on the Thermal and Mechanical Properties of Concrete. J. Adv. Concr. Technol. 2019, 17, 46–61. [Google Scholar] [CrossRef]
- Wadsö, L.; Karlsson, J.; Tammo, K. Thermal properties of concrete with various aggregates. J. Cem. Concr. Res. 2012. [Google Scholar]
- Wang, Y.; Huang, J.; Wang, D.; Liu, Y.; Zhao, Z.; Liu, J. Experimental study on hygrothermal characteristics of coral sand aggregate concrete and aerated concrete under different humidity and temperature conditions. Constr. Build. Mater. 2020, 230, 117034. [Google Scholar] [CrossRef]
- Payam, S.; Iman, A.; Norhayati, B. Concrete as a thermal mass material for building applications—A review. J. Build. Eng. 2018, 19, 14–25. [Google Scholar]
- Lee, Y.H.; Chua, N.; Amran, M.; Yong Lee, Y.; Hong Kueh, A.B.; Fediuk, R.; Vatin, N.; Vasilev, Y. Thermal performance of structural lightweight concrete composites for potential energy saving. J. Cryst. 2021, 11, 461. [Google Scholar] [CrossRef]
- Cao, V.D.; Pilehvar, S.; Salas-Bringas, C.; Szczotok, A.M.; Bui, T.Q.; Carmona, M.; Rodriguez, J.F.; Kjøniksen, A.-L. Thermal performance and numerical simulation of geopolymer concrete containing different types of thermoregulating materials for passive building applications. Energy Build. 2018, 173, 678–688. [Google Scholar] [CrossRef]
- Saboor, S.; Chelliah, A.; Gorantla, K.; Kim, K.-H.; Lee, S.-H.; Shon, Z.H.; Brown, R.J.C. Strategic design of wall envelopes for the enhancement of building thermal performance at reduced air-conditioning costs. J. Environ. Res. 2021, 193, 110577. [Google Scholar] [CrossRef]
- Asadi, I.; Shafigh, P.; Hassan, Z.F.B.A.; Mahyuddin, N.B. Thermal conductivity of concrete—A review. J. Build. Eng. 2018, 20, 81–93. [Google Scholar] [CrossRef]
- Choktaweekarn, P.; Saengsoy, W.; Tangtermsirikul, S. A model for predicting the specific heat capacity of fly-ash concrete. J. Sci. Asia 2009, 35, 178–182. [Google Scholar] [CrossRef]
- Robati, M.; McCarthy, T.J.; Kokogiannakis, G. Incorporating environmental evaluation and thermal properties of concrete mix designs. J. Constr. Build. Mater. 2016, 128, 422–435. [Google Scholar] [CrossRef]
- Ruijun, W.; Ningning, Y.; Yang, L. Methods for improving the microstructure of recycled concrete aggregate: A review. Constr. Build. Mater. 2020, 242, 118164. [Google Scholar]
- Zhengrong, L.; Dongkai, Z.; Cui, L. Experimental evaluation of indoor thermal environment with modularity radiant heating in low energy buildings. Int. J. Refrig. 2021, 123, 159–168. [Google Scholar]






| Coil Heating Temperature °C | Coil Spacing mm | Initial Temperature °C | Comprehensive Heat Transfer Coefficient W(/m2∙°C) |
|---|---|---|---|
| 42 | 200 | 15 | 10.5 |
| Name | Thermal Conductivity W(m·K) | Specific Heat Capacity J/(kg·K) | Density kg/m3 | Thermal Diffusivity m2/s | Volumetric Heat CapacitykJ/(m3·K) |
|---|---|---|---|---|---|
| FAC1 | 0.95 | 1050 | 1700 | 5.32 × 10−7 | 1785 |
| FAC2 | 0.7 | 1050 | 1500 | 4.44 × 10−7 | 1575 |
| SC | 1 | 1050 | 1700 | 5.6 × 10−7 | 1785 |
| CAC1 | 0.7 | 1050 | 1400 | 4.76 × 10−7 | 1470 |
| CAC2 | 0.84 | 1050 | 1600 | 5 × 10−7 | 1680 |
| Coil Heating Temperature °C | Coil Spacing mm | Initial Temperature °C | Literature Resource |
|---|---|---|---|
| 40 | 100 | 14 | [50] |
| Name | Fitting Expression | 0.5 h Total Heat Storage J | 7 h total Heat Storage J |
|---|---|---|---|
| FAC1 | 54.9031 | 763.743 | |
| FAC2 | 47.1078 | 655.021 | |
| SC | 61.0277 | 848.512 | |
| CAC1 | 51.2075 | 702.038 | |
| CAC2 | 53.7666 | 747.599 |
| Name | Section Location | Heat Storage Rate J/S | Comprehensive Heat Storage Rate J/S |
|---|---|---|---|
| FAC1 | Section1 | 0.38932 | 0.09469 |
| Section2 | 0.20665 | ||
| Section3 | 0.26407 | ||
| Section4 | 0.24693 | ||
| FAC1 | Section1 | 0.23293 | 0.09001 |
| Section2 | 0.20782 | ||
| Section3 | 0.22346 | ||
| Section4 | 0.15443 | ||
| SC | Section1 | 0.44923 | 0.09477 |
| Section2 | 0.20238 | ||
| Section3 | 0.34339 | ||
| Section4 | 0.2742 | ||
| CAC1 | Section1 | 0.22835 | 0.09314 |
| Section2 | 0.20373 | ||
| Section3 | 0.22999 | ||
| Section4 | 0.20615 | ||
| CAC2 | Section1 | 0.22094 | 0.09451 |
| Section2 | 0.16703 | ||
| Section3 | 0.24527 | ||
| Section4 | 0.1867 |
| Name | Index | Spearman Rank Correlation Coefficient Rs | 0.05 Level of Visibility |
|---|---|---|---|
| FAC1 | Surface heat flux of coil | 1 | Obviously |
| Floor surface temperature | −0.95421 | Obviously | |
| Heat storage rate in floor | 1 | Obviously | |
| SC | Surface heat flux of coil | 1 | Obviously |
| Floor surface temperature | −0.98577 | Obviously | |
| Heat storage rate in floor | 1 | Obviously | |
| ACA2 | Surface heat flux of coil | 1 | Obviously |
| Floor surface temperature | −0.94645 | Obviously | |
| Heat storage rate in floor | 1 | Obviously |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Y.; Xu, G. Numerical Simulation of Thermal Storage Performance of Different Concrete Floors. Sustainability 2022, 14, 12833. https://doi.org/10.3390/su141912833
Wang Y, Xu G. Numerical Simulation of Thermal Storage Performance of Different Concrete Floors. Sustainability. 2022; 14(19):12833. https://doi.org/10.3390/su141912833
Chicago/Turabian StyleWang, Yudi, and Guoqiang Xu. 2022. "Numerical Simulation of Thermal Storage Performance of Different Concrete Floors" Sustainability 14, no. 19: 12833. https://doi.org/10.3390/su141912833
APA StyleWang, Y., & Xu, G. (2022). Numerical Simulation of Thermal Storage Performance of Different Concrete Floors. Sustainability, 14(19), 12833. https://doi.org/10.3390/su141912833







