Mathematical Models for the Vehicle Routing Problem by Considering Balancing Load and Customer Compactness

Abstract

The vehicle routing problem seeking to minimize the traveled distance and the deviation of the total workload is known as the vehicle routing problem with workload balance (WBVRP). In the WBVRP, several elements are considered: (i) the total distance or driving time, (ii) the number of customers to be visited, and (iii) the total weight or amount of delivered goods. We have considered the WBVRP by adding a concept called customer compactness and the visual attractiveness of the routes. The WBVRP allows a similar workload for drivers to improve their well-being and social development. Unbalanced routes could generate high costs due to potential strikes by drivers seeking an equitable workload. We have proposed three mathematical formulations for solving the WBVRP by minimizing the customer compactness and the distance with and without considering workload balancing. The workload balancing is based on the deviation concerning the average load of the routes and considering waiting and driving time. We have tested the efficiency of the proposed models on a synthetic set of instances, analyzing different aspects such as depot location, customer location, and demand. The analysis of the results has been performed considering customer compactness and the visual attractiveness of the obtained solution. Computational experiments on generated random instances show the efficiency of the proposed approaches.

1. Introduction

Mathematical optimization models for the solution of the well-known vehicle routing problem (VRP) have been used for decades as a strategy to generate distribution plans. The proposed mathematical models consider maximizing the resources of the VRP (vehicles, drivers, cargo capacities, traveled distance, demands, depot location, and customers). Historically, the focus of these models has been aimed at reducing costs and increasing transportation revenues, solving the problem’s commercial aspect. However, experimentation over the years has concluded that the early proposed formulations generally do not consider the desired benefit due to the high dispersion of customers. This aspect leads to confusing and unintuitive routes (low visual attractiveness) and unbalanced routes in terms of the work by drivers. Both factors increase the disagreement of the main actors, triggering a low acceptance of distribution planning.

The use and experience of the published works over the years have led to the identification of certain shortcomings of the VRP in practice [1].

Dispersion of the customer set of the route. Usually, the traditional variants of the VRP consider a cost or income based on the distance the vehicle must travel to supply the customers’ demand. The outputs of the classic models provide a set of points to go through, which should offer the cheapest, simplest and shortest route at first glance. However, the cost is not directly related to the generation of simple routes by increasing the number of customers, vehicles, and demands. Therefore, having a set of customers with scattered locations exacerbates this problem.

Unbalance in the route’s workload. The workload is usually measured as a fixed or variable cost based on traveled distance or time. The workload metrics must consider the comparison between routes avoiding generating disproportionate VRP solutions concerning the required work of each route.

A high dispersion of customers (or low compactness) could generate challenging routes to be performed, longer service times, longer working hours, and the concentration of deliveries in some areas (leaving a group of dissatisfied customers). In addition, the scarce workload limitation produces unequal demands for the drivers who carry out the routes. Drivers could usually be dissatisfied due to unequal routes, increasing staff turnover, and decreasing service quality. On the other hand, it is essential to maintain drivers’ conformity to generate stability and service confidence. Otherwise, low customer satisfaction may occur, negatively affecting economic terms. It should be noted that currently, “a deficit of 10,000 professional drivers is estimated in Chile” [2] which aggravates the problem due to the complexity of supplying the demand in the event of medical licenses and resignations.

Given that some aspects of customer dispersion and lod balancing, including compactness of customer and visual attractiveness, are usually not covered by most VRP published variants, our interest is to create solution strategies to generate simple, ordered, and compensated routes. These aspects could be summarized as route balancing, which could be performed by compacting the customers based on a balance in the route’s workload. In this work, the problem of vehicle routing with load balancing with compactness and improvement of visual attractiveness of the routes is introduced. Three mathematical models are proposed for the problem, maximizing the group of customers and balancing the workload routes.

The paper’s main contribution is associated with some limitations and considerations that have yet to be studied deeply in the literature. First, the proposed models consider vehicles with homogeneous characteristics and travel times of a size predefined, separating the workload into costs associated with driving and waiting times at loading and unloading for the WBVRP. Drivers have been assigned to a single vehicle and a single route; therefore, “route workload” and “driver workload” are synonymous. The workload is distinguished into two types: driving time and waiting time. The waiting times correspond to the periods associated with the unloading time with which the driver is not associated. In contrast, driving time considers an amount of time related to the distance between nodes and the average speed of the trip.

Second, the proposed approaches integrate two additional concepts related to customer compactness and visual attractiveness of the routes for the WBVRP. The customer compactness concept allows for improving balanced work on routes, given the nature of the routes. We have proposed as a metric the distance as the primary attribute to calculate the customer compactness, to the detriment of travel time. The compactness for the entire system is determined by the sum of the individual route compactness. We have considered the maximum compactness, the minimum compactness, the minimum dispersion, and the maximum proximity as proposed metrics. In addition, the visual attractiveness concept allows drivers to perceive a similar workload, therefore improving their well-being and social development. Unbalanced visual routes could generate high costs due to potential strikes by drivers seeking equitable workloads.

This paper has been developed as follows. Section 2 details the literature related to the problem of customer compactness and load balancing in VRP. Section 3 details the proposed models. Section 4 presents the statistical analyses of the findings in the different sets of instances. Finally, Section 5 shows the conclusions and proposed future work.

2. Literature Review

The VRP consists of generating practical routes and using them to distribute or collect products. Basic VRP problems have a predefined number of vehicles that depart from a starting point (depot) to supply the other nodes within the route (customers). The main objective is to perform a set of efficient routes, minimizing costs or maximizing profits, under considerations specific to each problem. In general, drivers and dispatchers assigned to VRP problems may be reluctant to implement solutions that seem too complex and counterintuitive or require a high degree of coordination, even if these solutions are technically optimal concerning cost [3].

Similarly, the customers generally ask that their cargo not pass-through unwanted places before reaching the final destination. In this way, the VRP problem’s objective should be minimizing costs and achieving acceptance and success in generating balanced routes considering the drivers’ criteria and the customers’ perception. One of the ways to solve this problem is through the concept of visual attractiveness. This concept considers a solution within a short computing time and without modifications. It is also easy to understand and accept from the observation point. There is no precise definition for visual attractiveness; however, many authors agree on the characteristics of visually attractive routes: compact, short distances between customers, reduced overlap between routes, and simple routes in terms of their shape and path [4].

In parallel, a situation arises from acceptance of the routing plans. It occurs when the distribution plan generates routes disproportionately concerning the workload performed by the driver in terms of the traveled distance, driving times, loading and unloading times, and costs per vehicle, among other elements. This situation could be exemplified in cases of a system comprised of very long and short routes. Some vehicles and drivers are overexerting themselves, and others work less than average. Figure 1 shows an example of unbalanced versus balanced routes.

This problem is known as vehicle routing problem with workload balance (WBVRP). Its effects range from low acceptance of operating plans, decreased employee satisfaction, increased overtime, bottlenecks of some resources, irregular wear of equipment, visually unattractive routes, and unbalanced routes. In the long term, this situation could lead to adverse work environments and driver resignations, which are critical to transportation operations. It is necessary to consider both the visual aspect of the routes and the workload to generate balanced solutions for the drivers and carriers.

2.1. Customer Compactness

Achieving visual attractiveness requires a combination of compactness and balanced routes, decreased overlap, and simplicity in route shapes. One of the ways to group these elements is to work directly on maximizing compactness using a metric to reduce the dispersion of customers, which reduces the probability of overlapping, as well as the appearance of routes that are too long or too short.

Constructing a centroid for each route is necessary to generate a metric related to compactness. There are several definitions for the concept of route centroid: (i) the geometric center of a route [5] (ii) the customer closest to the geometric center of the route [6], (iii) the customer who is in the middle of the route in terms of the number of nodes [7], (iv) the customer with the minimum total distance to the rest of the nodes of its route [8], among others.

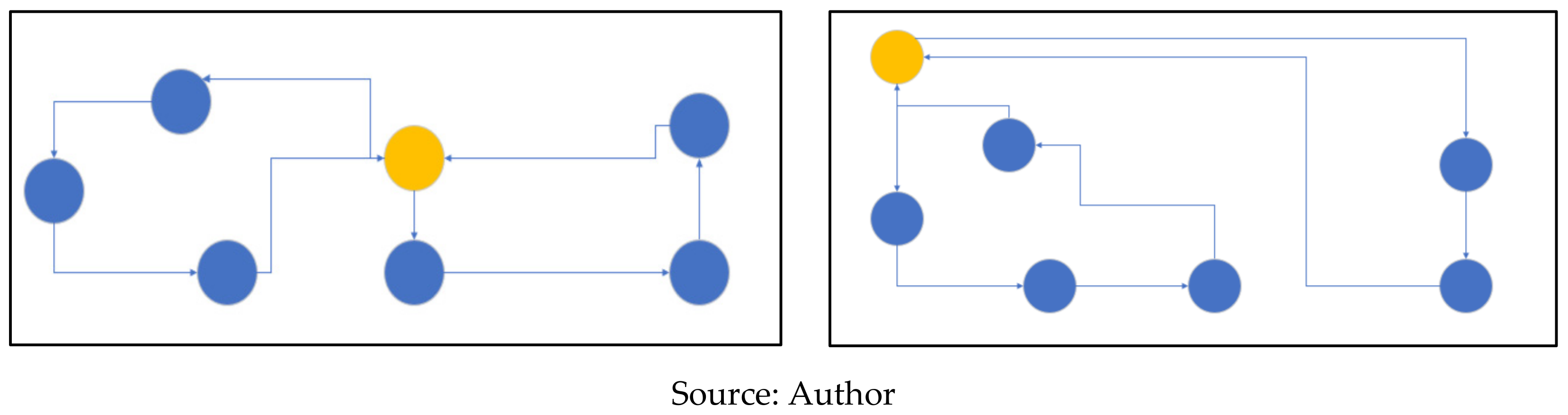
Figure 2 presents the example of a route with five customers of equal importance. The route centroid is highlighted in red, and the center of gravity with a cross. In case one, the centroid corresponds to the center of gravity. In case two, the centroid of the route corresponds to the node closest to the center of gravity. In case three, the middle node is the centroid (third of five points). Finally, in case four, the centroid of the route is the node with the smallest total distance from the rest of the nodes. The difference between these examples is the benefit of considering visual attractiveness. In this sense, the centroid that offers the best visualization is the most intuitive for identifying the route (case one).

The compactness calculation metrics are diverse. However, two representative indices operating with the center of gravity as a centroid are route compactness and route proximity. Route compactness of $i$($COM{P}_i$) calculates the distance from the different nodes of the route $i$ to their corresponding center of gravities $C_i$. This value is divided by the total number of nodes of the route ($\left|T_i\right|$). In this way, compactness allows comparison between different routes [9]. In addition, compactness is maximized when the metric is minimized according to (1). Route proximity $i$ ($PRO{X}_i$) is calculated according to (2). In particular, $O_i$ corresponds to the number of nodes of a route $i$ close to the center of another route $j$ (under a predefined threshold), with $j\ne i$ [6]. If this value is high, the routes are closed, and the compactness is high.

Note that the compactness is calculated independently by each route. In contrast, the proximity is calculated with the information of two close routes to compact the nodes, consequently generating overlapping routes. However, in both cases, the location of the center of gravity is necessary.

$$COM{P}_i=\frac{{{\displaystyle \sum }}_{i\in T_I}dist\left(i,C_1\right)}{\left|T_i\right|}$$

(1)

$$PRO{X}_i=\left[2\left(1-\frac{O_i}{\left|T_i\right|}\right)\right]-1$$

(2)

2.2. Workload

Balancing workloads between routes could serve as a metric to improve visual attractiveness since it is possible to have routes with a similar composition, reducing the customer’s dispersion and, therefore, the appearance of extremely short or long routes. This situation reduces the total compactness of the system and the overlapping of edges. However, it is difficult to quantify the workload since it generally involves vehicle drivers. A daily schedule driver is composed of driving and waiting times, finding VRP solutions with long driving times and fewer waiting times and vice versa. The published works have dealt with this situation, proposing the workload constraint under specific parameters.

Individual workloads (times) are likely to yield significant inequalities between drivers by maximizing or minimizing the sum of the total workload. The best way is to carry out this evaluation individually or to support the objective function in some metric that measures work balance. It may also be the case that the workload is used for other purposes, such as minimizing travel times and distances between nodes, maximizing benefits, and minimizing costs. Another option is to handle the workload as a constraint, limiting its maximum value, the minimum and the mean of the workload, and the standard deviation of the driver’s set. An individual approach is also possible, limiting each of the individual workloads. A survey of some routing problems considering variants of workload balance has been addressed by [10].

2.3. The Vehicle Routing Problem with Workload Balance (WBVRP)

The vehicle routing with balancing load has been studied by [11] and [12]. Two main aspects are highlighted from previous work: the total distance or driving time and the total weight or amount of goods delivered. One of the main challenges is to measure “workload balance” fairly. Lozano et al. [13] compare objective functions (OFs) to measure balanced route configurations. This work proposes a basic single-solution-based evolutionary algorithm to compare the quality of the Pareto approximations for the different conflict objective functions. Solution methods for bi-objective variants of the WBVRP have been proposed by [14,15,16,17,18]. Population-based algorithms for the WBVRP have been proposed by [17,19,20,21].

Real problems associated with WBVRP have been considered by [22], who address the problem from a real bottled beverage distribution company. The authors propose a bi-objective programming model where dispersion and balancing concerning the number of customers are used as performance criteria. In addition, [21] develops a multi-objective memetic algorithm (MMA) for the WBVRP, integrating a problem-specific local search procedure into a multi-objective evolutionary algorithm. Camacho-Vallejo et al. [23] consider the distribution process of a manufacturing company that supplies products to the customers. Lehuédé et al. [24] investigate the lexicographic minimax approach to research the balanced workload, rooted in social choice theory. The problem is solved by a heuristic based on the multi-directional local search framework.

Recently, [25] examined a centrally organized multi-period collaborative vehicle routing problem, where carriers can exchange customers who must be serviced regularly. Sartori et al. [26] consider vehicle routing and scheduling problems with interdependent routes arising when some services must be performed by at least two vehicles and temporal synchronization between the starting times of these services. Fallah et al. [27] present an improved two-approximation algorithm for the WBVRP. The authors focus on obtaining approximate solutions since finding balanced loads is NP-complete. In addition, Li et al. [28] addressed the vehicle routing problem with workload balance (WBVRP) and a microcluster-based VRPWB (MWBVRP) to minimize the total traveling costs and balance the workload. Jorge et al. [29] consider the smart waste collection problem concerning workload. The authors propose a look-ahead heuristic to decide when the collection is necessary and which bins must be collected considering the present bin fill levels.

Finally, variants of the WBVRP have been considered by several authors. The balanced cargo vehicle routing problem with time windows (BCVRPTW) has been studied by [30,31,32]. A combination of the WBVRP with loading constraints has been introduced by [33]. A real-world balanced open vehicle routing problem considering the minimization of the makespan is introduced by [34].

According to the literature review, the traditional approaches to measuring the workload balance have some problems. Traditionally, the workload balance is measured as the minimization of the duration of the longest route and the difference between the longest and the shortest routes, respectively. Instead, we propose a novel formulation for the WBVRP with the customers’ compactness and visual attractiveness by using several objectives to propose a practical framework for real rich routing problems.

3. Material and Methods

We have proposed three mathematical models to solve the WBVRP considering customer compactness and visual attractiveness. The proposed mathematical models use the following parameters and decision variables:

3.1. Parameters

• $coor{d}_{ij}=$ Coordinates of the nodes
• $d_i=$ Demand of customer $i$
• $t{d}_i=$ Loading and unloading time of customer $i$
• $c{t}_i=$ Cost per time associated with driving and waiting time for each node
• $N=$ Number of nodes
• $K=$ Number of vehicles
• $Q=$ Vehicle capacity
• $vel=$ Average vehicle speed
• $desv=$ Workload deviation
• $dis{t}_{ij}=$ Euclidean distances between nodes
• $\gamma =$ Factor for the considered distance.

3.2. Decision Variables

• $x_{ijv}=\left\{\begin{array}{c}1\\ 0\end{array}\right.$ If the vehicle $v$ travels the edge $\left(i,j\right)$, Otherwise

• $u_{iv}=$ Cumulative demand of the vehicle $v$ on node $i$

• $C{T}_v=$ Workload of the vehicle $v$

• $mCT=$ Workload average

• $C{G}_{vc}=$ Coordinate $X$ and $Y$ of the gravity center of the visited route by vehicle $v$

• $COM{P}_v=$ Compactness of the route $v$
• $dist{x}_{iv}=$ Squared difference between the x-coordinate of the nodes and their corresponding $C{G}_{vc}$
• $dist{y}_{iv}=$ Squared difference between the y-coordinate of the nodes and their corresponding $C{G}_{vc}$

3.3. Model with Minimum Compactness

The first model seeks to minimize the compactness expressed by (3). The compactness is calculated as the distance from the node $i$ to the center of gravity ($CG$) of the route $v$ plus the sum of a proportion of the total distance. This sum has been added to the compactness to give a logical order to the routes.

$$Minimize Z={\displaystyle \sum }_{v\in K}COM{P}_v+\gamma \left[{\displaystyle \sum }_{v\in K}{\displaystyle \sum }_{i\in N}{\displaystyle \sum }_{j\in N} dis{t}_{ij}\ast x_{ijv}\right]$$

(3)

Subject to

$$x_{iiv}=0\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\forall i\in N,v\in K$$

(4)

$${\displaystyle \sum }_{v\in K}{\displaystyle \sum }_{i\in N}{x}_{ijv}\le 1\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\forall j\in N$$

(5)

$${{\displaystyle \sum }}_{v\in K}{{\displaystyle \sum }}_{j\in N}{x}_{ijv}\le 1\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\forall i\in N$$

(6)

$${{\displaystyle \sum }}_{j\in N}{x}_{1jv}=1\hspace{1em}\hspace{1em}\hspace{1em}\forall v\in K$$

(7)

$${{\displaystyle \sum }}_{i\in N}{x}_{i1v}=1\hspace{1em}\hspace{1em}\hspace{1em}\forall v\in K$$

(8)

$${{\displaystyle \sum }}_{i\in N}{x}_{ijv}={{\displaystyle \sum }}_{i\in N}{x}_{jiv}\hspace{1em}\hspace{1em}\hspace{1em}\forall v\in K,\forall j\in N$$

(9)

$${\displaystyle \sum }_{v\in K}{\displaystyle \sum }_{i\in N}{\displaystyle \sum }_{j\in N}{x}_{jiv}=N+n-1$$

(10)

$${{\displaystyle \sum }}_{i,j\in N} d_j{x}_{ijv}\le Q\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\forall v\in K$$

(11)

$${\displaystyle \sum }_{i\in N}{\displaystyle \sum }_{j\in N}{\displaystyle \sum }_{v\in K}{d}_j{x}_{ijv}={\displaystyle \sum }_{j\in N}{d}_j$$

(12)

$$u_{iv}+d_j \le u_{jv}+Q\ast \left(1-x_{ijv}\right)\hspace{1em}\hspace{1em}\hspace{1em}\forall i,j\in N, v\in K, i,j\ne 1$$

(13)

$$u_{iv}\le Q\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\forall i\in N, v\in K, i\ne 1$$

(14)

$$C{G}_{v1}{\displaystyle \sum }_{i,j\in N}{x}_{ijv}={\displaystyle \sum }_{i,j\in N}Coor{d}_{ix}{x}_{ijv}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\forall v\in K$$

(15)

$$C{G}_{v2}{{\displaystyle \sum }}_{i,j\in N}{x}_{ijv}={{\displaystyle \sum }}_{i,j\in N}Coor{d}_{iy}{x}_{ijv}\hspace{1em}\hspace{1em}\hspace{1em}\forall v\in K$$

(16)

$$COM{P}_v{{\displaystyle \sum }}_{i,j\in N}{x}_{ijv}={{\displaystyle \sum }}_{i,j\in N}(dist{x}_{iv}{x}_{ijv}+dist{y}_{iv}{x}_{ijv})\hspace{1em}\hspace{1em}\hspace{1em}\forall v\in K$$

(17)

$${(Coor{d}_{i1}-C{G}_{v1})}^2=dist{x}_{iv\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}}\forall v\in K, \forall i\in N$$

(18)

$${(Coor{d}_{i2}-C{G}_{v2})}^2=dist{y}_{iv}\hspace{1em}\hspace{1em}\hspace{1em}\forall v\in K, \forall i\in N$$

(19)

$$x_{ijv}\in \left\{0,1\right\}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\forall \left(i,j\right)\in N$$

(20)

$$COM{P}_v\ge 0\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\forall v\in K$$

(21)

$$dist{x}_{iv}, dist{y}_{iv}\ge 0\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\forall v\in K, \forall i\in N$$

(22)

Equation (4) guarantees the continuity of the routes avoiding edges leaving and arriving at the same location. Equations (5) and (6) ensure that each customer is visited only once. Constraints (7) and (8) establish that exactly one vehicle must leave and arrive at the depot for each route. Equation (9) establishes that the number of arrivals at a node is precisely equal to the number of departures from it. At the same time, Equation (10) ensures that the number of edges is based on the set of customers, the vehicles, and the initial conditions.

Equation (11) defines that the fulfilled demand by each vehicle does not exceed its capacity. Equation (12) improves the model’s performance by equating the total demand with the requested demand. Equations (13) and (14) are related to the sub-tour elimination constraints. Constraints (15)–(17) calculate the center of gravity and compactness of the route. In particular, Equations (15) and (16) calculate the x and y coordinates of the gravity centers of the routes. On the other hand, (17) calculates the squared Euclidean distance between each visited node and its respective gravity center, making the value zero if the node is not visited for the given route. Note that this value is divided by the total sum of the number of nodes, obtaining a comparable compactness value. The sum of the route compactness is minimized in the objective function (3).

Equations (18) and (19) calculate the squared differences between the x and y coordinates of the nodes and their corresponding gravity center. Note that constraints (15)–(19) are quadratic, making the model nonlinear. Likewise, compactness does not operate directly with the Euclidean distance but rather with its square, which does not affect the relationship of distances between nodes. Finally, Equations (20)–(22) establish the variables’ nature and non-negativity.

3.4. Model with Minimum Distance and Workloading Balance Constraints

The second model considers the minimization of distance with the balance of workloads. The objective function is the following:

$$Minimize Z={\displaystyle \sum }_{v\in K}{\displaystyle \sum }_{i\in N}{\displaystyle \sum }_{j\in N} dis{t}_{ij} x_{ijv}$$

(23)

Equation (23) modifies the original objective function (3) to one of minimum distance.

Subject to constraints (4)–(16) and (18), (19) of the model minimize compactness with the distance factor (model 1). Additionally, the following constraints have been considered:

$${{\displaystyle \sum }}_{i,j\in N}(dis{t}_{ij}{x}_{ijv}c{t}_{1}Vel)+\left(c{t}_{2}t{d}_j{x}_{ijv}\right)=C{T}_v\hspace{1em}\forall v\in K$$

(24)

$$mCT=\frac{{{\displaystyle \sum }}_{v\in n}C{T}_v }{n}$$

(25)

$$C{T}_v\le \left(1+desv\right)mCT\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\forall v\in K$$

(26)

$$C{T}_v\ge \left(1-desv\right)mCT\hspace{1em}\hspace{1em}\hspace{1em}\forall v\in K$$

(27)

$$x_{ijv}\in \left\{0,1\right\}\hspace{1em}\hspace{1em}\forall \left(i,j\right)\in N$$

(28)

$$C{T}_v, mCT\ge 0\hspace{1em}\hspace{1em}\hspace{1em}\forall v\in K$$

(29)

Equations (24)–(27) incorporate the workload balance. The vector $C{T}_v$ equivalent to the workload for each route $v$ is calculated by (24). The workload cost is calculated as the driving time ($dis{t}_{ij}Vel$) and the waiting time ($t{d}_i$), multiplied by their respective costs $c{t}_i$. The average workload is obtained by (25). This value is used in (26) and (27) to limit the load on a percentage of the same average. Constraints (28) and (29) determine the nature of the variables.

3.5. Model with Classical Minimum Distance

The proposed mathematical model is the classical distance (23) and subject to constraints (4)–(16), (18), (19), and (28), (29).

4. Instances and Computational Results

The proposed methodology was solved using an Intel Core i5 3.1 GHz computer with 8 GB of RAM. The models were programmed in AMPL, and the CPLEX 12.4 solver was used. According to [35], it is recommended to carry out tests with variations in the depot location, customers’ location, and demand to reflect the effect of the initial data on the VRP approaches. In this way, different instances have been generated to test the efficiency of the proposed models.

4.1. Relationship between Route Balancing, Compactness, Workload, and Instance Generation

There is a relationship between route compactness and balancing, as well as between workload and balancing. However, the degree of influence of these factors could be determined by the initial data with which each model works, even canceling out the positive effect of compactness and workload balance—Figure 3 and Figure 4 show compactness and workload balancing with different instances, respectively.

In Figure 3, compact routes around their respective centroid are obtained. However, the right-side routes are more balanced than the left-side routes due to the difference in location and number of customers. In Figure 4, homogeneous demands, travel, and unload times have been considered. As can be seen, the first case consists of a central depot with customers on both sides, generating similar routes in terms of the number of nodes and distances. In the second case, the depot is located at one corner, causing the left-side route to be a shorter and more significant number of customers than the right-side route. Mathematically, if the distance traveled and the number of visited customers is considered, the workload can be balanced between both routes (Figure 4). However, for the driver, the routes are unbalanced due to visual attractiveness.

Instances have been generated to evaluate and compare the performance of the three models, mainly involving variations in the initial parameters. Comparisons of minimum distance concerning work balance and minimum compactness and comparisons of workload balance concerning minimum compactness have been performed.

We have used the following notation to explain and analyze the obtained results:

• Final objective function value ($z_{val}$).
• Difference between the optimal value of Z on the linear relaxation and the real value of Z ($z_{gap}$).
• Objective function value of Z on the linear relaxation ($z_{bou}$).
• Computing time of the model ($t_{cpu}$).
• Standard deviation of the compactness (considers the dispersion of the customers between routes) (${\sigma }_{comp}$).
• Dispersion graphs reflecting the figures of the performed routes. Observation allows evaluation of the traveled distance, the number of customers, and the degree of overlap of the routes (visual attractiveness).

We have generated three sets of instances for testing all the proposed models. The first set is a preliminary set seeking to avoid “data” which could fit into the models. This set of instances allows predicting the possible performance of the proposed approaches for given parameters. Then, two sets of instances with a different number of customers, vehicles, and vehicle capacities are generated to test the possible performance of the proposed approaches over the customer demand, depot, and customer location.

4.2. Preliminary Instances

Tests have been performed on changing parameter values (

Table 1. Parameters of preliminary instances.

Nodes	Vehicles	Deviation	Customers Location	Demand	Depot Location
10	2	0.500	Random (1–1000)	Random (1–100)	Center
15	3	0.250	80% center/20% external zone	80% small/20% large	Corner
30	6	0.125	Clustering	For each grid
60	12

Source: Author.

) to generate instances that do not fit into the proposed models. The computing time limit for the preliminary instances has been set to one hour for each instance.

Generally, the 80% center/20% external zone location strategy positions most customers near the center and a minority in external zones, generating inappropriate solutions regarding load balance. A high concentration of customers in the central zone causes overlapping routes and unbalanced load solutions. As the number of customers and vehicles increases, this result worsens. The demand per quadrant is not particularly unfavorable for the objectives of the three proposed models. However, it generates a range of complex possibilities to cover because the value assigned to each quadrant must be considered. Then the pattern of demands must be varied for many instances.

When considering a high value of $desv$, the balanced load constraints are irrelevant, generating unbalanced solutions. However, an excessive decrease of $desv$ generates a significant increase in the minimum work on the routes. For instances with many customers per route, more restrictive $desv$ values are used, while in instances with many vehicles and few customers per route, the value of $desv$ is low and flexible. A minimal value of the $desv$ parameter generates forced traversals that are longer than they should be, which balances the work between routes but unbalances the visual factor. Figure 5 and Figure 6 compare routes with low, high, and average $desv$ values.

4.3. Comparison of Models

New instances have been generated based on the preliminary comparison, seeking adverse effects for the different models, contrasting the minimum distance concerning the minimum compactness and the workload balance. The differences in the workload are the driving time (associated with the distance traveled) and the waiting time (associated with the demand of each customer). The time limit for each instance is set to one hour, and the outputs’ evaluation was performed visually. The summary of the characteristics of the instances are shown

Table 2. Parameters of first set of instances.

Instance	N	K	Q	Demand	Customers Location	Depot Location
1	10	3	40%	Random (1–100)	Random (0–1000)	Center
2	10	3	40%	Random (1–100)	Random (0–1000)	Corner
3	10	3	40%	Random (1–100)	Clustering	Center
4	10	3	40%	Random (1–100)	Clustering	Corner
5	10	3	40%	80% (1–50) and 20% (80–100)	Random (0–1000)	Center
6	10	3	40%	80% (1–50) and 20% (80–100)	Random (0–1000)	Corner
7	10	3	40%	80% (1–50) and 20% (80–100)	Clustering	Center
8	10	3	40%	80% (1–50) and 20% (80–100)	Clustering	Corner
9	10	2	60%	Random (1–100)	Random (0–1000)	Center
10	10	2	60%	Random (1–100)	Random (0–1000)	Corner
11	10	2	60%	Random (1–100)	Clustering	Center
12	10	2	60%	Random (1–100)	Clustering	Corner
13	10	2	60%	80% (1–50) and 20% (80–100)	Random (0–1000)	Center
14	10	2	60%	80% (1–50) and 20% (80–100)	Random (0–1000)	Corner
15	10	2	60%	80% (1–50) and 20% (80–100)	Clustering	Center
16	10	2	60%	80% (1–50) and 20% (80–100)	Clustering	Corner

Source: Author.

:

For example, with clustered customer locations, the minimum distance model performs routes mixing many and few customers. In this case, compactness reduces the traveled distance on the route with the most significant number of customers and increases it on routes with few customers. Regarding the depot node, an exciting situation occurred. When the depot is located in the center, the overlap is low. However, the overlap increases when the depot is positioned in a corner. It was possible to appreciate significant balance differences between routes. The workload balance considering the cost of waiting time (associated with demand per customer) shows a negative behavior when demands of the 80/20 types are considered to generate unbalanced routes visually. This situation creates exclusive routes for high-demand customers (Figure 7). Note that larger nodes correspond to nodes with higher demand.

The second set of instances has been generated to compare the values of compactness and workload concerning minimum distance. For this case, eight instances have been generated by

Table 3. Parameters of second set of instances.

Instance	N	K	Q	Demand	Customers Location	Depot Location
17	13	3	40%	Random (1–100)	Random (0–1000)	Center
18	13	3	40%	Random (1–100)	Random (0–1000)	Corner
19	13	3	40%	Random (1–100)	Clustering	Center
20	13	3	40%	Random (1–100)	Clustering	Corner
21	13	3	40%	80% (1–50) and 20% (80–100)	Random (0–1000)	Center
22	13	3	40%	80% (1–50) and 20% (80–100)	Random (0–1000)	Corner
23	13	3	40%	80% (1–50) and 20% (80–100)	Clustering	Center
24	13	3	40%	80% (1–50) and 20% (80–100)	Clustering	Corner

Source: Author.

:

Regarding the second set of instances, it is noted that for the workload constraints related to waiting times, no tests were carried out with demands of the 80/20 types for the reasons described above. Regarding the value of Z, the optimal workload balancing solutions focused on waiting time obtained values an average of 11% higher than the minimum distance. Figure 8 and Figure 9 shows the resulting routes for two instances considering workload with waiting time and minimum distance. In these figures, it is observed that although a perfect balance was not reached, it was possible to affirm that the constraints modified the solutions by the classic model.

Table 4. Obtained results for the second set of instances.

	Minimum Distance Model				Loading Balance Model by Considering Driving Time					Loading Balance Model by Considering Waiting Time
Instance	zval	zbou	zgap(%)	tcpu(s)	zval	zbou	zgap(%)	tcpu(s)	desv	zval	zbou	zgap(%)	tcpu(s)	desv
17	4.505	4.505	0.00	12.00	4.811	4.811	0.00	34.00	0.10	4.794	4.794	0.00	32.00	0.025
18	6.754	6.754	0.00	1.95	6.832	6.832	0.00	2.18	0.05	6.858	6.858	0.00	637.00	0.025
19	3.431	3.431	0.00	88.00	3.657	3.657	0.00	210.00	0.10	4.217	4.217	0.00	250.00	0.025
20	6.100	6.100	0.00	5.00	6.412	6.412	0.00	68.00	0.10	7.384	7.384	0.00	743.00	0.025
21	3.712	3.712	0.00	15.00	4.102	4.102	0.00	179.00	0.15	-	-	-	-	-
22	6.427	6.427	0.00	440.00	6.427	6.427	0.00	170.00	0.10	-	-	-	-	-
23	4.099	4.099	0.00	276.00	4.328	4.328	0.00	636.00	0.03	-	-	-	-	-
24	6.314	6.314	0.00	283.00	6.314	6.314	0.00	129.00	0.10	-	-	-	-	-

Source. Owner.

summarizes the obtained results for the second set of instances.

The obtained results with the workload constraints presented improvements concerning the minimum distance departures with the visual attractiveness and the load balance (by considering the distance and the number of customers per route).

Table 5. Summary of the obtained results for the compactness results on the second set of instances.

Instance	zval	zbou	zgap(%)	tcpu(s)
17	208.37	48.00	99.00	3600
18	483.77	61.00	99.00	3600
19	126.67	31.00	99.00	3600
20	408.09	65.00	99.00	3600
21	127.38	38.00	99.00	3600
22	454.25	65.00	99.00	3600
23	178.35	37.00	99.00	3600
24	416.51	64.00	99.00	3600

Source: Author.

shows the obtained results by compactness.

Note that the obtained results in Table 4 and Table 5 are not comparable. The minimum compactness considers two components. The first component minimizes the dispersion of each route (using quadratic calculations), and the second minimizes the total traveled distance. Differences in the compactness model cause values of $z_{bou}$ to be much lower than values of $z_{val}$, and all gaps remained above 99%. For the same reason, all outputs finished processing within their time limit. Beyond the factors described above, the minimum compactness provided two better-balanced solutions compared to the minimum distance (Figure 10 and Figure 11), achieving a good distribution of traveled distance, the number of customers per route, and improving visual attractiveness.

4.4. Comparison of Compactness and Loading Balance

Table 6. Comparison of the proposed models with loading balance and compactness.

Model	Instances with Balanced Results
Loading Balance with Driving Time	17, 18, 19, 20, 21, 22, 23 and 24
Loading Balance with Waiting Time	17, 18, 19 and 20
Compactness	17 and 21

Source: Author.

summarizes the results of the balanced loads comparing the workload models with driving time, waiting time, and compactness. The workload balances regarding driving and waiting times coincided in instances 17, 18, 19, and 20. The results of the Z values have a difference of 0.35%, 0.37%, 15.3%, and 15.2%, respectively (Table 4 and Table 5). The differentiating factor was presented when the customer location is a cluster shape, showing higher Z values for the balance due to waiting time. Regarding the execution time of instance 18, obtaining the optimal solution per waiting time load was 3.4 times faster than the solution per driving time load (notably, instance 18 was the only deviant in terms of execution time in the eight workload solutions per driving time.)

This situation could be linked to the fact that in the model constrained by waiting time, the random distribution of the demands (without bias) represents an advantage. In contrast, for the constraints by driving time (distance), the demands without a pattern represent a difficulty. In instances 19 and 20, the driving time equilibrium has observed a better balance for the obtained solutions.

The compactness and workload solutions per driving time show balanced outputs concerning the minimum distance for instances 17 and 21. In the second set of instances, the compactness outputs reached the time limit without reaching the optimum (Table 5). At the same time, the workload achieved optimal solutions in much less time. It generated more balanced sets than the minimum compactness in terms of distance traveled and satisfying demand by the route. The workload balancing method related to waiting time only coincided with compactness in instance 17. Similar to the previous case, the workload solution was more balanced and calculated in less time than the minimum solution compactness.

Finally, tests have been conducted on large instances (number of customers). The solution time limit for the following set of instances was set to two hours (

Table 7. Parameters of the third set of instances.

Instance	N	K	Q	Demand	Customers Location	Depot Location
25	20	3	40%	Random (1–100)	Random (0–1000)	Center
27	20	3	40%	Random (1–100)	Random (0–1000)	Corner
29	20	3	40%	Random (1–100)	Clustering	Center
31	20	3	40%	Random (1–100)	Clustering	Corner
33	20	3	40%	80% (1–50) and 20% (80–100)	Random (0–1000)	Center
35	20	3	40%	80% (1–50) and 20% (80–100)	Random (0–1000)	Corner
37	20	3	40%	80% (1–50) and 20% (80–100)	Clustering	Center
39	20	3	40%	80% (1–50) and 20% (80–100)	Clustering	Corner

Source: Author.

):

The obtained results of this set have been satisfactory, presenting the same trend as the previous set of instances. The minimum distance model generates routes with fewer nodes, while the workload model generates more balanced routes in the visual aspect (see Figure 12 and Figure 13). Regarding the standard deviation of compactness, a reduction was noted in the case of workload (9% down).

4.5. Discussion Results

At the operational level, dispatchers plan the available vehicle to drivers according to their current location, leading to disproportionate routes favoring the vehicle closest to the loading node. This situation generates discontent because the routes are unbalanced, generating long routes (with many traveled kilometers and long driving times). The final result, in terms of cost, is much more unfavorable than the generated optimization of the minimum distance. Without having a precise method to assign loads, biases are usually generated where certain companies position themselves better than others, even producing internal conflicts that lead to the departure of collaborators, reducing the number of available vehicles. The two described cases are aggravated when the customers become aware of the abovementioned situations, which affects their loyalty, increases mistrust, and makes it possible for competitors to enter.

The first observation throughout the three tests has been both the minimum compactness and the workload balance due to driving and waiting times. This situation increases the computing times and obtains longer routes than the minimum distance. However, more balanced routes are obtained, as seen in the figures, showing the number of visited customers and satisfying demands per route with a reduced standard deviation of compactness. However, the workloads and the minimization of the compactness did not have the same scope.

The minimum compactness does not offer optimal solutions for small instances, discouraging the performance of tests with more data. On the other hand, the results given by the workload balance due to waiting times and driving times were not the same, making it necessary to study them separately. The high difference occurred with the “80-20” demand, generated by a small group of nodes with atypically high demand, causing worse workload results due to waiting times. Therefore, the workload due to waiting times has been limited for use only with random demand distributions.

The experiments establish a set of the initial parameters for which the workload results obtained excellent results in balance. These parameters have been obtained through different degrees of adjustment for the loading constraints, which have been initially defined arbitrarily. These constraints have been modified at each experimentation stage according to the previous results, making their predetermination difficult.

The compaction maximization and workload balance models generate more balanced routes for real cases. However, both models make the original mathematical formulation challenging to solve, given the high computing times and the objective function values concerning the minimum distance model. This aspect is decisive for compaction since, considering the results, its use in real large-scale instances is unfeasible. However, customer compaction is a concept that contributes to balance and is one of many alternatives to address the WBVRP. Quadratic functions could be reformulated linearly to improve the results.

The proposed model considering workload balancing with a simple minimum distance objective function achieves the goal of balancing routes for drivers and carriers under a given set of initial parameters. Therefore, this model is a feasible alternative for real short and long-distance routing problems, especially for service providers that outsource transportation. In the case of long-distance carriers, it is common for trips to involve deliveries to several customers. However, there are occasions when weekly or even monthly cargo programs are used, which follow the same logic of last-mile routing decisions.

5. Concluding Remarks and Future Work

This paper proposes mathematical models to solve the vehicle routing problem considering balanced loads and customer compactness. The first model seeks compactness maximization, while the second model minimizes distance with load balance. Finally, the last model considers the minimization of the total distance. Maximizing compactness and work balance between routes is achieved to a greater or lesser extent to offer balanced outputs. The workload balance increases the mentioned criteria less abruptly. The compactness model involves quadratic functions that, if reformulated linearly, would probably improve the results. It is also important to mention that although the workload model has been studied by separating driving and waiting times, both should work together. However, the model is characterized by its versatility as it allows both elements to be combined.

According to the obtained results, the model considering workload balance achieves the objective of balancing the routes for drivers and carriers under a specific set of initial parameters within the limited computing times. This situation makes this model a feasible alternative for real short and long-distance routing problems and even for service outsourcing companies. In the case of long-distance carriers, it is not usual for routes to involve deliveries to several customers; however, there are times when weekly or even monthly charging schedules are used that follow the same logic as last-mile routing.

As future works, we propose the use of heuristic strategies based on granular search and genetic algorithms for the solution of the problem considered extensions of works proposed by [1,36,37,38,39,40,41]. In the same way, several objectives through multi-objective optimization methodologies should be considered.