Environmentally Friendly Concrete Compressive Strength Prediction Using Hybrid Machine Learning

Abstract

In order to reduce the adverse effects of concrete on the environment, options for eco-friendly and green concretes are required. For example, geopolymers can be an economically and environmentally sustainable alternative to portland cement. This is accomplished through the utilization of alumina-silicate waste materials as a cementitious binder. These geopolymers are synthesized by activating alumina-silicate minerals with alkali. This paper employs a three-step machine learning (ML) approach in order to estimate the compressive strength of geopolymer concrete. The ML methods include CatBoost regressors, extra trees regressors, and gradient boosting regressors. In addition to the 84 experiments in the literature, 63 geopolymer concretes were constructed and tested. Using Python language programming, machine learning models were built from 147 green concrete samples and four variables. Three of these models were combined using a blending technique. Model performance was evaluated using several metric indices. Both the individual and the hybrid models can predict the compressive strength of geopolymer concrete with high accuracy. However, the hybrid model is claimed to be able to improve the prediction accuracy by 13%.

1. Introduction

Nowadays, artificial intelligence methods are widely used in estimating concrete properties [1,2,3,4,5,6,7,8,9,10]. The demand for cement has significantly increased over the past few decades as a result of building new infrastructure and supporting global population growth. By 2050, the projected increase will reach 23%, posing numerous economic and environmental issues. [11,12].

An alkali-activated alumina-silicate mineral produces geopolymers, which are inorganic polymers [13]. Using alumina-silicate waste materials as a cementitious binder, geopolymer is an environmentally friendly and economic alternative to traditional ordinary portland cement (OPC). Fly ash-slag geopolymer mortar develops strength based on the chemical composition of the raw materials. The evaluation of molar ratios represents a good method for studying chemical components in geopolymers [14].

Thermal coal plants produce fly ash (FA), which is the unburned residual residue that is carried by gases released by the boiler’s burning zone [15]. Electrostatic separators or mechanical separators collect FA [16]. Each year, more than 375 million tons of FA are produced throughout the world, whose disposal costs range from $20 to $40 per ton [17]. There are several landfills in suburban areas where this waste is disposed of [18]. The environment is adversely affected by dumping tons of FA without any treatment [19]. Water, soil, and air pollution are caused by hazardous substances contained in FA. These include silica, alumina, and oxides such as ferric oxide (Fe₂O₃). Consequently, human health and the environment are also adversely affected [20]. A safe and sustainable environment requires good waste management employment [21]. The whole ecological cycle will be affected if FA is not properly disposed of.

The most commonly consumed material after water is concrete, which is used as a construction material worldwide [22,23]. Approximately three tons of concrete are produced for every human being [24]. The global production of concrete is estimated to be around 25 billion tons per year [25]. Cement is produced in excess of 2 billion tons annually around the world according to current statistics. In the next decade, this is expected to rise by 25 percent [26]. Cement manufacturing, however, has adverse environmental effects. Gene expression programming (GEP) has been used by a number of researchers in recent years to estimate various mechanical properties of concrete. Experimental and literature-based data are used to predict the compressive strength of sugar cane bagasse ash concrete (SCBA) [27]. In addition, these authors suggested a formula based on GEP to estimate concrete-filled steel tube (CFST) axial capacity based on just 277 examples. The GEP algorithms have also been used by Nour et al. [28] To determine the compressive strength of CFST which contains recycled aggregate.

Construction materials such as portland cement (PC) are commonly used throughout the world [29]. Despite its many benefits, PC production emits approximately 7% of the overall carbon dioxide emitted by humans [30]. It has been estimated that approximately 50% of the GHG emissions associated with cement production are caused by calcination (the process of forming CaO by converting CO₂ from CaCO₃), and the remaining 50% are caused by the energy used during the process [31]. Each year, the building industry produces approximately four billion tons of PC [32]. The estimated annual usage of PC within the next four decades is around 6 billion tons [33]. In response, it has become essential to develop new binders that use less energy to produce and result in fewer greenhouse gas emissions [34].

Researchers have been investigating the role of artificial intelligence (AI) and machine learning (ML) methods in the development of models that are reliable, accurate, and consistent for solving structural engineering problems. Wu and Li [35] used a hybrid particle swarm optimization-support vector machine (PSO-SVM) model for damage degree evaluation. Fan et al. [36] used an artificial neural network (ANN) to predict carbon prices using a multi-layer perceptron model. This model proved to be more accurate and fitter than many other simpler models. A support vector regression-particle swarm optimization (SVR-PSO) hybrid model was employed by Wu and Zhou [37], in which the SVR and PSO algorithms are combined for the prediction and feature analysis of punching shear strength of two-way reinforced concrete slabs. Wu and Zhou [38] showed that a hybrid ML model was able to accurately predict the splitting tensile strength prediction of sustainable high-performance concrete. Using 681 data records, Han et al. [39] employed three ML models to predict the compressive strength of high-strength concrete. Wu and Zhou [40] applied a hybrid ML model that combines the SVR model and grid search (GS) optimization algorithm to predict the compressive strength of sustainable concrete.

A least squares SVM (LSSVM) model was applied by Zhu et al. [41] in order to forecast energy prices due to its nonstationarity and nonlinearity, and its performance was superior to that of autoregressive integrated moving average (ARIMA) and ANN models. A hybrid model combining ANN and SVM, developed by Patel et al. [42], had the best overall prediction performance. Moreover, Dou et al. [43] pointed out that the long short-term memory (LSTM) model has advantages over the SVM method in prediction. A hybrid model that incorporates both a statistic and an AI model can also provide relatively better performance.

2. Dataset

This paper uses a set of 84 data points (shown in

Table A1. Dataset [40,41].

Reference	FA (%)	SF (%)	MK (%)	Bacillus Bacteria (mL/L)	f’c (MPa)
	30	0	0	0	44.87
	30	0	0	12.5	48.39
	30	0	0	25	49.44
	30	0	0	37.5	50.46
	30	0	0	50	51.48
	30	0	0	62.5	53.71
	30	0	0	75	54.82
	30	0	0	87.5	54.96
	30	0	0	100	55.1
	30	0	0	112.5	54.91
	30	0	0	125	54.73
	30	0	0	12.5	48.91
	30	0	0	23	50.65
	30	0	0	37.5	51.99
	30	0	0	50	53.42
	30	0	0	62.5	56.19
	30	0	0	75	57.06
	30	0	0	87.5	57.2
	30	0	0	100	57.33
	30	0	0	112.5	57.27
	30	0	0	125	57.13
	15	10	5	0	74.02
	15	10	5	12.5	80.07
	15	10	5	25	82.46
	15	10	5	37.5	83.53
	15	10	5	50	84.6
	15	10	5	62.5	88.43
	15	10	5	75	89.7
	15	10	5	87.5	90.26
	15	10	5	100	90.82
	15	10	5	112.5	90.61
	15	10	5	125	90.09
	15	10	5	12.5	80.11
	15	10	5	25	83.57
	15	10	5	37.5	85.12
	15	10	5	50	88.45
	15	10	5	62.5	91.39
	15	10	5	75	92.23
	15	10	5	87.5	93.97
	15	10	5	100	94.67
	15	10	5	112.5	93.48
	15	10	5	125	92.97
	17	5	8	0	74.07
	17	5	8	12.5	81.19
	17	5	8	25	83.01
	17	5	8	37.5	83.97
	17	5	8	50	85.31
	17	5	8	62.5	86.83
	17	5	8	75	90.51
	17	5	8	87.5	90.73
	17	5	8	100	90.95
	17	5	8	112.5	90.86
	17	5	8	125	90.44
	17	5	8	12.5	80.37
	17	5	8	25	83.76
	17	5	8	37.5	85.39
	17	5	8	50	88.27
	17	5	8	62.5	91.17
	17	5	8	75	92.05
	17	5	8	87.5	93.07
	17	5	8	100	94.89
	17	5	8	112.5	93.11
	17	5	8	125	92.63
	12	10	8	0	77.97
12	10	8	12.5	84.37
12	10	8	25	87.4
12	10	8	37.5	88.62
12	10	8	50	89.83
12	10	8	62.5	93.09
12	10	8	75	94.45
12	10	8	87.5	95.26
12	10	8	100	96.06
12	10	8	112.5	95.79
12	10	8	125	94.97
12	10	8	12.5	85.07
12	10	8	25	88.24
12	10	8	37.5	89.99
12	10	8	50	93.74
12	10	8	62.5	97.53
12	10	8	75	98.09
12	10	8	87.5	99.59
12	10	8	100	99.87
12	10	8	112.5	99.47
12	10	8	125	99.03
Authors	20	5	0	79.5	59.06
	20	5	0	39.3	61.32
	20	5	0	45.3	62.11
	20	5	0	79.7	57.59
	20	5	0	52.5	59.17
	20	5	0	37.8	61.88
	20	5	0	84.1	63.8
	20	5	0	64.3	63.12
	20	5	0	93.7	59.39
	20	5	0	59.7	64.71
	20	5	0	43.1	62.33
	20	5	0	132.5	59.96
	20	5	0	80.9	63.01
	20	5	0	83.6	55.21
	20	5	0	37.7	61.77
	20	5	0	63.3	62.45
	20	5	0	59.1	61.32
	20	5	0	56.3	64.93
	20	5	0	95.5	62.22
	20	5	0	70.4	59.85
	20	5	0	91	59.39
	20	10	5	29	97.97
	20	10	5	92.3	98.99
	20	10	5	46.4	99.89
	20	10	5	99.8	92.44
	20	10	5	67.3	102.61
	20	10	5	58.1	96.96
	20	10	5	34.4	97.52
	20	10	5	48.8	98.76
	20	10	5	64.2	97.41
	20	10	5	61.2	97.75
	20	10	5	95.9	96.16
	20	10	5	77.9	95.83
	20	10	5	86.7	98.09
	20	10	5	59.9	94.92
	20	10	5	45.3	99.1
	20	10	5	71.5	99.1
	20	10	5	104.5	101.02
	20	10	5	85.4	100.12
	20	10	5	69.3	101.25
	20	10	5	63.9	97.41
	20	10	5	88	97.97
	25	5	8	42.1	101
	25	5	8	66.2	97.72
	25	5	8	49.1	96.48
	25	5	8	52.5	103.14
	25	5	8	41.5	98.85
	25	5	8	32.9	100.21
	25	5	8	73.8	99.87
	25	5	8	49.1	102.24
	25	5	8	111.2	98.74
	25	5	8	14.1	93.43
	25	5	8	30.7	102.58
	25	5	8	95.2	98.4
	25	5	8	51.2	99.64
	25	5	8	58.5	97.95
	25	5	8	46	104.84
	25	5	8	71.5	99.41
	25	5	8	80.5	101.79
	25	5	8	59.5	98.62
	25	5	8	16.5	100.77
	25	5	8	44.9	97.15
	25	5	8	58.3	98.74

) available in the literature as well as 63 samples of green concrete that have been designed and prepared by the authors and tested [44,45]. A detailed investigation was conducted to develop a geopolymer concrete mix design method based on fly ash. The following parameters were chosen based on considerations of workability and compressive strength.

A geopolymer’s activation process is highly dependent on the amount and fineness of fly ash (FA). In previous studies, it has been shown that geopolymer concrete strength increases with increasing fly ash quantity and fineness [46,47]. With an early duration of heating, finer particles show higher workability and strength. For this reason, the proportioning procedure for geopolymer concrete is developed based on the quantities and fineness of fly ash. In the production of silicon and ferrosilicon alloys, quartz is reduced with coal to form a by-product known as silicon fume (SF) [48]. Silica fume is an extremely effective pozzolanic material as a result of its fineness and silica content. Several properties of concrete are improved by silica fumes, such as compressive strength, bond strength, abrasion resistance, and permeability. By reducing their permeability, silica fumes can also prevent the reinforcing steel from corroding [49]. The ureolytic bacillus species produce calcite to reduce concrete pores in order to increase strength and durability [50].

3. Machine Learning

By being specifically programmed, ML systems learn and improve independently. To provide systems with the ability to gather data and use that data to learn more, ML algorithms are designed to learn from observations. Data collected by systems are used by those systems to make vital decisions based on patterns that they find in the data. An ML algorithm’s most important step is training. ML models make predictions and find patterns from the prepared data during training. Thus, a model can accomplish the task set by learning from data. The model improves over time as it is trained. Training datasets were selected randomly for 80% of the paper and testing datasets were selected randomly for 20% of it. Figure 1 shows the research methodology. The purpose of this section is to provide a brief introduction to the theory behind the three ML algorithms used in this study. These algorithms were written in Python language and included a CatBoost regressor, extra trees regressor, and gradient boosting regressor. In this paper, the grid search method was used to perform hyperparameter tuning for ML models, which presents a list of values for each hyperparameter and evaluates the model for every combination of the values in this list.

3.1. CatBoost Regressor

CatBoost is a new type of gradient enhancement technology [51], which is a powerful ML technique. A number of fields have applied it due to its good performance, such as short-term weather forecasts [52], Kickstarter campaign predictions [53], driving style recognition [54], and diabetes prediction [55]. Additionally, CatBoost is increasingly used to estimate crop evapotranspiration.

In CatBoost, the model overfitting is dealt with by Bayesian estimators, which handle categorical and ordered features of the decision trees. CatBoost ranks the developed model’s features based on prediction values change (PVC) or loss function change (LFC). In PVC, a change in a feature value is calculated along with a change in prediction. ML models based on CatBoost use PVC as the default method. Models are generally ranked according to LFC using a range of models.

F = {f₁, f₂, f₃,……….. f_n}

(1)

P_i = β_i Fj

(2)

It is a set of input features called F, a numeric factor called β_i and a prediction step called P. In F = {f₁, f₂, f₃,……….. f_n} Equation (1) [56], the input features are given to the ML model. In P_i = β_i Fj Equation (2). Feature F_j represents a specific feature from the given feature set, P_i represents the prediction value, β_i represents the numeric factor, and P_i represents the substituted numeric factor.

P_i+1 = β_i+1 F_j

(3)

P_i=0 ≠ P_i ≠ P_i+1

(4)

P_i+1 = β_i+1 F_j Equation (3), where P_i+1 indicates the prediction value upon changing the numeric factor, and β_i+1 indicates the modified numeric factor. This particular feature becomes necessary when there is a change in the numeric factor that changes the prediction value, as shown in P_i=0 ≠ P_i ≠ P_i+1 Equation (4).

3.2. Extra Trees Regressor

Geurts et al. [57] presented an approach called extra tree regression (ETR) which evolved from the random forest (RF) model. Extra tree regression (ETR) constructs unpruned decision trees or regression trees during the process of applying the conventional top-down method [58].

Bootstrapping and bagging are utilized by the random forest (RF) model to perform regression. Each decision tree is grown using a random training dataset sample as part of the bootstrapping step. Once the ensemble has been achieved, the bagging step is used to divide the nodes in the decision tree. During this step, a number of random subsets of training data are selected. The best subset and its value are selected during the decision-making process [59].

As Breiman [60] described it, the RF model is a series of decision trees, wherein the predicting tree is the tree of results and the predicting vector is the uniform independent distribution vector that is assigned before the tree is expanded. In order to construct a forest using the Breiman equation, all trees are combined and averaged:

$$G\left(x,{\theta }_1,\dots ,{\theta }_r\right)=\frac{1}{R}{\displaystyle \sum _{r=1}^{R}G\left(x,{\theta }_r\right)}$$

(5)

ETRs and RF systems differ in two important ways. Firstly, the ETR selects random points from the cutting points and divides the nodes accordingly. Additionally, it minimizes bias by cultivating the trees based on the entire learning sample [57]. Two parameters govern the split process in the ETR approach: k and n_min, where k is the number of features sampled randomly in each node, and n_min is the minimum number of features to separate each node. Further, k and n_min are used to determine the strength of the selection of attributes and the strength of the average output noise. Using these parameters improves the model’s precision and reduces overfitting [61,62]. ETR structure is shown in Figure 2.

3.3. Gradient Boosting Regressor

As an ensemble technique for regression and classification, gradient boosting, was introduced by Friedman in 1999 [63]. Different boosting, such as gradient boosting, can be used for a variety of applications, but it is only effective when used for regression. It is shown in Figure 3 that every iteration of the randomly selected training set is checked against the base model in gradient boosting. It can be improved by subsampling the training data randomly, which prevents overfitting. By subsampling the training data randomly, gradient boosting performance can be improved. By fitting smaller data at each iteration, the regression model runs faster with a smaller fraction of training data. Gradient boosting regression requires tuning parameters: number of trees and shrinkage rate, where the number of trees refers to the number of trees to be grown. It is important to make sure that the number of trees is not set too low and that the shrinkage parameter, sometimes referred to as the learning rate, is applied to each tree in the expansion.

3.4. Hybrid Model

An ensemble ML technique called blending combines the predictions produced by multiple ensemble members by using an ML model. Thus, blending is also known as stacking, which is a framework for stacked generalizations. A stacking model uses two or more baseline models, termed level-0 models, combined with a meta-model, termed level-1 models, that combines the predictions from the bases. Data from the sample are used to train the meta-model.

3.5. Cross-Validation Using K Fold

ML models are evaluated using cross-validation by resampling them based on a restricted sample of data. A single parameter called k determines how many groups are to be split up from a given data sample. It is therefore sometimes referred to as k-fold cross-validation. It is possible to use a specific value for k to replace k in the model’s reference, e.g., k = 20 becomes 20-fold cross-validation. As an ML technique applying unseen data to a model, cross-validation is primarily used to estimate its skill. The model is used to make predictions based on data unused during training. This is carried out in order to estimate its performance in general when predicted based on new data. Due to its simplicity, it is a popular method since it generally leads to less biased or optimistic estimates of the model skill than other methods, such as simple trains and tests. It is important to note that each observation in the data sample is assigned to a particular group and remains within that group during the analysis. Each sample is used once in the hold-out set, once in the training set, and once in the hold-out set.

3.6. Feature Scaling

Scaling feature values is an important step before creating an ML model, as this is one of the most important techniques in ML. The goal of feature scaling is to use a common scale to change the values of columns. In one column, you can have values ranging from 0 to 1, and in another column, you can have values ranging from 1000 to 10,000. Trying to combine the values as features during modeling may be difficult due to the vast differences in scale. A weak ML model can be distinguished from a strong one by this factor. Scaling can be carried out in three ways: standardizing, normalizing, and scaling. In this paper, values in the dataset were scaled to change from 0 to 1.

4. Experiment and Results

In order to describe how well an ML model performs in making predictions, its accuracy must be evaluated. Several metrics are commonly used to evaluate the performance of regression models, including MSE, MAE, RMSE [65,66], and R².

• An average of the absolute difference over the data set represents the mean absolute error (MAE) between the original and predicted values.

$$MAE=\frac{1}{N}{\displaystyle \sum _{i=1}^N\left|y_i-\widehat{y}\right|}$$

(6)

• By taking the average difference over the data set and squaring it, MSE (mean squared error) is calculated.

$$MSE=\frac{1}{N}{{\displaystyle \sum _{i=1}^N\left(y_i-\widehat{y}\right)}}^2$$

(7)

• RMSE (root mean squared error) is the error rate by the square root of MSE.

$$RMSE=\sqrt{MSE}=\sqrt{\frac{1}{N}{{\displaystyle \sum _{i=1}^N\left(y_i-\widehat{y}\right)}}^2}$$

(8)

• The coefficient of determination (R²) [67] represents the degree to which the values fit the originals. Percentages ranging from 0 to 1. Models with higher values are better.

$$R^2=1-\frac{{{\displaystyle \sum _{}^{}\left(y_i-\widehat{y}\right)}}^2}{{{\displaystyle \sum _{}^{}\left(y_i-\overline{y}\right)}}^2}$$

(9)

where,

$$\begin{array}{l}\widehat{y}-\mathrm{predicted} \mathrm{value} \mathrm{of} \mathrm{y}\\ \overline{y}-\mathrm{mean} \mathrm{value} \mathrm{of} \mathrm{y}\end{array}$$

• As with standard MSE, RMSLE [66,68] measures exponents rather than values themselves.

$$RMSLE=\sqrt{\frac{1}{n}{\displaystyle \sum _{i=1}^n{\left(\log \left({\widehat{y}}_i+1\right)-\log \left(y_i+1\right)\right)}^2}}$$

(10)

• MAPE (mean absolute percentage error)

$$MAPE=\frac{1}{n}{\displaystyle \sum _{i=1}^n\frac{\left|y_i-{\widehat{y}}_i\right|}{\left|y_i\right|}}*100$$

(11)

The accuracy of the model is a combination of R and these error indexes that defines. Some disciplines, such as economy and health informatics, have thresholds for the MAE, MSE, etc values (e.g. blood pressure min level). However, there is no general rule for the ranges of MAE, MSE, etc. [69,70,71]. In general, the lower the better. R² is sufficient when its value reaches one. Higher R values and lower statistical indexes such as RMSE and MAE values indicate a more precise model.

Table 1. Statistical performance of ML models.

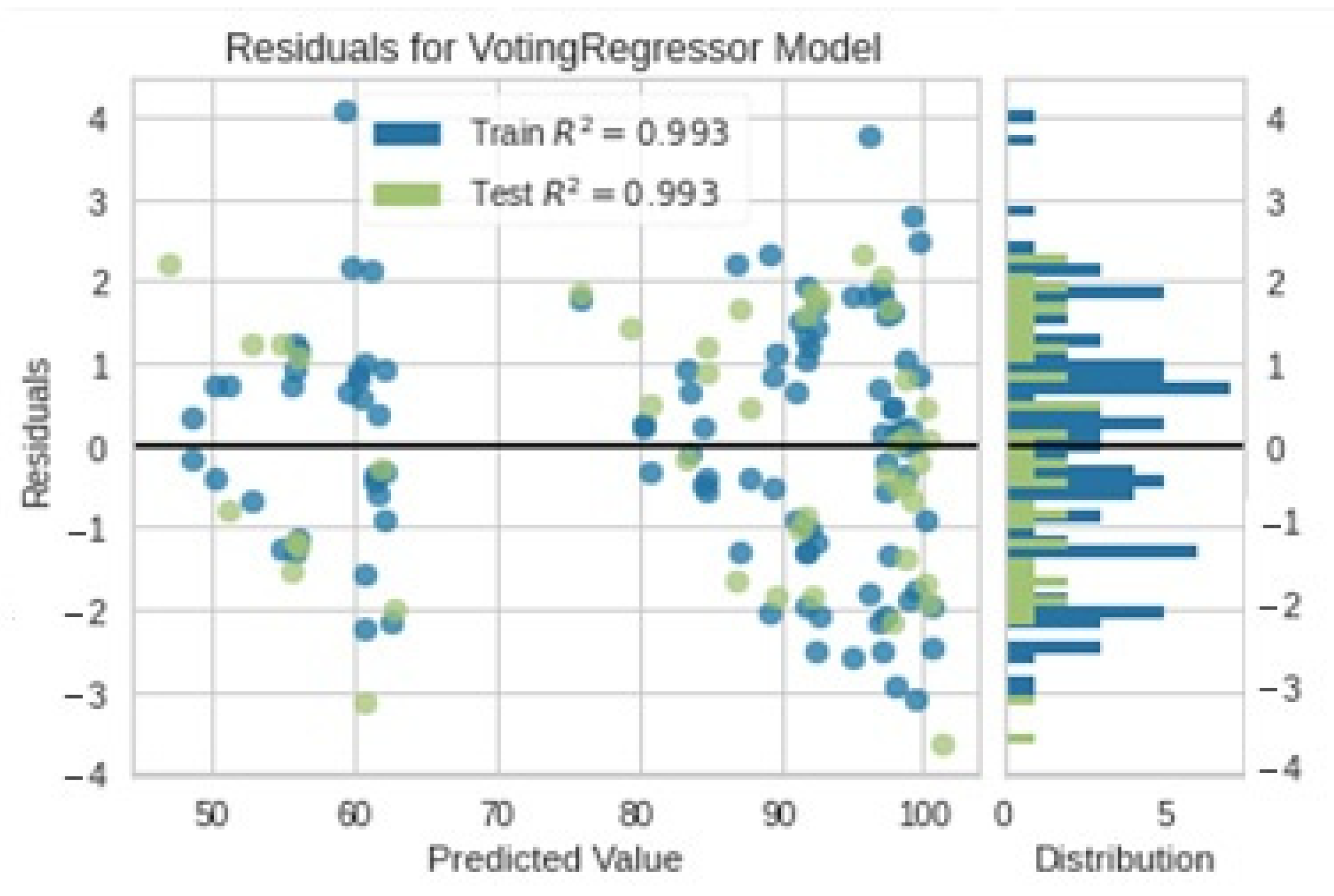
Model	MAE	MSE	RMSE	R2	RMSLE	MAPE
CatBoost Regressor	2.1116	7.2175	2.629	0.9565	0.0312	0.0254
Extra Trees Regressor	2.1126	8.1478	2.7518	0.9558	0.0333	0.0257
Gradient Boosting Regressor	2.175	7.6915	2.7279	0.9528	0.0327	0.0264

displays the error indices in each fold, sorted by RMSE value for the three ML models. According to Table 1, the CatBoost regressor performs best.

Using a higher iteration rate, the three models can be dynamically tuned to find more optimal hyperparameters. For each of the 120 iterations,

Table 2. Statistical performance of catboost regressor after 120 iterations.

Fold	MAE	MSE	RMSE	R2	RMSLE	MAPE
0	1.8879	4.6918	2.1661	0.9847	0.0282	0.0243
1	1.7773	6.0005	2.4496	0.9779	0.0312	0.0228
2	1.575	3.9003	1.9749	0.9868	0.0212	0.018
3	1.2351	2.0828	1.4432	0.994	0.0191	0.0171
4	1.3525	3.1442	1.7732	0.9906	0.0201	0.0166
5	1.9193	6.8454	2.6164	0.9648	0.0315	0.0241
6	1.5786	4.3335	2.0817	0.9847	0.0326	0.0236
7	2.802	11.0342	3.3218	0.961	0.0392	0.0332
8	2.0567	5.8858	2.4261	0.8381	0.0253	0.0217
9	2.6954	9.5568	3.0914	0.9686	0.0369	0.0313
Mean	1.888	5.7475	2.3344	0.9651	0.0285	0.0233
Std	0.4935	2.6549	0.5459	0.0436	0.0066	0.0053

,

Table 3. Statistical performance of extra trees regressor after 120 iterations.

Fold	MAE	MSE	RMSE	R2	RMSLE	MAPE
0	1.613	3.8801	1.9698	0.9874	0.0253	0.0206
1	2.7107	11.4503	3.3838	0.9578	0.0438	0.0358
2	1.3623	3.6744	1.9169	0.9876	0.0205	0.0155
3	1.7642	6.0952	2.4688	0.9824	0.032	0.0239
4	1.8849	4.8217	2.1958	0.9857	0.0284	0.0244
5	1.8805	6.0462	2.4589	0.9689	0.0282	0.023
6	1.574	4.8332	2.1984	0.9829	0.0344	0.0236
7	2.4592	7.8659	2.8046	0.9722	0.0307	0.0281
8	1.9959	5.5419	2.3541	0.8476	0.0247	0.0211
9	2.7254	9.2016	3.0334	0.9698	0.0349	0.0315
Mean	1.997	6.3411	2.4785	0.9642	0.0303	0.0248
Std	0.4542	2.3484	0.4452	0.04	0.0062	0.0055

and

Table 4. Statistical performance of gradient boosting regressor after 120 iterations.

Fold	MAE	MSE	RMSE	R2	RMSLE	MAPE
0	1.6887	4.0168	2.0042	0.9869	0.0247	0.0211
1	2.0354	6.4656	2.5428	0.9762	0.0326	0.0265
2	1.7395	5.4694	2.3387	0.9815	0.0262	0.0209
3	1.425	2.9556	1.7192	0.9915	0.0219	0.019
4	1.8397	4.6379	2.1536	0.9862	0.025	0.0224
5	1.9379	7.1815	2.6798	0.963	0.0333	0.0245
6	1.3919	5.0369	2.2443	0.9822	0.0369	0.0222
7	2.9093	16.3499	4.0435	0.9422	0.0423	0.0313
8	1.7562	5.5063	2.3466	0.8486	0.0245	0.0185
9	3.0088	10.4196	3.2279	0.9658	0.0409	0.0363
Mean	1.9733	6.804	2.5301	0.9624	0.0308	0.0243
Std	0.5285	3.719	0.6347	0.0404	0.007	0.0054

show the fitted 10 folds, resulting in 1200 fits in total. Figure 4 summarizes the results of Table 2, Table 3, Table 4 and

Table 5. Statistical performance of the hybrid ML model.

Fold	MAE	MSE	RMSE	R2	RMSLE	MAPE
0	1.6699	9.6212	2.2936	0.987	0.0234	0.0133
1	2.1309	13.8944	2.6276	0.995	0.0166	0.0175
2	1.9022	5.3901	2.0845	0.997	0.0325	0.0172
3	1.6091	7.2350	1.9028	0.993	0.0295	0.0159
4	1.8274	8.2654	1.6877	0.981	0.0312	0.0265
5	2.0111	6.3820	1.0339	0.985	0.0194	0.0270
6	1.4661	6.0591	2.9916	0.997	0.0263	0.0187
7	1.5413	7.0150	2.7520	0.952	0.0289	0.0226
8	1.8261	4.2140	2.1107	0.994	0.0264	0.0228
9	1.5823	8.6375	3.0620	0.976	0.0252	0.0149
Mean	1.7567	7.6714	2.2546	0.99	0.0259	0.0197
Std	0.2176	2.7050	0.6296	0.013818	0.0050	0.0048

.

According to Table 5, the combined model shows a 13% improvement over the individual methods if the above three methods are combined.

What follows here are the results related to the combined model. A hybrid model’s residuals are shown in Figure 5, A training dataset is represented by blue points and a testing dataset by green points. The R² of the hybrid model equals 0.99 as shown in Figure 6.

When performing a least-squares regression analysis, the Cook’s distance is commonly used as an estimate of the impact of a data point [72]. A Cook’s distance is an estimate of a data point’s influence. Outliers can be removed from a dataset using a variety of techniques. When analyzing regression data, the Cook’s distance is often used. Leverage and residual are taken into account for each observation. When you remove the i^th observation from a regression model, Cook’s distance suggests how much the model changes. Cook’s distance is a measure of how strongly the fitted values are influenced by a data point. Any data point with a Cook’s distance exceeding 4/n (where n is the total number of data points) is considered an outlier by default. For the hybrid model, Figure 7 shows the Cook’s distance.

An optimal loss function is plotted against a validation data set with the same parameter set used in the training data set to produce a learning curve in ML. This tool determines whether the estimator suffers more from variance or bias errors when adding more training data to a machine model. As the training set grows, it will not benefit much from more training data if both the validation and training scores are too low [73]. For the hybrid model, Figure 8 shows the learning curve.

The low-dimensional spaces reflect the parameters while the high-dimensional spaces are the features. Manifold learning is the process of uncovering these manifold structures in data sets. Dimensionality reduction is achieved through the use of manifold learning, which is a nonlinear method. High-dimensional data can be visualized using t-SNE [1]. In order to minimize the Kullback-Leibler divergence between the joint probabilities of the low-dimensional embedding and the high-dimensional data, the similarity between data points is converted into joint probabilities. Due to the non-convex nature of t-SNE’s cost function, different results can be obtained with different initializations [73]. Data with high dimensions are excluded from this study, as indicated in Figure 9.

In this section, by using three ML methods and combining them together, an estimation model with high accuracy was presented to predict the strength of green concrete. The strength of this study is the high accuracy of the model, but its weakness is that an engineer must be familiar with programming and ML algorithms to estimate concrete strength. In future works, using methods that are based on providing a formulation, a relationship can be presented so that the user can easily use it to obtain the resistance of green concrete.

5. Conclusions

A green concrete’s compressive strength was predicted using three ML methods. The CatBoost regressor, the extra trees regressor, and the gradient boosting regressor were evaluated using 147 samples. All of the models produced high accuracy predictions of the compressive strength of the geopolymer concrete. The models were evaluated using several statistical indices. A limited data sample was used for cross-validating ML models. Data samples were split into groups according to the single parameter “k”, hence the name “k-fold cross-validation”. Accordingly, a value of k = 10 has been chosen in this paper, implying that the model has 10-fold cross-validation. CatBoost regressor, extra trees regressor, and gradient boosting regressor models have an average RMSE of 2.63, 2.75, and 2.73. All three models were combined with blending, which is a method of ensemble ML. The hybrid model has a 13% greater accuracy in all statistical indices than the individual models. Additionally, the hybrid model could predict the compressive strength of green concrete based on other statistical concepts such as cook’s distance, learning curves, and manifold learning.