Optimal Operational Planning of RES and HESS in Smart Grids Considering Demand Response and DSTATCOM Functionality of the Interfacing Inverters
Abstract
:1. Introduction
2. Problem Formulation
2.1. Objective Function
2.2. Constraints
2.2.1. Distribution System Constraints
2.2.2. RES Constraints
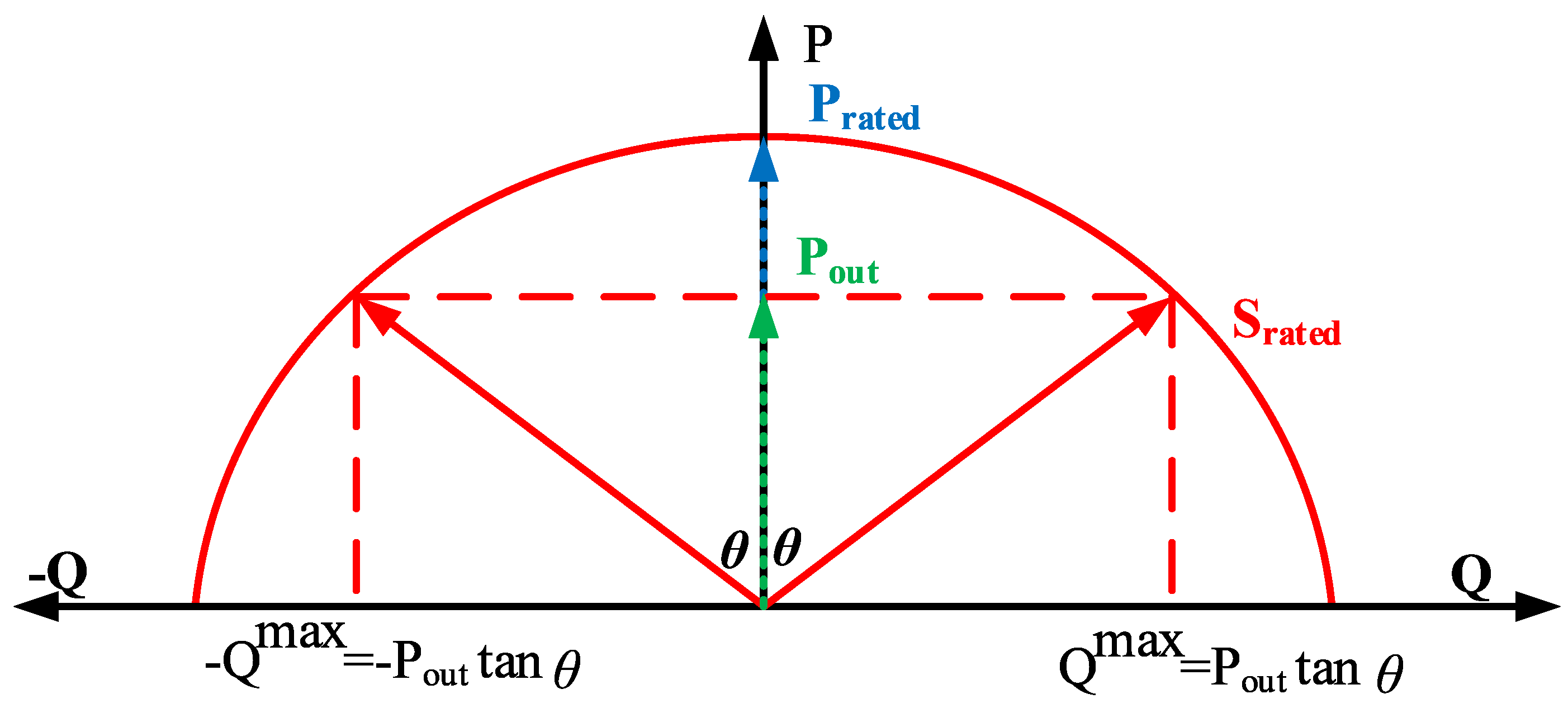
2.2.3. Constraints of RES Interfacing Inverters
2.2.4. ESS Constraints
2.2.5. Constraints of the DR Program
3. Uncertainty Modeling of RES and Load Demand
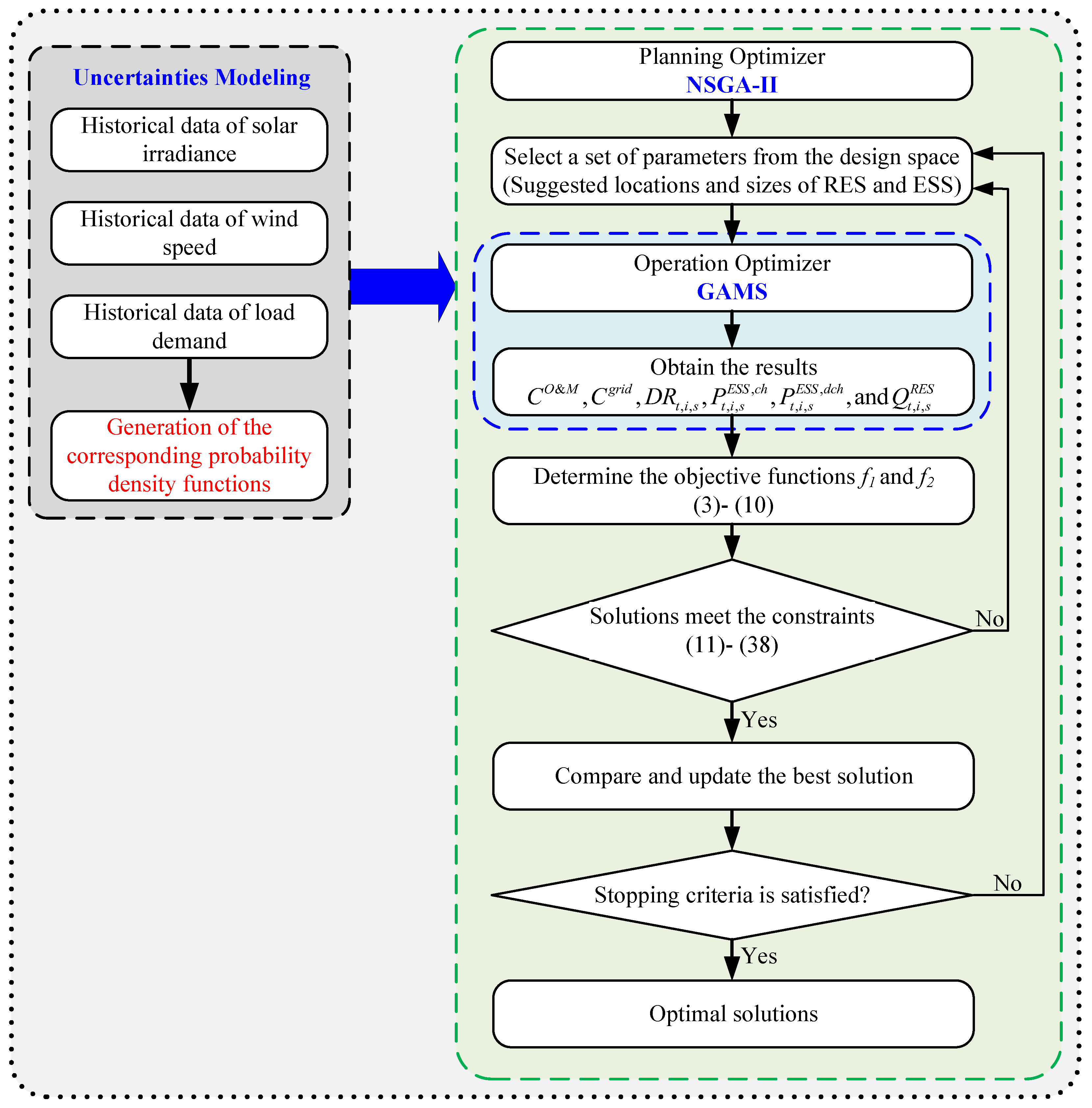
4. Nested Optimization of RES and HESS
- Take the suggested locations and sizes as the input of the inner optimizer from the design space of the NSGA-II;
- GAMS optimizer is employed to evaluate the optimal charging/discharging power of the ESS, optimal reactive power of the RES interfacing inverters, and the DR factor to minimize the cost of the imported energy from the upstream grid and O&M costs of RES and ESS;
- Repeat steps (1)–(4) until the stopping criteria are satisfied. Then, store the optimal obtained solutions.
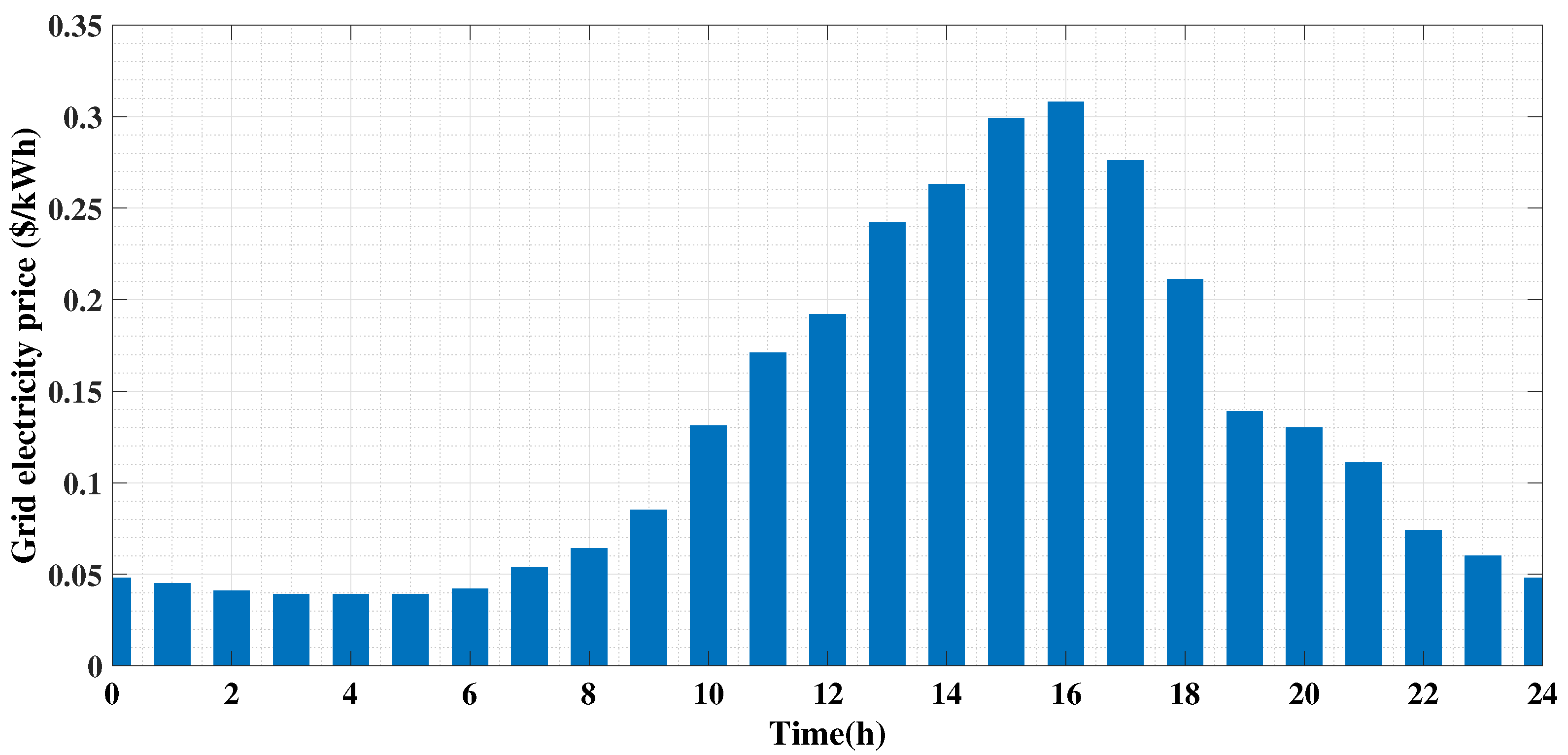
5. Results and Discussion
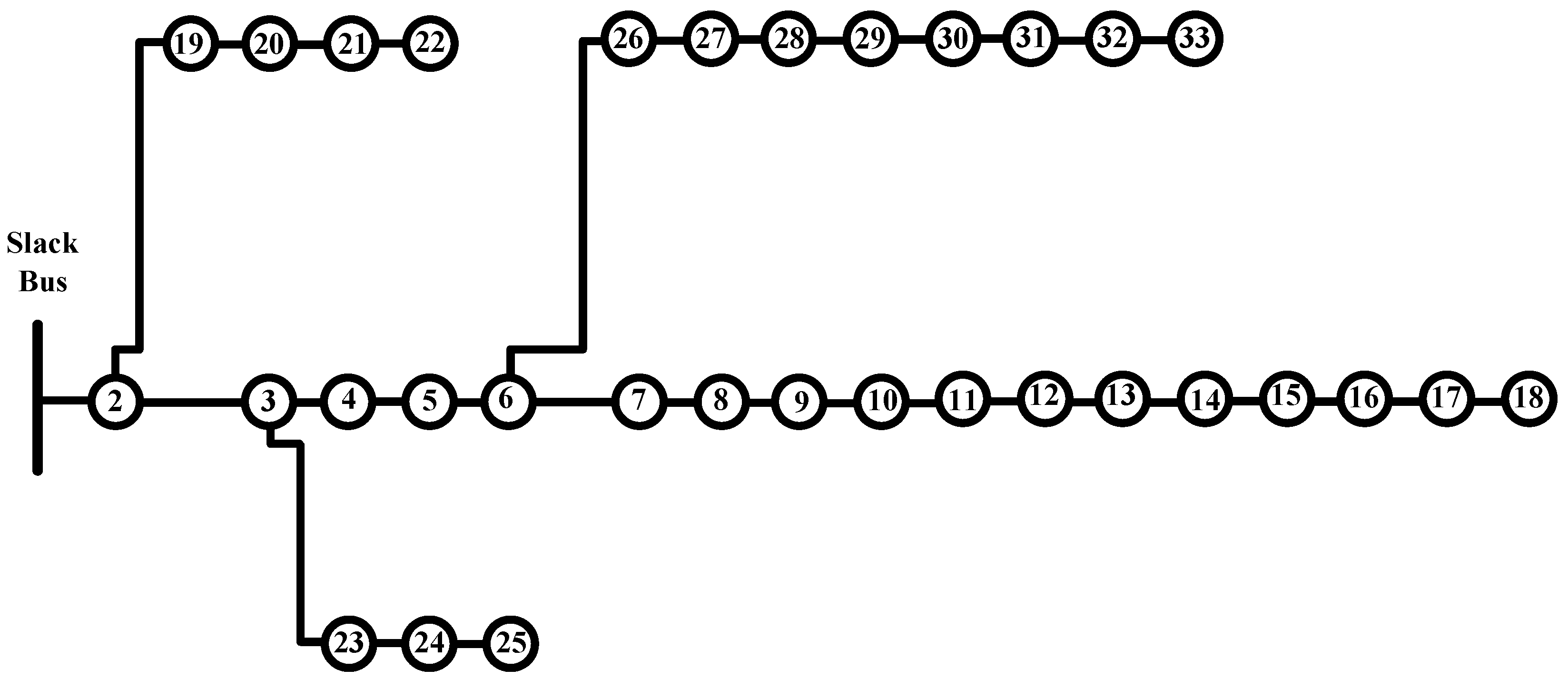
5.1. Test System
5.2. Case Studies
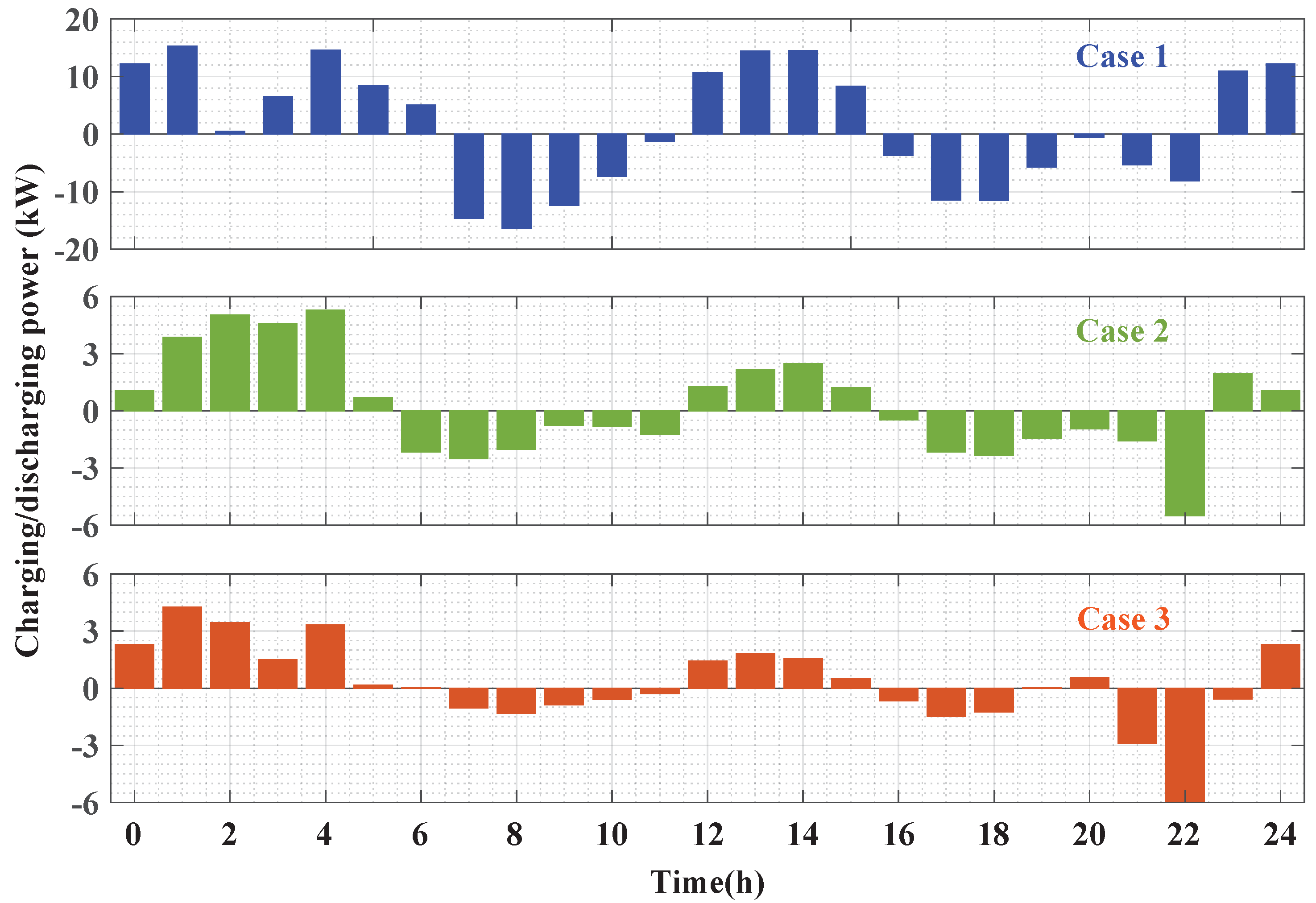
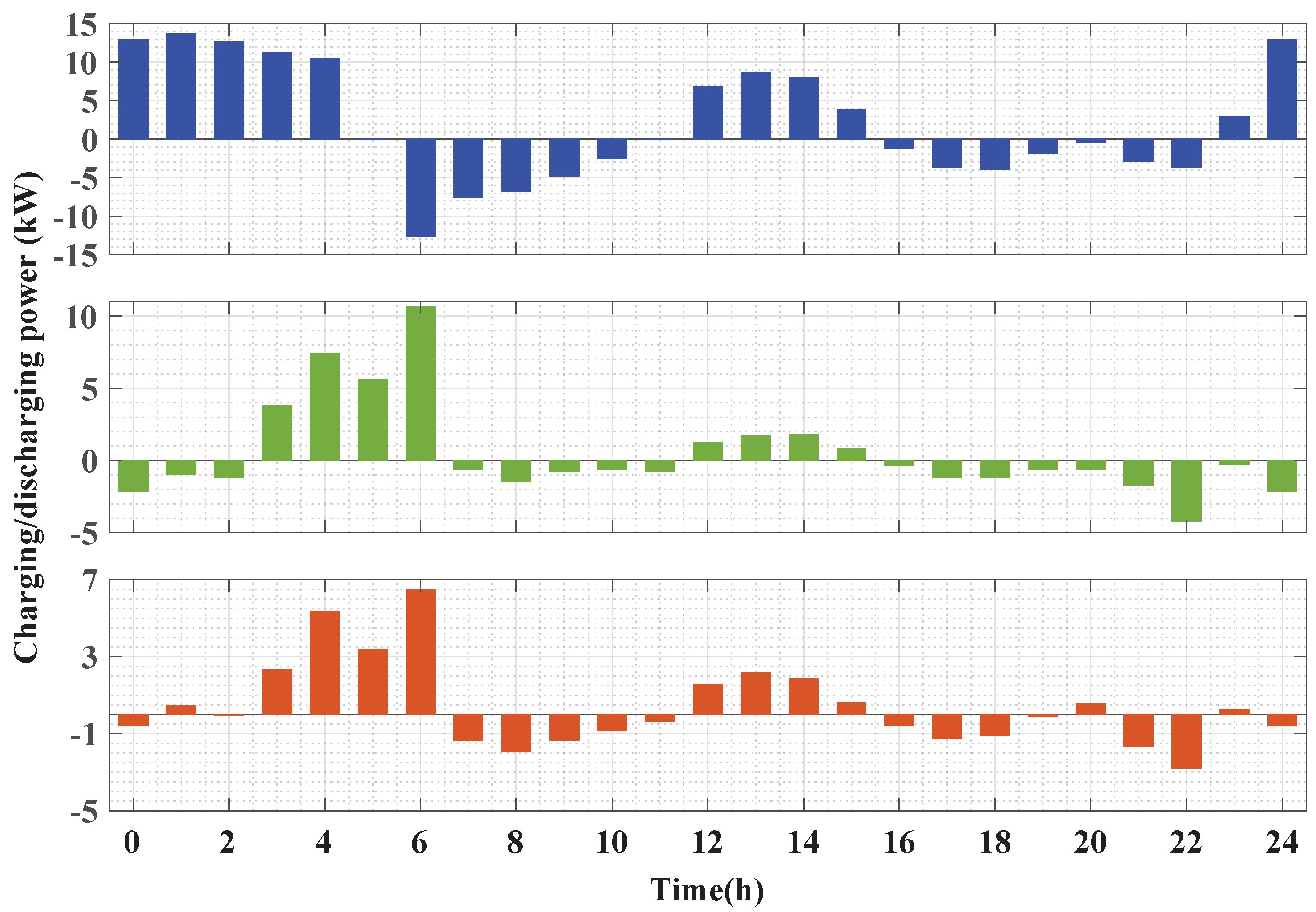
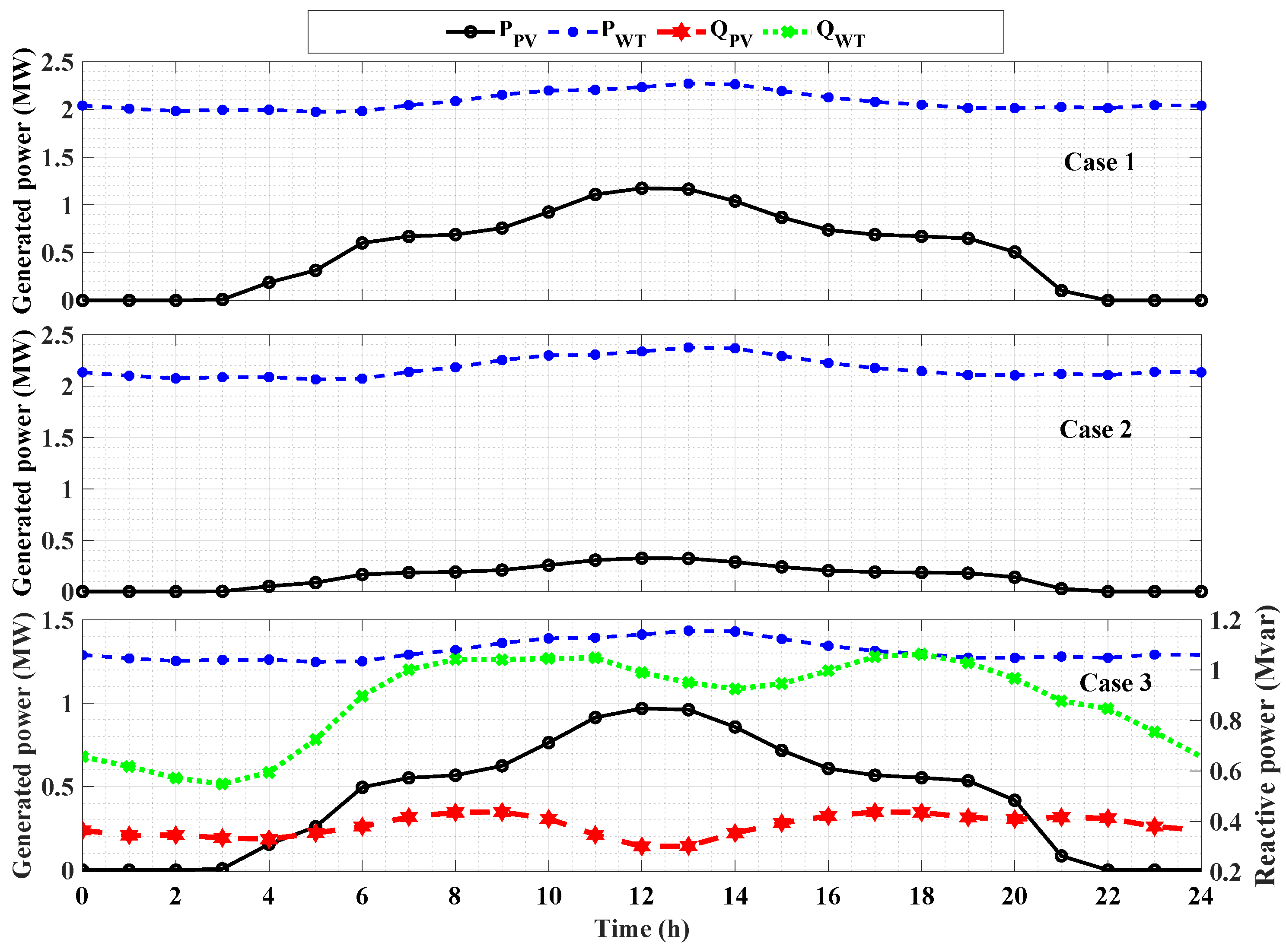
- Case 1: In this case, the RES are optimally allocated along with HESS without considering neither the DR program nor DSTATCOM functionality of the RES inverters;
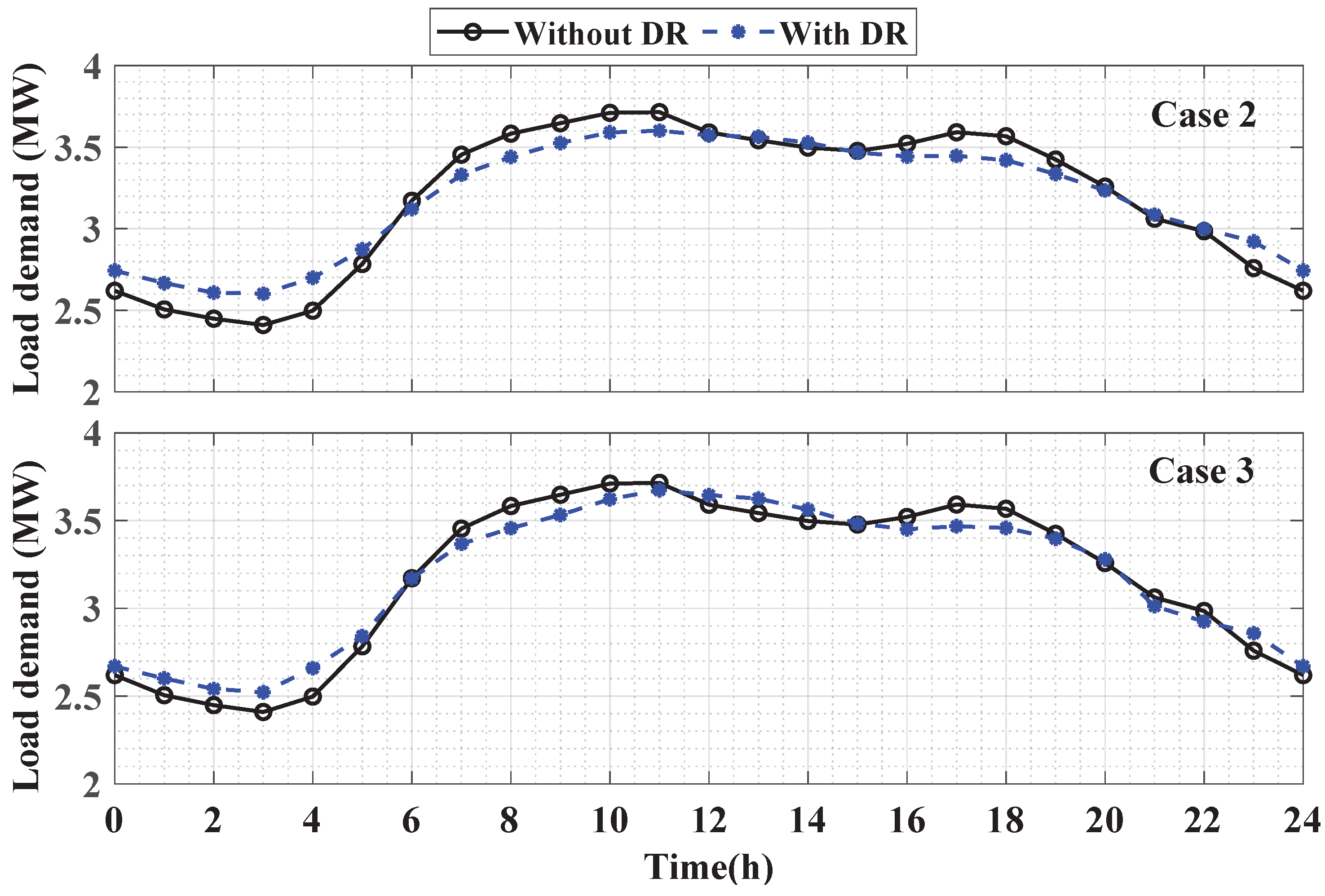
- Case 2: This case optimally allocates the RES and HESS considering the DR program only;
- Case 3: This case is the proposed approach in which the RES and HESS (as in Case 2) are optimally allocated considering both the DR program and DSTATCOM functionality of the RES interfacing inverters.
5.3. Performance of the Suggested Approach
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| BES | Battery energy storage |
| BESS | Battery energy storage system |
| CAES | Compressed air energy storage |
| DoD | Depth of discharge |
| DR | Demand response |
| DSTATCOM | Distribution static compensator |
| ESS | Energy storage systems |
| HESS | Hybrid energy storage systems |
| Li-ion | lithium-ion batteries |
| GAMS | General algebraic modeling system |
| NSGA-II | Non-dominated sorting genetic algorithm-II |
| O&M | Operation and maintenance cost |
| Probability distribution function | |
| PV | Photovoltaics |
| RES | Renewable energy sources |
| SC | Supercapacitors |
| SCES | supercapacitor energy storage |
| SoC | State of charge |
| VD | Total voltagemagnitude deviation |
| WT | Wind turbine |
References
- Li, J.; Hu, D.; Mu, G.; Wang, S.; Zhang, Z.; Zhang, X.; Lv, X.; Li, D.; Wang, J. Optimal control strategy for large-scale VRB energy storage auxiliary power system in peak shaving. Int. J. Electr. Power Energy Syst. 2020, 120, 106007. [Google Scholar] [CrossRef]
- Feng, L.; Zhang, X.; Li, X.; Li, B.; Li, Y.; Xu, Y.; Guo, H.; Zhou, X.; Chen, H. Performance analysis of hybrid energy storage integrated with distributed renewable energy. Energy Rep. 2022, 8, 1829–1838. [Google Scholar] [CrossRef]
- Zhong, S.; Qiu, J.; Sun, L.; Liu, Y.; Zhang, C.; Wang, G. Coordinated planning of distributed WT, shared BESS and individual VESS using a two-stage approach. Int. J. Electr. Power Energy Syst. 2020, 114, 105380. [Google Scholar] [CrossRef]
- Alobaidi, A.H.; Khodayar, M.; Vafamehr, A.; Gangammanavar, H.; Khodayar, M.E. Stochastic expansion planning of battery energy storage for the interconnected distribution and data networks. Int. J. Electr. Power Energy Syst. 2021, 133, 107231. [Google Scholar] [CrossRef]
- Yan, N.; Zhang, B.; Li, W.; Ma, S. Hybrid energy storage capacity allocation method for active distribution network considering demand side response. IEEE Trans. Appl. Supercond. 2018, 29, 1–4. [Google Scholar] [CrossRef]
- Campos, R.A.; do Nascimento, L.R.; Rüther, R. The complementary nature between wind and photovoltaic generation in Brazil and the role of energy storage in utility-scale hybrid power plants. Energy Convers. Manag. 2020, 221, 113160. [Google Scholar] [CrossRef]
- Sepulveda, N.A.; Jenkins, J.D.; Edington, A.; Mallapragada, D.S.; Lester, R.K. The design space for long-duration energy storage in decarbonized power systems. Nat. Energy 2021, 6, 506–516. [Google Scholar] [CrossRef]
- Arbabzadeh, M.; Sioshansi, R.; Johnson, J.X.; Keoleian, G.A. The role of energy storage in deep decarbonization of electricity production. Nat. Commun. 2019, 10, 1–11. [Google Scholar] [CrossRef] [Green Version]
- Yacar, D.; Tejada-Arango, D.A.; Wogrin, S. Storage allocation and investment optimisation for transmission-constrained networks considering losses and high renewable penetration. IET Renew. Power Gener. 2018, 12, 1949–1956. [Google Scholar] [CrossRef]
- Tan, K.M.; Babu, T.S.; Ramachandaramurthy, V.K.; Kasinathan, P.; Solanki, S.G.; Raveendran, S.K. Empowering smart grid: A comprehensive review of energy storage technology and application with renewable energy integration. J. Energy Storage 2021, 39, 102591. [Google Scholar] [CrossRef]
- Wen, S.; Lan, H.; Fu, Q.; David, C.Y.; Zhang, L. Economic allocation for energy storage system considering wind power distribution. IEEE Trans. Power Syst. 2014, 30, 644–652. [Google Scholar] [CrossRef]
- Wang, X.; Li, Z.; Shahidehpour, M.; Jiang, C. Robust line hardening strategies for improving the resilience of distribution systems with variable renewable resources. IEEE Trans. Sustain. Energy 2017, 10, 386–395. [Google Scholar] [CrossRef]
- Ali, A.; Mahmoud, K.; Lehtonen, M. Optimization of photovoltaic and wind generation systems for autonomous microgrids with PEV-parking lots. IEEE Syst. J. 2021, 16, 3260–3271. [Google Scholar] [CrossRef]
- Lara, J.D.; Olivares, D.E.; Canizares, C.A. Robust energy management of isolated microgrids. IEEE Syst. J. 2018, 13, 680–691. [Google Scholar] [CrossRef]
- Du, Y.; Wu, J.; Li, S.; Long, C.; Onori, S. Coordinated energy dispatch of autonomous microgrids with distributed MPC optimization. IEEE Trans. Ind. Inform. 2019, 15, 5289–5298. [Google Scholar] [CrossRef]
- Xu, D.; Zhou, B.; Wu, Q.; Chung, C.Y.; Li, C.; Huang, S.; Chen, S. Integrated modelling and enhanced utilization of power-to-ammonia for high renewable penetrated multi-energy systems. IEEE Trans. Power Syst. 2020, 35, 4769–4780. [Google Scholar] [CrossRef]
- Ali, A.; Mahmoud, K.; Lehtonen, M. Multiobjective photovoltaic sizing with diverse inverter control schemes in distribution systems hosting EVs. IEEE Trans. Ind. Inform. 2020, 17, 5982–5992. [Google Scholar] [CrossRef]
- Atwa, Y.M.; El-Saadany, E.F.; Salama, M.M.A.; Seethapathy, R. Optimal Renewable Resources Mix for Distribution System Energy Loss Minimization. IEEE Trans. Power Syst. 2010, 25, 360–370. [Google Scholar] [CrossRef]
- Alismail, F.; Xiong, P.; Singh, C. Optimal wind farm allocation in multi-area power systems using distributionally robust optimization approach. IEEE Trans. Power Syst. 2017, 33, 536–544. [Google Scholar] [CrossRef]
- Kumar, M.; Tyagi, B. An optimal multivariable constrained nonlinear (MVCNL) stochastic microgrid planning and operation problem with renewable penetration. IEEE Syst. J. 2020, 14, 4143–4154. [Google Scholar] [CrossRef]
- Akram, U.; Khalid, M.; Shafiq, S. Optimal sizing of a wind/solar/battery hybrid grid-connected microgrid system. IET Renew. Power Gener. 2018, 12, 72–80. [Google Scholar] [CrossRef]
- Vahidinasab, V. Optimal distributed energy resources planning in a competitive electricity market: Multiobjective optimization and probabilistic design. Renew. Energy 2014, 66, 354–363. [Google Scholar] [CrossRef]
- Somakumar, R.; Kasinathan, P.; Monicka, G.; Rajagopalan, A.; Ramachandaramurthy, V.K.; Subramaniam, U. Optimization of emission cost and economic analysis for microgrid by considering a metaheuristic algorithm-assisted dispatch model. Int. J. Numer. Model. Electron. Netw. Devices Fields 2022, 35, 1–25. [Google Scholar] [CrossRef]
- Ali, A.; Mahmoud, K.; Lehtonen, M. Maximizing hosting capacity of uncertain photovoltaics by coordinated management of OLTC, VAr sources and stochastic EVs. Int. J. Electr. Power Energy Syst. 2021, 127, 106627. [Google Scholar] [CrossRef]
- Aleem, S.A.; Hussain, S.S.; Ustun, T.S. A review of strategies to increase PV penetration level in smart grids. Energies 2020, 13, 636. [Google Scholar] [CrossRef] [Green Version]
- Ali, A.; Mahmoud, K.; Lehtonen, M. Enhancing hosting capacity of intermittent wind turbine systems using bi-level optimisation considering OLTC and electric vehicle charging stations. IET Renew. Power Gener. 2020, 14, 3558–3567. [Google Scholar] [CrossRef]
- Nguyen-Hong, N.; Nguyen-Duc, H.; Nakanishi, Y. Optimal sizing of energy storage devices in isolated wind-diesel systems considering load growth uncertainty. IEEE Trans. Ind. Appl. 2018, 54, 1983–1991. [Google Scholar] [CrossRef]
- Hajipour, E.; Bozorg, M.; Fotuhi-Firuzabad, M. Stochastic capacity expansion planning of remote microgrids with wind farms and energy storage. IEEE Trans. Sustain. Energy 2015, 6, 491–498. [Google Scholar] [CrossRef]
- Zheng, Y.; Hill, D.J.; Dong, Z.Y. Multi-agent optimal allocation of energy storage systems in distribution systems. IEEE Trans. Sustain. Energy 2017, 8, 1715–1725. [Google Scholar] [CrossRef]
- Soltani, N.Y.; Nasiri, A. Chance-constrained optimization of energy storage capacity for microgrids. IEEE Trans. Smart Grid 2020, 11, 2760–2770. [Google Scholar] [CrossRef]
- Zhao, B.; Ren, J.; Chen, J.; Lin, D.; Qin, R. Tri-level robust planning-operation co-optimization of distributed energy storage in distribution networks with high PV penetration. Appl. Energy 2020, 279, 115768. [Google Scholar] [CrossRef]
- Barani, M.; Aghaei, J.; Akbari, M.A.; Niknam, T.; Farahmand, H.; Korpås, M. Optimal partitioning of smart distribution systems into supply-sufficient microgrids. IEEE Trans. Smart Grid 2018, 10, 2523–2533. [Google Scholar] [CrossRef]
- Monteiro, M.R.; Alvarenga, G.F.; Rodrigues, Y.R.; de Souza, A.Z.; Lopes, B.; Passaro, M.C.; Abdelaziz, M. Network partitioning in coherent areas of static voltage stability applied to security region enhancement. Int. J. Electr. Power Energy Syst. 2020, 117, 105623. [Google Scholar] [CrossRef]
- Hosseinnezhad, V.; Rafiee, M.; Ahmadian, M.; Siano, P. A comprehensive framework for optimal day-ahead operational planning of self-healing smart distribution systems. Int. J. Electr. Power Energy Syst. 2018, 99, 28–44. [Google Scholar] [CrossRef]
- Oskouei, M.Z.; Mohammadi-Ivatloo, B.; Erdinc, O.; Erdinç, F.G. Optimal allocation of renewable sources and energy storage systems in partitioned power networks to create supply-sufficient areas. IEEE Trans. Sustain. Energy 2020, 12, 999–1008. [Google Scholar] [CrossRef]
- Fani, B.; Shahgholian, G.; Alhelou, H.H.; Siano, P. Inverter-Based Islanded Microgrid: A Review on Technologies and Control. e-Prime-Adv. Electr. Eng. Electron. Energy 2022, 2, 100068. [Google Scholar]
- Albadi, M.H.; El-Saadany, E.F. A summary of demand response in electricity markets. Electr. Power Syst. Res. 2008, 78, 1989–1996. [Google Scholar] [CrossRef]
- Ferreira, R.d.S.; Barroso, L.; Carvalho, M.M. Demand response models with correlated price data: A robust optimization approach. Appl. Energy 2012, 96, 133–149. [Google Scholar] [CrossRef]
- Lee, M.; Aslam, O.; Foster, B.; Kathan, D.; Kwok, J.; Medearis, L.; Palmer, R.; Sporborg, P.; Tita, M. Assessment of Demand Response and Advanced Metering; Tech. Rep.; Federal Energy Regulatory Commission: Washington, DC, USA, 2013.
- Aalami, H.; Moghaddam, M.P.; Yousefi, G. Modeling and prioritizing demand response programs in power markets. Electr. Power Syst. Res. 2010, 80, 426–435. [Google Scholar] [CrossRef]
- Deb, K.; Pratap, A.; Agarwal, S.; Meyarivan, T. A fast and elitist multiobjective genetic algorithm: NSGA-II. IEEE Trans. Evol. Comput. 2002, 6, 182–197. [Google Scholar] [CrossRef] [Green Version]
- General Algebraic Modeling System (GAMS). 2022. Available online: https://www.gams.com/ (accessed on 13 July 2022).
- IEEE Std. 1547-2018 (Revis. IEEE Std 1547-2003); IEEE Standard for Interconnection and Interoperability of Distributed Energy Resources with Associated Electric Power Systems Interfaces. IEEE: Piscataway, NJ, USA, 2018.
- Gangwar, T.; Padhy, N.P.; Jena, P. Storage Allocation in Active Distribution Networks considering Life-cycle and Uncertainty. IEEE Trans. Ind. Inform. 2022, 1. [Google Scholar] [CrossRef]
- Ali, A.; Raisz, D.; Mahmoud, K. Optimal oversizing of utility-owned renewable DG inverter for voltage rise prevention in MV distribution systems. Int. J. Electr. Power Energy Syst. 2019, 105, 500–513. [Google Scholar] [CrossRef]
- Ali, A.; Mahmoud, K.; Raisz, D.; Lehtonen, M. Probabilistic approach for hosting high PV penetration in distribution systems via optimal oversized inverter with watt-var functions. IEEE Syst. J. 2020, 15, 684–693. [Google Scholar] [CrossRef]
- Baran, M.E.; Wu, F.F. Network reconfiguration in distribution systems for loss reduction and load balancing. IEEE Power Eng. Rev. 1989, 9, 101–102. [Google Scholar] [CrossRef]
- Andreas, A.; Stoffel, T. Nevada Power: Clark Station; Las Vegas, Nevada (Data). 2006. Available online: https://midcdmz.nrel.gov/npcs/ (accessed on 1 June 2022).
- Historical Climate Data—Climate—Environment and Climate Change Canada. 2019. Available online: http://climate.weather.gc.ca/ (accessed on 1 June 2022).
- European Network of Transmission System Operators for Electricity. 2019. Available online: https://www.entsoe.eu/ (accessed on 1 June 2022).
- Wind Turbine Models. Available online: https://en.wind-turbine-models.com/turbines/1682-hummer-h25.0-100kw (accessed on 20 June 2022).
- Biswas, P.P.; Suganthan, P.; Amaratunga, G.A. Optimal power flow solutions incorporating stochastic wind and solar power. Energy Convers. Manag. 2017, 148, 1194–1207. [Google Scholar] [CrossRef]
- Blumsack, S. Basic economics of power generation, transmission and distribution. Energy Mark. Policy Regul. Course Pennstate Coll. Dep. Energy Miner. Eng. 2018, 13. Available online: https://www.e-education.psu.edu/eme801/node/530 (accessed on 20 June 2020).
- Peng, C.; Xiong, Z.; Zhang, Y.; Zheng, C. Multi-objective robust optimization allocation for energy storage using a novel confidence gap decision method. Int. J. Electr. Power Energy Syst. 2022, 138, 107902. [Google Scholar] [CrossRef]
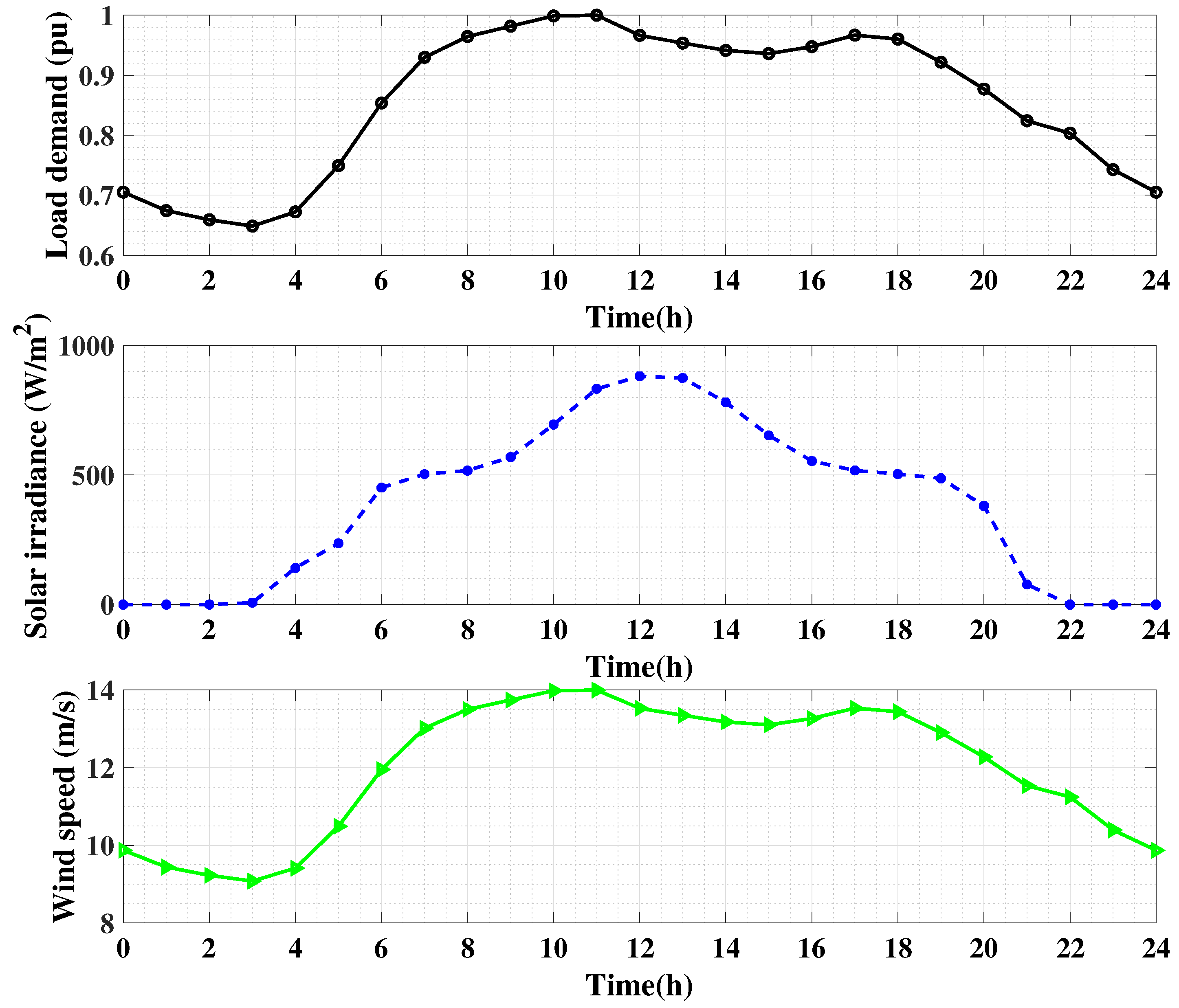




| Time | Solar Irradiance (kW/m2) | Wind Speed (m/s) | Load Demand (%) | |||
|---|---|---|---|---|---|---|
| Mean | SD | Mean | SD | Mean | SD | |
| 1 | 0.000 | 0.000 | 7.680 | 4.779 | 65.177 | 4.698 |
| 2 | 0.000 | 0.000 | 7.487 | 4.927 | 62.018 | 4.410 |
| 3 | 0.000 | 0.000 | 7.267 | 4.882 | 58.758 | 5.230 |
| 4 | 0.000 | 0.000 | 7.316 | 4.779 | 57.756 | 4.220 |
| 5 | 0.000 | 0.000 | 7.355 | 4.847 | 58.776 | 4.614 |
| 6 | 0.002 | 0.012 | 7.220 | 4.955 | 62.223 | 6.212 |
| 7 | 0.025 | 0.047 | 7.263 | 4.914 | 70.783 | 9.278 |
| 8 | 0.108 | 0.105 | 7.714 | 4.790 | 76.010 | 9.321 |
| 9 | 0.255 | 0.148 | 7.981 | 4.650 | 78.115 | 8.115 |
| 10 | 0.416 | 0.171 | 8.484 | 4.671 | 79.969 | 7.260 |
| 11 | 0.565 | 0.198 | 8.754 | 4.592 | 81.174 | 6.852 |
| 12 | 0.659 | 0.210 | 8.847 | 4.672 | 81.949 | 6.811 |
| 13 | 0.713 | 0.229 | 9.159 | 4.815 | 82.103 | 7.116 |
| 14 | 0.703 | 0.237 | 9.317 | 4.661 | 81.037 | 7.444 |
| 15 | 0.637 | 0.231 | 9.113 | 4.412 | 80.539 | 7.616 |
| 16 | 0.529 | 0.228 | 8.766 | 4.682 | 80.640 | 7.944 |
| 17 | 0.416 | 0.220 | 8.395 | 4.874 | 81.114 | 8.291 |
| 18 | 0.278 | 0.191 | 8.037 | 4.882 | 81.093 | 8.775 |
| 19 | 0.149 | 0.142 | 7.750 | 4.773 | 81.050 | 8.558 |
| 20 | 0.060 | 0.082 | 7.558 | 4.967 | 81.509 | 7.702 |
| 21 | 0.014 | 0.028 | 7.512 | 4.890 | 80.661 | 6.040 |
| 22 | 0.000 | 0.001 | 7.645 | 4.943 | 77.876 | 5.348 |
| 23 | 0.000 | 0.000 | 7.483 | 4.808 | 73.689 | 5.373 |
| 24 | 0.000 | 0.000 | 7.743 | 4.848 | 69.979 | 5.167 |
| Wind Turbine Parameters | PV Parameters | ||
|---|---|---|---|
| Unit price ($/kW) | 1075 | Unit price ($/kW) | 615 |
| Lifetime (years) | 20 | Lifetime (years) | 20 |
| Rated power(kW) | 100 | (W/m) | 1000 |
| Cut-in speed (m/s) | 2.5 | (W/m) | 120 |
| Rated speed (m/s) | 10 | O&M cost ($/kWh) | 0.01 |
| Cut-off speed (m/s) | 20 | ||
| O&M cost ($/kWh) | 0.01 | ||
| Index | Li-Ion Battery | Supercapacitor | CAES |
|---|---|---|---|
| Unit price of power | 770 ($/kW) | 70 ($/kW) | 920 ($/kW) |
| Unit price of capacity | 385 ($/kWh) | 1765 ($/kWh) | 230 ($/kWh) |
| Lifetime | 10 (years) | 10 (years) | 30 (years) |
| 100 (%) | 100 (%) | 100 (%) | |
| 20 (%) | 5 (%) | 10 (%) | |
| Charging efficiency | 90 (%) | 95 (%) | 75 (%) |
| Discharging efficiency | 90 (%) | 95 (%) | 75 (%) |
| Index | Case 1 | Case 2 | Case 3 |
|---|---|---|---|
| PV locations | 7 & 21 | 8 & 21 | 8 & 21 |
| PV capacities (MW) | 1.16 & 0.17 | 0.19 & 0.17 | 0.58 & 0.51 |
| WT locations | 12 & 29 | 15 & 31 | 14 & 30 |
| WT capacities(unit) | 22 & 15 | 19 & 21 | 12 & 12 |
| Battery location | 16 | 11 | 17 |
| Battery capacity (kWh) | 134 | 110 | 112 |
| Battery power (kW) | 26.80 | 22 | 22.4 |
| SC location | 22 | 20 | 21 |
| SC capacity (kWh) | 10.5 | 10 | 14 |
| SC power (kW) | 880 | 388 | 2000 |
| CAES location | 27 | 21 | 28 |
| CAES capacity (kWh) | 180 | 227 | 143 |
| CAES power (kW) | 18 | 22.7 | 14.3 |
| Annual cost (M$/yaer) | 0.685 | 0.618 | 0.477 |
| Total VD (pu) | 6.46 | 6.15 | 5.24 |
| Cost reduction (%) | - | 9.78 | 30.4 |
| Reduction of VD (%) | - | 4.80 | 19 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ali, A.; Shaaban, M.F.; Sindi, H.F. Optimal Operational Planning of RES and HESS in Smart Grids Considering Demand Response and DSTATCOM Functionality of the Interfacing Inverters. Sustainability 2022, 14, 13209. https://doi.org/10.3390/su142013209
Ali A, Shaaban MF, Sindi HF. Optimal Operational Planning of RES and HESS in Smart Grids Considering Demand Response and DSTATCOM Functionality of the Interfacing Inverters. Sustainability. 2022; 14(20):13209. https://doi.org/10.3390/su142013209
Chicago/Turabian StyleAli, Abdelfatah, Mostafa F. Shaaban, and Hatem F. Sindi. 2022. "Optimal Operational Planning of RES and HESS in Smart Grids Considering Demand Response and DSTATCOM Functionality of the Interfacing Inverters" Sustainability 14, no. 20: 13209. https://doi.org/10.3390/su142013209
APA StyleAli, A., Shaaban, M. F., & Sindi, H. F. (2022). Optimal Operational Planning of RES and HESS in Smart Grids Considering Demand Response and DSTATCOM Functionality of the Interfacing Inverters. Sustainability, 14(20), 13209. https://doi.org/10.3390/su142013209








