Impact Assessment of Diverse EV Charging Infrastructures on Overall Service Reliability

Abstract

A higher penetration of EVs may pose several challenges to the power systems, including reliability issues. To analyze the impact of EVs on the reliability of power systems, a detailed EV charging infrastructure is considered in this study. All possible charging locations (home, workplace, public locations, and commercial fast chargers) and different charging levels (level 1, level 2, and DC fast charging) are considered, and seven charging infrastructures are determined first. Then, the reliability impact of each charging infrastructure is determined using the two widely used reliability indices, i.e., the loss of load expectation (LOLE) and the loss of energy expectation (LOEE). The impact of mixed charging infrastructure portfolios is also analyzed by considering two different cases, which included the equal share of all charging infrastructure and charging infrastructure share based on consumer preferences. The performance is analyzed on a well-known reliability test system (Roy Billinton Test System) and different penetration levels of EVs are considered in each case. Test results have shown that fast-charging stations have the worst reliability impact. In addition, it was also observed that mixed charging portfolios have lower reliability impacts despite having a fair share of fast-charging stations.

1. Introduction

1.1. Research Background

The transportation sector contributes a major portion of the global greenhouse gas emissions and it is reported to be around one-quarter of the total global emissions [1]. Various efforts are underway to reduce/eliminate the consumption of fossil fuels from the transportation sector, which includes hydrogen cars, hybrid cars, and battery electric cars (known as electric vehicles, EVs). Due to the environmental friendliness, sustainable nature (especially when power is generated from renewables), and maturity in related technologies of EVs, it is expected that a major portion of future transportation will be composed of EVs [2,3,4]. Due to the increased penetration of EVs, the interdependence of transportation and power networks will further increase. This increased dependence brings both opportunities and challenges for both power and transportation networks. On one hand, EVs can serve as mobile energy storage units and increase the resilience/reliability of buildings, microgrids, and power networks [5]. On the other hand, during power system contingencies, the service reliability of transportation networks may also be jeopardized due to the absence of power [6].

1.2. Literature Review

Several studies are conducted on both of these aspects, i.e., reliability enhancement using EVs and the reliability assessment of power networks with a high penetration of EVs, which are discussed in the following paragraphs. In [7], it has been demonstrated through a reliability test system that the bidirectional charging control of EVs can benefit the reliability of power systems. The authors have also proposed an optimization method to obtain the optimal control strategy to enhance the system’s reliability. In [8], EVs are used as transportable power storage devices to feed the load of faulty areas. In addition, the priority of load is also considered in accordance with the fault occurrence time and outage scenario while analyzing the load pattern. The reliability of the power system is analyzed in [9] while considering EVs and different charging strategies are recommended for assisting the overall system reliability. This study has found that around 40% of public charging is the best ratio to maximize the power system reliability. Similarly, different studies are conducted on using EVs as a reliable resource for buildings [8], microgrids [10], and power distribution systems [11]. The reliability of EVs during power outages is also discussed in different studies. For example, the prioritization and allocation of available power to EVs during outages is proposed in [12] considering the impact of those EVs on individuals and the community. Similarly, a game-theoretic approach is proposed in [13] to manage the load of EVs locally by using the vehicle-to-vehicle service during system contingencies.

However, with a higher penetration of EVs, both the local distribution system load and the overall power system load could significantly increase. In addition, most EV owners may not agree to provide reliability-related services due to the potential degradation of the EV battery and available incentives [11]. Similarly, the availability of EVs and having sufficient surplus energy to feed the local loads at a particular location during the system contingency is also uncertain. Therefore, a higher power demand may introduce higher reliability risks during power contingencies [14] if no countermeasure is taken or new generation units are added [15]. Several articles have analyzed the reliability aspects of power systems under a high penetration of distributed energy sources and EVs [16,17]. Therefore, several studies are conducted to analyze the power system reliability under the high penetration of EVs.

For example, the impact of EVs on the power system is analyzed in [18] using two reliability indices such as the expected energy not served and the loss of load expectation. It has been concluded in this study that in order to mitigate the reliability issues due to EVs, appropriate charging/discharging schemes are required. A probabilistic method is proposed in [19] to assess the security of power systems during a steady state. The performance is analyzed by testing it with a real power system in South Korea. Similarly, a reliability assessment of power systems with a high penetration of EVs is carried out in [20]. It has been concluded that controlled charging can significantly reduce the reliability issues under the high penetration of EVs. Similarly, the reliability of power systems is assessed in [21,22] while considering different charging modes. Different outage scenarios are considered in [23] and a probabilistic method is used to evaluate the impact of EVs on the power network. A battery exchange mode of EVs is considered to analyze the reliability impact of EVs on the power system in [24]. Results have shown that a battery exchange mode has a lower impact on system reliability as compared to the plugin mode. A planning phase model for charging infrastructure is proposed in [25] considering the reliability of power systems. The adequacy of the power system is analyzed in [26] by considering the effective load demand, which is defined as the amount of extra generation required to restore the system to its initial reliability level. In addition to reliability issues, different power quality issues (voltage deviation, unbalance, and fluctuations) due to fast-charging stations are analyzed in [27]. Finally, the role of different reliability aspects in future power systems including EVs is analyzed in [28] and the reliability of EV components is analyzed in [29].

1.3. Research Gaps and Contributions

It can be observed from the literature that several studies are conducted on analyzing the reliability of power systems with a high penetration of EVs. However, different charging infrastructures used across the globe (residential, workplace, public, and commercial) for charging EVs are not considered in these studies. Different charging infrastructures with different charging levels (level1, level2, and DC fast charging) are used in different sectors to charge the EVs and due to the difference in the power requirements of each infrastructure, the reliability impact of each infrastructure could be different. In addition, the modeling of the EV load in each of the infrastructures is different due to differences in spatial and temporal location/distribution of EVs and chargers. Finally, well-known reliability indices need to be used for a better understanding of policymakers and to assist them in making well-informed decisions. In addition, it will provide guidelines for future generation expansion scenarios to avoid such reliability issues.

To address the shortcomings of the existing literature on the reliability analysis of EVs, a detailed charging infrastructure framework is considered in this study. Simulation results have shown that commercial chargers have the worst impact on the reliability of the power system and mixed charging portfolios are more suitable for enhancing the power system reliability. The major contributions of his study as compared to the existing studies are as follows.

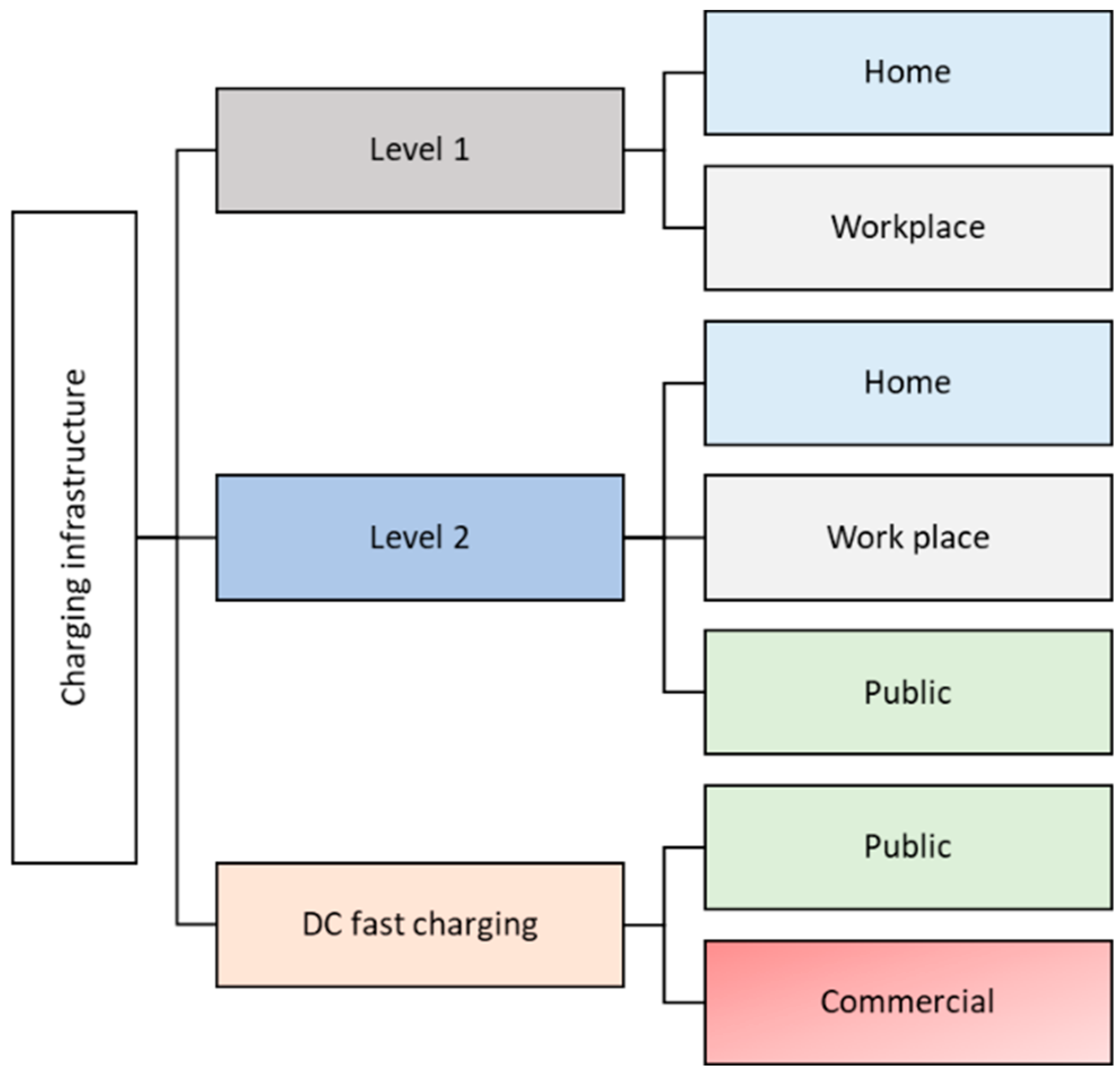
• All possible charger types (level 1, level 2, and DC fast charging) and charging locations (home, workplace, public locations, and commercial charging places) are considered and seven charging infrastructures are determined. EV load profiles are estimated for all seven charging infrastructures.
• The reliability impact of individual charger types and mixed portfolios is determined by considering the developed seven charging profiles.
• Two of the most widely used reliability indices, loss of load expectation (LOLE) and loss of energy expectation (LOEE) are used to evaluate the impact of individual and mixed charger portfolios.
• Various simulation studies are performed by considering different penetration levels of EVs.

2. Charging Infrastructures

The existing charging infrastructure can be divided into three main categories based on the type of charging levels, such as level 1, level 2, and DC fast charging. An overview of these three categories is shown in Figure 1. Level 1 chargers have lower power ratings and take a longer time for charging. Therefore, these chargers are generally preferred in locations where EVs are parked for longer durations, such as homes and workplaces. The ratings of level 2 chargers are higher than those of level 1 but still require a significant amount of time for charging EVs. Therefore, these chargers are also more suitable for locations where EVs remain parked for longer durations such as homes, workplaces, and those public areas where EV drivers tend to stay for a longer duration. Finally, DC fast chargers have significantly higher power ratings and thus can recharge the EVs in a very limited amount of time. Therefore, these chargers are generally deployed for commercial use and/or in those public areas where EV drivers tend to stay for a short time. The EV load estimation process for different charging infrastructures is different and it is discussed for each category in the subsequent sections.

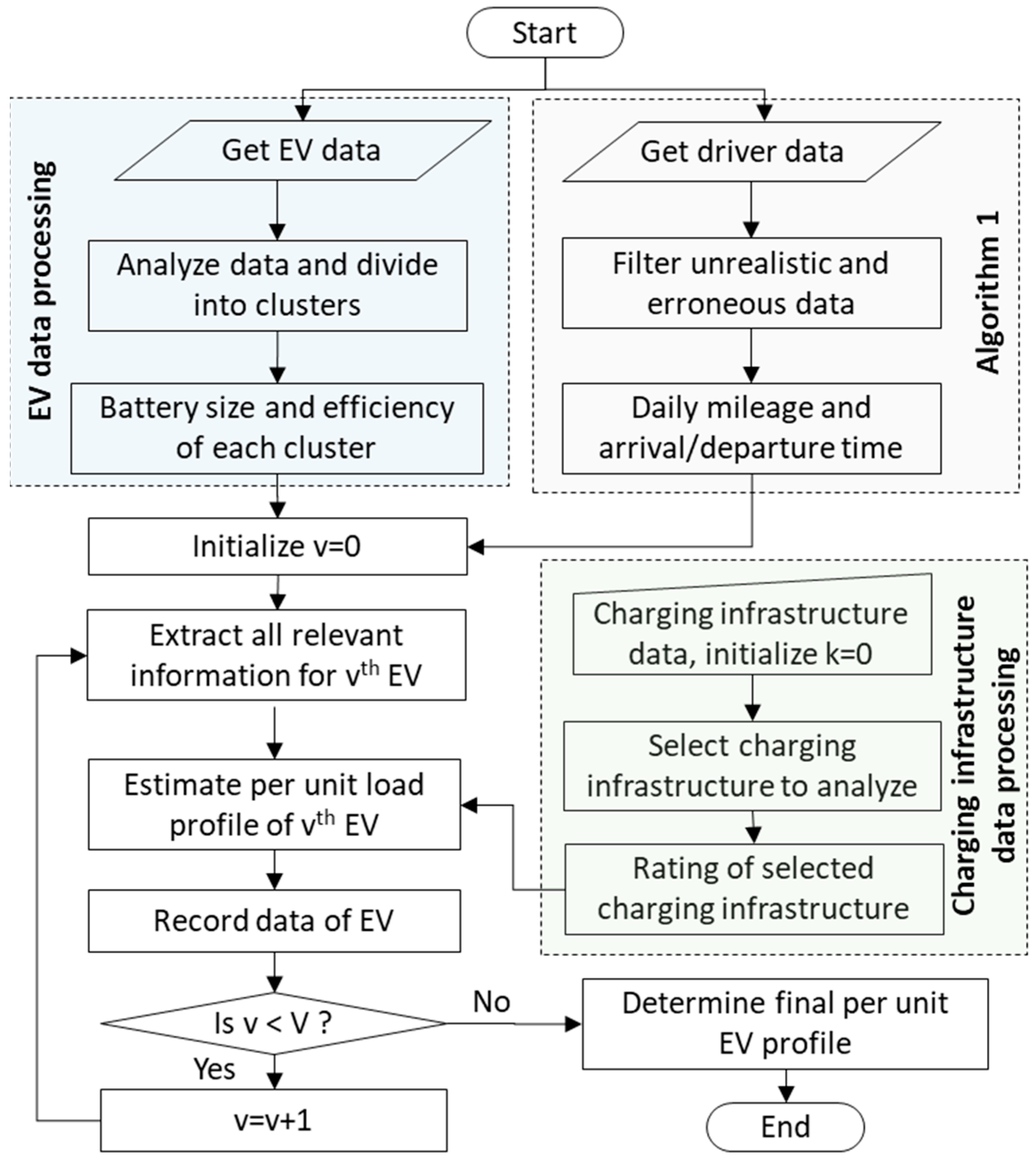
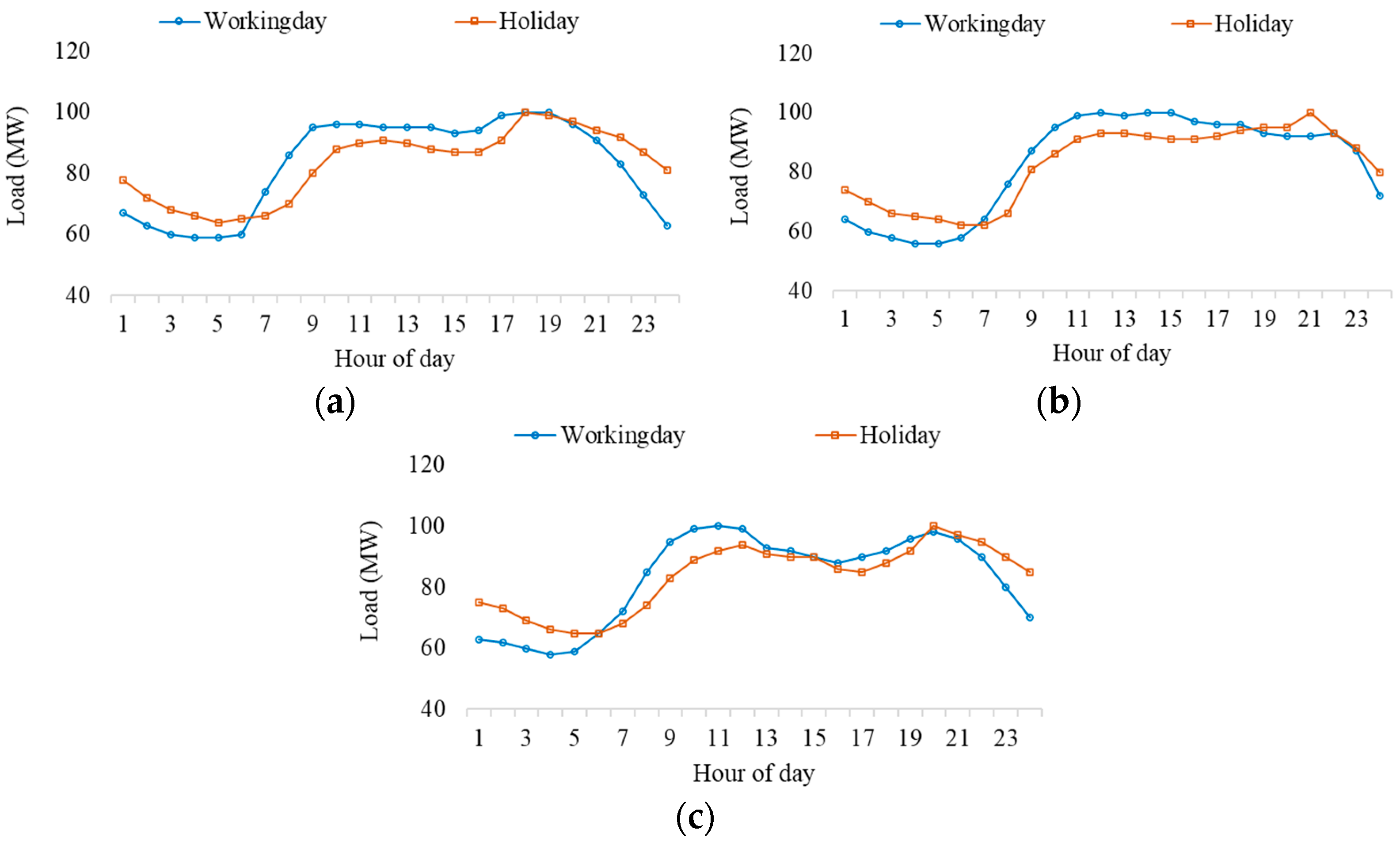
2.1. EV Load Estimation

To analyze the reliability impact of different charging infrastructures, EV load estimation is required for each infrastructure type. Therefore, in this section, details about EV load estimation in each infrastructure are presented. To estimate the EV load in each of the charging infrastructures, information regarding EVs, EV drivers, and charging infrastructure is required. A generalized framework for EV load estimation is shown in Figure 2. It can be observed that initially, EV data are processed and EVs are clustered into four groups, similar to [30]. This is due to the presence of several commercially available EV models; an overview of considered EV models can be seen in [31]. The EV parameters of interest for EV load estimation are the useable battery size and energy economy of each EV. Therefore, these two parameters are extracted for each EV cluster. Then, the EV driver data are analyzed. Due to the absence of reliable EV driver data, a survey is conducted by the author regarding the arrival and departure times of vehicles at different locations. Details about the survey data can be found in [32]. An overview of driver data processing for home is shown in Algorithm 1.

Algorithm 1: Vehicle driver data processing for home

The total number of vehicles in the dataset is counted and different filters are used to remove erroneous data or trips with incomplete information. Then, a loop is used for each vehicle to count the number of trips covered by each vehicle. Each trip is further analyzed to determine the departure time from home and the arrival time at home. This information is used to determine the parking period of each vehicle at home. The same process is repeated for vehicle arrival and departure time at the workplace. In this way, the parking period of EVs at the workplace is determined. In the case of public chargers, the available energy level of EVs is updated after each trip and if the state-of-charge (SOC) is below a certain level, the EV is scheduled to be charged before the next trip. During charging also, the SOC of the EV is updated after each interval. Finally, in the case of commercial chargers, the need for the next recharge is determined after each trip based on the distance and mileage efficiency of the EV. Then, similar to [33], the vehicle arrival rate is estimated using the decision tree. Similar to public chargers, the SOC of each EV is updated after each interval. Details about the charging process are presented in the following sub-sections.

Based on the charger type, this process is repeated for the whole fleet of EVs and the net EV load is determined using the following equation.

$$P_t^{fleet}={\displaystyle \sum _{v\in V}{P}_{t,v}^{}\forall \mathrm{t}\in \mathrm{T}}$$

(1)

where $P_t^{fleet}$ is the load of the EV fleet during interval t and $P_{t,v}^{}$ is the load of v^th EV during interval t in kW.

2.2. Level 1 Charging

Level 1 chargers are generally used at homes and workplaces since EVs tend to be parked for a longer duration in such locations. The voltage and current levels for level 1 chargers are 110 V and 12 A, respectively, thus having a charging power of 1.4 kW. Using the survey data [32], the arrival and departure times along with the daily mileage of EV drivers are extracted first. These data are used to develop probability density functions (PDFs) for the arrival, departure, and daily mileage of EVs. Then, data related to EVs are extracted from the database of commercially available EVs [31]. This database includes different types of EVs such as sedans, SUVs, minivans, etc. The same process is repeated for both homes and workplaces, except for the arrival and departure times, which are different based on the location (home or workplace). The SOC of v^th EV ($So{C}_v$), in %, can be updated using the following equation, where $R_v$ is the range of v^th EV in km and $M_v$ is the daily mileage of the v^th EV in km. It is assumed that the battery SOC decreases linearly with the distance traveled similar to [34,35].

$$So{C}_v=\left(\frac{R_v-M_v}{R_v}\right)\cdot 100\forall \mathrm{v}\in \mathrm{V}$$

(2)

Then, the arrival and departure times of EVs are generated using a normal distribution function and this information is used to determine the stay duration. The charging duration of an EV ($D_v$), in hours, is computed using the following equation

$$D_v=\frac{E_v}{{\eta }_v\cdot L^{ch}}\forall \mathrm{v}\in \mathrm{V}$$

(3)

where $E_v$ refers to the amount of energy required by v^th EV in kWh. Similarly, ${\eta }_v$ represents the mileage efficiency of v^th EV and $L^{ch}$ is the charging level of the charger, i.e., 1.4 kW in the case of the level 1 charger. This information is used to determine the EV load of individual EVs for different time intervals. The load of the whole EV fleet is determined using (1) and this process is repeated using Monte Carlo simulations till convergence.

2.3. Level 2 Charging

Level 2 chargers have higher power ratings as compared to level 1 chargers, and they can reduce the charging time. Therefore, level 2 chargers are commonly installed at homes, workplaces, and public places. Typical voltage and current ratings of a level 2 charger are 220 V and 30 A with a power rating of approximately 7.2 kW. The EV load estimation process of the level 2 charger is similar to that of level 1 with different power ratings. There are some differences in the EV load estimation process due to differences in the location of the charger, i.e., home, workplace, or public place. The EV load estimation process for the home and the workplace is the same as that of level 1, as explained in the previous section.

In the case of public charging stations, the SOC of the EV is updated after each trip using Equation (2). Then, a threshold level is used to determine the need for a recharge before the next trip, depending on the current SOC level. The EV load for any interval t ($P_{t,v}^{}$), in kW, is determined using the following equation

$$P_{t,v}^{}=\min \left\{{\eta }_v\cdot L^{ch},P_{v,t}\right\}\forall \mathrm{v}\in \mathrm{V}$$

(4)

where $P_{v,t}$ refers to the amount of power required by v^th EV in kW. Similarly, ${\eta }_v$ represents the mileage efficiency of v^th EV and $L^{ch}$ is the charging level of the charger, i.e., 7.2 kW in the case of a level 2 charger. Then, the SOC of the EV ($So{C}_{t,v}^{}$) is updated using the following equation

$$So{C}_{t,v}^{}=So{C}_{t-1,v}^{}+\Delta \mathrm{t}.\left(P_{t,v}^{}/P_v^{cap}\right)\cdot 100 \forall \mathrm{v}\in \mathrm{V}$$

(5)

where $P_v^{cap}$ is the capacity of the v^th EV in kWh and $\Delta \mathrm{t}$ is the length of the time interval in hours. This process is repeated after each interval till the EV is fully charged or it departs from the charging station. In this way, the EV load of EVs in public charging stations is estimated, and details about the process can be found in [33].

2.4. DC-Fast Charging

Fast charging stations tend to recharge the EV in a significantly lesser amount of time as compared to level 1 and level 2 chargers. However, they are not economically viable for several customers. Therefore, fast chargers are generally installed for commercial charging stations and/or public places, where EVs tend to stay for a shorter duration. Typically, fast charger ratings start from 480 V and 108 A, which provides approximately 50 kW of power. The EV load estimation process for fast chargers in public places is the same as that of level 2, explained in the previous section, except for different charger ratings. The EV load estimation process of commercial chargers is as follows.

In the case of commercial chargers, EV trips are tracked and the need for recharge is determined first. Then, a decision tree is used to estimate the arrival time of EVs at the commercial chargers, similar to [33]. The EV is scheduled to recharge if the SOC falls below 20% after completing any trip. Otherwise, the EV can carry out the next trip and the SOC will be updated again. The amount of power required to recharge the EV at any time t ($E_{t,v}^{}$) is determined using the following equation

$$E_{t,v}^{}=\left(So{C}^{\max }-So{C}_{t,v}^{}\right)\cdot \frac{P_v^{cap}}{100}\forall v\in \mathrm{V}$$

(6)

where $So{C}^{\max }$ is the upper SOC bound and $P_v^{cap}$ is the capacity of the v^th EV in kWh. The SOC of the EV is updated after each interval using (2) considering the traveled distance and the mileage efficiency of the v^th EV.

The same process is repeated for all the EVs and the load of the EV fleet is determined for each time interval t. Details about the EV load estimation for a fast-charging station can be found in [33].

3. Reliability Evaluation

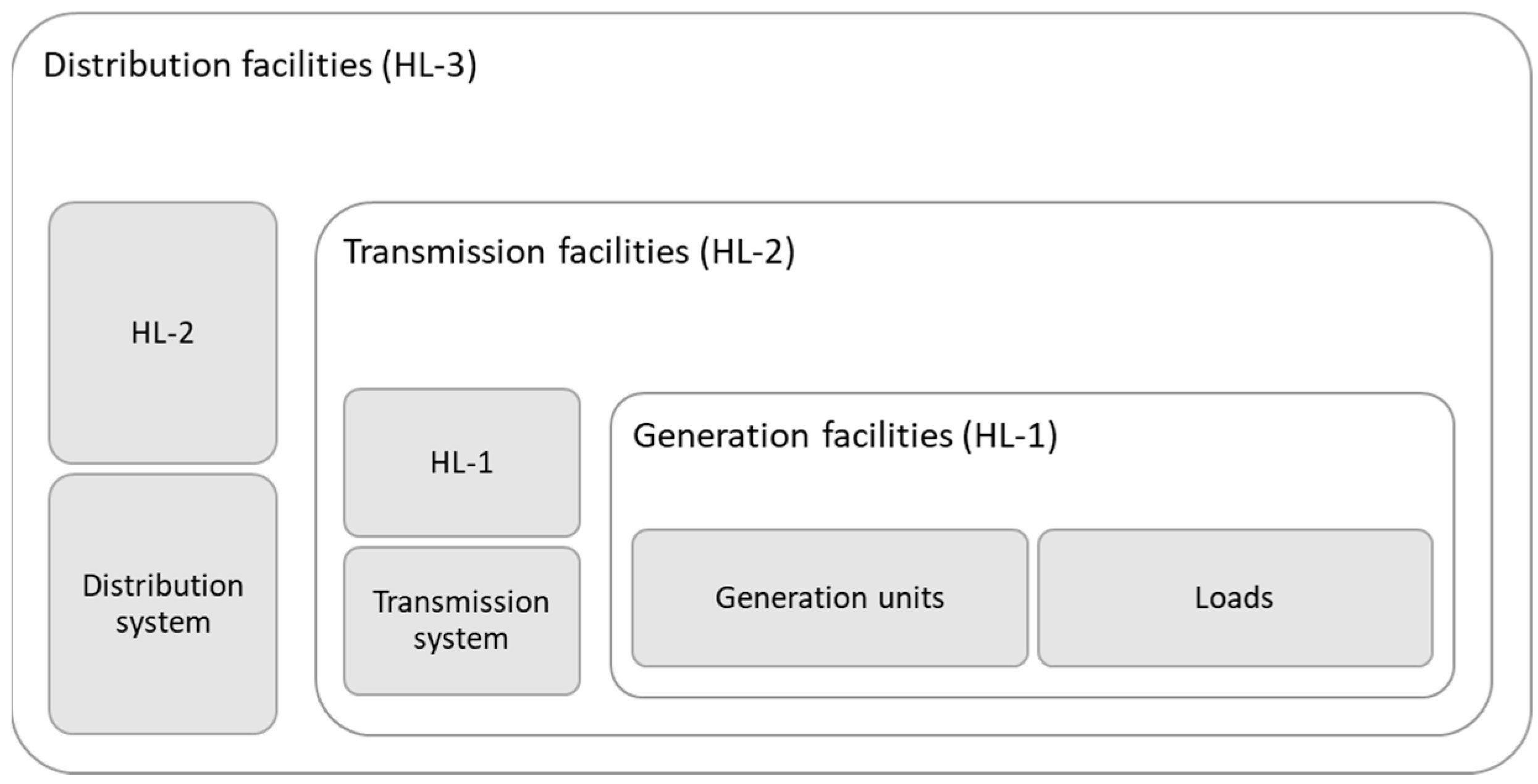
3.1. Reliability Evaluation Levels and Methods

Modern power systems are required to provide electricity to their customers with service reliability. This goal becomes significantly difficult with a higher penetration of distributed energy resources, including EVs. Different analyses are required at various levels of the power system to assure service reliability during the outage of power system components, such as generators and lines [36]. For reliability analysis purposes, modern power systems are divided into different hierarchical levels (HL), as shown in Figure 3.

Several methods are used in the existing literature for the reliability analysis of power systems at different hierarchical levels. These methods can be broadly categorized as deterministic and probabilistic methods. The probabilistic methods are further categorized as analytical and simulation-based methods [37]. Simulation-based methods are further categorized as sequential and non-sequential Monte Carlo simulations (MCS). An overview of probabilistic methods for the reliability evaluation of power systems is shown in Figure 4.

3.2. Analytical Method and Reliability Indices

In this section, an overview of reliability evaluation is presented for analytical methods. Details about analytical and other simulation-based methods can be found in [36].

In analytical methods, the capacity outage probability table (COPT) is used to represent the generation model. For a two-state model, the following equation can be used to represent the cumulative probability of a certain capacity level after adding a two-stage unit with unavailability (U).

$$P_X^A=\left(1-FOR\right)\cdot P_X^B+FOR\cdot P_{X-C}^B$$

(7)

where, $P_X^A$ is the cumulative probability of the system capacity outage level (X MW) after the addition of a two-stage unit. Similarly, $P_X^B$ is the cumulative probability before the addition of a two-stage unit. Finally, FOR refers to the forced outage rate of the generation unit. Similarly, for multi-stage units, the cumulative probability of the system capacity outage level can be represented as

$$P_X^A={\displaystyle \sum _{i\in n}{p}_i\cdot P_{X-C_i}^B}$$

(8)

Multi-stage generators could have n partial capacity outage states ($C_i$) with individual probabilities of ($p_i$).

Two of the most commonly used reliability indices are the loss of load expectation (LOLE) and the loss of energy expectation (LOEE). These two indices are used in this study to evaluate the reliability of power systems under a high penetration of EVs and these two indices are described in the following sub-sections.

3.2.1. Loss of Load Expectation (LOLE)

LOLE refers to the failed capacity level in hours per year or days per year depending on the model used. For example, LOLE will be in hours per year if the load duration curve (LDC) model is used and in days per year if the daily peak load variation curve (DPLVC) model is used. Mathematically, it can be represented as

$$LOLE={\displaystyle \sum _{k\in n}{t}_k\cdot P_k(X>C_{ins}-L)}$$

(9)

where $P_k$ is the probability of the existence of a capacity outage for outage k. X is the capacity outage state in COPT, and $C_{ins}$ is the installed capacity of the system. Similarly, $t_k$ is the time during which the loss of load will occur due to the capacity outage and L is the value of the load level in the system. Finally, n is the total number of encountering outages in the system.

It implies that the LOLE is the summation of the probability of load outage over the designated period and two major factors contribute to the LOLE, which are as follows

• Any capacity outage level that failed to meet the demand (probability of the existence of failed capacity level).
• The designated period of time.

3.2.2. Loss of Energy Expectation (LOEE)

Similarly, LOEE is also widely used in the power system to analyze network reliability. LOEE refers to the expected total amount of shortage energy that occurs when the available generation capacity fails to meet the demand over the specified period. It is generally computed by combining the COPT with the LDC load model. Mathematically, it can be represented as

$$LOEE={\displaystyle \sum _{k\in n}{t}_k\cdot (X-(C_{ins}-L))\cdot P_k(X>C_{ins}-L)}$$

(10)

It implies that three major factors contribute to the LOEE, two of them are same as that of LOLE and the third one is the amount of energy not supplied.

4. Reliability Evaluation of Individual Infrastructure

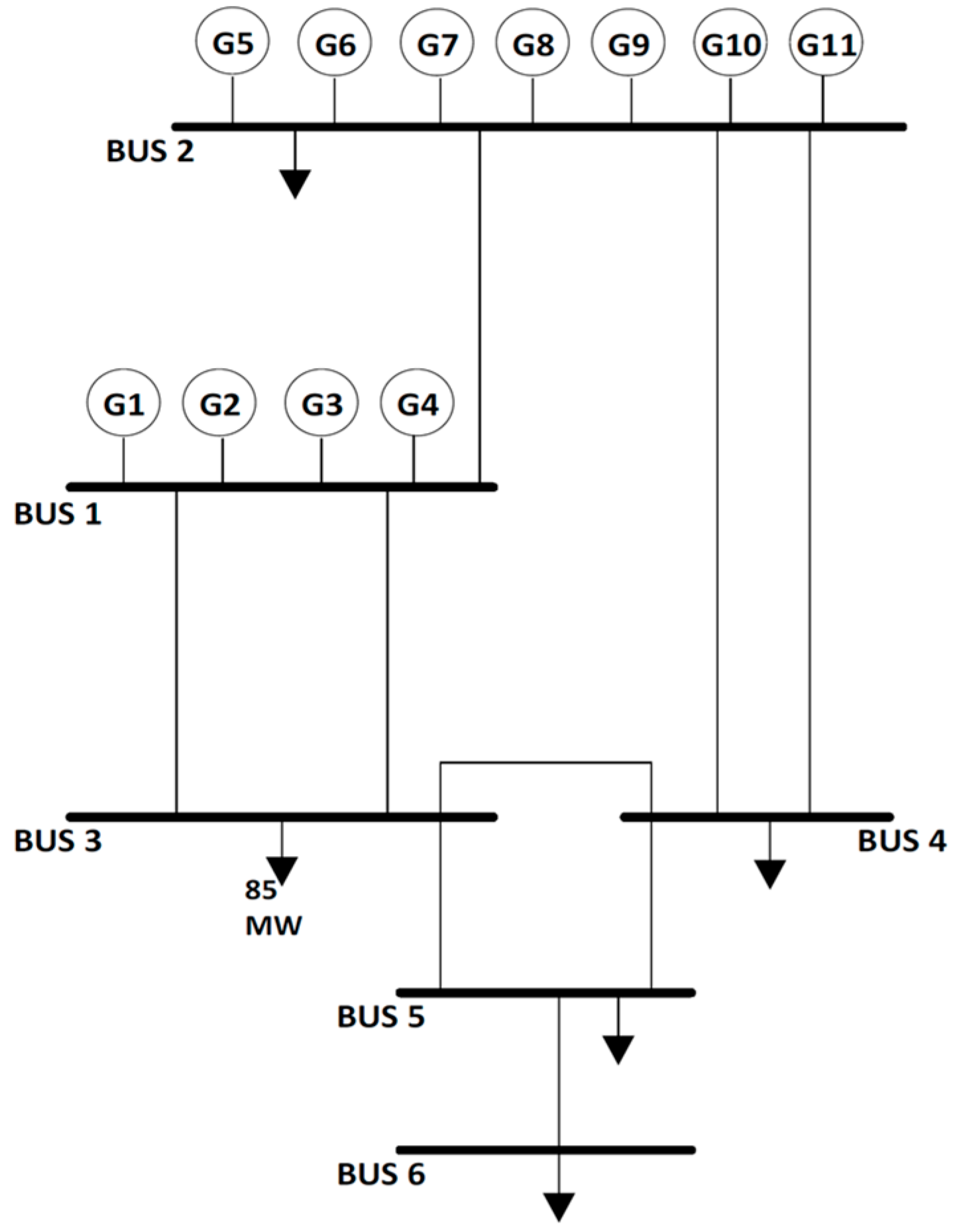
4.1. Input Data and Test System

In order to analyze the reliability performance of power systems under a high penetration of EVs, seven EV charging infrastructures are considered in this study, similar to [33]. These infrastructures include home level 1 (L1), workplace L1, home level 2 (L2), workplace L2, public L2, public fast-charging (FC) station, and commercial FC station. The load profiles are obtained by using the methods outlined in Section 2 and an overview of the daily load profiles is shown in Figure 5. It can be observed that the load profiles of level 1 are flatter as compared to level 2 and DC fast-charging stations have the highest peaks, as expected. The reliability analysis is performed for an entire year and load profiles of EVs are also generated for the whole year.

Similarly, the yearly load data of the power system is generated by considering representative days from different seasons of the year. The daily load profiles during weekdays and holidays for the representative days are taken from [38] and are shown in Figure 6. The difference in load profiles during weekdays and holidays along with differences in different seasons is evident in Figure 6.

Finally, the performance of the method under consideration is analyzed for the well-known reliability test system, the Roy Billinton Test System (RBTS) [39]. The single-line diagram of the RBTS test system is shown in Figure 7. The generation model of RBTS is comprised of 11 conventional generators. The capacities of generators in the model are ranging from 5 MW to 40 MW. The total installed capacity of the system is around 240 MW.

All generating units are represented by a two-state model and each generator is tripped one by one and their impact is analyzed for each of the charging infrastructures, as discussed in the previous paragraph. This process is repeated by considering all the tripping scenarios and the results are accumulated to compute the two indices (LOLE and LOEE) as discussed in the previous section.

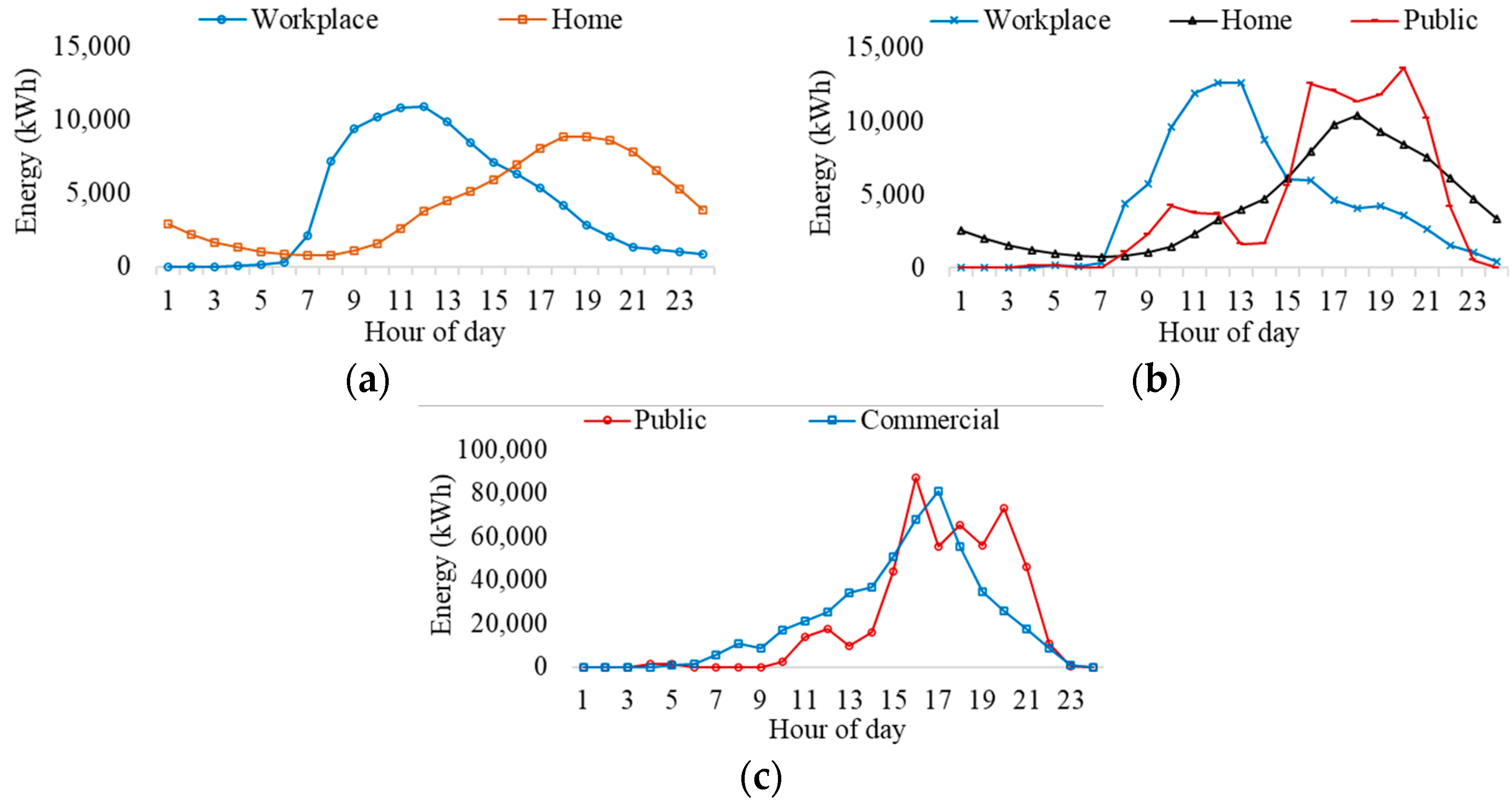
4.2. Loss of Load Expectation (LOLE)

In this section, each charging infrastructure is individually considered, assuming that all the EVs use the same charging infrastructure. The impact of a mixed charging infrastructure is presented in the following section. All seven infrastructures are considered and the LOLE is computed by using the analytical method, discussed in Section 3. The results of LOLE obtained for each infrastructure are tabulated in

Table 1. LOLE (h/year) results of seven charging infrastructures.

EV Ratio (%)	Work L1	Work L2	Public L2	Public FC	Home L1	Home L2	Commercial FC
10	1.43	1.46	1.45	1.52	1.36	1.40	3.24
25	2.12	2.21	2.28	2.55	1.96	2.06	65.28
50	3.98	4.21	5.05	7.12	3.43	4.11	357.29

. The LOLE of the Roy Billinton Test System turns out to be 1.09 h/year and the acceptable value of LOLE is 2.4 h/year, as stated in [40].

It can be observed from Table 1 that in the case of level 1 (workplace level 1 and home level 1) and level 2 (workplace level 2, home level 2, and public level 2) chargers, the value of LOLE is within the acceptable bound till the 25% penetration level of EVs. However, in the case of public fast chargers (FC), even a penetration of 25% EVs also violates the acceptable value of LOEE. Finally, in the case of commercial FC, the LOLE is violated even for the 10% EV penetration scenario. In the case of a 50% EV penetration scenario, the LOLE limit is violated for all the infrastructures. It implies that 50% of EV penetration is not acceptable (without adding a new generation) with any EV charging infrastructure considering the reliability standard of power systems.

Similarly, the increase in the LOLE value for all infrastructures, considering the 1.09 h/year as reference, is shown in Figure 8. It can be observed that in the case of a home, workplace, and public charging stations, the value of LOLE is almost doubled for the 25% penetration case. The higher impact of level 2 chargers is also evident in Figure 8a,b. The impact of FCs is significantly higher than those of level 1 and level 2 chargers, as expected, due to the higher power ratings of these chargers. Especially, in the case of commercial chargers, the value of LOLE is increased exponentially with the higher penetration of EVs. It can be concluded from this analysis that commercial FC has the worst reliability impact on the power systems.

4.3. Loss of Energy Expectation (LOEE)

Similar to the previous section, all seven infrastructures are considered and the LOEE is computed by using the analytical method, discussed in Section 3. The results of LOEE obtained for each infrastructure are tabulated in

Table 2. LOEE results (MWh/yr) of seven charging infrastructures.

EV Ratio (%)	Work L1	Work L2	Public L2	Public FC	Home L1	Home L2	Commercial FC
10	13.07	13.28	13.48	14.12	12.63	12.94	31.99
25	20.39	21.24	22.31	25.73	18.33	19.90	1206.10
50	42.38	46.22	53.27	74.89	34.05	41.82	18678.00

. The LOEE of the Roy Billinton Test System turns out to be 9.8 MWh/year. Similarly, the increase in the LOEE value for all infrastructures, considering the 9.8 MWh/year as a reference is shown in Figure 9.

It can be observed from Table 2 and Figure 9 that for level 1 chargers (home level 1 and workplace level 1), the value of LOEE is increased by approximately 1.3 times for the 10% penetration case and by approximately 4 times for the 50% penetration case. In the case of level 2 chargers (workplace level 2, home level 2, and public level 2), the value of LOEE is increased by approximately 1.4 times for the 10% penetration case and by approximately 5 times for the 50% penetration case. Finally, in the case of fast chargers, an exponential increase in the LOEE value is observed for the commercial FC, similar to LOLE in the previous section. It is worth noting that the increase in LOEE is not linearly correlated with an increase in the EV penetration level. It implies that higher penetrations have more significant impacts due to this non-linear relationship. This is especially evident in the case of fast-charging stations, as shown in Figure 9c,d. Especially, the impact of commercial FCs increases exponentially with an increase in the EV penetration level. It implies that commercial FC is the worst choice when the reliability of the power system is a major concern.

5. Reliability Evaluation of Mixed Infrastructure

In this section, the impact of different ratios of charging infrastructures on the reliability of the power system is analyzed. Two cases are simulated in this section. In the first case, an equal share of all infrastructure is considered while in the second case, customer preference for the charging infrastructure is considered. Details about each of the cases are presented in the following sections.

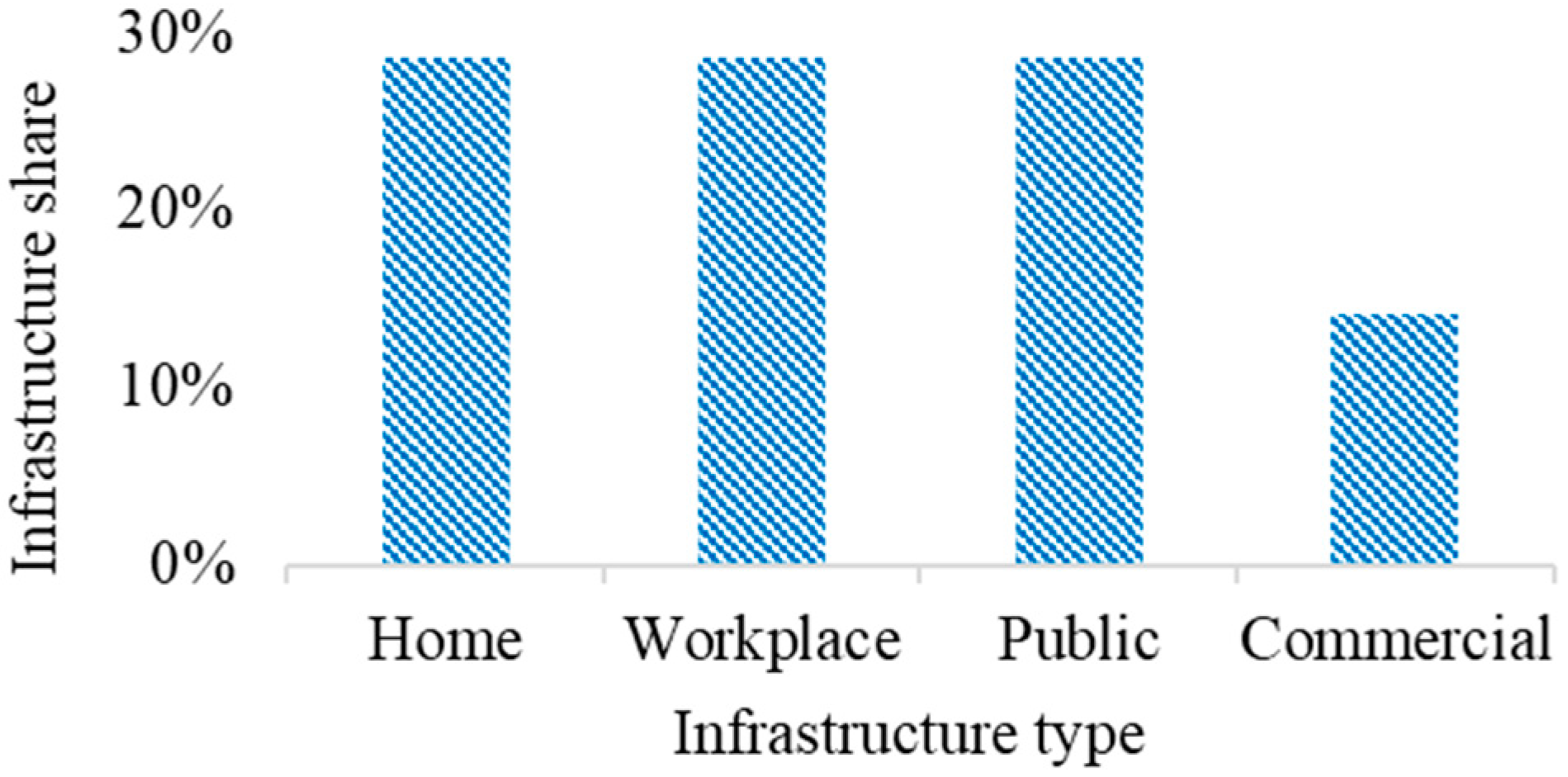
5.1. Case a: Equal Share of all Infrastructure

A total of seven charging infrastructures are considered in this study, which is explained in Section 2. Therefore, in this section, an equal share of all charging infrastructure is considered, i.e., 14.33% each. The location-wise share of charging infrastructure is shown in Figure 10. Home, workplace, and public each have two types of charging infrastructure. Therefore, the share of these three categories is approximately 29% each. However, there is only one charging infrastructure for commercial chargers. Therefore, the share of the commercial charging infrastructure is approximately 14%.

The value of LOLE and LOEE are tabulated for different EV penetration levels in

Table 3. Reliability indices for equal share of charging infrastructure case.

EV Penetration Level	10%	25%	50%
LOLE	1.47	2.31	5.78
LOEE	13.57	22.56	61.94

. It can be observed that with this charging infrastructure portfolio, the value of LOLE is within the acceptable bound for up to a 25% EV penetration scenario. Similarly, the rise in the value of LOEE with higher EV penetration levels is lower as compared to FC stations (as discussed in the previous section). It is worth noting that the values of LOLE and LOEE, in this case, are very similar to level 2 charging stations, despite having approximately a 25% share of FCs. It implies that mixed portfolios can mitigate the reliability impacts while having some ratio of FCs. Therefore, it can be concluded that mixed charging station portfolios are better than FC-only chargers in terms of system reliability.

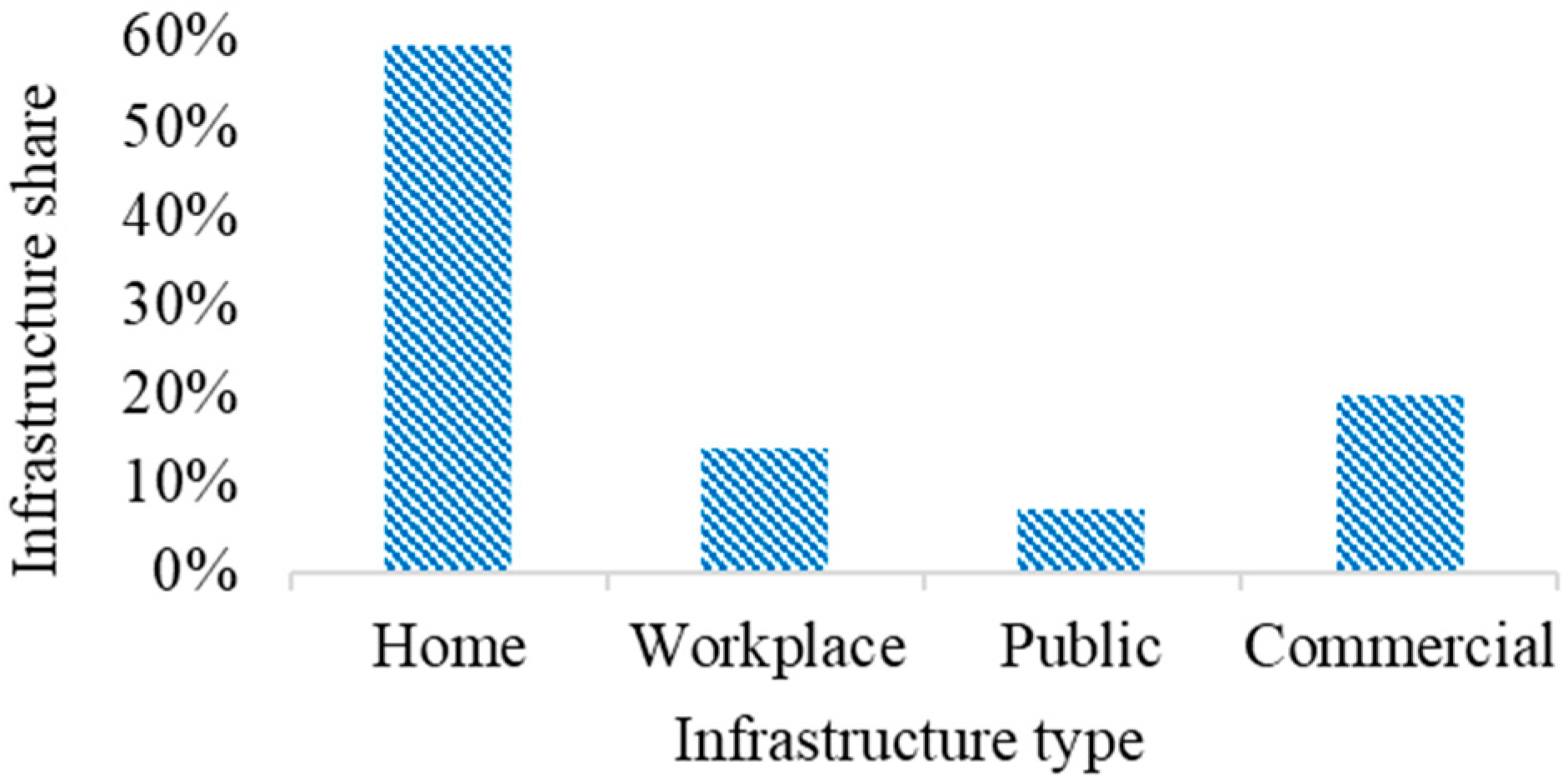
5.2. Case b: User Preference-Based Infrastructure Share

In this section, the share of charging infrastructure is based on customer preference for charging location, i.e., home, workplace, public, and commercial locations. The results are obtained from a real survey conducted by the author and details about the survey can be found in [32]. According to the survey, most EV owners prefer to charge their EVs at home, which is then followed by the commercial charging stations. Public location was the least preferred option, as shown in Figure 11.

The obtained results of LOLE and LOEE are shown in

Table 4. Reliability indices for preference-based share of charging infrastructure case.

EV Penetration Level	10%	25%	50%
LOLE	1.47	2.41	8.28
LOEE	13.63	23.89	92.63

. It can be observed from Table 4 that the value of LOLE is within the acceptable range for up to 25% of EV penetration, similar to the previous case. However, the value of LOLE and LOEE at different EV penetration ratios is higher as compared to the previous case. This is due to the higher ratio of fast charging infrastructure in this case (20% commercial and 10% public) as compared to the previous case (12% each). However, the impacts are still closer to level 2 chargers and significantly lower than the FC-only cases. It implies that the commercial charging infrastructure has a huge impact on the reliability of the power system. Therefore, it can be concluded that penetration of commercial FCs needs to be limited to enhance the system’s reliability.

6. Conclusions

The impact of electric vehicle charging load on the reliability of power systems is analyzed in this study. Seven infrastructures are modeled and different EV penetration scenarios are considered. Two of the most widely used reliability indices (LOLE and LOEE) are used to evaluate the reliability of the power system under different penetration levels of electric vehicles. Both single charger and mixed portfolio cases are evaluated.

• Test results have shown that commercial fast chargers have the worst impact on the reliability of the power system while level 1 and level 2 chargers have a lower impact.
• In the case of commercial fast chargers, the reliability of the system was below the acceptable range for only a 10% penetration of electric vehicles. In the case of level 1 and level 2 chargers, reliability was within the acceptable range for up to a 25% penetration of electric vehicles.
• It has also been observed that mixed charging infrastructure portfolios enhance the reliability of the power system, i.e., LOLE and LOEE are reduced as compared to the commercial-only case despite having a fair share of fast chargers in the portfolio.

The integration of renewables could differently impact the reliability of power systems even with a high penetration of EVs. Therefore, the author is planning to carry out a follow up research on his topic with the inclusion of renewables.