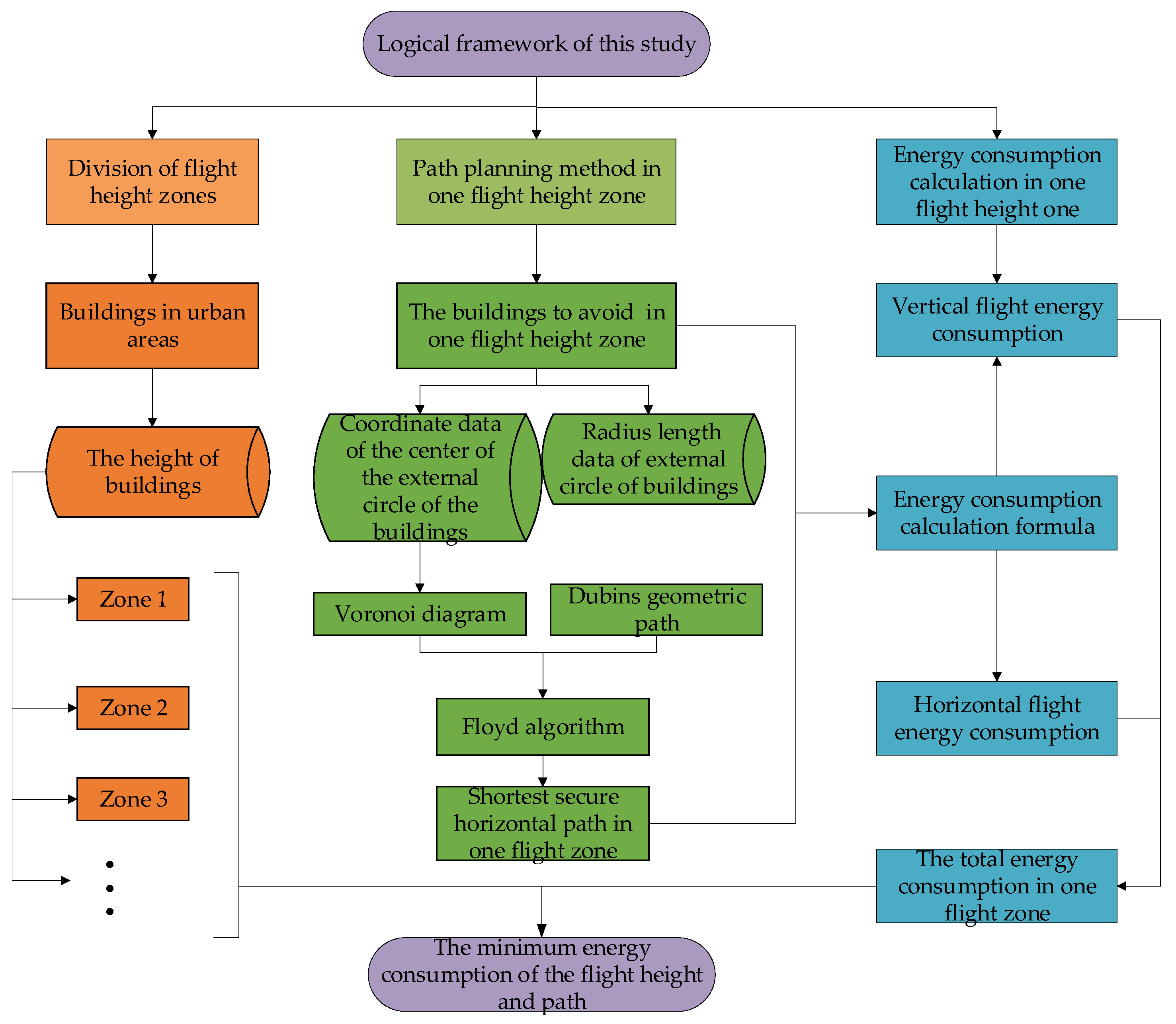
Path Planning of Electric VTOL UAV Considering Minimum Energy Consumption in Urban Areas
Abstract
:1. Introduction
2. Battery Output Power and Calculation of Energy Consumption
2.1. Battery Output Power
2.2. Energy Consumption Calculation
3. Safe Horizontal Path Planning Method
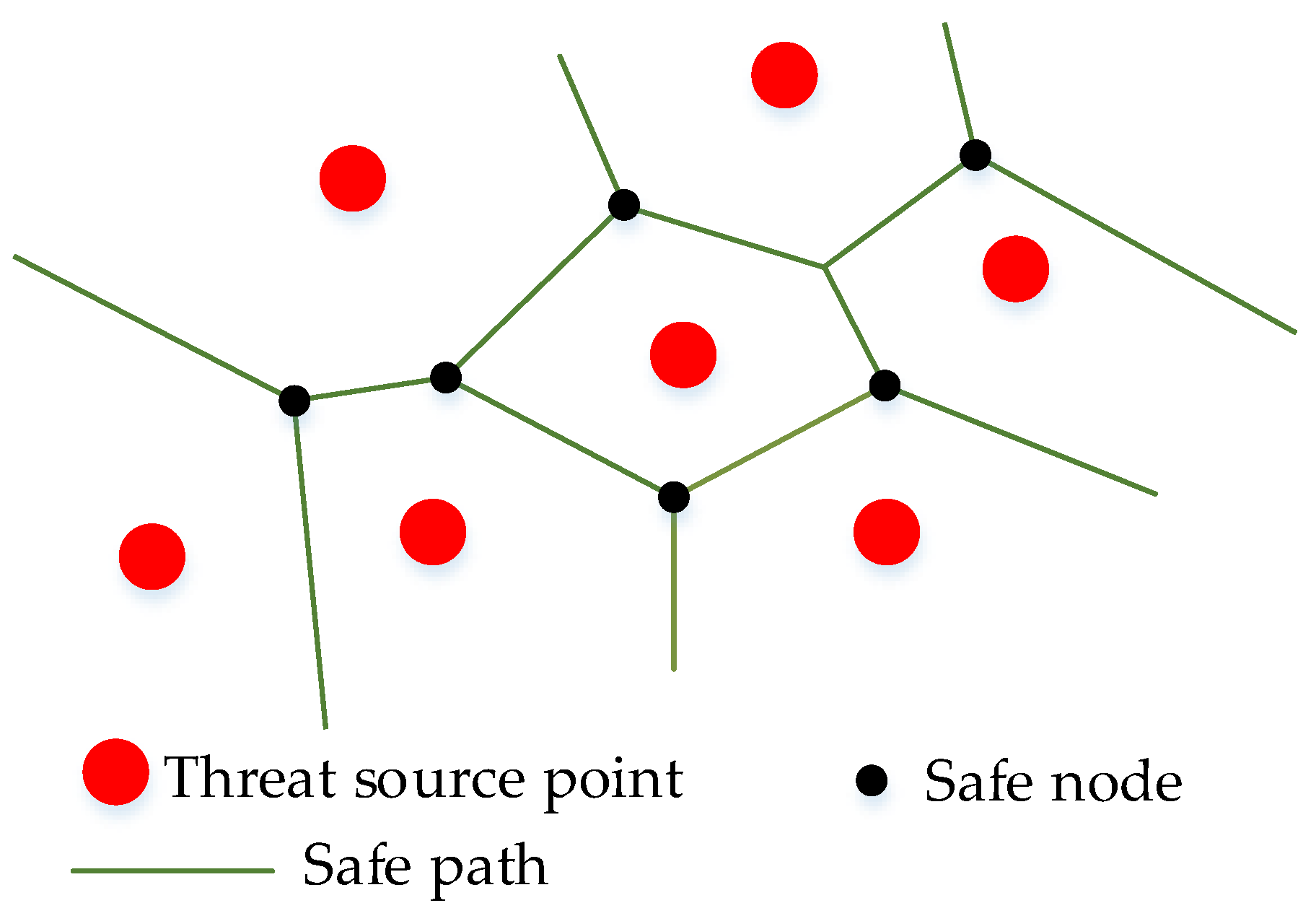
3.1. Generation of Safe Nodes
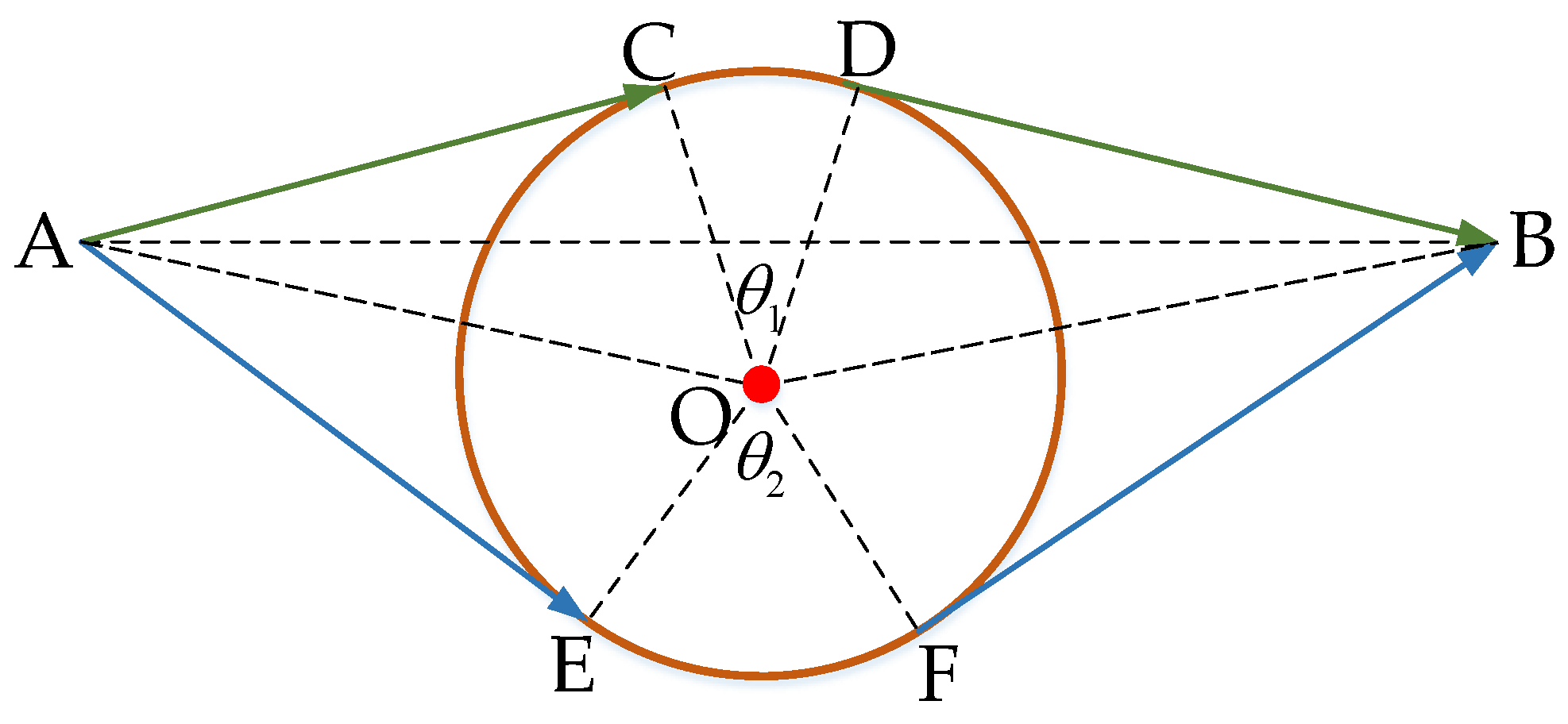
3.2. Dubins Geometric Path
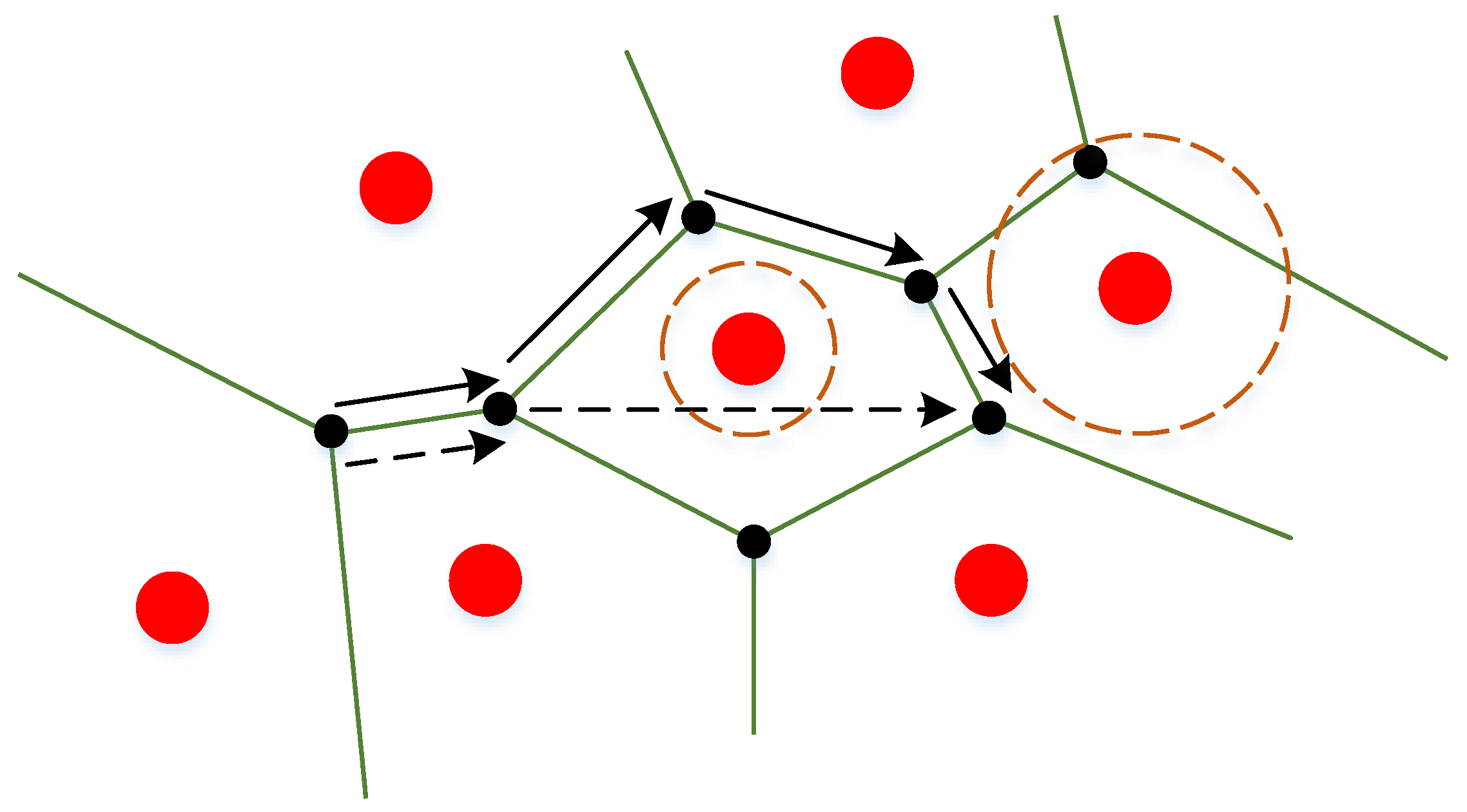
- In the Voronoi diagram, the lines between some non-adjacent safe nodes may be in the threat circle domain. The left dashed circle in Figure 4 is the external circle of the building, and the dashed line passes through the outer circle, indicating that it is extremely risky for the UAV to fly in a straight line between these two points.
- Some safe nodes may be influenced by buildings. The right dashed circle in Figure 4 contains a safety node, indicating that the safety node is located in the risky circle domain and should be discarded when planning the path.
3.3. The Shortest Path Planning Method Based on Floyd Algorithm
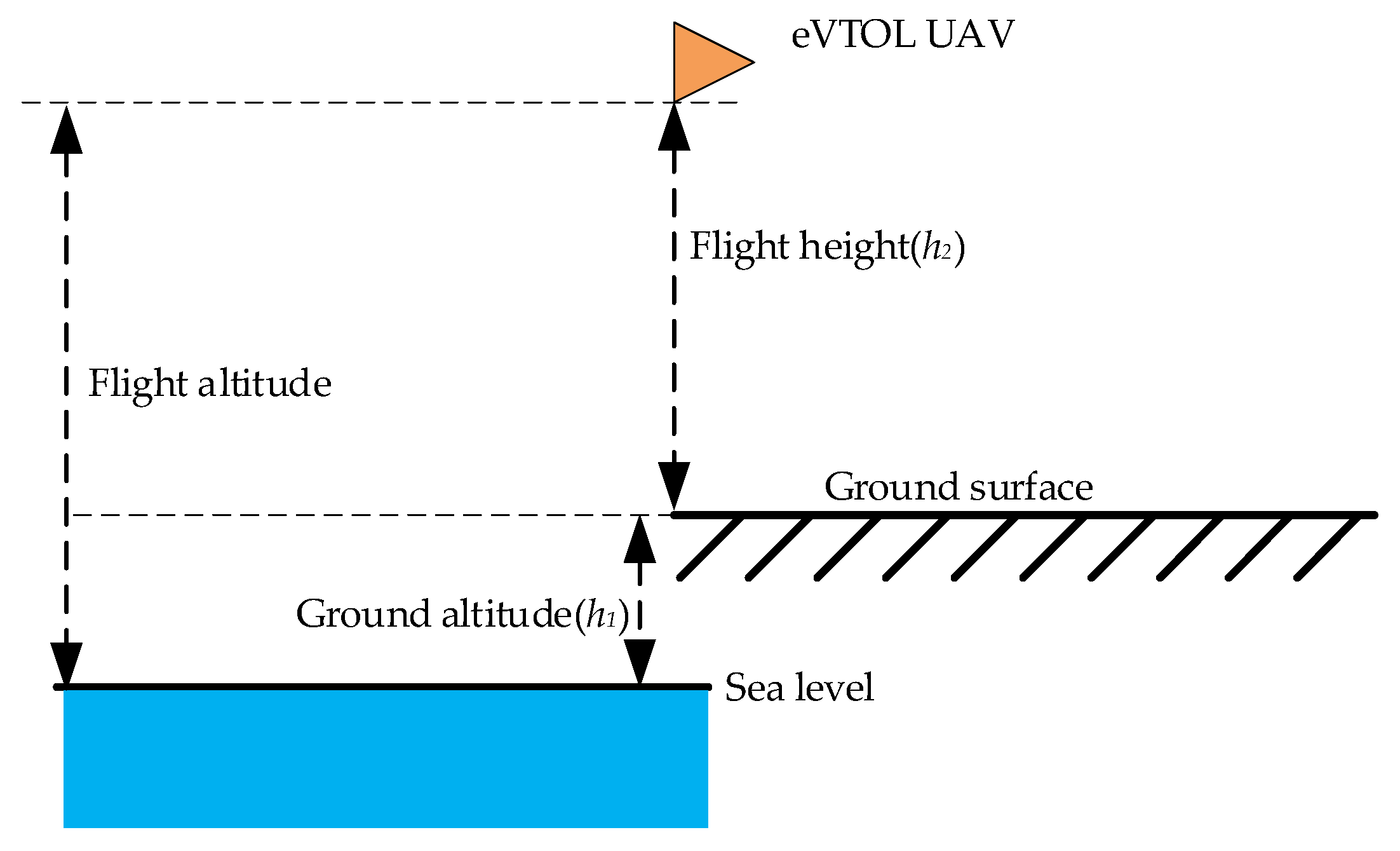
4. Optimum Flight Height
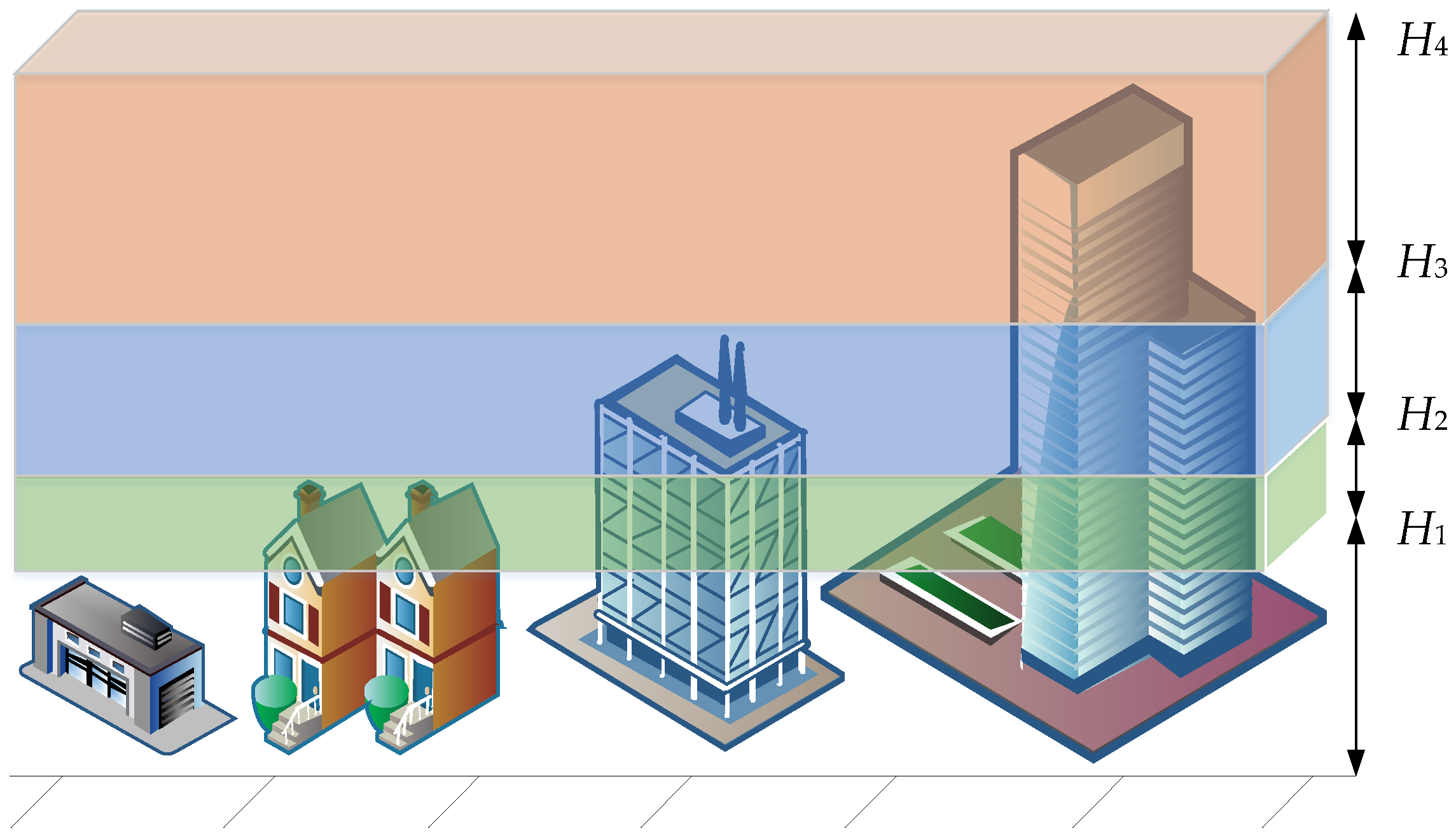
4.1. Division of the Flight Height Zones
4.2. The Flight Height with the Minimum Energy Consumption
- When the UAV is in the flight height zone (A, B), it can fly over buildings with height no higher than A, and it needs to bypass buildings with height no lower than B;
- In the same flight height range, when the flight height of the UAV changes within the range, the number and location of buildings affecting the flight safety of the UAV remain unchanged, and the safe horizontal path remains unchanged;
- In different flight height zones, the number and location of buildings affecting the safety of UAV flight are different, and the safe horizontal path is also different;
- In the lower flight height range, there are also more buildings that affect the safety of UAV flight.
5. Simulation Analysis and Discussion
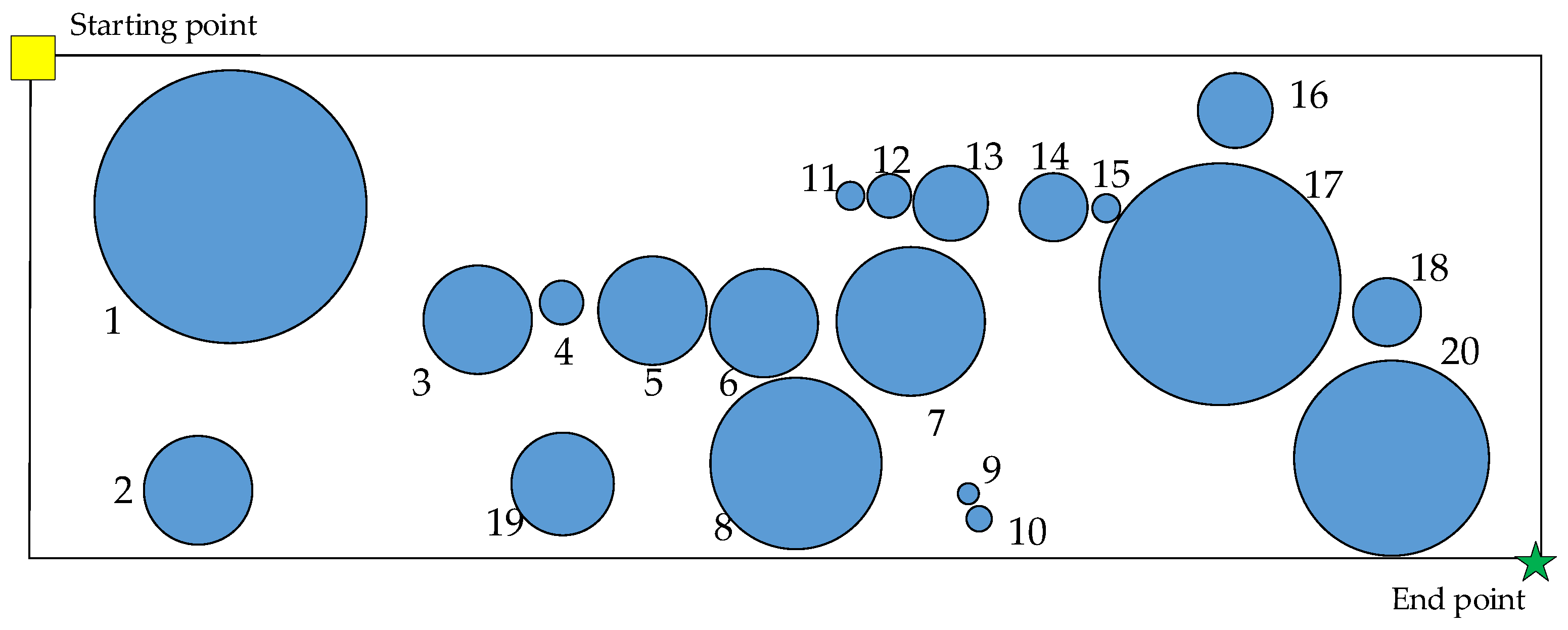
5.1. Flight Area Settings
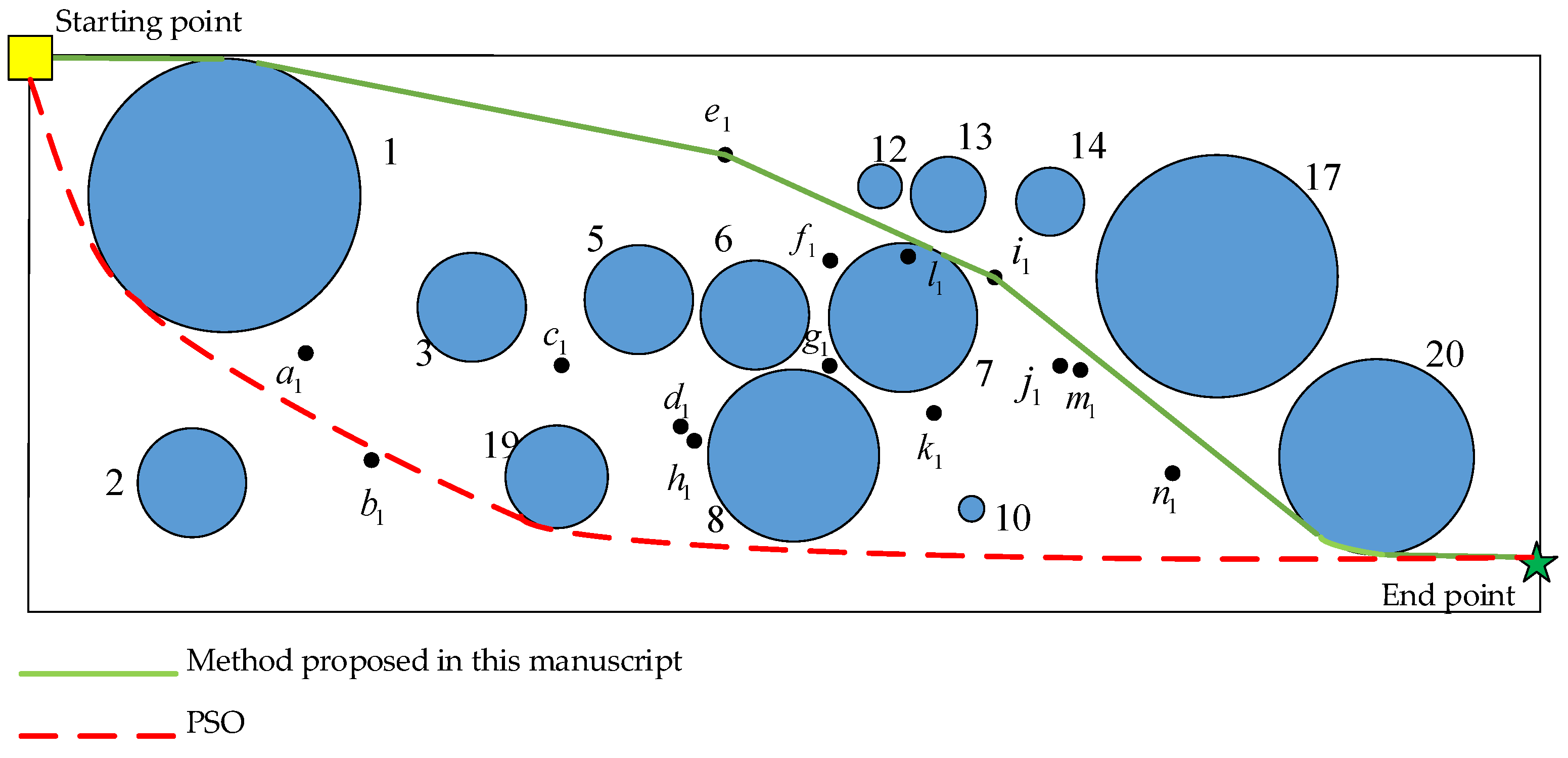
5.2. Horizontal Path Planning
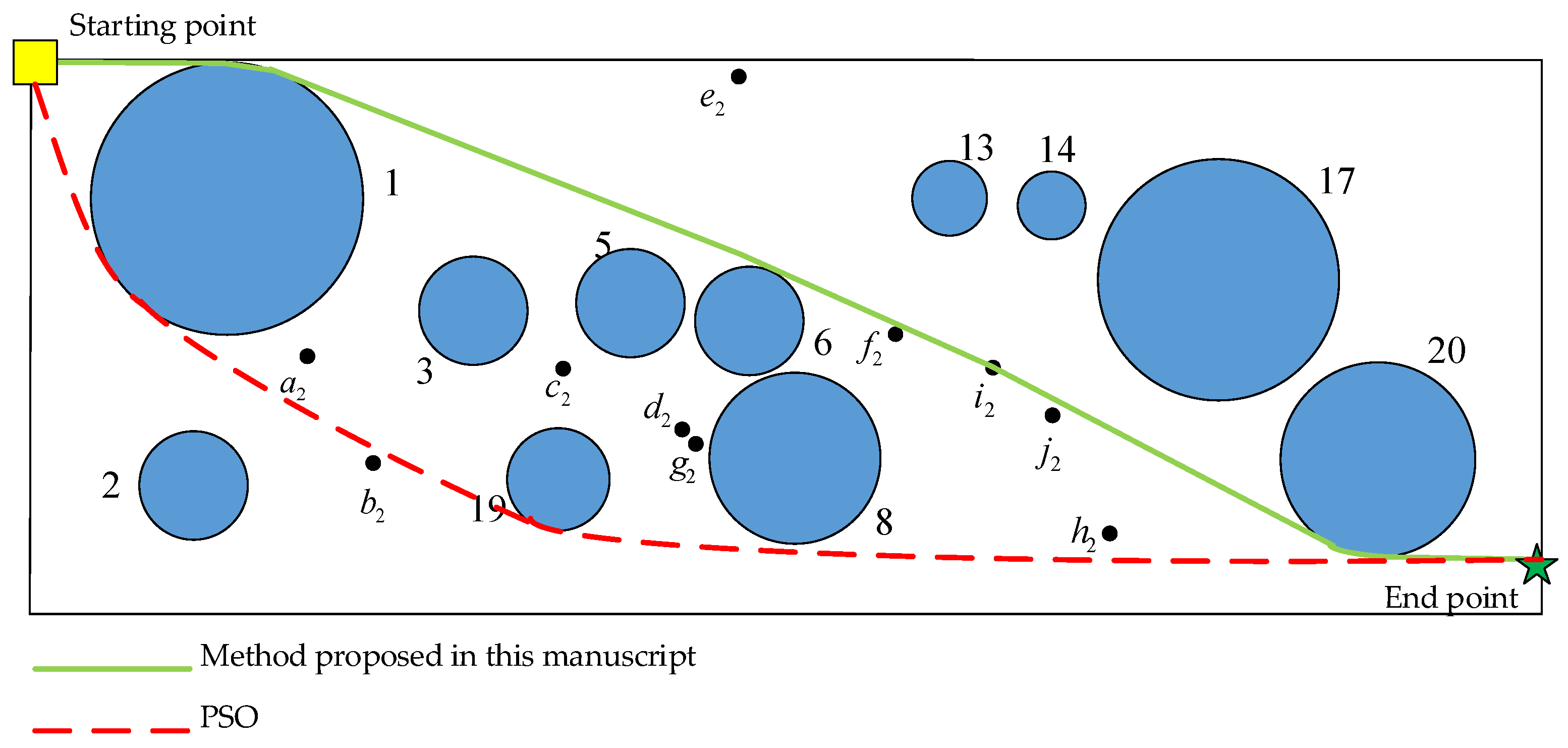
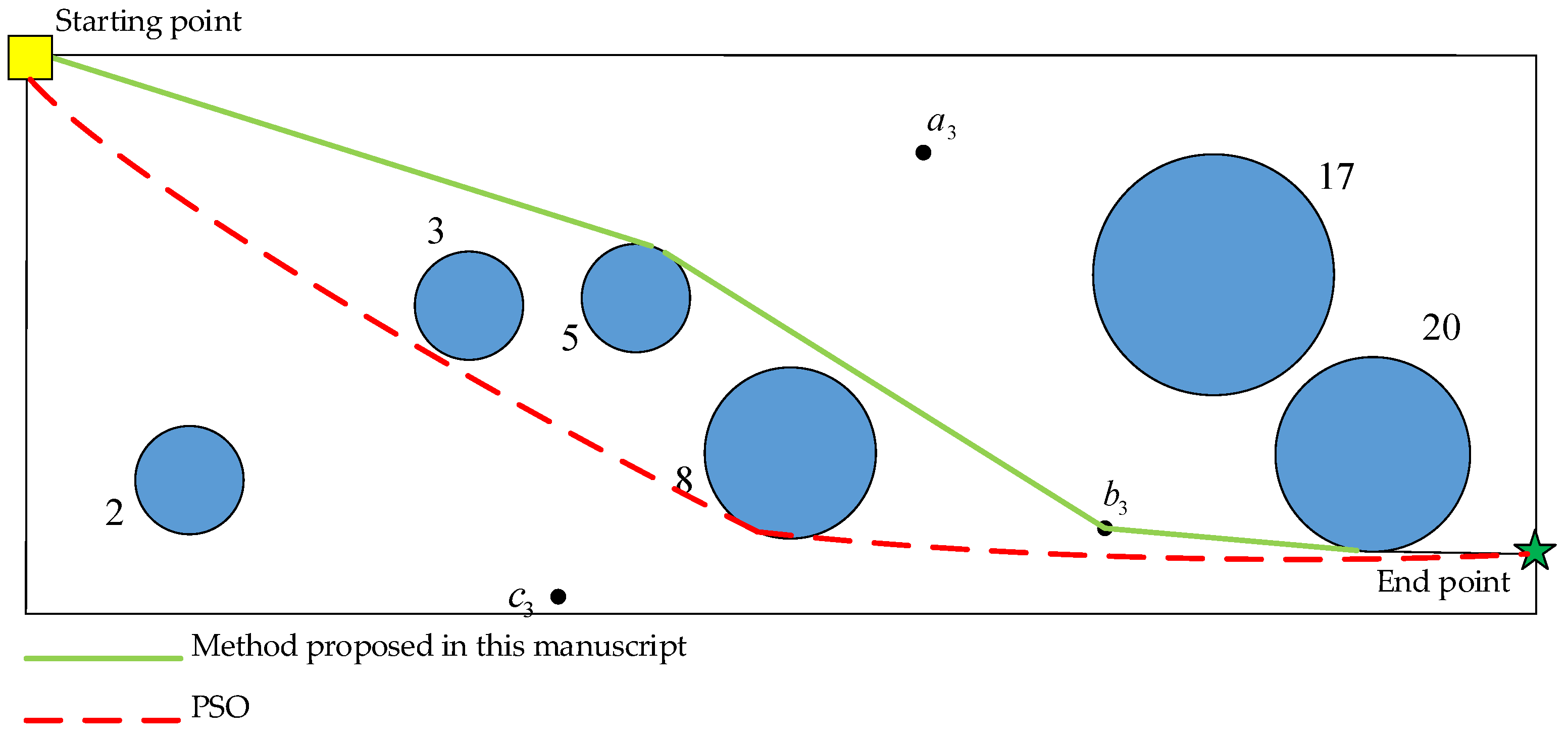
5.2.1. Planning Path by Method in This Manuscript and PSO
- Xk+ 1 is the position of particle i of the k + 1 generation;
- Xk is the position of particle i of the k generation;
- Vk+ 1 is the velocity of particle i of the k + 1 generation;
- Vk is the velocity of particle i of the k generation;
- Pkid is the position of the individual optimal particle i of the k generation;
- Pkgd is the position of the global optimal particle of the k generation;
- r1 and r2 are random numbers between (0, 1);
- c1 and i c2 are constants.
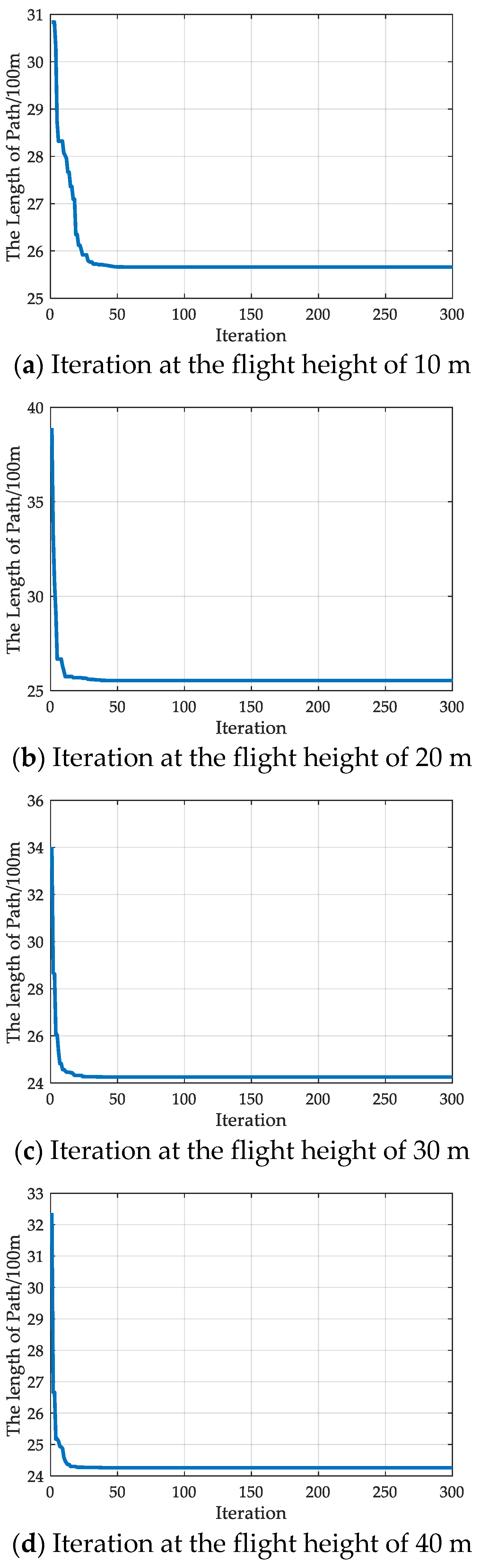
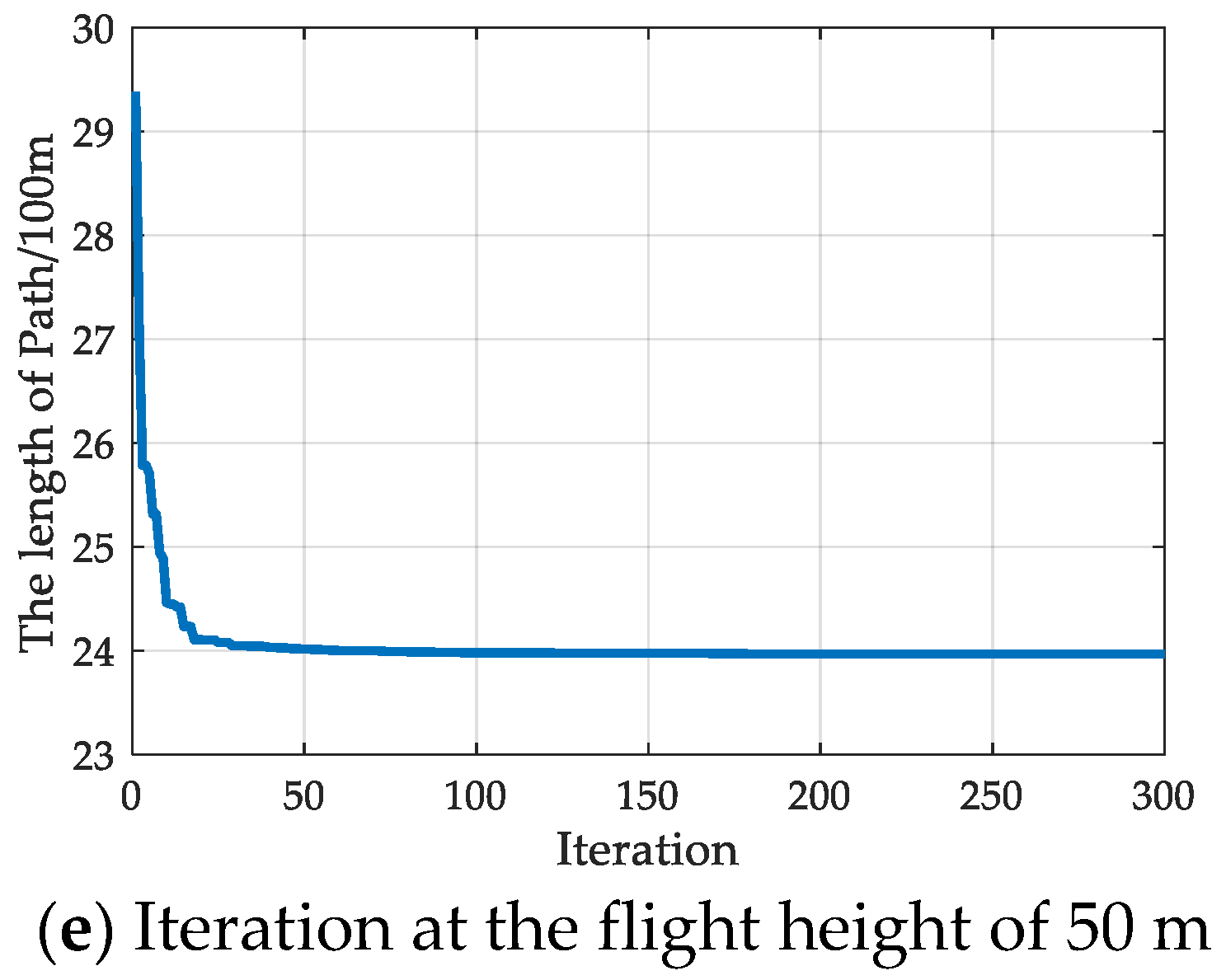
- The same method is used to divide the flight zones of the eVTOL UAV. According to the building height, the flight height zone is divided into (10 m, 20 m), (20 m, 30 m), (30 m, 40 m), (50 m, 60 m), corresponding to the flight height above the ground is 10 m, 20 m, 30 m, 40 m, 50 m, respectively. Find the paths at each of the five heights. Flight zone (10 m, 20 m);
- 2.
- Flight zone (20 m, 30 m);
- 3.
- Flight zone (30 m, 40 m);
- 4.
- Flight zone (40 m, 50 m)
- 5.
- Flight zone (50 m, 60 m)
5.2.2. Comparison of Path Planning Methods
5.3. Results and Analysis
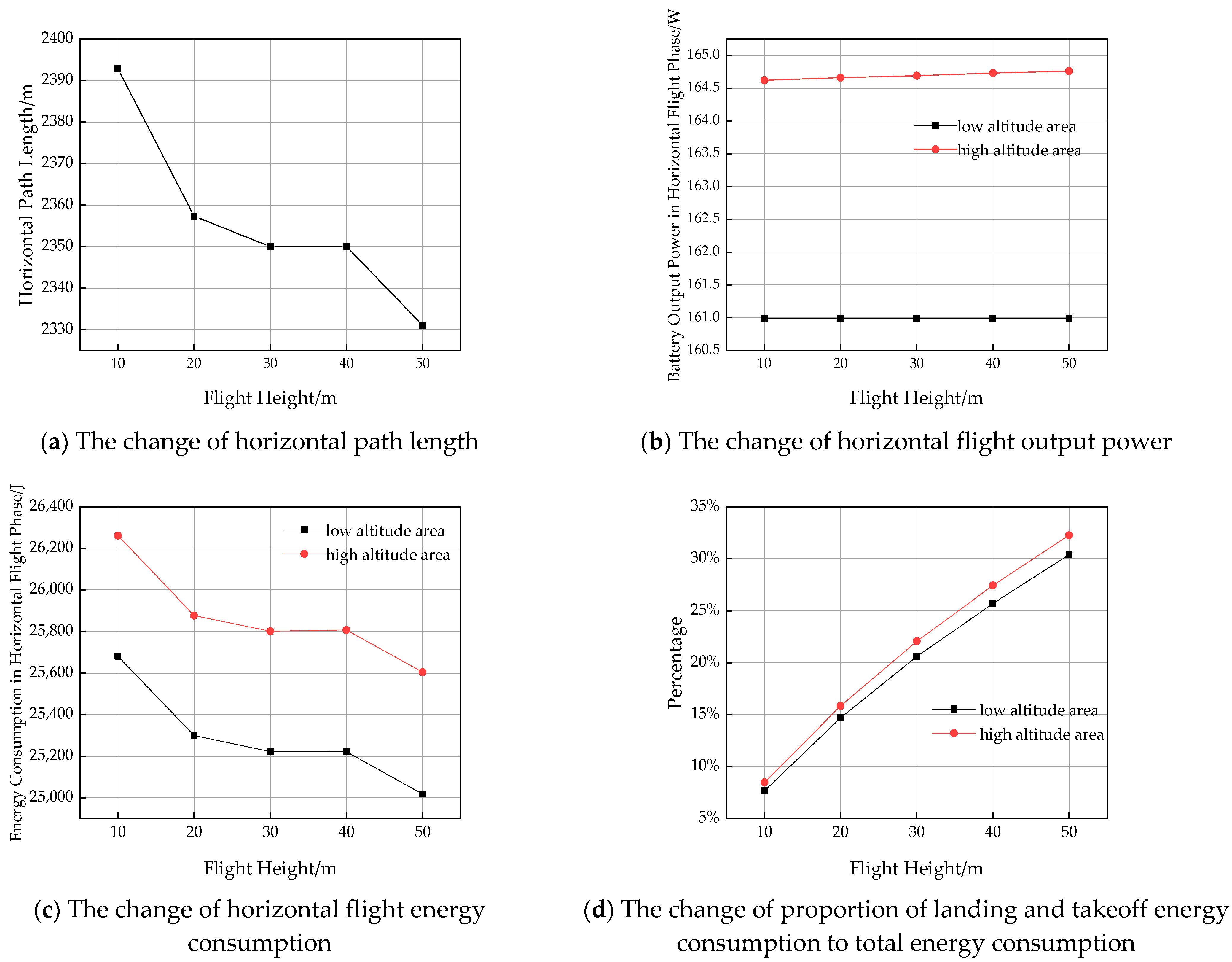
5.3.1. Low-Altitude Area and High-Altitude Area
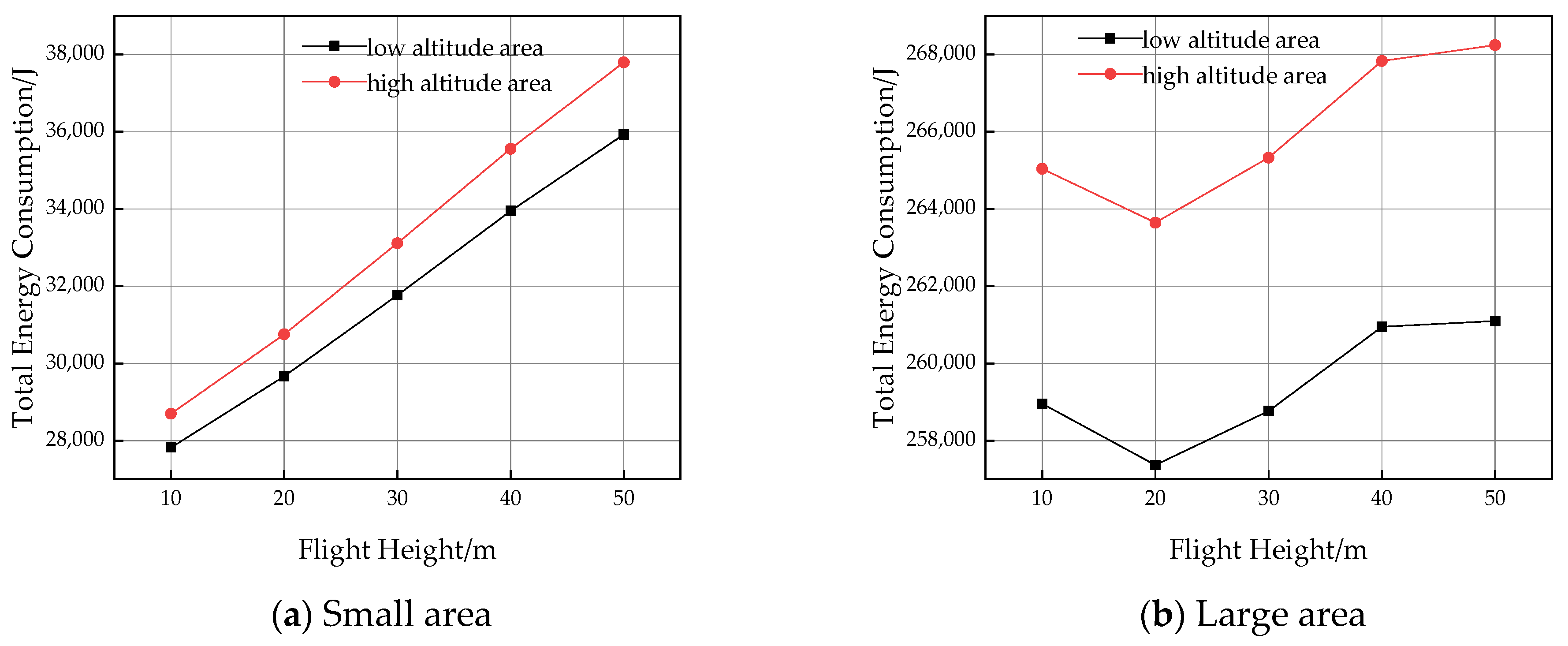
5.3.2. Small Area and Large Area
5.4. Discussion
6. Conclusions
- (1)
- The eVTOL UAV combines the advantages of multi-rotor UAV and fixed-wing UAV. Its operation is characterized by vertical takeoff first and then switching to a fixed wing attitude during the horizontal flight phase. Therefore, we first consider the flight height of the UAV and then plan the horizontal path of the UAV.
- (2)
- In both low-altitude and high-altitude areas, the proportion of take-off and landing energy consumption in the total energy consumption of UAV in the small area increases with the increase of flight height. The air at high altitudes is thinner and less dense. When flying at the same altitude, the battery output of a UAV at high altitudes is greater than that at low-altitudes.
- (3)
- In low-altitude and high-altitude areas, the total energy consumption of UAVs varies with flight altitude in the same way. However, in small and large areas, the variation of total energy consumption of UAV is different. In small area environment, the total energy consumption increases with the increase of flight altitude. In a large regional environment, the take-off and landing energy consumption takes a small proportion in the total energy consumption, and the total energy consumption fluctuates. Therefore, the energy consumption of the UAV at all flying altitudes should be analyzed and calculated, and the flying altitude with the minimum energy consumption can be obtained after comparison. The energy savings enable UAVs to cover longer distances, thus reducing operating costs for UAV operators.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Menouar, H.; Guvenc, I.; Akkaya, K.; Uluagac, A.S.; Kadri, A.; Tuncer, A. UAV-enabled intelligent transportation systems for the smart city: Applications and Challenges. IEEE Comun. Mag. 2017, 55, 22–28. [Google Scholar] [CrossRef]
- Cohen, A.P.; Shaheen, S.A.; Farrar, E.M. Urban Air Mobility: History, Ecosystem, Market Potential, and Challenges. IEEE Trans. Intell. Tansportation Syst. 2021, 22, 6074–6087. [Google Scholar] [CrossRef]
- Zhang, H.; Zou, Y.; Zhang, Q.; Liu, H. Future urban air mobility management: Review. Acta Aeronaut. Astronaut. Sin. 2021, 42, 82–106. [Google Scholar]
- Stahl, P.; Roessler, C.; Hornung, M. Modelling and Performance Impact of Different Battery Architectures for Fixed-Wing eVTOL UAV. In Proceedings of the AIAA Scitech 2020 Forum, Orlando, FL, USA, 6–10 January 2020; p. 11. [Google Scholar]
- Wang, B.; Hou, Z.; Wang, W. Performance analysis of propulsion system of miniature electric-powered vertical takeoff and landing air vehicles. J. Natl. Univ. Def. Technol. 2015, 37, 84–90. [Google Scholar]
- Vascik, P.D.; Hansman, R.J. Constraint identification in on demand mobility for aviation through an exploratory case study of Los Angeles. In Proceedings of the 17th AIAA Aviation Technology, Integration, and Operations Conference, Denver, CO, USA, 5–9 June 2017. [Google Scholar] [CrossRef]
- Vascik, P.D.; Balakrishnan, H.; Hansman, R.J. Assessment of air traffic control for urban air mobility and unmanned systems. In Proceedings of the 8th International Conference on Research in Air Transportation, Castelldefels, Spain, 25–29 June 2018. [Google Scholar]
- Zhang, X.; Jiao, Q. Research on UAS air traffic management system architecture. J. Wuhan Univ. Technol. 2020, 42, 29–37+58. [Google Scholar]
- Quan, Q.; Li, G.; Bai, Y.; Fu, R.; Li, M.; Ke, C.; Cai, K. Low altitude UAV traffic management: An introductory overview and proposal. Acta Aeronaut. Astronaut. Sin. 2020, 41, 6–34. [Google Scholar]
- Ramana, M.V.; Varma, S.A.; Kotharia, M. Motion planning for a fixed-wing UAV in urban environments. IFAC-Pap. Online 2016, 49, 419–424. [Google Scholar] [CrossRef]
- Filippis, L.D.; Guglieri, G.; Quagliotti, F. Path planning strategies for UAVS in 3D environments. J. Intell. Robot. Syst. 2012, 65, 247–264. [Google Scholar] [CrossRef]
- He, T.; Mantegh, I.; Chen, L.; Vidal, C.; Xie, W. UAS flight path planning for dynamic, multi-vehicle environment. In Proceedings of the 2020 International Conference on Unmanned Aircraft Systems (ICUAS), Dallas, TX, USA, 1–4 September 2020; pp. 211–219. [Google Scholar]
- Wu, P.; Xie, J.; Liu, Y.; Chen, J. Risk-bounded path planning for urban air mobility operations under uncertainty. arXiv 2021, arXiv:2109.04606. [Google Scholar] [CrossRef]
- Wu, Y.; Hu, X. An online route planning method for multi-rotor drone in urban environments. Control Decis. 2021, 36, 2851–2860. [Google Scholar]
- Muñoz, J.; López, B.; Quevedo, F.; Monje, C.A.; Garrido, S.; Moreno, L.E. Multi UAV Coverage Path Planning in Urban Environments. Sensors 2021, 21, 7365. [Google Scholar] [CrossRef]
- Zhang, H.; Gan, X.; Li, S.; Feng, Z.; Jin, Y. UAV route planning considering regional risk assessment under complex low altitude environment. Chin. J. Sci. Instrum. 2021, 42, 257–266. [Google Scholar]
- Majeed, A.; Hwang, S.O. A Multi-Objective Coverage Path Planning Algorithm for UAVs to Cover Spatially Distributed Regions in Urban Environments. Aerospace 2021, 8, 343. [Google Scholar] [CrossRef]
- Aggarwal, S.; Kumar, N. Path planning techniques for unmanned aerial vehicles: A review, solutions, and challenges. Comput. Commun. 2020, 149, 270–299. [Google Scholar] [CrossRef]
- Wang, M.; Diepolder, J.; Zhang, S.; Sopper, M.; Holzapfel, F. Trajectory optimization-based maneuverability assessment of eVTOL aircraft. Aerosp. Sci. Technol. 2021, 117, 106903. [Google Scholar] [CrossRef]
- Han, P.; Yang, X.; Zhao, Y.; Guan, X.; Wang, S. Quantitative Ground Risk Assessment for Urban Logistical Unmanned Aerial Vehicle (UAV) Based on Bayesian Network. Sustainability 2022, 14, 5733. [Google Scholar] [CrossRef]
- Dorling, K.; Heinrichs, J.; Messier, G.G.; Magierowski, S. Vehicle routing problems for drone delivery. IEEE Trans. Syst. Man Cybern. Syst. 2017, 47, 70–85. [Google Scholar] [CrossRef] [Green Version]
- Ahluwalia, R.K.; Peng, J.K.; Wang, X.; Papadias, D.; Kopasz, J. Performance and cost of fuel cells for urban air mobility. Int. J. Hydrog. Energy 2021, 46, 36917–36929. [Google Scholar] [CrossRef]
- Dukkanci, O.; Kara, B.Y.; Bektas, T. Minimizing energy and cost in range-limited drone deliveries with speed optimization. Transp. Res. Part C 2021, 125, 102985. [Google Scholar] [CrossRef]
- She, R.; Ouyang, Y. Efficiency of UAV-based last-mile delivery under congestion in low-altitude air. Transp. Res. Part C 2021, 122, 102878. [Google Scholar] [CrossRef]
- Cheng, C.; Adulyasak, Y.; Rousseau, L.M. Drone routing with energy function: Formulation and exact algorithm. Transp. Res. Part B 2020, 139, 364–387. [Google Scholar] [CrossRef]
- Shao, Q.; Shao, M.; Lu, Y. Terminal area control rules and eVTOL adaptive scheduling model for multi-vertiport system in urban air Mobility. Transp. Res. Part C Emerg. Technol. 2021, 132, 103385. [Google Scholar] [CrossRef]
- Fevgas, G.; Lagkas, T.; Argyriou, V.; Sarigiannidis, P. Coverage Path Planning Methods Focusing on Energy Efficient and Cooperative Strategies for Unmanned Aerial Vehicles. Sensors 2022, 22, 1235. [Google Scholar] [CrossRef] [PubMed]
- Aiello, G.; Valavanis, K.P.; Rizzo, A. Fixed-Wing UAV energy efficient 3D path planning in cluttered environments. J. Intell. Robot. Syst. 2022, 105, 60. [Google Scholar] [CrossRef]
- Han, P.; Zhang, B. Effect of track error on safety risk assessment of UAV ground impact. China Saf. Sci. J. 2021, 31, 106–111. [Google Scholar]
- Zhou, Q.; Xu, M. Research On Risk Assessment Of UAV To Buildings. In Proceedings of the 2021 International Conference on Information Control, Electrical Engineering and Rail Transit (ICEERT), Kunming, China, 30 October–1 November 2021; pp. 37–40. [Google Scholar] [CrossRef]
- Li, C.; Qu, W.; Li, Y.; Huang, L.; Wei, P. Overview of traffic management of urban air mobility (UAM) with eVTOL aircraft. J. Traffic Transp. Eng. 2020, 20, 35–54. [Google Scholar]
- Tang, W.; Song, B.; Cao, Y.; Yang, W. Preliminary design method for miniature electric-powered vertical take-off and landing unmanned aerial vehicle and effects of special parameters. Acta Aeronaut. Astronaut. Sin. 2017, 38, 120–133. [Google Scholar]
- Mouillet, V. Revision Summary Document for the Base of Aircraft Data (BADA); Revision 3.8; EUROCONTROL: Brussels, Belgium, 2009. [Google Scholar]
- Giesbrecht, J. Global Path Planning for Unmanned Ground Vehicles; Technical Report; Defence Research and Development Suffield (ALBERTA): Suffield, AB, Canada, 2004. [Google Scholar]
- Wang, Z.; Liu, C.; Cai, X. A path planning method based on Voronoi diagram. Shipboard Electron. Countermeas. 2017, 40, 76–80. [Google Scholar]
- Shi, H.; Liu, S. Unmanned aerial vehicle route improvement planning based on Voronoi diagram. J. Jilin Univ. (Sci. Ed.) 2018, 56, 945–952. [Google Scholar]
- Bhargav, J.; Zheng, C.; Tal, S. On shortest Dubins path via a circular boundary. Automatica 2020, 121, 109192. [Google Scholar]
- Li, H.; Chen, Y.; Zhang, Z.; Liu, X. UAV collision avoidance path planning based on Dubins method. Flight Dyn. 2020, 38, 44–49. [Google Scholar]
- Zhao, Y.; Zheng, Y. Construction and optimization of flight mission profile of urban logistics UAV. Flight Dyn. 2021, 39, 54–59+67. [Google Scholar]




| Parameter | Value | Parameter | Value |
|---|---|---|---|
| M | 6.2 Kg | κ | 0.94 |
| A | 1.313 m2 | ηp | 0.8 |
| VC | 15 m/s | ηM | 0.8 |
| VT | 5 m/s | ηESC | 0.8 |
| VL | 5 m/s | CD0 | 0.015 |
| k | 0.13 | g | 9.8 m/s2 |
| Serial Number | Center Coordinates (m) | Circle Diameter (m) | Height of Building (m) | Serial Number | Center Coordinates (m) | Circle Diameter (m) | Height of Building (m) |
|---|---|---|---|---|---|---|---|
| 1 | (286, 528) | 403 | 30 | 11 | (1185, 543) | 40 | 10 |
| 2 | (237, 114) | 160 | 40 | 12 | (1245, 541) | 60 | 20 |
| 3 | (644, 365) | 160 | 40 | 13 | (1335, 531) | 110 | 30 |
| 4 | (767, 387) | 70 | 10 | 14 | (1485, 525) | 100 | 30 |
| 5 | (899, 376) | 160 | 50 | 15 | (1560, 523) | 40 | 10 |
| 6 | (1060, 355) | 160 | 30 | 16 | (1747, 666) | 110 | 10 |
| 7 | (1276, 357) | 220 | 20 | 17 | (1726, 414) | 350 | 50 |
| 8 | (1108, 151) | 250 | 50 | 18 | (1968, 373) | 100 | 10 |
| 9 | (1360, 109) | 30 | 10 | 19 | (770, 124) | 150 | 30 |
| 10 | (1375, 73) | 40 | 20 | 20 | (1963, 144) | 286 | 60 |
| Safe Node | Coordinate (m) | Safe Node | Coordinate (m) |
|---|---|---|---|
| a1 | (400, 305) | h1 | (973, 167) |
| b1 | (503, 138) | i1 | (1405, 410) |
| c1 | (776, 281) | j1 | (1510, 279) |
| d1 | (954, 190) | k1 | (1318, 212) |
| e1 | (1011, 589) | l1 | (1281, 452) |
| f1 | (1167, 433) | m1 | (1517, 278) |
| g1 | (1169, 282) | n1 | (1667, 123) |
| Safe Node | Coordinate (m) | Safe Node | Coordinate (m) |
|---|---|---|---|
| a2 | (400, 305) | f2 | (1265, 37) |
| b2 | (503, 138) | g2 | (973, 167) |
| c2 | (776, 281) | h2 | (1571, 39) |
| d2 | (954, 190) | i2 | (1400, 282) |
| e2 | (1028, 708) | j2 | (1487, 212) |
| Safe Node | Coordinate (m) | Safe Node | Coordinate (m) |
|---|---|---|---|
| a3 | (1304, 592) | b3 | (1571, 39) |
| Safe Node | Coordinate (m) | Safe Node | Coordinate (m) |
|---|---|---|---|
| a4 | (1304, 592) | b4 | (1571, 39) |
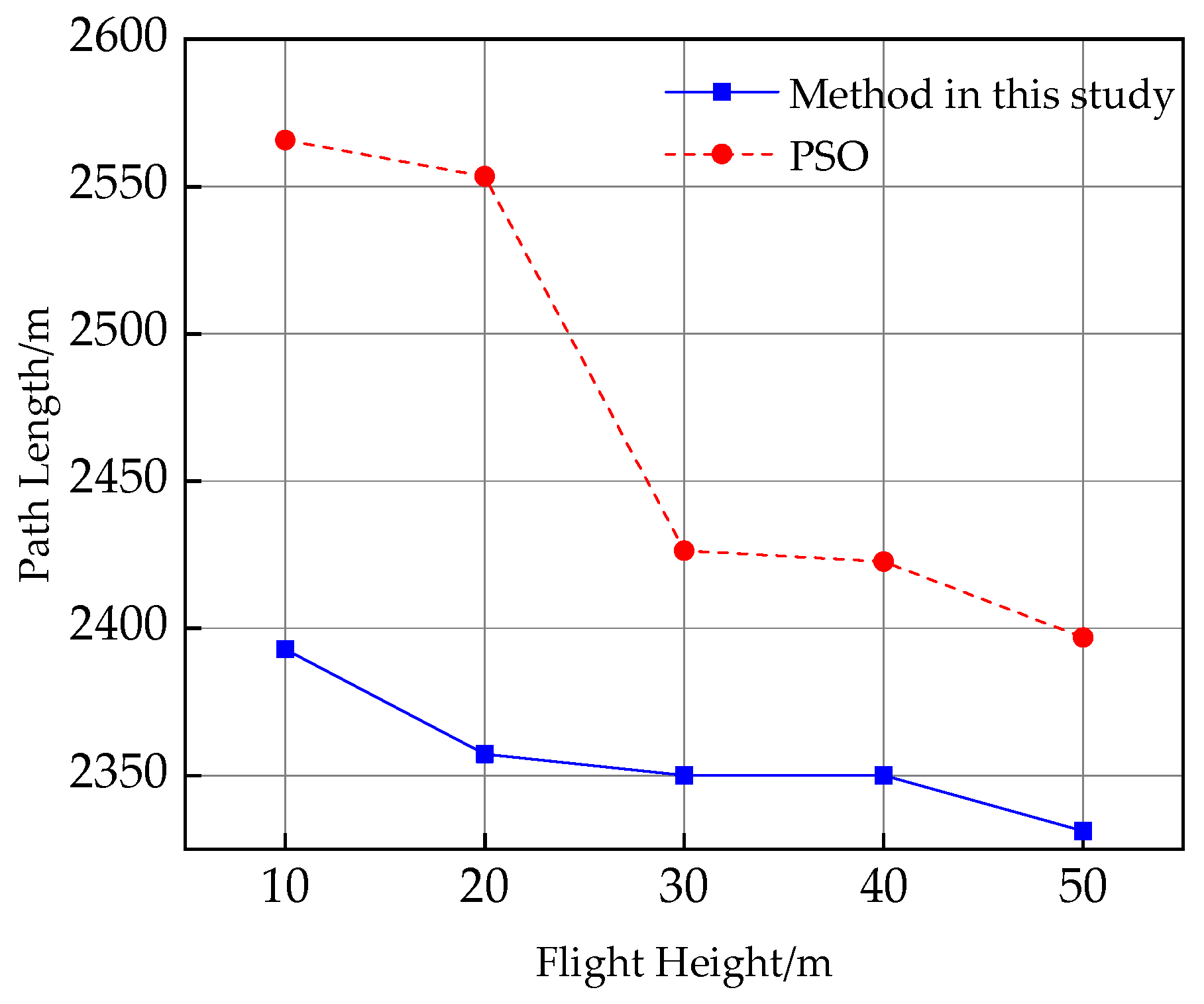
| Flight Height (m) | Path Length Obtained by the Method in This Study (m) | Path Length Obtained by PSO (m) |
|---|---|---|
| 10 | 2392.82 | 2565.8 |
| 20 | 2357.32 | 2553.45 |
| 30 | 2350.03 | 2426.37 |
| 40 | 2350.03 | 2422.67 |
| 50 | 2331.11 | 2396.9 |
| Flight Height (m) | Horizontal Path Length (m) | Battery Output Power in Horizontal Flight Phase (W) | Energy Consumption in Horizontal Flight Phase (J) | Energy Consumption in Take-off Phase (J) | Energy Consumption in Landing Phase (J) | Total Energy Consumption (J) |
|---|---|---|---|---|---|---|
| 10 | 2392.82 | 160.99 | 25,681.79 | 1069.23 | 1069.23 | 27,820.25 |
| 20 | 2357.32 | 160.99 | 25,300.34 | 2180.99 | 2180.99 | 29,662.32 |
| 30 | 2350.03 | 160.99 | 25,222.10 | 3272.27 | 3272.27 | 31,766.64 |
| 40 | 2350.03 | 160.99 | 25,221.93 | 4364.08 | 4364.08 | 33,950.09 |
| 50 | 2331.11 | 160.99 | 25,018.61 | 5456.41 | 5456.41 | 35,931.43 |
| Flight Height (m) | Horizontal Path Length (m) | Battery Output Power in Horizontal Flight Phase (W) | Energy Consumption in Horizontal Flight Phase (J) | Energy Consumption in Take-Off Phase (J) | Energy Consumption in Landing Phase (J) | Total Energy Consumption (J) |
|---|---|---|---|---|---|---|
| 10 | 2392.82 | 164.62 | 26,260.40 | 1218.07 | 1218.07 | 28,696.54 |
| 20 | 2357.32 | 164.66 | 25,877.09 | 2436.76 | 2436.76 | 30,750.61 |
| 30 | 2350.03 | 164.69 | 25,801.76 | 3656.07 | 3656.07 | 33,113.90 |
| 40 | 2350.03 | 164.73 | 25,808.03 | 4875.99 | 4875.99 | 35,560.01 |
| 50 | 2331.11 | 164.76 | 25,604.91 | 6096.54 | 6096.54 | 37,797.99 |
| Flight Height (m) | Horizontal Path Length (m) | Energy Consumption of Horizontal Flight at High-Altitude Area (J) | Energy Consumption of Horizontal Flight at Low Altitude Area (J) | Total Energy Consumption at High-Altitude Area/(J) | Total Energy Consumption at Low-Altitude Area/J (J) |
|---|---|---|---|---|---|
| 10 | 2392.82 | 262,604.00 | 256,817.90 | 265,040.20 | 258,956.30 |
| 20 | 2357.32 | 258,770.90 | 253,003.40 | 263,644.40 | 257,365.30 |
| 30 | 2350.03 | 258,017.60 | 252,221.10 | 265,329.30 | 258,765.60 |
| 40 | 2350.03 | 258,080.30 | 252,219.30 | 267,832.30 | 260,947.50 |
| 50 | 2331.11 | 256,049.10 | 250,618.10 | 268,242.20 | 261,098.90 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, Y.; Liu, M. Path Planning of Electric VTOL UAV Considering Minimum Energy Consumption in Urban Areas. Sustainability 2022, 14, 13421. https://doi.org/10.3390/su142013421
Li Y, Liu M. Path Planning of Electric VTOL UAV Considering Minimum Energy Consumption in Urban Areas. Sustainability. 2022; 14(20):13421. https://doi.org/10.3390/su142013421
Chicago/Turabian StyleLi, Yafei, and Minghuan Liu. 2022. "Path Planning of Electric VTOL UAV Considering Minimum Energy Consumption in Urban Areas" Sustainability 14, no. 20: 13421. https://doi.org/10.3390/su142013421





