Optimal Multi-Objective Power Scheduling of a Residential Microgrid Considering Renewable Sources and Demand Response Technique

Abstract

Microgrid optimization is one of the most promising solutions to power system issues and new city electrification. This paper presents a strategy for optimal power scheduling of a residential microgrid depending on renewable generating sources and hydrogen power. Five scenarios of the microgrid are introduced to show the effect of using biomass energy and a seawater electrolyzer on microgrid cost and CO${}_2$ emissions. Time of use demand response is applied to reshape the electric load demand and decrease the dependence on grid power. The obtained results from the multi-objective optimization verify that biomass has a significant role in minimizing the cost and CO${}_2$ emissions; the cost is decreased by 37.9% when comparing scenarios with and without biomass. Besides, the FC integration with seawater electrolyzer and tanks reduces the microgrid emissions by around 40%.

1. Introduction

1.1. Greenhouse Gas Emissions

The growth of devastating greenhouse gas emissions acts as one of the main challenges to the human race [1]. Global carbon emissions in 2014 exceeded 1.6 times their levels in the 1990s [2]. GHGs aided in the significant rise in global temperature, posing a threat to human health and many economies [3]. Following the Kyoto Protocol, several countries have taken measures to cut GHG emissions, especially CO${}_2$ emissions. GHGs half reduction by 2050 is a global target to face temperature increase [4]. In the power system sector, transferring to renewable sources is the best solution to achieve a significant reduction in GHG emissions [5].

1.2. Renewable Energy

Renewable power is generated from continuously rejuvenated energy flows such as wind, solar, geothermal heat, tidal, etc. [6]. Renewable energy sources are anticipated to provide 80% of global energy needs [7]. Globally, renewable energy capacity today stands at 2195 GW. The RES sector offered around 10.3 million jobs (directly and indirectly), with investments of over USD 280 billion [8]. A total of 145 countries have implemented programs to promote sustainable energy technologies during the last few decades. Biomass is a sustainable resource that may supplement other renewable energy sources. When combined with carbon capture, it creates no emissions [9]. Gasification is a reasonable method of generating electricity from biomass [10]. The growing popularity of renewable energy sources is helping to develop new microgrids.

1.3. Microgrid

Microgrids might be a viable solution to the current energy problems. A microgrid is made up of a group of dispersed electric sources and interconnected loads. Their operational modes are classified as isolated or grid-connected modes. Isolated microgrids are small power networks that produce and manage their own electricity needs. Grid connectivity improves system dependability and allows electricity trading with other grids [11,12]. Hydrogen technology is currently preferred in microgrids to store electric power. Electrolyzers normally produce hydrogen while power is available, while fuel cells generate energy from hydrogen during periods of low power [13]. The seawater electrolysis process produces chemical substances with hydrogen such as NaClO. It can be sold and manufactured to create revenue for the system. NaClO is used in drinking water disinfection, bleaching, and removing stains from clothing [14].

1.4. Motivations

The appropriate microgrid’s sizing has a major role in minimizing overall system costs, lowering CO${}_2$ emissions, and promoting community development. Investment in the power system sector is an essential target to reduce the burden on the economy and encourage business in the energy sector. Microgrid productivity can be boosted through power trading and hydrogen technology. CO${}_2$ emissions from power generation cannot be reduced without a reliance on renewable energy. Energy management technologies are strongly encouraged as a means of improving microgrid dependability and lowering microgrid costs [15].

1.5. Demand Response

Demand response programs support power system operators with cost-effective and energy-saving alternatives [16]. They represent customers’ adjustments to their energy consumption in response to changes in energy prices or incentive payments intended to limit power use at periods when the system’s stability is endangered [17]; they also help in reshaping load patterns. DR techniques are divided into price-based and incentive-based programs. In the price-based type, prices control electricity consumption by increasing peak-load hour tariffs while lowering them during off-peak hours. Consumers are rewarded for lowering their load during significant times via incentive-based demand response (DR) programs [18].

1.6. Related Literature

Many researchers have discussed the optimal design and operation of hybrid microgrids, considering renewable sources and demand response techniques. The appropriate power scheduling is greatly influenced by the desired sizing objectives. Cagnano et al. [19] outlined various control mechanisms required to achieve cost-effective, efficient, and secure operation of microgrids and reviewed the present primary design behaviors. A comprehensive literature assessment of existing microgrid-sizing methodologies was discussed in reference [20]. Cost-based and non-cost-based strategies are the two main sizing methodologies. For optimum energy cost and power supply probability, the Grasshopper Optimization Algorithm (GOA) was utilized for optimal microgrid sizing in [21]. In selecting the best size of microgrid, the net cost, renewable portion, energy cost, grid pricing rates, and greenhouse gas emissions were considered in [22]. Ref. [23] employed an evolutionary technique for optimum sizing of distributed energy sources to reduce the capital and yearly operating expenses. In ref. [24], HRES cost and different load values were considered for optimal microgrid sizing using the improved hybrid optimization genetic algorithm. Microgrid reliability was improved by connecting microgrids to the electric grid. Ref. [25] introduced a strategy for designing grid-connected microgrids that enhances their dependability while also serving the load at a low cost. For effective energy management of a grid-connected microgrid that depends on renewable energy, ref. [26] utilized the modified bat algorithm (MBA). MFABC+, MFABC, particle swarm algorithms, and HOMER software were utilized for optimal microgrid sizing in [27]. Ref. [28] used a multi-objective feasibility enhanced particle swarm optimization algorithm to reduce the microgrids’ operational costs and increase the renewable power use. Ref. [29] proposed optimal microgrid allocation based on renewable energy sources, demand response schemes, storage systems, and EV charging stations. Ref. [30] introduced optimal energy scheduling of grid-connected microgrids considering renewable sources uncertainty. Authors in [31] introduced two-step scheduling for microgrids using Monte Carlo and particle swarm optimization, considering sources’ uncertainty by grouping sources into basic load and frequency-modulated sources. Ref. [32] proposed an optimal energy management system for DC-microgrid composed of four nanogrids with a single energy storage system (ESS). Ref. [33] used genetic optimization to develop a novel multi-control scheme that maximized the power from renewable sources while minimizing total harmonic distortion. The results were compared with other optimization techniques. Power trading can enhance the system’s profit while lowering the total system cost via system sizing and optimization [34]. Ref. [35] demonstrated the impact of renewable sources on CO${}_2$ level reduction. Biomass energy has proven itself as a suitable alternative energy source in electric power production. It is now considered a renewable energy source [36]. It has zero emissions when the CO${}_2$ capture technique is employed [9]. Biomass gasification is a cheap solution for off-grid rural communities to produce electricity [10]. Ref. [37] researched biomass energy challenges as well as its large-scale employment. Ref. [38] studied the energy productivity of rice straw as a biomass fuel; it explored the burning of rice straw for energy and the issues associated with it. Ref. [39] discussed the latest microgrid control and power management studies. Ref. [40] presented different strategies for managing extra microgrid power with cost and emissions reduction as goals through selling surplus power to the grid, energy storage systems, and extra electricity conversion to hydrogen. The production of electricity from fuel cells via hydrogen production from seawater is regarded as the most abundant energy resource [41]. Hydrogen created from seawater in the morning can be used in fuel cells at night in microgrids that rely on PV [42]. Ref. [43] highlighted the need to reduce peak electricity demand.

Grid-purchased electricity and fuel costs can be reduced by employing DR schemes [44]. Ref. [45] studied the demand response objectives and classifications for facing electric power sector challenges. Demand response programs provide a cheap alternative to infrastructure upgrades in residential microgrids [46]. The restrictions and aims of demand response for diverse systems are described in [47]. Three types of demand response were compared in [48]; time-of-use demand response presents an effective and feasible technique to deal with peak load period problems. The barriers of participation in demand response were discussed in [49]. Ref. [50] used single- and multi-period load models to estimate emergency and time-of-use demand response programs based on load elasticity principles. The elasticity principal was used in ref 5 to address demand response [51]. With the help of thermostatically controlled and price-responsive loads, ref. [52] employed deep reinforcement learning algorithms to manage the energy of a grid-connected microgrid.

1.7. Paper Contribution

Regarding the previous literature, this paper’s contributions are outlined as follows:

• Multi-objective optimal power scheduling of a residential microgrid considering revenues and productivity maximization of the microgrid using seawater electrolyzer and biomass generation.
• The effects of load shifting techniques on reducing maximum demand and the grid’s power consumption, microgrid configuration, and emissions.
• Introducing a comparison between different configurations for system design to demonstrate the feasibility and productivity of the used technologies.

1.8. Paper Construction

The remainder of the paper is organized as follows: Section 2 describes the system, and Section 3 clarifies demand response techniques. Objective functions are explained in Section 4, and constraints are discussed in Section 5. The optimization technique is discussed in Section 6. Simulation results and discussion are introduced in Section 7. Section 8 contains the conclusion and future work.

2. Microgrid Modeling

Optimal power scheduling is essential in the establishment process of microgrids to reduce the cost, emissions, loss of power supply, and the number of required system components. The system being studied is a residential microgrid in the northern part of Egypt. The proposed microgrid aims to meet all of its energy requirements with minimum cost and the least possible CO${}_2$ emissions. Five case studies are discussed in this research to show the feasible system configuration. Figure 1 shows the available power generation units for all studied systems. The operation of each case study is demonstrated in Figure 2. Multi-objective genetic algorithm is utilized for the microgrid optimization with the help of MATLAB software.

2.1. Photovoltaic (PV) Modeling

PV transforms solar energy into electricity [53]. PV power is determined by solar radiation. Equation (1) describes the PV output power. This research uses Egyptian solar radiation data for the simulation; Egypt is considered one of the countries that has a wealth of solar power with a sunlight period of around 3500 to 4500 h/year [54].

$$P_{pv}\left(t\right)={\eta }_{pv}\times S_{pv}\times \frac{G\left(t\right)}{G_{Stc}}$$

(1)

where ${\eta }_{pv}$, $S_{pv}$, $I_d\left(t\right)$, and $I_{d,Stc}$ are the PV’s efficiency, the rated capacity, the incident solar radiation, and solar radiation at the stc, respectively [55].

2.2. Fuel Cell (FC) Modeling

Fuel cell (FC) uses hydrogen to generate DC power. It normally consists of an electrolyte and two terminals (anode and cathode). The chemical processes inside FC are described in the equations below [56].

$$H_2⟶2H^{+}+2e^{-}$$

(2)

$$0.5O_2+2e^{-}⟶O^{2-}$$

(3)

$$2H^{+}+\frac{1}{2}{O}_2^{2-}⟶H_{2}O+heat$$

(4)

The capital cost and operating and maintenance costs of the fuel cell are described in the following equations:

$$Ca{p}_{FC}={\alpha }_{FC}\times S_{FC}$$

(5)

$$O{M}_{FC}={\beta }_{FC}\times S_{FC}\times \sum _{j=1}^N{\left(\frac{1+{\mu }_{FC}}{1+i_r}\right)}^j$$

(6)

where $Ca{p}_{FC}$, ${\alpha }_{FC}$, $S_{FC}$, $O{M}_{FC}$, ${\beta }_{FC}$, ${\mu }_{FC}$, $i_r$, and N are the capital cost of FC, the investment cost of FC, FC capacity, operating and maintenance cost, the annual operating and maintenance cost, the escalation rate, interest rate, and project lifetime, respectively.

2.3. Sea Water Electrolyzer Modeling

Water covers approximately 75% of the earth’s surface. This water is mostly salty. Electrolysis of seawater can be utilized to create hydrogen as well as useful chemical substances [57]. The chemical reactions inside the electrolyzer are described by the following equations [58,59]:

$$NaCl+H_{2}O⟶NaClO+H_2$$

(7)

$$2N{a}^{+}+2H_{2}O+2e^{-}⟶2NaOH+H_2$$

(8)

$$2NaOH+C{l}_2⟶2NaClO+H_2$$

(9)

The overall equation during the electrolysis process is

$$NaCl+H_{2}O⟶NaClO+H_2$$

(10)

The most appropriate method of hydrogen storage is pressurized gas storage. This requires a compressor and a storage tank [60].

2.4. Electric Utility

The utility grid serves as a backup when the generated power is not enough to supply the microgrid’s load. It also adds selling power availability to the grid in case of excess generation.

The exported and imported powers at a given time can be described using the equations below:

$$P_{grp}:P_{grid}\left(t\right)>0incaseofimportingpower$$

(11)

$$P_{grs}:P_{grid}\left(t\right)<0incaseofexportingpower$$

(12)

The net grid cost is

$$C_{grid}=C_p\mid P_{grp}\mid -C_S\mid P_{grs}\mid$$

(13)

where $C_{grid}$, $C_p$, $P_{grp}$, $C_S$, and $P_{grs}$ are the grid cost, unit power purchasing price, purchased power, unit power selling price, and the sold power, respectively [61,62].

2.5. Biomass Modeling

Biomass gasification is the process of converting solid biowaste into a combustible gas mixture. It can be used as a source of heat or as a fuel in internal combustion engines to produce mechanical or electric power. The calorific value of biomass and the amount of biomass determine its power [63]:

$$P_{bio}=\frac{Totalbiomassavailable\left(\mathrm{Ton}/\mathrm{yr}\right)\times 1000\times C{V}_{bm}\times {\eta }_{bm}}{365\times 860\times Operating\mathrm{h}/\mathrm{day}}$$

(14)

The operating and maintaining cost of a biogas system is divided into two components (fixed and variable costs), which vary based on the anticipated power and the amount of fuel used:

$$O{M}_{bg,npv}=\theta 1_{bg}\times P_{bio}\sum _{j=1}^N{\left(\frac{1+{\mu }_{bg}}{1+i_r}\right)}^j+\theta 2_{bg}\times P{W}_{bg}^{yr}\times \sum _{j=1}^N{\left(\frac{1+{\mu }_{bg}}{1+i_r}\right)}^j$$

(15)

Equation (16) shows the amount of biogas fuel cost:

$$F_{bg,npv}=\theta 3_{bg}\times B{F}_r^{yr}\times \sum _{j=1}^N{\left(\frac{1+{\mu }_{bg}}{1+i_r}\right)}^j$$

(16)

Equations (17) and (18) explain the capital and salvage cost values of the biomass unit:

$$C_{bg}={\gamma }_{bg}\times P_{bio}$$

(17)

$$S{V}_{bg,npv}={\lambda }_{bg}\times P_{bio}\times {\left(\frac{1+\delta }{1+i_r}\right)}^N$$

(18)

where $C{V}_{bm}$, ${\eta }_{bm}$, $\theta 1_{bg}$, $P_{bio}$, and $i_r$ are the biomass calorific valve, the overall conversion efficiency, the annual fixed operation and maintenance cost (USD/kW/year), the power produced by biogas generator, and the interest rate, respectively. ${\mu }_{bg}$, $\theta 2_{bg}$, $P{W}_{bg}^{yr}$, and $\theta 3_{bg}$ are the escalation rate, the variable operation and maintenance cost (USD/kWh), the annual working power of biogas generator (kWh/year), and the biomass fuel cost (USD/ton), respectively. $B{F}_r^{yr}$, ${\gamma }_{bg}$, ${\lambda }_{bg}$, and $\delta$ are the annual required biomass fuel (ton/year), the initial cost of biogas system (USD/kW), the resale price of the system (USD/kW), and the inflation rate, respectively [64].

3. Demand Response

Demand response is an energy management approach that shifts energy usage from peak hours to other periods. This research studied time-of-use demand response as a time-based type.

3.1. Time-of-Use (ToU) Demand Response

In time-of-use demand response, peak load periods have higher prices, whereas off-peak hours have reduced prices according to predefined prices. In this work, price elasticity models are employed to structure the TOU demand response.

Elasticity Model

The change in load demand as a result of price swings is the price elasticity of electrical demand $El$ [65].

$$El=\frac{{\rho }_o}{d_o}\times \frac{\partial d}{\partial \rho }$$

(19)

where $\rho$, $d_o$, ${\rho }_o$, and d are the electricity price, the initial load demand, the nominal price, and the load demand, respectively.

The cross elasticity $El(i,j)$ illustrates how demand varies over time as a result of price changes at different time periods [66].

$$El(i,j)=\frac{{\rho }_o\left(j\right)}{d_o\left(i\right)}\times \frac{\partial d\left(i\right)}{\partial \rho \left(j\right)}$$

(20)

The customer benefits are depicted as [67]

$$S=B\left(d\right(i\left)\right)-d\left(i\right)\times \rho \left(i\right)$$

(21)

where $B\left(d\right(i\left)\right)$ denotes the revenue earned by the usage of electrical energy as follows [68]:

$$B\left(d\left(i\right)\right)=B_o\left(i\right)+{\rho }_o\left(i\right)[d\left(i\right)-d_o\left(i\right)]\{1+\frac{d\left(i\right)-d_o\left(i\right)}{2El\left(i\right)\times d_o\left(i\right)}\}$$

(22)

Demand response advantages are boosted by setting $\frac{\partial S}{\partial d\left(i\right)}$ to zero. As a result, the following is the consumer usage:

$$d\left(i\right)=d_o\left(i\right)\{1+El\left(i\right)\times \frac{\rho \left(i\right)-{\rho }_o\left(i\right)}{{\rho }_o\left(i\right)}\}$$

(23)

when the cross elasticity is taken into consideration, the load demand is expressed as follows:

$$d\left(i\right)=d_o\left(i\right)+\sum _{i=1,i\ne j}^{24}El(i,j)\times \frac{d_o\left(i\right)}{{\rho }_o\left(j\right)}\times [\rho \left(j\right)-{\rho }_o\left(j\right)]$$

(24)

The final load demand that fulfills the maximum gains of the customer’s usage during a 24 h period is demonstrated in the following equation [68]:

$$\begin{array}{c}\hfill d\left(i\right)=d_o\left(i\right)\{1+El\left(i\right)\times \frac{[\rho \left(i\right)-{\rho }_o\left(i\right)]}{{\rho }_o\left(i\right)}+\\ \hfill \sum _{i=1,i\ne j}^{24}El(i,j)\times \frac{[\rho \left(j\right)-{\rho }_o\left(j\right)]}{{\rho }_o\left(j\right)}\}\end{array}$$

(25)

The self and cross elasticities are set on the basis of prices and demand to represent the flexibility to change the load patterns by shifting a portion of load from one period to another. The values of self and cross elasticities are mentioned in

Table 1. Self and cross elasticity values.

	Peak	Off-Peak	Low
Peak	−0.1	0.016	0.012
Off-Peak	0.008	−0.1	0.01
Low	0.006	0.008	−0.1

[50].

4. Objective Function

This study introduces technical, economic, and environmental objectives for power scheduling of a residential microgrid, including PV, WG, and plug-in-electric vehicles. The first objective is the minimization of load-generation mismatch. The second objective is the minimization of total system cost. The third objective is CO${}_2$ emissions minimization. The following equations show the proposed objective functions.

$$F1=min:\left(LoPS\right)=min:\mid P_l\left(t\right)-\sum P_{gn}\left(t\right)\mid$$

(26)

$$F2=min:\left(cost\right)=min:\left(\sum C_{pv}+C_{FC}+C_{electrolyzer}+C_{grid}+C_{Bio}-C_{Revenues}\right)$$

(27)

$$F3=min:\left({\left(C{O}_2\right)}_{emissions}\right)$$

(28)

where $P_{gn}$, $C_{pv}$, $C_{FC}$, $C_{electrolyzer}$, $C_{grid}$, $C_{Bio}$, and $C_{Revenues}$ are the total generated power, PV cost, fuel cell cost, electrolyzer cost, grid cost, total biomass cost, and system’s revenue, respectively.

5. Constraints

Power balance constraints:

$$\begin{array}{c}\hfill P_{pv}\left(t\right)+P_{FC}\left(t\right)+P_{bio}+P_{grid\_buy}\left(t\right)-P_{grid\_sell}\left(t\right)-P_{electrolyzer}=P_l\left(t\right)\end{array}$$

(29)

Limits constraints:

$$0<P_{pv}<P_{pv,max}$$

(30)

$$0<P_{FC}<P_{FC,max}$$

(31)

$$P_{grs,max}<P_{grid}<P_{grp,max}$$

(32)

$$P_{bi{o}_{min}}<P_{bio}<P_{bi{o}_{max}}$$

(33)

$$H_{2_{tan{k}_{min}}}\le H_{2_{tank}}\le H_{2_{tan{k}_{max}}}$$

(34)

6. Multi-Objective Genetic Algorithm (MOGA)

The multi-objective genetic algorithm is a meta-heuristic mechanism motivated by the natural selection technique, which is a part of larger classes of evolutionary algorithms. Genetic algorithms are widely used and biologically inspired by developers to produce high-quality optimization and search prospects, such as mutation, crossover, and selection.

MOGA utilizes a weighted sum of various objective functions in the selection stage and merges them into a scalar fitness function. The design characteristics of the various objective functions weights are not specified and are randomly changed through each selection. Thus, the search orientation in this algorithm is not fixed.

At each generation over the process of MOGA, an empirical series of Pareto optimal solutions are stored and updated. Furthermore, a certain number of solutions are picked at random from the series. Those solutions are considered elite individuals. The elite mechanism has the benefit of preserving the diversity of each population [69].

The block diagram of the proposed MOGA algorithm is shown in Figure 3 and described below:

• Stage 1 (Initialization): generate an initial population.
• Stage 2 (Evaluation): calculate the values of the objective functions for the created population.
• Stage 3 (Selection): use random weights to determine each population’s fitness value; then, pick a pair of strings from the existing population.
• Stage 4 (Crossover and Mutation): a crossover strategy is implemented for each chosen pair to produce a new population via the crossover process; after that, the mutation process is carried out.
• Stage 5 (Elitist): delete some strings of created strings haphazardly and substitute them with elite strings picked at random from temporary Pareto optimal solutions.
• Stage 6 (Termination): if the stopping requirement is not satisfied, go to Stage 2.
• Stage 7 (Optimal Solution): the MOGA suggests the preferable options.

7. Results and Discussion

Microgrid sizing and optimization are important issues for power system developers. The system configuration could differ depending on the available technology and the design objectives or targets. In this study, five case studies are introduced. In all scenarios, solar power has the first priority to produce the required electrical energy. The first scenario consists of PV, FC, seawater electrolyzer, tank, and public grid. The second scenario introduces biomass power to the first scenario but without the dependence on public grid. The third scenario has the availability of biomass and grid-connection with FC and seawater electrolyzer to guarantee full system reliability. Scenario 4 is like the system of the first scenario but without sea water electrolyzer. Scenario 5 is the simplest one, with PV and the public grid as the only power sources. The simulation parameters are shown in Appendix A. The load and generation of each power unit for all studied case studies are displayed in Figure 4, Figure 5, Figure 6, Figure 7 and Figure 8.

The simulation results for the five scenarios confirm the following features:

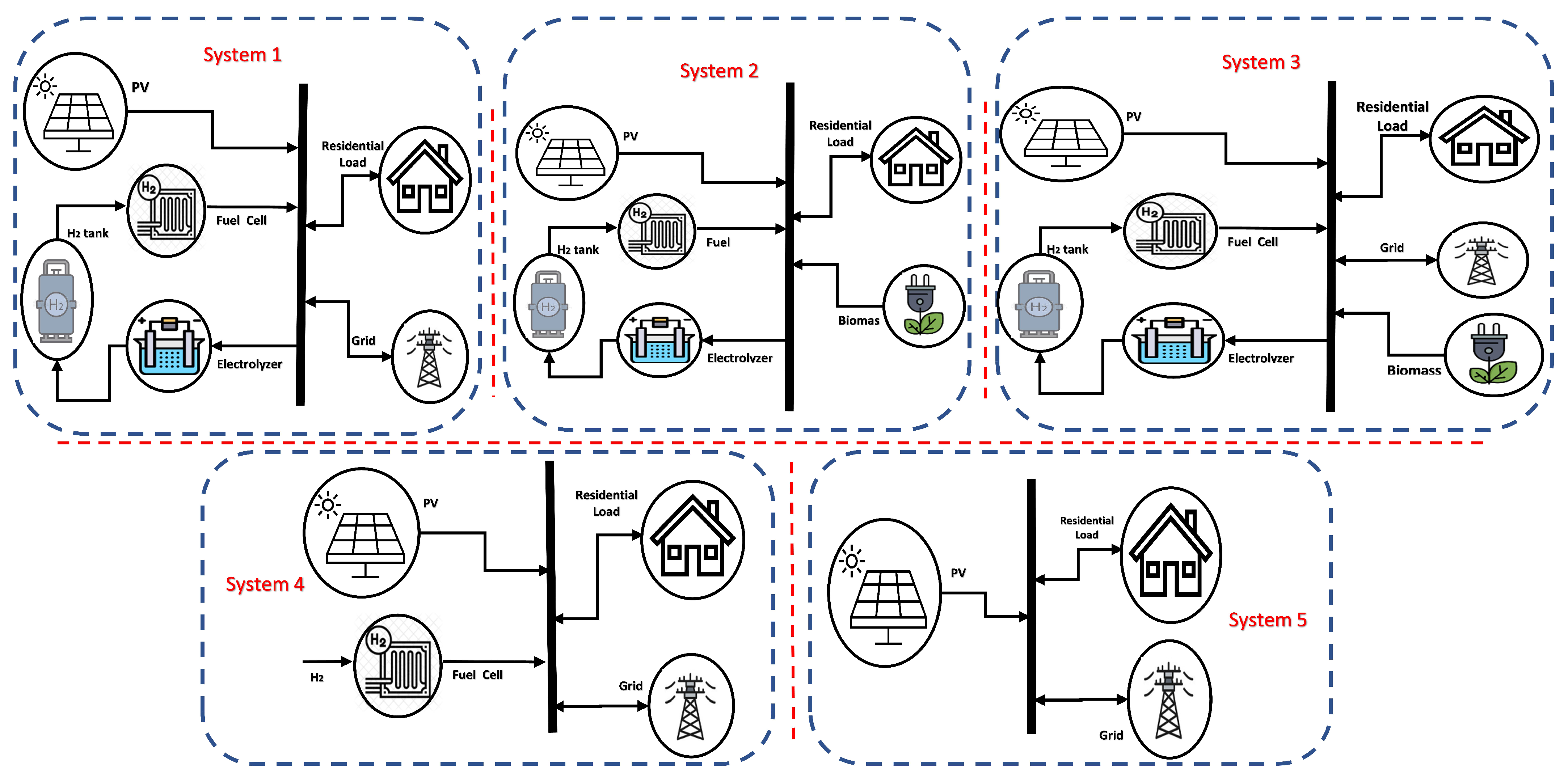
• By taking scenario 5 as a reference case study because it is the simplest system configuration with the minimum number of generating units, the FC integration with sea water electrolyzer and tanks reduces the system emissions by around 40% and slightly increases the cost by USD 0.093 million.
• If the microgrid that uses FC does not produce its own $H_2$, its cost is increased due to the cost of purchasing $H_2$. As seen from scenario 4’s results, its cost is greater than scenario 1’s cost by USD 0.246 million; the CO${}_2$ emissions are also higher by 150.6 kg/day.
• Relying on biomass has a great impact on cost and emissions. If biomass energy is used instead of depending on public grid power, the cost is decreased by 37.9%, as noticed by comparing scenarios 1 and 2. If both biomass power and electric utility are utilized in a hybrid microgrid as in scenario 3, the system has the lowest total cost of USD 1.186 million due to selling power back to the grid. Systems with biomass have zero emissions as they replace grid power use.
• The grid power share is decreased by using biomass energy and FC; it reached zero by integrating biomass energy units. It decreased by 6% and 10% when comparing scenario 5 with scenarios 4 and 1.
• Scenario 5 is the worst system configuration; it emits the highest emissions of 954.095 kg of CO${}_2$ per day. Scenario 4 has the highest system cost and a great amount of CO${}_2$ emissions, with roughly about 722.356 kg/day.
• By comparing the systems that have storage tanks (1, 2, and 3), scenario 1 has the largest storage tank capacity as it has the largest fuel cell capacity of 184 kW with a power share percentage of more than 10%, as clarified in Figure 9. Scenario 2 has the largest EL capacity of 701 kW as it produces more chemical substances and hydrogen to increase revenue and decrease the system cost, as there is no revenue from the grid in this scenario.

Figure 9 demonstrates the contribution of the kWh energy production share of each generating unit.

• In all the studied scenarios, the PV capacity ranges from 830 kW to 1000 kW. It provides more than 70% of the required power; the remaining percentage comes from the public grid, biomass, or stored energy in FC.
• The incorporation of biomass power decreases the dependence of FC; it reduces the FC energy share by around 50% by comparing scenario 1 and scenario 2.
• In scenario 3, the grid-connectivity is considered as a revenue tool to sell extra power back to the grid. It is regarded as a semi-grid-connected microgrid. Using seawater electrolyzers ensures the generation of the system’s required $H_2$.
• In scenario 3, the integration of biomass with EL and tank reduces the dependence on fuel cell; the capacity of the fuel cell is reduced to 30 kW.
• Systems with seawater electrolyzers have the lowest CO${}_2$ emissions. They reach 571.752 kg/day for systems without biomass energy.
• The electrolyzing process is regarded not only as a means of producing hydrogen but also as a means of increasing system income. System productivity can be increased by selling extra power back to the public grid and selling NACLO and extra $H_2$ produced from the electrolyzing process.
• Scenario 1 has a total system cost of USD 3.672 million with 571.752 kg of CO${}_2$ emissions per day. By introducing biomass, both the emissions and the cost are enhanced. The cost is reduced by USD 1.394 million in scenario 2 and by USD 2.486 million in scenario 3 when compared with scenario 1.

Table 2. Results for systems without DR.

	Case 1	Case 2	Case 3	Case 4	Case 5
Cost (million USD)	3.672	2.278	1.186	3.918	3.579
CO${}_2$ emissions (kg/day)	571.752	0	0	722.356	954.095
PV capacity (kW)	986.553	830.866	901.435	995.850	1000
FC capacity (kW)	184	66	30	97	0
EL capacity (kW)	294	701	336	0	0
Tank capacity (kg)	147.5	22	10	0	0
Maximum grid power (kW)	229.810	0	0	273.310	321.810
Biomass capacity (kW)	0	288.972	306.861	0	0

demonstrates the obtained results for all the studied scenario without DR programs.

• All systems create revenues of more than USD 4 million. Scenarios 1 and 2 have the highest revenues of USD 4.47 million and USD 4.34 million, respectively.
• The revenues from selling extra power back to the grid are decreased by introducing biomass to the system, in addition to the increase in selling chemical products and hydrogen produced from the seawater electrolyzer, as in scenario 3.
• Without seawater electrolyzers, the revenues are only from selling power back to the public grid or nearby microgrids.

Table 3. Revenues.

	Case 1	Case 2	Case 3	Case 4	Case 5
Grid revenue	2.104	0	1.469	4.232	4.253
Electrolyzing process revenue	2.366	4.182	2.875	0	0

shows the systems’ revenue for each scenario. Figure 10 displays the amount of revenue from selling power back to the grid and revenues from selling chemical products and hydrogen that are produced through the electrolysis process.

• Demand response programs reshape the load patterns by shifting a portion of off-peak load, which is usually at night, to other periods. Biomass unit capacity is reduced by applying demand response as it is always used at night; it is reduced by 12.5% and 12.9% for scenarios 2 and 3.
• By applying demand response schemes, the load curve is modified; the peak load is reduced by 10.88%, as seen in Figure 11.
• The microgrids’ overall cost and CO${}_2$ emissions are decreased with time-of-use demand response.
• In most studied cases, the total system cost is reduced by TOU-DR with different values within USD 0.356 million, as in scenario 5, and USD 0.277 million, as in scenario 2.
• The CO${}_2$ emissions are reduced by 63.658, 20.763, and 71.819 kg/day for scenarios 1, 4, and 5, respectively. The maximum value of the grid’s purchased power is decreased by 13.71%, 8.6%, and 10.88% for scenarios 1, 4, and 5, respectively.
• For scenarios without biomass, the FC capacity is decreased by applying DR schemes, while it is slightly increased for scenarios with biomass units to manage the decrease in biomass capacity.

Table 4. Results of systems with DR.

	Case 1	Case 2	Case3	Case4	Case5
Cost (million USD)	3.331	2.001	1.388	3.562	3.247
CO${}_2$ emissions (kg/day)	508.094	0	0	701.593	882.276
PV capacity (kW)	980.965	932.368	874.959	963.199	993.292
FC capacity (kW)	177	68	39	74	0
EL capacity (kW)	285	783	168	0	0
Tank capacity (kg)	147	23	83	0	0
Maximum grid power (kW)	198.297	0	0	249.797	286.797
Biomass capacity (kW)	0	252.934	267.413	0	0

shows the scenarios’ configuration, cost, and emissions with their participation in ToU-DR schemes.

8. Conclusions

Microgrid size optimization plays a critical role in lowering total system costs by avoiding needless investment in unused generation. This study introduces a power scheduling methodology for a grid-connected microgrid considering PV, biomass power, fuel cell, and seawater electrolyzer. CO${}_2$ emissions reduction, cost, and avoiding power outages are the main targets in the multi-objective scheduling process. The seawater electrolysis process is not only beneficial for producing hydrogen; it also serves as an income source for the system by selling the produced chemical compounds throughout the process. Time-of-use demand response is employed in this study to modify the load demand distribution and maximize the utilization of renewable energy sources. The research findings confirm that ToU-DR reduces the maximum load demand by 10.88%. They also confirm that CO${}_2$ emissions can be reduced to zero by introducing biomass and also reduced by 40% by integrating FC and seawater electrolyzers. Biomass has the ability to decrease the microgrid cost by USD 1.39 million, if it replaces the grid power. Moreover, the hybrid microgrid of biomass, grid, PV, FC with seawater electrolyzer, and hydrogen tank is the most economical configuration. Furthermore, microgrid productivity is increased by selling both extra power and produced chemical products; it reaches over USD 4.1 million in most studied scenarios. Studying the integration of other renewable sources such as wind generators and integrating electric vehicles into the studied system through vehicles-to-grid schemes with a deep analysis of the sensitivity to parameter fluctuations is the proposed future work to increase microgrid productivity and reduce GHG emissions.