Impact of Industrial Intelligence on Total Factor Productivity
Abstract
:1. Introduction
2. Literature Review and Theoretical Framework
2.1. Industrial Intelligence and Economic Development
2.2. Industrial Intelligence and Labor Skill
- Difference in defining the concepts. Compared with “industrial intelligence” being discussed in this paper, most research is related with “technical advancement” or “artificial intelligence”, covering all sectors in society, with more and more focus on the tertiary industry. There is a lack of overriding standards for choosing the principal variables.
- Current research is mainly about the relationship between industrial intelligence and either economic development or labor skill, rarely about the combination of the three.
- The research could lead to entirely different conclusions due to their different research angles and methods which result in their selection of different variables and empirical models.
3. Research Ideas and Framework
3.1. Research Ideas
3.2. Research Hypothesis
3.3. Creativity and Limitation of This Paper
4. Calculation of Whole-Factor Productivity
4.1. Calculation Methods and Model Selection
4.2. Data Treatment
4.3. Modeling Estimation Results and Testing
4.4. Model Set-Up and Modification
5. Empirical Test
5.1. Mediation Effect
5.2. Principal Variables and Descriptive Statistics
5.3. Regression Results
5.4. Robust and Endogenous Test
5.4.1. Endogenous Test
- In order to control the endogenous omitted variable bias, the following variables are added: the financial input of R&D of each province is used to measure the input of R&D (Rd), and the imported value of industrial equipment is to measure the investment of machines and equipment (Fdi). The first step test is made by combining these two additional variables with the previous explanatory variable. The results given in Table 7 show that the prominence level of different coefficients is under good control, and the coefficient of the industrial intelligence, being consistent with that of Table 5, is positive. The consistency of the conclusions is therefore guaranteed.
- The OLS regression is carried out in the second step to solve the reverse causality of two variables, i.e., industrial intelligence and labor skill, by the methodology of Mao Qilin and Sheng Bin [57], in which the industrial intelligence is an explained variable, and the explanatory variables include trade openness, financial development, industrial structure upgrading, infrastructure, R&D input, equipment investment and labor skill. The results in Table 8 exhibit that the prominence level of the industrial intelligence and other explanatory variables except labor skill is within 10%, and the correlation of the industrial intelligence and the labor skill (high, medium and low) is not prominent. This eliminates, to some extent, the possibility of reverse causality between industrial intelligence and labor skill.
5.4.2. Robust Test
6. Region-by-Region Test
7. Conclusions and Recommendations
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
| Region | High | TFP | Mid | TFP | Low | TFP | |
|---|---|---|---|---|---|---|---|
| East | lnt | 0.002 ** (0.001) | 0.255 *** (0.024) | −0.004 *** (0.001) | 0.271 *** (0.024) | −0.001 (0.001) | 0.232 *** (0.024) |
| high | −10.046 *** (2.441) | ||||||
| mid | 9.740 *** (2.089) | ||||||
| low | −4.342 * (2.222) | ||||||
| Df | 0.028 *** (0.009) | −1.720 *** (0.280) | −0.018 * (0.011) | −1.823 *** (0.271) | 0.005 (0.010) | −1.979 *** (0.283) | |
| Sr | 0.391 *** (0.114) | 13.212 *** (3.518) | −0.072 (0.131) | 9.989 *** (3.341) | −0.554 *** (0.131) | 6.881 * (3.739) | |
| Fra | 0.046 *** (0.013) | 1.745 *** (0.398) | −0.019 (0.015) | 1.464 *** (0.378) | −0.054 *** (0.015) | 1.046 ** (0.416) | |
| Trade | −0.056 *** (0.015) | −3.301 *** (0.469) | 0.101 *** (0.017) | −3.719 *** (0.490) | 0.022 (0.017) | −2.633 *** (0.470) | |
| Rd | 0.002 ** (0.001) | 0.085 *** (0.028) | −0.003 *** (0.001) | 0.094 *** (0.028) | 0.002 ** (0.001) | 0.075 ** (0.029) | |
| Fdi | 0.003 (0.002) | −0.168 *** (0.062) | −0.003 (0.002) | −0.168 *** (0.061) | −0.001 (0.002) | −0.202 *** (0.064) | |
| Middle | lnt | 0.008 *** (0.001) | 0.080 *** (0.027) | 0.006 ** (0.003) | 0.192 *** (0.020) | −0.015 *** (0.003) | 0.168 *** (0.023) |
| high | 3.342 (2.270) | ||||||
| mid | 2.539 *** (0.926) | ||||||
| low | −2.489 *** (0.854) | ||||||
| Df | 0.027 *** (0.007) | −0.146 (0.136) | 0.035 ** (0.016) | −0.146 (0.121) | −0.076 *** (0.017) | −0.245 * (0.133) | |
| Sr | 0.052 (0.080) | 2.696 * (1.449) | −0.828 *** (0.187) | 4.972 *** (1.586) | 0.589 *** (0.202) | 4.335 *** (1.467) | |
| Fra | 0.001 (0.014) | 3.160 *** (0.250) | −0.018 (0.032) | 3.210 *** (0.241) | −0.020 *** (0.035) | 3.114 *** (0.240) | |
| Trade | −0.110 (0.093) | 2.241 *** (1.702) | −0.466 ** (0.219) | 3.058 * (1.676) | 0.662 *** (0.235) | 3.522 ** (1.704) | |
| Rd | −0.004 ** (0.002) | −0.096 *** (0.033) | −0.009 ** (0.004) | −0.087 *** (0.032) | 0.016 *** (0.004) | −0.070 ** (0.033) | |
| Fdi | −0.006 ** (0.002) | −0.088 ** (0.046) | −0.016 *** (0.006) | −0.068 (0.044) | 0.017 *** (0.006) | −0.065 (0.044) | |
| lnt | 0.008 *** (0.001) | 0.202 *** (0.016) | 0.009 *** (0.002) | 0.155 *** (0.017) | −0.020 (0.002) | 0.186 *** (0.019) | |
| high | −6.222 *** (1.170) | ||||||
| West | mid | −0.213 (0.841) | |||||
| low | 1.696 *** (0.604) | ||||||
| Df | 0.005 (0.007) | −0.203 ** (0.096) | −0.072 *** (0.011) | −0.248 ** (0.122) | 0.070 *** (0.015) | ||
| Sr | 0.077 (0.103) | 5.883 *** (1.342) | −0.311 * (0.159) | 5.341 *** (1.508) | 0.018 (0.214) | −0.352 *** (0.111) | |
| Fra | −0.071 *** (0.013) | −1.433 *** (0.188) | −0.038 * (0.020) | −1.000 *** (0.189) | 0.131 *** (0.027) | −1.214 *** (0.197) | |
| Trade | −0.043 (0.058) | 0.539 (0.759) | −0.055 (0.090) | 0.798 (0.841) | 0.145 (0.121) | 0.563 (0.819) | |
| Rd | −0.001 (0.002) | 0.039 * (0.023) | 0.008 *** (0.003) | 0.041 (0.026) | −0.008 ** (0.004) | 0.053 ** (0.025) | |
| Fdi | −0.008 (0.040) | 0.280 *** (0.068) | −0.030 *** (0.008) | 0.324 ** (0.881) | 0.040 *** (0.011) | 0.262 *** (0.077) |
Appendix B
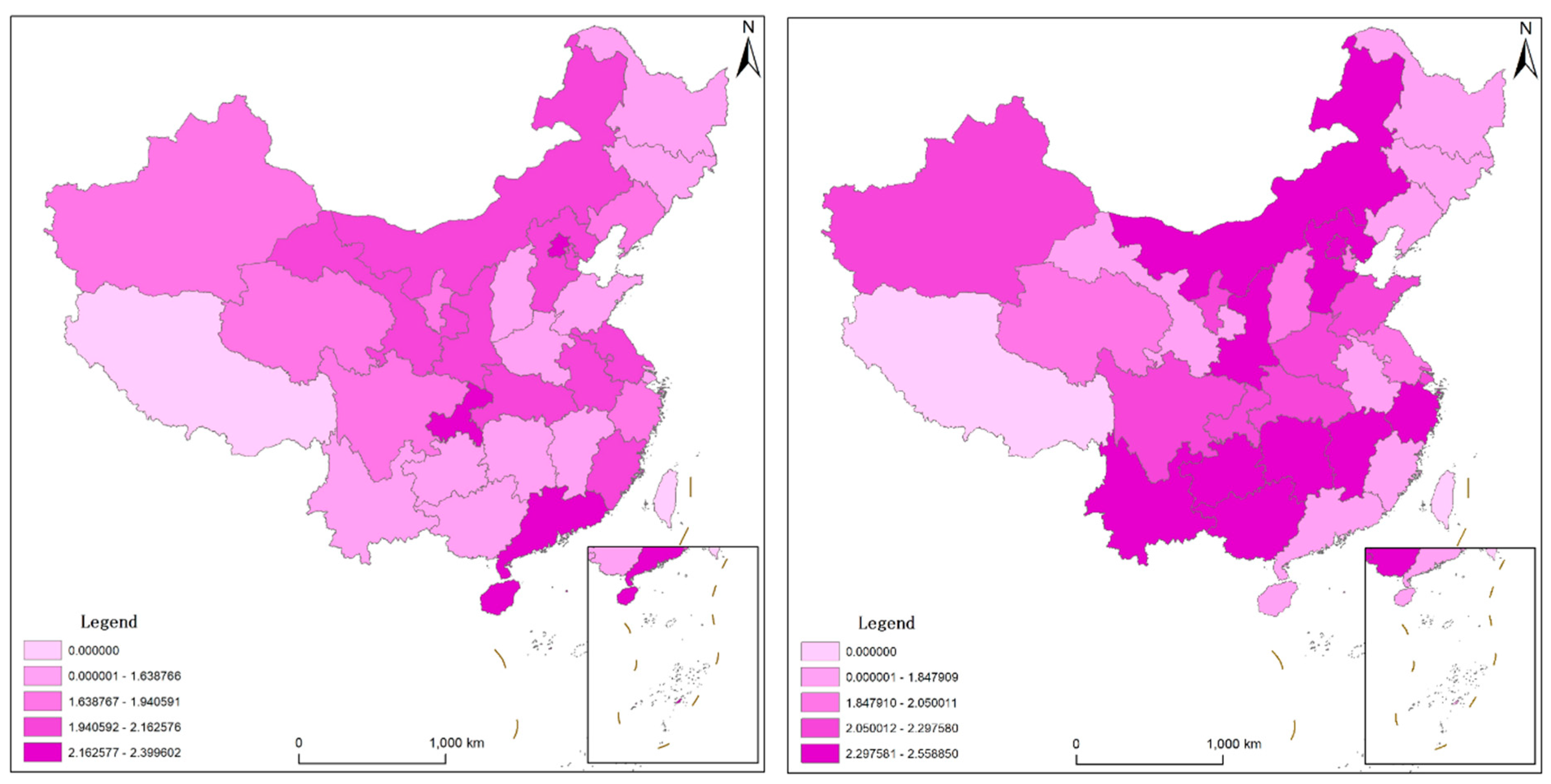



References
- Lai, D.; Meng, D.; Li, C.; Wang, Q. China Labor Market Development Report 2018; Beijing Normal University Press: Beijing, China, 2018; pp. 178–188. [Google Scholar]
- Fatima, S.; Desouza, K.C.; Dawson, G.S. National strategic artificial intelligence plans: A multi-dimensional analysis. Econ. Anal. Policy 2020, 67, 178–194. [Google Scholar] [CrossRef]
- Guerry, M.; Bieller, S.; Muller, C.; Kraus, W. Global Industrial Robotics Report 2020; IFR Press Conference: Frankfurt, Germany, 2020; pp. 1–32. [Google Scholar]
- Kromann, L.; Malchow-Møller, N.; Skaksen, J.R.; Sørensen, A. Automation and productivity? A cross-country, cross-industry comparison. Ind. Corp. Chang. 2019, 29, 265–287. [Google Scholar] [CrossRef] [Green Version]
- Brynjolfsson, E.; Rock, D.; Syverson, C. Artificial Intelligence and the Modern Produc-tivity Paradox: A Clash of Expectations and Statistics; University of Chicago Press: Chicago, IL, USA, 2019; pp. 23–60. [Google Scholar]
- Graetz, G.; Michaels, G. Robots at work. Rev. Econ. Stat. 2018, 100, 753–768. [Google Scholar] [CrossRef] [Green Version]
- Furman, J.; Seamans, R. AI and the economy. Innov. Policy Econ. 2019, 19, 161–191. [Google Scholar] [CrossRef]
- Prettner, K.; Strulik, H. The Lost Race Against the Machine: Automation, Education, and Inequality in an R&D-Based Growth Model. Cent. Eur. Gov. Econ. Dev. Res. Discuss. Pap. 2017, 8, 329–350. [Google Scholar]
- Prettner, K. A note on the implications of automation for economic growth and the labor share. Macroecon. Dyn. 2019, 23, 1294–1301. [Google Scholar] [CrossRef]
- Shi, B. An Explanation of the Mechanism of AI Promoting Economic High-quality Development. Reform 2020, 1, 30–38. [Google Scholar]
- Yang, C.; Liang, C.; Lee, C.C. How does the use of industrial robots affect the ecological footprint? International evidence. Ecol. Econ. 2022, 198, 107483. [Google Scholar]
- Acemoglu, D.; Restrepo, P. Low-skill and high-skill automation. J. Hum. Cap 2018, 12, 204–232. [Google Scholar] [CrossRef] [Green Version]
- Acemoglu, D.; Restrepo, P. The race between man and machine: Implications of tech-nology for growth, factor shares, and employment. Am. Econ. Rev. 2018, 108, 1488–1542. [Google Scholar] [CrossRef] [Green Version]
- Shackleton, J.R. Robocalypse now? Why we shouldn’t panic about automation, algorithms and artificial intelligence. Why We Shouldn’t Panic About Automation, Algorithmsand Artificial Intelligence (May 11, 2018). Inst. Econ. Aff. Curr. Controv. 2018, 61. [Google Scholar] [CrossRef]
- Chen, Y.B.; Lin, C.; Chen, X.L. Artificial Intelligence, Aging and Economic Growth. J. Econ. Res. 2019, 54, 47–63. [Google Scholar]
- Yang, G.; Hou, Y. The usage of industry robots, technology upgrade and economic growth. Chin. Ind. Econ. 2020, 10, 138–156. [Google Scholar]
- Cette, G.; Devillard, A.; Spiezia, V. Growth factors in developed countries: A 1960–2019 growth accounting decomposition. Comp. Econ. Stud. 2021, 64, 159–185. [Google Scholar] [CrossRef]
- Purdy, M.; Daugherty, P. Why Artificial Intelligence is the Future of Growth. 2016. Report. Accenture. Available online: https://max.book118.com/html/2017/1214/144058655.shtm (accessed on 1 November 2022).
- Bughin, J.; Seong, J.; Manyika, J.; Chui, M.; Joshi, R. Notes from the AI Frontier: Modeling the Impact of AI on the World Economy; Discussion Paper; McKinsey Global Institute, 2018; Available online: https://www.mckinsey.com/~/media/McKinsey/Featured%20Insights/Artificial%20Intelligence/Notes%20from%20the%20frontier%20Modeling%20the%20impact%20of%20AI%20on%20the%20world%20economy/MGI-Notes-from-the-AI-frontier-Modeling-the-impact-of-AI-on-the-world-economy-September-2018.ashx (accessed on 1 November 2022).
- Wei, W.; Hao, W.Y. Technology Choice and the Economic Growth Forced by Technological Progress—An Empirical Study of Chinese Experience. Res. Econ. Manag. 2015, 36, 33–39. [Google Scholar]
- Shen, G.J. “Capital-skill Complementarity” Hypothesis: Theory, Verification and Its Applications. Chin. Econ. Q. 2016, 15, 1653–1682. [Google Scholar]
- Benedetto, R.; Davide, R.; Paula, H.; Bianca, S.; Enrico, B. Ecological deficit and use of natural capital in Luxembourg from 1995 to 2009. Sci. Total Env. 2014, 468–469, 292–301. [Google Scholar]
- Bloom, D.E.; Mckenna, M.; Prettner, K. Demography, unemployment, automation, and digitalization: Implications for the creation of (decent) jobs, 2010–2030. NBER Work. Pap. 2018. Available online: https://www.econstor.eu/handle/10419/185199 (accessed on 1 November 2022).
- Jung, J.H.; Lim, D.G. Industrial robots, employment growth, and labor cost: A simultaneous equation analysis. Technol. Forecast. Soc. Chang. 2020, 159, 120202. [Google Scholar] [CrossRef]
- Wang, E.Z.; Lee, C.C.; Li, Y. Assessing the impact of industrial robots on manufacturing energy intensity in 38 countries. Energy Econ. 2022, 105, 105748. [Google Scholar] [CrossRef]
- Zhou, F.; Wen, H.; Lee, C.C. Broadband infrastructure and export growth. Telecommun. Policy 2022, 46, 102347. [Google Scholar] [CrossRef]
- Kanazawa, A.; Kinugawa, J.; Kosuge, K. Adaptive motion planning for a collaborative robot based on prediction uncertainty to enhance human safety and work efficiency. IEEE Trans. Robot. 2019, 35, 817–832. [Google Scholar] [CrossRef]
- Sachs, J.D.; Kotlikoff, L.J. Smart Machines and Long-Term Misery; National Bureau of Economic Research: Cambridge, UK, 2012. [Google Scholar]
- de Vries, G.J.; Gentile, E.; Miroudot, S.; Wacker, K.M. The rise of robots and the fall of routine jobs. Labour. Econ. 2020, 66, 101885. [Google Scholar] [CrossRef]
- Chen, Y.; Lee, C.C.; Chen, M. Ecological footprint, human capital, and urbanization. Energy Env. 2022, 33, 487–510. [Google Scholar] [CrossRef]
- Autor, D.H.; Dorn, D. The growth of low-skill service jobs and the polarization of the US labor market. Am. Econ. Rev. 2013, 103, 1553–1597. [Google Scholar] [CrossRef] [Green Version]
- Dauth, W.; Findeisen, S.; Südekum, J.; Woessner, N. German Robots-the Impact of Industrial Robots on Workers. CEPR Discussion Paper 12306. 2017. Available online: https://conference.iza.org/conference_files/MacroEcon_2018/suedekum_j1695.pdf (accessed on 1 November 2022).
- Chiacchio, F.; Petropoulos, G.; Pichler, D. The Impact of Industrial Robots on EU Employment and Wages: A Local Labour Market Approach. Technical Report, Issue 2. 2018. Available online: https://www.bruegel.org/sites/default/files/wp-content/uploads/2018/04/Working-Paper_02_2018.pdf (accessed on 1 November 2022).
- Acemoglu, D.; Restrepo, P. The wrong kind of AI? Artificial intelligence and the future of labour demand. Camb. J. Reg. Econ. Soc. 2020, 13, 25–35. [Google Scholar] [CrossRef]
- Arntz, M.; Gregory, T.; Zierahn, U. Revisiting the risk of automation. Econ. Lett. 2017, 159, 157–160. [Google Scholar] [CrossRef]
- Acemoglu, D.; Restrepo, P. Robots and jobs: Evidence from US labor markets. J. Polit. Econ. 2020, 128, 2188–2244. [Google Scholar] [CrossRef] [Green Version]
- Adachi, D.; Kawaguchi, D.; Saito, Y. Robots and Employment: Evidence from Japan, 1978–2017; Discussion papers; Research Institute of Economy, Trade and Industry (RIETI): Tokyo, Japan, 2020. [Google Scholar]
- Acemoglu, D.; Lelarge, C.; Restrepo, P. Competing with robots: Firm-level evidence from France. AEA Pap. Proc. 2020, 110, 383–388. [Google Scholar] [CrossRef]
- Goos, M.; Manning, A.; Salomons, A. Job Polarization in Europe. Am. Econ. Rev. 2009, 99, 58–63. [Google Scholar] [CrossRef] [Green Version]
- Lv, S.B.; Zhang, S.W. Employment “Polarization” in China: An empirical Research. Chin. Econ. Q. 2015, 14, 757–778. [Google Scholar]
- Hao, N.; Jiang, Y.H. What Affected Labor Employment Polarization in China? Res. Econ. Manag. 2017, 38, 75–85. [Google Scholar]
- Qu, X.B.; Cheng, J. Changes of Employment Structure in China Upgrading or Polarization? Stud. Lab. Econ. 2015, 3, 119–144. [Google Scholar]
- Xie, M.M.; Xia, Y.; Pan, J.F.; Guo, J.F. Artificial Intelligence, Technological Change and Low—Skill Employment. Empirical Evidence from Chinese Manufacturing Firms. Chin. J. Manag. Sci. 2020, 28, 54–66. [Google Scholar]
- Chen, Q.L.; Xu, D.; Zhou, Y. Labour Sbustitution Effect of Artificial Intelligence in the Era of Population Aging: Evidence from Panel Data across Countries and Panel Data at Provincial Level in China. Chin. J. Popul. Sci. 2018, 6, 30–42, 126–127. [Google Scholar]
- Cai, F. How can Chinese Economy Achieve the Transiton toward Total Factor Productivity Growth? Soc. Sci. Chin. 2013, 1, 56–71, 206. [Google Scholar]
- Wu, J.L. Deepen Reform to Establish A New Normal for Chinese Economy. Explor. Conten. 2015, 1, 4–7+2. [Google Scholar]
- Wen, Z.L.; Ye, B.J. Analyses of Mediating Effects: The Development of Methods and Models. Advanc. Psychol. Sci. 2014, 22, 731–745. [Google Scholar] [CrossRef]
- Duffy, J.; Papageorgiou, C.; Perez-Sebastian, F. Capital-skill complementarity? Evidence from a panel of countries. Rev. Econ. Stat. 2004, 86, 327–344. [Google Scholar] [CrossRef] [Green Version]
- Benabou, R. Inequality and growth. NBER Macroecon. Annu. 1996, 11, 11–74. [Google Scholar] [CrossRef]
- Forbes, K.J. A reassessment of the relationship between inequality and growth. Am. Econ. Rev. 2000, 90, 869–887. [Google Scholar] [CrossRef] [Green Version]
- Yu, Y.Z. Dynamic spatial convergence of provincial total factor productivity in China. Wor. Econ. 2015, 38, 30–55. [Google Scholar]
- Yu, Y.Z. Estimation of Total Factor Productivity in China from the Perspective of Heterogeneity:1978–2012. Chin. Econ. Q. 2017, 16, 1051–1072. [Google Scholar]
- Battese, G.E.; Coelli, T.J. Frontier production functions, technical efficiency and panel data: With application to paddy farmers in India. J. Prod. Anal. 1992, 3, 153–169. [Google Scholar] [CrossRef]
- Sun, Z.; Hou, Y.L. How Does Industrial Intelligence Reshape the Employment Structure of Chinese Labor Force. Chin. Indus. Econ. 2019, 5, 61–79. [Google Scholar]
- Chen, X.; Zheng, Y.L.; Yao, D. Industrial Intelligence, Employment Structure of Labor Force and Quality of Economic Growth: Empirical Test Based on Mediating Effect Model. Chin. Econ. Manag. 2020, b34, 56–64. [Google Scholar]
- Dai, X.; Liu, M.; Ren, Z.C. How Does Labor Evolution Affect China’s Industrial Development: Transfer or Transformation. Chin. Indus. Econ. 2016, 9, 24–40. [Google Scholar]
- Mao, Q.L.; Sheng, B. Trade Liberalization and Chinese Firms’ Export Behavior: Does WTO Entry Facilitate Export Participation? Chin. Econ. Q. 2014, 13, 647–674. [Google Scholar]
- Liu, L.; Li, L.S.; Liu, J.; Cheng, Z.H. Intelligentization and the Transformation of Economic Development Mode: Theoretical Mechanism and Empirical Evidence. Econ. Rev. 2020, 2, 3–19. [Google Scholar]
| Variant | Symbol | Average Value | Standard Deviation | Maximum Value | Minimum Value |
|---|---|---|---|---|---|
| Output | lnY | 8.959 | 0.964 | 6.143 | 10.963 |
| Capital input | lnK | 9.881 | 1.164 | 6.821 | 12.101 |
| Labor input | lnL | 7.59 | 0.81 | 5.673 | 8.814 |
| Time | T | 6.5 | 3.457 | 1 | 12 |
| Square of capital input | KK | 98.988 | 22.478 | 46.525 | 146.426 |
| Square of labor input | LL | 58.255 | 11.887 | 32.188 | 77.682 |
| Square of time | TT | 54.167 | 46.163 | 1 | 144 |
| Capital input multiplied by labor input | KL | 75.505 | 14.442 | 39.518 | 106.514 |
| Time multiplied by capital input | TK | 66.014 | 38.19 | 6.821 | 145.208 |
| Time multiplied by labor input | TL | 49.551 | 27.259 | 5.673 | 105.765 |
| Variant | Coefficient | Variant | Coefficient |
|---|---|---|---|
| C (constant) | 9.567 *** (0.999) | TK (time multi.by capital) | −2.372 (0.620) |
| lnK (capital input) | 2.113 ** (0.996) | TL (time multi.by labor) | 2.841 *** (0.714) |
| lnL (labor input) | 1.163 (0.997) | σ2 | 0.246 (0.999) |
| T (time) | 6.164 *** (0.998) | γ | 0.978 (0.998) |
| KK (square of capital) | 8.368 (0.381) | μ | 321.19 *** (0.998) |
| LL (square of labor) | 6.05 (0.587) | η | 74.746 *** (0.993) |
| TT (square of time) | −14.464 ** (6.896) | log likelihood funct. value | 370.61 |
| KL (capital multi. by labor) | −0.151 (0.805) | LR statistical amount | 930.472 |
| Test | Hypothesis | LLF | LR | Degree of Freedom K | Conclusion | |
|---|---|---|---|---|---|---|
| Step 1 | H1: not all binomial coefficients are 0. H0: all binomial coefficients are 0. | 370.61 329.099 | 83.022 | 3 | 7.05 | HO rejected |
| Step 2 | H1: not all time-varying coefficients are 0. H0: all time-varying coefficients are 0. | 329.099 451.587 | −244.976 | 3 | 7.05 | HO accepted |
| Variable | Symbol | Average Value | Standard Deviation | Maximum Value | Minimum Value |
|---|---|---|---|---|---|
| Total factor productivity | TFP | 1.261 | 0.731 | 2.661 | −0.130 |
| Industrial intelligence | lnt | 15.995 | 9.863 | 76.686 | 2.152 |
| Low-skill labor | low | 0.253 | 0.102 | 0.603 | 0.026 |
| Medium-skill labor | mid | 0.590 | 0.005 | 0.764 | 0.341 |
| High-skill labor | high | 0.141 | 0.005 | 0.559 | 0.030 |
| Trade openness | Trade | 0.311 | 0.020 | 1.662 | 0.016 |
| Financial development | Df | 2.855 | 0.059 | 8.131 | 1.288 |
| Industrial structure upgrade | Sr | 0.430 | 0.005 | 0.802 | 0.283 |
| Infrastructure | Fra | 0.858 | 0.025 | 2.438 | 0.066 |
| TFP (1) | TFP (2) | TFP (3) | TFP (4) | TFP (5) | |
|---|---|---|---|---|---|
| Lnt (industrial intelligence) | 0.077 *** (0.023) | 0.082 *** (0.023) | 0.100 *** (0.022) | 0.098 *** (0.022) | 0.054 ** (0.023) |
| Df (financial develp.) | −0.497 *** (0.165) | −1.055 *** (0.181) | −0.991 *** (0.185) | −0.968 *** (0.179) | |
| Sr (industrial structure) | 10.489 *** (1.696) | 10.348 *** (1.694) | 10.547 *** (1.646) | ||
| Fra (infrastructure) | 1.044 (0.662) | 1.257 * (0.644) | |||
| Trade (trade openness) | −2.280 *** (0.511) | ||||
| C (constant) | −3.121 *** (0.897) | −0.010 (1.363) | −4.688 *** (1.495) | −6.149 *** (1.756) | −2.067 (1.935) |
| Fixed effect of region | Control | Control | Control | Control | Control |
| Fixed effect of time | Control | Control | Control | Control | Control |
| R2 | 0.851 | 0.855 | 0.871 | 0.879 | 0.880 |
| OBS | 360 | 360 | 360 | 360 | 360 |
| F | 0.000 *** | 0.000 *** | 0.000 *** | 0.000 *** | 0.000 *** |
| High-Skill Labor (1) | TFP (2) | Medium-Skill Labor (3) | TFP (4) | Low-Skill Labor (5) | TFP (6) | |
|---|---|---|---|---|---|---|
| lnt (industrial intelligence) | 0.004 *** (0.001) | 0.243 *** (0.017) | 0.001 (0.001) | 0.227 *** (0.015) | −0.007 *** (0.001) | 0.223 *** (0.014) |
| high (high skill) | −3.826 *** (1.442) | |||||
| mid (mid skill) | 1.491 * (0.781) | |||||
| low (low skill) | −0.808 (0.660) | |||||
| Bootstrap test (indirect effect) | 0.015 ** (0.007) | 0.001 (0.001) | 0.006 (0.005) | |||
| Bootstrap test (direct effect) | 0.243 *** (0.027) | 0.227 *** (0.026) | 0.223 *** (0.027) | |||
| Df (financial development) | 0.024 *** (0.005) | −1.060 *** (0.136) | 0.050 *** (0.008) | −1.076 *** (0.140) | 0.032 *** (0.009) | −1.125 *** (0.135) |
| Sr (ind. str. upgrading) | 0.277 *** (0.064) | 3.849 ** (1.770) | −0.117 (0.103) | 2.962 * (1.737) | −0.327 *** (0.124) | 2.524 (1.755) |
| Fra(infrastructure) | −0.003 (0.007) | 0.516 *** (0.186) | −0.020 * (0.011) | 0.497 *** (0.188) | −0.020 (0.013) | 0.510 *** (0.188) |
| Trade (trade openness) | −0.004 (0.011) | −2.030 *** (0.285) | 0.080 *** (0.017) | −0.805 *** (0.280) | −0.013 (0.021) | −2.024 *** (0.288) |
| C (constant) | −0.103 *** (0.017) | 0.250 (0.474) | −0.728 *** (0.027) | −0.440 (0.792) | 0.434 *** (0.032) | 0.996 * (0.554) |
| R2 | 0.746 | 0.563 | 0.312 | 0.559 | 0.403 | 0.668 |
| OBS F | 360 0.000 *** | 360 0.000 *** | 360 0.000 *** | 360 0.000 *** | 360 0.000 *** | 360 0.000 *** |
| TFP | TFP | ||
|---|---|---|---|
| lnt (indus. intelligence) | 0.088 *** (0.021) | Rd (R&D input) | 0.324 *** (0.037) |
| Df (financial developt) | −0.889 *** (0.159) | Fdi (equipment invest.) | −0.144 *** (0.046) |
| Sr (indus.str.upgrading) | 8.799 *** (1.456) | C (constant) | −10.324 *** (1.969) |
| Fra (infrastructure) | 0.379 (0.574) | Fixed effect of region | control |
| Trade (trade openness) | −1.792 *** (0.461) | Fixed effect of time | control |
| OBS | 360 | R2 | 0.906 |
| Industrial Intelligence | Industrial Intelligence | ||
|---|---|---|---|
| Df (financial developmnt) | 1.178 *** (0.412) | high (high-skill labor) | 20.121 (11.638) |
| Sr (indus. str. upgrade) | −12.227 *** (4.039) | mid (medium-skill labor) | −5.174 (10.960) |
| Fra (infrastructure) | 2.546 * (1.512) | low (low-skill labor) | 0.116 (11.941) |
| Trade (trade openness) | −6.860 *** (1.309) | C (constant) | 45.912 *** (11.141) |
| Rd (R&D input) | −0.270 *** (0.093) | Fixed effect of region | Control |
| Fdi (equip. investment) | 0.179 (0.123) | Fixed effect of time | Control |
| OBS | 360 | R2 | 0.974 |
| TFP (1) | TFP (2) | TFP (3) | |
|---|---|---|---|
| lnt (indus. intelligence) | 0.239 *** (0.014) | 0.264 *** (0.013) | 0.217 *** (0.016) |
| high (high skill) | −1.742 (1.283) | ||
| lh (lnt*high) | −0.417 *** (0.042) | ||
| mid (medium skill) | 3.363 *** (0.751) | ||
| lm (lnt*mid) | 0.639 *** (0.055) | ||
| low (low skill) | 0.532 (0.805) | ||
| ll (lnt*low) | 0.271 *** (0.069) | ||
| Df (financial development) | −0.806 *** (0.122) | −0.755 *** (0.120) | −1.102 *** (0.131) |
| Sr (indus. str. upgrade) | 4.706 *** (1.509) | 2.607 * (1.437) | 4.369 ** (1.722) |
| Fra (infrastructure) | 0.344 ** (0.170) | 0.427 *** (0.165) | 0.365 * (0.192) |
| Trade (trade openness) | −2.593 *** (0.285) | −3.794 *** (0.308) | −2.007 *** (0.318) |
| Rd (R&D input) | 0.110 *** (0.018) | 0.103 *** (0.017 | 0.078 *** (0.020) |
| Fdi (equip. investment) | −0.120 *** (0.037) | −0.166 *** (0.035) | −0.186 *** (0.041) |
| C (constant) | −0.836 ** (0.425) | −2.647 *** (0.681) | 0.031 (0.625) |
| R2 | 0.687 | 0.704 | 0.604 |
| OBS | 360 | 360 | 360 |
| F | 0.000 *** | 0.000 *** | 0.000 *** |
| East | Middle | West | |
|---|---|---|---|
| Lnt (industrial intelligence) | 0.235 *** (0.024) | 0.206 *** (0.020) | 0.153 *** (0.015) |
| Df (financial development) | −2.001 *** (0.286) | −0.056 (0.122) | −0.233 ** (0.105) |
| Sr (industrial structure upgrade) | 9.284 *** (3.564) | 2.868 * (1.457) | 5.407 *** (1.479) |
| Fra (infrastructure) | 1.280 *** (0.402) | 3.163 *** (0.253) | −0.992 *** (0.186) |
| Trade (trade openness) | −2.731 *** (0.472) | 1.875 (1.699) | 0.810 (0.837) |
| Rd (R&D input) | 0.066 ** (0.029) | −0.109 *** (0.032) | 0.039 (0.025) |
| Fdi (equip. investment) C (constant) | −0.197 *** (0.065) −0.201 (0.892) | −0.108 ** (0.044) −4.180 *** (0.595) | 0.330 *** (0.075) −2.269 *** (0.576) |
| R2 | 0.610 | 0.916 | 0.690 |
| OBS | 360 | 360 | 360 |
| F | 0.000 *** | 0.000 *** | 0.000 *** |
| Region | High-Skill Labor | TFP | Medium-Skill Labor | TFP | Low-Skill Labor | TFP | |
|---|---|---|---|---|---|---|---|
| East | lnt | 0.002 ** (0.001) | 0.255 *** (0.024) | −0.004 *** (0.001) | 0.271 *** (0.024) | −0.001 (0.001) | 0.232 *** (0.024) |
| high | −10.046 *** (2.441) | ||||||
| mid | 9.740 *** (2.089) | ||||||
| low | −4.342 * (2.222) | ||||||
| Middle | lnt | 0.008 *** (0.001) | 0.080 *** (0.027) | 0.006 ** (0.003) | 0.192 *** (0.020) | −0.015 *** (0.003) | 0.168 *** (0.023) |
| high | 3.342 (2.270) | ||||||
| mid | 2.539 *** (0.926) | ||||||
| low | −2.489 *** (0.854) | ||||||
| West | lnt | 0.008 *** (0.001) | 0.202 *** (0.016) | 0.009 *** (0.002) | 0.155 *** (0.017) | −0.020 (0.002) | 0.186 *** (0.019) |
| high | −6.222 *** (1.170) | ||||||
| mid | −0.213 (0.841) | ||||||
| low | 1.696 *** (0.604) |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
An, K.; Shan, Y.; Shi, S. Impact of Industrial Intelligence on Total Factor Productivity. Sustainability 2022, 14, 14535. https://doi.org/10.3390/su142114535
An K, Shan Y, Shi S. Impact of Industrial Intelligence on Total Factor Productivity. Sustainability. 2022; 14(21):14535. https://doi.org/10.3390/su142114535
Chicago/Turabian StyleAn, Ke, Yike Shan, and Sheng Shi. 2022. "Impact of Industrial Intelligence on Total Factor Productivity" Sustainability 14, no. 21: 14535. https://doi.org/10.3390/su142114535
APA StyleAn, K., Shan, Y., & Shi, S. (2022). Impact of Industrial Intelligence on Total Factor Productivity. Sustainability, 14(21), 14535. https://doi.org/10.3390/su142114535




