A Multistage Time-Delay Control Model for COVID-19 Transmission
Abstract
1. Introduction
- (1)
- Based on a survey of the literature on epidemiology, due to the three periods of the development of the epidemic, a multistage time-delay COVID-19 transmission model is established in this paper. The classic SEIR model, the improved SEQIR (susceptible–exposed–quarantine–infected–recovered) model and the SEQIR Ⅱ (susceptible–exposed–quarantine–infected–recovered Ⅱ) model are adopted and used to model the outbreak period, the control period, and the steady period, respectively. These models could better simulate the transmission of three phases of COVID-19, and the results are more actual with the development of the epidemic.
- (2)
- Because COVID-19 has an incubation period, the state shall adopt prevention and control measures designed to provide prevention and control, isolating the close contacts of confirmed patients until they are cured; isolation, the spread of death and medical measures such as process improvement have a time lag. In this paper, the SEQIR model adds the isolation measures Q, considering the effective time of Q, that is, the delay time as a delay factor. In addition, several change rates are improved to better simulate the results.
- (3)
- Population mobility has a significant impact on the spread of COVID-19. The SEQIR II model used in this paper takes population mobility during the steady period, which includes both immigrating and emigrating populations.
- (4)
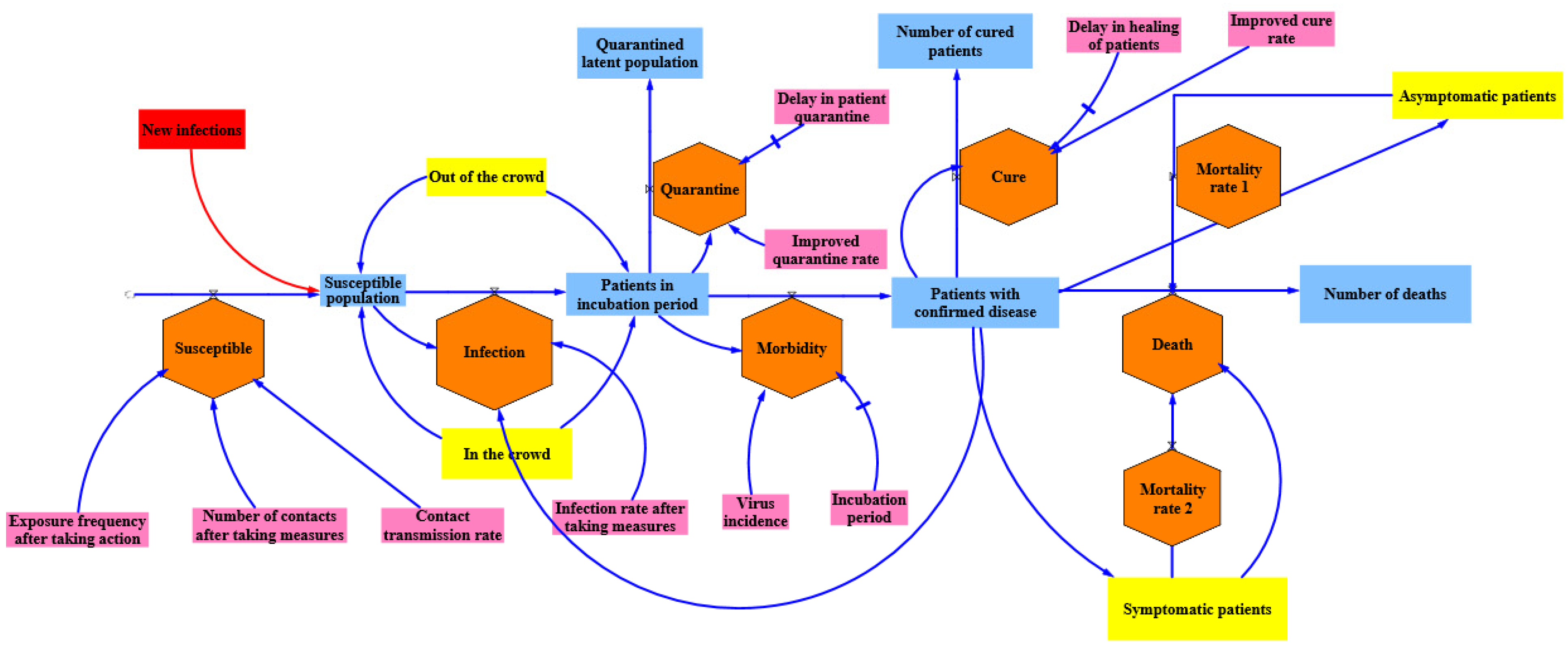
- In the steady period, this paper’s focus shifts from the cumulative number of confirmed patients to the number of new patients. In addition, the symptoms of patients are classified as asymptomatic and symptomatic. Therefore, at the beginning of the steady period, the new patients could be divided into symptomatic patients and asymptomatic patients, a division that is more consistent with the current transmission situation.
2. Related Work
3. Model Hypothesis and Parameter Design
3.1. Model Hypothesis
- (1)
- The initial number of virus transmission patients is a constant value, as is the number of new infections.
- (2)
- In the outbreak period and the control period, the effect of the prevention and control measures on the spread of the epidemic is mainly studied without considering the influence of the immigration and emigration population.
- (3)
- Confirmed patients can infect the susceptible population and transform them into latent patients.
- (4)
- Close contacts during the incubation period will be quarantined, assuming that all close contacts can accept the isolation.
- (5)
- There are certain antibodies in recovered patients, and although there is a risk of reinfection, its incidence is greatly reduced compared with normal people; therefore, reinfection in recovered patients was not considered.
- (6)
- It is assumed that all patients infected during the incubation period go to the hospital for testing after onset, become confirmed patients, and are hospitalized.
- (7)
- After recovery, the nucleic acid test of the confirmed patient becomes negative, the patient is kept in the hospital for 5 days for observation, and his or her body temperature is normal. After reexamination, the patient is discharged.
3.2. Parameter Design
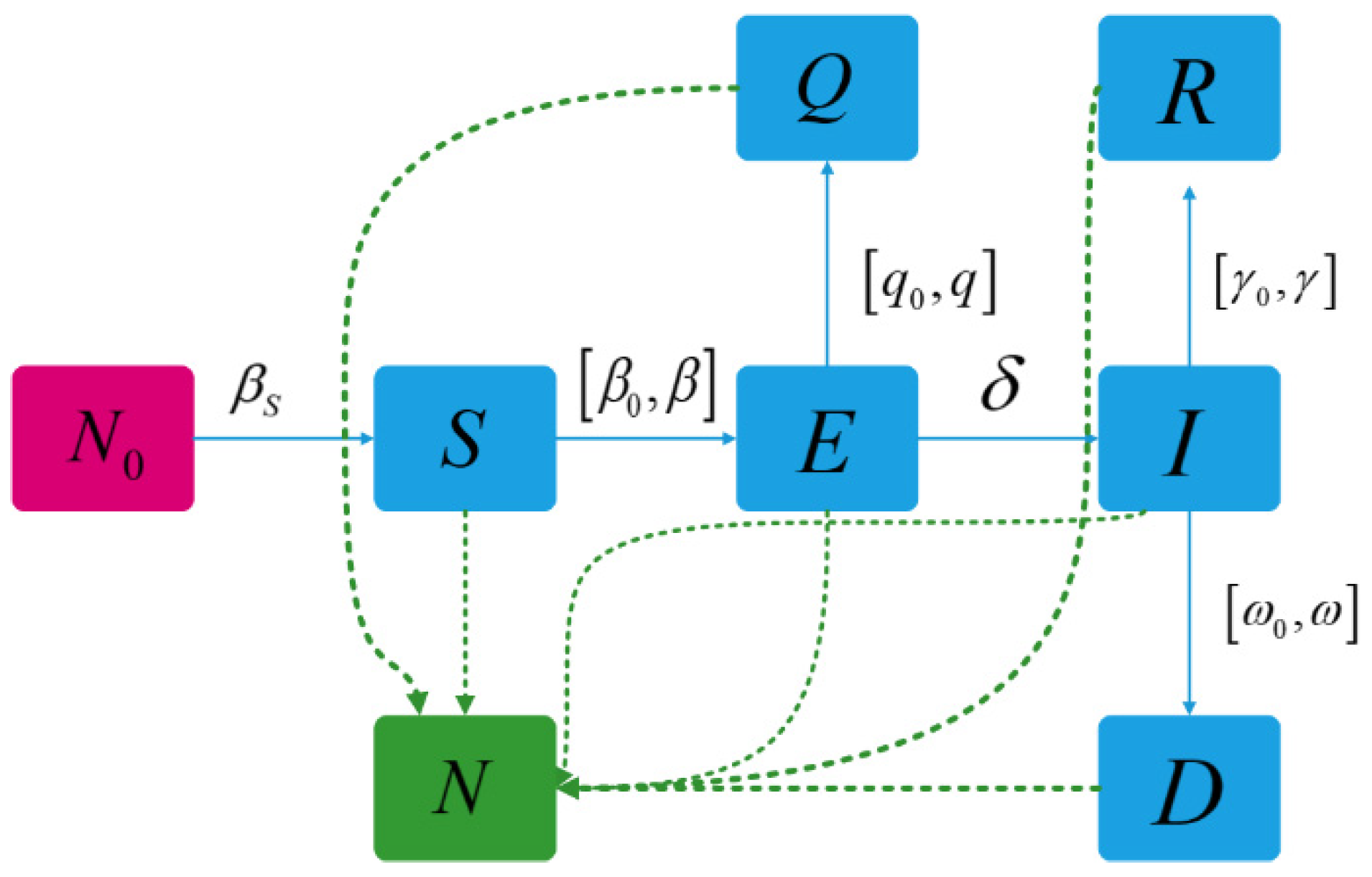
4. SEIR Model and SEQIR Ⅱ Model
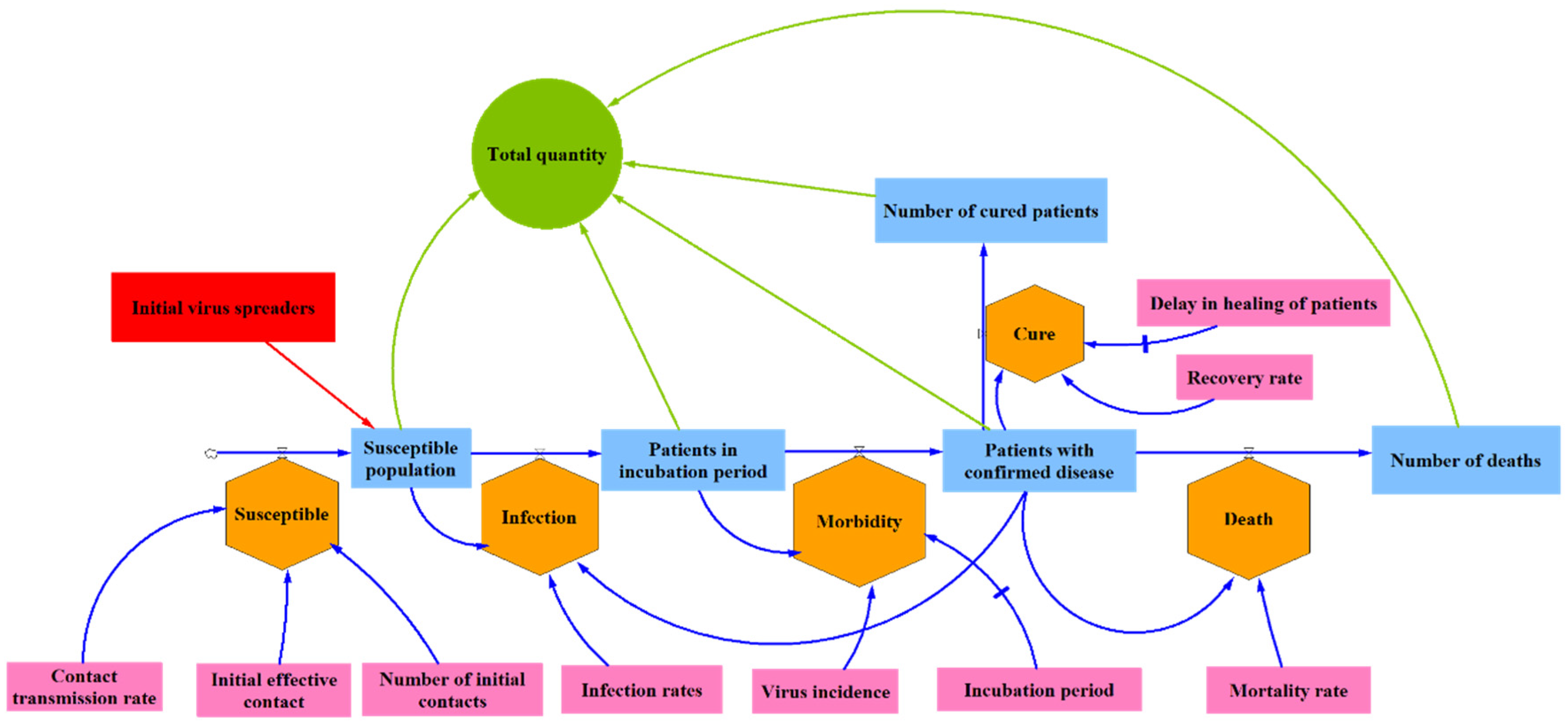
4.1. Classical SEIR Model
4.2. SEQIR Model
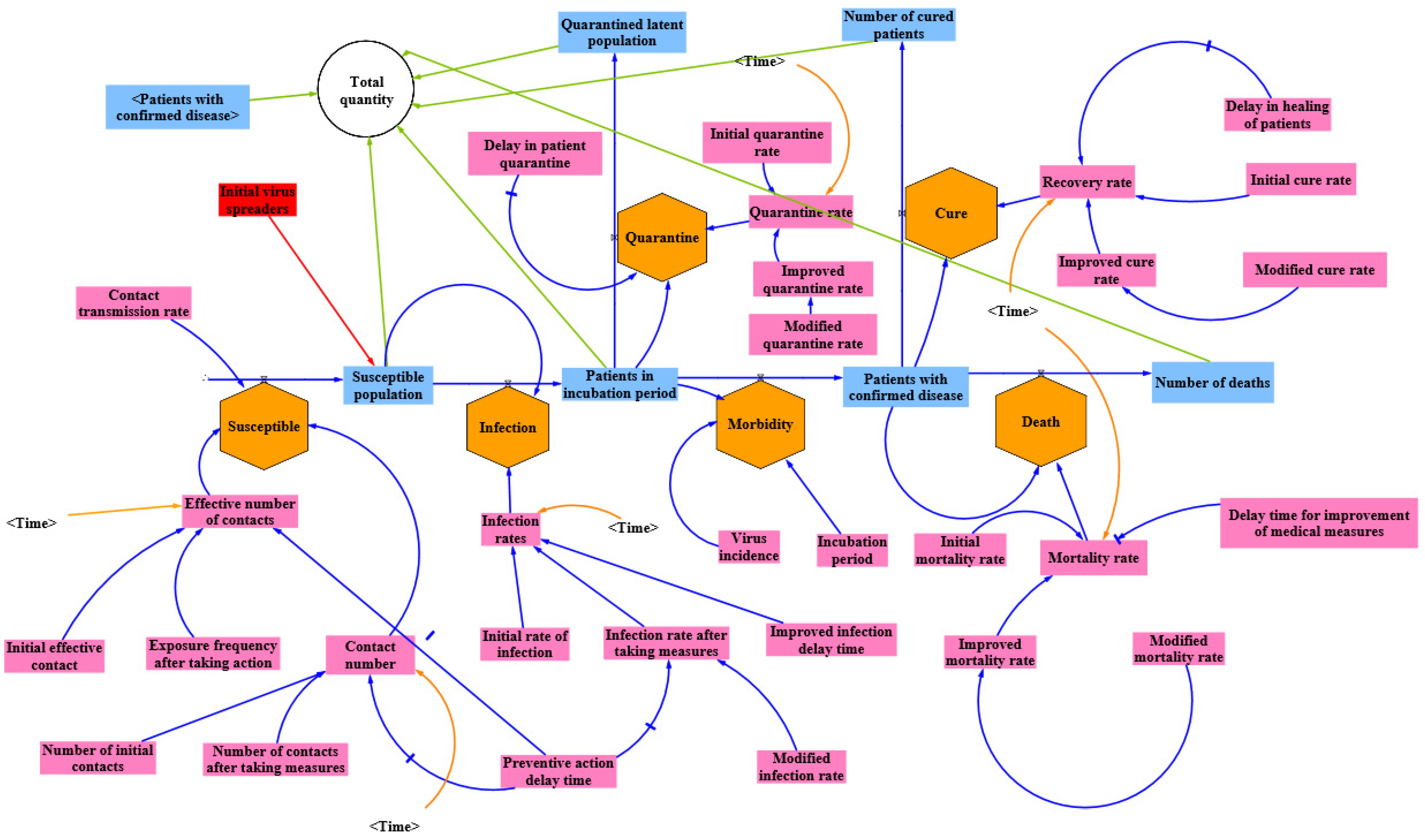
4.3. SEQIR II Model
4.4. Assignment of Model Parameters
5. Experimental Results and Analysis
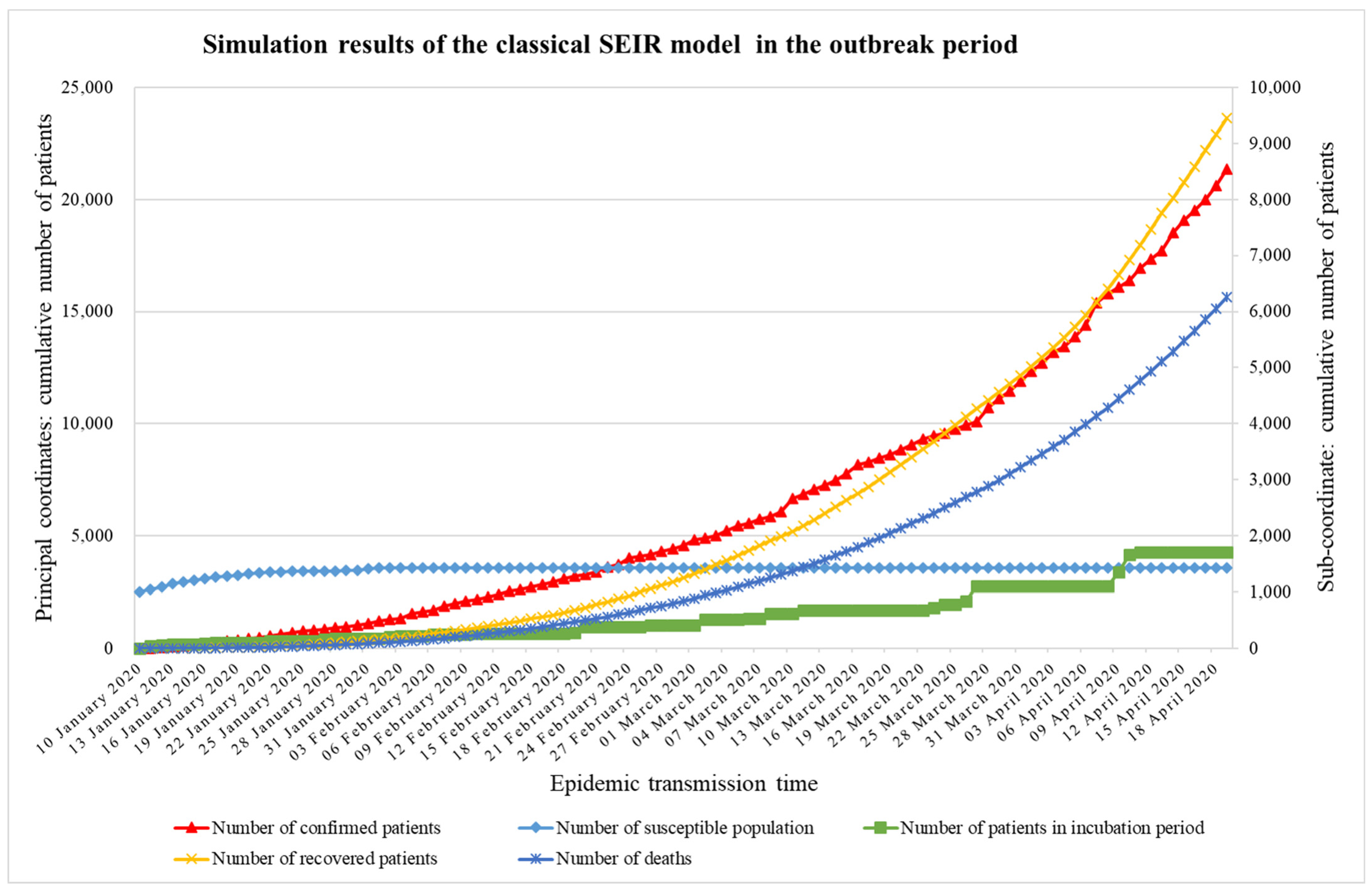
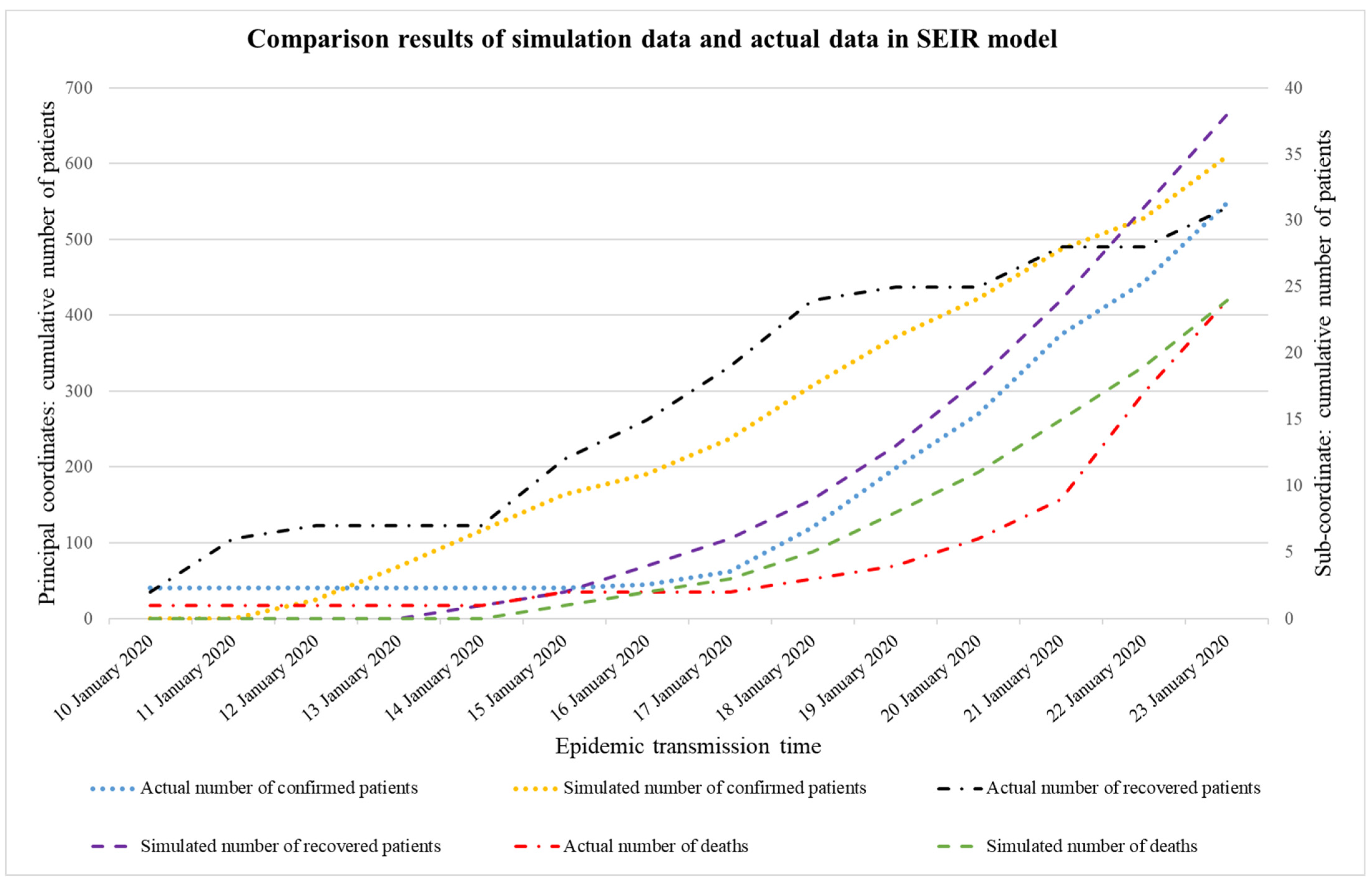
5.1. Outbreak Period
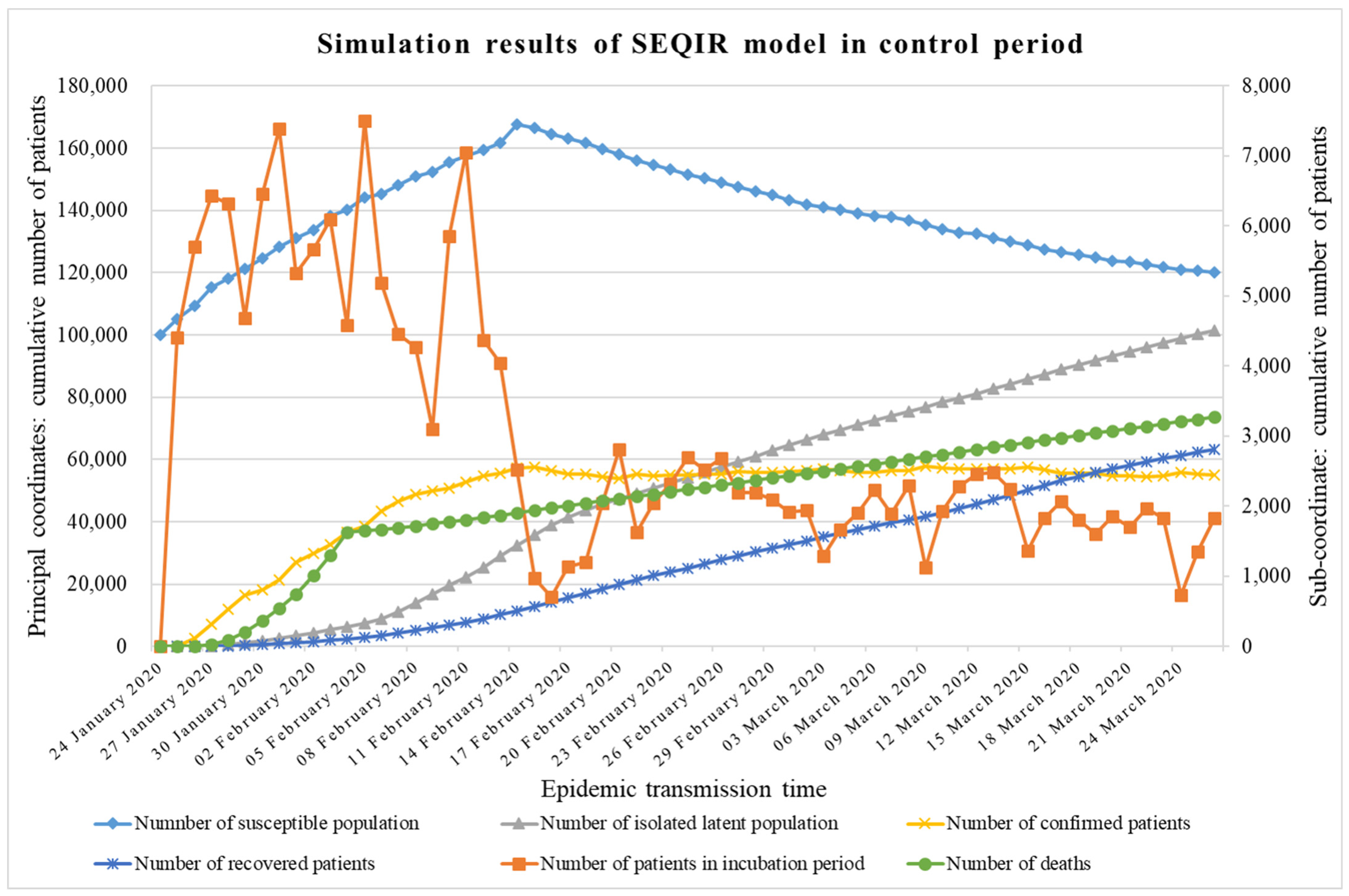
5.2. Control Period
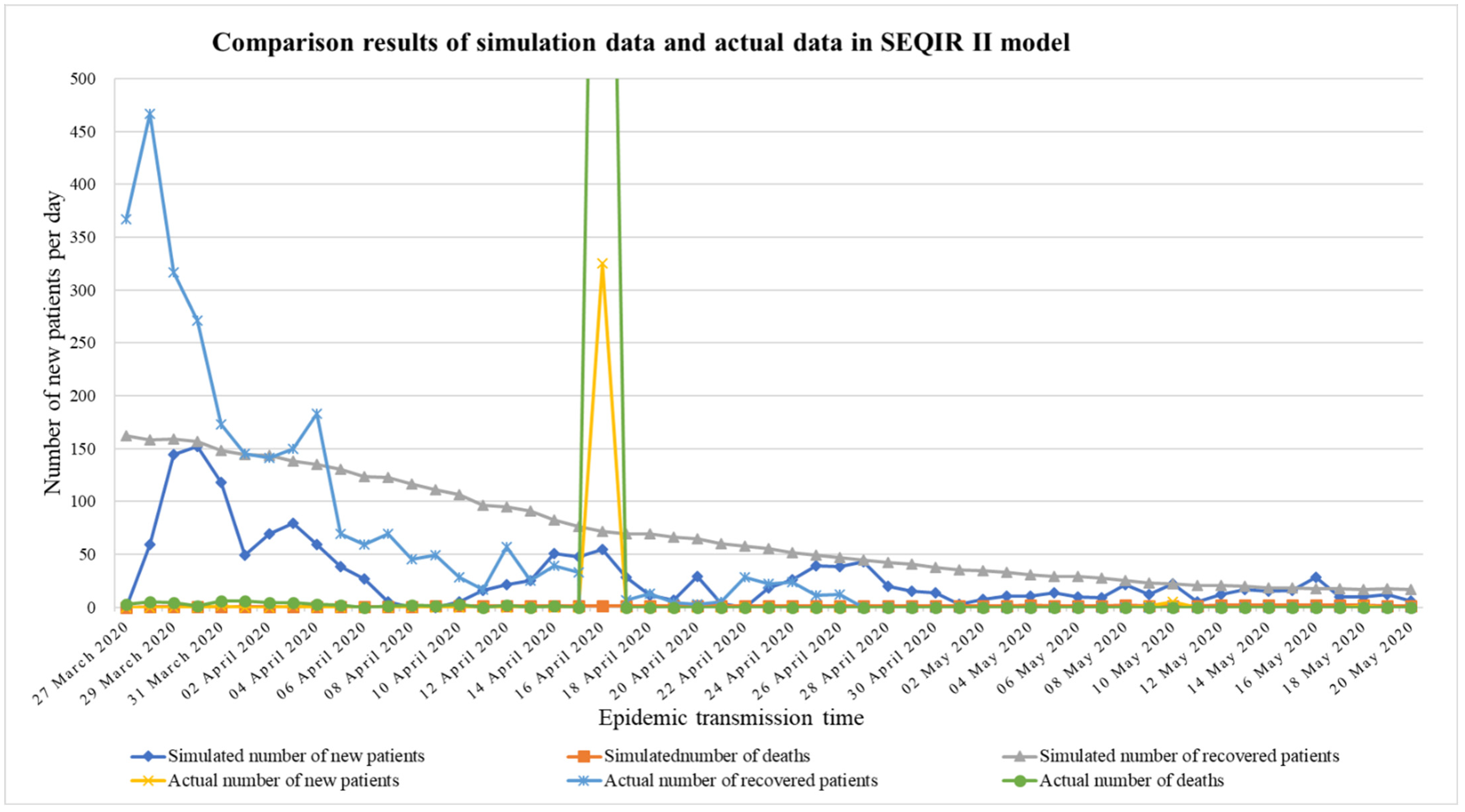
5.3. Steady Period
6. Conclusions and Discussion
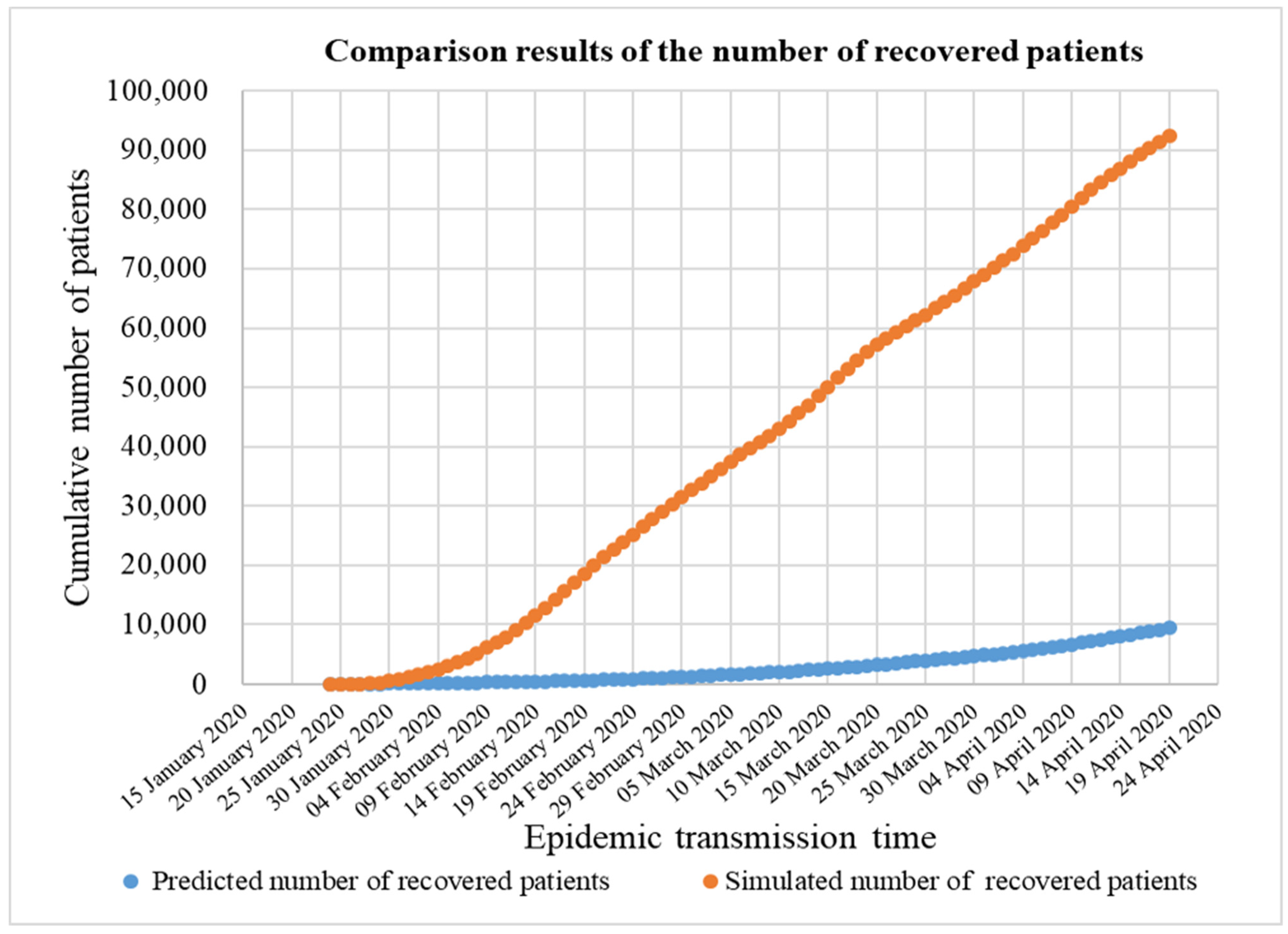
- For the comparison between the predicted data of the classical SEIR model and the simulated data of the improved SEQIR model for the control period, the actual data is not added for discussion, which needs to be improved later.
- Changes in mortality in the improved SEQIR model will be modified to make it more consistent with changes in the number of deaths during the control period.
- This may alter or improve aspects of the SEQIR Ⅱ model, in which the simulation effect of the number of recovered patients is poor.
- The SEQIR Ⅱ model will be modified to better simulate the process of a sudden and rapid decline in the number of recovered patients.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Kumar, P.; Morawska, L. Could fighting airborne transmission be the next line of defence against COVID-19 spread? City Environ. Interact. 2019, 4, 100033. [Google Scholar] [CrossRef] [PubMed]
- Shuai, Y.; Jiang, C.; Su, X.; Yuan, C.; Huang, X. A Hybrid Clustering Model for Analyzing COVID-19 National Prevention and Control Strategy. In Proceedings of the 2020 IEEE 6th International Conference on Control Science and Systems Engineering (ICCSSE), Beijing, China, 17–19 July 2020. [Google Scholar] [CrossRef]
- Spaan, W.; Cavanagh, D.; Horzinek, M.C. Coronaviruses: Structure and genome expression. J. Gen. Virol. 1988, 69 Pt 12, 2939–2952. [Google Scholar] [CrossRef]
- Zhu, N.; Zhang, D.; Wang, W.; Li, X.; Yang, B.; Song, J.; Zhao, X.; Huang, B.; Shi, W.; Lu, R.; et al. A Novel Coronavirus from Patients with Pneumonia in China, 2019. N. Engl. J. Med. 2020, 382, 727–733. [Google Scholar] [CrossRef] [PubMed]
- Chen, Y.; Liu, Q.; Guo, D. Emerging coronaviruses: Genome structure, replication, and pathogenesis. J. Med. Virol. 2020, 92, 418–423. [Google Scholar] [CrossRef] [PubMed]
- Prasse, B.; Achterberg, M.A.; Ma, L.; van Mieghem, P. Network-Based Prediction of the 2019-nCoV Epidemic Outbreak in the Chinese Province Hubei. Appl. Netw. Sci. 2020, 5, 1–11. [Google Scholar]
- Wang, D.; Tan, D.; Lei, L. Particle swarm optimization algorithm: An overview. Soft Comput. 2018, 22, 387–408. [Google Scholar] [CrossRef]
- He, S.; Banerjee, S. Epidemic outbreaks and its control using a fractional order model with seasonality and stochastic infection. Phys. A Stat. Mech. Its Appl. 2018, 501, 408–417. [Google Scholar] [CrossRef]
- Mei, W.; Liu, Z.; Zhu, J.; Du, L. Extreme IR Model for COVID-19 Real-Time Forecasting. J. Univ. Electron. Sci. Technol. China 2020, 49, 362–368. [Google Scholar] [CrossRef]
- Law, K.B.; Peariasamy, K.M.; Gill, B.S.; Singh, S.; Sundram, B.M.; Rajendran, K.; Dass, S.C.; Lee, Y.L.; Goh, P.P.; Ibrahim, H.; et al. Tracking the early depleting transmission dynamics of COVID-19 with a time-varying SIR model. Sci. Rep. 2020, 10, 21721. [Google Scholar] [CrossRef]
- Santos, I.D.; Almeida, G.; Moura, F.D. Adaptive SIR model for propagation of SARS-CoV-2 in Brazil. Phys. A Stat. Mech. Its Appl. 2021, 569, 125773. [Google Scholar] [CrossRef]
- Guerrero-Nancuante, C.; Manriquez, R. An epidemiological forecast of COVID-19 in Chile based on the generalized SEIR model and the concept of recovered. Medwave 2020, 20, e7898. [Google Scholar] [CrossRef] [PubMed]
- Wu, J.T.; Kathy, L.; Leung, G.M. Nowcasting and forecasting the potential domestic and international spread of the 2019-nCoV outbreak originating in Wuhan, China: A modelling study. Lancet 2020, 395, 689–697. [Google Scholar] [CrossRef]
- Yang, Z.; Zeng, Z.; Wang, K.; Wong, S.-S.; Liang, W.; Zanin, M.; Liu, P.; Cao, X.; Gao, Z.; Mai, Z.; et al. Modified SEIR and AI prediction of the epidemics trend of COVID-19 in China under public health interventionsy. J. Thorac. Dis. 2020, 12, 165–174. [Google Scholar] [CrossRef] [PubMed]
- Walker, P.G.T.; Whittaker, C.; Watson, O.; Baguelin, M.; Ainslie, K.E.C.; Bhatia, S.; Bhatt, S.; Boonyasiri, A.; Boyd, O.; Cattarino, L.; et al. Report 12: The Global Impact of COVID-19 and Strategies for Mitigation and Suppression; Imperial College London: London, UK, 2020. [Google Scholar]
- Driessche, P.; Watmough, J. A simple SIS epidemic model with a backward bifurcation. J. Math. Biol. 2000, 40, 525–540. [Google Scholar] [CrossRef] [PubMed]
- Cai, Y.; Kang, Y.; Wang, W. A stochastic SIRS epidemic model with nonlinear incidence rate. Appl. Math. Comput. 2017, 305, 221–240. [Google Scholar] [CrossRef]
- Chen, Y.C.; Lu, P.E.; Chang, C.S.; Liu, T.H. A Time-dependent SIR model for COVID-19. IEEE Trans. Netw. Sci. Eng. 2020, 7, 3279–3294. [Google Scholar] [CrossRef]
- Guo, W.; Xu, T.; Tang, K.M. Mestimator based online sequential extreme learning machine for predicting chatic time series with outilters. Neural Comput. Appl. 2017, 2017, 4093–4110. [Google Scholar] [CrossRef]
- Du, Z.; Wang, L.; Cauchemez, S.; Xu, X.; Wang, X.; Cowling, B.J.; Meyers, L.A. Risk for Transportation of 2019 Novel Coronavirus (COVID-19) from Wuhan to Cities in China. Emerg. Infect. Dis. 2020, 26, 1049–1052. [Google Scholar] [CrossRef]
- Boldog, P.; Tekeli, T.; Vizi, Z.; Dénes, A.; Bartha, F.A.; Röst, G. Risk assessment of novel coronavirus COVID-19 outbreaks outside China. J. Clin. Med. 2020, 9, 571. [Google Scholar] [CrossRef]
- Dong, E.; Du, H.; Gardner, L.M. An interactive web-based dashboard to track COVID-19 in real time. Appl. Math. Comput. 2017, 305, 221–240. [Google Scholar] [CrossRef]
- Gill, B.S.; Jayaraj, V.J.; Singh, S.; Mohd Ghazali, S.; Cheong, Y.L.; Md Iderus, N.H.; Sundram, B.M.; Aris, T.B.; Mohd Ibrahim, H.; Hong, B.H.; et al. Modelling the Effectiveness of Epidemic Control Measures in Preventing the Transmission of COVID-19 in Malaysia. Int. J. Environ. Res. Public Health 2020, 17, 5509. [Google Scholar] [CrossRef] [PubMed]
- Kock, R.A.; Karesh, W.B.; Veas, F.; Velavan, T.P.; Simons, D.; Mboera, L.E.G.; Dar, O.; Arruda, L.B.; Zumla, A. 2019-nCoV in context: Lessons learned? Lancet Planet. Health 2020, 4, e87–e88. [Google Scholar] [CrossRef]
- Mat, N.F.C.; Edinur, H.A.; Razab, M.K.A.A.; Safuan, S. A Single Mass Gathering Resulted in Massive Transmission of COVID-19 Infections in Malaysia with Further International Spread. J. Travel Med. 2020, 27, taaa059. [Google Scholar] [CrossRef] [PubMed]
- Fanelli, D.; Piazza, F. Analysis and forecast of COVID-19 spreading in China, Italy and France. Chaos Solitons Fractals 2020, 134, 109761. [Google Scholar] [CrossRef]
- Li, Q.; Guan, X.; Wu, P.; Wang, X.; Zhou, L.; Tong, Y.; Ren, R.; Leung, K.; Lau, E.H.Y.; Wong, J.Y.; et al. Early transmission dynamics in Wuhan, China, of novel coronavirus–infected pneumonia. N. Engl. J. Med. 2020, 382, 1199–1207. [Google Scholar] [CrossRef]
- Keeling, M.J.; Eames, K. Networks and epidemic models. J. R. Soc. Interface 2005, 2, 295–307. [Google Scholar] [CrossRef]
- Zhuang, Z.; Zhao, S.; Lin, Q.; Cao, P.; Lou, Y.; Yang, L.; Yang, S.; He, D. Preliminary estimating the reproduction number of the coronavirus disease (COVID-19) outbreak in Republic of Korea from 31 January to 1 March 2020. Int. J. Infect. Diseases 2020, 95, 308–310. [Google Scholar] [CrossRef]
- Keeling, M.J.; Danon, L. Mathematical modelling of infectious diseases. Br. Med. Bull. 2009, 92, 33–42. [Google Scholar] [CrossRef]
- Tang, B.; Wang, X.; Li, Q.; Bragazzi, N.L.; Tang, S.; Xiao, Y.; Wu, J. Estimation of the Transmission Risk of the 2019-nCoV and Its Implication for Public Health Interventions. J. Clin. Med. 2020, 9, 462. [Google Scholar] [CrossRef]






| Symbol | Meaning | Symbol | Meaning |
|---|---|---|---|
| Susceptible population | Number of initial contacts | ||
| Patients in incubation period | Number of contacts after taking measures | ||
| Patients with confirmed infection | Contact transmission rate | ||
| Isolated latent population | Preventive action delay time | ||
| Number of recovered patients | Improved infection delay time | ||
| Number of deaths by COVID-19 disease | Delay in recovery of patients | ||
| Initial virus spreaders | Delay time for improvement of medical measures | ||
| Total quantity (Stages 1 and 2) | Delay in patient isolation | ||
| Rate of susceptible population infected | Incubation period | ||
| Initial rate of infection | Immigration of susceptible groups | ||
| Infection rate after taking measures | Emigration of susceptible groups | ||
| Virus incidence | Immigration of patients in the incubation period | ||
| Initial isolation rate | Emigration of patients in the incubation period | ||
| Improved isolation rate | Current inflow of population in the province | ||
| Initial mortality rate | Current outflow of population in the province | ||
| Improved mortality rate | Probability of emigration of patients who are in the incubation period | ||
| Mortality rate 1 (Mortality in asymptomatic patients) | Probability of emigration of susceptible groups | ||
| Mortality rate 2 (Mortality among symptomatic patients) | Probability of immigration of patients who are in the incubation period | ||
| Initial recovery rate | Probability of immigration of susceptible groups | ||
| Improved recovery rate | Number of asymptomatic patients | ||
| Initial effective contact | Number of patients with symptoms | ||
| Exposure frequency after taking action | New infections |
| Outbreak Period | Control Period | ||||
|---|---|---|---|---|---|
| Symbol | Initial Value | Distribution | Symbol | Initial Value | Distribution |
| 1000 | - | 100,000 | - | ||
| 0.0002 | 0.0002 | ||||
| 9 | 9 | ||||
| 6 | 1 | ||||
| 0.02 | 6 | ||||
| 4 | 1 | ||||
| 0.01 | 10 | - | |||
| 5 | - | 10 | - | ||
| 0.01 | - | 5 | - | ||
| Steady Period | 10 | - | |||
| Symbol | Initial Value | Distribution | 5 | - | |
| 1000 | - | 4 | |||
| 0.0002 | 0.15 | ||||
| 9 | 0.6 | ||||
| 6 | 0.02 | ||||
| 0.02 | 0.01 | ||||
| 4 | 0.01 | ||||
| 0.01 | 0.01 | ||||
| 5 | - | 0.01 | - | ||
| 0.01 | - | 0.0005 | |||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, Z.; Wang, Y.; Gao, J.; Song, J.; Zhang, Y. A Multistage Time-Delay Control Model for COVID-19 Transmission. Sustainability 2022, 14, 14657. https://doi.org/10.3390/su142114657
Wu Z, Wang Y, Gao J, Song J, Zhang Y. A Multistage Time-Delay Control Model for COVID-19 Transmission. Sustainability. 2022; 14(21):14657. https://doi.org/10.3390/su142114657
Chicago/Turabian StyleWu, Zhuang, Yuanyuan Wang, Jing Gao, Jiayang Song, and Yi Zhang. 2022. "A Multistage Time-Delay Control Model for COVID-19 Transmission" Sustainability 14, no. 21: 14657. https://doi.org/10.3390/su142114657
APA StyleWu, Z., Wang, Y., Gao, J., Song, J., & Zhang, Y. (2022). A Multistage Time-Delay Control Model for COVID-19 Transmission. Sustainability, 14(21), 14657. https://doi.org/10.3390/su142114657






