A Steady-State Flight Control Algorithm Combining Stretching Ratio Coefficient and PID Control for UAVs in Uncertain Environments

Abstract

Unmanned aerial vehicle (UAV) has the advantages of flexible operation, simple structure, and low price, which has been widely researched. In recent years, the application of small UAVs has become more extensive, and the steady-state control of UAVs has great research prospects and value due to it being the key to better execute flight task. A PID steady-state control algorithm based on color recognition and target detection is designed herein. Firstly, it is necessary to calculate the distance between the coordinates of the center of the UAV screen and the geometric center of the target point. Secondly, a pixel distance correction algorithm based on actual distance is proposed so as to correct pixel distance deviation. Finally, it is necessary to control the speed of the UAV by a PID control algorithm to achieve the goal that the UAV is stable near the geometric center of the target point. In short, this algorithm realizes the functions of real-time video transmission of the UAV, flight data storage, color recognition, and speed control of the UAV based on the PID control algorithm and distance correction. The experimental results demonstrate that the proposed algorithm has good robustness, makes the UAV have better stability, and can be used for the process of target tracking in uncertain environments.

1. Introduction

With the characteristics of high flexibility, low cost, high reliability, free takeoff, landing, and hovering, quad-rotor helicopters (typical small UAVs) are widely used in various fields, such as rescue [1], plant protection [2], aerial photography [3], transportation [4], and so on. For example, quad-rotor helicopters applied to farmland can detect and spray crops by hovering at ultralow altitude, which is more flexible and efficient than manual work. On the one hand, a quad-rotor helicopter has four input channels and six degrees of freedom. It has an underactuated system, with nonlinear and strong coupling properties. On the other hand, in the process of flight, the external environment is uncertain, i.e., wind, load change, obstacles, and other factors will affect the control of the UAV, so the adaptive ability and robustness of UAV are required to be high [1,2,3,4,5,6]. To sum up, it is of great scientific research value and application value to study and design the steady-state control of quad-rotor helicopters [7,8,9,10]. For application in the maritime industry, UAVs usually collaborates with unmanned marine vehicles (UMVs) [11,12] to execute complex tasks. It is very important to implement stable-state flight for UAVs, especially in uncertain environments.

At present, the widely used quad-rotor helicopter attitude control methods mainly include PID control [13,14,15], sliding mode control [16,17,18], backstepping control [19,20,21], neural network control [22,23], active disturbance rejection control (ADRC) [24,25,26,27] and so on. PID control is composed of proportional, integral and differential parts. It uses deviation to eliminate deviation, and it has the characteristics of simple structure and easy parameter adjustment, but inaccurate input data and parameters have a great impact on results. Reference [28] proposes a nonlinear PID control method, which effectively enhances the robustness of the quad-rotor helicopter system. Sliding mode control is a typical variable structure control, which has good anti-disturbance for uncertain complex systems. However, due to the structure not being fixed, chattering may occur when the state trajectory reaches the sliding surface. Reference [29] proposes a second-order sliding mode controller method, which is applied to the height tracking of a quad-rotor helicopter, and the experiment proves that it can effectively reduce the jitter phenomenon. Backstepping control utilizes the idea of divide and conquer, which divides a high-order complex system into low-order simple subsystems, which is suitable for systems with uncertain parameters. As the order of the system increases, the complexity of the division will also increase. Reference [30] proposes a multi-UAV cooperative formation method based on backstepping control. Simulation experiments show that the UAV converges to the final trajectory faster. Neural network control has powerful learning ability and can learn in complex, uncertain and nonlinear situations. Compared with other algorithms, the control process needs to consume additional computing resources. Reference [31] proposes an intelligent control algorithm based on RBF neural network, which enhances the anti-jamming ability of the quad-rotor helicopter. Active disturbance rejection control is a control method that does not depend on the mathematical model of the controlled object. It mainly consists of a tracking differentiator (TD), an extended state observer (ESO) and a nonlinear state error feedback controller (NSEFC). Its disadvantage is that manual tuning parameters are more complicated than PID control. Reference [32] proposes a dual closed-loop quad-rotor helicopter attitude control algorithm: the outer loop adopts PID control, and the inner loop adopts active disturbance rejection control.

In this paper, a method based on computer vision is proposed for a quad-rotor helicopter to maintain a stable flight state after being disturbed by certain external forces. First, the system terminal collects the video stream returned by the quad-rotor helicopter, and uses color recognition and target detection algorithms to determine the boundary box of the object. Secondly, the pixel distance between the image frame center and the target geometric center is calculated, and the stretching coefficient is creatively introduced to correct the pixel distance deviation under different distance conditions. Using the stretching coefficient method, the target area proportion of different distances can be converted into depth information by a priori information, the relative distance between the UAV and the target can be obtained through the image frame collected by the monocular camera, and the information can be used to guide the UAV control, so as to improve the control accuracy of the UAV. Finally, a PID algorithm is used to control the UAV to maintain stability after receiving external force interference.

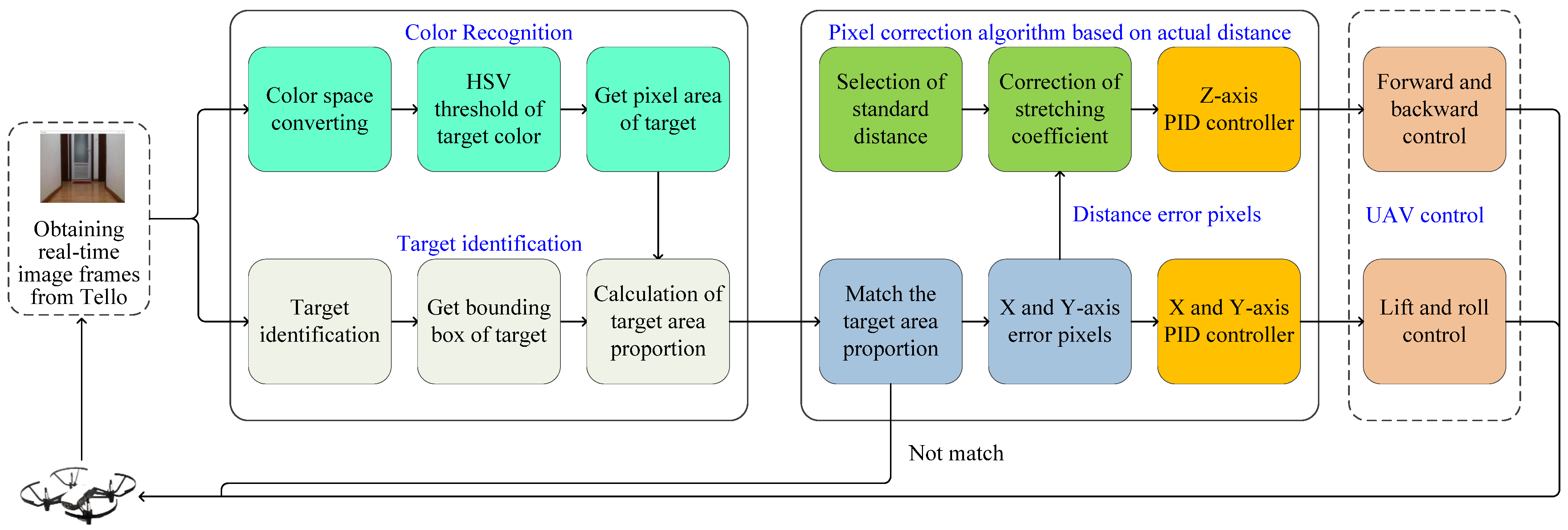
2. System Design

In order to implement stable flight of a quad-rotor helicopter, this paper combines color recognition and target detection, and proposes a pixel distance correction algorithm by stretching ratio coefficient and PID control, as Figure 1 shows.

Color recognition is implemented based on HSV color space, and target color matching combining HSV threshold is adopted so as to obtain the geometric center of the target. A pixel distance correction algorithm based on actual distance includes the calculation of pixel distance and target area proportion, selection of standard distance, calculation of stretching radio and stretching coefficient. According to last frame error information, PID control is used so as to implement the UAV control of forward and backward, lift and roll.

The expansion ratio coefficient can effectively correct the input error data. The results that affect PID control have two parts. One part is PID control parameters, the other part is the input error data. According to the predesigned standard distance, the expansion ratio coefficient can effectively correct the error data and make the control distance between the UAV and the object more accurate.

3. Function Implementation of System

3.1. Image Processing Combining Target Identification and Color Recognition

The UAV collects the video stream through the equipped front camera, and the system terminal processes the returned image. By identifying the fixed target, the UAV can fly stably near the geometric center of the target. During the flight, the images captured by the UAV will appear blurry. Therefore, the color recognition algorithm is used to optimize the target identification to improve the accuracy. The main process of identification is as follows.

Select the recognized target and color. Targets are identified using the yolov3 algorithm, which accurately and quickly identifies the bounding box of a specific target. Use HSV color space transformation to identify the target color. Compared with the RGB color model, the HSV color model can reflect the specific color information of objects well. The conversion from RGB color space to HSV color space is accomplished by calling cv2.cvtColor() method in the program and setting the parameter to cv2.COLOR_BGR2HSV.

After a specific color is identified, there may be other impurity areas with the same or similar color as the target in the image frame, but usually these have a small area. In order to avoid these areas being misidentified as the target, the region with the largest area in the identified color is selected for contour extraction, the cv2.findContours() method is used to find the contour, and the max() method is called to select the contour with the largest area.

Combining the results of color recognition and target recognition, calculate the ratio between the white area located in rectangular box of the binary image target recognition and the area of the rectangular box. If the ratio is larger than the preset ratio pr, target detection combined with color recognition can screen out more accurate targets.

The specific process of the algorithm is shown in Algorithm 1.

Algorithm 1: Combining object detection and color recognition.

Input:$\mathrm{Image} \mathrm{frame}: frame, \mathrm{Object} \mathrm{class}: obj\_id, \mathrm{Object} \mathrm{hsv}: obj\_\mathrm{hsv}, \mathrm{Preset} \mathrm{ratio}: pr$ $bbox\leftarrow \mathrm{getBBox}\left(frame, obj\_id\right)$ $img\_thr\leftarrow \mathrm{hsvThreshold}\left(frame, obj\_\mathrm{hsv}\right)$ $\mathrm{for} i\leftarrow 0 \mathrm{to} \mathrm{len}\left(bbox\right)-1 \mathrm{do}$ $x,y,w,h\leftarrow bbox\left[i\right]$ $crop\leftarrow \mathrm{img}\_\mathrm{thr}\left[y:\left(y+\mathrm{h}\right),x:\left(x+w\right)\right]$ $contours\leftarrow \mathrm{findContours}\left(crop\right)$ $\mathrm{if} \mathrm{len}\left(contours\right)>0 \mathrm{then}$ $biggestContour\leftarrow \mathrm{maxArea}\left(contours\right)$ $area\leftarrow \mathrm{contourArea}\left(biggestContour\right)$ $\mathrm{if} area/\left(\mathrm{w}\ast \mathrm{h}\right)\ge pr \mathrm{then}$ $\mathrm{controlTello}$ $\mathrm{else}$ $\mathrm{not} \mathrm{match}$ $\mathrm{end} \mathrm{if}$ $\mathrm{else}$ $\mathrm{not} \mathrm{found}$ $\mathrm{end} \mathrm{if}$ $\mathrm{end} \mathrm{for}$

3.2. UAV Pixel Distance Correction Algorithm

3.2.1. Pixel Distance Calculation

After obtaining the geometric center of the maximum contour, in order to determine the deviation degree between the current position of the UAV and the geometric center of the target, the deviation distance between the current position of the UAV and the X axis or Y axis directions should be calculated, respectively.

By default, the center of the image frame is taken as the position of the UAV, so the actual deviation distance can be converted into pixel deviation distance between the center coordinates of the image frame and the geometric center of the target.

In order to measure the stability effect of the UAV near the target point and facilitate data analysis, in addition to the pixel distance deviation in X axis and Y axis directions, the linear pixel distance between the two coordinates should also be introduced so as to characterize the overall distance deviation between the UAV and the geometric center of the target point, which can be calculated by $d=\sqrt{x^2+y^2}$.

After obtaining the pixel distance deviation of the X axis and Y axis, there exists the problem of enlarging or shrinking the pixel distance caused by different actual distances between the UAV and the target plane. To address this problem, the pixel distance correction method is proposed as below.

As shown in Figure 2, the distance from two image frames targeting the geometric center to center of the image is expressed by d, while observing the right target area is larger, which means the UAV is closer to the target plane, then the speed of the UAV adjustment should be smaller. The UAV speed (up and down, left and right) has a linear positive correlation with pixel distance, and the pixel distance $d$ in the two images is the same; therefore, the speed control command issued by the UAV is exactly the same, which is inconsistent with the actual situation, so it needs to be modified. Thus, while the UAV is closer to the target plane, the pixel distance should be reduced proportionally.

The pixel distance correction algorithm is composed of standard distance selection, obtaining stretching radio and stretching coefficient, and calculating stretching coefficient by combining area proportion.

3.2.2. Standard Distance Selection

As shown in Figure 3, when the actual distance between the UAV and the geometric center of the target is $d_0$ (that is, the UAV needs to fly the same distance to the right), when the distance between the UAV and the plane where the target is located is $D_1$, $D_2$ and $D_3$, the pixel distance between the center of the UAV image frame and the geometric center of the target is $d_1$, $d_2$ and $d_3$ respectively. It can be seen from Figure 3 that $D_1$ < $D_2$ < $D_3$ and $d_3$ < $d_2$ <$d_1$. Therefore, when the UAV makes the same horizontal displacement, the closer it is to the plane where the target is and the greater the change in pixel distance in the image frame.

Taking the X axis as an example, when the UAV is at different distances from the same central axis to the target plane, the pixel distance sequence of the X axis is listed as Formula (1).

$$X_n=\{x_1,x_2,x_3,\cdots ,x_n\},(x_1<x_2<x_3<\cdots <x_n)$$

(1)

After analysis of Figure 3, $\underset{D\to \infty }{\lim }d=d_0$. When the UAV is infinitely far away from the target plane, the pixel distance between the center of the UAV image frame and the target line is consistent with the actual distance. However, considering that the distance between the UAV and the target plane cannot reach an infinite distance in an actual situation, an appropriate distance as far as possible should be selected as the standard distance length, and $x_m$ in the pixel distance sequence is assumed to be the standard distance, where $x_0$ = $x_m$.

3.2.3. Stretching Ratio and Stretching Coefficient

Because the pixel length corresponding to the same length is different at different distances, the pixel length is small while the distance is far away, and the pixel length is large while the distance is close. This change is called stretching with respect to the standard length. The ratio between pixel length at different distances and standard distance length is called stretching ratio, which is described as Formula (2).

$$k_{x_i}=\frac{x_i}{x_0},(i=1,2,3,\cdots ,n)$$

(2)

Therefore, by dividing the pixel distance sequence X_n by x₀, then the corresponding stretching ratio sequence of X axis at different distances can be obtained by Formula (3).

$$K_{x_n}=\{k_{x_1},k_x{}_{{}_2},k_x{}_{{}_3},\cdots ,k_x{}_{{}_{(m-1)}},1,k_x{}_{{}_{(m+1)}},\cdots ,k_x{}_{{}_n}\}$$

(3)

The $K_{x_n}$ sequence reflects the stretching ratio compared to standard distance length $x_0$ at different distances, so the distance can be modified to standard distance through dividing pixel length at different distances by stretching ratio at the same distance.

The same is true for the stretching ratio in the Y axis. The pixel distance on the X axis and Y axis can be obtained by trigonometric function operation based on pixel distance $d$, and then dividing the corresponding stretching ratio under the same distance so as to obtain the corrected pixel distance on the X axis and Y axis, which is described as Formula (4).

$$x_{fix}=\frac{x_i}{k_{x_i}},y=\frac{y_i}{k_{y_i}},(i=1,2,3,\cdots ,n)$$

(4)

where $x_{fix}$ and $y_{fix}$ represent the pixel distance of X axis and Y axis after correction; $x_i$ and $y_i$ are the pixel distance under the condition of different distance. $k_{x_i}$ and $k_{y_i}$ are the stretching ratio of X axis and Y axis at different distances.

3.2.4. Calculating the Stretching Coefficient by Combing Target Area with Area Proportion

Assuming that the target points are rectangles of unknown size, assume that the height and width of the image obtained by the UAV camera are $H$ pixels and $W$ pixels respectively. Similarly, the length of the rectangle in image is $h$ pixels and $w$ pixels in X axis and Y axis respectively.

Then, the total pixels of the image is $S$ and the total pixels occupied by the target point is $S_i$. Supposing the targets are squares, and the UAV image frame is also set to a square, then $H=W$ and $h=w$. According to Section 3.2.2 and Section 3.2.3, the standard distance length $m_0$ is selected in the one-dimensional direction, and the stretching ratio sequence can be obtained as shown in Formula (5).

$$K_n=\{k_1,k_2,k_3,\cdots ,k_{m-1},1,k_{m+1},\cdots ,k_n\}, k_i=\frac{\sqrt{S_i}}{\sqrt{S_0}}$$

(5)

$S_0$ represents the area of the target corresponding to the standard distance length $m_0$, and $S_i$ represents the pixel area of the target in UAV image frame at different distances.

If the sampling time of the sampling distance points reaches accuracy requirement, then discrete sequence of the distance can be regarded as a continuous function, and the stretching ratio function can be calculated by Formula (6).

$$k(D)=\frac{\sqrt{S(D)}}{\sqrt{S_0}},D\in (0,+\infty )$$

(6)

where $S\left(D\right)$ represents the functional relationship between the distance $D$ (unit: meters) from UAV to target and the area (unit: the square of number) of the target in image; $k\left(D\right)$ is called the stretching coefficient.

Considering the possible change of set image frame size and target size, a new variable p is introduced to reduce unnecessary calculation and enhance the universality of Formula (6). Thus p represents the ratio of the target area to the whole image frame, and the stretching ratio formula can be transformed into Formula (7).

$$k(D)=\frac{\sqrt{S(D)}}{\sqrt{S_0}}=\frac{\sqrt{\frac{S(D)}{S}}}{\sqrt{\frac{S_0}{S}}}=\frac{\sqrt{p(D)}}{\sqrt{p_0}},D\in (0,+\infty )$$

(7)

Therefore, this formula can adapt to different image frames and target points, and determine the stretching coefficient.

4. Velocity Control of the UAV Based on PID

A PID formula is a commonly used control method in system process control. It is mainly composed of three parts: proportion, integral and derivative. A PID formula has the advantages of excellent negative feedback effect and simple parameter adjustment. It is mostly used in closed-loop systems with automatic correction. Position-type PID can be described as Formula (8).

$$u(t)=K_p[e(t)+\frac{1}{T_i}{\displaystyle {\int }_0^{t}e(t)}dt+T_d\frac{de(t)}{dt}]$$

(8)

where: $u\left(t\right)$ represents the output curve of system, which means it is the curve of PID output result changing with time; $K_p$ is the ratio factor; $e\left(t\right)$ represents the deviation curve, which means it is changing curve between the set value and the actual value changing with time; $T_i$ is integration time; $T_d$ stands for differential time. Expand the Formula (8) to obtain the Formula (9).

$$u(t)=K_{P}e(t)+K_I{\displaystyle {\int }_0^{t}e(t)}dt+K_D\frac{de(t)}{dt}$$

(9)

For UAV, the proportion part represents response speed of the UAV. Too much will exceed the target, and too little will not reach the target due to lack of power.

The integral part can make up for the problem that the proportion is too small, but it can only correct for small deviations. For the position-type PID formula, the integral will gradually increase with the accumulation of time, so it is necessary to set the upper and lower bounds.

The differential part can prevent the UAV from exceeding the target: if it is too small, it will exceed the target, and if it is too large, it will be sensitive to error and jitter near the target with high frequency.

4.1. Symbolic Control of the UAV Roll, Ascent and Descent Speed

In DJITelloPy project, velocity is a vector, and its positive and negative values have directional meaning. In a Cartesian three-dimensional coordinate system, the symbols of each axis and their corresponding velocity directions are shown in

Table 1. UAV orientation and symbol conversion.

Axis	(+)	(−)
x	Roll to right	Roll to left
y	Backward	Forward
z	Ascending	Descending

.

Since the coordinate system displayed in the computer image is different from the Cartesian coordinate system and considering the relative motion between the UAV and the target, its schematic diagram and transformation relationship are shown in Figure 4 and

Table 2. Relation between coordinate system and actual motion.

Area	Point	${\mathit{d}}_{\mathit{X}}$	${\mathit{d}}_{\mathit{Y}}$	x Axis Symbol	y Axis Symbol
Area1	P1	−	−	−	+
Area2	P2	+	−	+	+
Area3	P3	−	+	−	−
Area4	P4	+	+	+	−
Area5	P5	0	−	0	+
Area6	P6	+	0	+	0
Area7	P7	0	+	0	−
Area8	P8	−	0	−	0

Note: “+” Indicates a positive result, “−” Indicates a negative result, “0” Indicates the result is zero.

.

The red dotted line divides the UAV’s real-time image into four areas with the same area: Area₁, Area₂, Area₃ and Area₄. Area₅, Area₆, Area₇ and Area₈ are four dotted lines inside the image, and the red dots are the center of the image. P₁, P₂, P₃, P₄, P₅, P₆, P₇, and P₈ are the different positions of identified bullseye. In the calculation, the geometric center coordinates of the target point are subtracted from the corresponding coordinates of the center of the image frame.

$$d_X=c_X-\frac{width}{2},d_Y=c_Y-\frac{height}{2}$$

(10)

where: $d_X$ and $d_Y$ represents the pixel distance of X and Y axis respectively; $C_X$ and $C_Y$ represent the horizontal and vertical coordinates respectively of the geometric center of the target; $width$ and $height$ represent the width and height of image respectively.

Table 2 shows that the sign of $d_X$ is same as the sign of left and right motion, and the sign of $d_Y$ is opposite to the sign of up and down motion. Therefore, after PID control is used to calculate the speed in program, the upper and lower speeds obtained are taken to be negative, and other data remain unchanged.

4.2. UAV Roll, Lifting Speed Size Control

Pixel distance correction before PID controlling. In the process of the UAV control, it doesn’t need to accurately measure the distance between the UAV and the target plane. Instead, it calculates the proportion of pixel area within the scope of the target. Thus, it needs to measure the proportion of the target area with the distance it needs to keep, then it can maintain relative distance control between the UAV and the target plane. This method can keep relative distance between the UAV and the target under the unknown size of the target, as shown in the following

Table 3. Image target area and its proportion at different distances between the UAV and the target.

Distance to Target Plane	Image Frame	Pixel Area of the Target	Proportion of the Target Area
20 cm		61,618	0.267
25 cm		41,271	0.179
30 cm		28,959	0.126
35 cm		21,352	0.093
40 cm		16,420	0.071
45 cm		13,250	0.058
50 cm		10,573	0.046

Note: The calculated target area is obtained by computer terminal through cv2.contourArea() method, and the average value of the last five times of area is rounded. According to the pixel distance correction method in Section 3.2, 50 cm is selected as the standard distance from the above table. Then according to Formula (7), while 50 cm is regarded as the standard distance, the stretching ratio formula can be described as.

(UAV screen is set to 480 × 480 pixels):

Then, the area of the target point is obtained, and after calculating the area proportion P, the stretching ratio coefficient between the UAV and the target plane at the current distance can be calculated by Formula (11).

$$k(D)=\sqrt{\frac{p\left(D\right)}{\mathrm{p}(0.5)}}=\sqrt{\frac{p\left(D\right)}{0.046}}\approx 4.68\times \sqrt{p\left(D\right)}$$

(11)

The larger the object, the greater the recognition distance. Thus, take a small object apple as an example and test at a longer distance (150–275 cm), then the image target area and its proportion between the UAV and the target are obtained, as

Table 4. Image target area and its proportion at different distances between the UAV and the target (longer distance).

Distance to Target Plane	Image Frame	After Processing	Pixel Area of Target	Proportion of Target Area p
150 cm			3222	0.0057
175 cm			2652	0.0047
200 cm			2080	0.0037
225 cm			1515	0.0027
250 cm			1199	0.0021
275 cm			1056	0.0019

shows. From the experimental results, we know that the method is also applicable.

4.3. UAV Forward and Backward Speed Size Control

Observed many times by the flight control, when UAV forward or backward velocity $v\_fb$ is larger than 15 cm/s², it will generate a larger pitch angle (Figure 5) and lead to a spurt in pixel distance, which will affect the results of PID formulas used for UAV control. In order to avoid this situation, the forward or backward velocity maximum threshold is set to 10.

At the same time, relative distance control method is used to control the forward and backward speed of the UAV. Thus, it is not necessary to obtain an accurate distance between the UAV and the target plane, but it is necessary to maintain a stable distance between the UAV and the target plane by controlling the proportion of the target area in the image frame within a certain range. The specific process of the algorithm is shown in Algorithm 2.

Algorithm 2: UAV controlling algorithm

Input:$\mathrm{Bounding} \mathrm{box}:x,\mathrm{y},\mathrm{w},\mathrm{h},\mathrm{Image} \mathrm{window}: winW,winH,\Delta t,I\_lr,I\_ud,plr,pud$ $lr\leftarrow x+w/2-winW/2$ $ud\leftarrow y+h/2-winH/2$ $I\_lr\leftarrow I\_lr+lr\ast \Delta t/30$ $I\_ud\leftarrow I\_ud+ud\ast \Delta t/30$ $I\_lr\leftarrow clip\left(I\_lr,-60,60\right)$ $I\_ud\leftarrow clip\left(I\_ud,-60,60\right)$ $d\leftarrow sqrt\left(l{r}^2+u{d}^2\right)$ $k\leftarrow 4.68\ast sqrt\left(\left(w\ast h\right)/\left(winW\ast winH\right)\right)$ $lr\leftarrow int\left(lr/k\right)$ $ud\leftarrow int\left(ud/k\right)$ $v\_lr\leftarrow int\left(pid\left[0\left]\ast lr+pid\right[1\left]\ast I\_lr+pid\right[2\right]\ast \left(lr-plr\right)\right)$ $v\_ud\leftarrow int\left(pid\left[0\left]\ast ud+pid\right[1\left]\ast I\_ud+pid\right[2\right]\ast \left(ud-pud\right)\right)$ $v\_lr\leftarrow clip\left(v\_lr,-60,60\right)$ $v\_ud\leftarrow clip\left(v\_ud,-60,60\right)$ $s\leftarrow w\ast h$ $\mathrm{if} s>\mathrm{10,000} \mathrm{then}$ $v\_fb\leftarrow -10$ $\mathrm{elif} \mathrm{10,000}>s>7500 \mathrm{then}$ $v\_fb\leftarrow 0$ $\mathrm{else}$ $v\_fb\leftarrow 5$ $send\_rc\_control\left(v\_lr,v\_fb,v\_ud,0\right)$ Output:$\mathrm{I}\_\mathrm{lr},\mathrm{I}\_\mathrm{ud},\mathrm{lr},\mathrm{ud}$

5. Experiment

5.1. Experimental Platform Tello

Tello is equipped with visual positioning system and integrated flight control system for stable hovering and flight. The Tello front camera can take 5-megapixel photos and 720p HD video, and the electronic shake protection makes the pictures more stable. The physical picture of Tello as shown in Figure 6.

5.2. Experiment to Determine the Parameters of the PID Formula

5.2.1. Determining K_P

By adjusting different values of proportionality coefficient K_P and observing motion state of the UAV, the appropriate proportionality coefficient K_P value of the UAV response speed is determined, so that UAV has sufficient response speed and no strong shock when moving.

The flight duration of each experiment is about 80 s. After obtaining the image, the distance between the center of the UAV image frame and the center of the target began to be recorded. The experimental data are shown in Figure 7, the horizontal axis is UAV flight time (unit: s), the vertical axis is pixel distance of plane straight line between the center of the UAV image frame and the center of the target (unit: number of pixels).

By analyzing experimental data, it can be seen that when K_P value is too large (K_P > 0.1), UAV power is too large, and it is easy to generate vibration, so that UAV flies out of the range of identifiable targets, resulting in the inability to identify target, and the experimental data is less than 80 s. After that, the value of K_P (Figure 7a–d) was determined by the dichotomization method in the experiment. After comparison, while K_P = 0.06, UAV has sufficient power and moderate size.

5.2.2. Determining K_D

After basically determining the range of proportion coefficient K_P, the differential coefficient K_D is added to the joint experiment, and K_D can also be adjusted to fine-tune K_P to finally achieve the effect of steady-state.

When there are only two parameters K_P and K_D, the proportional part provides the appropriate response speed of the UAV, and the differential part complements the difference. Eventually there will be some time after t, for any given $t_1$ and $t_2$:

$$e(t_1)\equiv e(t_2), \frac{de(t)}{dt}=\frac{e(t_2)-e(t_1)}{t_2-t_1}=0,t_1,t_2\in (t,+\infty )$$

(12)

At this time, the steady-state error will be generated, and the influence caused by proportion P and the influence caused by differential D on UAV will cancel each other. Therefore, the experimental effect expected to be achieved in this part of the experiment is that the linear pixel distance between Tello UAV and geometric center of the target point will maintain a stable distance.

At the same time, average error is calculated to measure the stability of distance. For a set of experimental data samples pixel distance $D=\left\{x_1,x_2,\dots ,x_n\right\}$, the following result is obtained:

$$\eta =\frac{1}{n}{\displaystyle \sum _{i=1}^n|x_i-\overline{x}|}$$

(13)

where: $\eta$ is the average error of experimental samples in this group, and $\overline{x}$ is the average of experimental samples in this group.

This group of experiments focuses on the stability of pixel distance between the UAV and the target after finding the target, so the flight data after 20 s (after 20 s, UAV has been kept flying around the target) is selected as sample to calculate the average error, and calculation results $\eta$ and parameter values are shown in Figure 8. All horizontal axes represent time (unit: s), and all vertical axes represent straight-line pixel distance (unit: number of pixels) between the UAV image frame center and the geometric center of the target.

The stretching coefficient K_P = 0.06 was determined from the previous set of experiments, and K_D = 0.5 was initially set. The experimental results (Figure 7a) show that under this parameter combination, the response speed of the UAV is slow and the oscillation amplitude is large. When differential coefficient is adjusted to K_D = 0.25 and K_D = 0.13 respectively (Figure 8b,c), the UAV pixel distance becomes more and more stable, so proportion coefficient K_P = 0.06 is kept unchanged and differential coefficient K_D is continuously reduced. By comparing the average error of each experiment, it is found that while K_P = 0.06 and K_D = 0.13, UAV flight error is the most stable and the value reaches the smallest.

5.2.3. Determining K_I

After steady-state error is generated, the integral coefficient K_I is added to eliminate the steady-state error, so the steady-state error is compensated to achieve the final target consistently with the geometric center of the target.

Keeping K_P = 0.06 and K_D = 0.13, while K_I = 0.01 (Figure 9a), it has a great influence on the steady-state control of the UAV, and UAV produces large oscillations near the target, which proves that the differential coefficient K_D set at this time is too small and insensitive to the error, so the values of K_P and K_D are increased in experiment (b) (Figure 9b). It was observed that the mean value of pixel distance decreased, but the oscillation phenomenon still occurred after the target object was identified, indicating that the integral did not make up the steady-state error in time. Therefore, the integral coefficient K_I was increased in Figure 9c,d, and K_I achieved a more obvious effect in experiment (d). Keep K_I = 0.03, and continue to adjust the values of K_P and K_D in Figure 9e–g, so that UAV has a faster response after identifying the target while maintaining a small average error. Finally, in Figure 9h, the reaction speed and average error of the UAV are better than those of the previous experiment, so it is believed that UAV flight control reaches the local optimal solution under each parameter of experiment (h). Finally, the stretching coefficients K_P = 0.05, K_I = 0.035, K_D = 0.2 are determined.

5.3. External Force Disturbance Test of UAV

The experimental design of the steady-state algorithm for the UAV is as follows:

(1)

A small wooden block is suspended under the UAV by a string to simulate the aircraft under load;

(2)

A red apple is used as the object to be recognized and placed on a chair to simulate the object to be recognized by the UAV;

(3)

When the UAV takes off and is hovering in a stable state, the UAV is simulated to be disturbed by external forces by manually pulling the string.

The whole experiment was divided into four stages. The scene diagram and system terminal processing diagram of the takeoff stage are shown in Figure 10a,b. The UAV is in a stable state, and the center of the image frame coincides with the geometric center of object. The scene diagram and the system terminal processing diagram of the predisturbance stage are shown in Figure 10c,d. The state of external interference of the UAV is simulated by manually pulling the string. The scene diagram and the system terminal processing diagram of the disturbance stage are shown in Figure 10e,f. The UAV is pulled to the right, then the center of the target object shifts to the left, so the UAV is in the disturbed state. The scene diagram and system terminal processing diagram of the post-disturbance stage are shown in Figure 10g,h. The UAV is restored to the stable state through the pixel correction algorithm, which is consistent with the takeoff state.

5.4. Perturbation Experiment of X, Y, Z Axes

This test simulated the degree of stability of the UAV in the harsh environment of strong wind with variable wind direction. The UAV took off after reaching a steady state. We chose different times to exert force with variable direction for the UAV. At the same time X, Y, Z axis acceleration, linear pixel distance to the target, and minimum circumscribed rectangular area were recorded, and the record length is 120 s.

A string is attached to the bottom of the UAV. While the UAV is in a stable hovering state, external force is applied to it by pulling the string to induce a disturbed state. As the acceleration value of the UAV can be obtained in real time during its flight, at the same time, the weight of the UAV is known. According to Newton’s second formula $\overrightarrow{\mathrm{F}}=\mathrm{m}\overrightarrow{\mathrm{a}}$, on the premise of knowing the weight and acceleration of the UAV, the direction and magnitude of external disturbance of the UAV can be calculated.

5.4.1. X Axis Perturbation Experiment

In this experiment, the direction of force applied to the UAV was the X axis direction of the UAV coordinate system. At the same time, the acceleration of the UAV in the X axis direction and the size of the target pixel area were recorded, and the target area identified by the UAV was controlled in the range of 7500–10,000 units.

The results are shown in Figure 11: In this experiment, the UAV was perturbed times at 28.1 s, 48.4 s, and 68.9 s.

Observing the experimental results, it can be seen that a force of about 19.36 × 10⁻² N is applied to the UAV at t = 28.1 s, which makes it produce an acceleration of −242 cm/s² in the X axis direction. The disturbance has great impact on the UAV, changes the target area by about 3000 units, and returns to a stable state after about 10 s.

At t = 48.4 s, a force of about 9.6 × 10⁻² N is applied to the UAV, which makes it produce an acceleration of −120 cm/s² in the X axis direction, and produces a small disturbance to the UAV, which changes the target area by about 5000 units. After about 12 s, the UAV basically returns to a stable state.

At t = 68.9 s, a force of about 6.88 × 10⁻² N is applied to UAV, which is the weakest one of the three disturbances, resulting in an acceleration of 86 cm/s² in the X axis of the UAV. However, due to the different acceleration directions of external force, the target area changes by nearly 14,000 units, and finally returns to stability after about 6 s.

When setting the forward and backward speed of the UAV, the factors that have inconsistent effects on target area change rate are considered, so the backward speed of the UAV is greater than the forward speed to compensate for area loss, so as to balance the recovery ability of the UAV in the X axis direction.

5.4.2. Y Axis Perturbation Experiment

Under this experiment, the direction of force applied to UAV is all the Y axis direction of the UAV coordinate system.

The results are shown in Figure 12: In this experiment, UAV was perturbed for a total of three times at 31.5 s, 49.3 s and 69.9 s, respectively.

Observing the experimental results, it can be seen that a force of about 6.96 × 10⁻² N is applied to UAV at t = 31.6 s, which makes UAV produce an acceleration of −87 cm/s² in the Y axis, which has little impact on UAV. The pixel offset of the Y axis reaches 66 units, and UAV returns to a stable state after 7 s.

At t = 49.3 s and t = 69.9 s, the force applied to UAV is more than 9.5 × 10⁻² N, and the maximum disturbance is generated at t = 49.3 s, so that the resulting Y axis acceleration reaches −186 cm/s², and the disturbance causes the Y axis pixel distance to be shifted by 160 units. After being disturbed at t = 49.3 s and t = 69.9 s, UAV returned to the stable state in about 10 s.

5.4.3. Z Axis Perturbation Experiment

Under this experiment, the direction of force applied to UAV is all the Z axis direction of the UAV coordinate system.

The results are shown in Figure 13: In this experiment, the UAV was perturbed for totally three times at 37.3 s, 58.8 s, and 76.6 s, respectively.

By observing the experimental results, it can be seen that the Z axis acceleration has an initial value (the value is about −1000), so the relative acceleration is used to calculate the force of the UAV in the Z axis direction.

At t = 37.3 s, a small disturbance is applied to UAV, and UAV returns to a stable state after about 5 s.

At t = 58.8 s, the maximum disturbance of this experiment is applied to the UAV, the magnitude of force is about 14.88 × 10⁻² N, the Z axis pixel offset is 163 units, and the UAV returns to a stable state after about 10 s.

At t = 76.6 s, a force of 12.96 × 10⁻² N is applied to the UAV, which makes the UAV produce an acceleration of −162 cm/s² in the Z axis, which causes a large disturbance to the UAV. Finally, the UAV returns to a stable state after about 8 s.

6. Discussion

In recent years, the application of small UAVs has become more extensive in various environments, such as aerial photography, rescue operation, exploration, logistics, etc. As the steady-state flight directly determines the completion quality of flight mission, so the steady-state control of UAVs has great research prospects and value. However, wind and other factors will affect the control of UAVs, so it is very important to implement stable-state flight for UAV, especially in uncertain environments. Compared with other sensors such as radar and laser range finder and so on, the camera is more common, so the algorithm relying only on camera is suitable for more UAV platforms.

The essence of this method is to map a 3D object with depth information to a 2D plane and modify it according to the object center. In the experiment of the thesis, only the rolling angle is verified by experiments.

As shown in Figure 14, when the UAV is in a stable state under different yaw angles, roll angles and pitch angles, the geometric center of the target object projected on the image frame of the UAV camera remains unchanged. When interfered by external force, the geometric center of the object changes on the image frame, and the UAV can be returned to the original state by the correction algorithm, which is also applicable to the different attitude (yaw and pitch angles controlling) of the UAV.

The proposed algorithm only relies on the image frames provided by the front camera of the UAV, so as to realize the steady flight of the UAV. Therefore, this algorithm is suitable for any UAV platform equipped with a front camera.

7. Conclusions

In addition to considering the pixel distance between target center and two-dimensional plane of the center of the UAV frame, it also focuses on the different distances between the UAV and the target in the three-dimensional space. Similar triangle principle is used to stretch the pixel distance so as to achieve accurate control of the UAV. In this paper, by combining color recognition with target detection, the frame returned by the UAV to the terminal is analyzed to identify specific target, and the pixel distance correction algorithm is proposed to modify the results of PID control algorithm so as to solve the problem of inaccurate UAV control caused by different distance from the target. By analyzing the results of the PID control algorithm and pixel distance correction algorithm and sending control commands to UAV in a closed-loop way, the system realizes steady-state control of the UAV, and makes it have a certain ability to resist external interference. Finally, the disturbance experiment is conducted in order to test the anti-interference ability of the UAV, which proves that the proposed algorithm can be used for steady-state control of UAVs under uncertain environments.

Limitations: The method proposed in this paper is to realize steady-state control of a UAV by identifying objects with the help of visual sensors. When the object is blocked, far away, or the ambient light is weak, the tracking of the object by the UAV will be greatly affected, and the stable state of the UAV will be affected.