Non-Intrusive Load Monitoring of Residential Loads via Laplacian Eigenmaps and Hybrid Deep Learning Procedures

Abstract

Today, introducing useful and practical solutions to residential load disaggregation as subsets of energy management has created numerous challenges. In this study, an intelligence hybrid solution based on manifold learning and deep learning applications is presented. The proposed solution presents a combined structure of Laplacian eigenmaps (LE), a convolutional neural network (CNN), and a recurrent neural network (RNN), called LE-CRNN. In the proposed model architecture, LE, with its high ability in dimensional reduction, transfers the salient features and specific values of power consumption curves (PCCs) of household electrical appliances (HEAs) to a low-dimensional space. Then, the combined model of CRNN significantly improves the structure of CNN in fully connected layers so that the process of identification and separation of the HEA type can be performed without overfitting problems and with very high accuracy. In order to implement the suggested model, two real-world databases have been used. In a separate scenario, a conventional CNN is applied to the data for comparing the performance of the suggested model with the CNN. The designed networks are trained and validated using the PCCs of HEAs. Then, the whole energy consumption of the building obtained from the smart meter is used for load disaggregation. The trained networks, which contain features extracted from PCCs of HEAs, prove that they can disaggregate the total power consumption for houses intended for the Reference Energy Disaggregation Data Set (REDD) and Almanac of Minutely Power Dataset (AMPds) with average accuracies (Acc) of 97.59% and 97.03%, respectively. Finally, in order to show the accuracy of the developed hybrid model, the obtained results in this study are compared with the results of similar works for the same datasets.

1. Introduction

In a global scenario, energy is one of the most important needs of daily human life and the rational use of energy resources is of the utmost importance. Accordingly, energy management and saving have posed many challenges worldwide. Due to the increasing costs of energy production and consumption, and its environmental effects, the importance of energy saving planning is growing significantly [1,2,3]. Based on this, future energy systems must have the ability to guarantee sustainable and affordable energy development for consumers. Therefore, the processes related to planning to save and monitor energy consumption in buildings are considered as an energy management program in line with sustainable energy development. Today, energy demand is growing significantly and is expected to double by 2030. Based on this, it can be seen that several kinds of research have been conducted in the field of effective management of energy supply and demand [4,5].

Recent studies have shown that today a large percentage of the world’s energy is consumed in residential and commercial buildings. Nowadays, smart electricity meters are widely employed in all types of residential and commercial buildings around the world. Based on various studies, it was estimated that smart electricity meters will be installed in approximately 72% of European homes by the end of 2020 [6]. Adding salient features such as power/energy consumption onto the surface of HEAs makes them “smart” energy users. By improving this process, consumers will be able to monitor and manage the energy consumption of each HEA in addition to monitoring the energy consumption of the whole home [7]. Therefore, managing and improving energy efficiency in buildings can play an important role in potential energy savings [8,9].

Residential load monitoring and providing real and direct feedback on the amount of electrical equipment consumption in buildings to consumers can have high potential in various beneficial applications such as awareness of energy consumption and conservation, controllable load quantitative assessment, providing accurate planning of energy consumption, and, finally, leading to minimizing the mismanagement of energy consumption [10,11]. This can also facilitate interactions between energy users and producers through load management programs, so that energy producers will be able to formulate energy saving policies for the use of individual appliances and consumers, based on the feedback from the producers, will be consciously able to do saving options [12,13]. A customer’s awareness of the mean consumption of each of their household electrical appliances (HEAs) enables them to save on the use of inefficient appliances and be able to control their consumption at peak hours to avoid penalties. These data provide a great opportunity for the application of data-driven methods in residential energy sectors. For example, by monitoring the energy consumption trend of a specific device, the partial faults of that device can be diagnosed. Load monitoring can be accomplished in two types, intrusive load monitoring (ILM) and non-intrusive load monitoring (NILM) [14]. ILM points to the use of a large number of sensors and intelligent sockets to directly monitor the power consumption of HEAs. Encroaching on family privacy and being costly are the most important problems of this method. The NILM method has been suggested to eliminate the ILM problems and reduce costs. In general, NILM can disaggregate electrical appliance-level data using data captured by a smart electric meter [14,15]. Figure 1 shows the difference between the two methods of ILM and NILM in residential load disaggregation.

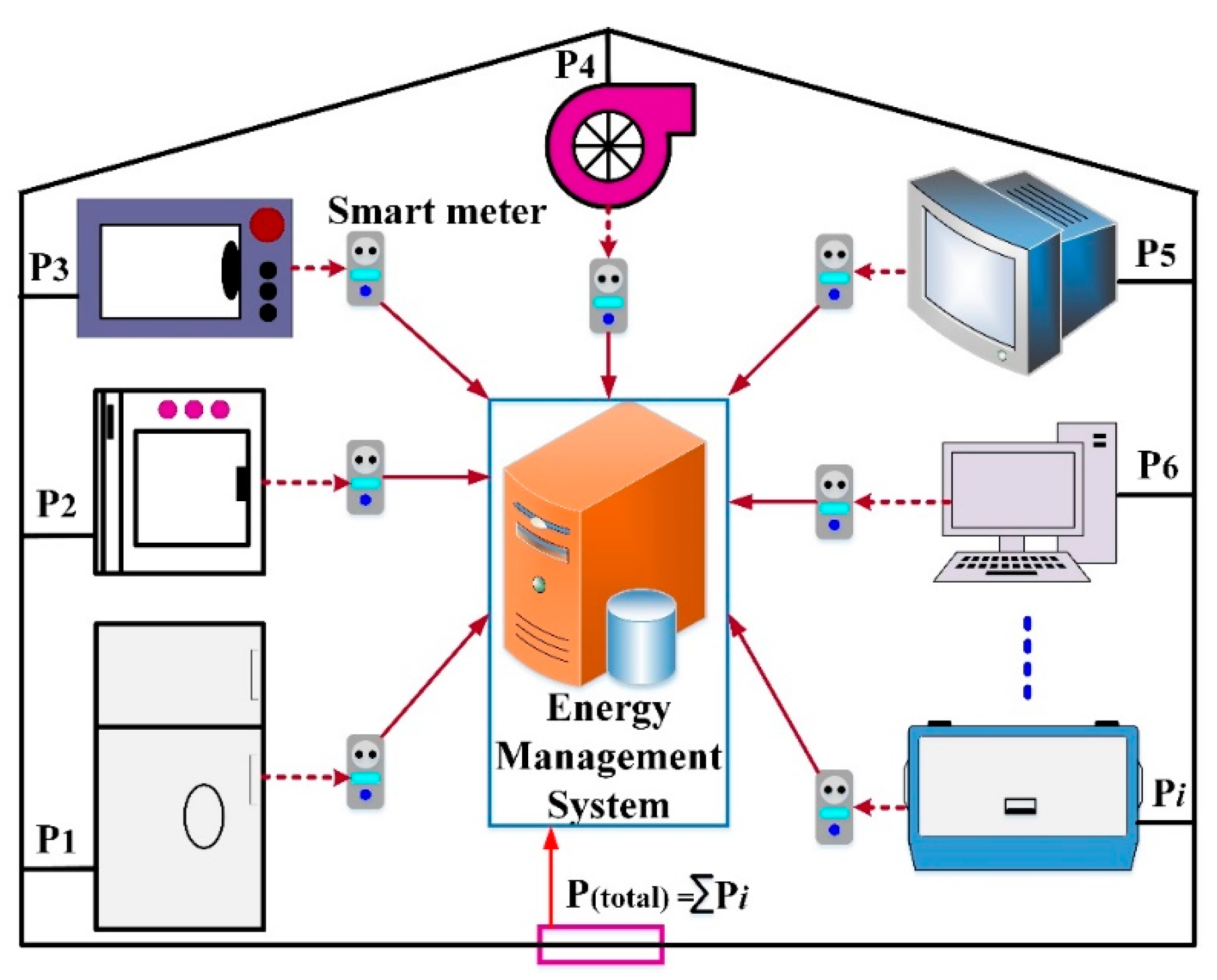
NILM was first proposed in 1992 by Hart as a process for analyzing residential loads and disaggregating the power consumption of HEAs [16]. The main idea of NILM is to extract the energy consumption of HEA using the original readings in the smart electric meter. Research has shown that NILM could empower residential consumers to reduce energy consumption by 15% [10]. In addition, fault detection in the home appliance motor, and a variety of programs for energy-efficient homes (i.e., automatic home energy management and end-use diagnostics and troubleshooting) are important applications of NILM [17]. The use of NILM has flourished in recent years due to the growing use of smart electric meters and the availability of accurate measurements of the consumption of HEAs. However, energy disaggregation and management are very challenging issues and research in this field is still in its infancy and needs to eliminate many technical and practical problems.

So far, several review studies have introduced NILM, described its applications, and categorized various NILM methods [18,19,20,21]. Reference [18], considering the application areas and studies performed on NILM, has categorized its various methods. A thorough review of the conventional and advanced methods of the NILM approach has been performed in [19]. This study, in addition to introducing various NILM methods, also reviewed various metrics for evaluating methods, which finally introduces hybrid deep learning-based methods as leading models in this field. In [20], by introducing the important applications of NILM in different fields, a comprehensive review of the types of algorithms used to develop NILM in the field of energy management has been performed. A comprehensive review of the 42 NILM datasets has been performed in [21], addressing their various features and finally providing a comparison of the performance of each data. This paper provides an overview of the performance of various NILM algorithms in processing various data for NILM researchers. Additionally, much research has proposed various approaches to address these problems of NILM and improve it. In some of them, the hidden Markov models (HMM) [22] are used to improve the NILM and disaggregate the residential load. A finite-state machine method based on fuzzy transitions is proposed in [23] to the NILM of HEAs. In order for NILM development, a new appliance detection solution based on an imbalance classification for electrical appliances switching ON/OFF has been utilized in [14]. In [24,25], load disaggregation has been performed based on a well-known regression-based method called WaveNILM. In [26], the improvement of the NILM process has been performed established on the introduction of an event-based approach. The proposed model accurately detects all events by filtering the power signals. Additionally, it extracts the features related to each of the HEAs from their power signals in the training dataset. In [24], the process of implementing the proposed approach was performed in two states using deferred loads and using all input features, where the network accuracy for each state was 94.70% and 88.40%, respectively. Residential load disaggregation and recognizing the power consumption of HEAs in [27] have been performed using a two-stage optimization model based on Mixed-Integer Nonlinear Programming. In some studies [10,28,29], unsupervised methods have been used to improve NILM. In [10], a dimension reduction-based method called principal component analysis (PCA) has been used to improve NILM performance by extracting power consumption patterns from HEAs and disaggregating them in a low-dimensional space. The additive factorial approximate maximum a posteriori (AFAMAP) method has been utilized in [28] for load disaggregation. The problems related to load disaggregation in [30] have been overcome by proposing a new NILM model based on alternating optimization that is called NILM-AO. The proposed model in this study was compared with methods based on graph signal processing and the presented results show the superiority of the NILM-AO model. Some other studies have benefited from supervised methods such as deep learning and machine learning applications for NILM and improved residential load disaggregation problems. The improvement of the NILM process in [29] has been achieved by presenting a hybrid unsupervised approach based on the joint adaptation network and the adversarial network. In this study, the performance of the developed model with other models based on machine learning was evaluated and the results show the high accuracy of the developed model. In [31], various machine learning solutions such as label power-set, support vector machine (SVM), and decision tree are used for disaggregating the power consumption of each electrical appliance via monitored data. In [32], the SVM has been employed as one of the most widely used machine learning models to disaggregate the consumption of HEAs. In this study, the load disaggregation process has been performed based on the classification of the amount of consumption associated with each HEA at different hours of the day and night. Deep learning methods are utilized dramatically in all scientific and industrial fields due to their capabilities. Deep learning applications over the past few years have increasingly solved many load disaggregation problems and become a viable solution for utilization in NILM. A deep learning-based procedure called long short-term memory (LSTM) has been used in [33] for residential load disaggregation and classifying the types of electrical appliances. Estimating the energy consumption of each electrical appliance from obtained smart meter data has been performed in [34] via a CNN and an auto-encoder. In [35], the identification of residential electric loads has been performed via a CNN-based NILM technique. In this study, the lack of a need for double processing and the reduction of calculation time for the simultaneous detection and classification of events are considered as obvious advantages of the proposed model. Residential load disaggregation has been performed in [36] by developing one of the deep learning solutions called adversarial autoencoder. The improvement of the NILM process has been performed based on the computational costs reduction and the optimization of feature spaces in [37] by presenting a trimming feature selection model for a microcontroller unit (MCU)-based Edge NILM. In [38], various hybrid structures of intelligence procedures, including recurrent neural network (RNN) architectures and CNNs, have been adopted for residential load disaggregation. A practical approach based on the CNN method has been presented in [39] to improve the NILM process and separate the load consumption of household electrical appliances. In [40], load disaggregation and estimating the power consumption of HEAs were accomplished via deep transform learning and deep dictionary learning techniques. In [41], NILM has been performed to extract the pattern of HEA power consumption using deep learning applications called conditional generative adversarial networks. In that study, in order to present a comparative approach and evaluate the performance of the proposed model, other conventional models such as U-Net and Instance Normalization have been utilized for load disaggregation. In [42], residential load disaggregation has been performed by developing a deep learning-based model called deep sparse coding, in which the performance of the proposed model was evaluated by applying it to various data. A deep learning-based architecture called bidirectional encoder representation from transformers and a modified objective function have been proposed in [43] for load disaggregation. In this study, the main focus is on adapting the architecture of the bidirectional transformer to the field of load disaggregation.

A review of the literature shows that residential load disaggregations as an energy management approach have long been performed based on various techniques. A look at recent studies confirms the capability of intelligent techniques, as it can be seen that today deep learning-based solutions have been able to significantly improve the process of NILM and solve problems related to other previous methods. However, conventional deep learning methods such as CNN, LSTM, etc., also suffer from high-dimensional data processing and time-series modeling of power consumption data. In addition, processing NILM-related data, which typically contains sampling noise at different frequencies and user-patterned consumption discrepancies, is a difficult task for conventional techniques. In general, based on achievements in recent studies, the shortcomings of conventional deep learning models can be pointed out as follows:

➢

In the face of noisy data, they need a pre-processing step so that the accuracy of the results does not decrease.

➢

They suffer significantly from overfitting, vanishing, and gradient explosion problems.

➢

The training process is very time-consuming and requires a high memory in the used system.

➢

In time-series data where the features are sequential, it is difficult and even impossible to model and extract the input features.

➢

The choice of model parameters has a significant effect on the feature extraction process, which is a tedious task and requires experienced people.

In this paper, to solve this problem and prevent overfitting, based on the idea of combining models, a hybrid structure of Laplacian eigenmaps (LE), a CNN, and an improved RNN is developed that is called LE-CRNN. In this structure, the LE technique eliminates the extra data and noise associated with the input data, preparing a dimensional reduced version of the power consumption curves (PCCs) as the input to the hybrid deep learning network. The deep learning-based hybrid model is a combined architecture of CNN and bidirectional LSTM (Bi-LSTM) techniques. This architecture was developed by removing fully connected layers of the CNN structure and replacing them with Bi-LSTM. After designing the presented hybrid model, the Reference Energy Disaggregation Data Set (REDD) [25] and Almanac of Minutely Power dataset (AMPds) [44] as two freely available data sets are used to apply the proposed method. The PCCs of each electrical appliance in the mentioned data sets were used as the designed network inputs to train and extract the power consumption features of each electrical appliance. Finally, the PCCs of total homes obtained from smart electric meters were used to test the designed model and recognize the type of each residential electrical appliance. It should be noted that the employed LE-CRNN technique can be considered a strong structure for solutions that are well compatible with the practical models. In addition, since the suggested technique performs the load disaggregation operation based on the extraction of features related to the power consumption of each household electrical appliance accordingly, it can also be utilized for unseen households. In general, the paper contribution is listed as follows:

➢

Introducing a novel hybrid model based on manifold learning and deep learning that is utilized for the first time for NILM.

➢

Feature extraction from input data and implementation of the training process based on the extracted features and behavioral patterns of each HEA to process large volumes of data and avoid overfitting problems.

➢

Generalizability of the developed model for NILM in residential buildings for which no data are available from electrical appliances.

➢

The ability of the proposed model to disaggregate the consumption of different types of HEAs, even residential cooling and heating loads, based on their consumption pattern.

➢

Reducing the volume of data to extract features from the input data so that none of the behavior patterns related to each HEA are lost.

➢

Removing noises related to data to improve the performance of the proposed hybrid model in the process of training and disaggregating the consumption of each HEA.

➢

Presenting a model that has the ability to disaggregate the power consumption of the entire building at different hours of the day and night and allows the consumer to control the power consumption of any HEA at any moment of time in addition to the consumption of the entire building.

➢

Providing a more accurate model for disaggregating residential loads to inform consumers about the consumption of each HEA for energy management and to prevent excessive consumption during peak hours.

The organization of the paper in the following sections is presented as follows: Section 2 explains the architecture and design of LE-CRNN. Section 3 illustrates the results. The comparison of the results obtained in this paper with other similar studies is presented in Section 4. Finally, Section 5 concludes the paper.

2. Architecture and Design of Hybrid LE and CRNN

2.1. Laplacian Eigenmaps (LE) Structure

Linear and non-linear dimensionality reduction methods are the two main groups of dimensionality reduction techniques. Each of these dimensional reduction techniques has many applications in solving problems related to high-dimensional data [45]. However, since real-world data are often hidden on a complex non-linear manifold, the use of non-linear dimensional reduction techniques is recommended to discover the intrinsic structure of such data [46]. In recent years, manifold learning has been developed and utilized as a non-linear dimensionality reduction application. A sampling of data points in a high dimensional observation space in a manifold formed in a low observation space is the principal idea of manifold learning. Manifold learning transfers data from a high-dimensional space to a low-dimensional space by preserving maximum variance and the inherent nature of the data.

LE is one of the most efficient manifold learning algorithms, presented by Belkin and Niyogi in 2003. LE provides a graph-based dimensionality-reduction procedure in order to maintain the distance graph of the input data points and extract a low-dimensional manifold figure from the original data space. LE accomplishes dimensional reduction for the input space of $X=\left\{x_1, x_2, \dots , x_T\right\}, x_i \in R^M, 1\le i\le T$ to obtain output matrix $Y=\left\{y_1, y_2, \dots , y_T\right\}, y_i \in R^N, 1\le i\le T$ by minimizing the following function [46]:

$${\displaystyle \sum }_{i,j}{\parallel \left(y_{*,i}-y_{*,j}\right)\parallel }_2^2{W}_{i,j}$$

(1)

where $M$ represents the dimensions of the input space, $N$ demonstrates the dimensions of the output space so that the $N\ll M$ condition is always present, $*,i$ and $*,j$ are column vectors of $Y$ corresponding to N-dimensional output points at edges $i$ and $j$, respectively. $W_{i,j}$ is an element of the data’s dependency matrix $W$ by a weight inversely proportional to the distance between points $x_i$ and $x_j$. LE attempts to map analogous points as closely as possible. The distance metric selection based on the heat kernel is expressed according to the following objective function [47]:

$$W_{i,j}=\{\begin{array}{cc}{e}^{-\frac{\parallel x_i-x_j{\parallel }_2^2}{a}}& for \parallel x_i-x_j{\parallel }_2^2<\epsilon \\ 0& otherwise,\end{array}$$

(2)

where ε denotes a threshold value and a is a fixed scale parameter. The role of heat kernel function $e^{-\parallel x_i-x_j{\parallel }_2^2/a}$ is heavy penalizing points $x_i$ and $x_j$, if they are mapped far apart in the low-dimensional space. Assume a suitable constraint as follows [46]:

$$\begin{array}{cc}{\displaystyle \sum _{ij}}{\left(y_i-y_j\right)}^2{W}_{ij}& ={\displaystyle \sum _{ij}}\left(y_i^2+y_j^2-2y_i{y}_j\right)W_{ij}\hfill \\ & ={\displaystyle \sum _i}{y}_i^2{D}_{ii}+{\displaystyle \sum _j}{y}_j^2{D}_{jj}-2{\displaystyle \sum _{ij}}{y}_i{y}_j{W}_{ij}=2y^{T}Ly\hfill \end{array}$$

(3)

where D is a degree matrix and $D_{ii}$ is a diagonal matrix that is defined as:

$$D_{ii}={\displaystyle \sum }_j{W}_{ij}L$$

(4)

where L is the Laplacian matrix that is a symmetric positive semidefinite matrix and defined as:

$$L=D-W$$

(5)

From Equation (3), the optimization problem turns to minimization of the following function [47]:

$$\begin{array}{c}min \\ y\end{array}\begin{array}{c}tr\left(y^{T}Ly\right) s.t. y^{T}Dy=1\\ \end{array}$$

(6)

where the $i$th row of $y$ is $y_i^T$. The optimization problem can be diminished to a generalized eigenvalue problem as [48]:

$$L{y}_{n,*}=\lambda D{y}_{n,*}$$

(7)

where $y_{n,*}$ shows the $n$th row of $Y$ and is the eigenvector corresponding to the $n$th nonzero eigenvalue $\lambda$. The structure of a non-linear polar-metric manifold can be obtained using low-dimensional delegation and can be utilized for classification.

2.2. Convolutional Recurrent Neural Network (CRNN) Structure

The proposed CRNN model is a combination of CNN and Bi-LSTM techniques. Each of the CNN and Bi-LSTM techniques are well-known applications of deep learning procedures. As Figure 2 shows, the proposed CRNN network architecture consists of three components, including convolutional layers, recurrent layers, and a classification layer. In the first step of the CRNN architecture, convolutional layers automatically extract a feature map from the input data. A convolution layer has a number of independent filters in structures to extract the features [49]. The convolution operation occurs when the input data passes through filters. The features in the input samples are extracted by these filters and become a feature space [50]. Each filter consists of kernels that split images or input data into small pieces. Dividing the inputs into small pieces facilitates the feature extraction process from the data. The process of kernel performance in each convolutional layer is expressed as follows [51]:

$$f_l^k(p,q)={\displaystyle \sum _c{\displaystyle \sum _{x,y}{i}_c(x,y)·}}{e}_l^k(u,v)$$

(8)

where, $c$ is the index of the channel, $\left(x,y\right)$ shows the image coordinates, and $\left(u,v\right)$ represents the row and column under consideration. $i_c\left(x,y\right)$ demonstrate an element related to the input data/image tensor IC. After performing the convolution operation, one of the most important stages is selecting and pooling the most features extracted from the data. This is performed by the pooling layer. The average pooling and max pooling are two types of pooling operations. The max pooling takes the highest values of the features extracted and transfers them to the next convolution layer. Accordingly, in CNN typically, max pooling is utilized. The type of pooling that is also used in this paper divides the input image into a set of non-overlapping rectangles and transfers the maximum value of features for each subsequent convolution layer [39]. The pooling layer is parameterized as the following equation [50]:

$$x_j^l=f\left({\beta }_j^{l}pooling\left(x_j^{l-1}\right)+b_j^l\right)$$

(9)

where $pooling ()$ shows the pooling operation and $\beta$ represents the pooling kernel. Eliminating the unusable variables and achieving a low-dimension space, which ensures the loss of prominent features and invariances to shift and distortion, are the prominent features of pooling layers. After extracting the features of the input data (PCCs in this study) during several layer-to-layer convolution and pooling processes, the main feature map is generated.

Due to the structure of CNN, after the formation of the final feature map in the last convolutional layer, the fully connected layers are utilized. Receiving the output of the last convolution layer as input, these layers perform the training process and determine the weight and bias of the data based on a feed-forward neural network. These layers compute the weight and biases related to the extracted features until they reach the highest scores for identifying and classifying the features for each class [38,39]. The number of hidden neurons in the fully connected layers by default is always set to 1024 or 2048. This makes it more difficult to categorize small samples. Additionally, fully connected layers, despite the strength of the time sequence, cannot maintain high classification accuracy and stability, and in most cases suffer from the problem of overfitting, which leads to time-consuming and reduced network accuracy. In this paper, these problems are solved by presenting a new hybrid structure called CRNN. As shown in Figure 2, in the proposed structure, the fully connected layer, which contains more redundancy, is removed and replaced with a Bi-LSTM structure.

The Bi-LSTM network as an RNN structure and improved LSTM network is a powerful tool for modeling a general-purpose sequence with time-series dependencies. Given that the PCCs collected from HEAs are a time-based sequence, their current state is strongly related to the previous state. Accordingly, the Bi-LSTM model is the best tool for solving this problem and modeling them. As shown in Figure 2, the structural schematic for Bi-LSTM, the training process of this network is based on a forward layer and a backward layer by utilizing the hidden state [52]. This structure enables the Bi-LSTM network to model the time series mode of the data and use the maximum extracted features to estimate the final output. At time t, the hidden layer and the output layer are computed in two directions as follows [52]:

$${\overrightarrow{h}}_t=\sigma \left({\overrightarrow{W}}_i{x}_t+{\overrightarrow{V}}_i{\overrightarrow{h}}_{t-1}+\overrightarrow{b}\right)$$

(10)

$${\overleftarrow{h}}_t=\sigma \left({\overleftarrow{W}}_i{x}_t+{\overleftarrow{V}}_i{h}_{t+1}+\overleftarrow{b}\right)$$

(11)

$$y_t=\sigma \left(U\left[{\overrightarrow{h}}_t;{\overleftarrow{h}}_t\right]+c\right)$$

(12)

where $h_t$ is the hidden state and $c_t$ depicts the current memory cell. σ denotes the activation function. $x_t$ and $h_{t-1}$ demonstrate the input value at time $t$ and the hidden state at the previous time step, respectively. $W_i$ and $b$ shows the weight matrix associated with the input gate and bias values, respectively. $y_t$ is the output of the last Bi-LSTM layer. Finally, at the last layer of the CRNN structure, the classification of features is performed via a Softmax function as follows [39]:

$$O_j=\left[\begin{array}{c}P\left(y=1\right)|x;\theta \\ P\left(y=2\right)|x;\theta \\ \dots \\ P\left(y=c\right)|x;\theta \end{array}\right]=\frac{1}{{{\displaystyle \sum }}_{j=1}^k\exp \left({\theta }^{j}x\right)}\left[\begin{array}{c}\exp \left({\theta }^{1}x\right)\\ \exp \left({\theta }^{1}x\right)\\ \dots \\ \exp \left({\theta }^{c}x\right)\end{array}\right]$$

(13)

where $P$ is the output related to each input and ${\theta }^{j}x$ shows the factors of the classification layer.

2.3. LE + CRNN Structure

In the proposed LE-CRNN structure (as seen in Figure 2), the main purpose is to extract the maximum feature from the PCCs and to disaggregate the load of the entire building based on the extracted features. The high volume of data and the time-series state of PCCs data related to HEAs cause some major problems in this process that conventional techniques are not easily able to solve. However, the step-by-step implementation of the proposed method can easily solve these problems and provide ideal results of load disaggregation related to the buildings studied. In the first stage, LE transfers the PCCs to a low-dimensional space with a high resolution based on a dimensional reduction approach. During this process, the main information and the most significant behavioral pattern related to PCCs are extracted. Then, the deep learning-based hybrid CRNN architecture is developed to categorize and disaggregate the building load. The features extracted from the LE technique are considered as the input of the suggested CRNN structure.

3. Experimental Results

In this paper, two distinct real-world REDD [25] and AMPds [44] datasets are utilized to show the accuracy of the proposed solution. The REDD dataset includes real energy consumption for six houses in Massachusetts, USA. This dataset is the result of monitoring for two weeks at 3 s sampling intervals. The AMPds dataset includes the power consumption of a one-unit house in Vancouver, Canada. The AMPds dataset was collected over two years from 2012 to 2014 and at one-minute sampling intervals. Both datasets include the low-frequency real power consumption of HEAs. In this study, for the REDD dataset, the power consumption data of HEAs in REDD house 1, REDD house 2, REDD house 3, and REDD house 4 are used. In the AMPds dataset, all available data are used to simulate and apply the proposed model. Improving the NILM and residential load disaggregation in order to know the power consumption of HEAs requires the identification of the consumption patterns of electrical appliances and extraction of the features available in their PCCs. In this paper, this goal is achieved via the hybrid model of LE-CRNN. Implementing the proposed solution requires a dataset including the PCCs of HEAs as the input. Each appliance whose power consumption curve is used as the input must have a target number. The target numbers of HEAs for each of the REED and AMPds datasets when their PCCs are used as the input for the designed network are assigned based on the targets labeled in [39].

From each of the introduced HEAs, seven-day power consumption is selected as input. So, one-day (24 h) power consumption was assumed as a signal and a total of seven one-day PCCs of each electrical appliance constitute the input data. Figure 3 shows examples of electrical appliance PCCs from REDD and AMPds homes that are considered as inputs. It can be seen that the power consumption of each HEA is different at various hours of the day and night. The parameters related to the tuning of the structure of the hybrid CRNN model are presented in

Table 1. CRNN model parameters.

Model	Layer (Type)	Parameter
CNN	No. filters in first convolutional layer	3
	No. filters in second convolutional layer	16
	No. filters in third convolutional layer	20
	Filter size in first convolutional layer	4 × 4
	Filter size in second convolutional layer	3 × 3
	Filter size in third convolutional layer	3 × 3
	Stride in convolutional layers	1
	Window size in each max pooling layer	2 × 2
	Stride in max pooling layers	2
Bi-LSTM	Biddirectional_1	44
	Dropout_1 (Dropout)	0.4
	Flatten_1 (Flatten)	22
	Dense_1 (Dense)	12
	Sequence length	1
	Hidden layer	4
	Hidden unit	100

. After designing the network models and determining the input dataset for each of them, each network can be trained and tested. To do this, in each dataset, we select 70% of the data as training data and the rest of the data to test for each network.

It should be noted that despite the selection of the amount of data for training and test stages by users, the network itself randomly performs the selection of data for training and test. Each designed network is trained using training data. Network tests and validation are performed using test data. In a conventional CNN structure, after applying the convolution and pooling layers, the extracted feature maps are transferred to the fully connected layers to determine the weight and bias. However, in the hybrid LE-CRNN model, feature maps are used as Bi-LSTM layer inputs to calculate weights and biases for transfer to the classification layer. The extracted features from the PCCs in the LE layer are presented for some examples of input data in Figure 4. These features are passed as inputs to the hybrid CRNN architecture.

Performance appraisal of classification results of each network for data related to each home was performed using a performance metric called accuracy ($\mathrm{Acc}$). This metric is calculated according to the following equations:

$$\mathrm{Acc}=\frac{\mathrm{TI}}{\mathrm{TI}+\mathrm{FI}}$$

(14)

where $\mathrm{TI}$ indicates the number of samples that have been correctly detected and $\mathrm{FI}$ represents the number of samples that have been misdiagnosed. Given that the number of samples belonging to each class is equal, the $\mathrm{Acc}$ metric can be useful for performance analysis of the network classification.

Table 2. Accuracy coefficient of each network in the training and initial test stages.

	Training		Test
Models	CNN	LE-CRNN	CNN	LE-CRNN
REDD house 1	0.9682	0.9751	0.9259	0.9499
REDD house 2	0.9642	0.9861	0.9583	0.9721
REDD house 3	0.9610	0.9803	0.9410	0.9770
REDD house 4	0.9714	0.9911	0.9609	0.9827
AMPds	0.9642	0.9798	0.9518	0.9716

shows the results of the accuracy coefficient of each of the CNN and LE-CRNN networks in the training and initial test stages for each house. The presented results in Table 2 show the high correlation between LE-CRNN prediction and target data in the classification of HEA types based on their power consumption patterns in all houses. When the network passes the training stage with good accuracy, it means that it has been able to extract the inherent features of data and identify power consumption patterns related to HEAs. Therefore, the trained networks will be able to identify test data. The reported results for the initial test stage show the accuracy and precision of the trained networks in classifying test data. Each network is saved after training and contains extracted features from the data. These networks can also identify and categorize new and unknown data. At another stage of the test, we considered the new and unknown PCCs of HEAs as inputs to the saved networks in order to perform the test operation, this time with the data of our selection. To do this, 25 samples of PCCs of each electrical appliance from each REDD and AMPds houses were considered for four hours.

Figure 5 shows the confusion matrices for the networks for the new test data of REDD house 1, REDD house 2, REDD house 3, REDD house 4, and the AMPds dataset, respectively. In these figures, the level of accuracy of each network in recognizing and classifying each of the PCC corresponding to each HEA at different hours is shown. In order to confirm the accuracy and efficiency of the developed solution compared to a conventional CNN, the desired tests were performed once using the CNN method.

Table 3. Performance evaluation of two models CNN and LE-CRNN for identifying the HEAs types.

Houses	CNN	LE-CRNN
REDD house 1	0.9688	0.9733
REDD house 2	0.9750	0.9900
REDD house 3	0.9709	0.9854
REDD house 4	0.9720	0.9881
AMPds	0.9700	0.9850

compares the $\mathrm{Acc}$ of the two models for the same test data. The presented results in Table 3 shows the ability of the proposed solution compared to a conventional CNN. In the presented results, it can be seen that the LE-CRNN for all cases had the highest $\mathrm{Acc}$. The LE-CRNN for the REDD dataset had an $\mathrm{Acc}$ value of 0.9842 and for the AMPds dataset it had an $\mathrm{Acc}$ value of 0.9850, while the CNN had $\mathrm{Acc}$ values of 0.9716 and 0.9700 for REDD and AMPds datasets, respectively. At present, the power consumption patterns of HEAs have been identified using the hybrid model of LE-CRNN and their features have been extracted. The most important step in residential load disaggregation and improving the NILM is to use these features to disaggregate the total home power consumption in order to identify and predict the level of consumption of each electrical appliance at any given time.

In this paper, to achieve this goal, samples of the total power consumption of each house were selected as the input to each network. For each house, 135 samples of the PCC obtained by the smart electricity meter, each related to four hours, were considered. At this stage, in order to compare the results and assess the accuracy of the proposed hybrid method, both CNN and LE-CRNN models were applied to the same data.

Table 4. The results of identifying the total home power consumption via trained networks.

		CNN			LE-CRNN
House	Number of Samples	TI	FI	Acc	TI	FI	Acc
REDD 1	135	127	8	0.9408	131	4	0.9703
REDD 2	135	130	5	0.9629	132	3	0.9777
REDD 3	135	129	5	0.9629	131	4	0.9703
REDD 4	135	131	4	0.9703	133	2	0.9851
General	540	518	22	0.9596	527	13	0.9759
AMPds	135	129	6	0.9555	131	4	0.9703

presents the results of the identification of PCCs of the total home power consumption via trained networks for load disaggregation in selected houses. In a way, at this stage of the work, the improvement of the NILM process has been presented, in that each designed network can disaggregate and categorize the behavior pattern and the amount of power consumption related to each HEA from the amount of consumption of the whole house. The results presented in Table 4 show that the design of CNN networks has a significant impact on their performance and results. It can be seen that the designed hybrid model of LE-CRNN with a high accuracy compared to conventional CNNs was able to improve the NILM and load disaggregation in both utilized datasets. It is noteworthy that the reduction of the computational costs of data measurement and the absence of the need for complex calculations in diagnostic operations are the most important advantages of using transient state signals from the power consumption of HEAs and the suggested method in this paper.

4. Comparison of Solutions

To evaluate the effectiveness of the methods, it is necessary to compare the results of the used methods to improve the NILM. A comparison of the results should be performed in accordance with the principles of using the same data. Therefore, the average accuracy obtained for all HEAs studied in this study is compared with the results gained in other studies, so that all comparisons are performed for the same data. However, given that in each of the performed studies in this regard, the division of the dataset is not the same for the training, test, and validation operations, direct comparisons must be performed with caution.

Table 5. Comparison of the accuracy of various solutions using the REDD and AMPds datasets and the number of categorized HEAs types.

REDD Dataset			AMPds Dataset
Appliance Identification Method	Remarks	Acc (%)	Appliance Identification Method	Remarks	Acc (%)
LE-CRNN	Utilizing all HEAs from REDD houses 1, 2, 3, and 4	97.59	LE-CRNN	Using eight appliances selected from the AMPds	97.03
CNN	Utilizing all HEAs from REDD houses 1, 2, 3, and 4	95.96	CNN	Using eight appliances selected from the AMPds	95.55
AANNs [15]	Using 7 appliances selected from the REDD	95.40	AFAMAP [28]	Using six appliances selected from the AMPds	74.90
PCA [10]	Utilizing all HEAs from REDD houses 1, 2, and 3	94.68	HMM [53]	Utilizing all HEAs from AMPds	71
CNN [34]	Utilizing all HEAs from REDD houses 1, 2, 3, 4, and 5	93.80	Combinatorial Optimization (CO) [53]	Utilizing all HEAs from AMPds	55
CNN [39]	Utilizing all HEAs from REDD houses 1,2, 3, and 4	96.17
PBN [54]	Utilizing all HEAs from REDD	85.50

compares the results of the utilized methods in this paper with the results presented in other studies.

Considering that, in this study, the proposed model was performed on two different datasets, REDD and AMPds, the results were compared separately for both datasets. As can be seen, Table 5 is divided into two parts, each part representing the results of different methods implemented on each of the datasets. The evaluation of the results shows that the proposed hybrid model has been able to perform better than other previous methods under the same conditions and significantly improve the process of NILM.

5. Conclusions

Residential load disaggregation and knowing the power consumption of HEAs is the most effective solution for energy management in residential consumption. The pattern recognition of power consumption time series is an efficient way to improve NILM. To do this, in this paper, the hybrid applications of manifold learning and deep learning, as an effective approach of pattern recognition, have been employed to extract obvious features from power consumption data to identify the type of consumer. The proposed model encompasses the hybrid of the LE, CNN, and Bi-LSTM so that, in order to accurately extract the features and prevent overfitting, a layer of Bi-LSTM was used in the structure of the CNN instead of the fully connected layers. To test the suggested method and compare its results with the conventional CNN, low-frequency sampling data from REDD and AMPds were used. The PCCs received from HEAs at various times were selected as input data for the training and validation of CNN and LE-CRNN networks. After training, the power consumption patterns of HEAs are saved as a black box model in the network. Then, in order to total the home load disaggregation, the saved networks were implemented to the power consumption samples of the total home. Finally, the power consumption of HEAs was disaggregated and predicted from the total home power consumption at various times. Predicting the consumption of HEAs with the Acc values of 97.59% and 97.03%, respectively, for the REDD and AMPds datasets using the LE-CRNN and comparing the results with the presented results in other studies makes the suggested hybrid model desirable. It should be noted that despite the proposed model being utilized for energy management in residential buildings, it can be selected in commercial buildings and industrial plants where the management of power consumption is of great importance.

A significant point raised today with the advent of intelligent energy systems and Internet of Things-based equipment is data security, which is especially important in industrial applications and operational areas. Accordingly, the models proposed to solve NILM-related problems must be secure against cyber-attacks and protect the privacy of the data; this issue can be considered a limitation of the proposed model. Solving this problem and presenting a cyber-resilient model is an important issue that should be addressed in the future. Additionally, disaggregating the residential and industrial loads in a power system and then monitoring the industrial loads and extracting their consumption pattern can be considered valuable work for future studies.