Wave Propagation and Scattering around a Radially Inhomogeneous Cylindrical Inclusion in a Full Space

Abstract

The geological structure, such as inclusions, may strongly affect the wave propagation and underground motions during earthquakes. Previous studies mainly focus on geological inclusion with the homogeneous medium. In this paper, the propagation and scattering of incident plane SH waves in and around an inhomogeneous cylindrical inclusion with a radially-varying modulus is studied. In terms of a radial wave function expansion, a rigorous analytical approach is formulated for general computation for the elastodynamic problem. A comprehensive set of numerical examples are presented to illustrate the sensitivity of the underground motion to the rigidity profile of the geological inclusion.

1. Introduction

The influence of local irregular geological structure on ground and underground motions is an important research topic in seismology and earthquake engineering [1,2]. The underground inclusion, as one kind of local irregular geological structures, has different properties, such as rigidity from the surrounding medium. Therefore, it may affect the earthquake wave propagation and cause nearby engineering structures, such as tunnels to suffer stronger seismic action [3,4,5,6]. However, there are still no relevant provisions to follow in the engineering seismic code. Thus, the propagation and scattering of seismic waves in sites containing inclusions will affect the sustainability of the safety of engineering structures.

To reveal the propagation mechanism of seismic waves around the inclusion, a lot of numerical and analytical studies have been carried out. The numerical research based on the boundary type method is the most fruitful due to its advantage to accurately satisfy the boundary radiation condition of infinite space. For example, Dravinski [7] used the boundary integral method to solve the problem of elastic inclusion in a half space. Hadley [8] used the dynamic full plane boundary element method to study the scattering of seismic waves by inclusions in a non-uniform elastic half space. Heymsfield [9] solved the two-dimensional scattering of SH waves by rock inclusions in the soil layer by using the direct boundary element method. Dravinski and Sheikhhasani [10] used the same method to study the scattering of plane harmonic SH waves by arbitrarily shaped multilayer inclusions embedded in a half space. Dong et al. [11] also solved the inclusion problem in an elastic half space using different integral equation methods. Rus and Gallego [12] proposed a direct differentiation-based boundary integral equation method for sensitivity analysis of inclusions in elastodynamic media. Parvanova et al. [13] used a direct displacement-based boundary element method to study the dynamic response of a medium with multiple inclusions under anti plane strain conditions. Liu et al. [14] studied the scattering of plane SH waves by a group of inclusions in an elastic half space based on the indirect boundary element method. Panji et al. [15] proposed a direct time-domain numerical method based on the half space Green’s function to study the scattering of SH waves by arbitrary shaped inclusions. Mojtabazadeh-Hasanlouei et al. [16] analyzed the underground multiple inclusions model under the propagation of SH wave based on the time-domain boundary element method established by the half space Green’s function. Qi et al. [17] calculated the displacement field and stress field of a half space with elliptical inclusion under a line source load using the Green’s function method, and analyzed the factors affecting the dynamic stress concentration factor (DSCF) around the elliptical inclusion.

Numerical methods can deal with more real and complex cases, but their accuracy often needs to be verified by analytical solutions. Pao and Mow [18] first established the model of scattering of SH waves by a cylindrical inclusion in a full space, and derived the wave function series solution to it. Later, Smerzini et al. [19] used the wave function expansion method to analyze the scattering of SH waves by a cylindrical inclusion in a half space. Jiang et al. [20] studied the dynamic response of a shallow circular inclusion under incident SH waves in a radially inhomogeneous half space by applying complex function theory and multipolar coordinate system. Recently, Tokmechi et al. [21] proposed the wave function series solution for SH wave scattering by a semicircular inclusion in a half space.

It is worth noting that the above studies all assume that the inclusions are of a homogeneous and an elastic medium. However, the actual inclusions are often inhomogeneous. Previous studies have shown that the propagation law of waves in the inhomogeneous medium is different from that in the homogeneous medium [22,23,24]. Accordingly, the wave field in a full space containing inhomogeneous inclusions may be different as well. To reveal the mechanism of an inhomogeneous inclusion modifying the wave field, the wave function series solution to SH wave scattering by a cylindrical inclusion whose shear modulus varies continuously in the form of power function in the radial direction is derived in this paper. The contribution of this paper is twofold. One is to fill the gap of analytical solution to SH wave scattering by an inhomogeneous inclusion; the other is to reveal the influence of the inhomogeneous rigidity distribution characteristics of the inclusion on the seismic field around it through frequency-domain and time-domain parameter analysis.

2. Model and Theoretical Formulations

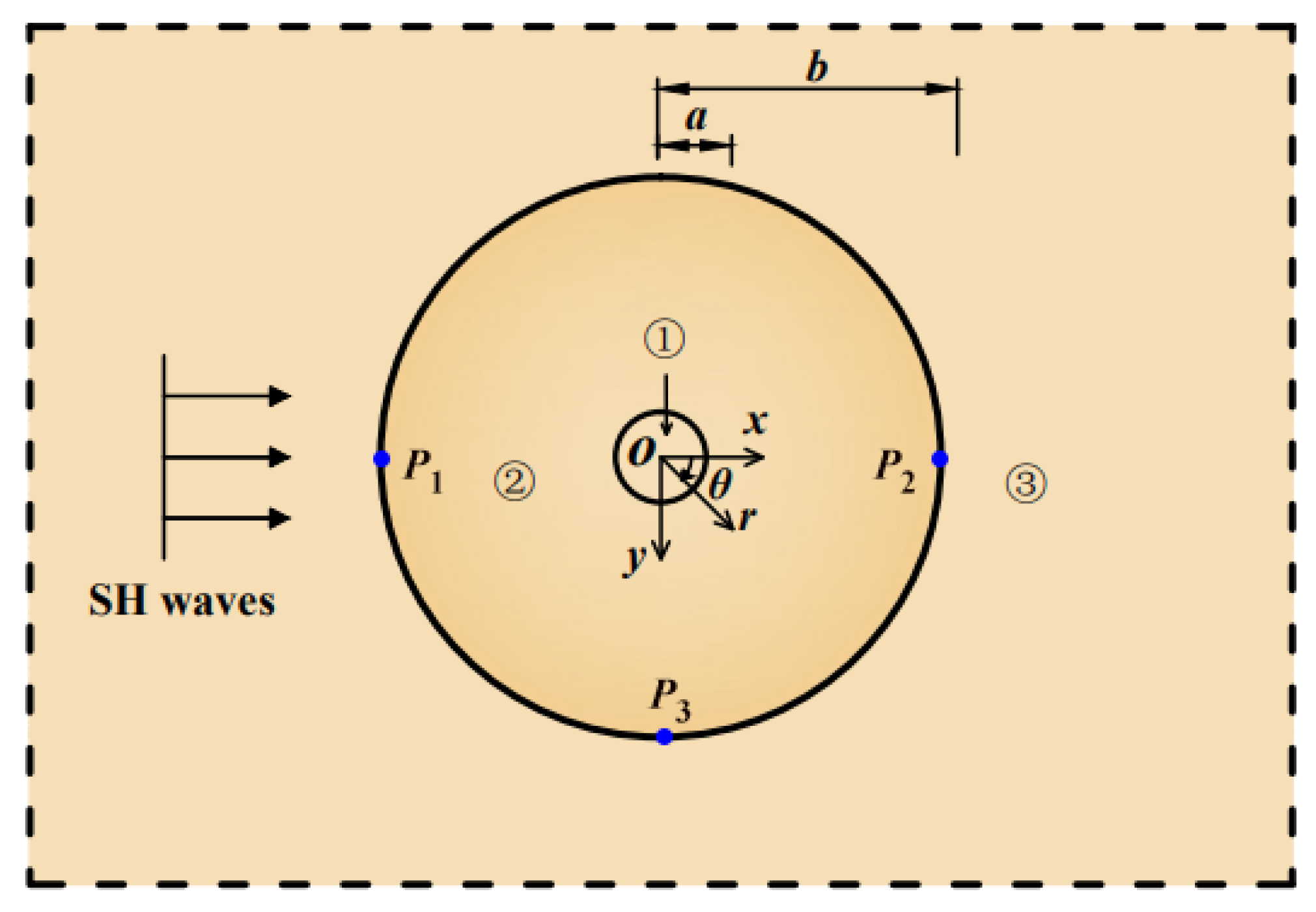
2.1. Model and Excitation

The two-dimensional model studied in this paper is shown in Figure 1. It represents a cylindrical inclusion with radius b in a full space. The inclusion is composed of two parts defined as region ① for r < a and region ② for a ≤ r ≤ b, respectively. It is assumed that the materials of the core region ① of the inclusion and the full space denoted as region ③ where the inclusion is located are both elastic, homogeneous and isotropic with constant density ρ_j, shear modulus µ_j and shear wave velocity c_j (j = 1 or 3, indicating region ① or region ③). In contrast, the material in the region ② of the inclusion is elastic, isotropic but inhomogeneous with a continuously varying rigidity in the radial direction. To facilitate the analytical solution, the shear modulus μ₂ and shear wave velocity c₂ are assumed as power functions of radial distance r and the mass density ρ₂ remains constant. The continuously varying rigidity profile of the inhomogeneous region of the inclusion can be expressed as follows:

$${\mu }_2(r)={\mu }_0{\left(\frac{r}{a}\right)}^{2\beta }\begin{array}{cc},& a\le r\le b\end{array}$$

(1)

$$c_2(r)=c_0{\left(\frac{r}{a}\right)}^{\beta }\begin{array}{cc},& a\le r\le b\end{array}$$

(2)

where β is the inhomogeneity exponent, and μ₀ and c₀ are the shear modulus and shear wave velocity at the inner surface of region ②, respectively. It should be noted that β can be any positive or negative number depending on the actual inhomogeneity profile and there is no rigorous limit of its value.

To focus on the effect of continuous change of wave velocity across the interfaces among the three regions, it is assumed that c₂(a) = c₁ and c₂(b) = c₃. The variation of the wave velocity along the x-axis in the cross section at y = 0 of the model is shown in Figure 2. One can see that the wave velocity profile of the inhomogeneous inclusion is dependent on the key parameter of c₁/c₃.

The excitation of the model is a plane SH wave of unit amplitude with harmonic vibration in the z direction. To facilitate the solution, a Cartesian coordinate system (x, y) and a polar coordinate system (r, θ) are established with the origin O at the center of the inclusion. The definition of x-axis, y-axis, and the angle θ can be seen in Figure 1.

2.2. Construction of Wavefields

The wave field w₁ in region ① should satisfy the Helmholtz equation in the polar coordinate system (r, θ):

$$\frac{{\partial }^2{w}_1}{\partial r^2}+\frac{1}{r}\frac{\partial w_1}{\partial r}+\frac{1}{r^2}\frac{{\partial }^2{w}_1}{\partial {\theta }^2}+k_1^2{w}_1=0,0\le r\le a,0\le \theta \le 2\pi$$

(3)

where k₁ = ω₁/c₁ is the shear wave number.

By solving Equation (3) with the method of separating variables, the standing wave field in region ① can be constructed as follows:

$$w_1(r,\theta )={\displaystyle \sum _{n=-\infty }^{+\infty }{A}_n{J}_n(k_{1}r)e^{in\theta }}$$

(4)

where A_n is the wave field coefficient to be determined, and J_n (·) is the first kind Bessel function of order n.

According to Zhang et al. [25], the wave fields in regions ② and ③ can be directly expressed as:

$$w_2(r,\theta )={\displaystyle \sum _{n=-\infty }^{+\infty }{B}_n{U}_n(r)e^{in\theta }}+{\displaystyle \sum _{n=-\infty }^{+\infty }{C}_n{V}_n(r)e^{in\theta }}$$

(5)

$$w_3(r,\theta )={\displaystyle \sum _{n=-\infty }^{+\infty }{i}^n{J}_n(k_{3}r)e^{in\theta }}+{\displaystyle \sum _{n=-\infty }^{+\infty }{D}_n{H}_n^{(1)}(k_{3}r)e^{in\theta }},r\ge b,0\le \theta \le 2\pi$$

(6)

where B_n, C_n and D_n are coefficients to be determined. The expressions of U_n(r) and V_n(r) are consistent with Equations (18) and (19) in Zhang et al. [25], respectively. H_n⁽¹⁾ (·) is the first kind Hankel function of order n.

2.3. Boundary Conditions

The displacement and stress continuity conditions on the two circular interfaces at r = a and b among the three regions need to be satisfied, i.e.,

$$w_1(r,\theta )=w_2(r,\theta )\begin{array}{cc},& r=a,0\le \theta \le 2\pi \end{array}$$

(7)

$${\tau }_{rz}^{(1)}(r,\theta )={\tau }_{rz}^{(2)}(r,\theta )\begin{array}{cc},& r=a,0\le \theta \le 2\pi \end{array}$$

(8)

$$w_2(r,\theta )=w_3(r,\theta )\begin{array}{cc},& r=b,0\le \theta \le 2\pi \end{array}$$

(9)

$${\tau }_{rz}^{(2)}(r,\theta )={\tau }_{rz}^{(3)}(r,\theta )\begin{array}{cc},& r=b,0\le \theta \le 2\pi \end{array}$$

(10)

2.4. Determination of Unknown Coefficients of Wave Fields

Substituting Equations (4) and (5) into (7), one has:

$${\displaystyle \sum _{n=-\infty }^{+\infty }{A}_n{J}_n(k_{1}r)e^{in\theta }=}{\displaystyle \sum _{n=-\infty }^{+\infty }{B}_n{U}_n(r)e^{in\theta }}+{\displaystyle \sum _{n=-\infty }^{+\infty }{C}_n{V}_n(r)e^{in\theta }}$$

(11)

Using the orthogonality of complex exponential function, i.e.,

$${\displaystyle {\int }_0^{2\pi }{e}^{in\theta }{e}^{iq\theta }}d\theta =\{\begin{array}{l}2\pi , n+q=0\\ 0, n+q\ne 0\end{array}$$

(12)

Equation (11) can be simplified as:

$$A_n{J}_n(k_{1}a)=B_n{U}_n(a)+C_n{V}_n(a)\begin{array}{cc},& n=0,\pm 1,\pm 2,\dots \end{array}$$

(13)

Substituting Equations (4) and (5) into (8) and also taking advantage of Equation (12), the following relational equation can be obtained as:

$$A_n{\mu }_1{k}_1{J}_n^{\prime }(k_{1}a)=B_n{\mu }_2(a)U_n^{\prime }(a)+C_n{\mu }_2(a)V_n^{\prime }(a)\begin{array}{cc},& n=0,\pm 1,\pm 2,\dots \end{array}$$

(14)

Similarly, substituting Equations (4) and (5) into (9) and (10), one has:

$$B_n{U}_n(b)+C_n{V}_n(b)=i^n{J}_n(k_{3}b)+D_n{H}_n^{(1)}(k_{3}b)\begin{array}{cc},& n=0,\pm 1,\pm 2,\dots \end{array}$$

(15)

$$B_n{\mu }_2(b)U_n^{\prime }(b)+C_n{\mu }_2(b)V_n^{\prime }(b)=i^n{\mu }_3{k}_3{J}_n^{\prime }(k_{3}b)+D_n{\mu }_3{k}_3{H_n^{\prime }}^{(1)}(k_{3}b), n=0,\pm 1,\pm 2,\dots$$

(16)

Combining Equations (13) and (14) to eliminate A_n, the following relational equation can be obtained as:

$$B_n{E}_n^a+C_n{F}_n^a=0$$

(17)

where

$$E_n^a=U_n(a)J_n^{\prime }(k_{1}a)-U_n^{\prime }(a)J_n(k_{1}a){\mu }_2(a)/{\mu }_1{k}_1$$

(18)

$$F_n^a=V_n(a)J_n^{\prime }(k_{1}a)-V_n^{\prime }(a)J_n(k_{1}a){\mu }_2(a)/{\mu }_1{k}_1$$

(19)

Similarly, combining Equations (15) and (16) to eliminate D_n, and taking advantage of the Wronskian formula of Bessel function, the following relational equation can be obtained as:

$$B_n{U}_n^b+C_n{V}_n^b=2i^{n+1}/\pi k_{3}b$$

(20)

where

$$U_n^b=U_n(b){H_n^{\prime }}^{(1)}(k_{3}b)-U_n^{\prime }(b)H_n^{(1)}(k_{3}b){\mu }_2(b)/{\mu }_3{k}_3$$

(21)

$$V_n^b=V_n(b){H_n^{\prime }}^{(1)}(k_{3}b)-V_n^{\prime }(b)H_n^{(1)}(k_{3}b){\mu }_2(b)/{\mu }_3{k}_3$$

(22)

Combining Equations (17) and (20), the coefficients B_n and C_n can be derived as:

$$B_n=\frac{2i^{n+1}{F}_n^a}{\pi k_{3}b\left(U_n^b{F}_n^a-V_n^b{E}_n^a\right)}$$

(23)

$$C_n=-\frac{2i^{n+1}{E}_n^a}{\pi k_{3}b\left(U_n^b{F}_n^a-V_n^b{E}_n^a\right)}$$

(24)

Taking Equations (23) and (24) into (13) and (15), respectively, the coefficients A_n and D_n can be obtained as:

$$A_n=\frac{2i^{n+1}\left[U_n(a)F_n^a-V_n(a)E_n^a\right]}{\pi k_{3}b\left(U_n^b{F}_n^a-V_n^b{E}_n^a\right)J_n(k_{1}a)}$$

(25)

$$D_n=\frac{i^n}{H_n^{(1)}(k_{3}b)}\left\{\frac{2i\left[U_n(b)F_n^a-V_n(b)E_n^a\right]}{\pi k_{3}b\left(U_n^b{F}_n^a-V_n^b{E}_n^a\right)}-J_n(k_{3}b)\right\}$$

(26)

Thus, all coefficients of wave fields have been obtained in an explicit form through rigorous mathematical derivation. After a truncation of the infinite term series in Equations (4)–(6) into finite terms, the wave field in each region can be calculated. In order to ensure the accuracy of the calculation results, convergence tests have been conducted and a frequency dependent truncation of the series term at n ≧ 3 + 4η is found to be enough for high accuracy of the results. The convergence test examples are shown in Figure 3 for four representative positions (O, P₁, P₂ and P₃ in Figure 1). For the calculation cases involved in this paper, a high enough calculation accuracy can be achieved by truncating the series term to n = 15 for brevity.

3. Verification of Model and Solution

3.1. Comparison with an Exact Solution by Pao and Mow

If the inhomogeneity component β is set to be 0 and the material parameters in regions ① and ② are set to be identical but different from that in region ③ (ρ₁ = ρ₂ ≠ ρ₃, c₁ = c₂ ≠ c₃), the model in this paper can theoretically be degenerated into the homogeneous inclusion model in Pao and Mow [18]. Here is the process of the theoretical degeneration.

When β = 0, ρ₁ = ρ₂ ≠ ρ₃, c₁ = c₂ ≠ c₃, one can find:

$$k_1=k_2\ne k_3$$

(27)

According to Zhang et al. [25], in Equation (5), one has:

$$U_n(r)=J_n(kr)$$

(28)

$$V_n(r)=Y_n(kr)$$

(29)

then Equations (18) and (21) can be reduced as:

$$E_n^a=0$$

(30)

$$U_n^b=J_n(k_{2}b){H_n^{\prime }}^{(1)}(k_{3}b)-J_n^{\prime }(k_{2}b)H_n^{(1)}(k_{3}b){\mu }_2{k}_2/{\mu }_3{k}_3$$

(31)

Substituting Equations (30) and (31) into Equations (23)–(26), the coefficients A_n, B_n, C_n and D_n can be degenerated into:

$$A_n=B_n=\frac{i^n{\mu }_3{k}_3\left[J_n^{\prime }(k_{3}b)H_n^{(1)}(k_{3}b)-J_n(k_{3}b){H_n^{\prime }}^{(1)}(k_{3}b)\right]}{{\mu }_2{k}_2{J}_n^{\prime }(k_{2}b)H_n^{(1)}(k_{3}b)-{\mu }_3{k}_3{J}_n(k_{2}b){H_n^{\prime }}^{(1)}(k_{3}b)}$$

(32)

$$C_n=0$$

(33)

$$D_n=\frac{-i^n\left[{\mu }_2{k}_2{J}_n(k_{3}b)J_n^{\prime }(k_{2}b)-{\mu }_3{k}_3{J}_n(k_{2}b)J_n^{\prime }(k_{3}b)\right]}{{\mu }_2{k}_2{J}_n^{\prime }(k_{2}b)H_n^{(1)}(k_{3}b)-{\mu }_3{k}_3{J}_n(k_{2}b){H_n^{\prime }}^{(1)}(k_{3}b)}$$

(34)

Since the series terms in the Equations (16) and (20) in Pao and Mow [18] are n = 0, 1, 2, …, +∞ and those of the model in this paper are n = −∞, …, +∞, one can substitute Equation (32) into Equations (4) and (5) and unify them in the same series form as follows for the convenience of comparison.

$$\begin{array}{ll}{w}_1(r,\theta )& =w_2(r,\theta )\\ & ={\displaystyle \sum _{n=0}^{+\infty }\frac{i^n{\epsilon }_n{\mu }_3{k}_3\left[J_n^{\prime }(k_{3}b)H_n^{(1)}(k_{3}b)-J_n(k_{3}b){H_n^{\prime }}^{(1)}(k_{3}b)\right]}{{\mu }_2{k}_2{J}_n^{\prime }(k_{2}b)H_n^{(1)}(k_{3}b)-{\mu }_3{k}_3{J}_n(k_{2}b){H_n^{\prime }}^{(1)}(k_{3}b)}{J}_n(k_{1}r)\cos \left(n\theta \right)}\end{array}$$

(35)

Similarly, taking Equation (32) into Equation (6), one has:

$$\begin{array}{ll}{w}_3(r,\theta )& ={\displaystyle \sum _{n=0}^{+\infty }{i}^n{\epsilon }_n{J}_n(k_{3}r)\cos \left(n\theta \right)}\\ & -{\displaystyle \sum _{n=0}^{+\infty }\frac{i^n{\epsilon }_n\left[{\mu }_2{k}_2{J}_n(k_{3}b)J_n^{\prime }(k_{2}b)-{\mu }_3{k}_3{J}_n(k_{2}b)J_n^{\prime }(k_{3}b)\right]}{{\mu }_2{k}_2{J}_n^{\prime }(k_{2}b)H_n^{(1)}(k_{3}b)-{\mu }_3{k}_3{J}_n(k_{2}b){H_n^{\prime }}^{(1)}(k_{3}b)}{H}_n^{(1)}(k_{3}r)\cos \left(n\theta \right)}\end{array}$$

(36)

Note that Equations (35) and (36) are completely consistent with Equations (16) and (20) in Pao and Mow [18], which verifies the correctness of the theory in this paper.

3.2. Comparison with the Exact Solution for Free Field

Setting the parameters of the radially inhomogeneous cylindrical inclusion model in this paper as β = 0.01, ρ₁/ρ₃ = ρ₂/ρ₃ = 1, c₁/c₃ = 1, the model can be approximately degenerated into a homogeneous free field model in a full space. The displacement amplitudes |u| at the inner surface (r = a) and the outer surface (r = b) of the inclusion are calculated to be approximately 1, as shown in Figure 4. This agreement with that predicted by the exact solution for a free field in a full space verifies the accuracy of the method in this paper as well.

4. Results and Discussions in Both Frequency and Time Domains

4.1. Effect of the Rigidity Profile of the Inclusion on the Frequency Domain Displacement and DSCF

To reveal the influence of the inhomogeneous rigidity or wave velocity profile on the seismic response of the inclusion, the surface displacement amplitudes as well as the dynamic stress concentration factors of both soft and hard inclusions at different dimensionless frequencies are calculated, as shown in Figure 5, Figure 6 and Figure 7. The dimensionless parameters in the calculation model are set as a/b = 0.1, ρ₁/ρ₃ = ρ₂/ρ₃ = 1, and c₂ (b)/c₃ = 1. For the soft inclusion, the wave velocity in the region ① is set as c₁/c₃ = c₂ (a)/c₃ = 0.5, while c₁/c₃ = c₂ (a)/c₃ =2 is taken for the hard inclusion.

It is obvious from Figure 5, Figure 6 and Figure 7 that the right side of soft inclusion experiences a more intense response than that of the hard one in terms of both |u| and DSCF. In contrast, the left sides of both inclusions have a similar dynamic response. To explain this phenomenon, the wave propagation process in the time domain is illustrated as follows.

4.2. Propagation Process of the Ricker Wavelet in the Full Space Containing Soft and Hard Inclusions

The propagation process of the Ricker wavelet in a full space containing a soft or hard inclusion is shown in Figure 8 and Figure 9, respectively. The dimensionless parameters in the calculation model are consistent with those in the frequency domain analysis.

Figure 8 shows the propagation process of incident Ricker wavelet in a full space with a soft inclusion. It is set that the Ricker wavelet reaches the soft inclusion at t = 7.5 s (Figure 8a). When the Ricker wavelet enters the soft inclusion, the wave in the soft inclusion gradually lags behind the wave in the full space due to the difference in wave velocity (c₂ < c₃). Therefore, the overall wavefront in the soft inclusion becomes concave and curved backward as shown in Figure 8b–e. When the Ricker wavelet passes through the soft core of the inclusion, the core acts as a secondary wave source and generates a scattered wave that begins to propagate outward as shown in Figure 8f. A superposition between the scattered wave and the direct wave can be observed in Figure 8g–i.

The wave progress in Figure 9 for the hard inclusion is different from that in Figure 8 after a similar start at t = 7.5 s. When the Ricker wavelet enters the hard inclusion, the wave in the inclusion propagates faster than that in the full space due to the larger wave velocity c₂ of the hard inclusion. The overall waveform is convex and curved forward as shown in Figure 9b–e. Comparing Figure 9f–i to Figure 8f–i, it can be found that the scattered wave generated by the hard inclusion is less obvious than that generated by the soft inclusion. The superposition of energy between the scattered wave by the hard inclusion and the direct wave is not so concentrated comparing to that in the case of soft inclusion. This explains the more intense response of the soft inclusion relative to the hard one.

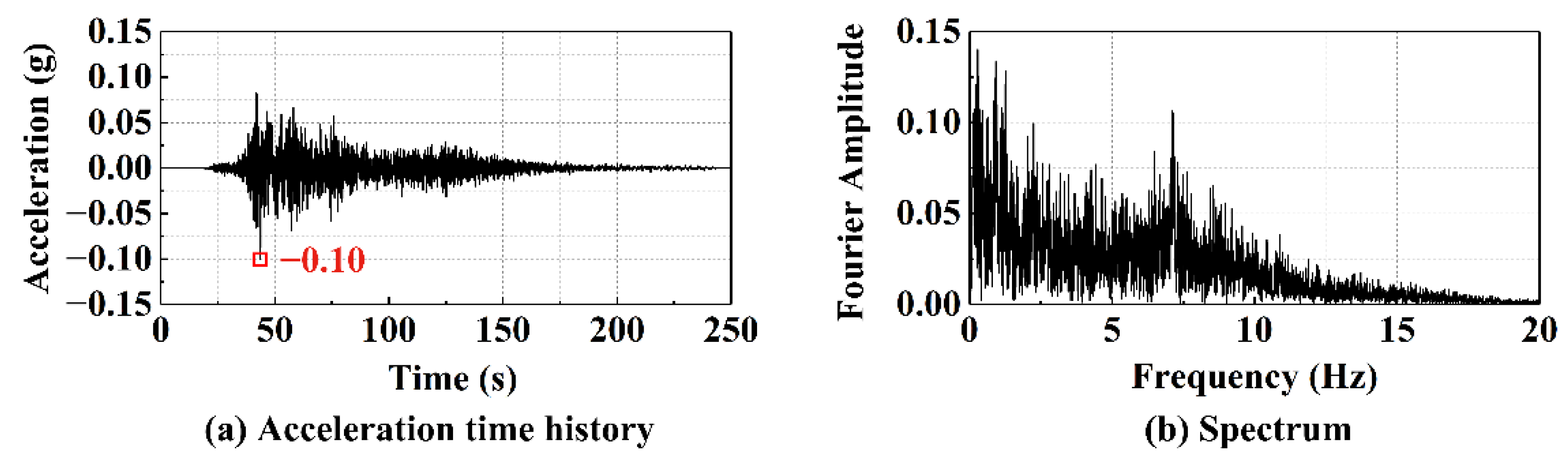
4.3. Acceleration Time Histories at Three Representative Positions of Soft and Hard Inclusions

To be more useful in engineering, a procedure based on the transfer function will be adopted in this section to obtain the acceleration response in the time domain. There are three major steps to obtain the results from the frequency domain to the time domain. Firstly, the input displacement time history can be obtained after twice numerical integration on the incident acceleration time history. Secondly, the input displacement Fourier spectrum obtained with the fast Fourier transform technique (FFT) should be multiplied by the frequency domain displacement transfer functions to obtain the response Fourier spectrum at the targeted locations. Finally, through the inverse fast Fourier transform (iFFT) and twice numerical differentiation, the earthquake acceleration response in the time domain can be obtained. In this way, the amplification or de-amplification of the wave at each frequency is taken into account in the site responses. The transfer functions and acceleration time histories of three representative positions (P₁, O and P₂ in Figure 1) around both the soft and hard inclusions are presented. The calculation parameters are set as a = 100 m, b = 1000 m, c₃ = 1000 m/s, ρ₁ = ρ₂ = ρ₃ = 2700 kg/m³.

For a specific seismic wave time history, such as Deyang wave and El Centro wave widely used in the literature, it is more than sufficient to compute the transfer functions in its major frequency band within 20 Hz. Assuming the incident Deyang wave and El Centro wave both have a PGA of 0.1 g, their acceleration time histories and Fourier spectrums are both plotted in Figure 10 and Figure 11, respectively.

Figure 12 shows the displacement transfer functions at three representative positions O, P₁ and P₂ for both soft (c₁/c₃ = 1/2) and hard (c₁/c₃ = 2) inclusions under incident SH wave at varying frequencies. It can be seen from Figure 12a for the soft inclusion case that the displacement transfer function amplitude |u| at position P₁ is around 1 and |u| at position O reaches 2 for most frequencies, while |u| at position P₂ oscillates between 1 and 2. These values means that there is no amplification of displacement amplitudes at position P₁, there is an amplification of 200% at position O and below 200% at position P₂ for most frequencies. When it comes to the case of a hard inclusion in Figure 12b, there is no obvious amplification in transfer function at position P₁ (|u| ≈ 1) but an obvious reduction at position O (|u| ≈ 0.5) and position P₂ (|u| ≈ 0.25) for most frequencies.

To take into account the frequency dependent modification of motions, an acceleration time history synthesizing procedure in Dai et al. [26] is adopted. Figure 13 shows the acceleration time histories at three positions of soft (Figure 13a–c) and hard (Figure 13d–f) inclusions under the Deyang (NS) wave recorded during the 2008 Wenchuan earthquake in China. It can be found that the PGA at positions P₁, O and P₂ of the soft inclusion is 1.0, 2.0 and 1.5 times that of the original Deyang (NS) wave (Figure 10a), while the PGA at positions P₁, O and P₂ of the hard inclusion is 1.0, 0.5 and 0.4 times that of the original wave.

Similarly, Figure 14 shows the acceleration time histories of three positions of soft (Figure 14a–c) and hard (Figure 14d–f) inclusions under El Centro wave. It can be found that the PGA at positions P₁, O and P₂ of the soft inclusion is 1.3, 2.8 and 1.7 times that of the original El Centro wave (Figure 10a), while the PGA at positions P₁, O and P₂ of the hard inclusion is 1.3, 0.7 and 0.3 times that of the original wave. Overall, the amplification or reduction effect on the incident El Centro wave is stronger than that on Deyang (NS) wave due to the difference in the frequency content between the two incident waves.

5. Conclusions

An analytical solution to SH wave scattering by a cylindrical inclusion with inhomogeneous elastic modulus in a full space is derived based on the wave function expansion method in this paper. The frequency domain results show that the rigidity profile of the inclusion has a great influence on both the displacement and stress around the inclusion. Generally, a softer inclusion will experience larger displacement and stress due to the superposition between scattered and direct waves, especially in its core and shaded side. Time domain results also illustrate that the soft inclusion may amplify the PGA of acceleration by more than 150% in the shaded side of the inclusion. This warrant special attention paid on the modification of earthquake input for underground structures built near inhomogeneous inclusions. Extension of the single layer inclusion model herein to a multilayer one is helpful for studying the inclusion problem with a more generous inhomogeneous profile.