A New Method to Assess Thick, Hard Roof-Induced Rock Burst Risk Based on Mining Speed Effect on Key Energy Strata
Abstract
:1. Introduction
2. The Principle and Discriminant Criterion of KES for RTRB
2.1. The Principle of KES for RTRB
2.2. The Discriminant Criterion of KES
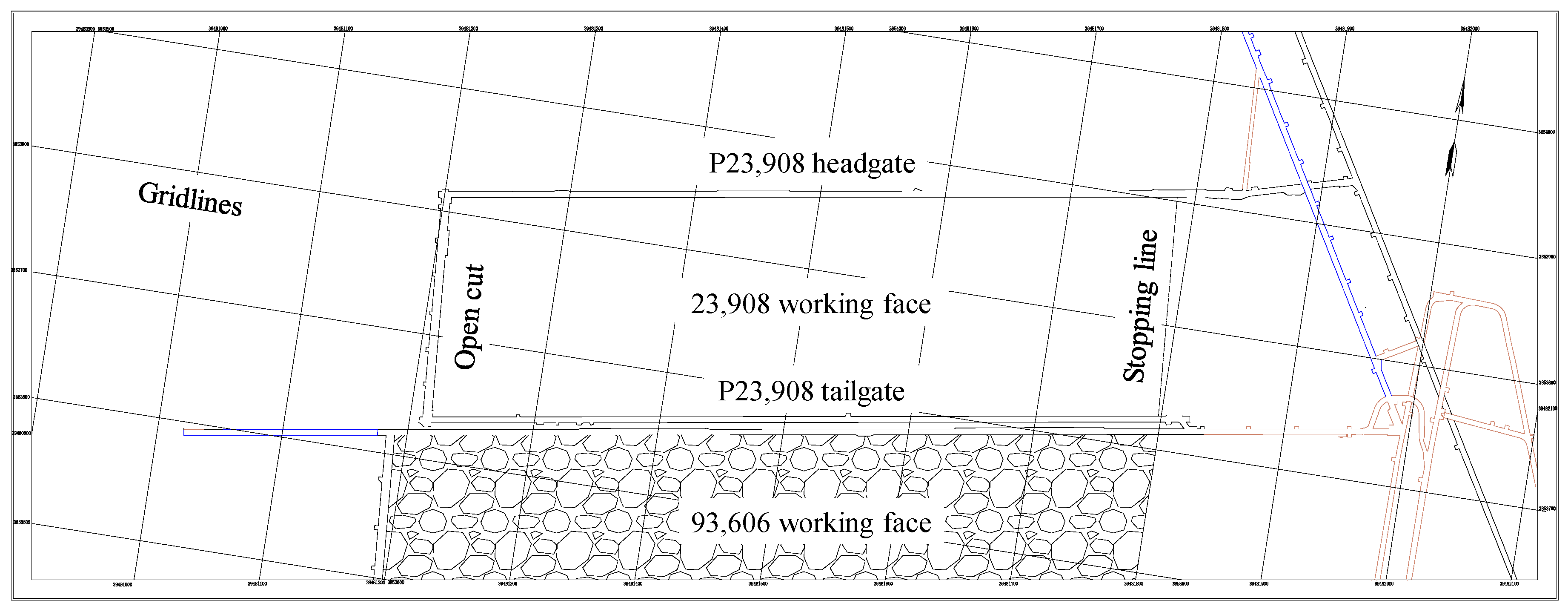
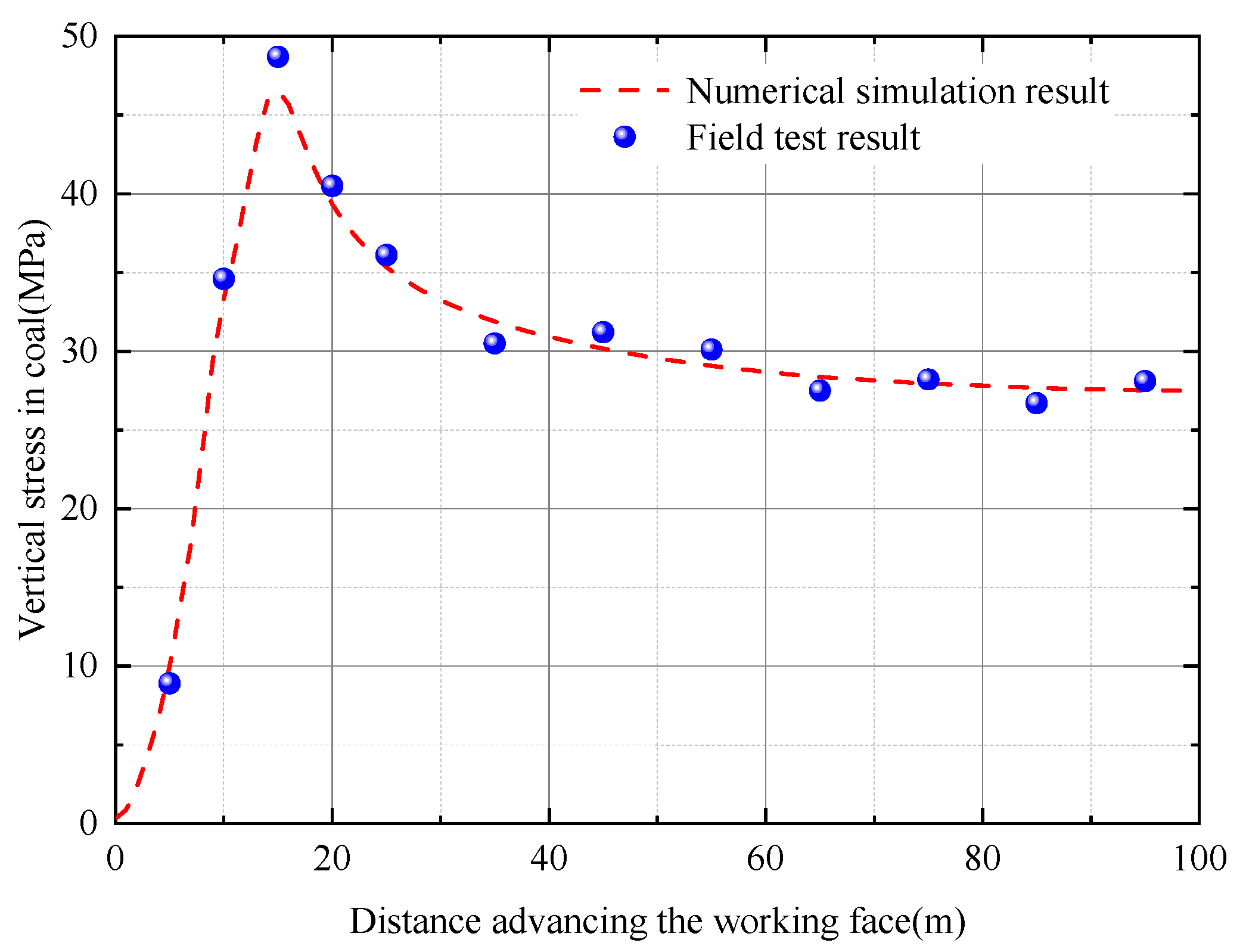
2.3. Engineering Example Analysis
3. Numerical Simulation Analysis of Mining Speed Effect on Energy Accumulation of Coal and Energy Release of KES
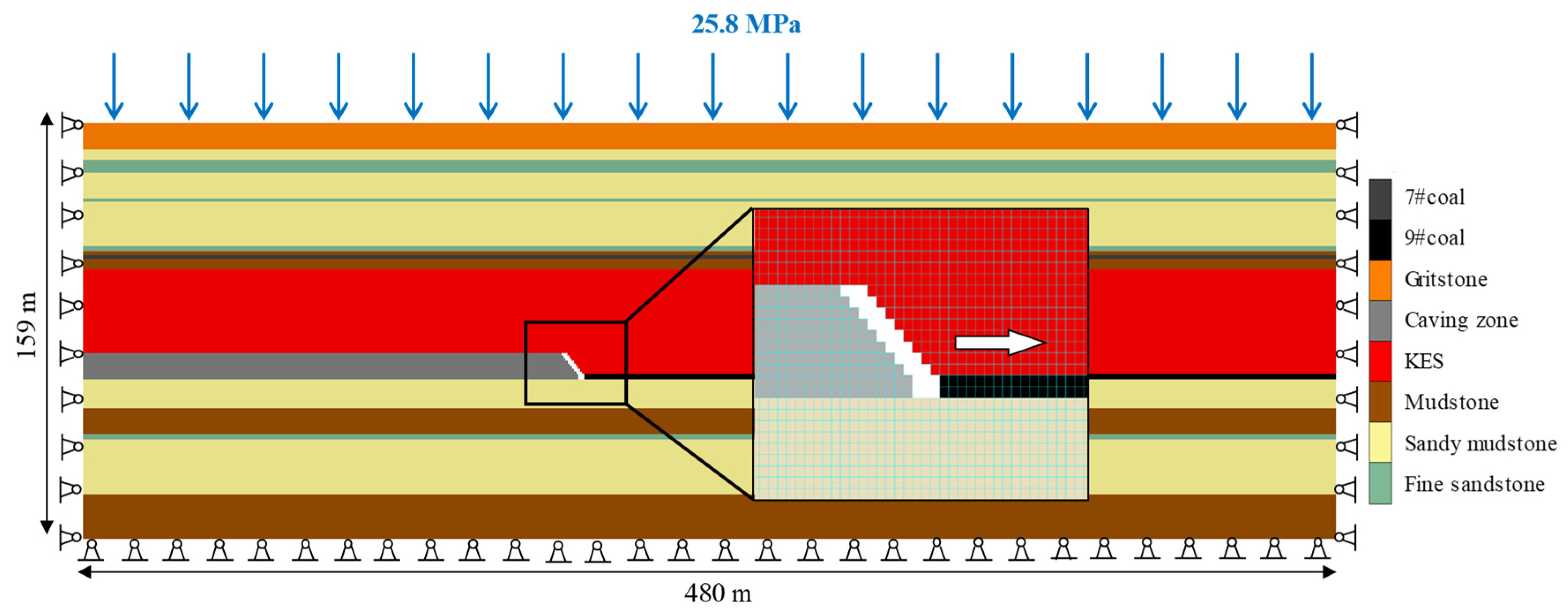
3.1. Numerical Simulation Methods
3.2. Results Analysis
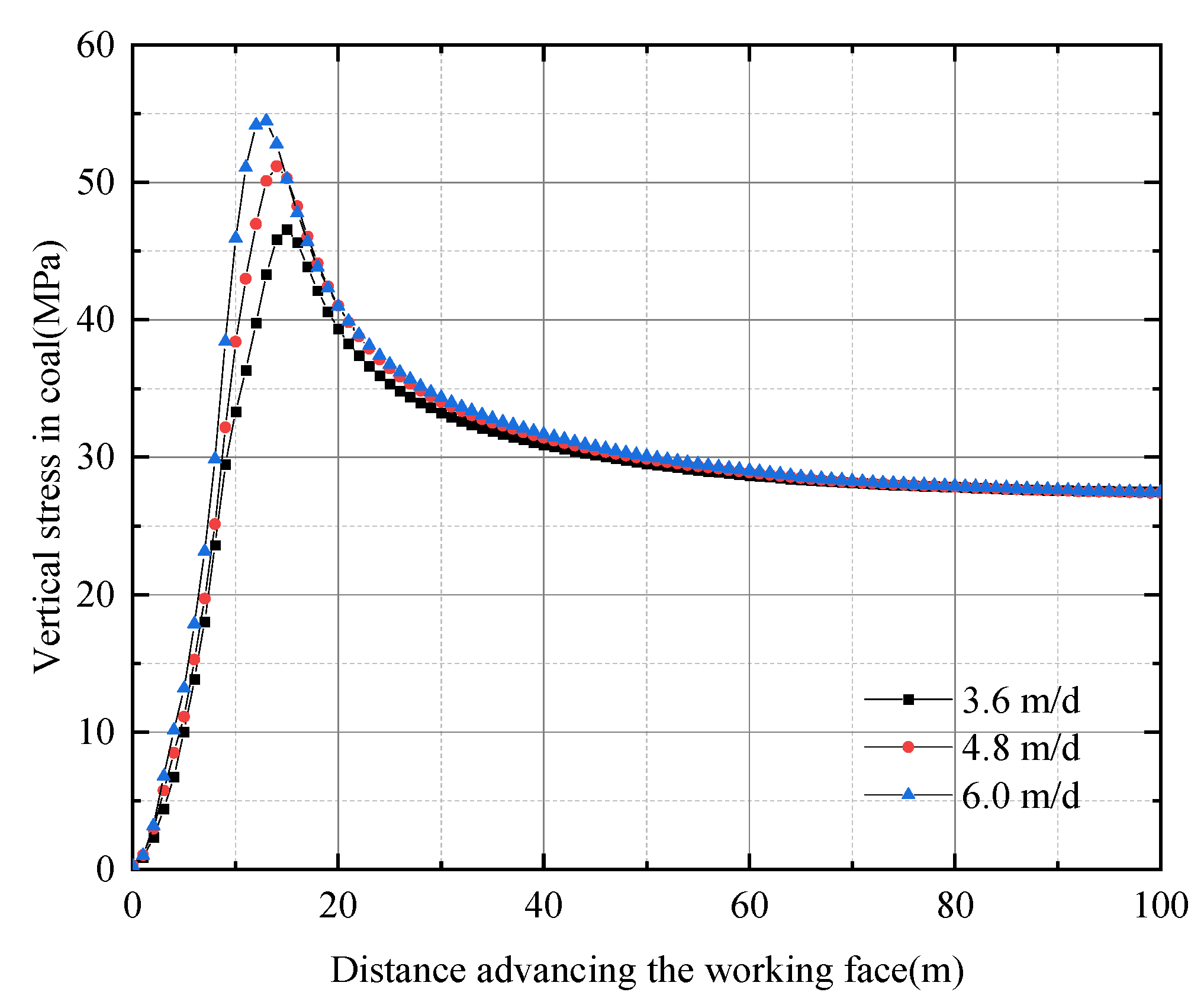
3.2.1. Evolution of Peak Vertical Stress in Coal
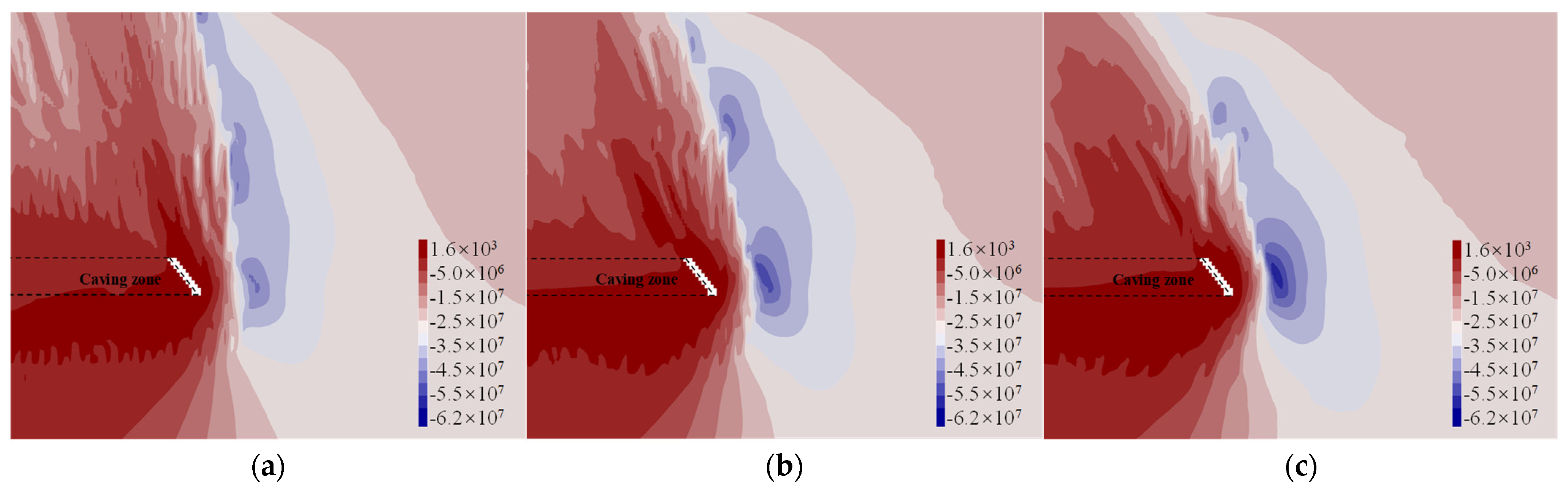
3.2.2. Distribution Characteristics of Vertical Stress
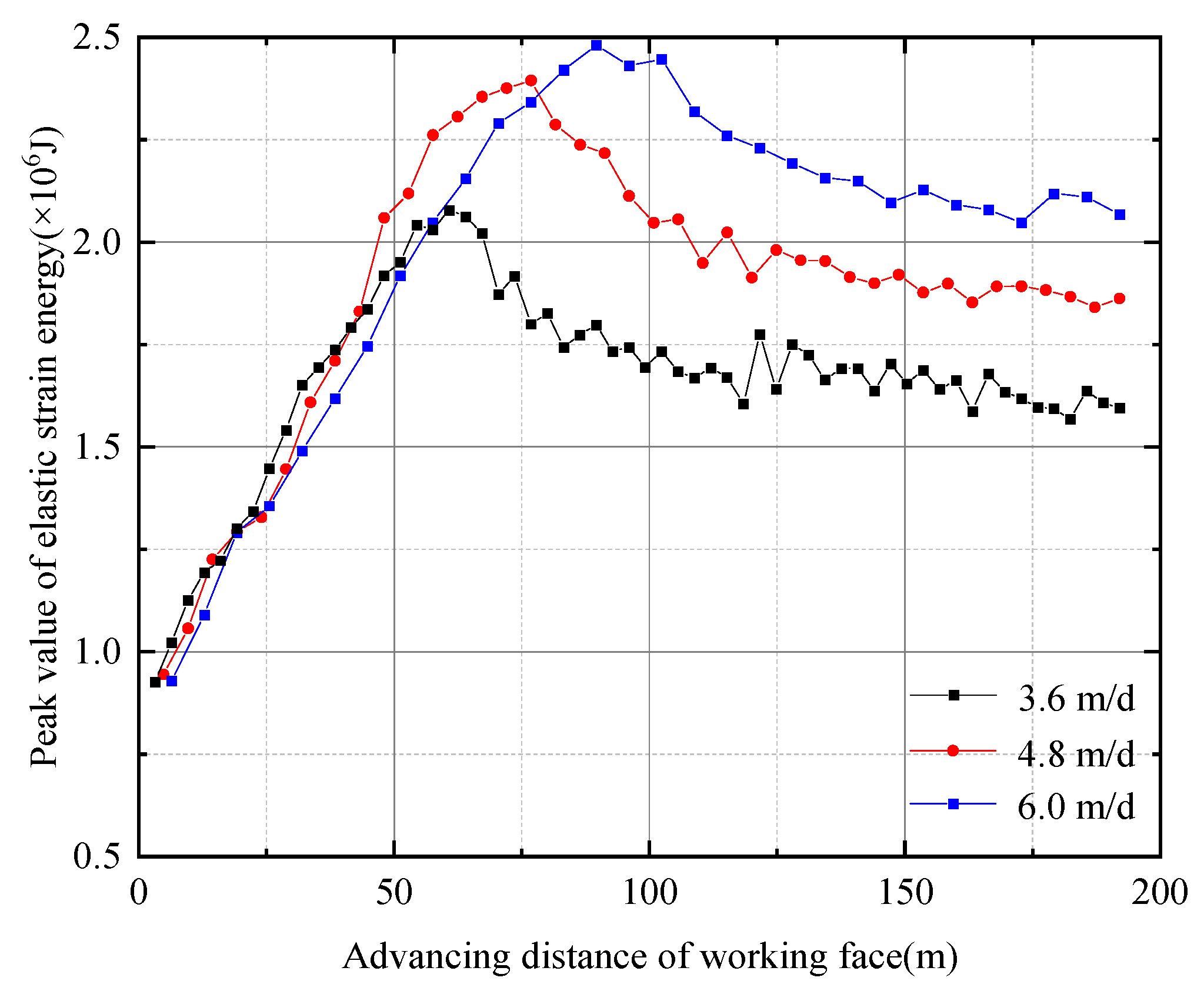
3.2.3. Evolution of Peak Elastic Strain Energy in Coal
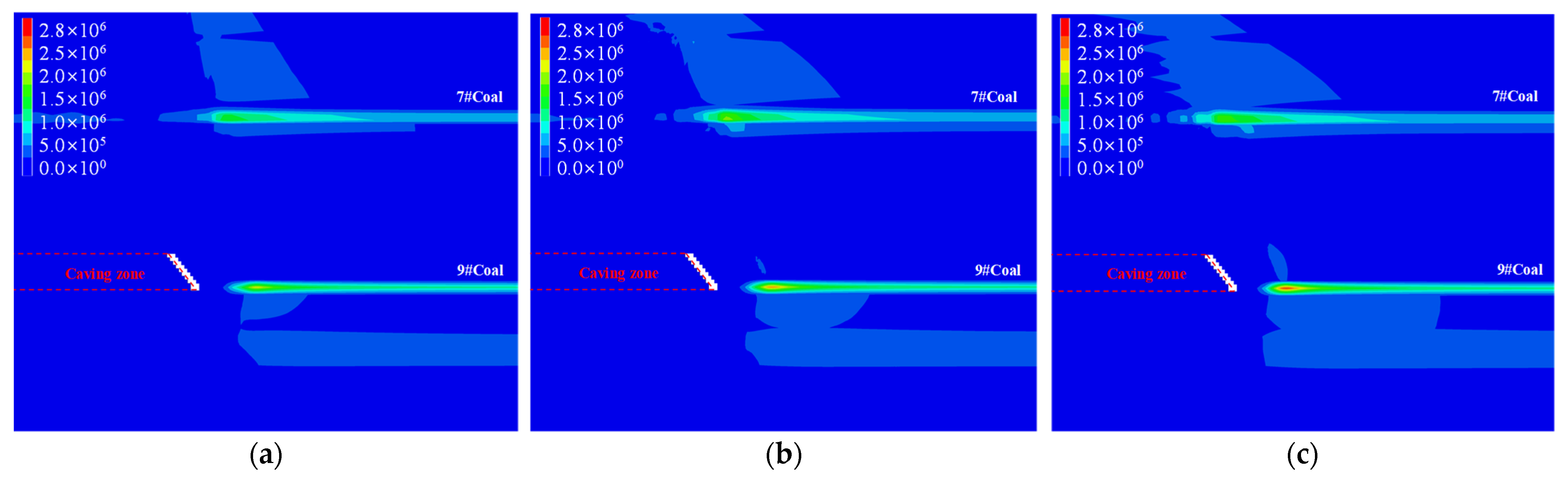
3.2.4. Distribution Characteristics of Elastic Strain Energy
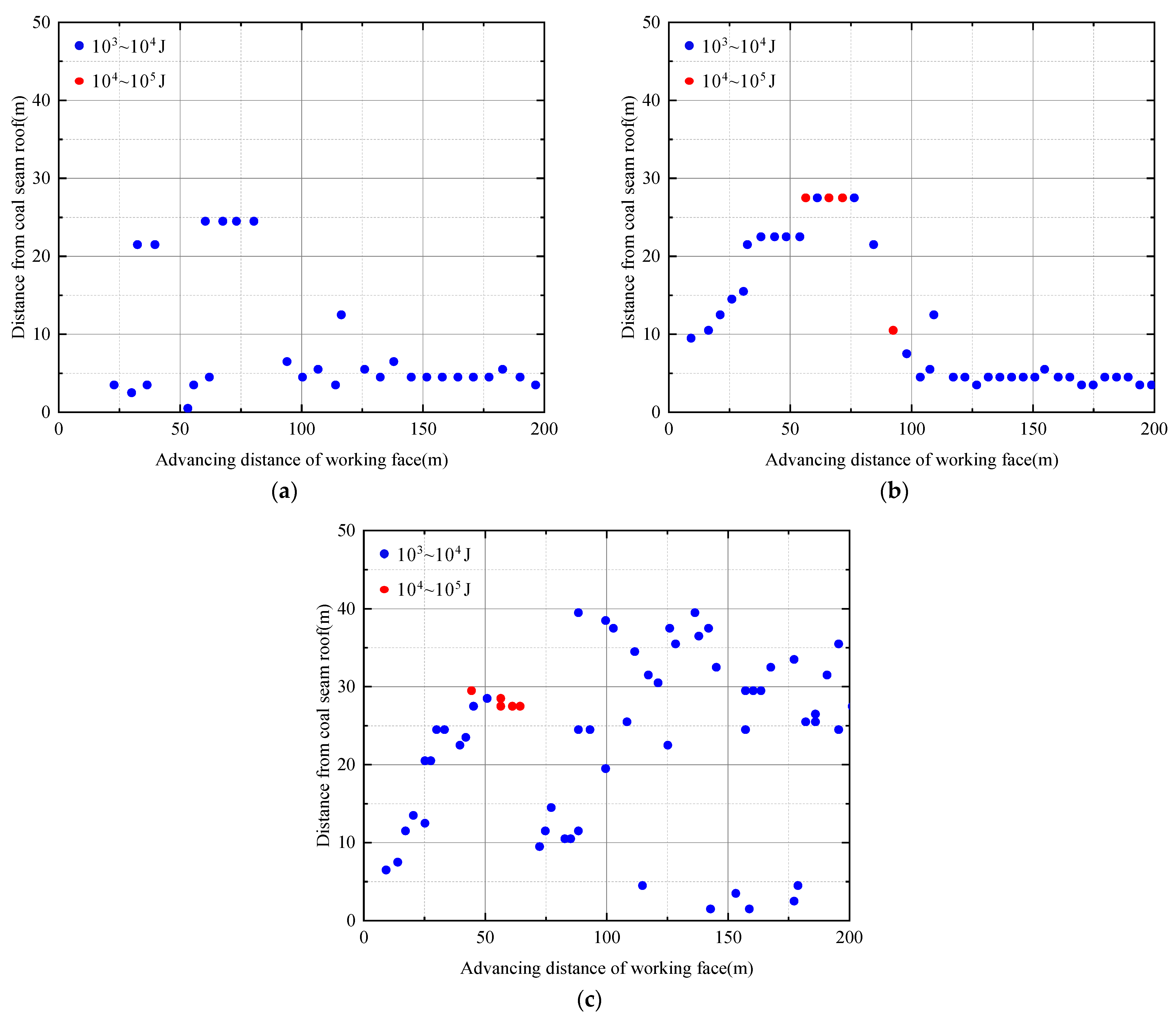
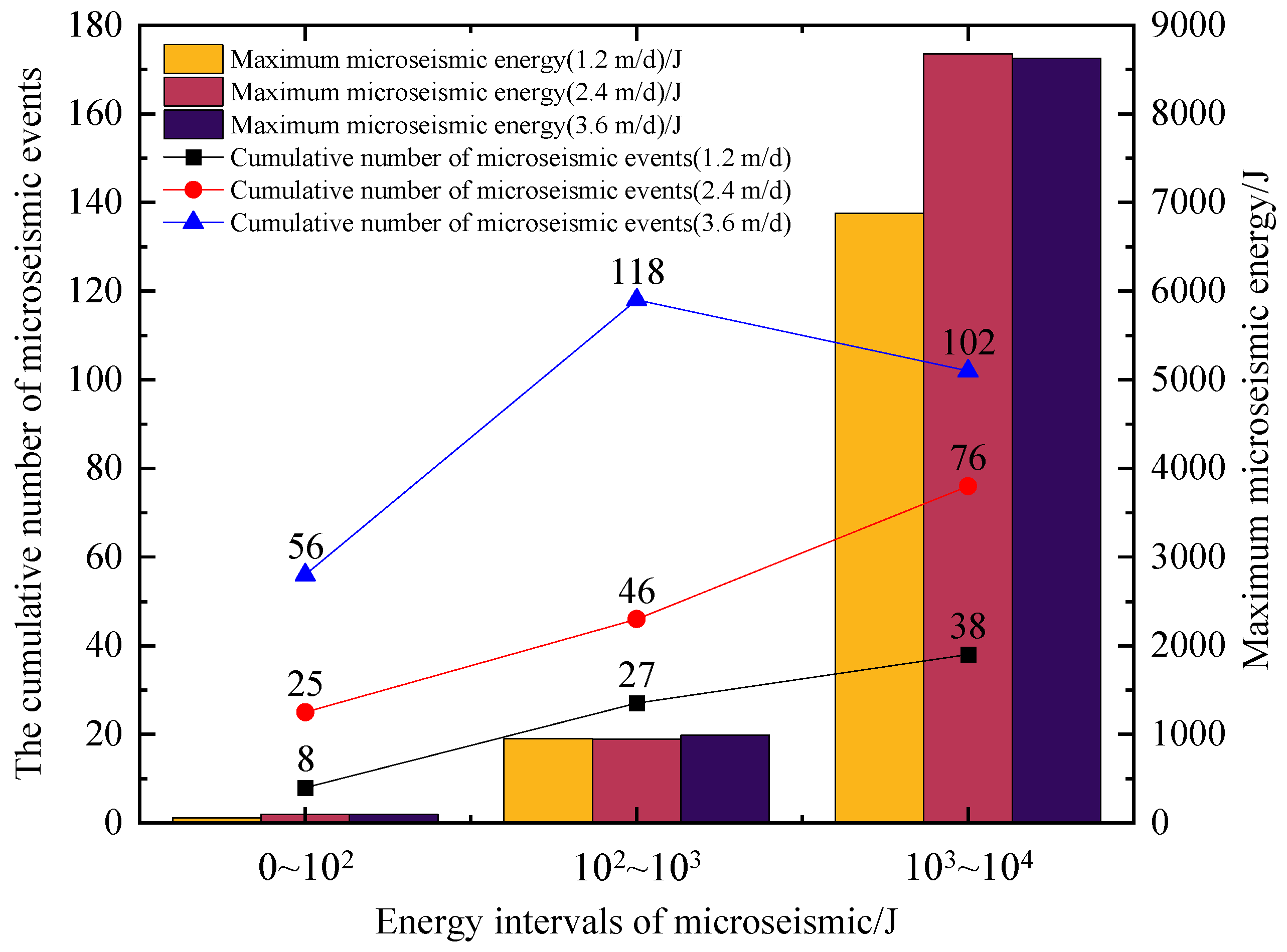
3.2.5. Evolution Characteristics of Energy Release in KES
4. Discussion
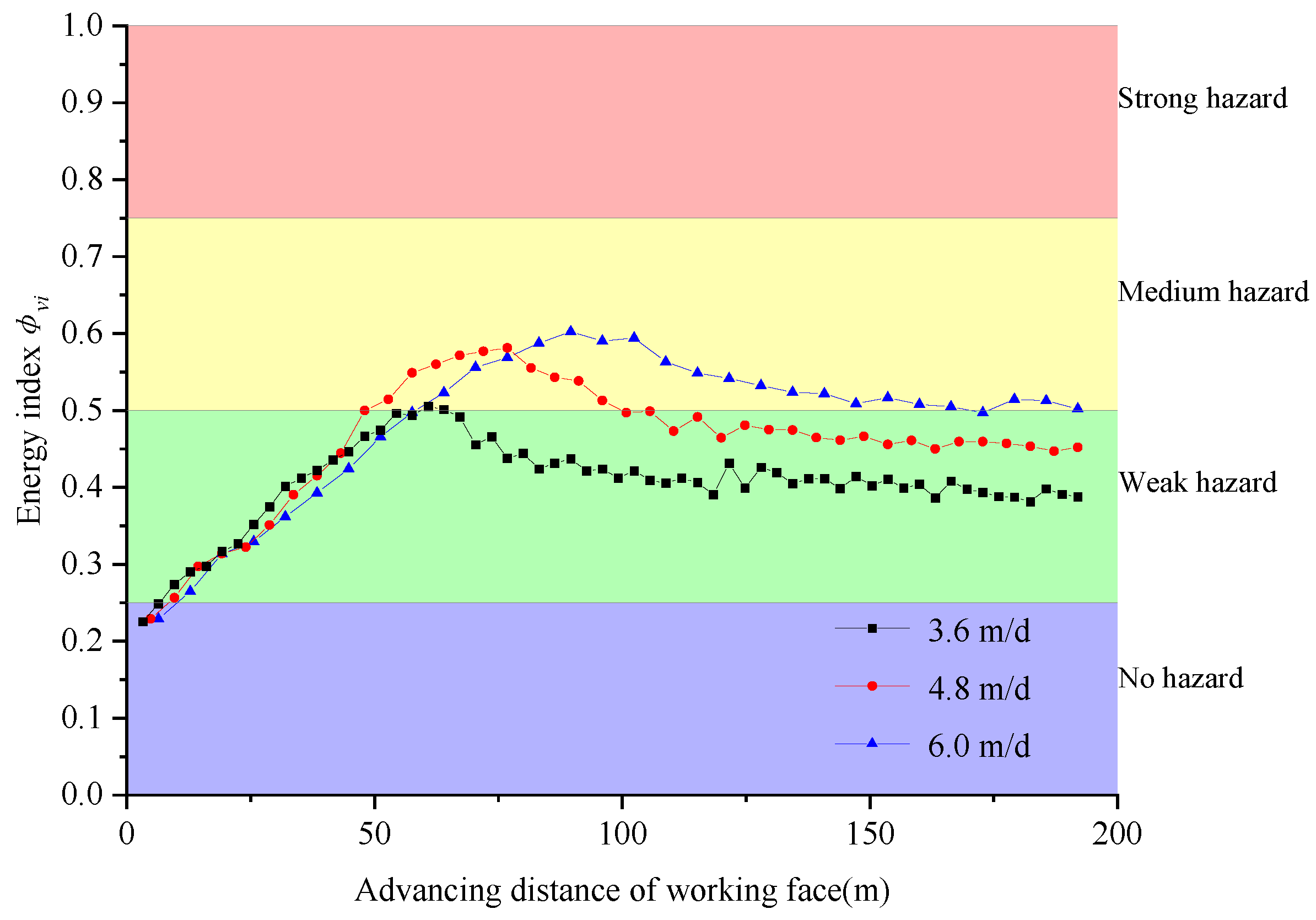
4.1. Rock Burst Risk Assessment Considering Mining Speed Effect
4.2. Engineering Practice Test
5. Summaries and Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Mazaira, A.; Konicek, P. Intense rockburst impacts in deep underground construction and their prevention. Can. Geotech. J. 2015, 52, 1426–1439. [Google Scholar] [CrossRef]
- Zhang, C.G.; Canbulat, I.; Hebblewhite, B.; Ward, C.R. Assessing coal burst phenomena in mining and insights into directions for future research. Int. J. Coal Geol. 2017, 179, 28–44. [Google Scholar] [CrossRef]
- Li, T.; Cai, M.F.; Cai, M. A review of mining-induced seismicity in China. Int. J. Rock Mech. Min. Sci. 2007, 44, 1149–1171. [Google Scholar] [CrossRef]
- Chen, S.J.; Zhao, Z.H.; Feng, F.; Zhang, M.Z. Stress evolution of deep surrounding rock under characteristics of bi-modulus and strength drop. J. Cent. South Univ. 2022, 29, 680–692. [Google Scholar] [CrossRef]
- Chen, S.J.; Yin, D.W.; Jiang, N.; Wang, F.; Zhao, Z. Mechanical properties of oil shale-coal composite samples. Int. J. Rock Mech. Min. Sci. 2019, 123, 104120. [Google Scholar] [CrossRef]
- Chen, S.J.; Feng, F.; Wang, Y.; Li, D.Y.; Huang, W.P.; Zhao, X.D.; Jiang, N. Tunnel failure in hard rock with multiple weak planes due to excavation unloading of in-situ stress. J. Cent. South Univ. 2020, 27, 2864–2882. [Google Scholar] [CrossRef]
- Li, X.L.; Chen, S.J.; Li, Z.H.; Wang, E.Y. Rockburst mechanism in coal rock with structural surface and the microseismic (MS) and electromagnetic radiation (EMR) response. Eng. Fail. Anal. 2021, 124, 105396. [Google Scholar] [CrossRef]
- Li, X.L.; Chen, S.J.; Liu, S.M.; Li, Z.H. AE waveform characteristics of rock mass under uniaxial loading based on Hilbert-Huang transform. J. Cent. South Univ. 2021, 28, 1843–1856. [Google Scholar] [CrossRef]
- Liu, S.M.; Li, X.L.; Wang, D.K.; Zhang, D. Investigations on the mechanism of the microstructural evolution of different coal ranks under liquid nitrogen cold soaking. Energy Sources Part A Recovery Util. Environ. Eff. 2020, 42, 1–17. [Google Scholar] [CrossRef]
- Zhou, X.M.; Wang, S.; Li, X.L. Research on theory and technology of floor heave control in semicoal rock roadway: Taking longhu coal mine in Qitaihe mining area as an Example. Lithosphere 2022, 2022, 3810988. [Google Scholar] [CrossRef]
- Wang, S.; Li, X.L.; Qin, Q.Z. Study on surrounding rock control and support stability of Ultra-large height mining face. Energies 2022, 15, 6811. [Google Scholar] [CrossRef]
- Li, X.L.; Chen, S.J.; Wang, S. Study on in situ stress distribution law of the deep mine taking Linyi Mining area as an example. Adv. Mater. Sci. Eng. 2021, 9, 5594181. [Google Scholar] [CrossRef]
- Liu, H.Y.; Zhang, B.Y.; Li, X.L. Research on roof damage mechanism and control technology of gob-side entry retaining under close distance gob. Eng. Fail. Anal. 2022, 138, 106331. [Google Scholar] [CrossRef]
- He, J.; Dou, L.M.; Mu, Z.L.; Cao, A.Y.; Gong, S.Y. Numerical simulation study on hard-thick roof inducing rock burst in coal mine. J. Cent. South Univ. 2016, 23, 2314–2320. [Google Scholar] [CrossRef]
- Wang, W.; Cheng, Y.P.; Wang, H.F.; Liu, H.Y.; Wang, L.; Li, W.; Jiang, J.Y. Fracture failure analysis of hard-thick sandstone roof and its controlling effect on gas emission in underground ultra-thick coal extraction. Eng. Fail. Anal. 2015, 54, 150–162. [Google Scholar] [CrossRef]
- Jiang, L.S.; Wu, Q.S.; Wu, Q.L.; Wang, P.; Xue, Y.C.; Kong, P.; Gong, B. Fracture failure analysis of hard and thick key layer and its dynamic response characteristics. Eng. Fail. Anal. 2019, 98, 118–130. [Google Scholar] [CrossRef]
- Wang, P.; Jiang, L.S.; Zheng, P.Q.; Qin, G.P.; Zhang, C. Inducing mode analysis of rock burst in fault-affected zone with a hard-thick stratum occurrence. Environ. Earth Sci. 2019, 78, 15. [Google Scholar] [CrossRef]
- Zhang, Q.M.; Wang, E.Y.; Feng, X.J.; Niu, Y.; Ali, M.; Lin, S.; Wang, H. Rockburst Risk Analysis During High-Hard Roof Breaking in Deep Mines. Nat. Resour. Res. 2020, 29, 4085–4101. [Google Scholar] [CrossRef]
- Cui, F.; Dong, S.; Lai, X.P.; Chen, J.Q.; Cao, J.T.; Shan, P.F. Study on Rule of Overburden Failure and Rock Burst Hazard under Repeated Mining in Fully Mechanized Top-Coal Caving Face with Hard Roof. Energies 2019, 12, 24. [Google Scholar] [CrossRef] [Green Version]
- Lu, C.P.; Liu, G.J.; Liu, Y.; Zhang, N.; Xue, J.H.; Zhang, L. Microseismic multi-parameter characteristics of rockburst hazard induced by hard roof fall and high stress concentration. Int. J. Rock Mech. Min. Sci. 2015, 76, 18–32. [Google Scholar] [CrossRef]
- Zhang, J.X.; Li, B.Y.; Zhou, N.; Zhang, Q. Application of solid backfilling to reduce hard-roof caving and longwall coal face burst potential. Int. J. Rock Mech. Min. Sci. 2016, 88, 197–205. [Google Scholar] [CrossRef]
- Ge, M.C. Efficient mine microseismic monitoring. Int. J. Coal Geol. 2005, 64, 44–56. [Google Scholar] [CrossRef]
- Cao, A.Y.; Dou, L.M.; Wang, C.B.; Yao, X.X.; Dong, J.Y.; Gu, Y. Microseismic Precursory Characteristics of Rock Burst Hazard in Mining Areas Near a Large Residual Coal Pillar: A Case Study from Xuzhuang Coal Mine, Xuzhou, China. Rock Mech. Rock Eng. 2016, 49, 4407–4422. [Google Scholar] [CrossRef]
- Zhu, G.A.; Dou, L.M.; Cai, W.; Li, Z.L.; Zhang, M.; Kong, Y.; Shen, W. Case Study of Passive Seismic Velocity Tomography in Rock Burst Hazard Assessment During Underground Coal Entry Excavation. Rock Mech. Rock Eng. 2016, 49, 4945–4955. [Google Scholar] [CrossRef]
- Cai, W.; Dou, L.M.; Si, G.Y.; Cao, A.Y.; Gong, S.Y.; Wang, G.F.; Yuan, S.S. A new seismic-based strain energy methodology for coal burst forecasting in underground coal mines. Int. J. Rock Mech. Min. Sci. 2019, 123, 104086. [Google Scholar] [CrossRef]
- Chen, F.; Cao, A.Y.; Liang, Z.Z.; Liu, Y.Q. A Coal Burst Risk Assessment Model of Seismic Events Based on Multiple Seismic Source Parameters: A Case Study of the Huating Coal Mine, Gansu Province, China. Nat. Resour. Res. 2021, 30, 4515–4532. [Google Scholar] [CrossRef]
- Liu, Y.Q.; Cao, A.Y.; Wang, S.W.; Yang, Y.; Guo, W.H.; Xue, C.C.; Li, X.W. Attenuation Characteristics Analysis of Seismic Energy and Its Application to Risk Assessment in Underground Coal Mines. Geomat. Nat. Hazards Risk 2022, 13, 1014–1042. [Google Scholar] [CrossRef]
- He, H.; Dou, L.M.; Gong, S.Y.; He, J.; Zheng, Y.L.; Zhang, X. Microseismic and electromagnetic coupling method for coal bump risk assessment based on dynamic static energy principles. Saf. Sci. 2018, 114, 30–39. [Google Scholar] [CrossRef]
- Li, H.; Cao, A.Y.; Gong, S.Y.; Wang, C.B.; Zhang, R.P. Evolution Characteristics of Seismic Detection Probability in Underground Mines and Its Application for Assessing Seismic Risks-A Case Study. Sensors 2022, 22, 10. [Google Scholar] [CrossRef]
- Wang, J.A.; Jiao, S.H.; Xie, G.X. Study on Influence of Mining Rate on Stress Environment in Surrounding Rock of Mechanized Top Caving Mining Face. China J. Rock Mech. Eng. 2006, 06, 1118–1124. [Google Scholar]
- Xie, G.X.; Chang, J.C.; Hua, X.Z. Influence of Mining Velocity on Mechanical Characteristics of Surrounding Rock in Fully Mechanized Top-Coal Caving Face. Chin. J. Geotech. Eng. 2007, 29, 963–967. [Google Scholar]
- Yang, S.L.; Wang, Z.H.; Jiang, W.; Yang, J.H. Advancing Rate Effect on Rock and Coal Failure Format in High Intensity Mining Face. J. China Coal Soc. 2016, 41, 586–594. [Google Scholar]
- Zhao, T.B.; Guo, W.Y.; Han, F.; Gu, S.D. Analysis on Energy Accumulation and Release of Roof under Influence of Mining Speed. Coal Sci. Technol. 2018, 46, 37–44. [Google Scholar]
- Feng, L.F.; Dou, L.M.; Wang, X.D. Mechanism of Mining Advance Speed on Energy Release from Hard Roof Movement. J. China Coal Soc. 2019, 44, 3329–3339. [Google Scholar]
- Qian, M.G.; Miao, X.X.; Xu, J.L.; Mao, X.B. Key Strata Theory in Ground Control, 2nd ed.; China University of Mining and Technology Press: Xuzhou, China, 2003; pp. 10–18. [Google Scholar]
- Cao, A.Y. Research on Seismic Effort of Burst and Failure of Coal-rock Mass Associated with Mining and Its Application. J. China Coal Soc. 2011, 36, 177–178. [Google Scholar]
- Jiang, F.X.; Liu, Y.; Zhang, Y.C.; Wen, J.L.; Yang, W.L.; An, J. A Three-Zone Structure Loading Model of Overlying Strata and Its Application on Rockburst Prevention. China J. Rock Mech. Eng. 2016, 35, 2398–2408. [Google Scholar]
- Gao, M.S.; Xu, D.; He, Y.L.; Zhang, Z.G.; Yu, X. Investigation on the Near-Far Field Effect of Rock Burst Subject to the Breakage of Thick and Hard Overburden. J. Min. Saf. Eng. 2022, 02, 215–226. [Google Scholar]
- Chen, G.B.; Li, T.; Zhang, G.H.; Lv, P.F.; Wu, X.Y. Experimental Study on the Law of Energy Accumulation before Failure of Coal-Rock Combined Body. J. China Coal Soc. 2021, 46, 174–186. [Google Scholar]
- Mu, Z.L. Study of the Burst-Energy Principle of Rock Burst Induced by Roof Stratum and Its Application. J. China Univ. Min. Technol. 2009, 38, 149–150. [Google Scholar]
- Yang, Z.Q. Occurrence Mechanism of Rock Burst and Its Prevention Methods under Complicated Geological Conditions. Ph.D. Thesis, China University of Mining and Technology (Beijing), Beijing, China, 2018. [Google Scholar]
- Zhu, S.T.; Liu, J.H.; Jiang, F.X. Classification, Prediction, Prevention and Control of Roof Movement-Type Mine Earthquake and Induced Disasters in China’s Coal Mines. J. China Coal Soc. 2022, 47, 807–816. [Google Scholar]
- Liu, Y.Q.; Cao, A.Y.; Wang, S.W. Prediction Method of Coal Burst Based on Attenuation Characteristics of Seismic Cluster Energy. J. China Coal Soc. 2022, 47, 1523–1533. [Google Scholar]
- Xu, J.L. Green Mining of Coal Mine, 3rd ed.; China University of Mining and Technology Press: Xuzhou, China, 2011. [Google Scholar]
- Bai, Q.S.; Tu, S.H.; Yuan, Y.; Wang, F.T. Back Analysis of Mining induced Responses on the Basis of Goaf Compaction Theory. J. China Univ. Min. Technol. 2013, 42, 355–361. [Google Scholar]
- Zhang, M.; Jiang, F.X.; Li, K.Q.; Sun, C.D.; Zhai, M.H. A Study of Surface Seismic Damage Boundary Based on the Break and Movement of Extremely Thick Key Stratum. J. China Univ. Min. Technol. 2017, 46, 514–520. [Google Scholar]
- Wang, L.; Xie, G. Influence of Mining Velocity on Dynamic Disasters in the Coal and Rock Mass at a Fully Mechanized Mining Face. J. China Univ. Min. Technol. 2010, 39, 70–74. [Google Scholar]
- Dou, L.M.; He, J.; Cao, A.Y.; Gong, S.Y.; Cai, W. Rock Burst Prevention Methods Based on Theory of Dynamic and Static Combined Load Induced in Coal Mine. J. China Coal Soc. 2015, 40, 1469–1476. [Google Scholar]
- Qi, Q.X.; Dou, L.M. Theory and Technology of Rock Burst; China University of Mining and Technology Press: Xuzhou, China, 2008. [Google Scholar]




| Range of Energy Level | Energy Attenuation Coefficient η |
|---|---|
| 102~103 J | 1.3968 × 10−3 |
| 103~104 J | 1.2046 × 10−3 |
| 104~105 J | 9.1698 × 10−4 |
| 105~106 J | 7.2674 × 10−4 |
| 106~107 J | 5.5714 × 10−4 |
| Lithology of Overlying Rock (UCS)/MPa | Computing Formula |
|---|---|
| Hard rock (40~80) | |
| Medium hard rock (20~40) | |
| Weak rock (10~20) | |
| Extremely weak rock (<10) |
| Rock Strata | Fine Sandstone I | Mudstone II | Mudstone III | Fine Sandstone II | Sandy Mudstone |
|---|---|---|---|---|---|
| h/m | 40.80 | 3.80 | 1.50 | 2.20 | 16.80 |
| RT/MPa | 5.86 | 2.00 | 2.00 | 5.86 | 2.46 |
| Er/GPa | 9.70 | 4.50 | 4.50 | 9.70 | 5.46 |
| Ud/J | 6.27 × 107 | 7.97 × 104 | 1.24 × 104 | 1.82 × 105 | 2.16 × 106 |
| η | 5.5714 × 10−4 | 1.2046 × 10−3 | 1.3968 × 10−3 | 1.2046 × 10−3 | 9.1698 × 10−4 |
| Udh/J | 1.05 × 105 | 3.47 × 101 | 4.51 × 100 | 6.21 × 101 | 5.30 × 102 |
| kr | 10.47 | 0 | 0 | 0 | 0.05 |
| Rock Strata | Elastic Modulus/GPa | Poisson Ratio | Tensile Strength/MPa | Cohesion/MPa | Internal Friction Angle/° | Density /kg·m−3 | Residual Tensile Strength/MPa | Residual Cohesion/MPa |
|---|---|---|---|---|---|---|---|---|
| Sandy mudstone | 5.46 | 0.22 | 2.46 | 2.00 | 32 | 2200 | 0.12 | 0.10 |
| Gritstone | 10.00 | 0.20 | 2.50 | 2.00 | 35 | 2600 | 0.13 | 0.10 |
| Mudstone | 4.50 | 0.28 | 2.00 | 1.20 | 27 | 2700 | 0.10 | 0.06 |
| Fine sandstone | 9.70 | 0.17 | 5.86 | 3.00 | 38 | 2800 | 0.29 | 0.15 |
| Coal | 1.19 | 0.36 | 0.50 | 0.80 | 23 | 1400 | 0.03 | 0.04 |
| Density/kg·m−3 | Bulk Modulus/GPa | Shear Modulus/GPa | Internal Friction Angle/° | Dilation Angle/° |
|---|---|---|---|---|
| 1700 | 9.58 | 5.32 | 30 | 10 |
| Type of Immediate Roof | UCS/MPa | Coefficient | |
|---|---|---|---|
| c1 | c2 | ||
| Hard | >40 | 2.1 | 16 |
| Medium–hard | 20~40 | 4.7 | 19 |
| Weak | <20 | 6.2 | 32 |
| Φvi | Rock Burst Risk Level |
|---|---|
| 0 < Φvi ≤ 0.25 | None |
| 0.25 < Φvi ≤ 0.5 | Weak |
| 0.5 < Φvi ≤ 0.75 | Medium |
| 0.75 < Φvi ≤ 1 | Strong |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, W.; Tu, S.; Tu, H.; Liu, X.; Miao, K.; Zhao, H.; Ma, J.; Tang, L.; Li, Y. A New Method to Assess Thick, Hard Roof-Induced Rock Burst Risk Based on Mining Speed Effect on Key Energy Strata. Sustainability 2022, 14, 15054. https://doi.org/10.3390/su142215054
Li W, Tu S, Tu H, Liu X, Miao K, Zhao H, Ma J, Tang L, Li Y. A New Method to Assess Thick, Hard Roof-Induced Rock Burst Risk Based on Mining Speed Effect on Key Energy Strata. Sustainability. 2022; 14(22):15054. https://doi.org/10.3390/su142215054
Chicago/Turabian StyleLi, Wenlong, Shihao Tu, Hongsheng Tu, Xun Liu, Kaijun Miao, Hongbin Zhao, Jieyang Ma, Long Tang, and Yan Li. 2022. "A New Method to Assess Thick, Hard Roof-Induced Rock Burst Risk Based on Mining Speed Effect on Key Energy Strata" Sustainability 14, no. 22: 15054. https://doi.org/10.3390/su142215054
APA StyleLi, W., Tu, S., Tu, H., Liu, X., Miao, K., Zhao, H., Ma, J., Tang, L., & Li, Y. (2022). A New Method to Assess Thick, Hard Roof-Induced Rock Burst Risk Based on Mining Speed Effect on Key Energy Strata. Sustainability, 14(22), 15054. https://doi.org/10.3390/su142215054









