A Decision-Making Model for Remanufacturing Facility Location in Underdeveloped Countries: A Capacitated Facility Location Problem Approach
Abstract
:1. Introduction
2. Literature Review
3. Materials and Methods
3.1. CFLP Formulation
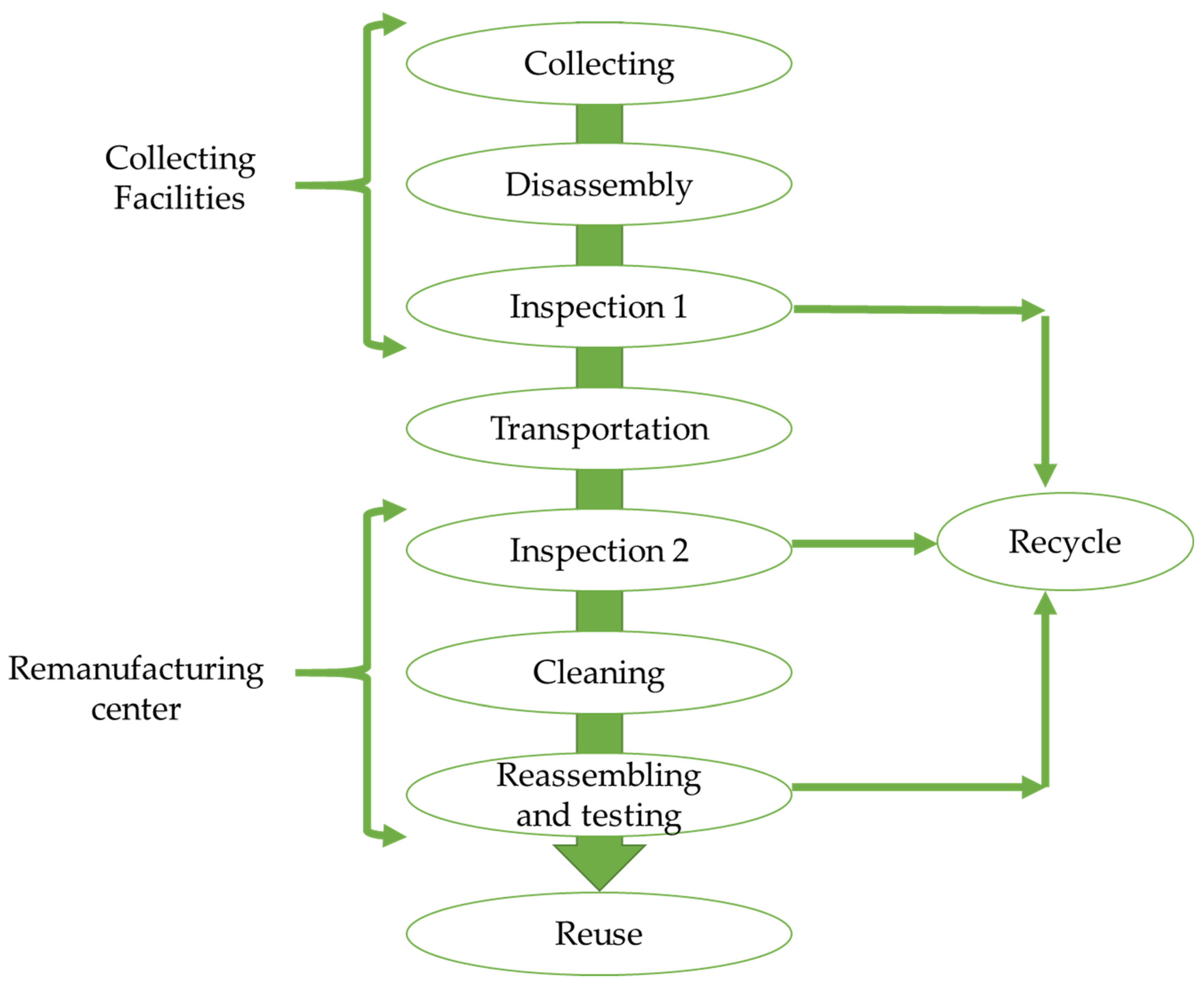
3.2. Current Network
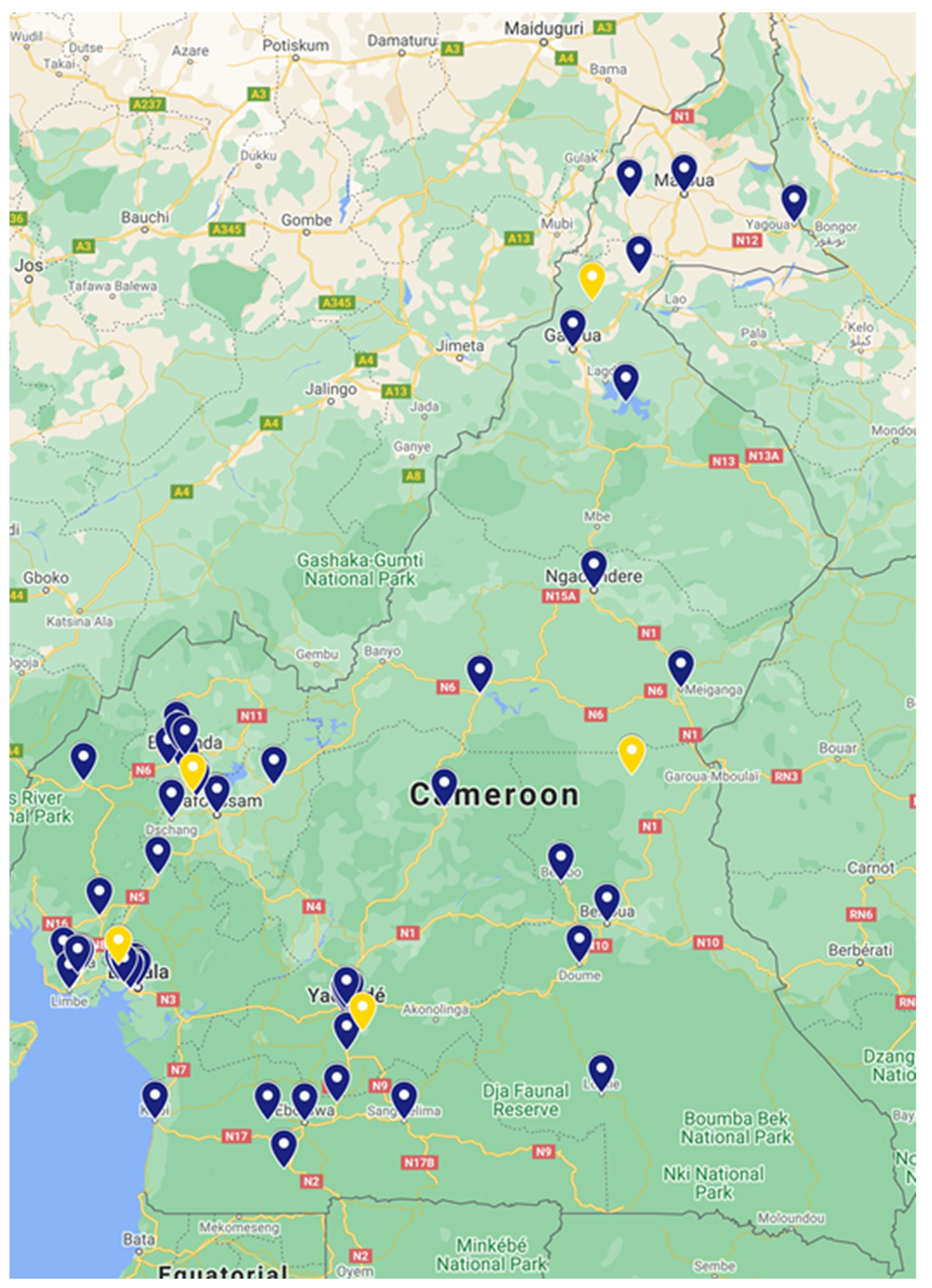
4. Illustrative Case
4.1. Background
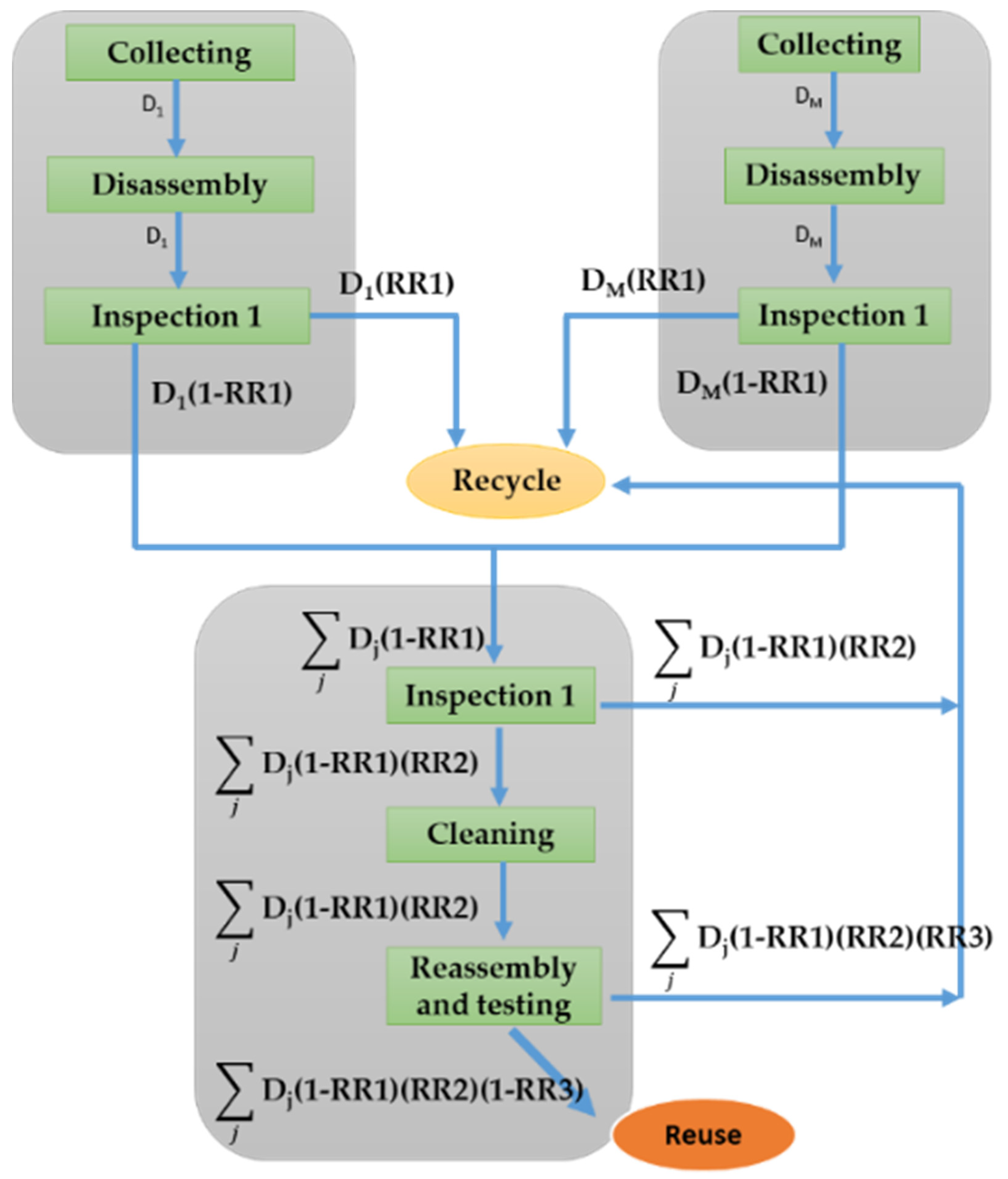
4.2. CFLP Model Reformulation
4.3. Proposed Mathematical Model
5. Results and Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| CFLP | Capacitated-Facility Location Problem |
| TSCFLP | Two-stage Capacitated-Facility Location Problem |
| SLD heuristic | Supervised Learning-driven heuristic |
| AHP | Analytic Heuristic Process |
| EOL | End-of-life |
| MILP | “Mixed-integer linear programming” |
| MINLP | “Mixed-integer non-linear programming” |
| MIQP | “Mixed-integer quadratic programming” |
| ARAS | Additive Ratio Analysis |
| T2NN | “Type-2 neutrosophic number” |
| CODAS | “Combinative distance-based assessment” |
| SWOT | Strength, weakness, opportunity, and threats |
| MIP | Mixed-integer programming |
| IT2F | Interval Type-2 Fuzzy |
| BRKGA | Biased Random-key Genetic Algorithm |
Appendix A
- * OPL 12.8.0.0 Model
- * Author: Raoul Fonkoua Fofou
- * Creation Date: Aug 27, 2021 at 8:22:25 PM
- int rem_facility=...; range RF=1..rem_facility;
- int coll_facility=...; range CF=1..coll_facility;
- int fixcost[RF]=...;
- int capacity[RF]=...;
- int demand[CF]=...;
- int transp_cost[RF][CF]=...;
- dvar float+ Q[RF][CF];
- dvar boolean y[RF];
- forall(j in CF)
- sum(i in RF)Q[i][j]==demand[j];
- forall(i in RF)
- sum(j in CF)Q[i][j]<=capacity[i]*y[i];
- * OPL 12.8.0.0 Model
- * Author: Raoul Fonkoua Fofou
- * Creation Date: Aug 27, 2021 at 8:53:26 PM
- int supp_region=...; range SR=1..supp_region;
- int dem_region=...; range DR=1..dem_region;
- int fixcost[SR]=...;
- int capacity[SR]=...;
- int demand[DR]=...;
- int transp_cost[SR][DR]=...;
- dvar float+ Q[SR][DR];
- dvar boolean y[SR];
- forall(j in DR)
- sum(i in SR)Q[i][j]==demand[j];
- forall(i in SR)
- sum(j in DR)Q[i][j]<=capacity[i]*y[i];
References
- Fofou, R.F.; Jiang, Z.; Wang, Y. A review on the lifecycle strategies enhancing remanufacturing. Appl. Sci. 2021, 11, 5937. [Google Scholar] [CrossRef]
- Ahmed, R.R.; Zhang, X. Multi-stage network-based two-type cost minimization for the reverse logistics management of inert construction waste. Waste Manag. 2021, 120, 805–819. [Google Scholar] [CrossRef] [PubMed]
- Hauschild, M.Z.; Kara, S.; Røpke, I. Absolute sustainability: Challenges to life cycle engineering. CIRP Ann. 2020, 69, 533–553. [Google Scholar] [CrossRef]
- Doni, F.; Corvino, A.; Bianchi Martini, S. Servitization and sustainability actions. Evidence from European manufacturing companies. J. Environ. Manag. 2019, 234, 367–378. [Google Scholar] [CrossRef]
- Ahmadi-Javid, A.; Seyedi, P.; Syam, S.S. A survey of healthcare facility location. Comput. Oper. Res. 2017, 79, 223–263. [Google Scholar] [CrossRef]
- Girma, Y.; Terefe, H.; Pauleit, S.; Kindu, M. Urban green infrastructure planning in Ethiopia: The case of emerging towns of Oromia special zone surrounding Finfinne. J. Urban Manag. 2019, 8, 75–88. [Google Scholar] [CrossRef]
- Romero-Duque, L.P.; Trilleras, J.M.; Castellarini, F.; Quijas, S. Ecosystem services in urban ecological infrastructure of Latin America and the Caribbean: How do they contribute to urban planning? Sci. Total Environ. 2020, 728, 138780. [Google Scholar] [CrossRef]
- Makvandi, M.; Li, B.; Elsadek, M.; Khodabakhshi, Z.; Ahmadi, M. The Interactive Impact of Building Diversity on the Thermal Balance and Micro-Climate Change under the Influence of Rapid Urbanization. Sustainability 2019, 11, 1662. [Google Scholar] [CrossRef] [Green Version]
- Ochola, E.M.; Fakharizadehshirazi, E.; Adimo, A.O.; Mukundi, J.B.; Wesonga, J.M.; Sodoudi, S. Inter-local climate zone differentiation of land surface temperatures for Management of Urban Heat in Nairobi City, Kenya. Urban Clim. 2020, 31, 100540. [Google Scholar] [CrossRef]
- Chen, W.Y. The role of urban green infrastructure in offsetting carbon emissions in 35 major Chinese cities: A nationwide estimate. Cities 2015, 44, 112–120. [Google Scholar] [CrossRef]
- Garcia Martin, P.C.; Schroeder, A.; Ziaee Bigdeli, A. The value architecture of servitization: Expanding the research scope. J. Bus. Res. 2019, 104, 438–449. [Google Scholar] [CrossRef]
- Xing, Y.; Liu, Y.; Tarba, S.; Cooper, S.C.L. Servitization in mergers and acquisitions: Manufacturing firms venturing from emerging markets into advanced economies. Int. J. Prod. Econ. 2017, 192, 9–18. [Google Scholar] [CrossRef] [Green Version]
- Liang, Z.; He, Y.; Wu, T.; Zhang, C. An informative column generation and decomposition method for a production planning and facility location problem. Int. J. Prod. Econ. 2015, 170, 88–96. [Google Scholar] [CrossRef]
- Wu, T.; Shi, Z.; Liang, Z.; Zhang, X.; Zhang, C. Dantzig-Wolfe decomposition for the facility location and production planning problem. Comput. Oper. Res. 2020, 124, 105068. [Google Scholar] [CrossRef]
- Sharkey, T.C.; Geunes, J.; Edwin Romeijn, H.; Shen, Z.J.M. Exact algorithms for integrated facility location and production planning problems. Nav. Res. Logist. 2011, 58, 419–436. [Google Scholar] [CrossRef] [Green Version]
- Romeijn, H.E.; Sharkey, T.C.; Shen, Z.J.M.; Zhang, J. Integrating facility location and production planning decisions. Networks 2010, 55, 78–89. [Google Scholar] [CrossRef] [Green Version]
- Kizilboga, G.; Mandil, G.; Genevois, M.E.; Zwolinski, P. Remanufacturing Network Design Modeling: A Case of Diesel Particulate Filter. Procedia CIRP 2013, 11, 163–168. [Google Scholar] [CrossRef]
- Fernández, E.; Landete, M. Fixed-Charge Facility Location Problems. Locat. Sci. 2015, 47–77. [Google Scholar] [CrossRef]
- Farahani, R.Z.; Hekmatfar, M.; Fahimnia, B.; Kazemzadeh, N. Hierarchical facility location problem: Models, classifications, techniques, and applications. Comput. Ind. Eng. 2014, 68, 104–117. [Google Scholar] [CrossRef]
- Weber, A.; Friedrich, C.J.; Cooke, F.B. Alfred Weber’s Theory of the Location of Industries. Geogr. J. 1930. Available online: https://agris.fao.org/agris-search/search.do?recordID=US201300608114 (accessed on 22 March 2022).
- Farahani, R.Z.; Fallah, S.; Ruiz, R.; Hosseini, S.; Asgari, N. OR models in urban service facility location: A critical review of applications and future developments. Eur. J. Oper. Res. 2019, 276, 1–27. [Google Scholar] [CrossRef]
- Lin, Y.H.; Tian, Q. Branch-and-cut approach based on generalized benders decomposition for facility location with limited choice rule. Eur. J. Oper. Res. 2021, 293, 109–119. [Google Scholar] [CrossRef]
- Silva, A.; Aloise, D.; Coelho, L.C.; Rocha, C. Heuristics for the dynamic facility location problem with modular capacities. Eur. J. Oper. Res. 2021, 290, 435–452. [Google Scholar] [CrossRef]
- Wei, M.; Qi, M.; Wu, T.; Zhang, C. Distance and matching-induced search algorithm for the multi-level lot-sizing problem with substitutable bill of materials. Eur. J. Oper. Res. 2019, 277, 521–541. [Google Scholar] [CrossRef]
- Silwal, S. A concentration inequality for the facility location problem. Oper. Res. Lett. 2022, 50, 213–217. [Google Scholar] [CrossRef]
- Wang, W.; Wu, S.; Wang, S.; Zhen, L.; Qu, X. Emergency facility location problems in logistics: Status and perspectives. Transp. Res. Part E Logist. Transp. Rev. 2021, 154, 102465. [Google Scholar] [CrossRef]
- Wu, T.; Huang, L.; Liang, Z.; Zhang, X.; Zhang, C. A supervised learning-driven heuristic for solving the facility location and production planning problem. Eur. J. Oper. Res. 2021, 301, 785–796. [Google Scholar] [CrossRef]
- Chouksey, A.; Agrawal, A.K.; Tanksale, A.N. A hierarchical capacitated facility location-allocation model for planning maternal healthcare facilities in India. Comput. Ind. Eng. 2022, 167, 107991. [Google Scholar] [CrossRef]
- Han, J.; Zhang, J.; Zeng, B.; Mao, M. Optimizing dynamic facility location-allocation for agricultural machinery maintenance using Benders decomposition. Omega 2021, 105, 102498. [Google Scholar] [CrossRef]
- Zhu, T.; Boyles, S.D.; Unnikrishnan, A. Two-stage robust facility location problem with drones. Transp. Res. Part C Emerg. Technol. 2022, 137, 103563. [Google Scholar] [CrossRef]
- Byrne, T.; Kalcsics, J. Conditional facility location problems with continuous demand and a polygonal barrier. Eur. J. Oper. Res. 2022, 296, 22–43. [Google Scholar] [CrossRef]
- Karagöz, S.; Deveci, M.; Simic, V.; Aydin, N. Interval type-2 Fuzzy ARAS method for recycling facility location problems. Appl. Soft Comput. 2021, 102, 107107. [Google Scholar] [CrossRef]
- Ryu, J.; Park, S. A branch-and-price algorithm for the robust single-source capacitated facility location problem under demand uncertainty. EURO J. Transp. Logist. 2022, 11, 100069. [Google Scholar] [CrossRef]
- Biajoli, F.L.; Chaves, A.A.; Lorena, L.A.N. A biased random-key genetic algorithm for the two-stage capacitated facility location problem. Expert Syst. Appl. 2019, 115, 418–426. [Google Scholar] [CrossRef]
- Gadegaard, S.L.; Klose, A.; Nielsen, L.R. An improved cut-and-solve algorithm for the single-source capacitated facility location problem. EURO J. Comput. Optim. 2018, 6, 1–27. [Google Scholar] [CrossRef] [Green Version]
- Souto, G.; Morais, I.; Mauri, G.R.; Ribeiro, G.M.; González, P.H. A hybrid matheuristic for the Two-Stage Capacitated Facility Location problem. Expert Syst. Appl. 2021, 185, 115501. [Google Scholar] [CrossRef]
- Liu, W.; Kong, N.; Wang, M.; Zhang, L. Sustainable multi-commodity capacitated facility location problem with complementarity demand functions. Transp. Res. Part E Logist. Transp. Rev. 2021, 145, 102165. [Google Scholar] [CrossRef]
- Saif, A.; Delage, E. Data-driven distributionally robust capacitated facility location problem. Eur. J. Oper. Res. 2021, 291, 995–1007. [Google Scholar] [CrossRef]
- Chandra, S.; Sarkhel, M.; Vatsa, A.K. Capacitated facility location–allocation problem for wastewater treatment in an industrial cluster. Comput. Oper. Res. 2021, 132, 105338. [Google Scholar] [CrossRef]
- Lu, Z.; Bostel, N. A facility location model for logistics systems including reverse flows: The case of remanufacturing activities. Comput. Oper. Res. 2007, 34, 299–323. [Google Scholar] [CrossRef]
- Abdulrahman, M.D.A.; Subramanian, N.; Liu, C.; Shu, C. Viability of remanufacturing practice: A strategic decision making framework for Chinese auto-parts companies. J. Clean. Prod. 2015, 105, 311–323. [Google Scholar] [CrossRef]
- D’Adamo, I.; Rosa, P. Remanufacturing in industry: Advices from the field. Int. J. Adv. Manuf. Technol. 2016, 86, 2575–2584. [Google Scholar] [CrossRef]
- Deveci, M.; Simic, V.; Torkayesh, A.E. Remanufacturing facility location for automotive Lithium-ion batteries: An integrated neutrosophic decision-making model. J. Clean. Prod. 2021, 317, 128438. [Google Scholar] [CrossRef]
- Du, Y.; Zheng, Y.; Wu, G.; Tang, Y. Decision-making method of heavy-duty machine tool remanufacturing based on AHP-entropy weight and extension theory. J. Clean. Prod. 2020, 252, 119607. [Google Scholar] [CrossRef]
- Duberg, J.V.; Johansson, G.; Sundin, E.; Tang, O. Economic evaluation of potential locations for remanufacturing in an extended supply chain—A case study on robotic lawn mowers. Procedia CIRP 2020, 90, 14–18. [Google Scholar] [CrossRef]
- Wu, L.Y.; Zhang, X.S.; Zhang, J.L. Capacitated facility location problem with general setup cost. Comput. Oper. Res. 2006, 33, 1226–1241. [Google Scholar] [CrossRef]
- GlobalPetrolPrices.com. Diesel Prices Around the World, 22 June 2015. 2015. Available online: http://www.globalpetrolprices.com/diesel_prices/ (accessed on 11 October 2021).
- ILOG CPLEX Optimization Studio | IBM. Available online: https://www.ibm.com/products/ilog-cplex-optimization-studio (accessed on 12 November 2022).
- Jiang, Z.; Ding, Z.; Liu, Y.; Wang, Y.; Hu, X.; Yang, Y. A data-driven based decomposition–integration method for remanufacturing cost prediction of end-of-life products. Robot. Comput. Integr. Manuf. 2020, 61, 101838. [Google Scholar] [CrossRef]

| References | Decision Variables and Objectives | Properties | Case Study | Approach | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Plant Opening | Production | Transportation | Inventory | Multi-Plant | Multi-Customer | Multi-Products | Multi-Period | Capacity | |||
| [39] | √ | √ | √ | √ | √ | √ | MINLP | ||||
| [43] | √ | √ | √ | √ | √ | T2NN, CODAS | |||||
| [37] | √ | √ | √ | √ | √ | MIQP | |||||
| [33] | √ | Robust Optimization | |||||||||
| [30] | √ | √ | √ | √ | √ | √ | √ | Robust Optimization | |||
| [34] | √ | √ | √ | √ | √ | TSCFLP, BRKGA | |||||
| [35] | √ | √ | Cut-and-solve algorithm | ||||||||
| [36] | √ | √ | √ | √ | √ | TSCFLP | |||||
| [27] | √ | √ | SLD heuristic | ||||||||
| [28] | √ | √ | √ | √ | √ | √ | √ | MILP | |||
| [29] | √ | √ | √ | √ | √ | √ | √ | MIP | |||
| [31] | √ | √ | √ | √ | Voronoi diagrams | ||||||
| [32] | √ | √ | √ | √ | √ | IT2F ARAS | |||||
| [44] | √ | √ | √ | √ | √ | AHP-entropy weight | |||||
| [41] | √ | √ | √ | AHP, strategic decision-making | |||||||
| [42] | √ | √ | √ | SWOT analysis, AHP | |||||||
| [45] | √ | √ | √ | √ | √ | √ | Economic Evaluation | ||||
| Variable | Definition |
|---|---|
| R C | The set of new remanufacturing facilities, denoted by m = {1, …, i} The set of collecting facilities, denoted by n = {1, …, j} |
| Xmn | The section of collecting facility n’s demand met by remanufacturing facility m |
| K | The set of capacities of remanufacturing centers, denoted by k = {1, …, k} |
| smk | kth capacity of remanufacturing center m |
| ymk | Binary variable assumed as 1 if the facility is opened at location m, otherwise 0 |
| fmk | Cost of opening new remanufacturing center m depending on the change in capacity k |
| Dmn | Distance between collecting facility n and remanufacturing facility m |
| Dn | Demand at collection facility n |
| UIC | Unit testing and inspection cost |
| UTC | Transportation cost of one remanufactured tractor per mile |
| UTCmn | Unit transportation cost between collecting facility n and remanufacturing facility m |
| URC | Remanufacturing cost for a single product |
| Cmn(Dn) | General transportation cost |
| RR1 | First inspection return rate |
| RR2 | Second inspection return rate |
| RR3 | Third inspection return rate |
| WT | LT | CE | NW | SW | NT | FN | AD | ST | ET |
|---|---|---|---|---|---|---|---|---|---|
| West Region. | Littoral region | Center Region | Northwest Region | Southwest region | North Region | Far North Region | Adamawa Region | South Region | East Region |
| Regions | WT | LT | CE | NW | SW | NT | FN | AD | ST | ET |
|---|---|---|---|---|---|---|---|---|---|---|
| WT | 50 | 125 | 140 | 110 | 120 | 340 | 410 | 175 | 190 | 250 |
| LT | 125 | 50 | 135 | 195 | 50 | 390 | 500 | 240 | 140 | 260 |
| CE | 140 | 130 | 80 | 199 | 190 | 210 | 430 | 200 | 150 | 140 |
| NW | 110 | 195 | 199 | 60 | 140 | 405 | 460 | 225 | 240 | 310 |
| SW | 120 | 50 | 190 | 140 | 50 | 450 | 510 | 270 | 200 | 330 |
| NT | 340 | 390 | 210 | 405 | 450 | 70 | 210 | 150 | 320 | 290 |
| FN | 410 | 500 | 430 | 460 | 510 | 210 | 60 | 220 | 620 | 580 |
| AD | 175 | 240 | 200 | 225 | 270 | 150 | 220 | 80 | 220 | 100 |
| ST | 190 | 140 | 150 | 240 | 200 | 320 | 620 | 220 | 80 | 140 |
| ET | 250 | 260 | 140 | 310 | 330 | 290 | 580 | 100 | 140 | 90 |
| Case Number | Capacity | Total Budget (CNY) | Opening Budget (CNY) | Transportation (CNY) | Number of Facilities |
|---|---|---|---|---|---|
| 1 | 250 | 6,583,564,250 | 1,333,300,000 | 264,250 | 60 |
| 2 | 500 | 5,912,153,000 | 661,677,750 | 475,250 | 30 |
| 3 | 750 | 5,692,277,895 | 441,677,750 | 600,145 | 20 |
| 4 | 1000 | 5,582,290,100 | 331,644,750 | 645,350 | 15 |
| 5 | 1250 | 5,516,251,250 | 265,471,000 | 780,250 | 12 |
| 6 | 1500 | 5,472,485,500 | 221,677,750 | 807,750 | 10 |
| 7 | 1750 | 5,450,378,250 | 199,452,250 | 926,000 | 9 |
| 8 | 2000 | 5,428,664,520 | 177,541,000 | 1,123,520 | 8 |
| 9 | 2500 | 5,385,171,000 | 133,610,500 | 1,560,500 | 6 |
| 10 | 3000 | 5,363,190,500 | 111,850,500 | 1,340,000 | 5 |
| 11 | 3500 | 5,363,217,000 | 111,566,000 | 1,591,000 | 5 |
| 12 | 4000 | 5,365,215,000 | 94,250,520 | 2,247,000 | 4 |
| 13 | 4500 | 5,389,637,550 | 91,550,500 | 2,395,650 | 4 |
| 14 | 5000 | 5,432,201,360 | 76,684,360 | 3,121,000 | 3 |
| 15 | 6000 | 5,469,365,250 | 71,986,750 | 3,365,500 | 3 |
| 16 | 7000 | 5,498,751,000 | 57,648,500 | 3,525,500 | 3 |
| 17 | 8000 | 5,532,213,250 | 49,448,400 | 4,095,850 | 2 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fofou, R.F.; Jiang, Z.; Gong, Q.; Yang, Y. A Decision-Making Model for Remanufacturing Facility Location in Underdeveloped Countries: A Capacitated Facility Location Problem Approach. Sustainability 2022, 14, 15204. https://doi.org/10.3390/su142215204
Fofou RF, Jiang Z, Gong Q, Yang Y. A Decision-Making Model for Remanufacturing Facility Location in Underdeveloped Countries: A Capacitated Facility Location Problem Approach. Sustainability. 2022; 14(22):15204. https://doi.org/10.3390/su142215204
Chicago/Turabian StyleFofou, Raoul Fonkoua, Zhigang Jiang, Qingshan Gong, and Yihua Yang. 2022. "A Decision-Making Model for Remanufacturing Facility Location in Underdeveloped Countries: A Capacitated Facility Location Problem Approach" Sustainability 14, no. 22: 15204. https://doi.org/10.3390/su142215204
APA StyleFofou, R. F., Jiang, Z., Gong, Q., & Yang, Y. (2022). A Decision-Making Model for Remanufacturing Facility Location in Underdeveloped Countries: A Capacitated Facility Location Problem Approach. Sustainability, 14(22), 15204. https://doi.org/10.3390/su142215204








