Exploring the Continuous Motivation of Algorithm Engineers under Multiple Objectives: A Mixed-Methods Study
Abstract
1. Introduction
2. Theoretical Background
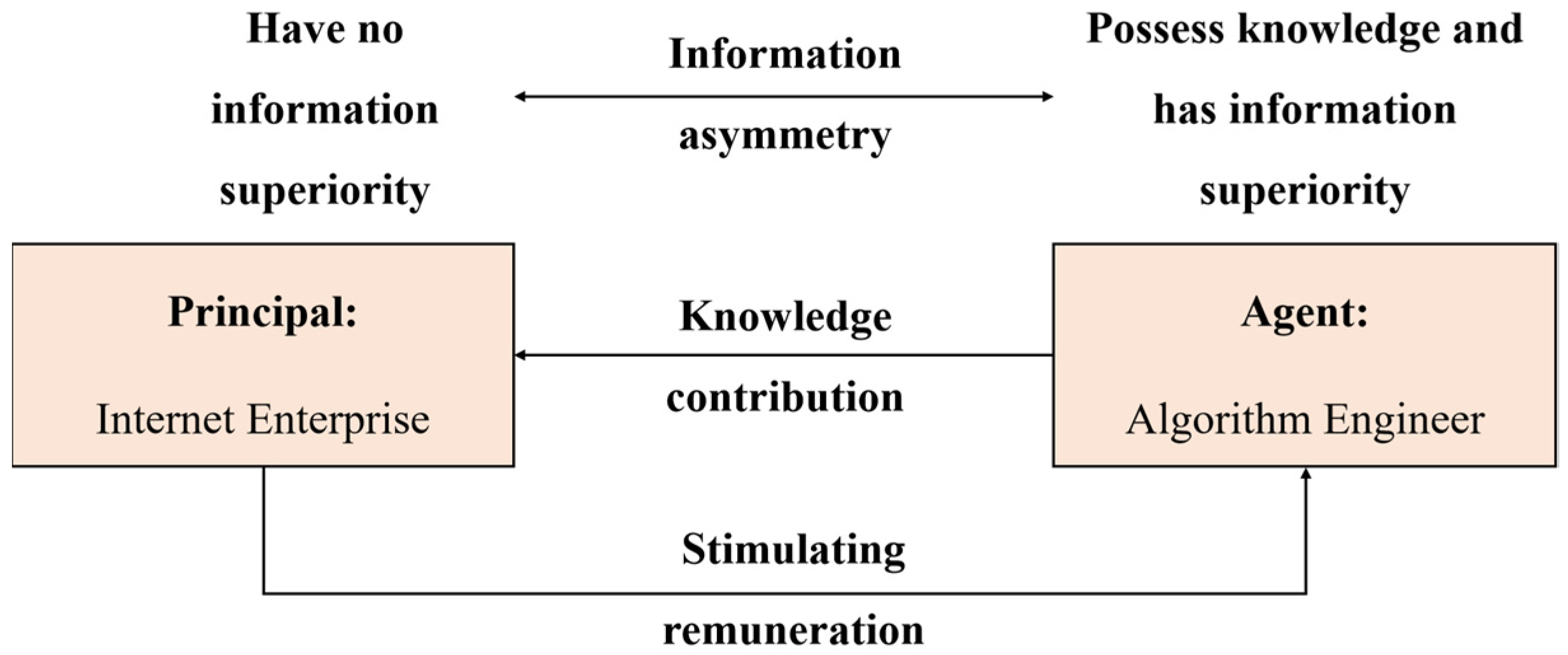
2.1. Multi-Task Principal–Agent Theory
2.2. Performance Management Systems and Sustainable Development
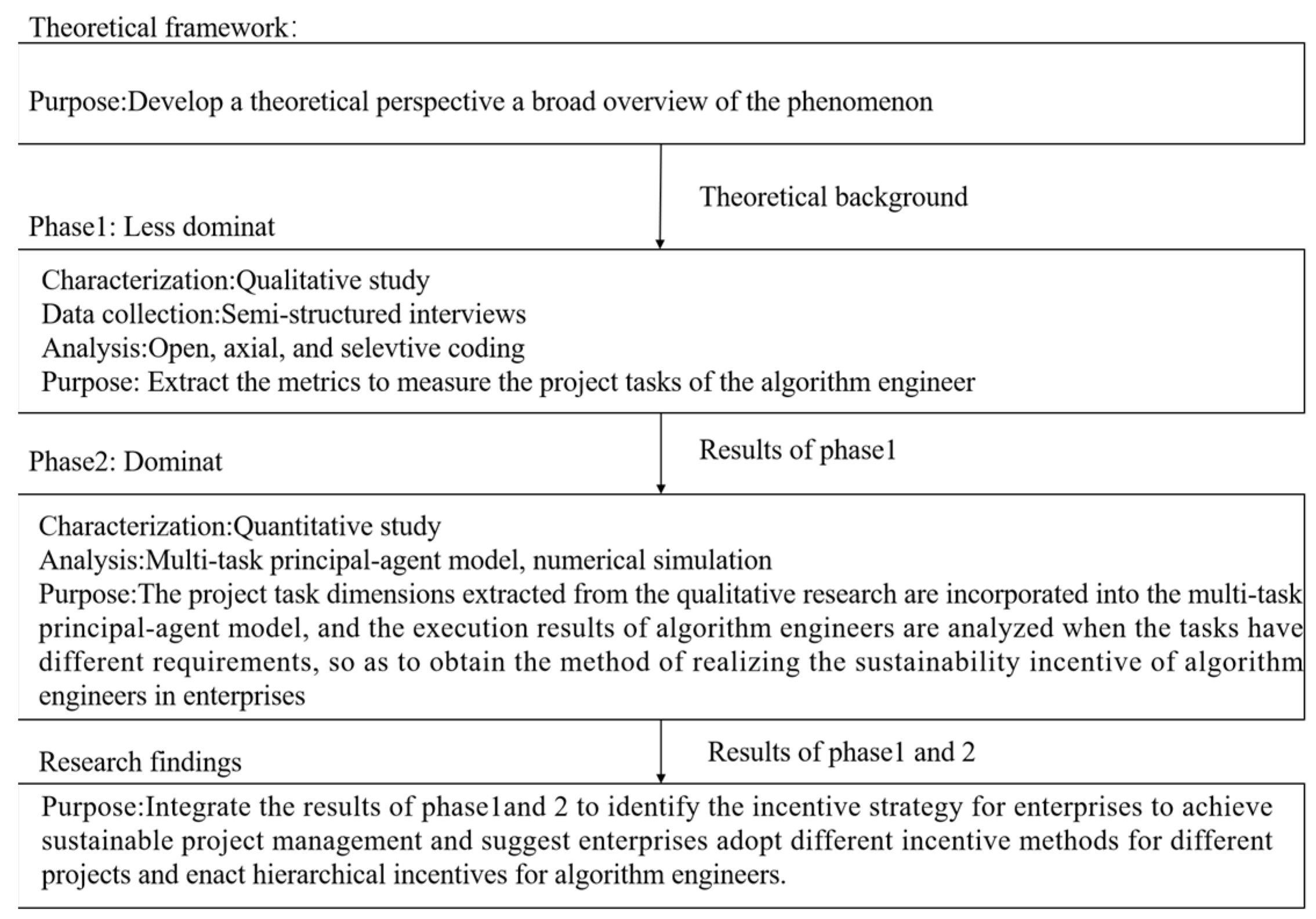
3. Mixed-Methods Design
Qualitative Analysis and Findings
4. Results
4.1. Qualitative Data Analysis
4.2. Problem Description and Model Assumptions
5. Model Construction
6. Model Analysis and Insights
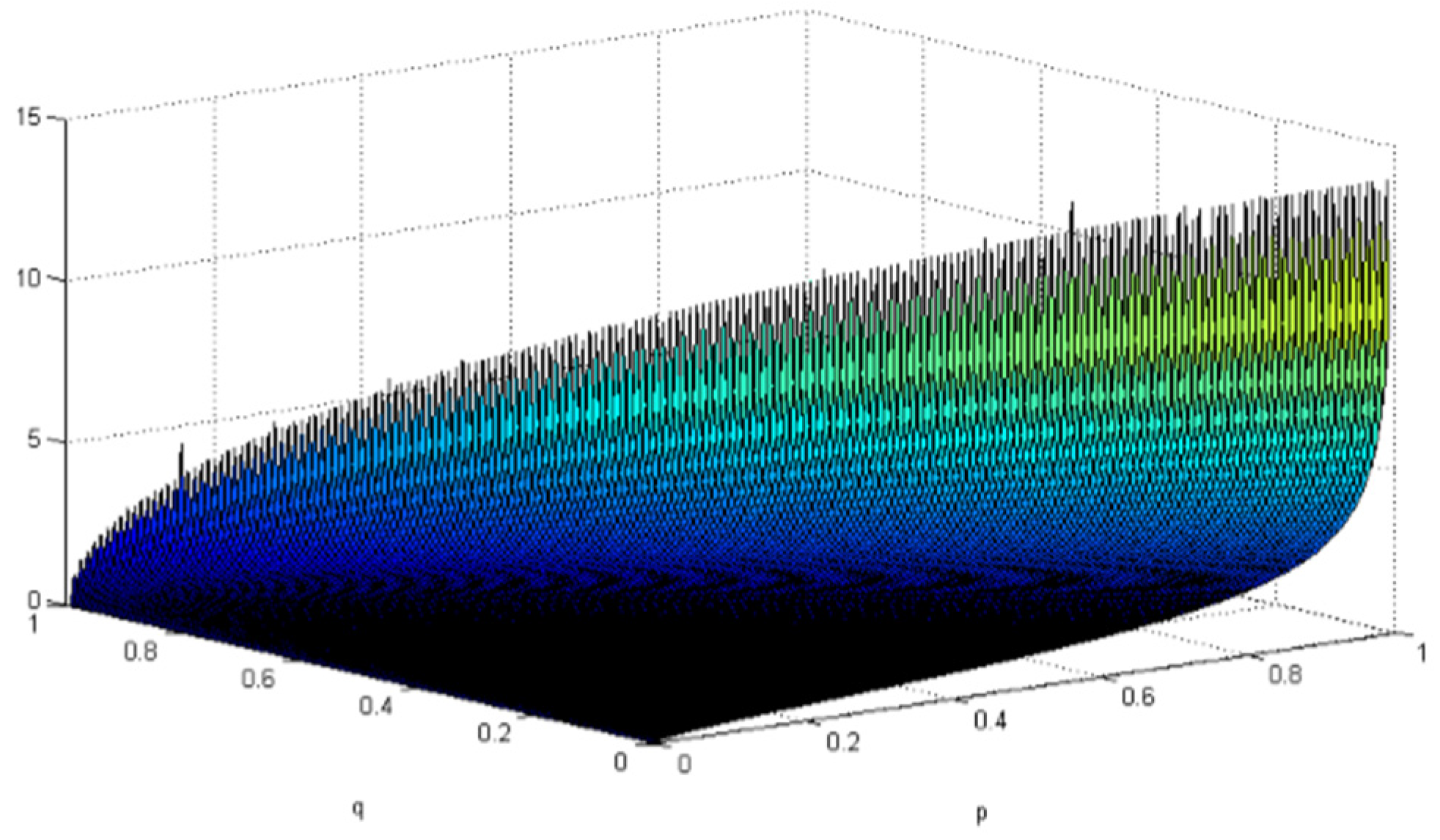
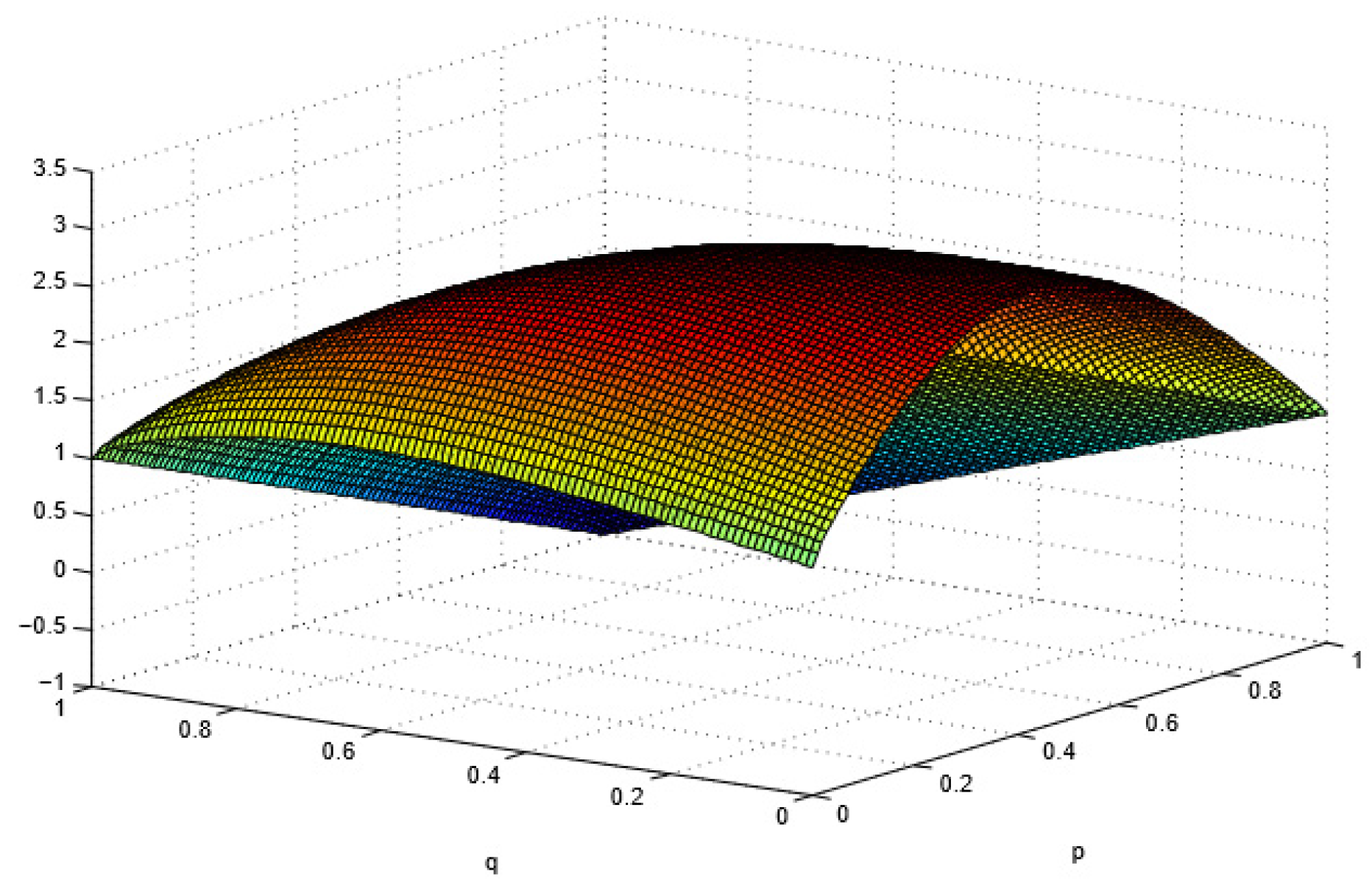
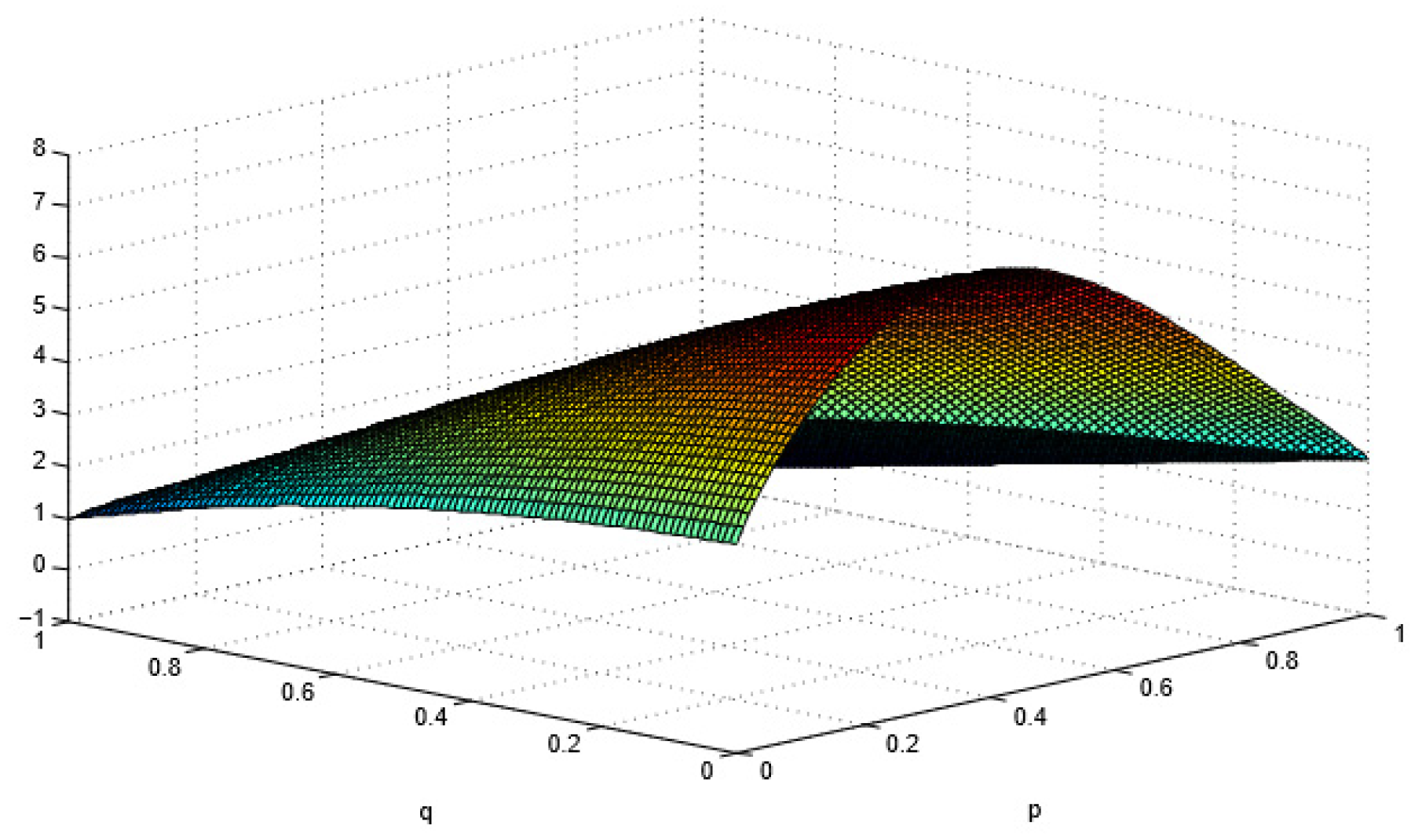
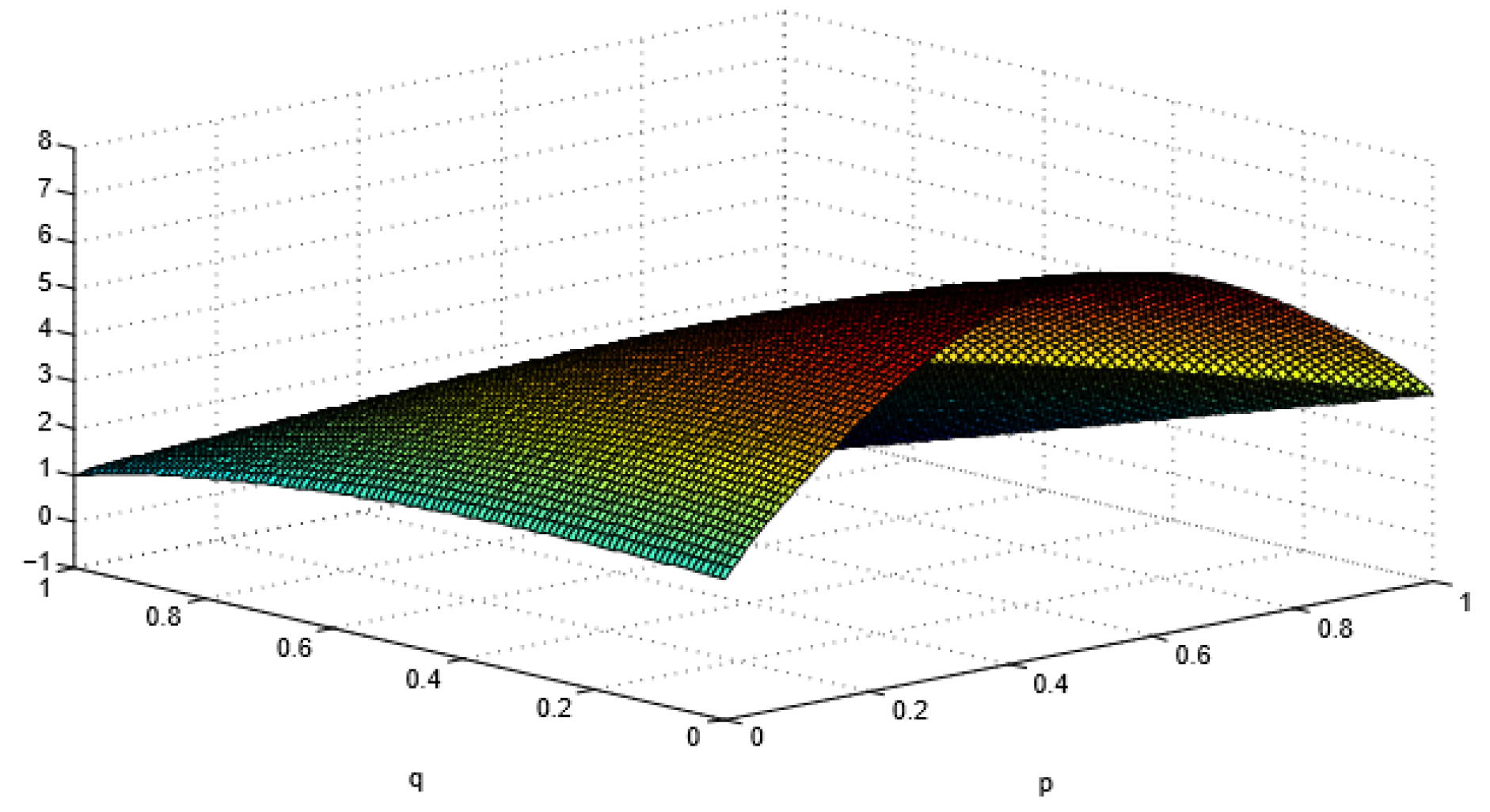
6.1. LOE Analysis of Algorithm Engineers with Different Ways of Working
6.2. Analysis of the Optimal Incentive Coefficient
7. Conclusions
7.1. Theoretical Contribution
7.2. Practical Implications
7.3. Limitations
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Holmstrom, B.; Milgrom, P. Multitask principal-agent analyses: Incentive contracts, asset ownership, and job design. J. Law Econ. Organ. 1991, 7, 24–52. [Google Scholar] [CrossRef]
- Baker, G.; Gibbons, R.; Murphy, K.J. Subjective performance measures in optimal incentive contracts. Q. J. Econ. 1994, 109, 1125–1156. [Google Scholar] [CrossRef]
- Schnedler, W. Task Difficulty, Performance Measure Characteristics, and the Trade-Off between Insurance and Well-Allocated Effort; AWI Discussion Paper Series; Discussion Paper Series No. 425; Alfred-Weber-Institut für Wirtschaftswissenschaften, Universität Heidelberg: Heidelberg, Germany, 2006; Available online: http://hdl.handle.net/10419/127245 (accessed on 17 May 2006).
- Edmans, A.; Gabaix, X.; Sadzik, T.; Sannikov, Y. Dynamic Incentive Accounts. National Bureau of Economic Research Working Papers No. 15324. 2009. Available online: https://econpapers.repec.org/paper/nbrnberwo/15324.htm (accessed on 1 September 2009).
- Banker, R.D.; Thevaranjan, A. Goal Congruence and Evaluation of Performance Measures; School of Management, University of Texas at Dallas: Dallas, TX, USA, 2000; Unpublished Manuscript. [Google Scholar]
- Datar, S.; Kulp, S.C.; Lambert, A. Balancing performance measures. J. Account. Res. 2001, 39, 75–92. [Google Scholar] [CrossRef]
- Gibbons, R.; Waldman, M. A theory of wage and promotion dynamics inside firms. J. Labor Econ. 2006, 24, 59–107. [Google Scholar] [CrossRef]
- Baker, G.P. Incentive contracts and performance measurement. J. Political Econ. 1992, 100, 598–614. [Google Scholar] [CrossRef]
- Le, C.Y. A multi-task principal agent model for knowledge contribution of enterprise staff. Interdiscip. J. Inf. Knowl. Manag. 2016, 11, 261–271. [Google Scholar] [CrossRef][Green Version]
- Xin, Y.; Liu, D.; Li, X. Modeling of Multitask Principal-Agent Based on Accounts Receivable. Math. Probl. Eng. 2022, 2022, 506150. [Google Scholar] [CrossRef]
- Buchen, C.; Kragl, J.; Palermo, A. Specialist vs. generalist: Efficiency in multitasking. Econ. Lett. 2021, 199, 109699. [Google Scholar] [CrossRef]
- DeVaro, J.; Gürtler, O. Strategic shirking in competitive labor markets: A general model of multi-task promotion tournaments with employer learning. J. Econ. Manag. Strategy 2020, 29, 335–376. [Google Scholar] [CrossRef]
- Cresti, E. Sustainability management control systems: Towards a socially responsible planning and control framework. In Proceedings of the Oxford Business and Economics Conference Program, Oxford, UK, 24–26 June 2009. [Google Scholar]
- Epstein, M.J.; Wisner, P.S. Actions and measures to improve sustainability. In The Accountable Corporation; Epstein, M.J., Hanson, K.O., Eds.; Praeger Publishers: Westport, CT, USA, 2006; Volume 3, pp. 207–234. [Google Scholar]
- Rouse, P.; Putterill, M. An integral framework for performance measurement. Manag. Decis. 2003, 41, 791–805. [Google Scholar] [CrossRef]
- Zampou, E.; Karagiannaki, A.; Plitsos, S. Sustainability performance measurement in manufacturing: Integrating environmental and operational aspects. In Proceedings of the 17th EMAN Conference, Rotterdam, The Netherlands, 27–28 March 2014. [Google Scholar]
- Adams, C.A.; McNicholas, P. Making a difference: Sustainability reporting, accountability and organizational change. Account. Audit. Account. J. 2007, 20, 382–402. [Google Scholar] [CrossRef]
- Songini, L.; Pistoni, A. Accounting, auditing and control for sustainability. Manag. Account. Res. 2012, 23, 202–204. [Google Scholar] [CrossRef]
- Durden, C. Towards a socially responsible management control system. Account. Audit. Account. J. 2008, 21, 671–694. [Google Scholar] [CrossRef]
- Herzig, C.; Viere, T.; Schaltegger, S.; Burritt, R. Environmental Management Accounting: Case Studies in South-East Asian Companies, 1st ed.; Routledge: Oxford, UK; New York, NY, USA, 2012. [Google Scholar]
- Schaltegger, S. Sustainability as a driver for corporate economic success. Consequences for the development of sustainability management control. Soc. Econ. 2011, 33, 15–28. [Google Scholar]
- Venkatesh, V.; Brown, S.A.; Sullivan, Y.W. Guidelines for conducting mixed–methods research: An extension and illustration. J. Assoc. Inform. Sys. 2016, 17, 435–495. [Google Scholar] [CrossRef]
- Hannah, D.P.; Tidhar, R.; Eisenhardt, K.M. Analytic models in strategy, organizations, and management research: A guide for consumers. Strat. Manag. J. 2021, 42, 329–360. [Google Scholar] [CrossRef]
- Venkatesh, V.; Brown, S.A.; Bala, H. Bridging the qualitative–quantitative divide: Guidelines for conducting mixed methods research in information systems. MIS Q. 2013, 37, 21–54. [Google Scholar] [CrossRef]
- Wu, J.; Zheng, Z.; Zhao, J.L. FairPlay: Detecting and deterring online customer misbehavior. Inform. Sys. Res. 2021, 32, 1323–1346. [Google Scholar] [CrossRef]
- Zhang, N.; Wei, X.; Zhang, Z. Game theory analysis on credit risk assessment in e-commerce. Inform. Process. Manag. 2022, 59, 102763. [Google Scholar]
- Miles, M.; Huberman, A. Qualitative Data Analysis: An Expanded Sourcebook; SAGE Publications: Thousand Oaks, CA, USA, 1994. [Google Scholar]

| Objects | Executives | Project Managers | Algorithm Engineers |
|---|---|---|---|
| Job Titles | Chief Executive Officer (CEO), Executive Assistant, Vice President | Project managers (A1–A8) | Algorithm engineers (Virtual online project development) (B1–B4) Algorithm engineers (Game Project Development) (B5–B14) |
| No. of interviewees | 3 s | 8 | 14 |
| Recording Time | 135 min | 270 min | 487 min |
| Category | Construct | Selected Quote |
|---|---|---|
| Project Completion Time | Project Completion Requirements | ‘Each project has a defined completion cycle, which is determined during project planning’. (I7) |
| Perceived Urgency | ‘There is uncertainty in the project development process, and every time we think about the completion time, it makes us nervous’. (I12) | |
| Project Difficulty | Difficulty of Project Planning | ‘The first step of the project is to make a complete plan, which needs to be negotiated by the team’. (I9) |
| Difficulty of Project Implementation | ‘The implementation process often deviates from the planning, which requires constant adjustment of the program and solution of project problems’. (I2) | |
| Project Quality | Quality of Algorithmic Code | ‘The same project may have different algorithmic solutions where the length and efficiency of the program are important’. (I9) |
| Quality of Algorithmic Application | ‘Another important criterion of the project is the efficiency of the algorithm and the frequency of errors. We want the algorithm to run well and fast’. (I1) |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, F.; Wu, X.; Zhang, S. Exploring the Continuous Motivation of Algorithm Engineers under Multiple Objectives: A Mixed-Methods Study. Sustainability 2022, 14, 15371. https://doi.org/10.3390/su142215371
Zhang F, Wu X, Zhang S. Exploring the Continuous Motivation of Algorithm Engineers under Multiple Objectives: A Mixed-Methods Study. Sustainability. 2022; 14(22):15371. https://doi.org/10.3390/su142215371
Chicago/Turabian StyleZhang, Fangqing, Xiaolong Wu, and Shujun Zhang. 2022. "Exploring the Continuous Motivation of Algorithm Engineers under Multiple Objectives: A Mixed-Methods Study" Sustainability 14, no. 22: 15371. https://doi.org/10.3390/su142215371
APA StyleZhang, F., Wu, X., & Zhang, S. (2022). Exploring the Continuous Motivation of Algorithm Engineers under Multiple Objectives: A Mixed-Methods Study. Sustainability, 14(22), 15371. https://doi.org/10.3390/su142215371






