Machine Learning Prediction Model for Shear Capacity of FRP-RC Slender and Deep Beams
Abstract
:1. Introduction
2. Existing Shear Strength Models
2.1. Shear Model by ACI 440-15
2.2. Shear Model by ACI 440-22
2.3. Shear Model by Canadian Standard Code CAN/CSA S806 (2012)
2.4. Shear Model by JSCE-97
2.5. Shear Model by Nehdi et al. (2007)
2.6. Shear Model by Hoult et al. (2008)
2.7. Shear Model by Kara (2011)
2.8. Shear Model by Mari et al. (2013)
2.9. Shear Model by Bažant and Yu (2005)
2.10. Shear Model by ACI 318-19
2.11. Shear Model by Kaszubska et al. (2018)
2.12. Shear Model by Ebid and Deifalla (2021)
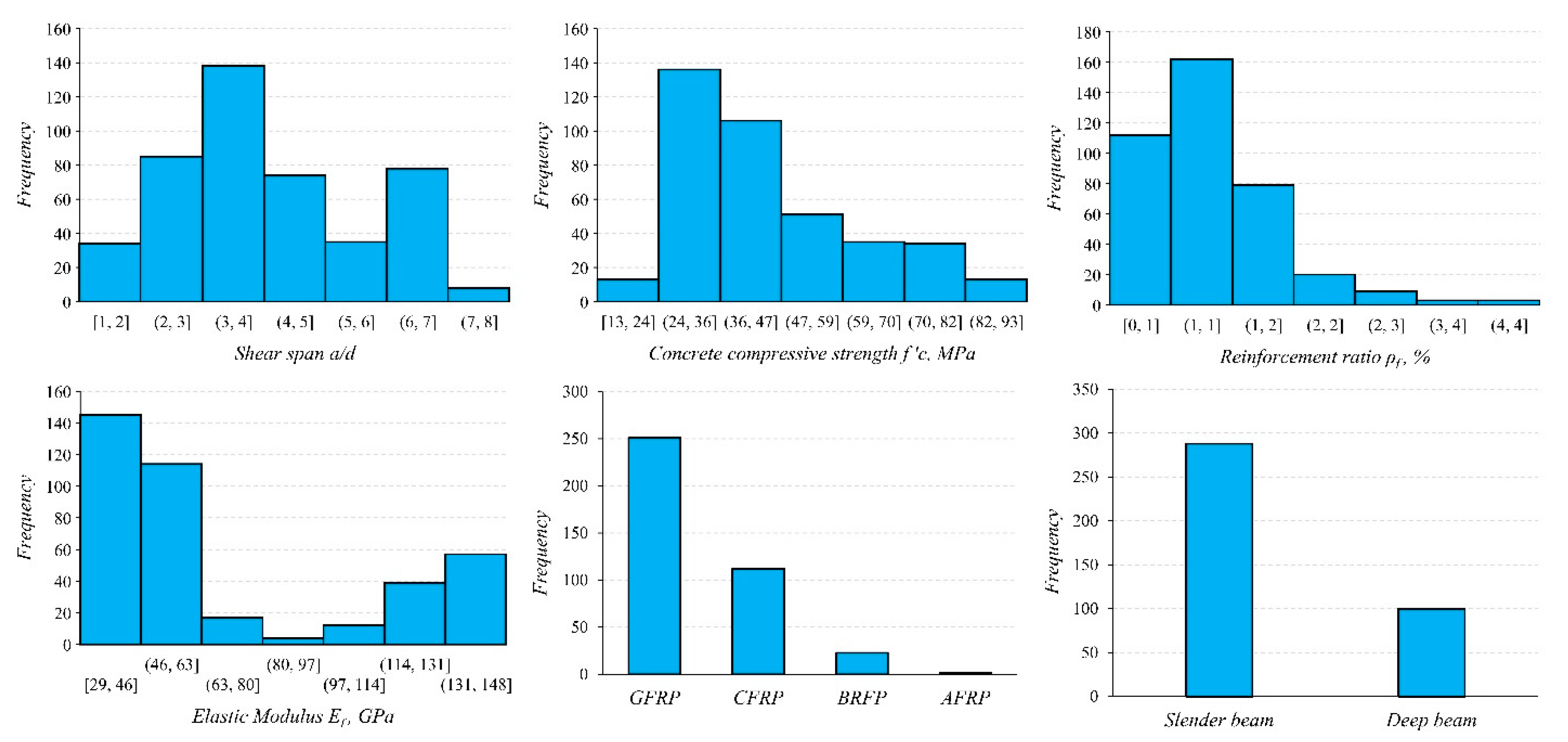
3. Surveyed Database
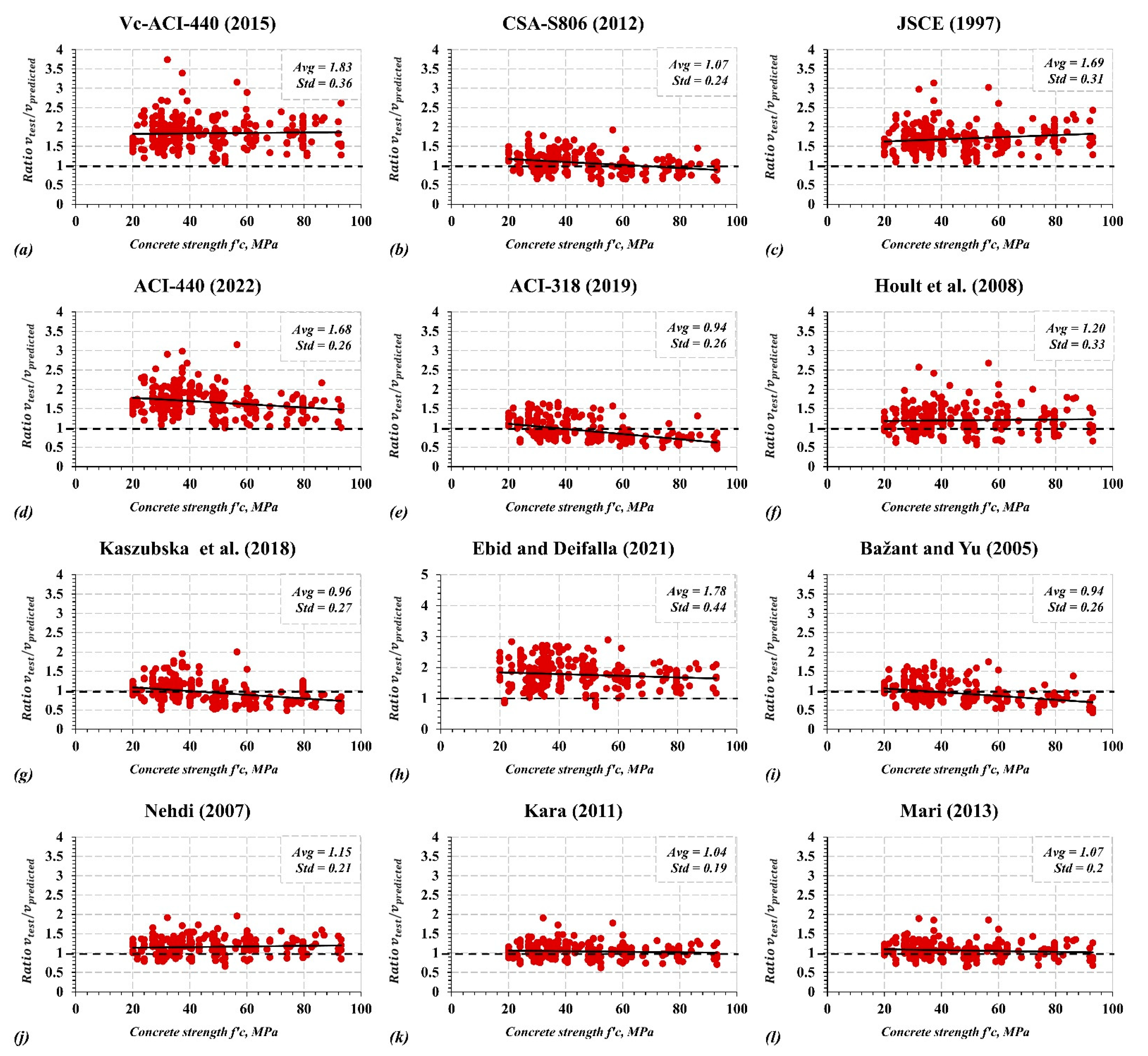
4. Performance of Shear Strength Models
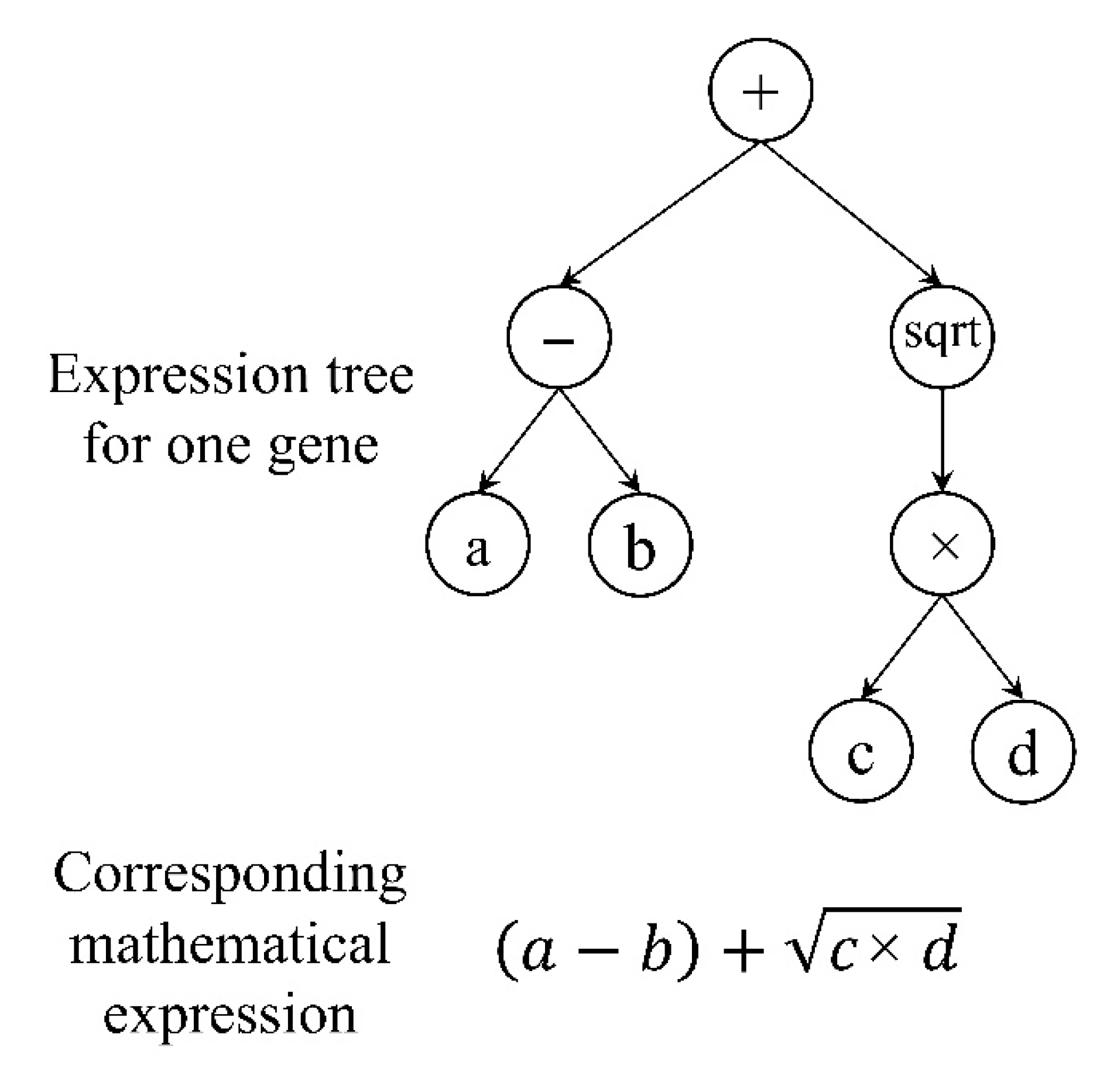
5. Gene Expression Programming (GEP)
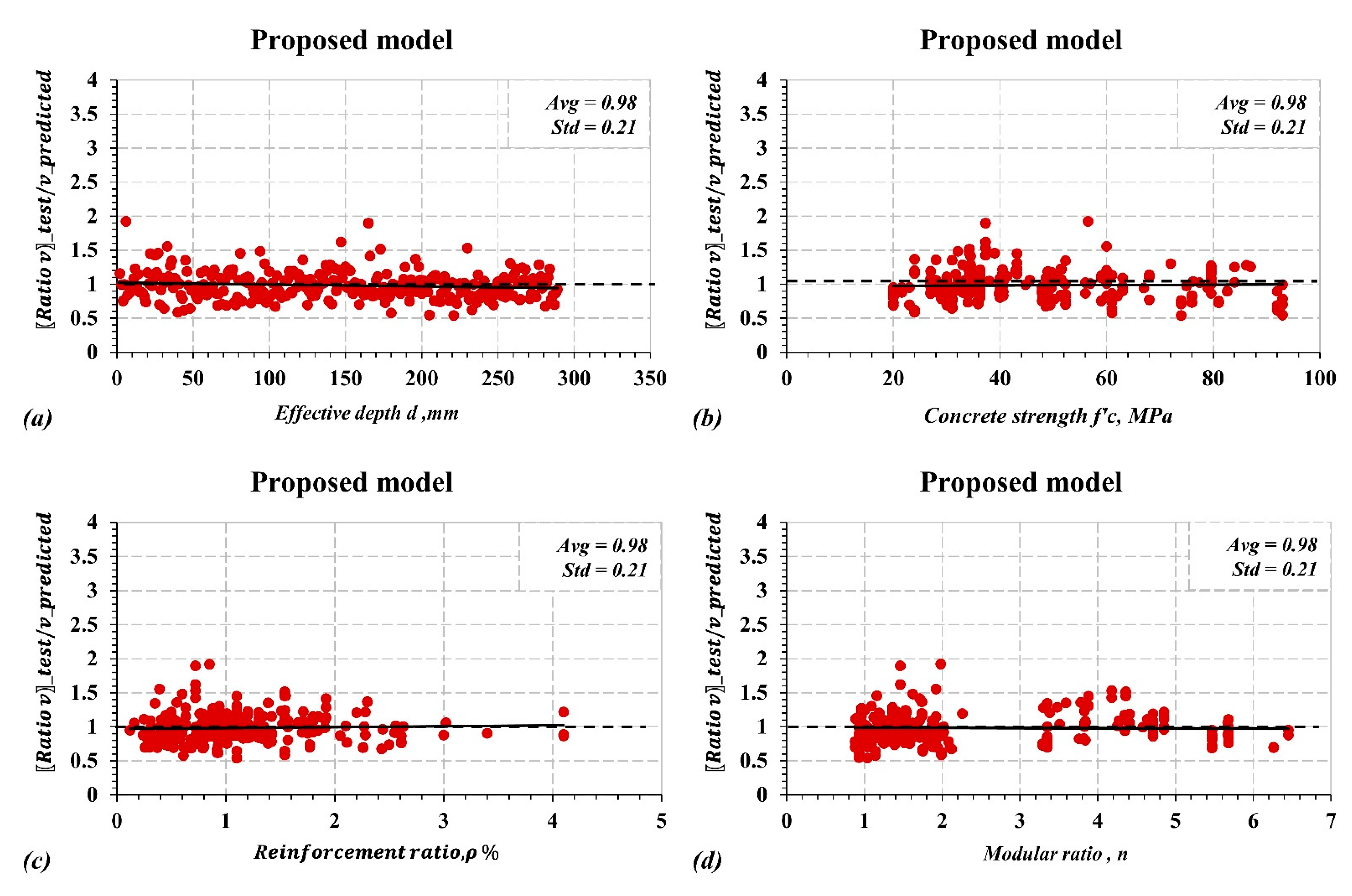
6. Proposed Model
7. Conclusions
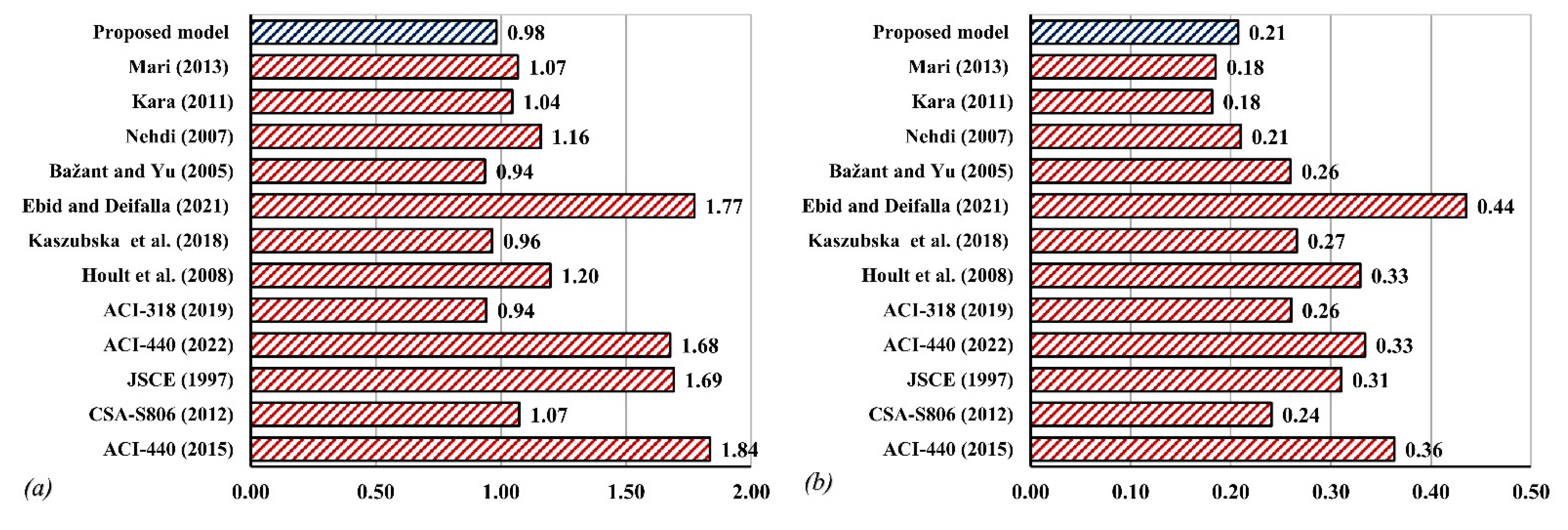
- For slender beams (a/d < 2.5), the ACI 318-19, Bažant and Yu, Kara, and Mari et al. models demonstrate less scatteredness compared to other models. Interestingly, the ACI 318 model resulted in high accuracy with an average Vc test/Vc predicted = 0.92 and a standard deviation of 0.24, although it was developed for steel-RC beams. In contrast, the Ebid and Deifalla, and ACI 440 (2015) models provided the highest scatteredness and standard deviation.
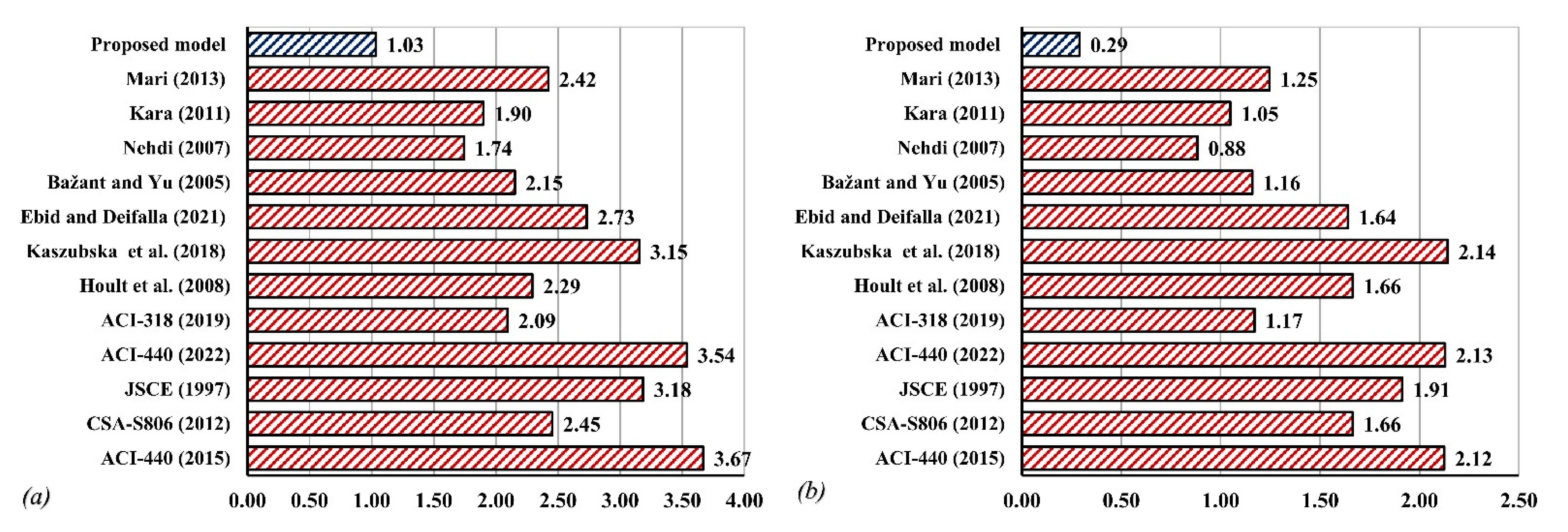
- Including the size effect in the ACI 440-22 (public draft) has notably improved the prediction by reducing model error (Vc test/Vc predicted) and the standard deviation from 1.82 to 1.66 and from 0.37 to 0.34, respectively, highlighting the importance of including this effect.
- Gene expression programming (GEP) has been utilized along with the compiled database to develop shear models for slender and deep beams. The proposed model yielded a superior accuracy over other models with an average Vc test/Vc predicted = 0.98 and a standard deviation of 0.21 for slender beams. For deep beams, the proposed model resulted in an average Vc test/Vc predicted = 1.03 and a standard deviation of 0.29. The proposed models are a function of concrete compressive strength, reinforcement ratio, effective depth, modular ratio, and shear span-to-depth ratio. In addition to the accuracy of the GEP models, the proposed models are much simpler than some of the design models, such as the JSCE and CSA S806 models.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Tarawneh, A.; Almasabha, G.; Murad, Y. ColumnsNet: Neural Network Model for Constructing Interaction Diagrams and Slenderness Limit for FRP-RC Columns. J. Struct. Eng. 2022, 148, 04022089. [Google Scholar] [CrossRef]
- Almasabha, G.; Tarawneh, A.; Saleh, E.; Alajarmeh, O. Data-Driven Flexural Stiffness Model of FRP-Reinforced Concrete Slender Columns. J. Compos. Constr. 2022, 26, 04022024. [Google Scholar] [CrossRef]
- Guadagnini, M.; Pilakoutas, K.; Waldron, P. Shear resistance of FRP RC beams: Experimental study. J. Compos. Constr. 2006, 10, 464–473. [Google Scholar] [CrossRef]
- Alam, M.S.; Sultana, N.; Hossain, S.Z. Bayesian optimization algorithm based support vector regression analysis for estimation of shear capacity of FRP reinforced concrete members. Appl. Soft Comput. 2021, 105, 107281. [Google Scholar] [CrossRef]
- Solhmirzaei, R.; Salehi, H.; Kodur, V.; Naser, M.Z. Machine learning framework for predicting failure mode and shear capacity of ultra high performance concrete beams. Eng. Struct. 2020, 224, 111221. [Google Scholar] [CrossRef]
- Saleh, E.; Tarawneh, A.N.; Naser, M.Z. Failure mode classification and deformability evaluation for concrete beams reinforced with FRP bars. Compos. Struct. 2022, 292, 115651. [Google Scholar] [CrossRef]
- Almasabha, G.; Alshboul, O.; Shehadeh, A.; Almuflih, A.S. Machine Learning Algorithm for Shear Strength Prediction of Short Links for Steel Buildings. Buildings 2022, 12, 775. [Google Scholar] [CrossRef]
- Alshboul, O.; Shehadeh, A.; Almasabha, G.; Mamlook, R.E.A.; Almuflih, A.S. Evaluating the impact of external support on green building construction cost: A hybrid mathematical and machine learning prediction approach. Buildings 2022, 12, 1256. [Google Scholar] [CrossRef]
- Tarawneh, A.; Almasabha, G.; Alawadi, R.; Tarawneh, M. Innovative and reliable model for shear strength of steel fibers reinforced concrete beams. Structures 2021, 32, 1015–1025. [Google Scholar] [CrossRef]
- Bashir, R.; Ashour, A. Neural network modelling for shear strength of concrete members reinforced with FRP bars. Compos. Part B: Eng. 2012, 43, 3198–3207. [Google Scholar] [CrossRef]
- Lee, S.; Lee, C. Prediction of shear strength of FRP-reinforced concrete flexural members without stirrups using artificial neural networks. Eng. Struct. 2014, 61, 99–112. [Google Scholar] [CrossRef]
- Jumaa, G.B.; Yousif, A.R. Predicting shear capacity of FRP-reinforced concrete beams without stirrups by artificial neural networks, gene expression programming, and regression analysis. Adv. Civ. Eng. 2018, 2018, 5157824. [Google Scholar] [CrossRef]
- Naderpour, H.; Haji, M.; Mirrashid, M. Shear capacity estimation of FRP-reinforced concrete beams using computational intelligence. Structures 2020, 28, 321–328. [Google Scholar] [CrossRef]
- Murad, Y.Z. Predictive model for bidirectional shear strength of reinforced concrete columns subjected to biaxial cyclic loading. Eng. Struct. 2021, 244, 112781. [Google Scholar] [CrossRef]
- Murad, Y.; Tarawneh, A.; Arar, F.; Al-Zu’bi, A.; Al-Ghwairi, A.; Al-Jaafreh, A.; Tarawneh, M. Flexural strength prediction for concrete beams reinforced with FRP bars using gene expression programming. Structures 2021, 33, 3163–3172. [Google Scholar] [CrossRef]
- Wight, J.K.; MacGregor, J.G. Reinforced Concrete; Pearson Education: London, UK, 2016. [Google Scholar]
- American Concrete Institute. Guide for the Design and Construction of Structural Concrete Reinforced with Fiber-Reinforced Polymer (FRP) Bars. (ACI 440.1 R-15); American Concrete Institute: Farmington Hills, MI, USA, 2015. [Google Scholar]
- Tureyen, A.K.; Frosch, R.J. Shear Tests of FRP Reinforced Concrete Beams without Stirrups. ACI Struct. J. 2002, 99, 427–434. [Google Scholar]
- Nanni, A.; de Luca, A.; Zadeh, H.J. FRP Reinforced Concrete Structures—Theory, Design and 33 Practice; CRC Press: Boca Raton, FL, USA, 2014; 400p, ISBN 978-0-415-77882-4. [Google Scholar]
- Canadian Standards Association. Design and Construction of Building Components with Fibre-Reinforced Polymers (No. 2); Canadian Standards Association: Toronto, ON, Canada, 2002. [Google Scholar]
- Wu, Z.; Wang, X.; Iwashita, K.; Sasaki, T.; Hamaguchi, Y. Tensile fatigue behaviour of FRP and hybrid FRP sheets. Compos. Part B Eng. 2010, 41, 396–402. [Google Scholar] [CrossRef]
- Japan Society of Civil Engineers. Recommendations for Design and Construction of Concrete Structures Using Continuous Fiber Reinforcing Materials; JSCE: Tokyo, Japan, 1997. [Google Scholar]
- Nehdi, M.; El Chabib, H.; Saïd, A.A. Proposed shear design equations for FRP-reinforced concrete beams based on genetic algorithms approach. J. Mater. Civ. Eng. 2007, 19, 1033–1042. [Google Scholar] [CrossRef]
- Hoult, N.A.; Sherwood, E.G.; Bentz, E.C.; Collins, M.P. Does the use of FRP reinforcement change the one-way shear behavior of reinforced concrete slabs? J. Compos. Constr. 2008, 12, 125. [Google Scholar] [CrossRef]
- Kara, I.F. Prediction of shear strength of FRP-reinforced concrete beams without stirrups based on genetic programming. Adv. Eng. Softw. 2011, 42, 295–304. [Google Scholar] [CrossRef]
- Mari, A.; Cladera, A.; Oller, E.; Bairan, J. Shear design of FRP reinforced concrete beams without transverse reinforcement. Compos. Part B Eng. 2014, 57, 228–241. [Google Scholar] [CrossRef]
- Bazant, Z.P.; Yu, Q. Designing against size effect on shear strength of reinforced concrete beams without stirrups: I. Formulation. J. Struct. Eng. (N. Y.) 2005, 131, 1877. [Google Scholar] [CrossRef] [Green Version]
- ACI Committee 318. Building Code Requirements for Structural Concrete (ACI 318-19); American Concrete Institute: Farmington Hills, MI, USA, 2019; p. 988. [Google Scholar]
- Kaszubska, M.; Kotynia, R.; Barros, J.A.; Baghi, H. Shear behavior of concrete beams reinforced exclusively with longitudinal glass fiber reinforced polymer bars: Experimental research. Struct. Concr. 2018, 19, 152–161. [Google Scholar] [CrossRef] [Green Version]
- Ebid, A.M.; Deifalla, A. Prediction of shear strength of FRP reinforced beams with and without stirrups using (GP) technique. Ain Shams Eng. J. 2021, 12, 2493–2510. [Google Scholar] [CrossRef]
- Razaqpur, A.G.; Isgor, B.O.; Greenaway, S.; Selley, A. Concrete contribution to the shear resistance of fiber reinforced polymer reinforced concrete members. J. Compos. Constr. 2004, 8, 452–460. [Google Scholar] [CrossRef]
- El-Sayed, A.; El-Salakawy, E.; Benmokrane, B. Shear strength of one-way concrete slabs reinforced with fiber-reinforced polymer composite bars. J. Compos. Constr. 2005, 9, 147–157. [Google Scholar] [CrossRef]
- Issa, M.A.; Ovitigala, T.; Ibrahim, M. Shear behavior of basalt fiber reinforced concrete beams with and without basalt FRP stirrups. J. Compos. Constr. 2016, 20, 04015083. [Google Scholar] [CrossRef]
- El Refai, A.; Abed, F. Concrete contribution to shear strength of beams reinforced with basalt fiber-reinforced bars. J. Compos. Constr. 2016, 20, 04015082. [Google Scholar] [CrossRef]
- Tomlinson, D.; Fam, A. Performance of concrete beams reinforced with basalt FRP for flexure and shear. J. Compos. Constr. 2015, 19, 04014036. [Google Scholar] [CrossRef]
- Khaja, M.N.; Sherwood, E.G. Does the shear strength of reinforced concrete beams and slabs depend upon the flexural reinforcement ratio or the reinforcement strain? Can. J. Civ. Eng. 2013, 40, 1068–1081. [Google Scholar] [CrossRef]
- Abdul-Salam, B. Behaviour of Shear Critical FRP Reinforced Concrete One-Way Slabs. Ph.D. Thesis, Université de Sherbrooke, Sherbrooke, QC, Canada, 2014. [Google Scholar]
- Razaqpur, A.G.; Shedid, M.; Isgor, B. Shear strength of fiber-reinforced polymer reinforced concrete beams subject to unsymmetric loading. J. Compos. Constr. 2011, 15, 500–512. [Google Scholar] [CrossRef]
- Chang, K.; Seo, D. Behavior of one-way concrete slabs reinforced with GFRP bars. J. Asian Archit. Build. Eng. 2012, 11, 351–358. [Google Scholar] [CrossRef] [Green Version]
- Ashour, A.F.; Kara, I.F. Size effect on shear strength of FRP reinforced concrete beams. Compos. Part B Eng. 2014, 60, 612–620. [Google Scholar] [CrossRef] [Green Version]
- Ashour, A.F. Flexural and shear capacities of concrete beams reinforced with GFRP bars. Constr. Build. Mater. 2006, 20, 1005–1015. [Google Scholar] [CrossRef]
- Tariq, M.; Newhook, J.P. Shear testing of FRP reinforced concrete without transverse reinforcement. In Proceedings of the Annual Conference of the Canadian Society for Civil Engineering, Moncton, NB, Canada, 4–7 June 2003; pp. 1330–1339. [Google Scholar]
- Kim, C.H.; Jang, H.S. Concrete Shear Strength of Normal and Lightweight Concrete Beams Reinforced with FRP Bars. J. Compos. Constr. 2014, 18, 04013038. [Google Scholar] [CrossRef]
- El-Sayed, A.K.; Soudki, K.; Kling, E. Flexural behaviour of self-consolidating concrete slabs reinforced with GFRP bars. In Proceedings of the 9th International Symposium on Fiber Reinforced Polymer Reinforcement for Reinforced Concrete Structures, Sydney, Australia, 13–15 July 2009; pp. 13–15. [Google Scholar]
- Zhao, W.; Maruyama, K.; Suzuki, H. Shear behavior of concrete beams reinforced by FRP rods as longitudinal and shear reinforcement. In Proceedings of the Rilem Proceedings, Ghent, Belgium, 23–25 August 1995; Chapman & Hall: London, UK, 1995; p. 352. [Google Scholar]
- Alkhrdaji, T.; Wideman, M.; Belarbi, A.; Nanni, A. Shear strength of GFRP RC beams and slabs. In Proceedings of the International Conference, Composites in Construction-CCC, Porto, Portugal, 10–12 October 2001; pp. 409–414. [Google Scholar]
- Deitz, D.H.; Harik, I.E.; Gesund, H. One-way slabs reinforced with glass fiber reinforced polymer reinforcing bars. Spec. Publ. 1999, 188, 279–286. [Google Scholar]
- Duranovic, N.; Pilakoutas, K.; Waldron, P. Tests on concrete beams reinforced with glass fibre reinforced plastic bars. Non-Met. (FRP) Reinf. Concr. Struct. 1997, 2, 479–486. [Google Scholar]
- Matta, F.; El-Sayed, A.K.; Nanni, A.; Benmokrane, B. Size Effect on Concrete Shear Strength in Beams Reinforced with Fiber-Reinforced Polymer Bars. ACI Struct. J. 2013, 110, 617–628. [Google Scholar]
- Yost, J.R.; Gross, S.P.; Dinehart, D.W. Shear strength of normal strength concrete beams reinforced with deformed GFRP bars. J. Compos. Constr. 2001, 5, 268–275. [Google Scholar] [CrossRef]
- Alam, M.S. Influence of Different Parameters on Shear Strength of FRP Reinforced Concrete Beams without Web Reinforcement. Ph.D. Thesis, Memorial University of Newfoundland, St. John’s, NL, Canada, 2010. [Google Scholar]
- Olivito, R.S.; Zuccarello, F.A. On the shear behaviour of concrete beams reinforced by carbon fibre-reinforced polymer bars: An experimental investigation by means of acoustic emission technique. Strain 2010, 46, 470–481. [Google Scholar] [CrossRef]
- Bentz, E.C.; Massam, L.; Collins, M.P. Shear strength of large concrete members with FRP reinforcement. J. Compos. Constr. 2010, 14, 637–646. [Google Scholar] [CrossRef]
- Gross, S.P.; Yost, J.R.; Dinehart, D.W.; Svensen, E.; Liu, N. Shear strength of normal and high strength concrete beams reinforced with GFRP bars. In Proceedings of the High Performance Materials in Bridges, Kona, HI, USA, 29 July–3 August 2003; pp. 426–437. [Google Scholar]
- Ali, I.; Thamrin, R.; Abdul, A.A.S.; Noridah, M. Diagonal shear cracks and size effect in concrete beams reinforced with glass fiber reinforced polymer (GFRP) bars. Appl. Mech. Mater. 2014, 621, 113–119. [Google Scholar]
- Nakamura, H.; Higai, T. Evaluation of shear strength of concrete beams reinforced with FRP. Doboku Gakkai Ronbunshu 1995, 1995, 89–100. [Google Scholar] [CrossRef] [Green Version]
- Swamy, N.; Aburawi, M. Structural implications of using GFRP bars as concrete reinforcement. In Proceedings of the 3rd International Symposium, FRPRCS. Sapporo, Japan, 14–16 October 1997; Volume 3, pp. 503–510. [Google Scholar]
- Liu, R. Precast Concrete Bridge Deck Panels Reinforced with Glass Fiber Reinforced Polymer Bars; The University of Utah: Salt Lake City, UT, USA, 2011. [Google Scholar]
- Farahmand, F. Shear Behaviour of Concrete Beams Reinforced with Glass Fibre Reinforced Plastic. Struct. Eng. Div. Dep. Civ. Geol. Eng. Univ. Manit. 1996, 234–345. [Google Scholar]
- Gross, S.P.; Dinehart, D.W.; Yost, J.R.; Theisz, P.M. Experimental tests of high-strength concrete beams reinforced with CFRP bars. In Proceedings of the 4th International Conference on Advanced Composite Materials in Bridges and Structures (ACMBS-4), Calgary, AB, Canada, 20–23 July 2004; quoted from Razaqpur and Isgor. 2006. [Google Scholar]
- Maruyama, K.; Zhao, W.J. Flexural and shear behaviour of concrete beams reinforced with FRP rods. Corros. Corros. Prot. Steel Concr. 1994, 1330–1339. [Google Scholar]
- Caporale, A.; Luciano, R. Indagine sperimentale e numerica sulla resistenza a taglio di travi di calcestruzzo armate con barre di GFRP. In Proceedings of the XXXVIII Convegno Nazionale AIAS, Torino, Italy, 9–11 September 2009. [Google Scholar]
- Kilpatrick, A.E.; Easden, L. Shear capacity of GFRP reinforced high strength concrete slabs. Dev. Mech. Struct. Mater. 2005, 1, 119–124. [Google Scholar]
- Kilpatrick, A.E.; Dawborn, R. Flexural Shear Capacity of High Strength Concrete Slabs Reinforced with Longitudinal GFRP Bars; FIB: Naples, Italy, 2006; pp. 1–10. [Google Scholar]
- Zeidan, M.; Barakat, M.A.; Mahmoud, Z.; Khalifa, A. Evaluation of concrete shear strength for FRP reinforced beams. In Proceedings of the Structures Congress 2011, Las Vegas, NV, USA, 14–16 April 2011; pp. 1816–1826. [Google Scholar]
- Andermatt, M.F.; Lubell, A.S. Behavior of concrete deep beams reinforced with internal fiber-reinforced polymer-experimental study. ACI Struct. J. 2013, 110, 585. [Google Scholar]
- Abed, F.; El-Chabib, H.; AlHamaydeh, M. Shear characteristics of GFRP-reinforced concrete deep beams without web reinforcement. J. Reinf. Plast. Compos. 2012, 31, 1063–1073. [Google Scholar] [CrossRef]
- Thomas, J.; Ramadass, S. Parametric study of shear strength of concrete beams reinforced with FRP bars. J. Inst. Eng. (India) Ser. A 2016, 97, 273–284. [Google Scholar] [CrossRef]
- Omeman, Z.; Nehdi, M.; El-Chabib, H. Experimental study on shear behavior of carbon-fiber-reinforced polymer reinforced concrete short beams without web reinforcement. Can. J. Civ. Eng. 2008, 35, 1–10. [Google Scholar] [CrossRef]
- Holland, J.H. Genetic algorithms. Sci. Am. 1992, 267, 66–73. [Google Scholar] [CrossRef]
- Cramer, N.L. A representation for the adaptive generation of simple sequential programs. In Proceedings of the First International Conference on Genetic Algorithms, Pittsburgh, PA, USA, 24–26 June 1985; pp. 183–187. [Google Scholar]
- Koza, J.R. Evolution of subsumption using genetic programming. In Proceedings of the First European Conference on Artificial Life; MIT Press: Cambridge, MA, USA, 1992; pp. 110–119. [Google Scholar]
- Ferreira, C. Gene expression programming: A new adaptive algorithm for solving problems. arXiv 2001, arXiv:cs/0102027. [Google Scholar]
- Soleimani-Babakamali, M.H.; Esteghamati, M.Z. Estimating seismic demand models of a building inventory from nonlinear static analysis using deep learning methods. Eng. Struct. 2022, 266, 114576. [Google Scholar] [CrossRef]
- Cakiroglu, C.; Islam, K.; Bekdaş, G.; Kim, S.; Geem, Z.W. Interpretable Machine Learning Algorithms to Predict the Axial Capacity of FRP-Reinforced Concrete Columns. Materials 2022, 15, 2742. [Google Scholar] [CrossRef] [PubMed]
- Esteghamati, M.Z.; Flint, M.M. Developing data-driven surrogate models for holistic performance-based assessment of mid-rise RC frame buildings at early design. Eng. Struct. 2021, 245, 112971. [Google Scholar] [CrossRef]





| Reference | N | b | a/d | f′c | ||
|---|---|---|---|---|---|---|
| Razaqpur, A. G. et al. (2004) [31] | 6 | 200 | (2.67–4.5) | (40.5–49.5) | (0.25–0.88) | 145 |
| El-sayed et al. (2005) [32] | 8 | 1000 | ((6–6.4)) | 40 | (0.39–2.44) | (40–114) |
| Issa et al. (2016) [33] | 7 | 300 | (5.65–7) | 35.9 | (0.68–3.4) | (48–53) |
| Tureyen and Frosch (2002) [18] | 6 | 457 | 3.4 | 34.5 | (0.96–1.92) | (37.5–47.1) |
| El Refai and Abed (2016) [34] | 5 | 152 | 3.3 | 49 | (0.31–1.52) | 50 |
| Tomlinson and Fam (2015) [35] | 3 | 150 | 4 | (56.5–60) | (0.39–0.81) | 70 |
| Khaja and Sherwood (2013) [36] | 11 | 400 | (3–8) | (47.8–51.4) | (0.57–4.1) | (47.5–51.9) |
| Abdul-Salam (2014) [37] | 18 | 100 | (5.92–6.18) | (47.9–86.2) | (0.45–1.42) | (69.5–144) |
| Razaqpur et al. (2011) [38] | 6 | 300 | (3.5–6.5) | 52.3 | (0.28–0.35) | 114 |
| Chang and Seo (2012) [39] | 6 | 1200 | 5.8 | 30 | (0.73–1.22) | (44–50) |
| Kaszubska et al. (2018) [29] | 7 | 150 | (2.9–3) | (28.8–31.7) | (0.99–1.85) | (50.2–50.9) |
| Ashour and Kara (2014) [40] | 6 | 200 | (2.7–5.9) | (21.6–28) | (0.12–0.51) | (32–38) |
| Ashour (2006) [41] | 6 | 150 | (2.7–3.7) | (34–59) | (0.45–1.15) | 32 |
| Tariq and Newhook (2003) [42] | 12 | (130–160) | (2.7–3.3) | (34.7–43.2) | (0.72–1.54) | (42–120) |
| Kim and Jang (2014) [43] | 24 | 150 | (3–4.5) | 30 | (0.31–0.71) | (48.2–146.2) |
| El-sayed A et al. (2009) [44] | 2 | 600 | 6.68 | 68 | (0.53–0.77) | 48 |
| Zhao et al. (1995) [45] | 3 | 150 | 3 | 34 | (1.51–3.02) | 105 |
| Alkhrdaji et al. (2001) [46] | 3 | 178 | (2.61–2.69) | 24 | (0.77–2.3) | 40 |
| Deitz et al. (1999) [47] | 3 | 305 | (4.5–5.8) | (27–30) | 0.73 | 40 |
| Duranovic et al. (1997) [48] | 2 | 150 | 3.65 | (33–38) | (1.31–1.36) | 45 |
| Matta et al. (2013) [49] | 9 | (114–229) | 3.1 | (32.1–59.7) | (0.13–0.28) | (43.2–48.2) |
| Joseph R et al. (2001) [50] | 18 | (178–279) | 4.06 | 36.3 | (0.86–1.75) | 40.336 |
| Alam (2010) [51] | 2 | 250 | 3.5 | (34.5–39.8) | (0.42–0.84) | (48–120) |
| Olivito and Zuccarello (2010) [52] | 20 | 150 | 5.56 | (30–40) | (0.786–1.3) | 115 |
| Bentz et al. (2010) [53] | 4 | 450 | (3.48–3.05) | 35 | (0.48–1.91) | 37 |
| Gross et al. (2003) [54] | 12 | (152–203) | 4.06 | 79.6 | (1.25–2.1) | 40.3 |
| Ali et al. (2014) [55] | 4 | 130 | 3 | (31–33.5) | (0.6–0.91) | 51.5 |
| Guadagnini et al. (2006) [3] | 1 | 150 | 3.3 | 40 | 1.1 | 45 |
| Nakamura and Higai (1995) [56] | 2 | 300 | 4 | (23–28) | (1.34–1.79) | 29 |
| Swamy (1997) [57] | 1 | 155 | 3.15 | 39 | 1.55 | 34 |
| Liu (2011) [58] | 20 | (635–1854) | 6.04 | (65–87) | (0.54–0.94) | 43.3 |
| Farahmand (1996) [59] | 6 | 200 | (3,4) | (31–35) | (0.51 1.08) | 41.3 |
| Gross et al. (2004) [60] | 4 | (89–159) | (6.35–6.45) | (60–81) | (0.33–0.76) | 139 |
| Maruyama and Zhao (1994) [61] | 4 | 150 | 3 | (28–35) | (0.55–2.2) | 94 |
| Caporale and Luciano (2009) [62] | 4 | 150 | 4.12 | (24–31) | (0.92–1.54) | 45.8 |
| Kilpatrick and Easden (2005) [63] | 12 | 420 | (3.61–6.41) | (61–93) | (0.61–2.61) | (40–42) |
| Kilpatrick and Dawborn (2006) [64] | 9 | 420 | (6–6.16) | (48–92) | (0.68–1.16) | 42 |
| Zeidan et al. (2011) [65] | 1 | 150 | 5 | 49 | 0.105 | 148 |
| Reference | N | B | a/d | f′c | ||
|---|---|---|---|---|---|---|
| Matthias F and Lubell. (2013) [66] | 8 | (300–310) | (1.1–2.06) | (39.9–68.5) | (1.47–2.13) | (64.1–72) |
| Abed et al. (2012) [67] | 9 | 200 | (1–1.52) | (43–65) | (0.92–1.84) | 51 |
| Thomas and S. Ramadass (2016) [68] | 8 | (100–170) | (0.5–1.75) | (40.6–59.5) | (1.16–1.75) | 40 |
| Zeidan et al. (2011) [65] | 3 | 150 | 2.5 | (24–46) | (0.105–0.21) | 148 |
| Omeman et al. (2008) [69] | 8 | (150–350) | (1.36–1.86) | (35–60) | (1.13–2.26) | 134 |
| Kim and Jang (2014) [43] | 29 | (150–200) | (1.5–2.5) | 30 | (0.31–0.71) | (48.2–146.2) |
| Alam (2010) [51] | 24 | (250–300) | (1.5–2.5) | (34.3–88.3) | (0.18–1.51) | (48–120) |
| Ali et al. (2014) [55] | 4 | 130 | 2.3 | (13–33.5) | (0.6–0.91) | 51.5 |
| Razaqpur, A. G. et al. (2004) [31] | 1 | 200 | 1.82 | 40.5 | 0.5 | 145 |
| El Refai and Abed (2016) [34] | 3 | 152 | 2.5 | 49 | (0.31–0.69) | 50 |
| Khaja and Sherwood (2013) [36] | 3 | 400 | 2 | (50.8–51.6) | (0.57–2.28) | 47.5 |
| Parameter | Selected Value |
|---|---|
| Dependent variable (shear stress) | 1 |
| Independent variables | 5,6 |
| Genes | 3 |
| Function set | |
| Head size | 6,8 |
| Linking function between ETs | Multiplication |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tarawneh, A.; Alghossoon, A.; Saleh, E.; Almasabha, G.; Murad, Y.; Abu-Rayyan, M.; Aldiabat, A. Machine Learning Prediction Model for Shear Capacity of FRP-RC Slender and Deep Beams. Sustainability 2022, 14, 15609. https://doi.org/10.3390/su142315609
Tarawneh A, Alghossoon A, Saleh E, Almasabha G, Murad Y, Abu-Rayyan M, Aldiabat A. Machine Learning Prediction Model for Shear Capacity of FRP-RC Slender and Deep Beams. Sustainability. 2022; 14(23):15609. https://doi.org/10.3390/su142315609
Chicago/Turabian StyleTarawneh, Ahmad, Abdullah Alghossoon, Eman Saleh, Ghassan Almasabha, Yasmin Murad, Mahmoud Abu-Rayyan, and Ahmad Aldiabat. 2022. "Machine Learning Prediction Model for Shear Capacity of FRP-RC Slender and Deep Beams" Sustainability 14, no. 23: 15609. https://doi.org/10.3390/su142315609
APA StyleTarawneh, A., Alghossoon, A., Saleh, E., Almasabha, G., Murad, Y., Abu-Rayyan, M., & Aldiabat, A. (2022). Machine Learning Prediction Model for Shear Capacity of FRP-RC Slender and Deep Beams. Sustainability, 14(23), 15609. https://doi.org/10.3390/su142315609








