Comparative Study of Geological Hazard Evaluation Systems Using Grid Units and Slope Units under Different Rainfall Conditions
Abstract
:1. Introduction
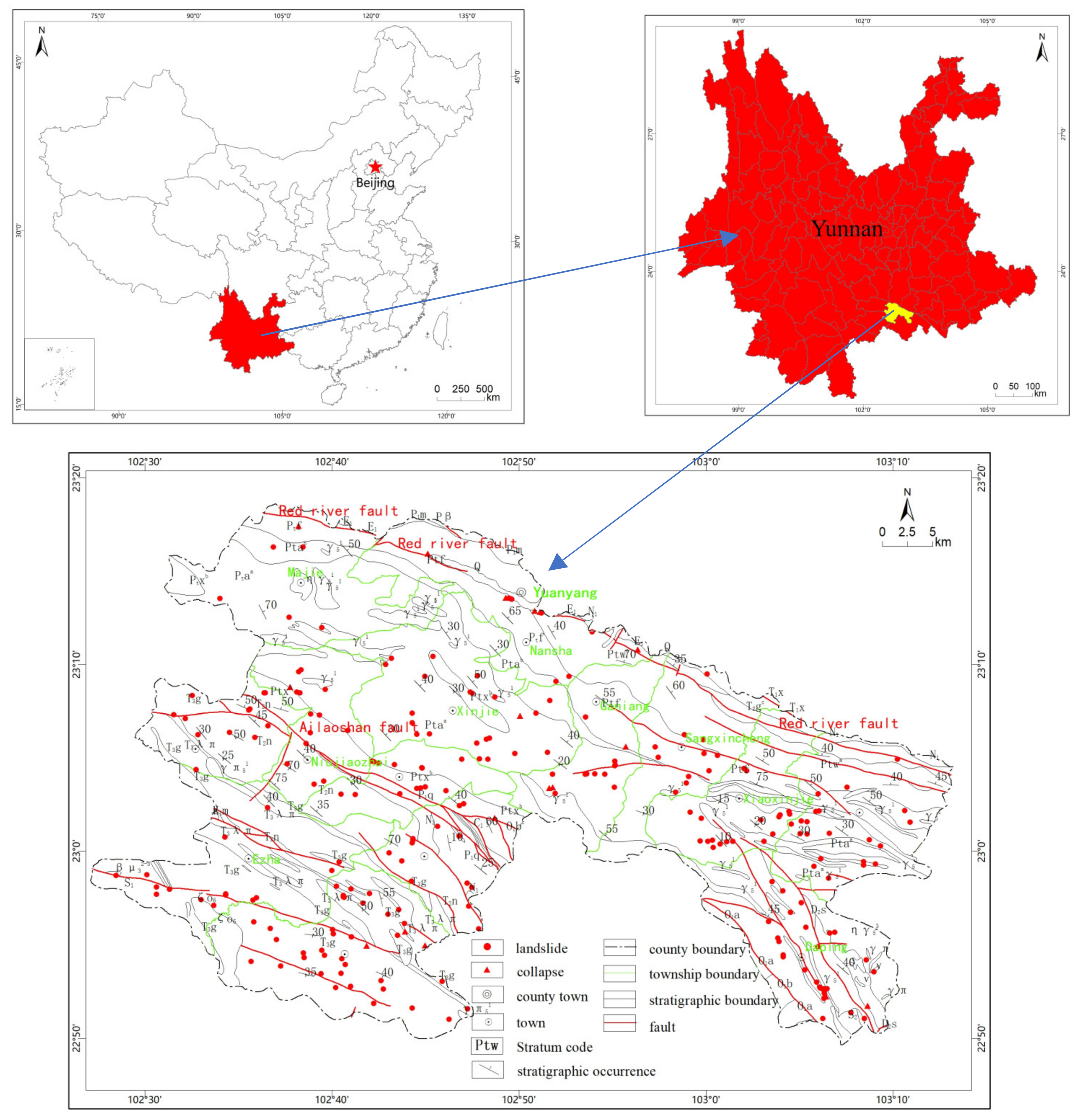
2. Overview of the Research Area
3. Materials and Methods of Evaluation
3.1. Establishment of Evaluation Method
3.1.1. Establishment of Susceptibility Evaluation Method
- (1)
- ICM (Information Content Method)
- (2)
- AHP (Analytic Hierarchy Process)
- (3)
- Weighted Information Method
3.1.2. Establishment of the Risk Evaluation Method
3.2. Selection of Evaluation Factors
3.2.1. Selection of Susceptibility Evaluation Factors
3.2.2. Selection of Risk Evaluation Factors
3.3. Evaluation Unit Demarcation
- (1)
- Grid Units
- (2)
- Slope Units
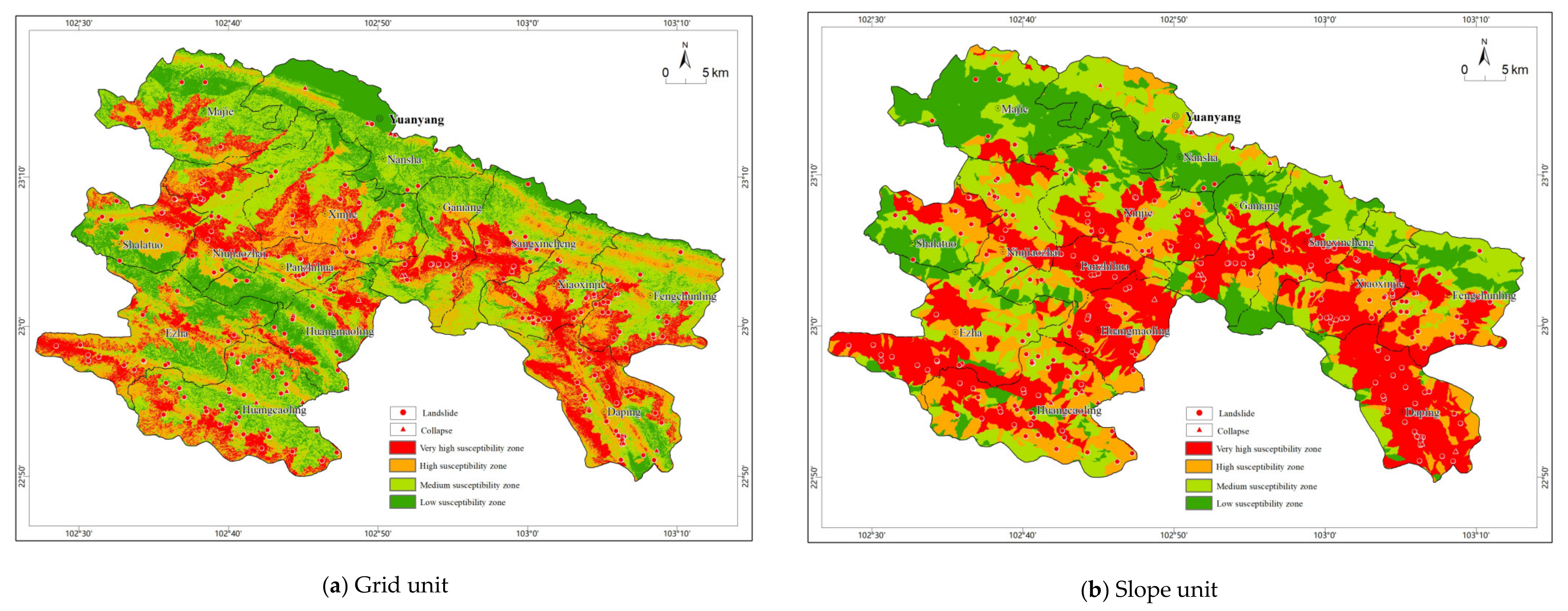
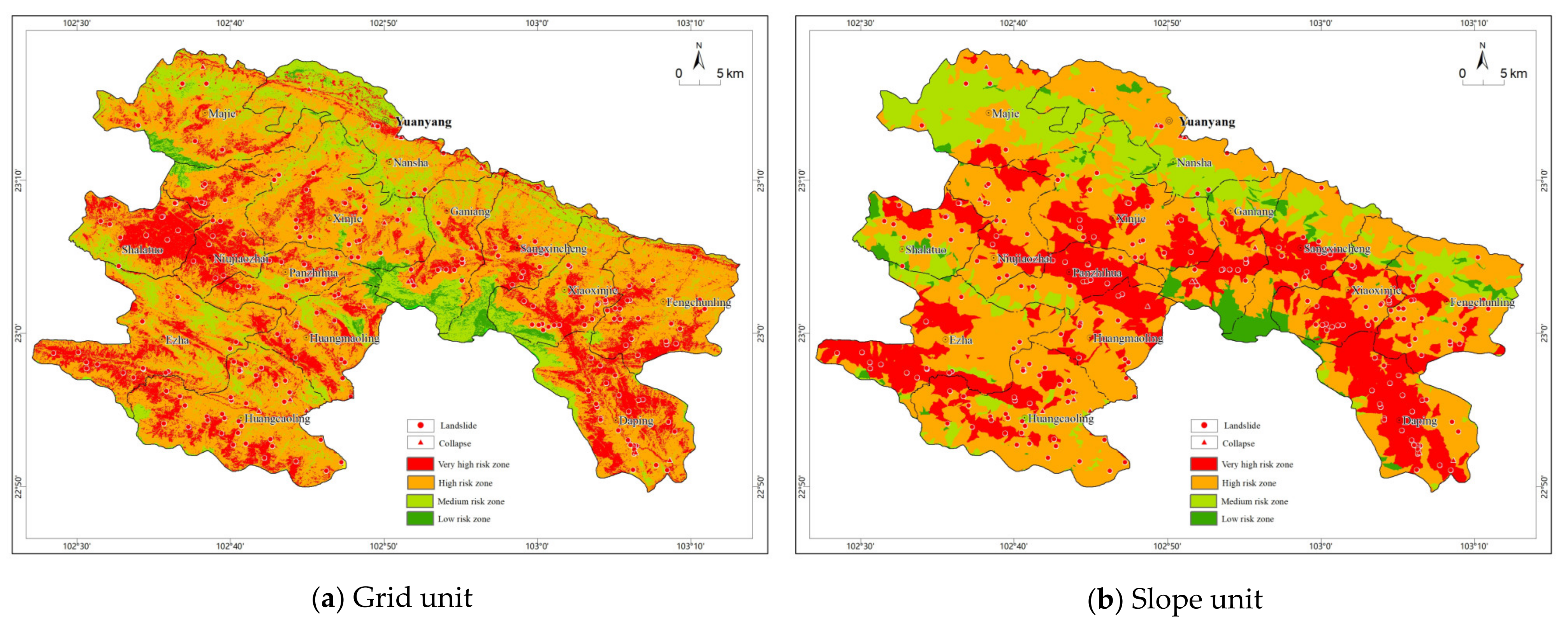
3.4. Regionalization of Collapse and Landslide Geological Hazard Susceptibilities
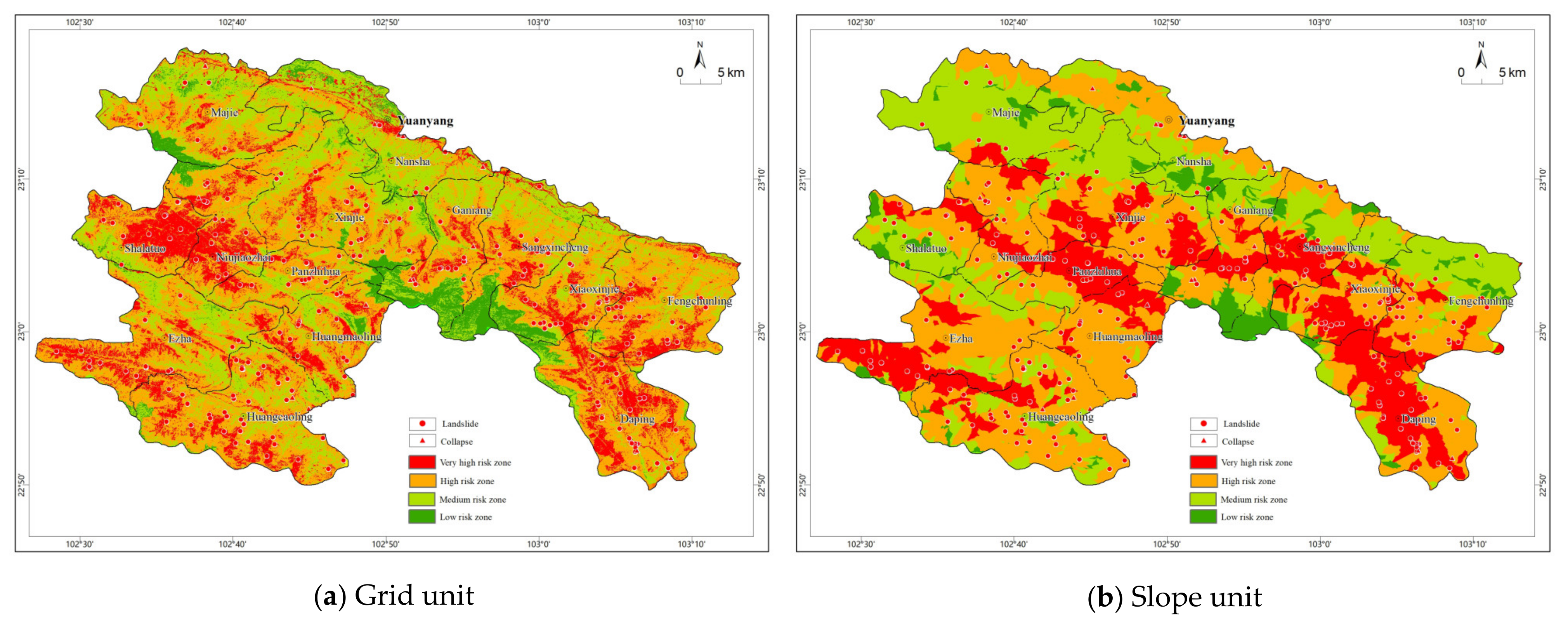
3.5. Regionalization of Geological Hazard Risk of Collapse and Landslide
4. Comparison of Results
4.1. Result Data Comparison
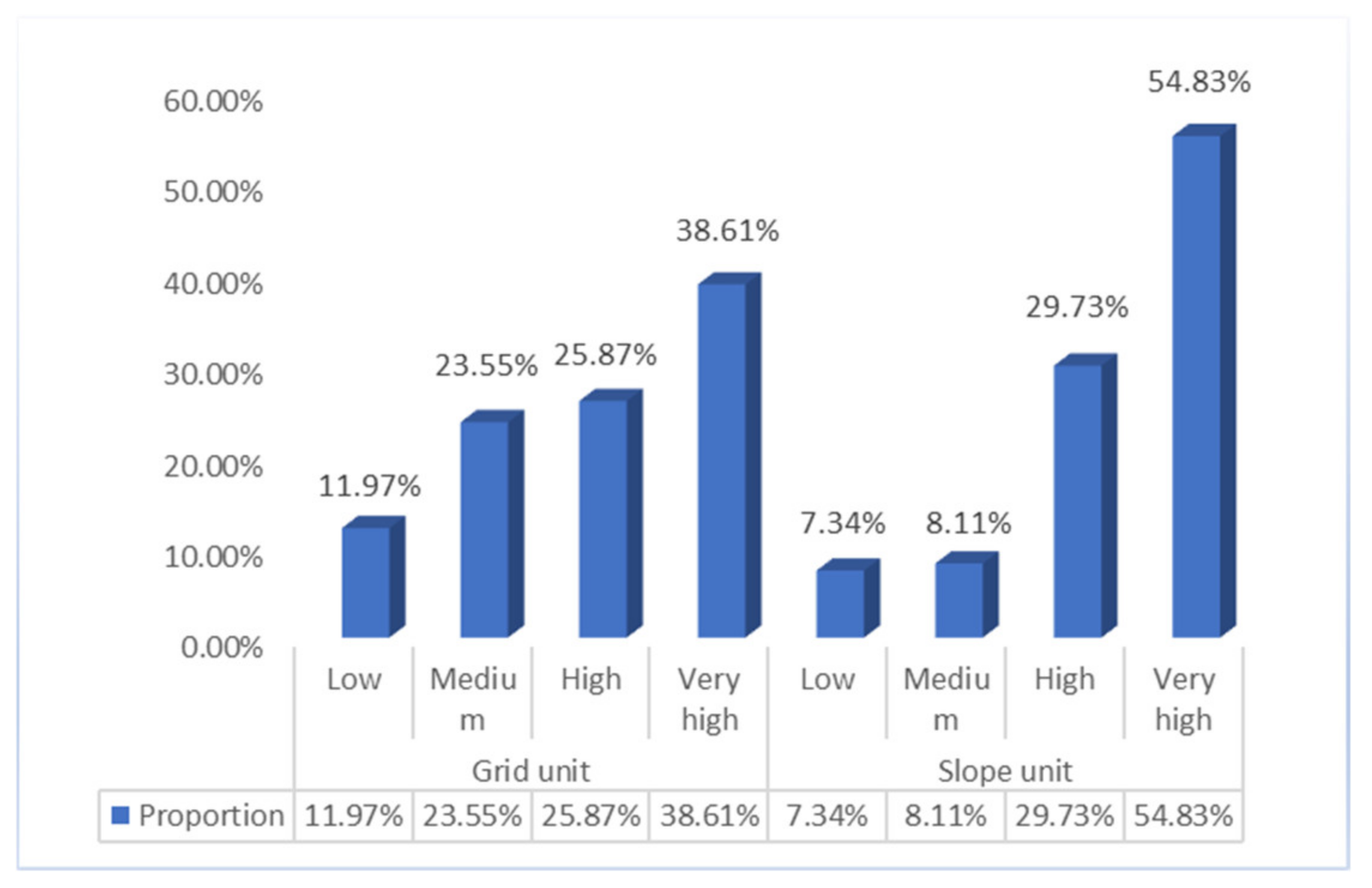
4.1.1. Comparison of Susceptibility Result Data
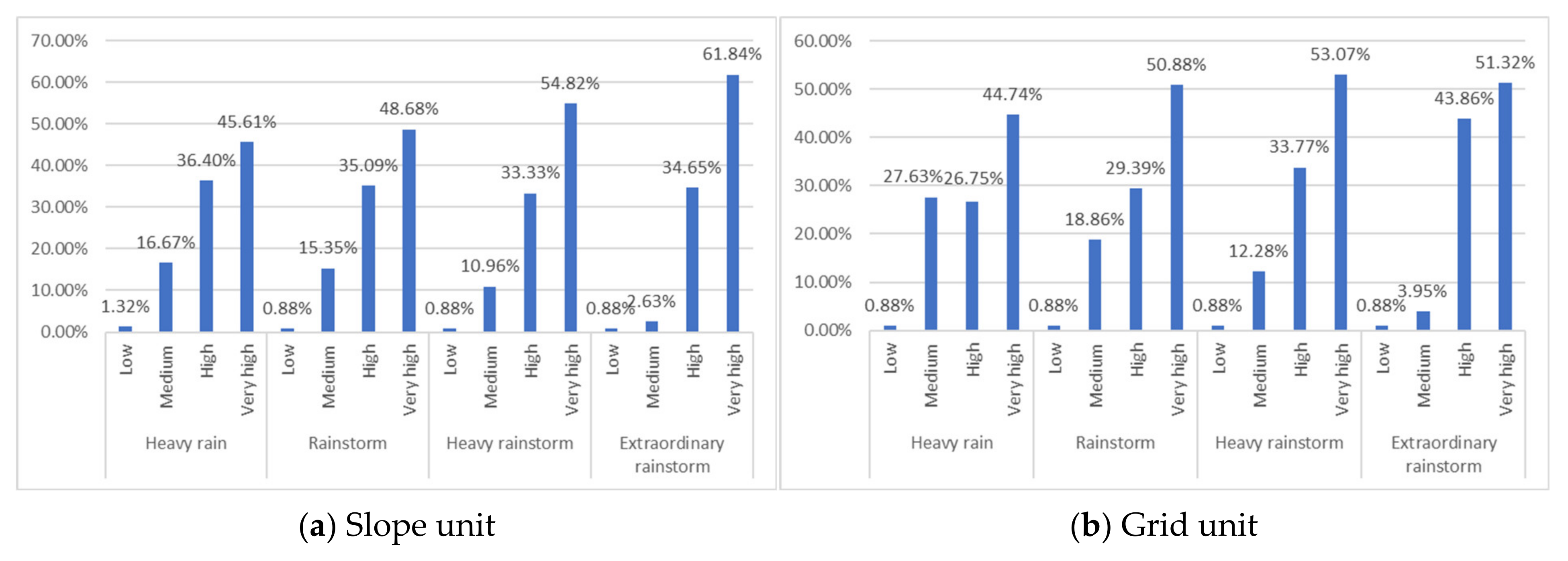
4.1.2. Comparison of Risk Result Data
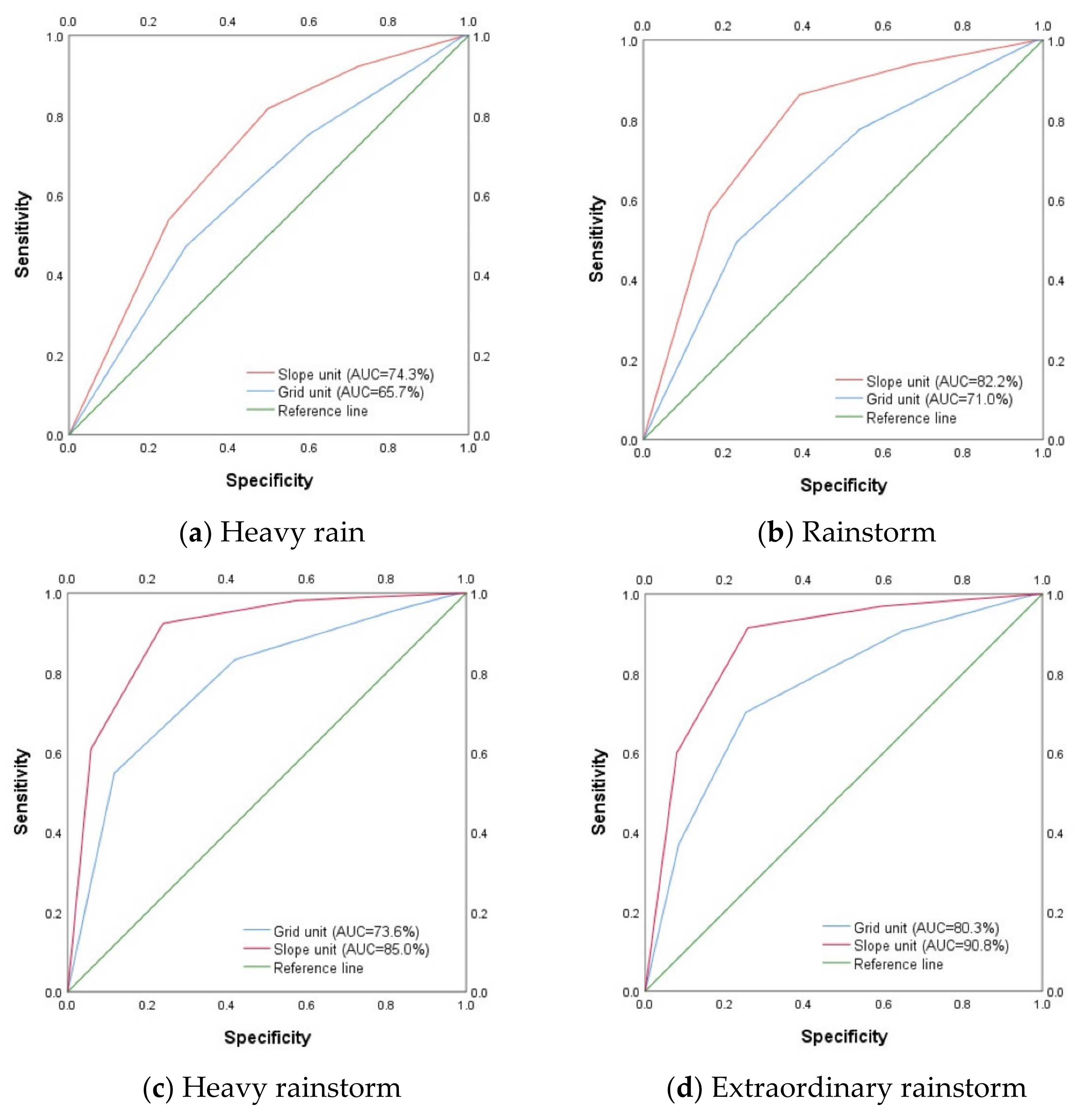
4.2. Comparison of Model Accuracy
4.2.1. Precision Comparison of Susceptibility Zoning Results
4.2.2. Precision Comparison of Risk Zoning Results
4.3. Comparison of Slope Unit Evaluation Results with the Actual Situation
4.3.1. Results of the Susceptibility Evaluation
4.3.2. Results of Risk Evaluation
5. Discussion
6. Conclusions
- (1)
- In the study area, a total of 7851 slope units were divided by ArcGis using DEM data. The boundaries of slope units were highly consistent with the ridge lines and valley lines, and the divided slope units were in line with the topographic and geomorphic characteristics of the study area, indicating that the method proposed in this paper can be used to divide slope units in large study areas.
- (2)
- Taking grid units and slope units as evaluation units and taking maximum annual average daily rainfall as the inducing factor, the risk evaluation results for collapse and landslide under four different rainfall conditions—heavy rain, rainstorm, heavy rainstorm, and extraordinary rainstorm—were obtained, which improved the disadvantage of using the rainfall inducing factor as a single evaluation factor in the calculations of the geological hazard risk evaluation model. The degrees and regional distribution characteristics of geological hazards induced by rainfall grade were clarified, providing a basis for the implementation of geological hazard prevention and control by means of prevention, avoidance, control, rescue, or a combination thereof, which is conducive to improving the operability and timeliness of hazard prevention and mitigation. At the same time, the geological hazard risk assessment system under different rainfall conditions proposed in this paper provides a reference for geological hazard risk assessment in other regions.
- (3)
- In this paper, grid units and slope units were used as the evaluation units in a collapse and landslide geological hazard evaluation system. According to the statistical analysis and comparison of the results, the proportions of hazards in the very high and high-susceptibility areas and risk areas under the slope unit system were higher than those under the grid unit system. In the comparison of model accuracy tests, the AUC values for susceptibility and risk assessment results obtained with slope units were higher than those obtained with grid units. Based on the comparison of the susceptibility and risk assessment results under the slope unit evaluation system and the actual survey data, it was concluded that the geological hazard assessment results under the slope unit system were in good agreement with the actual situation, and, finally, it was concluded that the geological hazard assessment results under the slope unit system were more reasonable and accurate. Thus, a scientific basis has been provided for the selection of evaluation units in large-scale regional geological hazard assessments undertaken for the prevention and control of geological hazards.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Sun, S.; Huang, R. Risk assessment of urban geological disasters in Suining. J. Chengdu Univ. Technol. 2010, 37, 174–180. [Google Scholar]
- Cong, W.; Pan, Y.; Li, T. Research on the Key Problems of landslide and debris flow Hazard Zoning based on GIS. Earth Sci. Front. 2006, 13, 185–190. [Google Scholar]
- Xu, Q.; Wang, J.; Shi, W. Effect of landscape pattern change on soil and water loss in large open-pit coal mine area: A Case study of Pingshuo Mining area, Shanxi Province. China Land Sci. 2022, 36, 96–106. [Google Scholar]
- Tian, S.; Zhang, S.; Tang, Q.; Fan, X.; Han, P. Comparative study on landslide susceptibility evaluation based on different evaluation units. J. Nat. Hazards 2019, 28, 137–145. [Google Scholar]
- Yin, K.; Zhang, G. Geological hazard risk regionalization and comprehensive control countermeasures. Saf. Environ. Eng. 2003, 10, 32–35. [Google Scholar]
- Wang, L.; Chang, M.; Xing, Y. Risk assessment of landslide geological hazards based on information method model and GIS. Geol. Hazards Environ. Prot. 2021, 32, 14–20. [Google Scholar]
- Yu, C. Study on Risk Zoning of Typical Geological Hazards and Comprehensive Evaluation of Geological Environment Carrying Capacity in Helong City. Ph.D. Thesis, Jilin University, Jilin, China, 2021. [Google Scholar]
- Zhu, H.; Ma, X.; Zhang, Y.; Zhu, H. Application of Analytic Hierarchy Process (AHP) based on slope element in geological hazard susceptibility zoning. Prevention and control of local hazards and settlement. In Proceedings of the 2017 Academic Annual Conference of Zhejiang Geological Society, Hangzhou, China, 26 November 2017; Zhejiang Provincial Department of Land and Resources, Zhejiang Geological Society: Zhejiang Association for Science and Technology: Hangzhou, China, 2017; pp. 79–84. Available online: https://kns.cnki.net/kcms/detail/detail.aspx?dbcode=CPFD&dbname=CPFDLAST2018&filename=ZJKX201711005013&uniplatform=NZKPT&v=JC-T0Vlt7t6M1csaf9e5TtEWD6u-4HY8zclOupHc18fYLtSiHGd1hVh9wq41tjxsB31hFGyxsSk%3d (accessed on 4 October 2022).
- Zhao, X.; Tan, S.; Li, Y. Risk assessment of geological hazards in dongchuan district based on slope unit and combination weighting method. J. Yunnan Univ. 2021, 43, 299–305. [Google Scholar]
- Min, Y.; Sun, T. Application of spot quality evaluation in subgrade settlement monitoring system. Laser Optoelectron. Prog. 2022, 2022, 1–16. Available online: https://kns.cnki.net/kcms/detail/31.1690.TN.20220713.1912.559.html (accessed on 4 October 2022).
- Zhang, Y. Geological Hazard Assessment of Zhaojue County Based on GIS. Master’s Thesis, Southwest University of Science and Technology, Mianyang, China, 2022. [Google Scholar]
- Yi, J.; Wang, F.; Cheng, Y.; Zhang, Y. Risk assessment of geological hazards in high mountain and canyon areas: A case study of Aba County, Sichuan Province. Chin. J. Geol. Hazard Control 2022, 33, 134–142. [Google Scholar]
- Liu, F.; Dai, T.; Wang, J.; Wang, L.; Su, Y.; Liu, H.; Zhang, H.; Wang, Y. Evaluation of geological hazard susceptibility coupled with Random Forest and information information model: A case study of Gongbujiangda County, Tibet Autonomous Region. J. Saf. Environ. 2022, 2022, 1–12. Available online: https://kns.cnki.net/kcms/detail/detail.aspx?dbcode=CAPJ&dbname=CAPJLAST&filename=AQHJ2022061700H&uniplatform=NZKPT&v=8I6eb9my9pNNM07sqjNo8OGVbydKpXRd0hUQOm2aEvEGgPIm0rvI_U09OjWMowc8 (accessed on 4 October 2022).
- Shen, Z.; Zhang, Q.; Wu, W.; Song, C. Spatial pattern and driving factors of geological hazard prone areas in the Tibetan Plateau and Hengduan Mountain region. Acta Geogr. Sin. 2022, 77, 1211–1224. [Google Scholar]
- Zhao, Y.; Wang, H.; Liu, Z.; Wu, S.; Ma, Q. Multi-scenario waterlogging hazard risk assessment based on combination weighting. Water Resour. Hydropower Technol. 2022, 53, 1–12. [Google Scholar]
- Tao, X.; Liu, J.; Huang, Z.; Zhuo, M.B.; Chen, J.; Bin, X.; Gao, Y.; Fei, X. Regionalization of highway geological hazard susceptibility and meteorological forecast model in Nyingchi city. Bull. Soil Water Conserv. 2022, 42, 195–202+209. [Google Scholar]
- Li, J.; Wang, H.; Wang, R. Evaluation of landslide susceptibility in Fuzhou area based on machine learning model. J. Hydraul. Eng. Civ. Eng. 2022, 20, 146–152. [Google Scholar]
- Pang, D.; Liu, G.; He, J.; Wang, B.; Zhao, M. Risk assessment and analysis of geological hazards in Gansu Province based on analytic hierarchy Process. Land Resour. Inf. 2021, 23, 41–47. [Google Scholar]
- Zhu, C.; Wu, Q.; Tan, J. Landslide risk assessment based on entropy weight method: A case study of Qinglong County, Guizhou Province. J. Guilin Univ. Technol. 2022, 42, 100–108. [Google Scholar]
- Yang, S.; Li, D.; Yan, L.; Huang, Y.; Wang, M. Evaluation of geological hazard susceptibility of landslide on high steep bank slope of Wujiang River based on random forest model. Saf. Environ. Eng. 2021, 28, 131–138. [Google Scholar]
- Qi, Y.; Wang, L. Application of AHP and entropy weight method to the vulnerability evaluation of urban geological hazards in mountainous areas. Bull. Surv. Mapp. 2021, 35, 112–116. [Google Scholar]
- Qi, Q. Study on the Evaluation of Geological Hazard Vulnerability Degree in Yuanyang County Based on GIS and target Hierarchy Combined Analysis Method. Master’s Thesis, China University of Geosciences, Beijing, China, 2012. [Google Scholar]
- Zhang, Z.; Xu, S.; Li, C.; Guan, X.; Li, W.; Deng, S.; Zheng, X. Evaluation of geological hazard susceptibility in Luchun County based on GIS and weighted information information model. Geol. Hazards Environ. Prot. 2022, 33, 37–43. [Google Scholar]
- Zhao, Z.; Xie, C.; Li, S. Evaluation of landslide susceptibility based on slope unit: A case study of mountain basin in Huichuan District, Zunyi City. Groundwater 2022, 44, 200–202. [Google Scholar]
- Hu, R.; Chen, P.; Zhuang, M.; Gao, W.; Sui, H.; Luo, G.; Gao, W.; Pan, S. Establishment and technical points of “Slope Length System For Geological Hazard Prevention and Control System. J. Eng. Geol. 2020, 28, 748–761. [Google Scholar]
- Lin, S.; Huang, Y.; Lin, J.; Jiang, F.; Yao, Y.; Ji, X. Comparative assessment of slope collapse risk based on information information model and random forest model. J. Mt. Sci. 2021, 39, 539–551. [Google Scholar]
- Ji, Y.; Wang, X.; Hao, Y.; Hu, P.; Wang, X.; Han, X.; Qiao, D. Survey and evaluation of urban geological hazard risk in Shaanxi Province based on slope unit: A case study of Jiangcun Subdistrict in Xi’an City. Hazard 2021, 34, 1–12. [Google Scholar]
- Tu, S.; Zhang, Z.; Fu, H.; Xu, S.; Deng, M.; He, X.; Liu, J. Evaluation of geological hazard susceptibility based on CF model and CF-LR model. Chin. J. Geol. Hazard Prev. 2019, 28, 1–10. [Google Scholar]
- Yao, J.; Ren, T.; Zhai, X.; Yuan, X.; Du, G. Evaluation of geological hazard susceptibility in Pingshan County based on GIS and weighted information information model. J. Hebei Univ. Geosci. 2021, 44, 47–53. [Google Scholar]
- Gao, L.; Su, J. Risk assessment method of debris flow in small area based on information entropy and AHP model. Res. Soil Water Conserv. 2017, 24, 376–380+2. [Google Scholar]
- Małka, A. Landslide susceptibility mapping of Gdynia using geographic information system-based statistical models. Nat. Hazards 2021, 107, 639–674. [Google Scholar] [CrossRef]
- Zeng, B.; Chen, X. Assessment of shallow landslide susceptibility using an artificial neural network. Arab. J. Geosci. 2021, 14, 1–18. [Google Scholar] [CrossRef]
- Lu, Y. Environmental FACTORS of URBAN CONSTRUCTION in mountainous areas from The Landslide hazard of Yuanyang County. Yunnan Environ. Sci. 1993, 23, 39–41. [Google Scholar]
- Li, Y.; Li, Z.; Zhao, Z. Evaluation of debris flow susceptibility based on deterministic coefficient model in lushui city. Res. Soil Water Conserv. 2019, 26, 336–342. [Google Scholar]
- Zou, F.; Leng, Y.; Tao, X.; He, S. Landslide risk identification based on slope unit: A case study of shallow soil slope in Wanshan, Guizhou Province. Chin. J. Geol. Hazard Prev. 2022, 33, 114–122. [Google Scholar]
- Liang, J. Decision analysis of ecological restoration of Tarim River Slope based on AHP. Water Conserv. Sci. Cold Reg. Eng. 2022, 5, 24–27. [Google Scholar]
- Wang, Z.; Guo, X.; Yu, Y.; Wang, N. Comprehensive evaluation of geoenvironmental quality of Beijing-Tianjin-Hebei urban agglomeration under multiple index system. Bull. Surv. Mapp. 2022, 47, 89–95+104. [Google Scholar]
- Liu, Y.; Huang, J.; Xiao, R.; Fang, R. Research on the early warning model of regional landslide disaster in Fujian Province based on random forest. Eng. Geol. 2022, 30, 944–955. [Google Scholar]
- Dang, J.; Dong, J.; He, S.; Fan, X.M. Application of Airborne LiDAR and Terrestrial 3D Laser Scanning in Risk Investigation of Collapse Geological Disasters in Duzhuzhai, Shuicheng, Guizhou. Chin. J. Geol. Disasters Prev. 2022, 33, 106–113. [Google Scholar]
- Zhou, S.H.; Fu, Y.H.; Xu, Z.W.; Yang, M.H.; Han, W.J. Evaluation of geological hazard susceptibility in Fujian Province based on subjective and objective weighting method. J. Saf. Environ. 2020, 37, 1–12. [Google Scholar]
- Xie, Z.; Peng, Z. Sensitivity evaluation and visual analysis of geological disasters in Tongliang, Chongqing. Geotech. Found. 2022, 36, 602–606. [Google Scholar]
- Li, P.; Li, L.H.; Liu, H.; Qi, S.W.; Deng, Q.H. Risk assessment of disturbance disaster for major hydropower projects in Lancang River basin. J. Eng. Geol. 2022, 30, 635–647. [Google Scholar]
- Qin, H.F.; Tan, S.C.; Shi, Y.Q.; Li, H.M.; Wang, B.X. Geological disaster susceptibility assessment based on CF-LR combined model—A case study of Ninger Hani and Yi Autonomous County, Yunnan Province. Renmin Chang. 2022, 53, 119–127. [Google Scholar]
- Li, T. On the risk assessment of geological disasters in construction sites-Taking Hengtai Huayuan Community in Wanrong County as an example. North China Nat. Resour. 2022, 21, 154–156. [Google Scholar]
- Mao, Q.X.; Hu, Y.P.; Liu, W.L.; Weng, M.Z.; Duan, X.F. Susceptibility Assessment of Slope Geological Disasters in Lichuan Mudao-Jiannan Linear Corridor Area Based on Information Quantity Model. Resour. Environ. Eng. 2022, 36, 175–180+217. [Google Scholar]
- Zhang, W. Analysis of the relationship between geological disasters and stratigraphic lithology in Guangdong Province. West. Resour. 2017, 62, 104–105+107. [Google Scholar]
- Yang, K.; Xue, X.; Li, S. Geological hazard susceptibility evaluation based on information content integrated into GA-optimized SVM model. Saf. Environ. Eng. 2022, 29, 109–118. [Google Scholar]
- Fan, Y.; Fan, X.; Fang, C. Modeling of county comprehensive geological hazards based on grid maximum method. Bull. Geol. Sci. Technol. 2022, 41, 197–208. [Google Scholar]
- Zhao, Y.; Deng, B.; Wang, X. Regionalization of geological hazard vulnerability based on Logistic and information information coupling model: A case study of a key town in southern Jiangxi Province. Geol. Hazards Environ. Prot. 2021, 32, 45–51. [Google Scholar]
- Zang, R. GIS-Based Risk Assessment of Geological Hazards in Yuanmou County; Kunming University of Science and Technology: Kunming, China, 2021. [Google Scholar]
- Shi, Y. Research on Landslide Monitoring and Identification and Susceptibility Evaluation in Reservoir Area Based on Time-Series InSAR; Kunming University of Science and Technology: Kunming, China, 2021. [Google Scholar]
- Li, H.L.; Huang, H.; Li, Y.L.; Zhang, J.J.; Wang, L.; Li, B.X. Study on the Effect of Geological Disasters in the Plate Suture Zone along the Sichuan-Tibet Railway. In Earth Sciences; Prentice Hall: Hoboken, NJ, USA, 1991; pp. 1–26. [Google Scholar]
- Wen, X.; Fan, X.M.; Chen, L.; Liu, S.K. Geological disaster susceptibility assessment based on information quantity model: A case study of Gulin County, Southeastern Sichuan. Geol. Sci. Technol. Bull. 2022, 41, 290–299. [Google Scholar]
- Bravo-Lopez, E.; Del Castillo, T.M.F.; Sellers, C.; Delgado-garcia, J. Landslide Susceptibility Mapping of Landslide Susceptibility, Landslide with Artificial Neural Networks: Multi-Approach Analysis of a Backpropagation Algorithm Applying the Neuralnet Package in Cuenca, Ecuador. Remote Sens. 2022, 14, 3495. [Google Scholar] [CrossRef]
- Wang, J.; Gao, Y.; Tie, Y.; Xu, W.; Bai, Y.; Zhang, Y. Evaluation of landslide hazard susceptibility in mountainous towns based on slope unit: A case study of Kangding. Sediment. Tethyan Geol. 2022, 39, 1–17. [Google Scholar]
- Wu, R.; Hu, X.; Mei, H.; He, J.; Yang, J. Spatial susceptibility assessment of landslides based on random forest: A case study of the Hubei section of the Three Gorges Reservoir Area. Earth Sci. 2021, 46, 321–330. [Google Scholar]
- Yuan, X.; Liu, C.; Nie, R.; Yang, Z.; Li, W.; Dai, X.; Cheng, J.; Zhang, J.; Ma, L.; Fu, X.; et al. A Comparative Analysis of Certainty Factor-Based Machine Learning Methods for Collapse and Landslide Susceptibility Mapping in Wenchuan County, China. Remote Sens. 2022, 14, 3259. [Google Scholar] [CrossRef]
- Jin, B.; In, K.; Li, Q.; Gui, L.; Yang, T.; Zhao, B.; Guo, B.; Zeng, T.; Ma, Z. Susceptibility Analysis of Land Subsidence along the Transmission Line in the Salt Lake Area Based on Remote Sensing Interpretation. Remote Sens. 2022, 14, 3229. [Google Scholar] [CrossRef]
- Xu, L.; Chen, C.L.; Qing, F.; Meng, X.; Zhao, Y.; Qi, T.; Miao, T. Graph-Represented Broad Learning System for Landslide Susceptibility Mapping in Alpine-Canyon Region. Remote Sens. 2022, 14, 2773. [Google Scholar] [CrossRef]
- Chang, L.; Zhang, R.; Wang, C. Evaluation and Prediction of Landslide Susceptibility in Yichang Section of Yangtze River Basin Based on Integrated Deep Learning Algorithm. Remote Sens. 2022, 14, 2717. [Google Scholar] [CrossRef]
- Zhu, L. Comprehensive Application and Research of Machine Learning in Sensitivity Assessment of Shallow Landslide; Jilin University: Jilin, China, 2021. [Google Scholar]
- Gao, H.; Zhang, X. Landslide Susceptibility Assessment Considering Landslide Volume: A Case Study of Yangou Watershed on the Loess Plateau (China). Appl. Sci. 2022, 12, 4381. [Google Scholar] [CrossRef]
- Sun, X.; Chen, J.; Li, Y.; Rene, N. Landslide Susceptibility Mapping along a Rapidly Uplifting River Valley of the Upper Jinsha River, Southeastern Tibetan Plateau, China. Remote Sens. 2022, 14, 1730. [Google Scholar] [CrossRef]
- Liu, S. Research on Risk Assessment and Early Warning Technology of Transmission Line Landslide under Rainfall Conditions; China University of Geosciences: Wuhan, China, 2021. [Google Scholar]
- Bruzon, A.G.; Arrogante-Funes, P.; Arrogante-Funes, F.; Martin—Gonzalez, F.; Novillo, C.J.; Fernandez, R.R.; Vazquez-Jimenez, R.; Alarcon-Paredes, A.; Alonso-Silverio, G.A.; Cantu-Ramirez, C.A.; et al. Landslide Susceptibility Assessment Using an Automl Framework. Int. J. Environ. Res. Public Health 2021, 18, 10971. [Google Scholar] [CrossRef]
- Qin, Y.; Cao, L.; Darvishi Boloorani, A.; Wu, W. High-Resolution Mining-Induced Geo-Hazard Mapping Using Random Forest: A Case Study of Liaojiaping Orefield, Central China. Remote Sens. 2021, 13, 3638. [Google Scholar] [CrossRef]
- Qin, Y.; Yang, G.; Lu, K.; Sun, Q.; Xie, J.; Wu, Y. Performance Evaluation of Five GIS-Based Models for Landslide Susceptibility Prediction and Mapping: A Case Study of Kaiyang County, China. Sustainability 2021, 13, 6441. [Google Scholar] [CrossRef]
- Rui-chi, X. Probabilistic Identification and Prediction of Potential Landslide Hazard Area in Sichuan-Tibet Traffic Corridor Based on Slope Unit; University of Chinese Academy of Sciences (Chengdu Institute of Mountain Hazards and Environment, Ministry of Water Resources, Chinese Academy of Sciences): Beijing, China, 2020. [Google Scholar]
- Kontoes, C.; Loupasakis, C.; Papoutsis, I.; Alatza, S.; Poyiadji, E.; Ganas, A.; Psychogyiou, C.; Kaskara, M.; Antoniadi, S.; Spanou, N. Landslide Susceptibility Mapping of Central and Western Greece, Combining NGI and WoE Methods, with Remote Sensing and Ground Truth Data. Land 2021, 10, 402. [Google Scholar] [CrossRef]
- Bi, H.J.; Nie, L.; Zeng, C.; Fan, C.; Zhou, T.L.; Liu, X. Evaluation of geological hazard susceptibility in Wenchuan County based on three multivariate instability index analysis models. Chin. J. Geol. Hazards Prev. 2022, 33, 123–131. [Google Scholar]









| Evaluation Factors | Classification | Si | Si/S | Ni | Ni/N | Amount of Information | Weight | CR | |||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Grid Unit | Slope Unit | Grid Unit | Slope Unit | Grid Unit | Slope Unit | ||||||
| Geomorphic types | Stacked valley landform | 238,887 | 672 | 0.07 | 0.09 | 22 | 0.09 | 0.25 | 0.05 | 0.0391 | 0.0462 |
| Karst mountain landform | 238,887 | 726 | 0.07 | 0.09 | 24 | 0.10 | 0.33 | 0.06 | |||
| Tectonically eroded mid-mountain landform | 2,873,413 | 6446 | 0.84 | 0.82 | 199 | 0.81 | −0.04 | −0.01 | |||
| Tectonically eroded low mountain landform | 53,971 | 52 | 0.02 | 0.01 | 0 | 0.00 | 0.00 | 0.00 | |||
| Land-use type | Woodland | 2,601,414 | 5757 | 0.73 | 0.73 | 120 | 0.49 | −0.41 | −0.40 | 0.0680 | |
| Shrubs | 2993 | 7 | 0.00 | 0.00 | 0 | 0.00 | 0.00 | 0.00 | |||
| Grass | 580,768 | 1095 | 0.16 | 0.14 | 19 | 0.08 | −0.75 | −0.58 | |||
| Arable land | 232,178 | 562 | 0.07 | 0.07 | 7 | 0.03 | −0.83 | −0.91 | |||
| Land for construction | 30,571 | 84 | 0.01 | 0.01 | 44 | 0.18 | 3.04 | 2.83 | |||
| Bare ground or sparse vegetation | 78,435 | 226 | 0.02 | 0.03 | 55 | 0.22 | 2.32 | 2.06 | |||
| Open waters | 14,991 | 73 | 0.00 | 0.01 | 0 | 0.00 | 0.00 | 0.00 | |||
| Herb wetland | 61 | 2 | 0.00 | 0.00 | 0 | 0.00 | 0.00 | 0.00 | |||
| Distance from fault (m) | 50 | 63,229 | 156 | 0.02 | 0.02 | 4 | 0.02 | −0.09 | −0.19 | 0.1314 | |
| 100 | 63,331 | 160 | 0.02 | 0.02 | 5 | 0.02 | 0.13 | 0.01 | |||
| 300 | 246,527 | 581 | 0.07 | 0.07 | 28 | 0.11 | 0.50 | 0.44 | |||
| 500 | 235,754 | 496 | 0.07 | 0.06 | 23 | 0.09 | 0.34 | 0.40 | |||
| 1000 | 541,180 | 1158 | 0.15 | 0.15 | 38 | 0.16 | 0.01 | 0.06 | |||
| 3000 | 1,281,573 | 2767 | 0.36 | 0.35 | 91 | 0.37 | 0.03 | 0.06 | |||
| >3000 | 1,109,778 | 2578 | 0.31 | 0.33 | 56 | 0.23 | −0.32 | −0.36 | |||
| Elevation (m) | 110–650 | 408,649 | 913 | 0.12 | 0.12 | 21 | 0.09 | −0.30 | −0.30 | 0.1634 | |
| 650–1050 | 729,924 | 1652 | 0.21 | 0.21 | 23 | 0.09 | −0.79 | −0.80 | |||
| 1050–1400 | 846,548 | 1900 | 0.24 | 0.24 | 52 | 0.21 | −0.12 | −0.13 | |||
| 1400–1700 | 811,256 | 1681 | 0.23 | 0.21 | 118 | 0.48 | 0.74 | 0.82 | |||
| 1700–2150 | 545,512 | 1241 | 0.15 | 0.16 | 30 | 0.12 | −0.23 | −0.25 | |||
| 2150–2950 | 199,476 | 509 | 0.06 | 0.06 | 1 | 0.00 | −2.62 | −2.76 | |||
| Engineering geological rock group | Thin–medium-form soft mudstone, argillaceous siltstone rock group | 142,964 | 205 | 0.04 | 0.03 | 3 | 0.01 | −1.19 | −0.75 | 0.0888 | |
| Medium–thick layer of hard strong karstic limestone, dolomite, dolomite limestone group | 55,908 | 93 | 0.02 | 0.01 | 1 | 0.00 | −1.35 | −1.06 | |||
| Clay and sandy clay mixed with gravel multilayer soil | 14,812 | 59 | 0.00 | 0.01 | 1 | 0.00 | −0.02 | −0.60 | |||
| Formation of thin–medium hard gneiss and metamorphic rocks | 1,658,434 | 3880 | 0.47 | 0.49 | 117 | 0.48 | 0.02 | −0.03 | |||
| Thin–medium hard marble, amphibolite, metamorphic rock group | 131,907 | 327 | 0.04 | 0.04 | 4 | 0.02 | −0.82 | −0.93 | |||
| Thin–medium form of hard mud shale, siltstone rocks | 541,466 | 1198 | 0.15 | 0.15 | 49 | 0.20 | 0.27 | 0.28 | |||
| Massive hard intrusive rock formation | 441,545 | 1011 | 0.12 | 0.13 | 38 | 0.16 | 0.22 | 0.19 | |||
| Fragmented, massive, relatively hard extruded rock group | 196,231 | 398 | 0.06 | 0.05 | 7 | 0.03 | −0.66 | −0.57 | |||
| Medium–thick layer of hard weakly karstic limestone and dolomite splint rock group | 303,885 | 613 | 0.09 | 0.08 | 23 | 0.09 | 0.09 | 0.19 | |||
| Medium–thick stratified hard sandstone, quartz sandstone rock group | 7250 | 18 | 0.00 | 0.00 | 2 | 0.01 | 1.38 | 1.28 | |||
| Medium–thick stratified hard medium karstic limestone and dolomitic limestone group | 29,680 | 67 | 0.01 | 0.01 | 0 | 0.00 | 0.00 | 0.00 | |||
| Thin-bedded hard slate rock group | 16,893 | 27 | 0.00 | 0.00 | 0 | 0.00 | 0.00 | 0.00 | |||
| Slope (°) | 0–8 | 131,433 | 1022 | 0.04 | 0.13 | 7 | 0.03 | −0.27 | −1.51 | 0.1694 | |
| 8–15 | 450,167 | 1374 | 0.13 | 0.17 | 51 | 0.21 | 0.49 | 0.18 | |||
| 15–25 | 1,235,738 | 2487 | 0.35 | 0.31 | 103 | 0.42 | 0.18 | 0.29 | |||
| 25–35 | 1,161,406 | 2022 | 0.33 | 0.26 | 64 | 0.26 | −0.23 | 0.02 | |||
| 35–90 | 550,193 | 991 | 0.16 | 0.13 | 20 | 0.08 | −0.65 | −0.43 | |||
| Aspect | Plane | 28,351 | 79 | 0.01 | 0.01 | 1 | 0.00 | −0.68 | −0.90 | 0.0870 | |
| North | 315,913 | 636 | 0.09 | 0.08 | 19 | 0.08 | −0.14 | −0.04 | |||
| Northeast | 534,362 | 1362 | 0.15 | 0.17 | 37 | 0.15 | 0.00 | −0.13 | |||
| East | 405,228 | 916 | 0.11 | 0.12 | 31 | 0.13 | 0.10 | 0.09 | |||
| Southeast | 449,606 | 981 | 0.13 | 0.12 | 29 | 0.12 | −0.07 | −0.05 | |||
| South | 408,220 | 859 | 0.12 | 0.11 | 38 | 0.16 | 0.30 | 0.35 | |||
| Southwest | 335,603 | 804 | 0.09 | 0.10 | 21 | 0.09 | −0.10 | −0.17 | |||
| West | 317,065 | 697 | 0.09 | 0.09 | 22 | 0.09 | 0.00 | 0.02 | |||
| Northwest | 442,634 | 958 | 0.13 | 0.12 | 27 | 0.11 | −0.13 | −0.10 | |||
| North | 298,057 | 604 | 0.08 | 0.08 | 20 | 0.08 | −0.03 | 0.07 | |||
| Curvature | Concave type slope | 934,362 | 2222 | 0.26 | 0.28 | 49 | 0.20 | −0.28 | −0.34 | 0.0304 | |
| Flat surface slope | 1,528,094 | 3333 | 0.43 | 0.42 | 121 | 0.49 | 0.13 | 0.16 | |||
| Convex type slope | 1,069,874 | 2341 | 0.30 | 0.30 | 75 | 0.31 | 0.01 | 0.03 | |||
| Distance from river (m) | 50 | 419,847 | 1579 | 0.12 | 0.20 | 33 | 0.13 | 0.13 | −0.40 | 0.0532 | |
| 100 | 376,932 | 628 | 0.11 | 0.08 | 25 | 0.10 | −0.04 | 0.25 | |||
| 300 | 1,189,564 | 2375 | 0.34 | 0.30 | 74 | 0.30 | −0.11 | 0.00 | |||
| 500 | 746,745 | 1472 | 0.21 | 0.19 | 55 | 0.22 | 0.06 | 0.19 | |||
| 1000 | 698,574 | 1562 | 0.20 | 0.20 | 55 | 0.22 | 0.13 | 0.13 | |||
| 3000 | 109,676 | 280 | 0.03 | 0.04 | 3 | 0.01 | −0.93 | −1.06 | |||
| Evaluation Unit | Susceptibility Grade | Number of Damage Points | Proportion | Interval Area (km2) | Proportion |
|---|---|---|---|---|---|
| Grid unit | Low | 31 | 11.97% | 475.55 | 21.55% |
| Medium | 61 | 23.55% | 782.7 | 35.46% | |
| High | 67 | 25.87% | 556.89 | 25.23% | |
| Very high | 100 | 38.61% | 392.01 | 17.16% | |
| Slope unit | Low | 19 | 7.34% | 410.06 | 18.58% |
| Medium | 21 | 8.11% | 470.21 | 21.30% | |
| High | 77 | 29.73% | 550.02 | 24.92% | |
| Very high | 142 | 54.83% | 776.87 | 35.20% |
| Evaluation Unit | Working Condition of Rainfall | Level of Risk | Area (km2) | Proportion (%) | Number of Damage Points | Proportion (%) |
|---|---|---|---|---|---|---|
| Slope unit | Heavy rain | Low | 285.47 | 12.88% | 3 | 1.32% |
| Medium | 897.58 | 40.51% | 38 | 16.67% | ||
| High | 796.35 | 35.94% | 83 | 36.40% | ||
| Very high | 236.47 | 10.67% | 104 | 45.61% | ||
| Rainstorm | Low | 211.76 | 9.56% | 2 | 0.88% | |
| Medium | 785.26 | 35.44% | 35 | 15.35% | ||
| High | 923.09 | 41.66% | 80 | 35.09% | ||
| Very high | 295.77 | 13.35% | 111 | 48.68% | ||
| Heavy rainstorm | Low | 117.02 | 5.28% | 2 | 0.88% | |
| Medium | 640.59 | 28.91% | 25 | 10.96% | ||
| High | 1077.75 | 48.64% | 76 | 33.33% | ||
| Very high | 380.52 | 17.17% | 125 | 54.82% | ||
| Extraordinary rainstorm | Low | 46.52 | 2.10% | 2 | 0.88% | |
| Medium | 391.71 | 17.68% | 6 | 2.63% | ||
| High | 1300.44 | 58.69% | 79 | 34.65% | ||
| Very high | 477.21 | 21.54% | 141 | 61.84% | ||
| Grid unit | Heavy rain | Low | 300.75 | 13.57% | 2 | 0.88% |
| Medium | 872.18 | 39.36% | 63 | 27.63% | ||
| High | 736.89 | 33.25% | 61 | 26.75% | ||
| Very high | 306.06 | 13.81% | 102 | 44.74% | ||
| Rainstorm | Low | 248.97 | 11.24% | 2 | 0.88% | |
| Medium | 765.52 | 34.55% | 43 | 18.86% | ||
| High | 860.20 | 38.82% | 67 | 29.39% | ||
| Very high | 341.19 | 15.40% | 116 | 50.88% | ||
| Heavy rainstorm | Low | 118.80 | 5.36% | 2 | 0.88% | |
| Medium | 644.32 | 29.08% | 28 | 12.28% | ||
| High | 954.51 | 43.08% | 77 | 33.77% | ||
| Very high | 498.24 | 22.49% | 121 | 53.07% | ||
| Extraordinary rainstorm | Low | 79.85 | 3.60% | 2 | 0.88% | |
| Medium | 356.23 | 16.08% | 9 | 3.95% | ||
| High | 1196.48 | 54.00% | 100 | 43.86% | ||
| Very high | 583.32 | 26.32% | 117 | 51.32% |
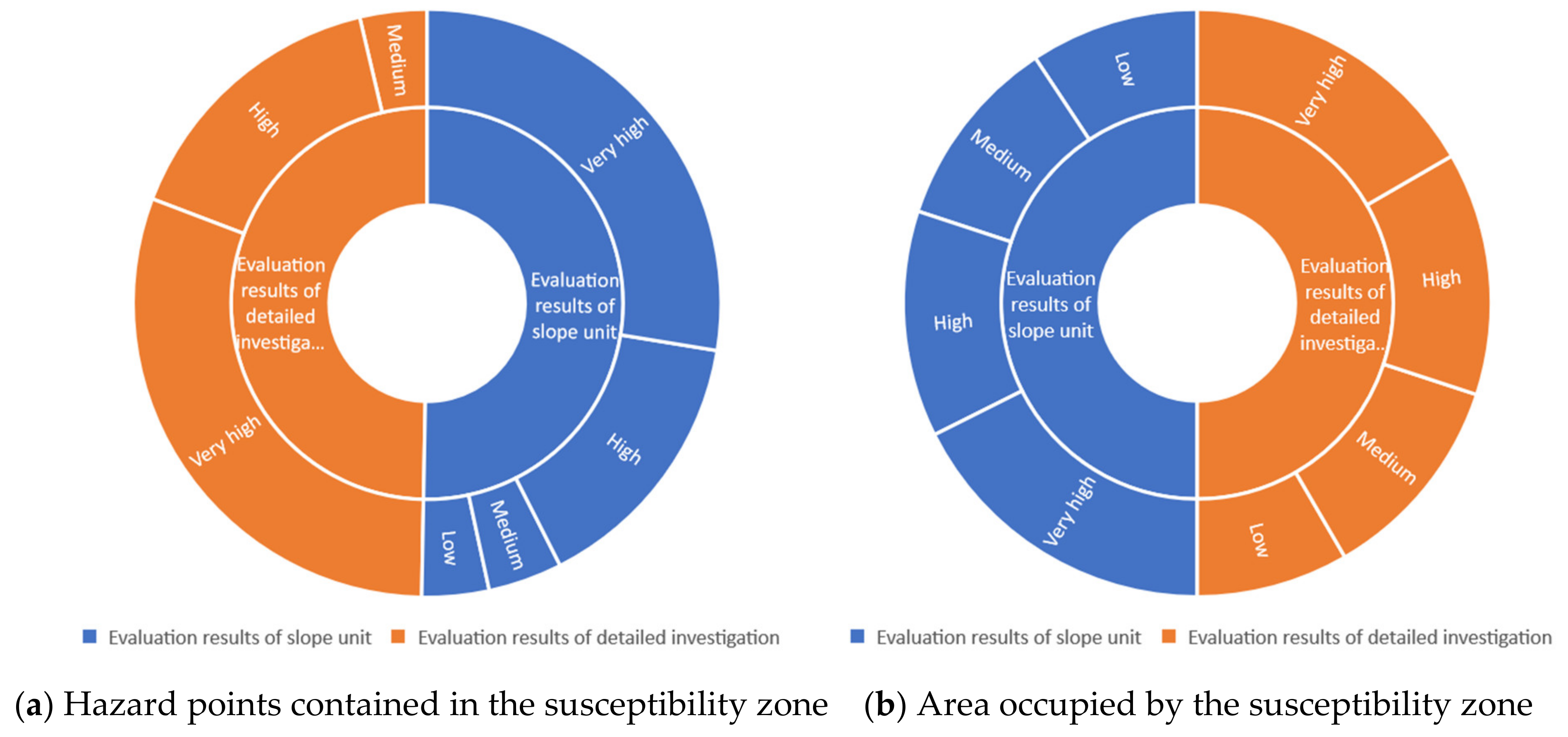
| Result Source | Susceptibility Grade | Number of Hazard Sites | Proportion | Interval Area (km2) | Proportion |
|---|---|---|---|---|---|
| Evaluation results of slope unit system | Low | 19 | 7.34% | 410.06 | 18.58% |
| Medium | 21 | 8.11% | 470.21 | 21.30% | |
| High | 77 | 29.73% | 550.02 | 24.92% | |
| Very high | 142 | 54.83% | 776.87 | 35.20% | |
| Evaluation results of detailed investigation | Low | 0 | 0.00% | 369.70 | 16.75% |
| Medium | 19 | 7.34% | 511.18 | 23.16% | |
| High | 80 | 30.89% | 591.30 | 26.79% | |
| Very high | 157 | 60.62% | 734.98 | 33.30% |
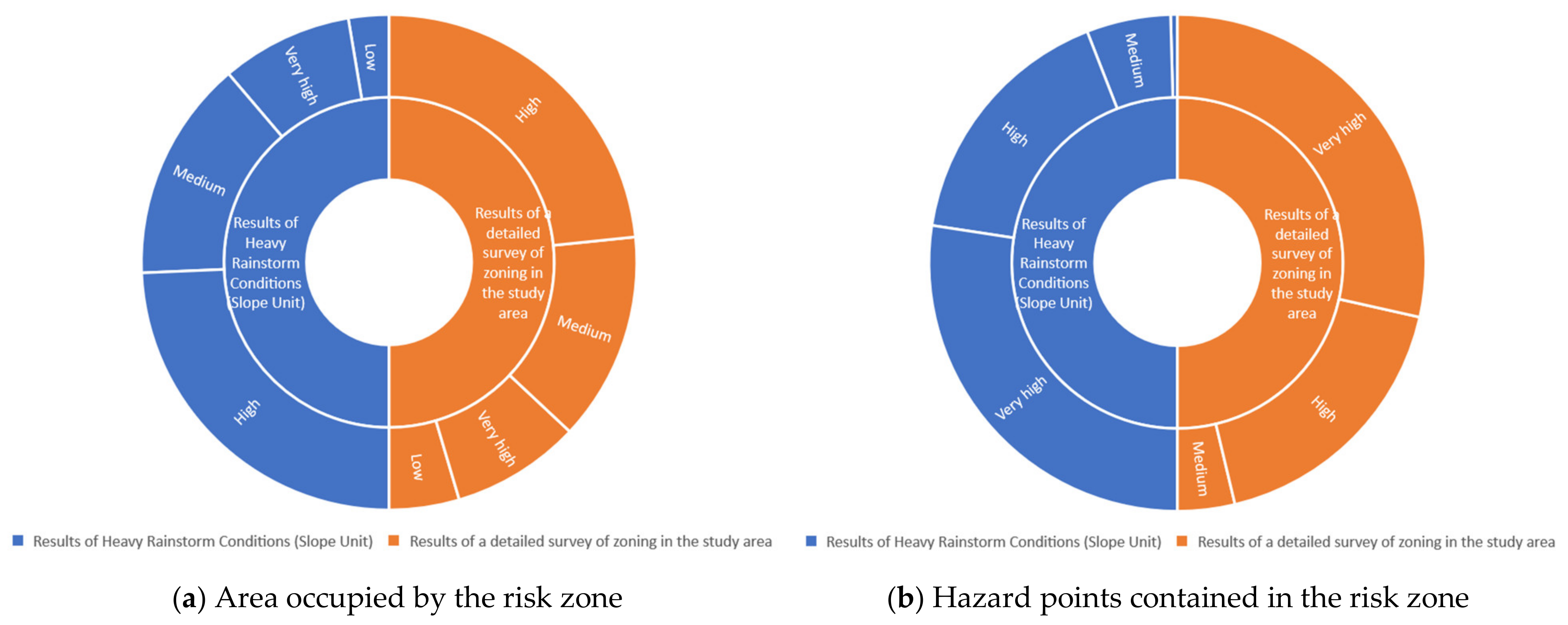
| Results the Source | Level of Risk | Interval Area (km2) | Proportion (%) | Number of Hazard Sites | Proportion (%) |
|---|---|---|---|---|---|
| Results for heavy rainstorm conditions (slope unit system) | Low | 117.02 | 5.28% | 2 | 0.88% |
| Medium | 640.59 | 28.91% | 25 | 10.96% | |
| High | 1077.75 | 48.64% | 76 | 33.33% | |
| Very high | 380.52 | 17.17% | 125 | 54.82% | |
| Results of a detailed survey of zoning in the study area | Low | 202.77 | 9.15% | 0 | 0.00% |
| Medium | 603.41 | 27.23% | 17 | 7.46% | |
| High | 1035.42 | 46.73% | 81 | 35.53% | |
| Very high | 374.28 | 16.89% | 130 | 57.02% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, S.; Zhu, J.; Yang, D.; Ma, B. Comparative Study of Geological Hazard Evaluation Systems Using Grid Units and Slope Units under Different Rainfall Conditions. Sustainability 2022, 14, 16153. https://doi.org/10.3390/su142316153
Liu S, Zhu J, Yang D, Ma B. Comparative Study of Geological Hazard Evaluation Systems Using Grid Units and Slope Units under Different Rainfall Conditions. Sustainability. 2022; 14(23):16153. https://doi.org/10.3390/su142316153
Chicago/Turabian StyleLiu, Shuai, Jieyong Zhu, Dehu Yang, and Bo Ma. 2022. "Comparative Study of Geological Hazard Evaluation Systems Using Grid Units and Slope Units under Different Rainfall Conditions" Sustainability 14, no. 23: 16153. https://doi.org/10.3390/su142316153
APA StyleLiu, S., Zhu, J., Yang, D., & Ma, B. (2022). Comparative Study of Geological Hazard Evaluation Systems Using Grid Units and Slope Units under Different Rainfall Conditions. Sustainability, 14(23), 16153. https://doi.org/10.3390/su142316153







