A Multi-Equipment Task Assignment Model for the Horizontal Stripe Pre-Cut Mining Method
Abstract
1. Introduction
2. Literature Review
3. Analysis of the Horizontal Stripe Pre-Cut Mining Method
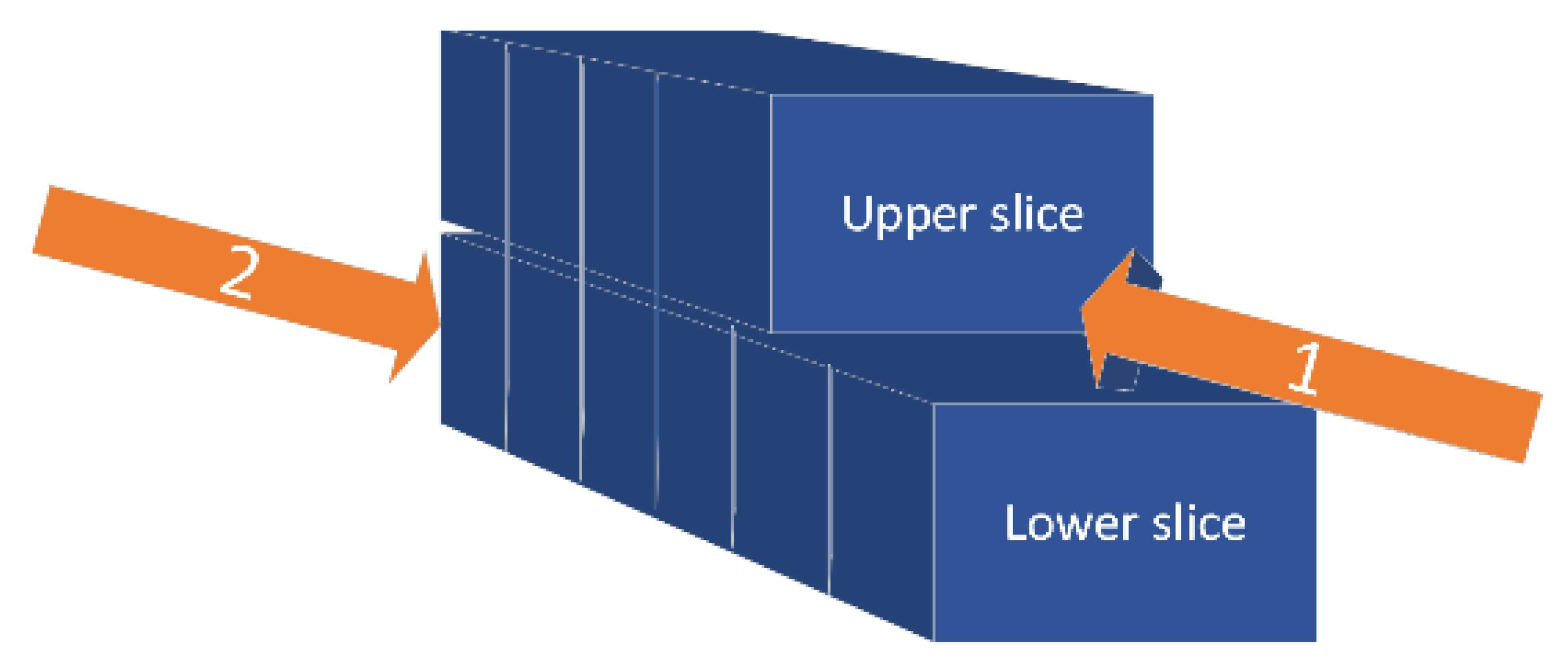
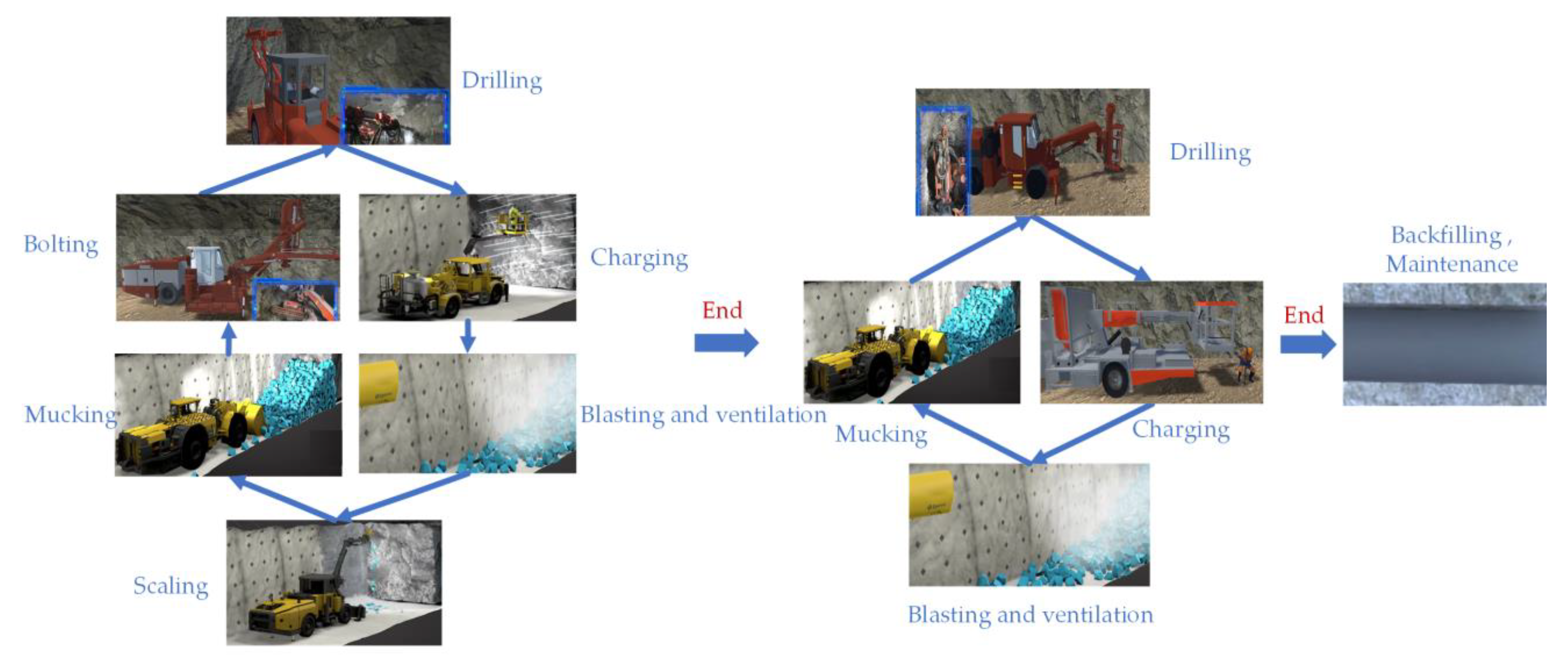
3.1. Mining Method Process Analysis
3.2. Multi-Equipment Task Assignment Definition
4. Modeling and Solution Methodology
4.1. Notations
4.2. Mathematical Model
4.2.1. Objective Functions
4.2.2. Equivalent Relations
4.2.3. Constraints
4.3. Solution Method
5. Case Study
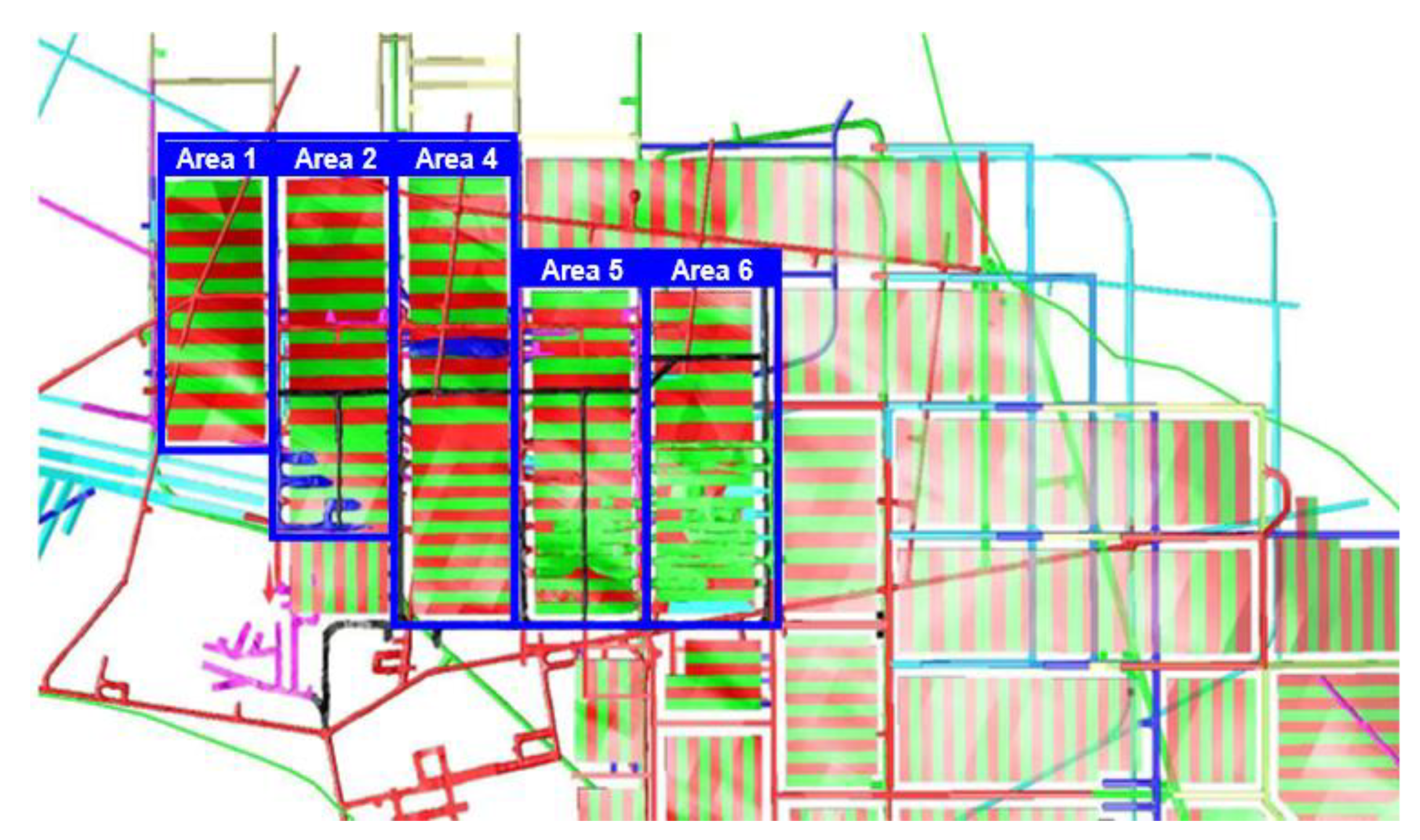
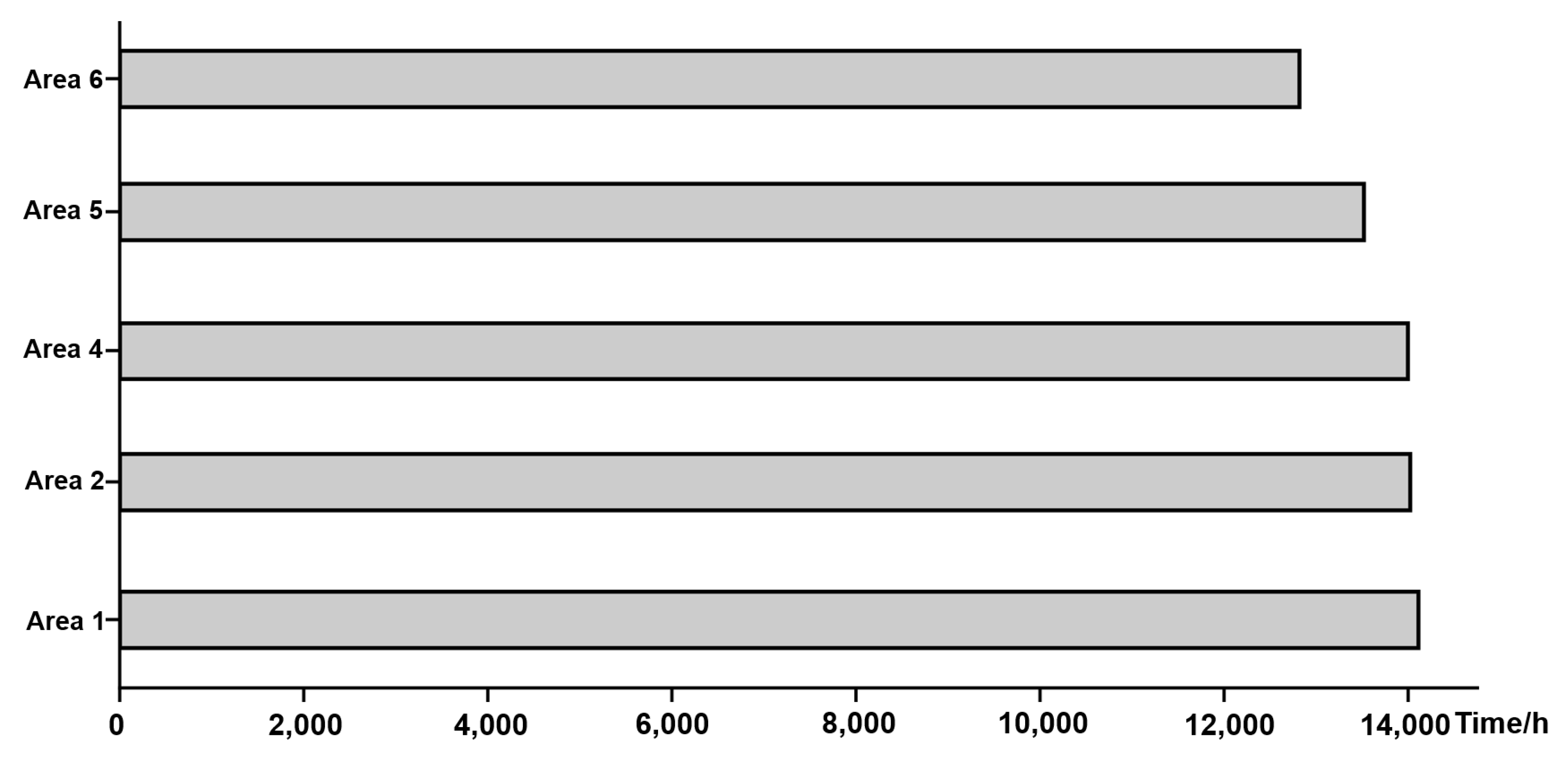
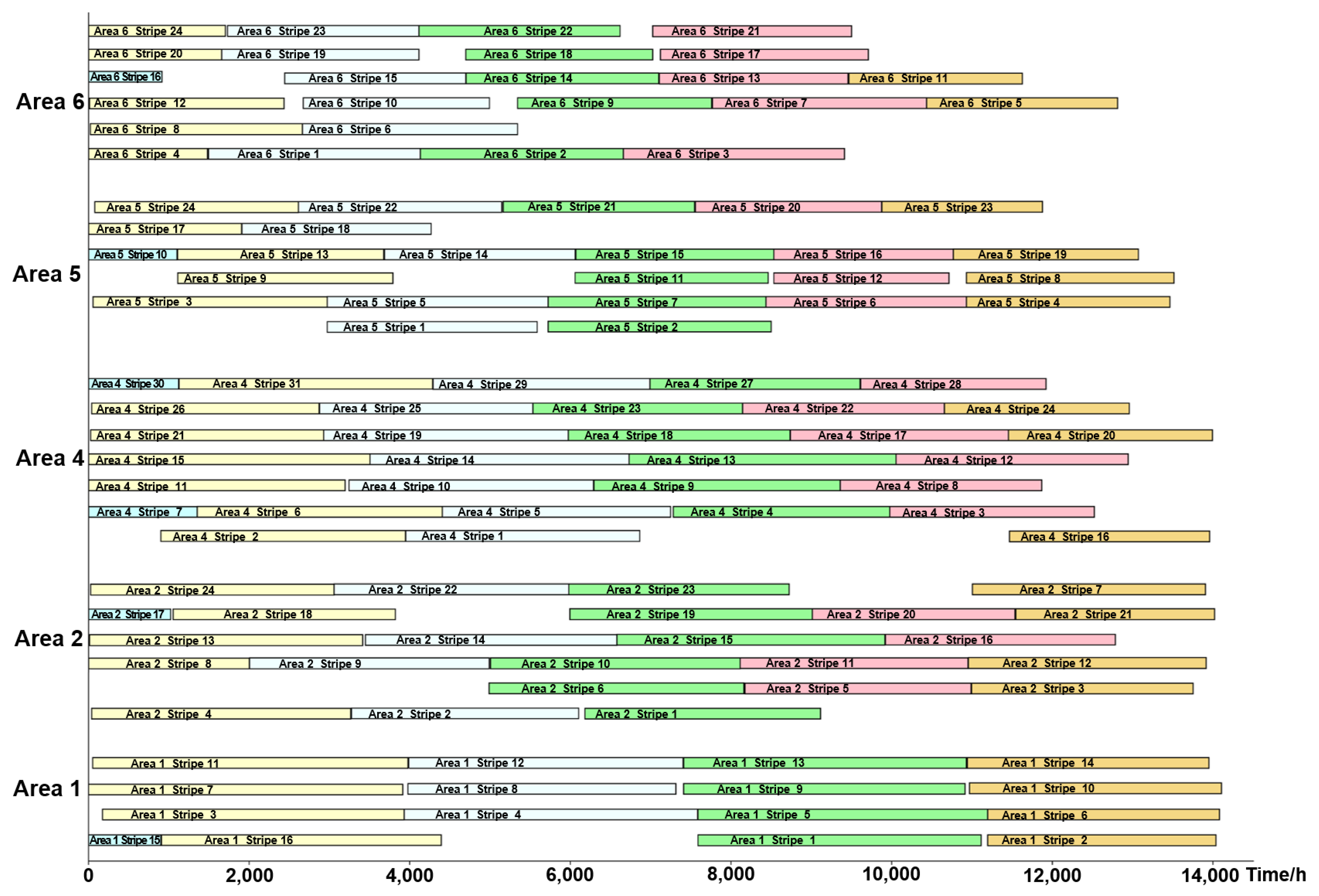
5.1. Datasets
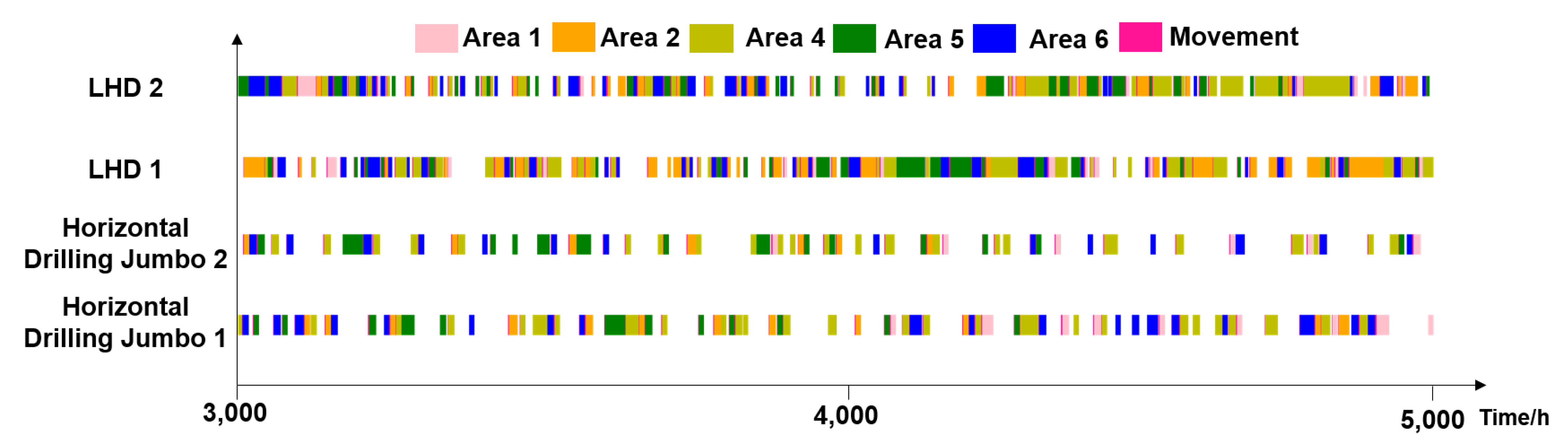
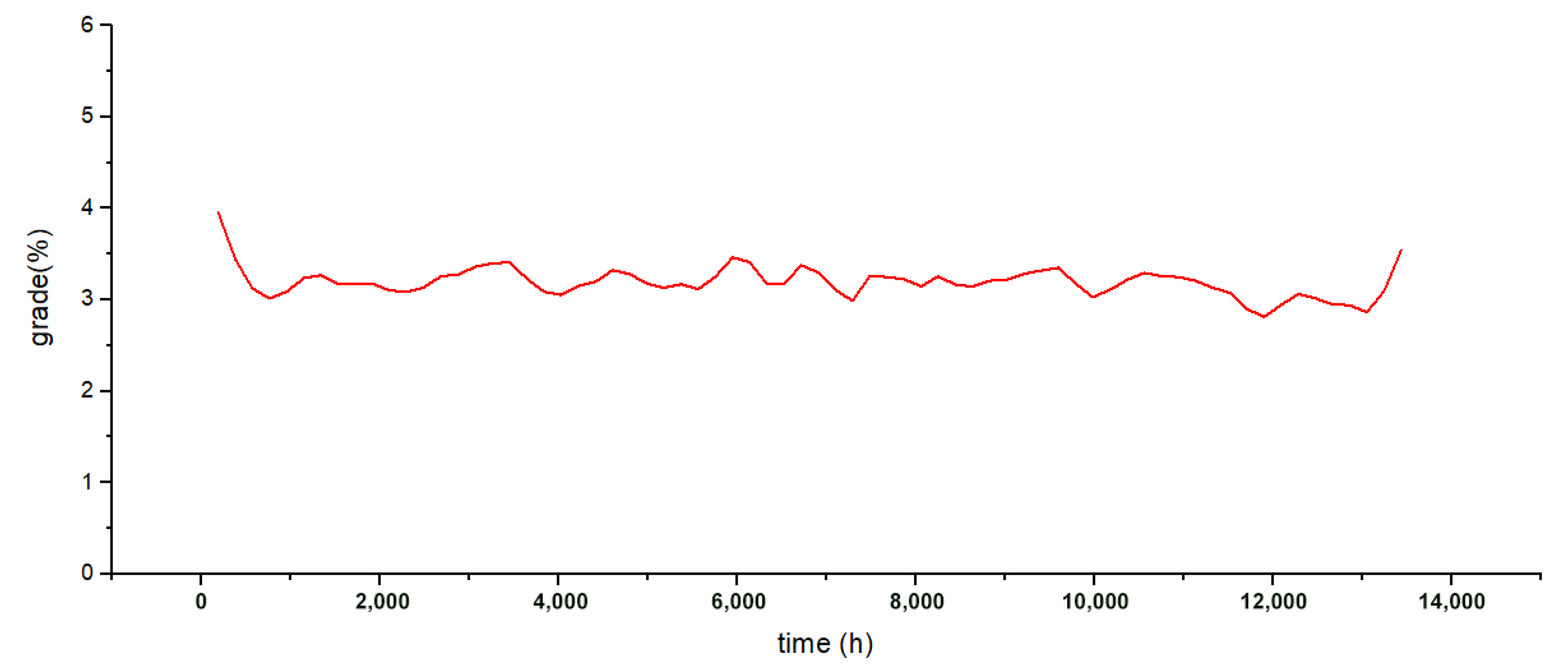
5.2. Result
5.3. Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Li, J.; Zhan, K. Intelligent Mining Technology for an Underground Metal Mine Based on Unmanned Equipment. Engineering 2018, 4, 381–391. [Google Scholar] [CrossRef]
- Guo, Q.; Cai, M.; Wu, X.; Xi, X.; Ma, M.; Zhang, J. Technological strategies for intelligent mining subject to multifield couplings in deep metal mines toward 2035. Chin. J. Eng. 2022, 44, 476–486. [Google Scholar]
- Yu, H.; Zhao, C.; Li, S.; Wang, Z.; Zhang, Y. Pre-Work for the Birth of Driver-Less Scraper (LHD) in the Underground Mine: The Path Tracking Control Based on an LQR Controller and Algorithms Comparison. Sensors 2021, 21, 7839. [Google Scholar] [CrossRef]
- Xiao, W.; Liu, M.; Chen, X. Research Status and Development Trend of Underground Intelligent Load-Haul-Dump Vehicle—A Comprehensive Review. Appl. Sci. 2022, 12, 9290. [Google Scholar] [CrossRef]
- Zhang, T.; Fu, T.; Cui, Y.; Song, X. Toward Autonomous Mining: Design and Development of an Unmanned Electric Shovel via Point Cloud-Based Optimal Trajectory Planning. Front. Mech. Eng. 2022, 17, 30. [Google Scholar] [CrossRef]
- Wang, Y.; van Stein, B.; Back, T.; Emmerich, M. A Tailored NSGA-III for Multi-Objective Flexible Job Shop Scheduling. In Proceedings of the 2020 IEEE Symposium Series on Computational Intelligence (SSCI), Canberra, Australia, 1–4 December 2020; IEEE: New York, NY, USA, 2020; pp. 2746–2753. [Google Scholar]
- Sang, Y.; Tan, J.; Liu, W. Research on Many-Objective Flexible Job Shop Intelligent Scheduling Problem Based on Improved NSGA-III. IEEE Access 2020, 8, 157676–157690. [Google Scholar] [CrossRef]
- Sun, X.; Wang, Y.; Kang, H.; Shen, Y.; Chen, Q.; Wang, D. Modified Multi-Crossover Operator NSGA-III for Solving Low Carbon Flexible Job Shop Scheduling Problem. Processes 2021, 9, 62. [Google Scholar] [CrossRef]
- Ioan, D.; Prodan, I.; Olaru, S.; Stoican, F.; Niculescu, S.-I. Mixed-Integer Programming in Motion Planning. Annu. Rev. Control 2021, 51, 65–87. [Google Scholar] [CrossRef]
- Nguyen, T.-D.; Nguyen-Quang, T.; Venkatadri, U.; Diallo, C.; Adams, M. Mathematical Programming Models for Fresh Fruit Supply Chain Optimization: A Review of the Literature and Emerging Trends. AgriEngineering 2021, 3, 519–541. [Google Scholar] [CrossRef]
- Yin, T.; Zhang, Z.; Zhang, Y.; Wu, T.; Liang, W. Mixed-Integer Programming Model and Hybrid Driving Algorithm for Multi-Product Partial Disassembly Line Balancing Problem with Multi-Robot Workstations. Robot. Comput.-Integr. Manuf. 2022, 73, 102251. [Google Scholar] [CrossRef]
- Zhao, Y.; Zhang, C.; Wang, Y.; Lin, H. Shear-Related Roughness Classification and Strength Model of Natural Rock Joint Based on Fuzzy Comprehensive Evaluation. Int. J. Rock Mech. Min. Sci. 2021, 137, 104550. [Google Scholar] [CrossRef]
- Zhao, Y.; Liu, Q.; Zhang, C.; Liao, J.; Lin, H.; Wang, Y. Coupled Seepage-Damage Effect in Fractured Rock Masses: Model Development and a Case Study. Int. J. Rock Mech. Min. Sci. 2021, 144, 104822. [Google Scholar] [CrossRef]
- Liu, J.; Zhao, Y.; Tan, T.; Zhang, L.; Zhu, S.; Xu, F. Evolution and Modeling of Mine Water Inflow and Hazard Characteristics in Southern Coalfields of China: A Case of Meitanba Mine. Int. J. Min. Sci. Technol. 2022, 32, 513–524. [Google Scholar] [CrossRef]
- Williams, J.K.; Smith, L.; Wells, P.M. Planning of Underground Copper Mining. In In Proceedings of the 10th International Symposium on Application of Computer Methods in the Mineral Industry, Johannesburg, Republic of South Africa, 10–14 April 1972; pp. 251–254. Available online: https://www.saimm.co.za/Conferences/Apcom72/251-Williams.pdf (accessed on 3 November 2022).
- Trout, L. Underground Mine Production Scheduling Using Mixed Integer Programming. In Proceedings of the 25th International APCOM Symposium Proceedings, Brisbane, Australia, 9–14 July 1995; The Australasian Institute of Mining and Metallurgy Melbourne: Melbourne, Australia, 1995; pp. 395–400. [Google Scholar]
- Carlyle, W.M.; Eaves, B.C. Underground Planning at Stillwater Mining Company. Interfaces 2001, 31, 50–60. [Google Scholar] [CrossRef]
- Topal, E. Advanced Underground Mine Scheduling Using Mixed Integer Programming; Colorado School of Mines: Golden, CO, USA, 2004. [Google Scholar]
- Kuchta, M.; Newman, A.; Topal, E. Implementing a Production Schedule at LKAB’s Kiruna Mine. Interfaces 2004, 34, 124–134. [Google Scholar] [CrossRef]
- Nehring, M.; Topal, E. Production Schedule Optimisation in Underground Hard Rock Mining Using Mixed Integer Programming. In Proceedings of the Project Evaluation Conference, Melbourne, Australia, 19–20 June 2007; pp. 169–175. [Google Scholar]
- Topal, E. Early Start and Late Start Algorithms to Improve the Solution Time for Long-Term Underground Mine Production Scheduling. J. South. Afr. Inst. Min. Metall. 2008, 108, 99–107. [Google Scholar]
- Campeau, L.-P.; Gamache, M. Short-Term Planning Optimization Model for Underground Mines. Comput. Oper. Res. 2020, 115, 104642. [Google Scholar] [CrossRef]
- Newman, A.M.; Kuchta, M.; Martinez, M. Long- and Short-Term Production Scheduling at Lkab’s Kiruna Mine. In Handbook Of Operations Research In Natural Resources; Springer International Publishing: Boston, MA, USA, 2007; pp. 579–593. [Google Scholar]
- Martinez, M.A.; Newman, A.M. A Solution Approach for Optimizing Long- and Short-Term Production Scheduling at LKAB’s Kiruna Mine. Eur. J. Oper. Res. 2011, 211, 184–197. [Google Scholar] [CrossRef]
- Nehring, M.; Topal, E.; Kizil, M.; Knights, P. Integrated Short- and Medium-Term Underground Mine Production Scheduling. J. South. Afr. Inst. Min. Metall. 2012, 112, 365–378. [Google Scholar]
- Little, J.; Knights, P.; Topal, E. Integrated Optimization of Underground Mine Design and Scheduling. J. South. Afr. Inst. Min. Metall. 2013, 113, 775–785. [Google Scholar]
- Campeau, L.-P.; Gamache, M.; Martinelli, R. Integrated Optimisation of Short- and Medium-Term Planning in Underground Mines. Int. J. Min. Reclam. Environ. 2022, 36, 235–253. [Google Scholar] [CrossRef]
- Chanda, E.C.K. An Application of Integer Programming and Simulation to Production Planning for a Stratiform Ore Body. Min. Sci. Technol. 1990, 11, 165–172. [Google Scholar] [CrossRef]
- Nehring, M.; Topal, E.; Little, J. A New Mathematical Programming Model for Production Schedule Optimization in Underground Mining Operations. J. South. Afr. Inst. Min. Metall. 2010, 110, 437–446. [Google Scholar]
- O’Sullivan, D.; Newman, A. Extraction and Backfill Scheduling in a Complex Underground Mine. Interfaces 2014, 44, 204–221. [Google Scholar] [CrossRef]
- Foroughi, S.; Hamidi, J.K.; Monjezi, M.; Nehring, M. The Integrated Optimization of Underground Stope Layout Designing and Production Scheduling Incorporating a Non-Dominated Sorting Genetic Algorithm (NSGA-II). Resour. Policy 2019, 63, 101408. [Google Scholar] [CrossRef]
- Lindh, E.; Olsson, K.; Rönnberg, E. Scheduling of an Underground Mine by Combining Logic-Based Benders Decomposition and a Priority-Based Heuristic. In Proceedings of the 13th International Conference on the Practice and Theory of Automated Timetabling—PATAT, Leuven, Belgium, 2–30 August 2022; pp. 95–114, accepted for publication. [Google Scholar]
- Tsomondo, C.M. Short-Term Production Scheduling and Equipment Dispatching for Underground Metal Mines; McGill University: Montréal, QC, Canada, 1996. [Google Scholar]
- Nehring, M.; Topal, E.; Knights, P. Dynamic Short Term Production Scheduling and Machine Allocation in Underground Mining Using Mathematical Programming. Trans. Inst. Min. Metall. Sect. A 2010, 119, 212–220. [Google Scholar] [CrossRef]
- Song, Z.; Schunnesson, H.; Rinne, M.; Sturgul, J. Intelligent Scheduling for Underground Mobile Mining Equipment. PLoS ONE 2015, 10, e0131003. [Google Scholar] [CrossRef]
- Li, G.; Hou, J.; Hu, N. Integrated Optimization Model for Production and Equipment Dispatching in Underground Mines. Chin. J. Eng. 2018, 40, 1050–1057. [Google Scholar]
- Wang, H.; Tenorio, V.; Li, G.; Hou, J.; Hu, N. Optimization of Trackless Equipment Scheduling in Underground Mines Using Genetic Algorithms. Min. Metall. Explor. 2020, 37, 1531–1544. [Google Scholar] [CrossRef]
- Hou, J.; Li, G.; Wang, H.; Hu, N. Genetic Algorithm to Simultaneously Optimise Stope Sequencing and Equipment Dispatching in Underground Short-Term Mine Planning under Time Uncertainty. Int. J. Min. Reclam. Environ. 2020, 34, 307–325. [Google Scholar] [CrossRef]
- Åstrand, M.; Johansson, M.; Zanarini, A. Fleet Scheduling in Underground Mines Using Constraint Programming. In Proceedings of the Integration of Constraint Programming, Artificial Intelligence, and Operations Research, Delft, The Netherlands, 26–29 June 2018; Springer International Publishing: Cham, Switzerland, 2018; pp. 605–613. [Google Scholar]
- Åstrand, M.; Johansson, M.; Zanarini, A. Underground Mine Scheduling of Mobile Machines Using Constraint Programming and Large Neighborhood Search. Comput. Oper. Res. 2020, 123, 105036. [Google Scholar] [CrossRef]
- Åstrand, M.; Johansson, M.; Feyzmahdavian, H.R. Short-Term Scheduling of Production Fleets in Underground Mines Using CP-Based LNS. In Proceedings of the Integration of Constraint Programming, Artificial Intelligence, and Operations Research, Vienna, Austria, 5–8 July 2021; Springer International Publishing: Cham, Switzerland, 2021; pp. 365–382. [Google Scholar]
- Hammami, N.E.H.; Jaoua, A.; Layeb, S.B. Equipment Dispatching Problem for Underground Mine Under Stochastic Working Times. In Proceedings of the International Conference on Computational Logistics, Enschede, The Netherlands, 27–29 September 2021; Springer International Publishing: Cham, Switzerland, 2021; pp. 429–441. [Google Scholar]
- Huang, X.; Chen, S.; Zhou, T.; Sun, Y. Survey on genetic algorithms for solving flexible job-shop scheduling problem. Comput. Integr. Manuf. Syst. 2022, 28, 536–551. [Google Scholar]
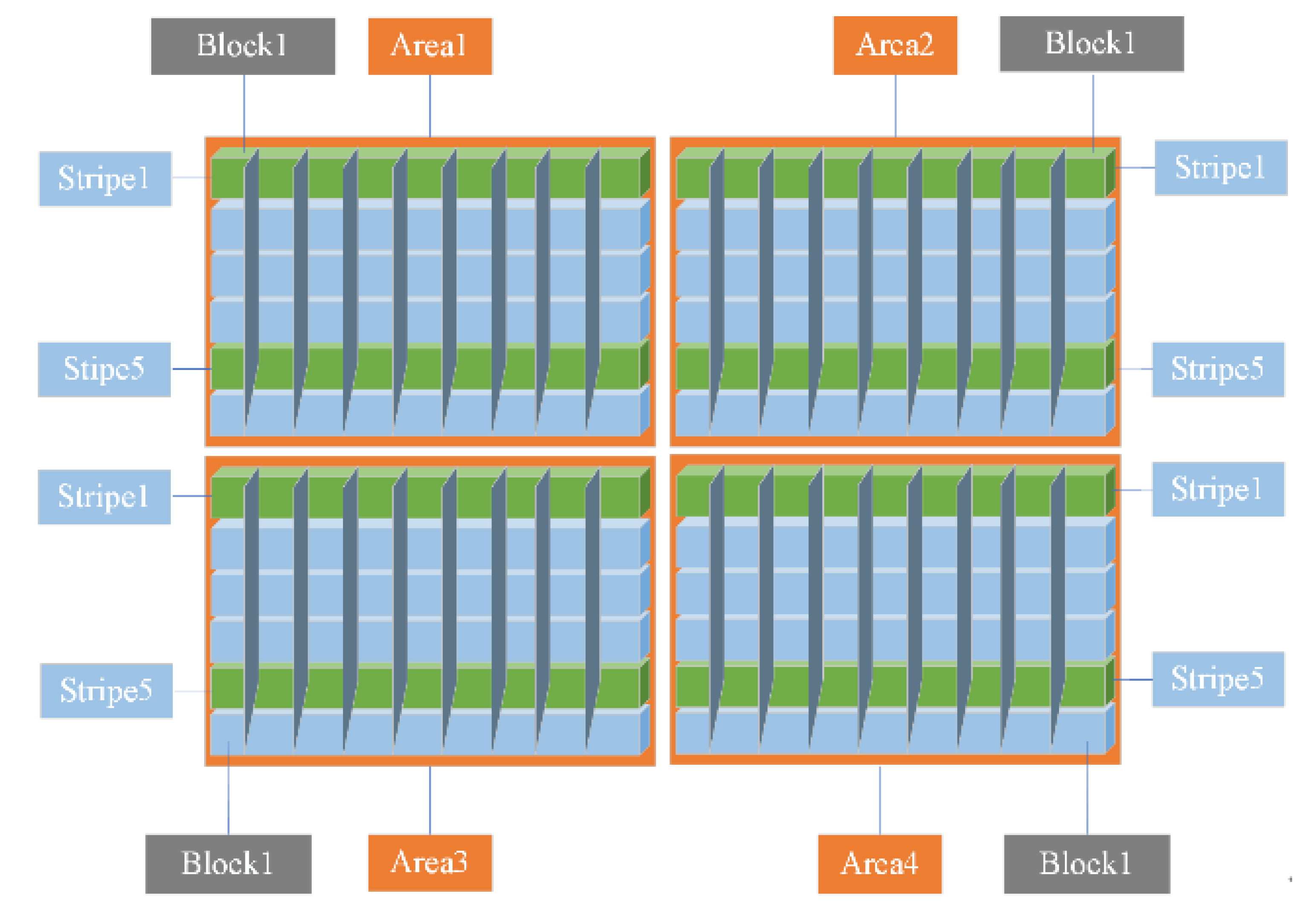


| Name | Meaning |
|---|---|
| A | Set of areas, A = {A1, A2…, Ai}, |
| Bi | Set of stripes, Bi = {Bi1, Bi2, …, Bik}, |
| Cik | Set of all blocks, represents blocks of the upper slice, represents blocks of the lower slice) |
| D | Set of horizontal drilling jumbos, D = {D1, D2, …, Dh}, |
| Z | Set of downward drilling jumbos, Z = {Z1, Z2, …, Zr}, |
| C | Set of charging dollies, C = {C1, C2, …, Cu}, |
| S | Set of scaling jumbos, S = {S1, S2, …, Sx}, |
| L | Set of LHDs, L = {L1, L2, …, Ly}, |
| B | Set of bolting jumbos, B = {B1, B2, …, Bw}, |
| F | Set of filling pipelines, F = {F1, F2, …, Fv}, |
| J | Set of processes, J = {J1, J2, …, Jm}, , J1 = 1 (Drilling), J2 = 2 (Charging), J3 = 3 (Blasting and ventilation), J4 = 4 (Scaling), J5 = 5 (Mucking), J6 = 6 (Bolting), J7 = 7 (Backfilling), J8 = 8 (Maintenance) |
| Name | Meaning |
|---|---|
| Qikn | Ore volume of Cikn, t, |
| G+ | Upper limit of ore grade, g·t−1 |
| G− | Lower limit of ore grade, g·t−1 |
| Ph | Operational efficiency of Dh, m/h |
| Pr | Operational efficiency of Zr, m/h |
| Pu | Operational efficiency of Cu, m/h |
| Pw | Operational efficiency of Bw, anchors/h |
| Pv | Filling capacity of Fv, m3/h |
| Py | Ideal operational efficiency of Ly, t·m/h |
| Operational efficiency discount factor of Ly in Cikn, %, | |
| Distance factor from Cikn to the corresponding ore pass, m, | |
| Ventilation factor, | |
| Distance between adjacent areas, m | |
| Distance between different stripes in Ai, m, | |
| Vel | Walking speed of any equipment, m/h |
| qikn | Avalanche ore volume per meter of Cikn, t/m, |
| Vikn | Volume of Cikn, m3, |
| Gikn | Grade of Cikn, g·t−1, |
| Hikn | Height of Cikn, m, |
| Nikn | Number of anchors per square meter of Cikn, anchors/m2, |
| Tmt,ik | Maintenance time of Bik, h |
| Name | Meaning |
|---|---|
| Lpao,ikn | Total length of the blasting hole for Cikn, m, |
| Th,ikn | Operation time of Dh in Cikn, h, |
| Tr,ikn | Operation time of Zr in Cikn, h, |
| Tu,ikn | Operation time of Cu in Cikn, h, |
| Tven,ikn | Blasting and ventilation time in Cikn, h, |
| Tx,ikn | Operation time of Sx in Cikn, h, |
| Ty,ikn | Operation time of Ly in Cikn, h, |
| Tw,ikn | Operation time of Bw in Cikn, h, |
| Tv,ik | Backfilling time of Fv in Bik, h |
| Its value is equal to any of {Th,ikn, Tr,ikn, Tu,ikn, Tx,ikn, Ty,ikn, Tw,ikn, Tv,ik, Tmt,ik } | |
| TSiknm | Starting time of jm in Cikn, h, , |
| TSikm | Starting time of jm in Bik, h, |
| TEiknm | Ending time of jm in Cikn, h, , |
| TEikm | Ending time of jm in Bik, h, |
| DTikn,m,m+1 | The interval time between the ending time of jm and the starting time of jm+1 in Cikn, h, , |
| DTik,m,m+1 | The interval time between the ending time of jm and the starting time of jm+1 in Bik, h, |
| Time of movement between Ai and Ai+1 with any equipment, h | |
| Time of movement between Bik and with any equipment, h | |
| Number of blasting and ventilation for jm in Cikn, |
| Name of Areas | Number of Stripes | Number of Ore Blocks | Total Quantities of Ores/Million Tons | Average Grade Cu | Average Grade Co |
|---|---|---|---|---|---|
| Area1 | 16 | 256 | 49.59 | 2.42 | 0.12 |
| Area2 | 24 | 766 | 86.93 | 2.18 | 0.14 |
| Area4 | 31 | 984 | 115.16 | 2.88 | 0.08 |
| Area1 | 24 | 768 | 69.78 | 2.73 | 0.12 |
| Area6 | 24 | 768 | 70.11 | 2.74 | 0.12 |
| Total | 119 | 3798 | 391.57 | 2.61 | 0.11 |
| Category | Operation Content | Operational Capacity | Average Movement Speed | Number of Equipment |
|---|---|---|---|---|
| Horizontal drilling jumbo | Drilling horizontal holes | 40 m/h | 1000 m/h | 4 |
| Downward drilling jumbo | Drilling vertical holes | 30 m/h | 1000 m/h | 2 |
| Charging dolly | Drilling holes for charging | 90 m/h | 1000 m/h | 3 |
| Scaling jumbo | Roof scaling | 10 m2/h | 1000 m/h | 1 |
| LHD | Ore mucking | 1500 t·m/h | 1000 m/h | 4 |
| Bolting jumbo | Anchor support | 10 anchors/h | 1000 m/h | 3 |
| Name | Total Time (Days) | Stripe Average Time (Days) | Process Interval (Days) | Block Interval (Days) | Equipment Utilization Rate (%) | Ore Grade Fluctuation (Dimensionless) | |
|---|---|---|---|---|---|---|---|
| Multi-objects | 587.67 | 111.15 | 2914.54 | 525.75 | 51.25 | 0.06 | |
| Single object | Total time | 549.43 | 110.06 | 3620.48 | 751.81 | 49.62 | 0.34 |
| Stripe average time | 567.91 | 109.59 | 3561.94 | 519.07 | 50.24 | 0.11 | |
| Process interval | 600.61 | 111.94 | 2734.91 | 571.94 | 46.19 | 0.24 | |
| Block interval | 626.16 | 124.09 | 3381.57 | 492.44 | 47.94 | 0.19 | |
| Equipment utilization rate | 591.61 | 116.80 | 3519.07 | 749.51 | 53.46 | 0.24 | |
| Ore grade fluctuation | 604.58 | 121.09 | 3705.06 | 934.83 | 47.24 | 0.04 | |
| Category | Equipment Utilization Rate | ||
|---|---|---|---|
| Average | Maximum | Minimum | |
| Horizontal drilling jumbo | 44.27 | 42.91 | 45.73 |
| Downward drilling jumbo | 48.43 | 47.95 | 49.54 |
| Charging dolly | 51.43 | 49.29 | 53.08 |
| Scaling jumbo | 45.05 | 45.05 | 45.05 |
| LHD | 63.84 | 65.28 | 61.34 |
| Bolting jumbo | 46.74 | 47.67 | 45.33 |
| Average | 51.25 | 65.28 | 45.05 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tu, S.; Jia, M.; Wang, L.; Feng, S.; Huang, S. A Multi-Equipment Task Assignment Model for the Horizontal Stripe Pre-Cut Mining Method. Sustainability 2022, 14, 16379. https://doi.org/10.3390/su142416379
Tu S, Jia M, Wang L, Feng S, Huang S. A Multi-Equipment Task Assignment Model for the Horizontal Stripe Pre-Cut Mining Method. Sustainability. 2022; 14(24):16379. https://doi.org/10.3390/su142416379
Chicago/Turabian StyleTu, Siyu, Mingtao Jia, Liguan Wang, Shuzhao Feng, and Shuang Huang. 2022. "A Multi-Equipment Task Assignment Model for the Horizontal Stripe Pre-Cut Mining Method" Sustainability 14, no. 24: 16379. https://doi.org/10.3390/su142416379
APA StyleTu, S., Jia, M., Wang, L., Feng, S., & Huang, S. (2022). A Multi-Equipment Task Assignment Model for the Horizontal Stripe Pre-Cut Mining Method. Sustainability, 14(24), 16379. https://doi.org/10.3390/su142416379







