Modeling and Nonlinear Control of dc–dc Converters for Microgrid Applications
Abstract
1. Introduction
2. Unified Average Model of the Converters
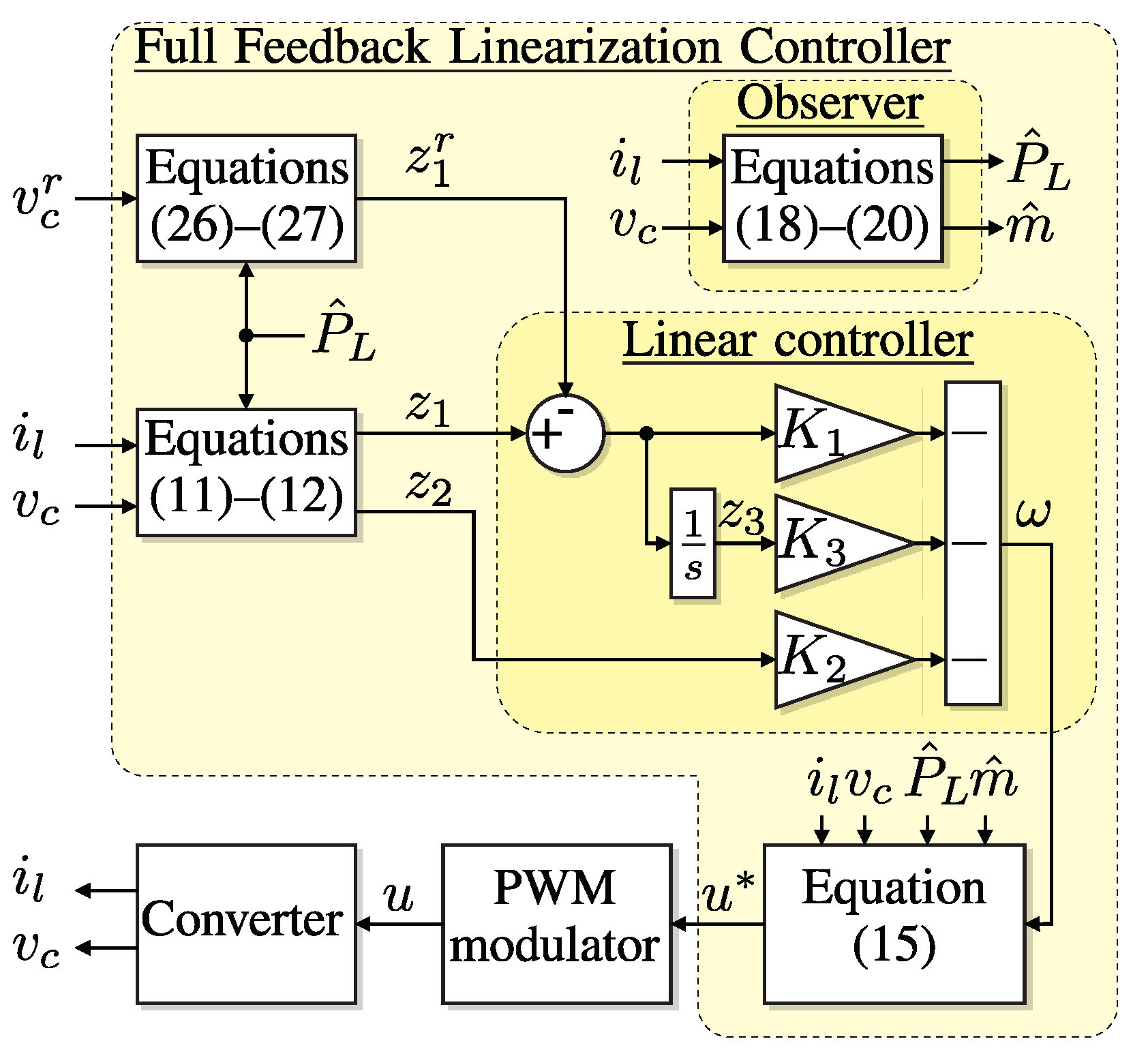
3. Proposed Full FL Scheme
4. Combined Load Power Observer
Tuning Criteria
5. Proposed Controller for the Linearized System
5.1. Tuning Criteria
5.2. Control Loop Summary
5.3. Comments about Other Strategies
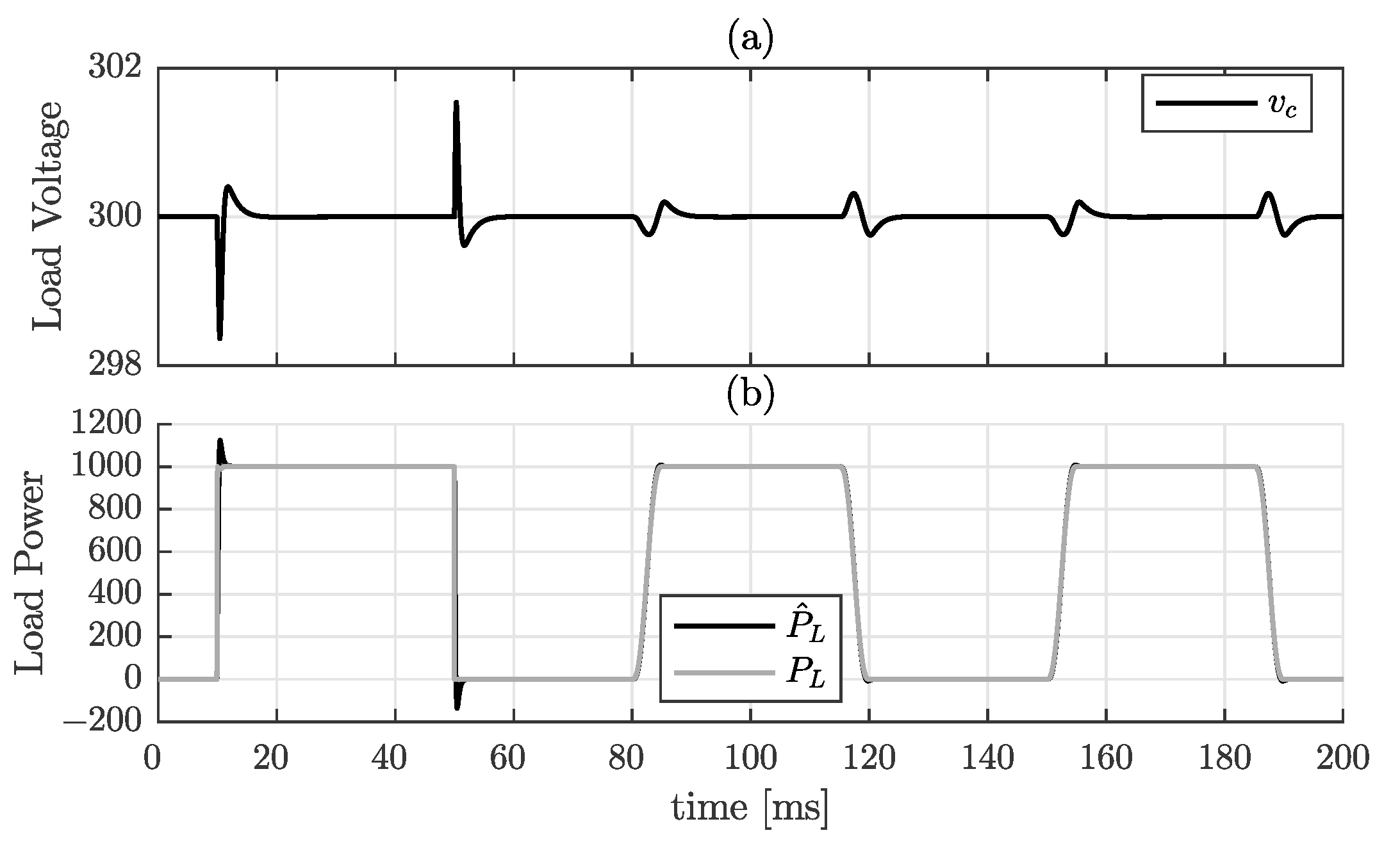
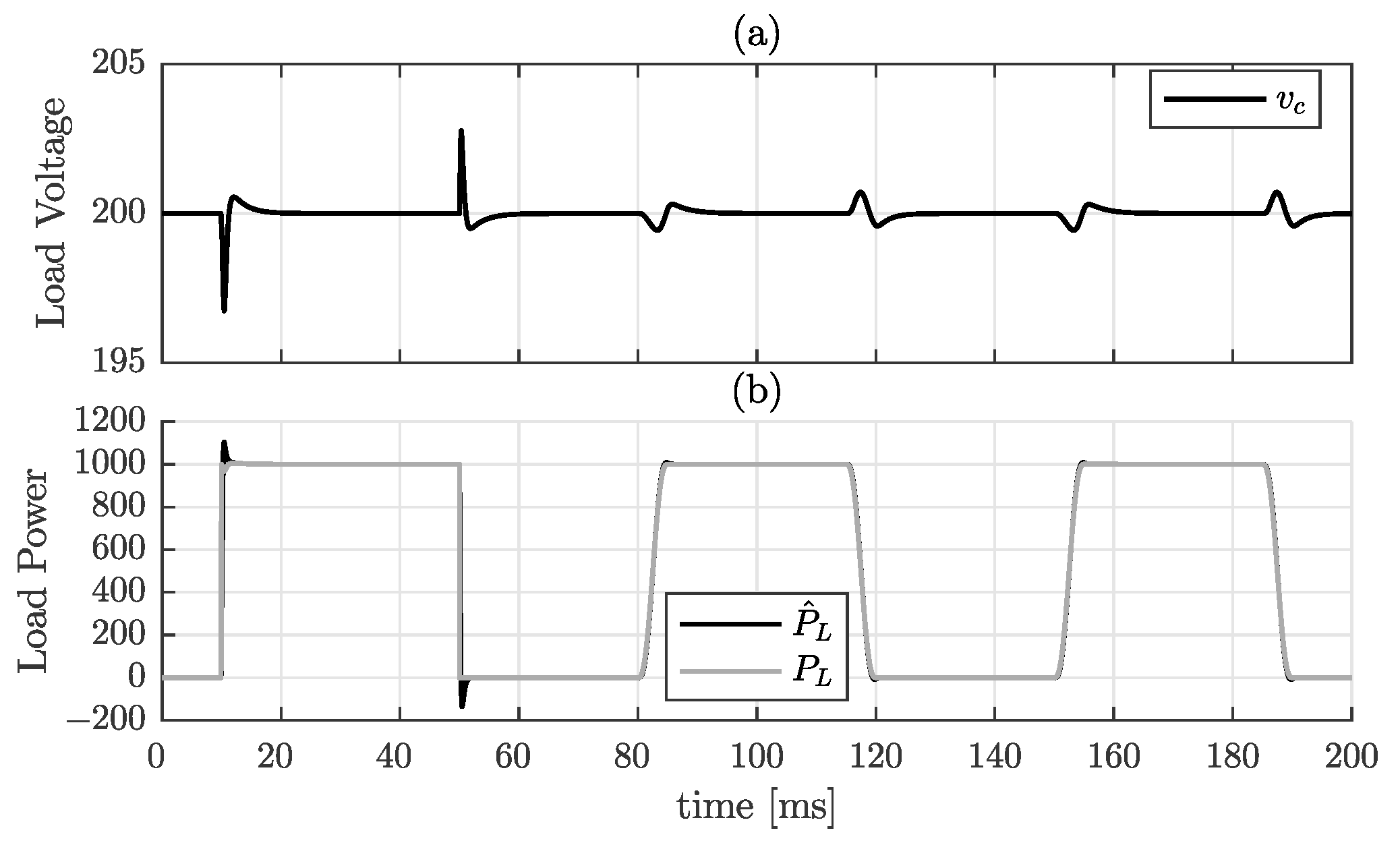
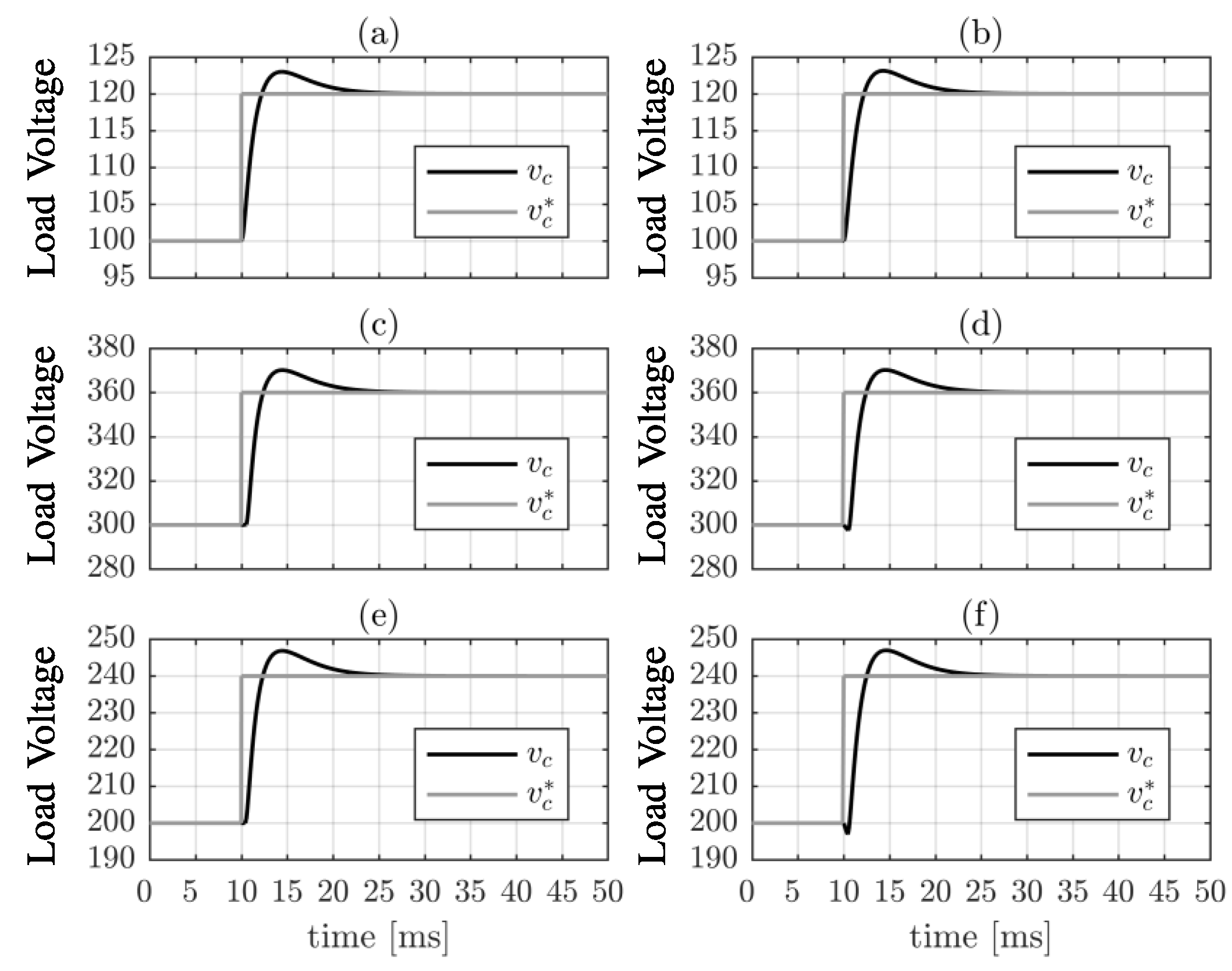
6. Simulation Results
7. Experimental Results: Application Cases
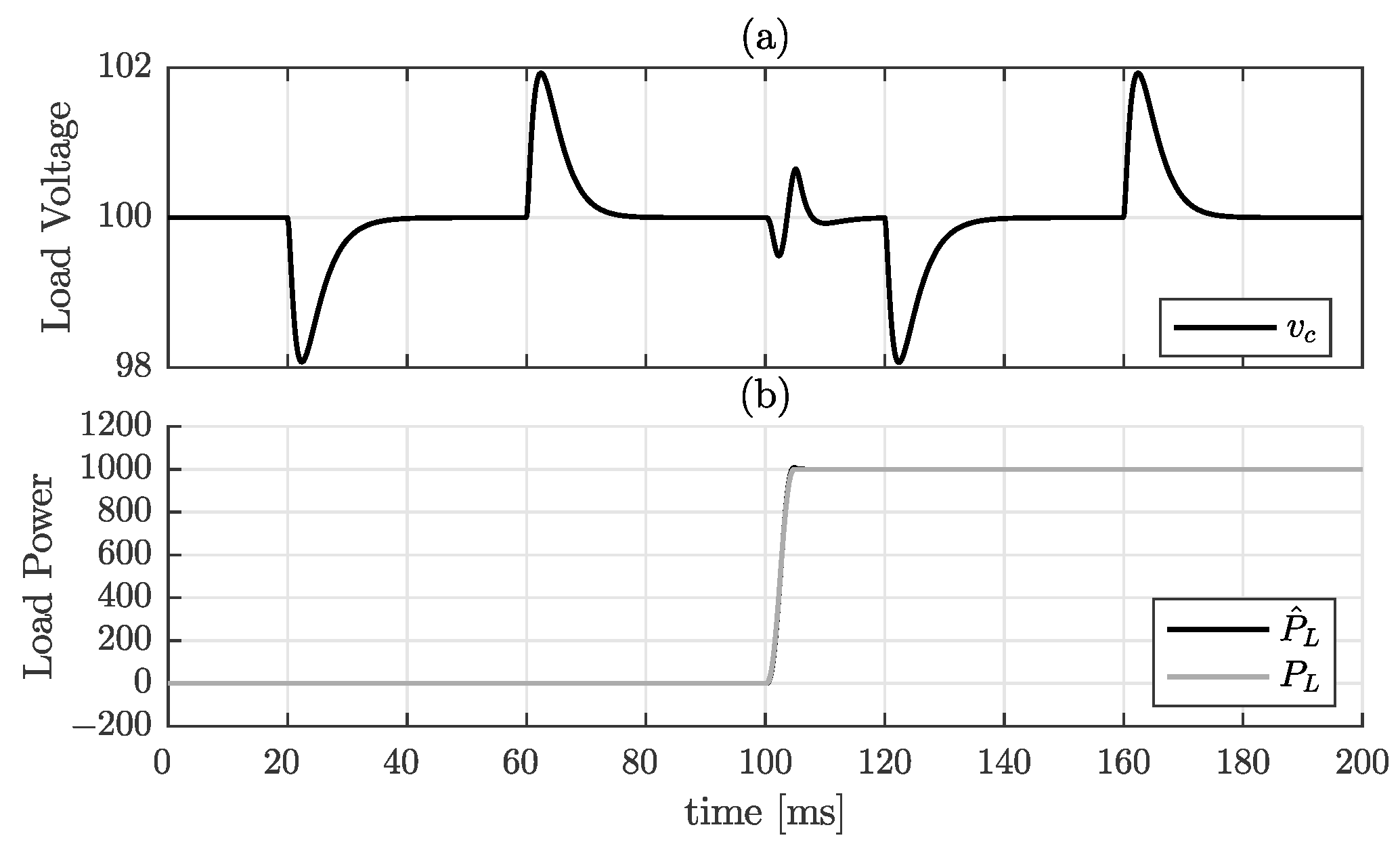
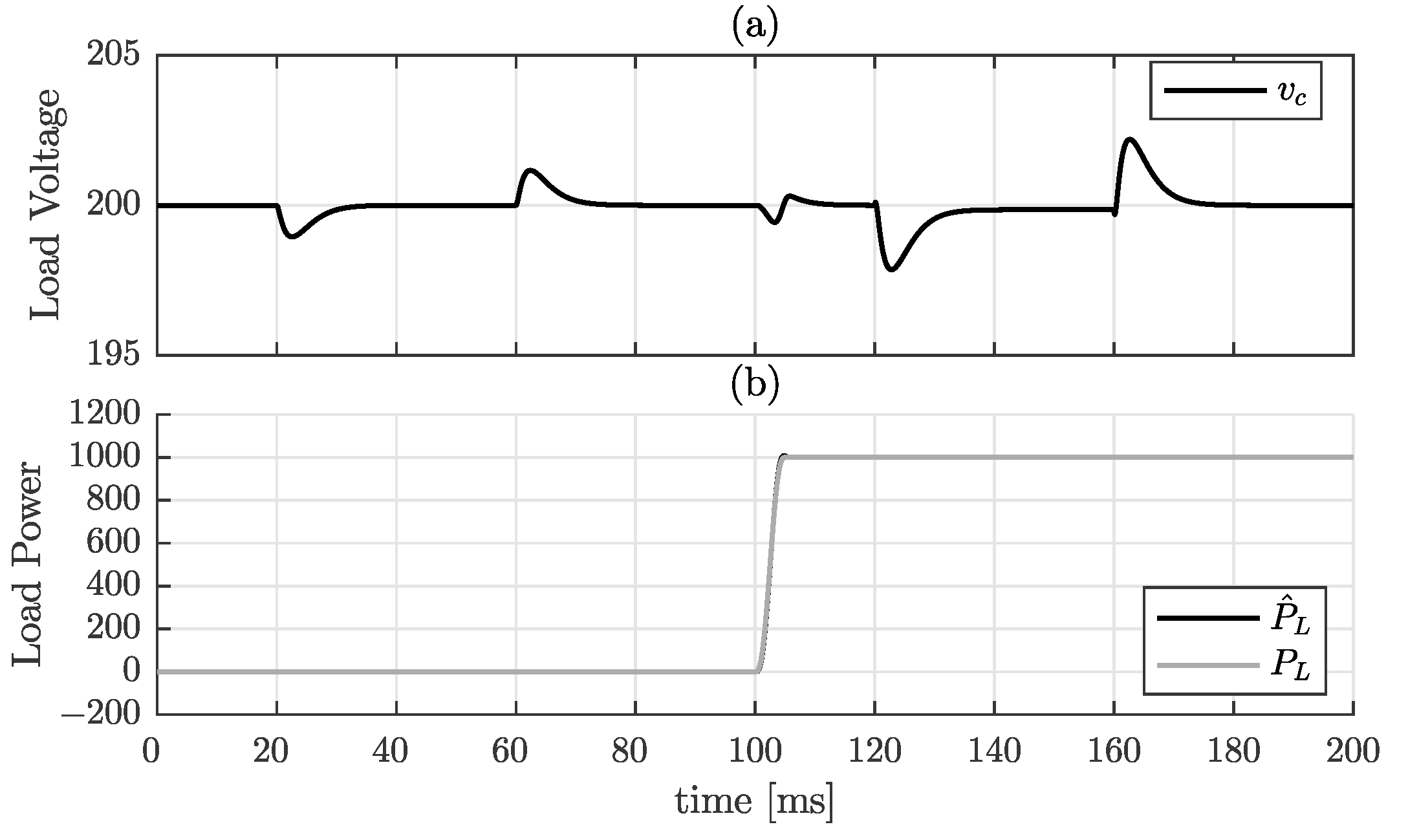
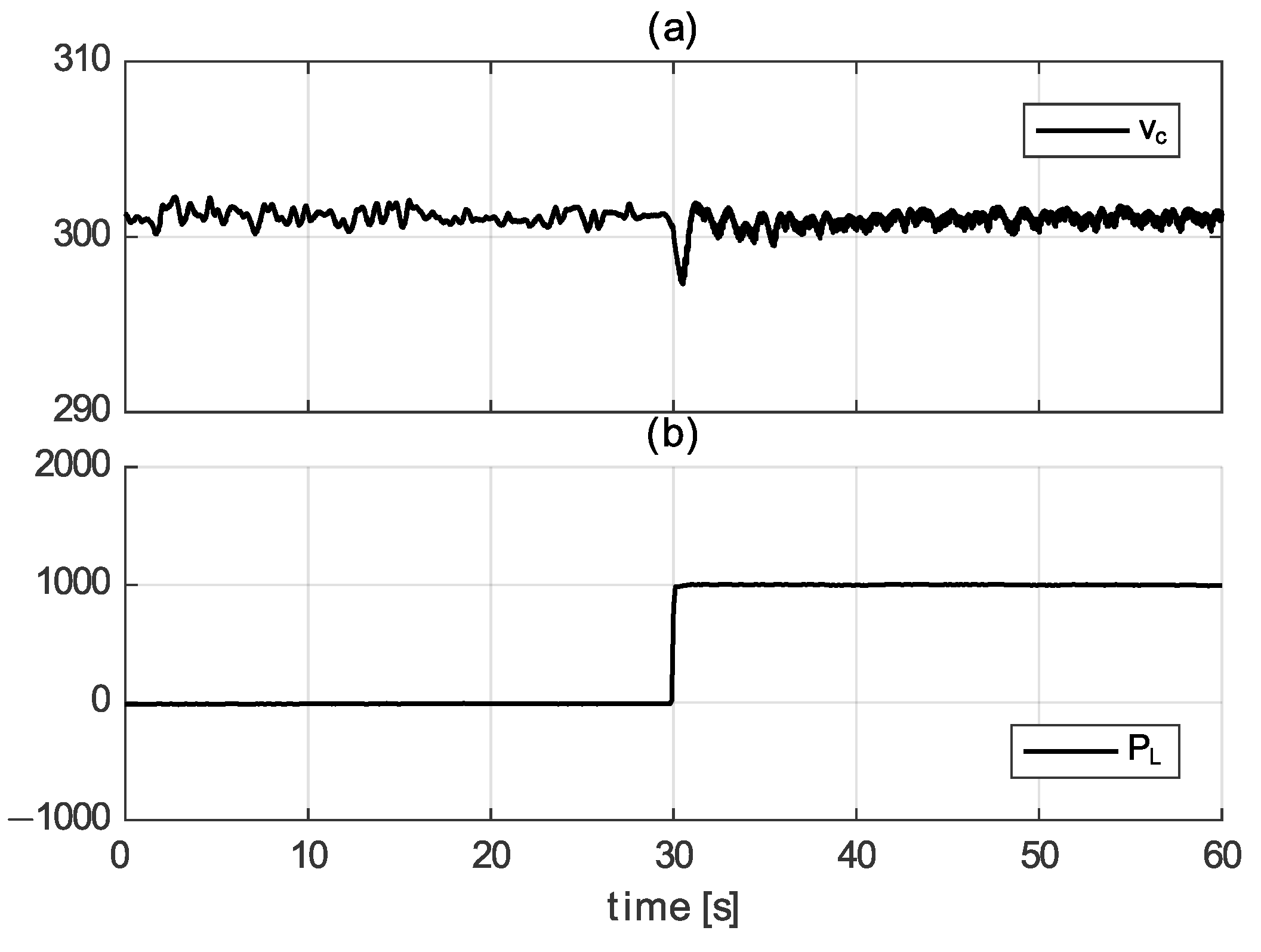
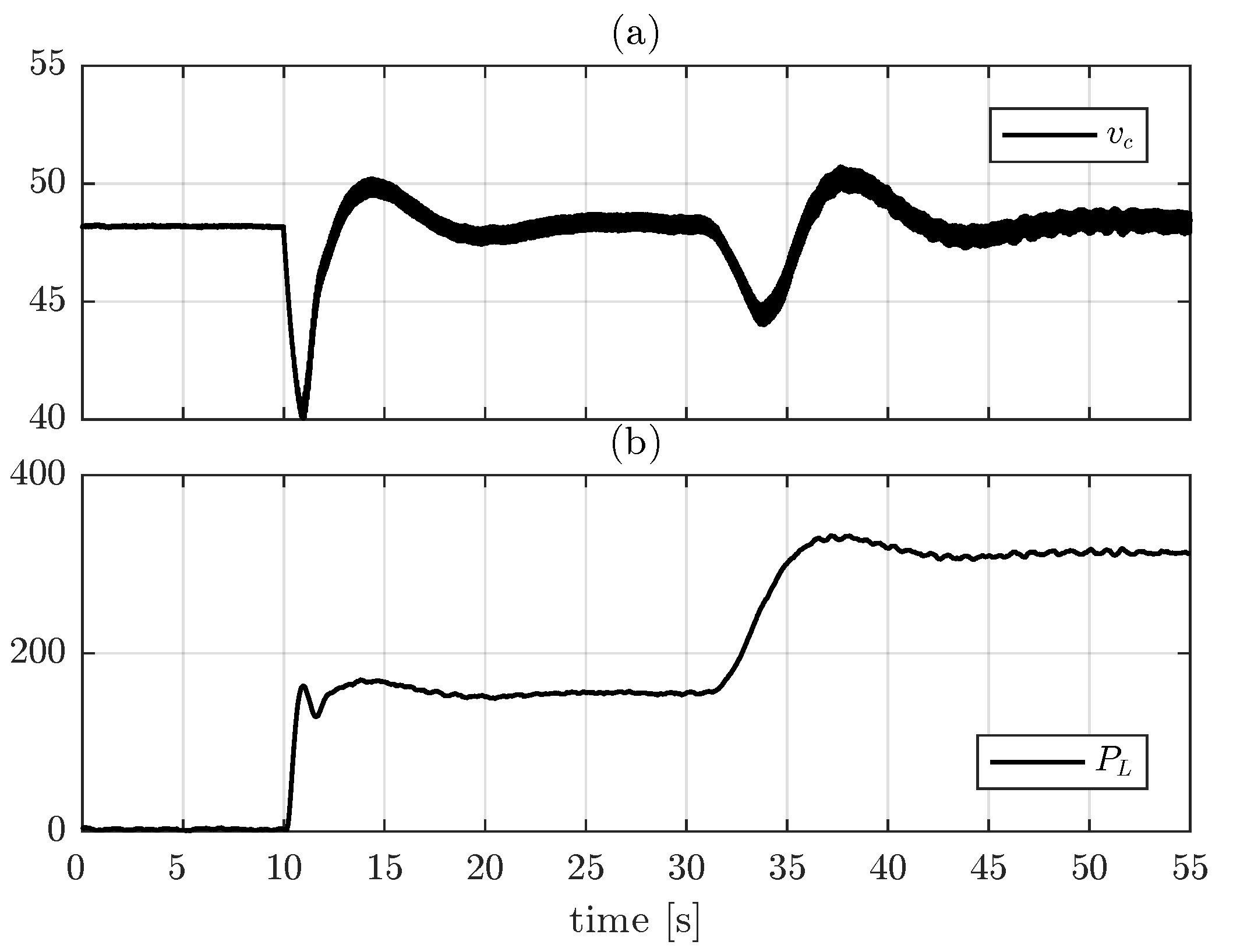
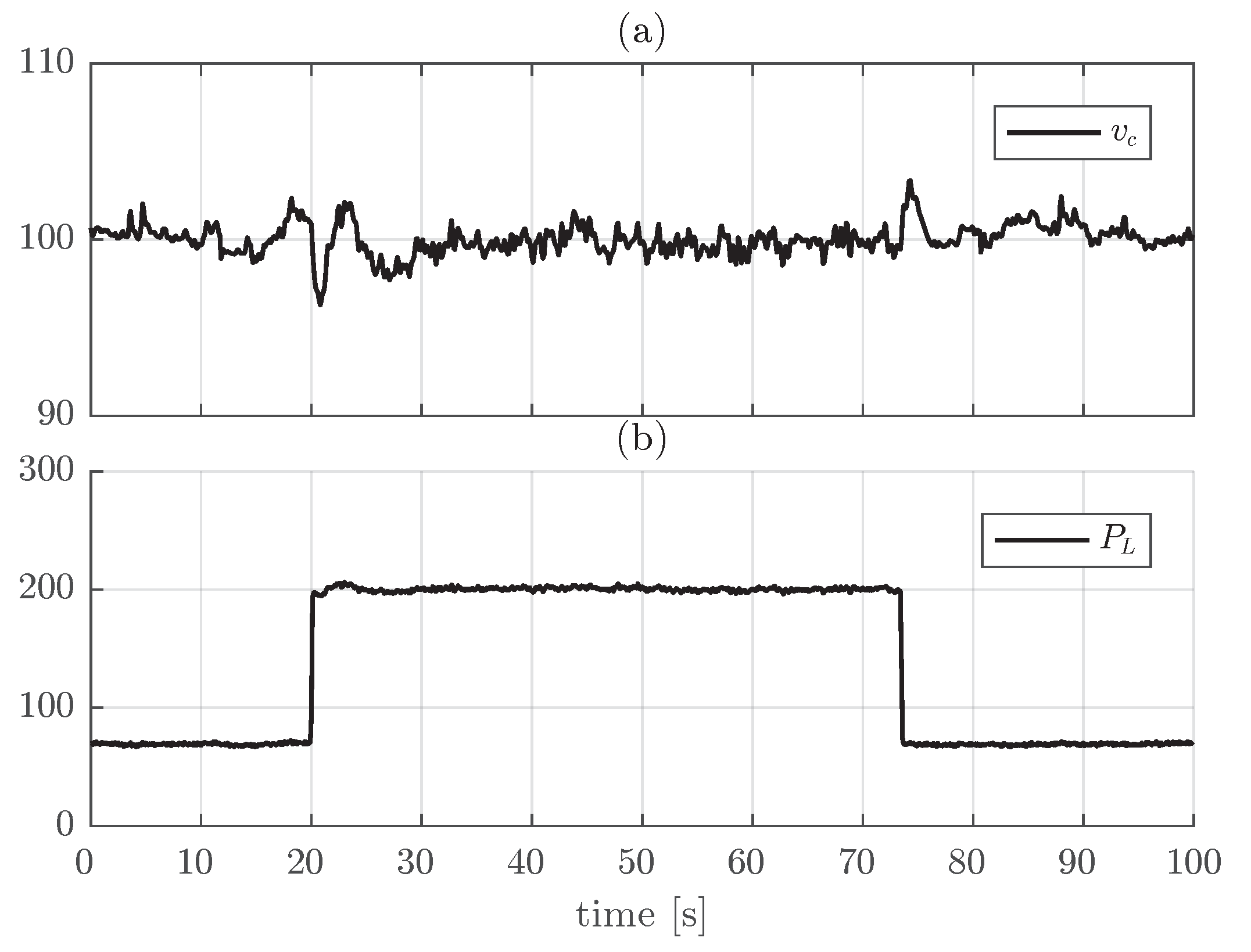
7.1. Boost Converter with CCL
7.2. Boost Converter with Resistive Load and CPL
7.3. Buck Converter with CCL
8. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Abbasi, M.; Abbasi, E.; Li, L.; Tousi, B. Design and analysis of a high-gain step-up/down modular DC–DC converter with continuous input current and decreased voltage stress on power switches and switched-capacitors. Sustainability 2021, 13, 5243. [Google Scholar] [CrossRef]
- Worku, M.Y. Recent Advances in Energy Storage Systems for Renewable Source Grid Integration: A Comprehensive Review. Sustainability 2022, 14, 5985. [Google Scholar] [CrossRef]
- Khan, M.Y.A.; Liu, H.; Habib, S.; Khan, D.; Yuan, X. Design and performance evaluation of a step-up DC–DC converter with dual loop controllers for two stages grid connected PV inverter. Sustainability 2022, 14, 811. [Google Scholar] [CrossRef]
- Jorge, S.G.; Solsona, J.A.; Busada, C.A. Nonlinear Control of a Two-Stage Single-Phase DC–AC Converter. IEEE J. Emerg. Sel. Top. Ind. Electron. 2022, 3, 1038–1045. [Google Scholar] [CrossRef]
- Hossain, E.; Perez, R.; Nasiri, A.; Bayindir, R. Stability improvement of microgrids in the presence of constant power loads. Int. J. Electr. Power Energy Syst. 2018, 96, 442–456. [Google Scholar] [CrossRef]
- Lenz, E.; Pagano, D.J.; Stramosk, V. Nonlinear control applied to a dc-dc power converter and the load sharing problem in a dc microgrid. IFAC Proc. Vol. 2014, 47, 534–539. [Google Scholar] [CrossRef]
- Behera, R.; Parida, S. DC microgrid management using power electronics converters. In Proceedings of the 2014 Eighteenth National Power Systems Conference (NPSC), Guwahati, India, 18–20 December 2014; pp. 1–6. [Google Scholar]
- Herrera, L.; Zhang, W.; Wang, J. Stability Analysis and Controller Design of DC Microgrids With Constant Power Loads. IEEE Trans. Smart Grid 2017, 8, 881–888. [Google Scholar]
- Schmidt, S.; Richter, M.; Oberrath, J.; Mercorelli, P. Control oriented modeling of DC-DC converters. IFAC-PapersOnLine 2018, 51, 331–336. [Google Scholar]
- Hossain, E.; Perez, R.; Nasiri, A.; Padmanaban, S. A comprehensive review on constant power loads compensation techniques. IEEE Access 2018, 6, 33285–33305. [Google Scholar] [CrossRef]
- Cabana-Jiménez, K.; Candelo-Becerra, J.E.; Sousa Santos, V. Comprehensive analysis of microgrids configurations and topologies. Sustainability 2022, 14, 1056. [Google Scholar] [CrossRef]
- Souza Junior, M.E.T.; Freitas, L.C.G. Power Electronics for Modern Sustainable Power Systems: Distributed Generation, Microgrids and Smart Grids-A Review. Sustainability 2022, 14, 3597. [Google Scholar] [CrossRef]
- Zolfaghari, M.; Gharehpetian, G.B.; Shafie-khah, M.; Catalão, J.P. Comprehensive review on the strategies for controlling the interconnection of AC and DC microgrids. Int. J. Electr. Power Energy Syst. 2022, 136, 107742. [Google Scholar] [CrossRef]
- ShahidUllah; Haidar, A.M.; Hoole, P.; Zen, H.; Ahfock, T. The current state of Distributed Renewable Generation, challenges of interconnection and opportunities for energy conversion based DC microgrids. J. Clean. Prod. 2020, 273, 122777. [Google Scholar] [CrossRef]
- Nasir, M.; Iqbal, S.; Khan, H.A.; Vasquez, J.C.; Guerrero, J.M. Sustainable rural electrification through solar PV DC microgrids-An architecture-based assessment. Processes 2020, 8, 1417. [Google Scholar] [CrossRef]
- Ali, S.; Zheng, Z.; Aillerie, M.; Sawicki, J.P.; Pera, M.C.; Hissel, D. A review of DC Microgrid energy management systems dedicated to residential applications. Energies 2021, 14, 4308. [Google Scholar] [CrossRef]
- Erenturk, K.; Draou, A.; AlKassem, A. Design and Comparison of Different Types of Synergetic Controllers for Islanded DC Microgrids. Sustainability 2022, 14, 8792. [Google Scholar] [CrossRef]
- Muñoz, C.; Rivera, M.; Villalón, A.; Baier, C.R.; Muñoz, J.; Ramirez, R.O.; Wheeler, P. Predictive Control with Current-Based Maximum Power Point-Tracking for On-Grid Photovoltaic Applications. Sustainability 2021, 13, 3037. [Google Scholar] [CrossRef]
- Azar, A.T.; Abed, A.M.; Abdulmajeed, F.A.; Hameed, I.A.; Kamal, N.A.; Jawad, A.J.M.; Abbas, A.H.; Rashed, Z.A.; Hashim, Z.S.; Sahib, M.A.; et al. A New Nonlinear Controller for the Maximum Power Point Tracking of Photovoltaic Systems in Micro Grid Applications Based on Modified Anti-Disturbance Compensation. Sustainability 2022, 14, 10511. [Google Scholar] [CrossRef]
- Francés, A.; Asensi, R.; García, O.; Prieto, R.; Uceda, J. Modeling Electronic Power Converters in Smart DC Microgrids-An Overview. IEEE Trans. Smart Grid. 2018, 9, 6274–6287. [Google Scholar] [CrossRef]
- Mosskull, H. Constant power load stabilization. Control Eng. Pract. 2018, 72, 114–124. [Google Scholar] [CrossRef]
- Mayo-Maldonado, J.; Ruiz-Martinez, O.; Escobar, G.; Maupong, T.; Valdez-Resendiz, J.; Rosas-Caro, J. Power shaping control of DC–DC converters with constant power loads. Control Eng. Pract. 2020, 105, 104639. [Google Scholar] [CrossRef]
- Negri, S.; Tironi, E.; Superti-Furga, G.; Ubezio, G. Control and fault analysis of multiport converters for low voltage DC distribution systems. Int. J. Electr. Power Energy Syst. 2013, 124, 106335. [Google Scholar] [CrossRef]
- Srinivasan, M.; Kwasinski, A. Control analysis of parallel DC-DC converters in a DC microgrid with constant power loads. Int. J. Electr. Power Energy Syst. 2020, 122, 106207. [Google Scholar] [CrossRef]
- Rani, P.H.; Navasree, S.; George, S.; Ashok, S. Fuzzy logic supervisory controller for multi-input non-isolated DC to DC converter connected to DC grid. Int. J. Electr. Power Energy Syst. 2019, 112, 49–60. [Google Scholar] [CrossRef]
- Pavlovic, T.; Bjazic, T.; Ban, Z. Simplified averaged models of DC–DC power converters suitable for controller design and microgrid simulation. IEEE Trans. Power Electron. 2013, 28, 3266–3275. [Google Scholar] [CrossRef]
- Utkin, V. Sliding mode control of DC/DC converters. J. Frankl. Inst. 2013, 350, 2146–2165. [Google Scholar] [CrossRef]
- Tan, S.C.; Lai, Y.M.; Tse, C.K. A unified approach to the design of PWM-based sliding-mode voltage controllers for basic DC-DC converters in continuous conduction mode. IEEE Trans. Circuits Syst. I Regul. Pap. 2006, 53, 1816–1827. [Google Scholar]
- Pandey, S.K.; Patil, S.L.; Ginoya, D.; Chaskar, U.M.; Phadke, S.B. Robust control of mismatched buck dc–dc converters by pwm-based sliding mode control schemes. Control Eng. Pract. 2019, 84, 183–193. [Google Scholar] [CrossRef]
- Tian, Z.; Lyu, Z.; Yuan, J.; Wang, C. UDE-based sliding mode control of DC–DC power converters with uncertainties. Control Eng. Pract. 2019, 83, 116–128. [Google Scholar] [CrossRef]
- Sferlazza, A.; Albea-Sanchez, C.; Martínez-Salamero, L.; Garcia, G.; Alonso, C. Min-Type Control Strategy of a DC–DC Synchronous Boost Converter. IEEE Trans. Ind. Electron. 2020, 67, 3167–3179. [Google Scholar] [CrossRef]
- Hassan, M.A.; Li, E.P.; Li, X.; Li, T.; Duan, C.; Chi, S. Adaptive Passivity-Based Control of DC-DC Buck Power Converter with Constant Power Load in DC Microgrid Systems. IEEE J. Emerg. Sel. Top. Power Electron. 2018, 7, 2029–2040. [Google Scholar] [CrossRef]
- He, W.; Soriano-Rangel, C.A.; Ortega, R.; Astolfi, A.; Mancilla-David, F.; Li, S. Energy shaping control for buck–boost converters with unknown constant power load. Control Eng. Pract. 2018, 74, 33–43. [Google Scholar] [CrossRef]
- He, W.; Ortega, R.; Machado, J.E.; Li, S. An Adaptive Passivity-Based Controller of a Buck-Boost Converter with a Constant Power Load. Asian J. Control 2017, 21, 581–595. [Google Scholar] [CrossRef]
- Geyer, T.; Papafotiou, G.; Morari, M. Hybrid model predictive control of the step-down DC–DC converter. IEEE Trans. Control Syst. Technol. 2008, 16, 1112–1124. [Google Scholar] [CrossRef]
- Xie, Y.; Ghaemi, R.; Sun, J.; Freudenberg, J.S. Model predictive control for a full bridge DC/DC converter. IEEE Trans. Control Syst. Technol. 2011, 20, 164–172. [Google Scholar]
- Karamanakos, P.; Geyer, T.; Manias, S. Direct voltage control of DC–DC boost converters using enumeration-based model predictive control. IEEE Trans. Power Electron. 2013, 29, 968–978. [Google Scholar] [CrossRef]
- Dehghanzadeh, A.; Farahani, G.; Vahedi, H.; Al-Haddad, K. Model predictive control design for DC-DC converters applied to a photovoltaic system. Int. J. Electr. Power Energy Syst. 2018, 103, 537–544. [Google Scholar] [CrossRef]
- Hausberger, T.; Kugi, A.; Eder, A.; Kemmetmüller, W. High-speed nonlinear model predictive control of an interleaved switching DC/DC-converter. Control Eng. Pract. 2020, 103, 104576. [Google Scholar] [CrossRef]
- Andres-Martinez, O.; Flores-Tlacuahuac, A.; Ruiz-Martinez, O.; Mayo-Maldonado, J. Nonlinear Model Predictive Stabilization of DC-DC Boost Converters with Constant Power Loads. IEEE J. Emerg. Sel. Top. Power Electron. 2020, 9, 822–830. [Google Scholar] [CrossRef]
- Babes, B.; Hamouda, N.; Albalawi, F.; Aissa, O.; Ghoneim, S.S.; Abdelwahab, S.A.M. Experimental Investigation of an Adaptive Fuzzy-Neural Fast Terminal Synergetic Controller for Buck DC/DC Converters. Sustainability 2022, 14, 7967. [Google Scholar] [CrossRef]
- Sira-Ramirez, H.; Ilic-Spong, M. Exact linearization in switched-mode DC-to-DC power converters. Int. J. Control 1989, 50, 511–524. [Google Scholar] [CrossRef]
- Roshan, Y.M.; Moallem, M. Control of nonminimum phase load current in a boost converter using output redefinition. IEEE Trans. Power Electron. 2014, 29, 5054–5062. [Google Scholar] [CrossRef]
- Arora, S.; Balsara, P.; Bhatia, D. Input–Output Linearization of a Boost Converter With Mixed Load (Constant Voltage Load and Constant Power Load). IEEE Trans. Power Electron. 2019, 34, 815–825. [Google Scholar] [CrossRef]
- Martinez-Treviño, B.A.; El Aroudi, A.; Cid-Pastor, A.; Martinez-Salamero, L. Nonlinear Control for Output Voltage Regulation of a Boost Converter With a Constant Power Load. IEEE Trans. Power Electron. 2019, 34, 10381–10385. [Google Scholar] [CrossRef]
- Bhattacharyya, D.; Padhee, S.; Pati, K.C. Modeling of DC–DC converter using exact feedback linearization method: A discussion. IETE J. Res. 2019, 65, 843–854. [Google Scholar] [CrossRef]
- Solsona, J.A.; Jorge, S.G.; Busada, C.A. Nonlinear Control of a Buck Converter Which Feeds a Constant Power Load. IEEE Trans. Power Electron. 2015, 30, 7193–7201. [Google Scholar] [CrossRef]
- Gensior, A.; Woywode, O.; Rudolph, J.; Guldner, H. On differential flatness, trajectory planning, observers, and stabilization for DC–DC converters. IEEE Trans. Circuits Syst. I Regul. Pap. 2006, 53, 2000–2010. [Google Scholar] [CrossRef]
- Cimini, G.; Ippoliti, G.; Orlando, G.; Longhi, S.; Miceli, R. A unified observer for robust sensorless control of DC–DC converters. Control Eng. Pract. 2017, 61, 21–27. [Google Scholar] [CrossRef]
- Franklin, G.F.; Powell, J.D.; Emami-Naeini, A. Feedback Control of Dynamic Systems; Addison-Wesley Longman Publishing Co., Inc.: Boston, MA, USA, 1993. [Google Scholar]
- Kobaku, T.; Patwardhan, S.C.; Agarwal, V. Experimental evaluation of internal model control scheme on a DC–DC boost converter exhibiting nonminimum phase behavior. IEEE Trans. Power Electron. 2017, 32, 8880–8891. [Google Scholar] [CrossRef]
- Ahmad, S.; Ali, A. Active disturbance rejection control of DC–DC boost converter: A review with modifications for improved performance. IET Power Electron. 2019, 12, 2095–2107. [Google Scholar] [CrossRef]
- Isidori, A. The zero dynamics of a nonlinear system: From the origin to the latest progresses of a long successful story. Eur. Control 2013, 19, 369–378. [Google Scholar] [CrossRef]
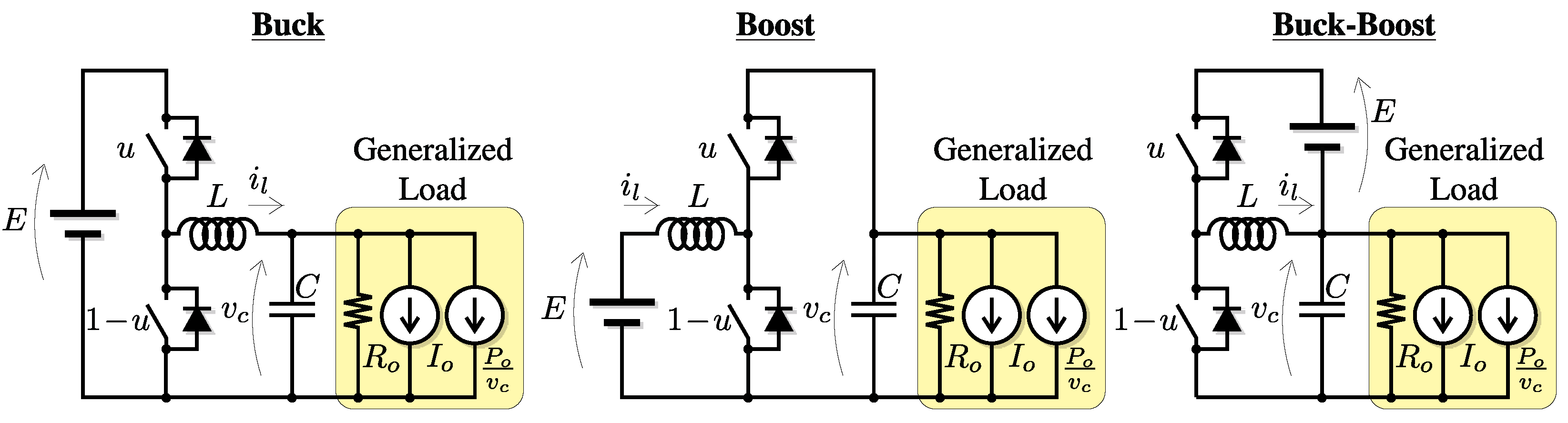




| Buck | |
| Boost | |
| Buck–Boost |
| Parameter | Value | Description |
|---|---|---|
| L | 3.78 mH | Filter Inductor |
| C | 470 F | Filter Capacitor |
| , , | , 5520, | Controller Gains |
| , , | , , | Observer Gains |
| E | 200 V | Input Voltage |
| Parameter | Value | Description |
|---|---|---|
| L | 800 H | Filter Inductor |
| C | 220 F | Filter Capacitor |
| E | 24 V | Input Voltage |
| Parameter | Value | Description |
|---|---|---|
| L | 3.78 mH | Filter Inductor |
| C | 100 F | Filter Capacitor |
| E | 200 V | Input Voltage |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Solsona, J.A.; Gomez Jorge, S.; Busada, C.A. Modeling and Nonlinear Control of dc–dc Converters for Microgrid Applications. Sustainability 2022, 14, 16889. https://doi.org/10.3390/su142416889
Solsona JA, Gomez Jorge S, Busada CA. Modeling and Nonlinear Control of dc–dc Converters for Microgrid Applications. Sustainability. 2022; 14(24):16889. https://doi.org/10.3390/su142416889
Chicago/Turabian StyleSolsona, Jorge A., Sebastian Gomez Jorge, and Claudio A. Busada. 2022. "Modeling and Nonlinear Control of dc–dc Converters for Microgrid Applications" Sustainability 14, no. 24: 16889. https://doi.org/10.3390/su142416889
APA StyleSolsona, J. A., Gomez Jorge, S., & Busada, C. A. (2022). Modeling and Nonlinear Control of dc–dc Converters for Microgrid Applications. Sustainability, 14(24), 16889. https://doi.org/10.3390/su142416889






