Sensitivity of EPA of Ground Motion to Soil Slope Dynamic Response
Abstract
:1. Introduction
2. Methods
2.1. Calculation Method
2.1.1. Finite Element Analysis of Seismic Response of Soil Slope
2.1.2. Definition of Effective Peak Acceleration
2.1.3. Correlation Calculation Method
2.2. Modeling
3. Results
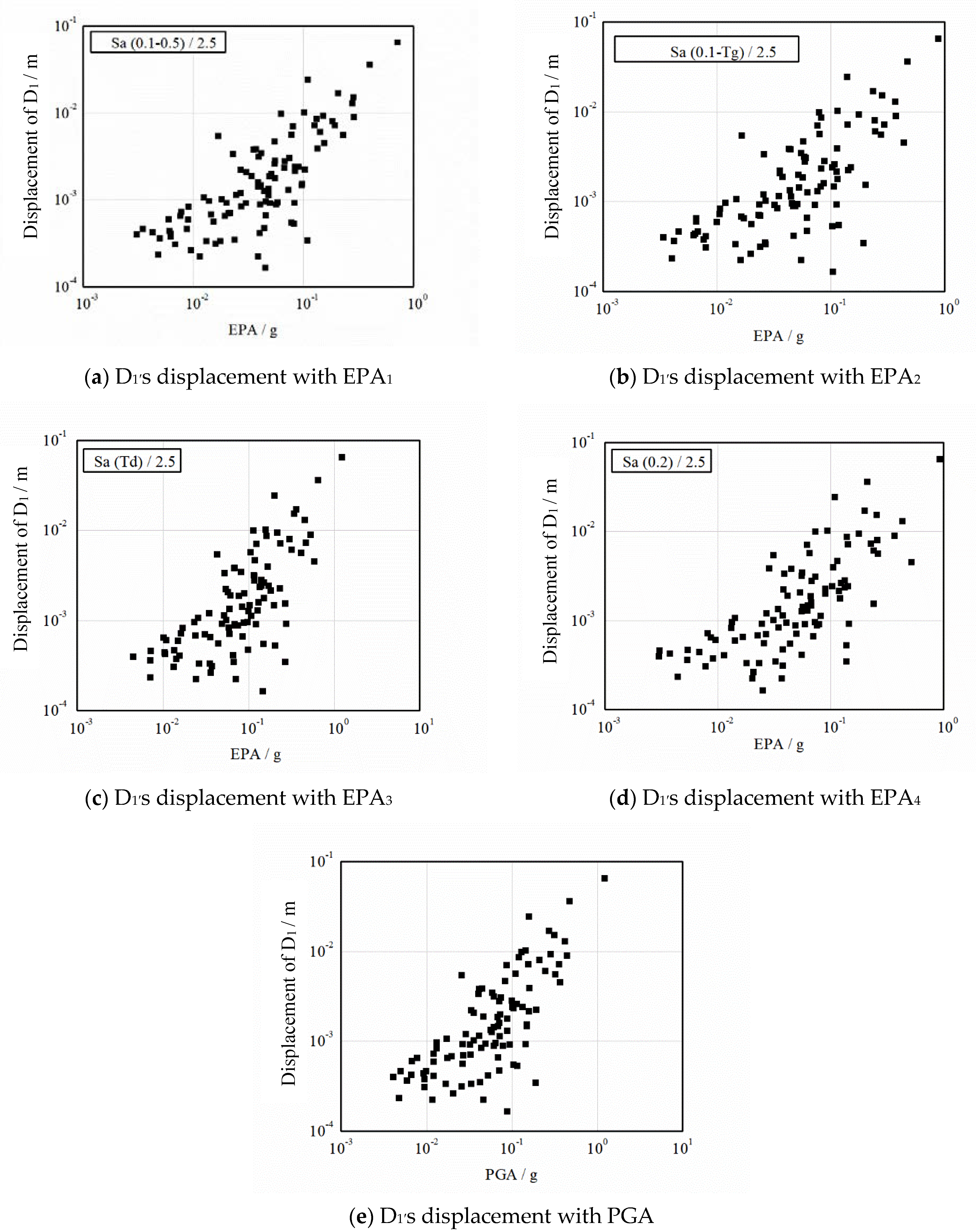
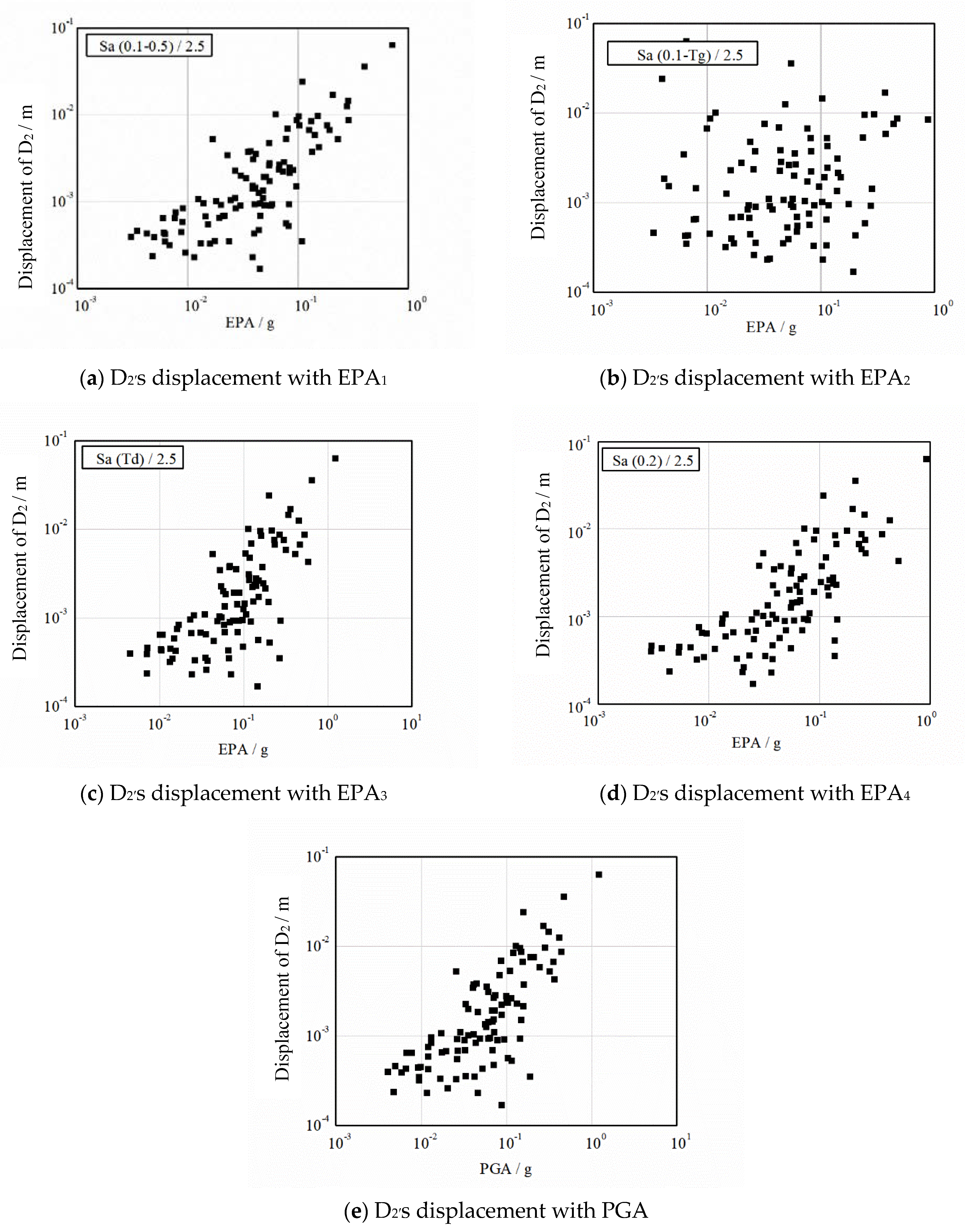
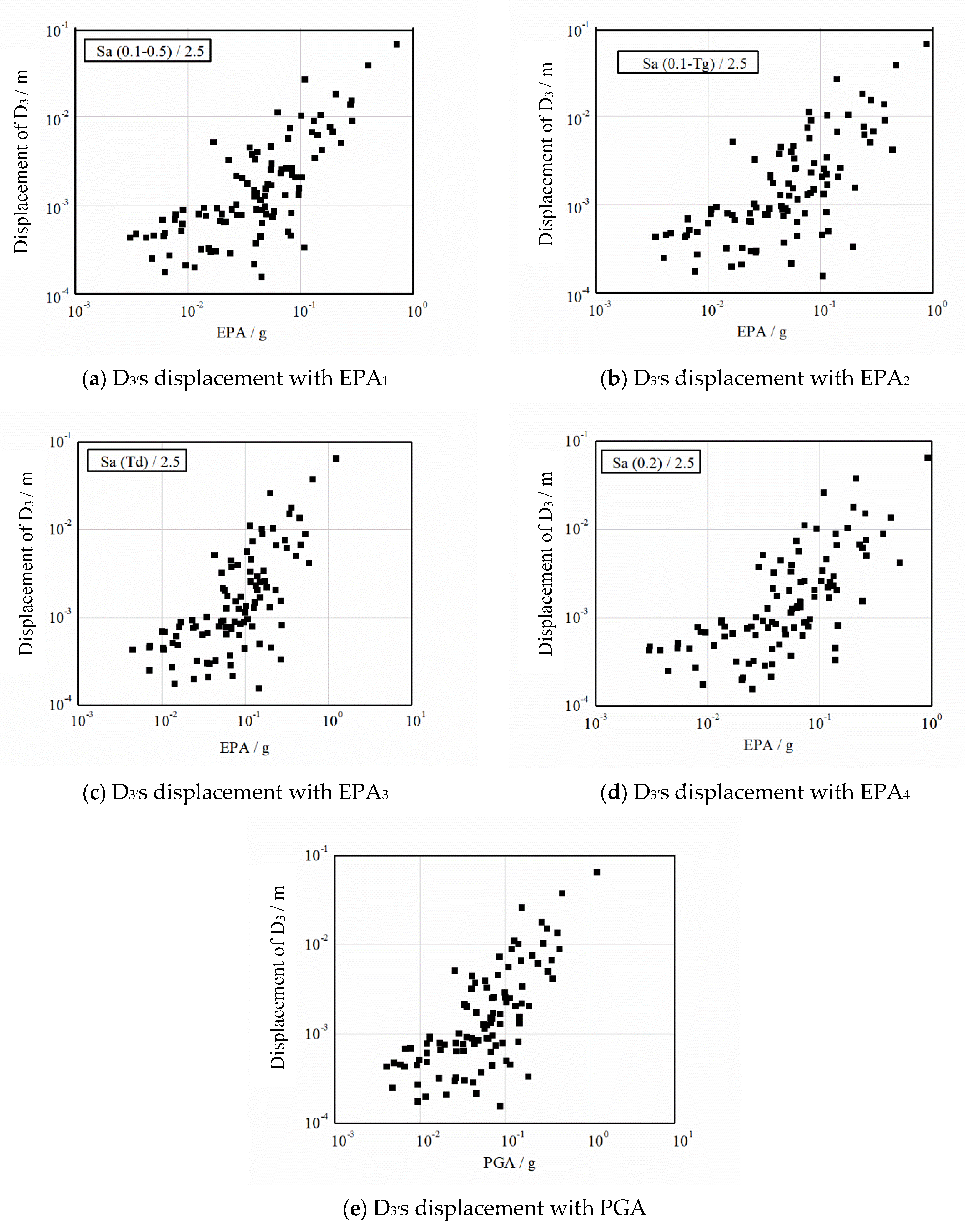
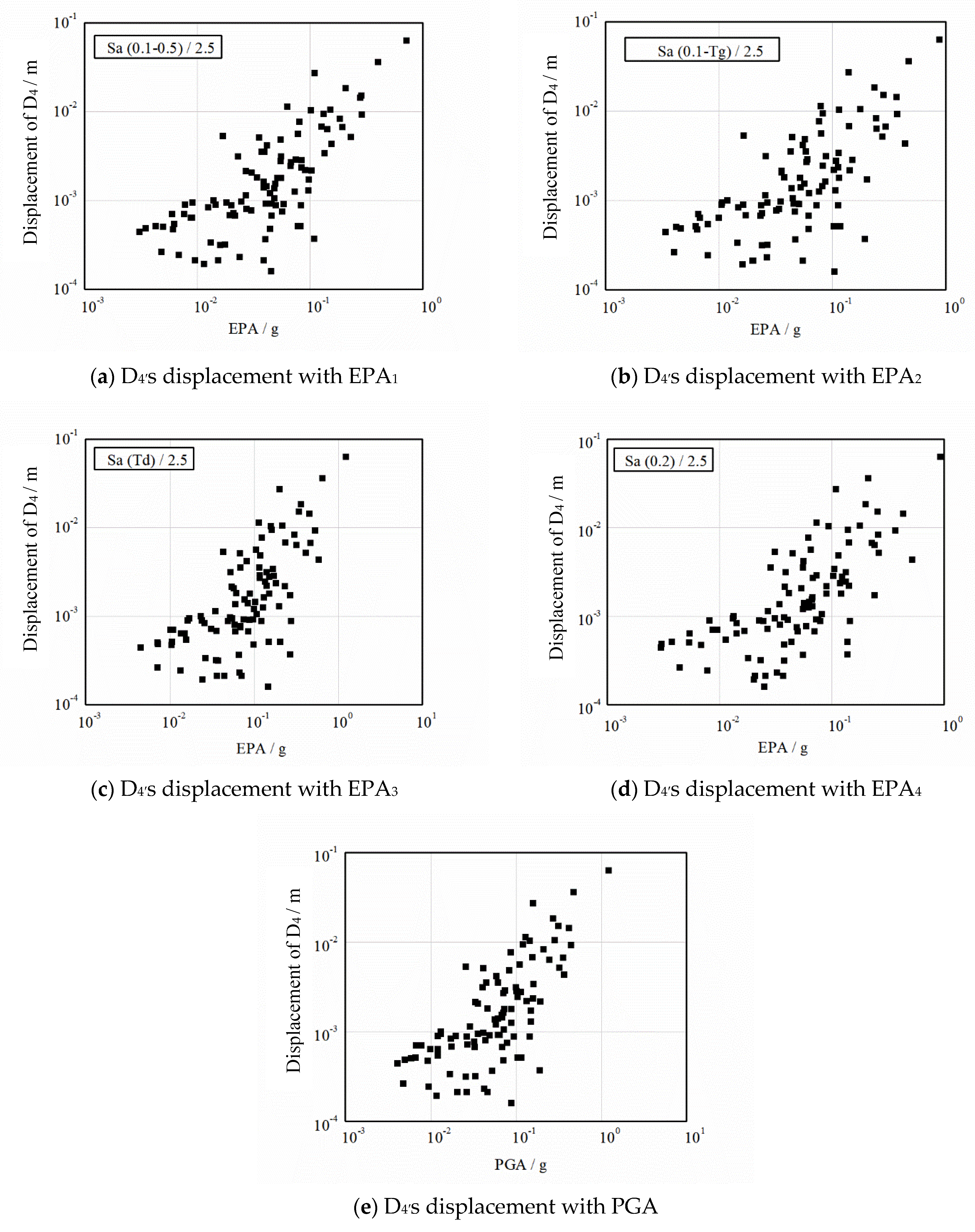
3.1. Influence Law of EPA on Slope Seismic Deformation Response
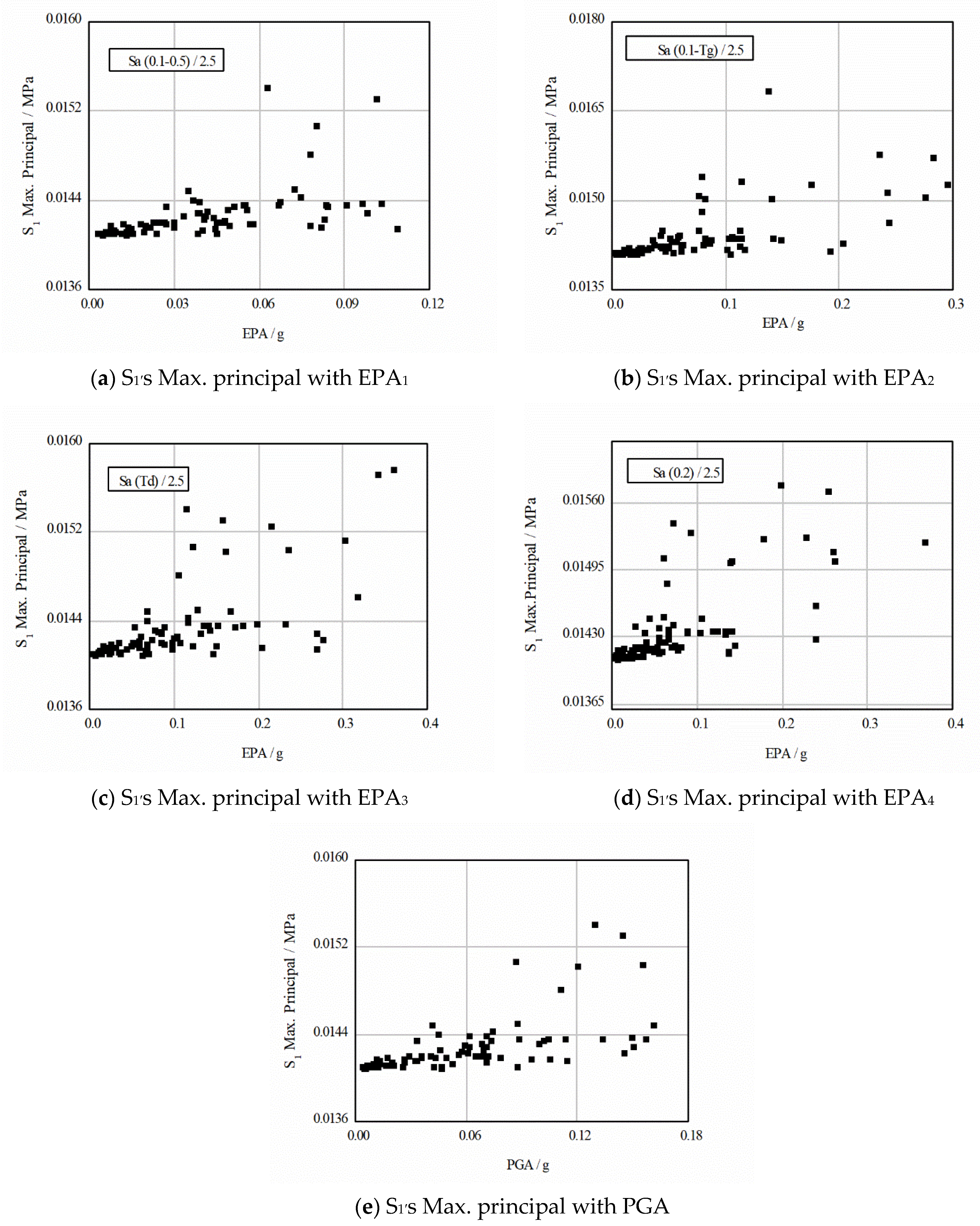
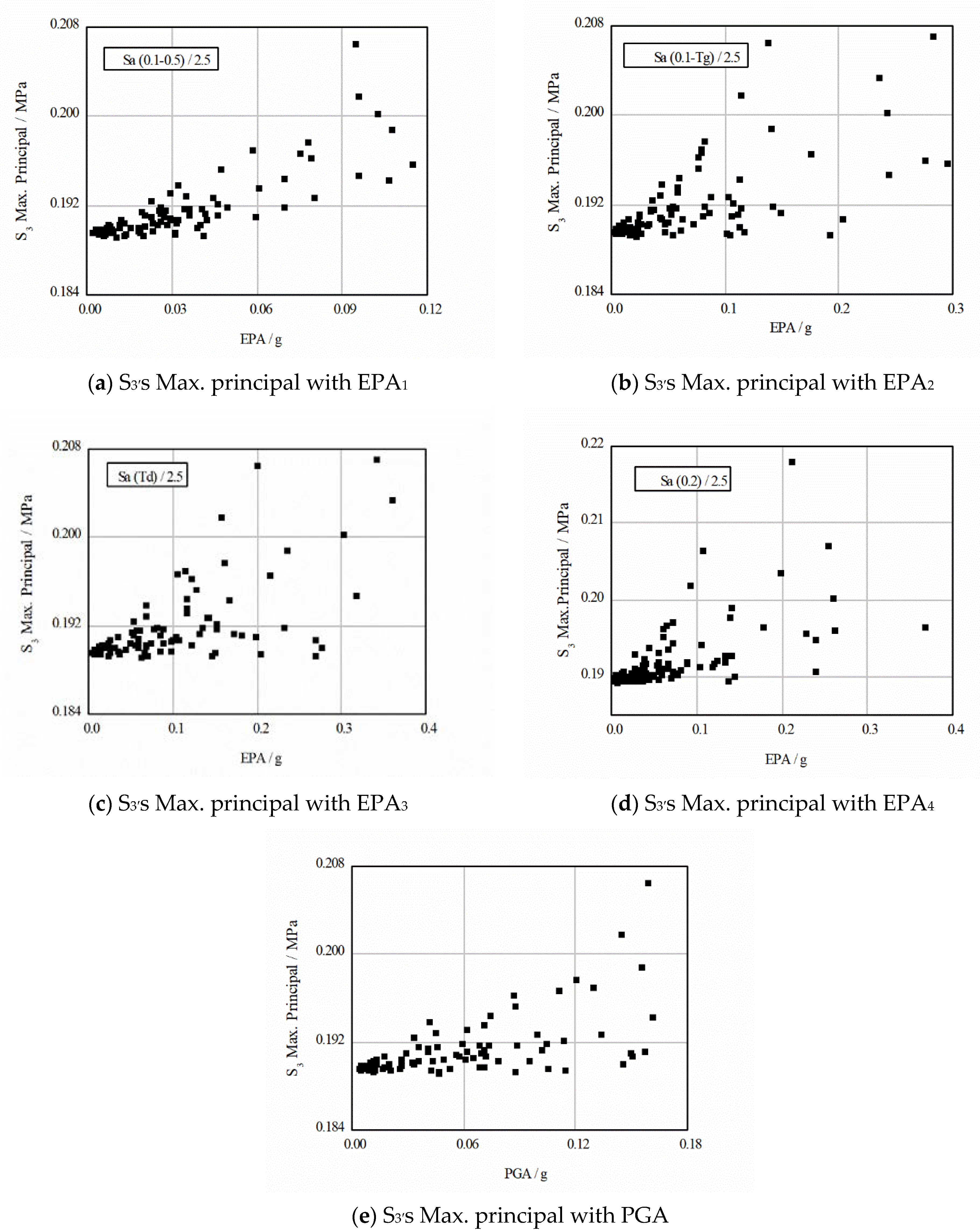
3.2. Influence Law of EPA on Seismic Stress of Slope
4. Discussion
5. Conclusions
- (1)
- As a whole, the displacement and stress responses of slope under earthquake action increase with the increase in PGA and EPA under different definitions, showing a positive linear relationship.
- (2)
- In the quantitative analysis, the linear correlation coefficients of PGA and EPA under different definitions on soil slope deformation displacement and stress response are different. Among them, EPA1 and PGA have the highest correlation coefficients with soil slope deformation displacement and stress response, followed by EPA2, EPA3 and EPA4.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- GB 50011-2010; Code for Seismic Design of Buildings. Construction Industry Press: Beijing, China, 2010.
- Long, C.; Lai, M.; Yu, H.; Li, D.H. Correlation between effective peak acceleration and seismic intensity. Earthq. Res. Sichuan 2011, 2, 26–31. [Google Scholar]
- Chang, L.; Liao, Y.; Wang, Y. EPA-based adjustment method of seismic ground motion record and its application. Build. Struct. 2020, 50, 13–17. [Google Scholar]
- Chen, H.; Guo, M. Selection of ground motion parameters for design of major engineering sites. In Advances in Modern Earthquake Engineering; Southeast University Press: Nanjing, China, 2020; pp. 25–39. [Google Scholar]
- An, D. Comparative analysis and improvement of different adjustment methods of effective peak acceleration. J. Build. Struct. 2020, 41 (Suppl. 1), 417–424. [Google Scholar]
- Basu, B.; Gupta, V.K. A damage-based definition of effective peak acceleration. Earthq. Eng. Struct. Dyn. 1998, 27, 503–512. [Google Scholar] [CrossRef]
- Cao, S.; Wang, Y.; Li, Z. Statistical analysis of seismic effective peak acceleration. Build. Struct. 2019, 49, 73–76. [Google Scholar]
- Zhong, J.; Hu, X.; Yi, L.; Wu, S.X. Study on relations of effective peak acceleration and peak ground acceleration. World Earthq. Eng. 2006, 22, 34–38. [Google Scholar]
- Yi, L.; Hu, X.; Zhong, Y. Major engineering design seismic determination based on EPA. J. Seismol. Res. 2004, 27, 271–276. [Google Scholar]
- Guo, M.; Zhang, J.; Tang, B. The relationship between bedrock seismic peak acceleration and effective peak acceleration was studied. In Proceedings of the 7th National Academic Conference on Earthquake Engineering (I), Guangzhou, China, 16–19 November 2006; pp. 83–88. [Google Scholar]
- Zhang, J.; Li, X.; Qi, J.; Wang, Y.S.; He, Q.M. Effect of influence weights of ground motion parameters on soil slope seismic response. J. Vib. Shock. 2018, 37, 225–230. [Google Scholar]
- Zhang, J.; Chen, S.; Wang, T.; Wu, F. Study on correlation between ground motion parameters and soil slope seismic response. Bull. Eng. Geol. Environ. 2022, 81, 226. [Google Scholar] [CrossRef]
- Huang, F.; Cao, Z.; Guo, J.; Jiang, S.; Guo, Z. Comparisons of heuristic, general statistical and machine learning models for landslide susceptibility prediction and mapping. CATENA 2020, 191, 104580. [Google Scholar] [CrossRef]
- Chang, Z.; Du, Z.; Zhang, F.; Huang, F.; Chen, J.; Li, W.; Guo, Z. Landslide Susceptibility Prediction Based on Remote Sensing Images and GIS: Comparisons of Supervised and Unsupervised Machine Learning Models. Remote Sens. 2020, 12, 502. [Google Scholar] [CrossRef] [Green Version]
- Huang, F.; Zhang, J.; Zhou, C.; Wang, Y.; Huang, J.; Zhu, L. A deep learning algorithm using a fully connected sparse autoencoder neural network for landslide susceptibility prediction. Landslides 2020, 17, 217–229. [Google Scholar] [CrossRef]
- Huang, F.; Cao, Z.; Guo, J.; Jiang, S.; Zhou, C.; Guo, Z. Landslide susceptibility prediction based on a semi-supervised multiple-layer perceptron model. Landslides 2020, 17, 2919–2930. [Google Scholar] [CrossRef]
- Jiang, S.; Huang, J.; Huang, F.; Yang, Y.; Yao, C.; Zhou, C. Modelling of spatial variability of soil undrained shear strength by conditional random fields for slope reliability analysis. Appl. Math. Model. 2018, 63, 374–389. [Google Scholar] [CrossRef]
- Yuan, R.; Xu, X.; Chen, G.; Tan, X.B.; Klinger, Y.; Xing, H.L. Ejection Landslide at Northern Terminus of Beichuan Rupture Triggered by 2008 Mw 7.9 Wenchuan Earthquake. Bull. Seismol. Soc. Am. 2010, 100, 2689–2699. [Google Scholar] [CrossRef]
- Xu, C.; Xu, X.W.; Yu, G.H.; Wu, X.Y. Susceptibility Analysis of Impact Factors of Landslides Triggered by Yushu Earthquake. Sci. Technol. Rev. 2012, 30, 18–24. [Google Scholar]
- Tian, Y.Y.; Xu, C.; Xu, X.W.; Chen, J. Analysis of Parameters of Landslides Triggered by the Minxian-Zhangxian Ms 6.6 Earthquake. China Earthq. Eng. J. 2013, 35, 616–626. [Google Scholar]
- Chang, Z.; Catani, F.; Huang, F.; Liu, C.; Meena, S.; Huang, J.; Zhou, C. Landslide susceptibility prediction using slope unit-based machine learning models considering the heterogeneity of conditioning factors. J. Rock Mech. Geotech. Eng. 2022; in press. [Google Scholar] [CrossRef]
- Du, W. Effects of directionality and vertical component of ground motions on seismic slope displacements in Newmark sliding-block analysis. Eng. Geol. 2018, 239, 13–21. [Google Scholar] [CrossRef]
- Huang, F.; Tao, S.; Li, D.; Lian, Z.; Catani, Z.; Huang, J.; Li, K.; Zhang, C. Landslide susceptibility prediction considering neighborhood characteristics of landslide spatial datasets and hydrological slope units using remote sensing and GIS technologies. Remote Sens. 2022, 14, 4436. [Google Scholar] [CrossRef]
- Huang, F.; Chen, J.; Liu, W.; Huang, J.; Hong, H.; Chen, W. Regional rainfall-induced landslide hazard warning based on landslide susceptibility mapping and a critical rainfall threshold. Geomorphology 2022, 408, 108236. [Google Scholar] [CrossRef]
- Hu, Y. Earthquake Engineering, 2nd ed.; Seismological Press: Beijing, China, 2006; pp. 104–109. [Google Scholar]
- Liu, J.; Du, X. Structural Dynamics; Mechanical Industry Press: Beijing, China, 2004; pp. 98–104. [Google Scholar]
- Applied Technology Council, and Structural Engineers Association of California. Tentative Provisions for the Development of Seismic Regulations for Buildings: ATC-3; Applied Technology Council: Palo Alto, CA, USA, 1978. [Google Scholar]
- GB 18306-2015; Seismic Ground Motion Parameters Zonation Map of China. Standards Press: Beijing, China, 2015.
- Frankel, A.; Mueller, C.; Barnhard, T.; Perkins, D.; Leyendecker, E.V.; Dickman, N.; Hanson, S.; Hopper, M. National Seismic Hazard Maps-Documentation; Geological Survey Open-File Report 96-532; USGS: Reston, VA, USA, 1996; pp. 96–532.
- Li, X.; Li, Y.; Wu, D. Correlation between ground motion intensity and structural seismic response. J. Vib. Shock. 2014, 33, 184–189. [Google Scholar]
- Zhang, J.; Li, X.; Wang, X.; Chi, M.; Wang, Y. Method for judging seismic stability state of soil slopes. Chin. J. Geotech. Eng. 2018, 40, 2096–2102. [Google Scholar]
- Lysmer, J.; Kuhlemeyer, R. Finite dynamic model for infinite media. J. Eng. Mech. Div. 1969, 95, 859–877. [Google Scholar] [CrossRef]
- Li, B.; Gui, Y. Study on dynamic response of homogeneous cutting slope under finite element-based earthquake action. Front. Earth Sci. 2020, 10, 45–48. [Google Scholar] [PubMed]
- Liu, H.; Chen, S. Research advances in dynamic constitutive models and dynamic analysis of soils. In Proceedings of the Yong Specialists in Geotechnical Engineering Academic Forum; Construction Industry Press: Beijing, China, 1998; pp. 29–42. [Google Scholar]
- Editorial Board of Engineering Geology Manual. Engineering Geology Manual, 4th ed.; China Construction Industry Press: Beijing, China, 2006; pp. 22–28. [Google Scholar]
- Li, X.; Liao, Z.; Du, X. An explicit finite difference method for viscoelastic dynamic problem. J. Earthq. Eng. Eng. Vib. 1992, 9, 74–80. [Google Scholar]
- Deeks, A.; Randolph, M. Axisymmetric time domain transmitting boundaries. J. Eng. Mech. 1994, 120, 25–42. [Google Scholar] [CrossRef]
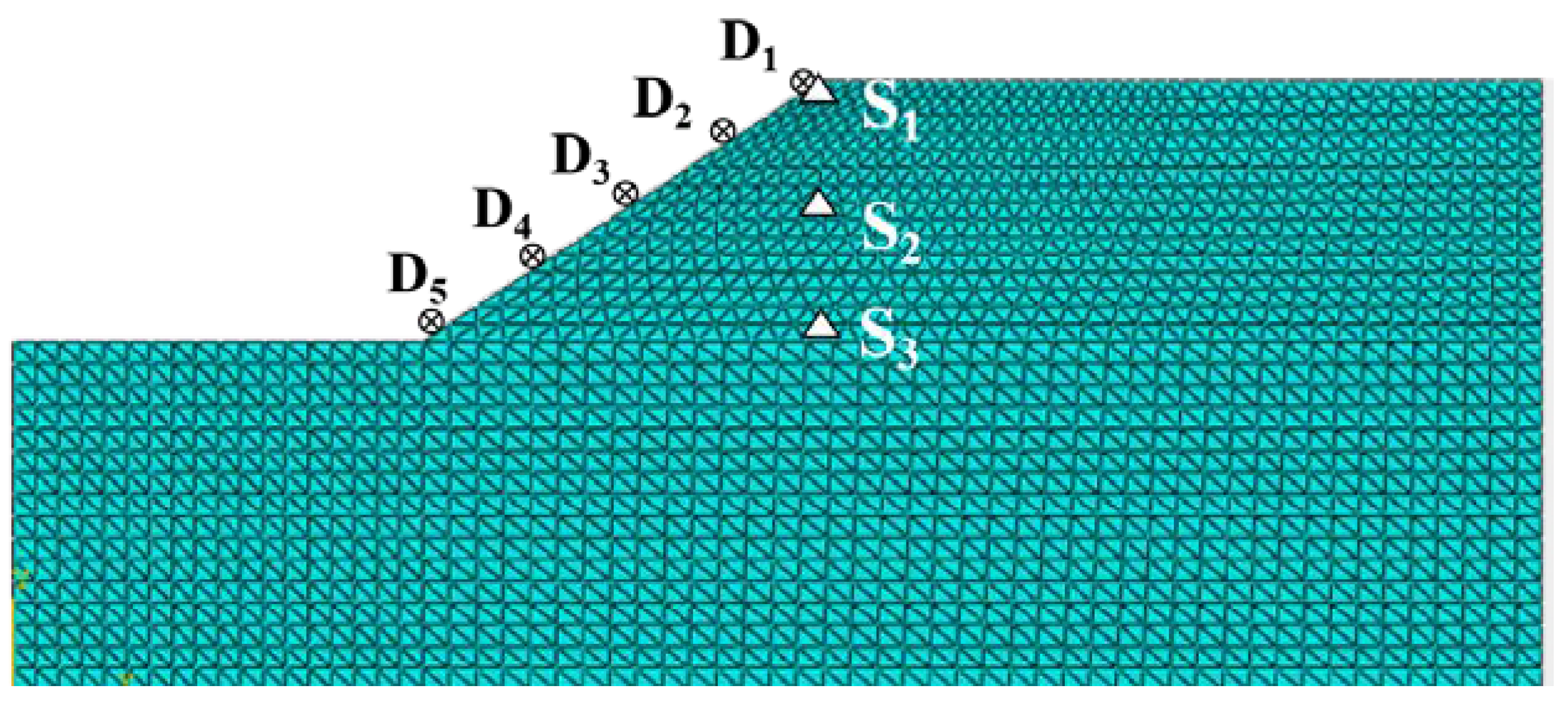


| Parameters | Density/ (kg·m−3) | Dynamic Modulus of Elasticity/MPa | Poisson’s Ratio | Cohesive Force/kPa | Internal Friction Angle/° |
|---|---|---|---|---|---|
| Number | 2070 | 90.8 | 0.3 | 13.99 | 25 |
| Slope Responses | EPA1 | EPA2 | EPA3 | EPA4 | PGA |
|---|---|---|---|---|---|
| D1 displacement | 0.890 | 0.826 | 0.823 | 0.732 | 0.869 |
| D2 displacement | 0.889 | 0.832 | 0.828 | 0.737 | 0.861 |
| D3 displacement | 0.881 | 0.817 | 0.813 | 0.720 | 0.863 |
| D4 displacement | 0.880 | 0.817 | 0.812 | 0.720 | 0.874 |
| D5 displacement | 0.890 | 0.827 | 0.822 | 0.730 | 0.873 |
| Mean value | 0.886 | 0.824 | 0.820 | 0.727 | 0.868 |
| Slope Responses | EPA1 | EPA2 | EPA3 | EPA4 | PGA |
|---|---|---|---|---|---|
| S1 Max. Principal | 0.890 | 0.828 | 0.824 | 0.717 | 0.858 |
| S2 Max. Principal | 0.895 | 0.828 | 0.819 | 0.716 | 0.845 |
| S3 Max. Principal | 0.911 | 0.843 | 0.832 | 0.747 | 0.869 |
| Mean value | 0.897 | 0.833 | 0.825 | 0.727 | 0.857 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, J.; Shen, Y.; Lu, T.; Yuan, Y.; Zhang, C. Sensitivity of EPA of Ground Motion to Soil Slope Dynamic Response. Sustainability 2022, 14, 16985. https://doi.org/10.3390/su142416985
Zhang J, Shen Y, Lu T, Yuan Y, Zhang C. Sensitivity of EPA of Ground Motion to Soil Slope Dynamic Response. Sustainability. 2022; 14(24):16985. https://doi.org/10.3390/su142416985
Chicago/Turabian StyleZhang, Jiangwei, Yan Shen, Tao Lu, Ying Yuan, and Chengda Zhang. 2022. "Sensitivity of EPA of Ground Motion to Soil Slope Dynamic Response" Sustainability 14, no. 24: 16985. https://doi.org/10.3390/su142416985
APA StyleZhang, J., Shen, Y., Lu, T., Yuan, Y., & Zhang, C. (2022). Sensitivity of EPA of Ground Motion to Soil Slope Dynamic Response. Sustainability, 14(24), 16985. https://doi.org/10.3390/su142416985









