A Sustainable Production Scheduling with Backorders under Different Forms of Rework Process and Green Investment
Abstract
:1. Introduction
1.1. Literature Review
1.2. Research Gaps and Contributions
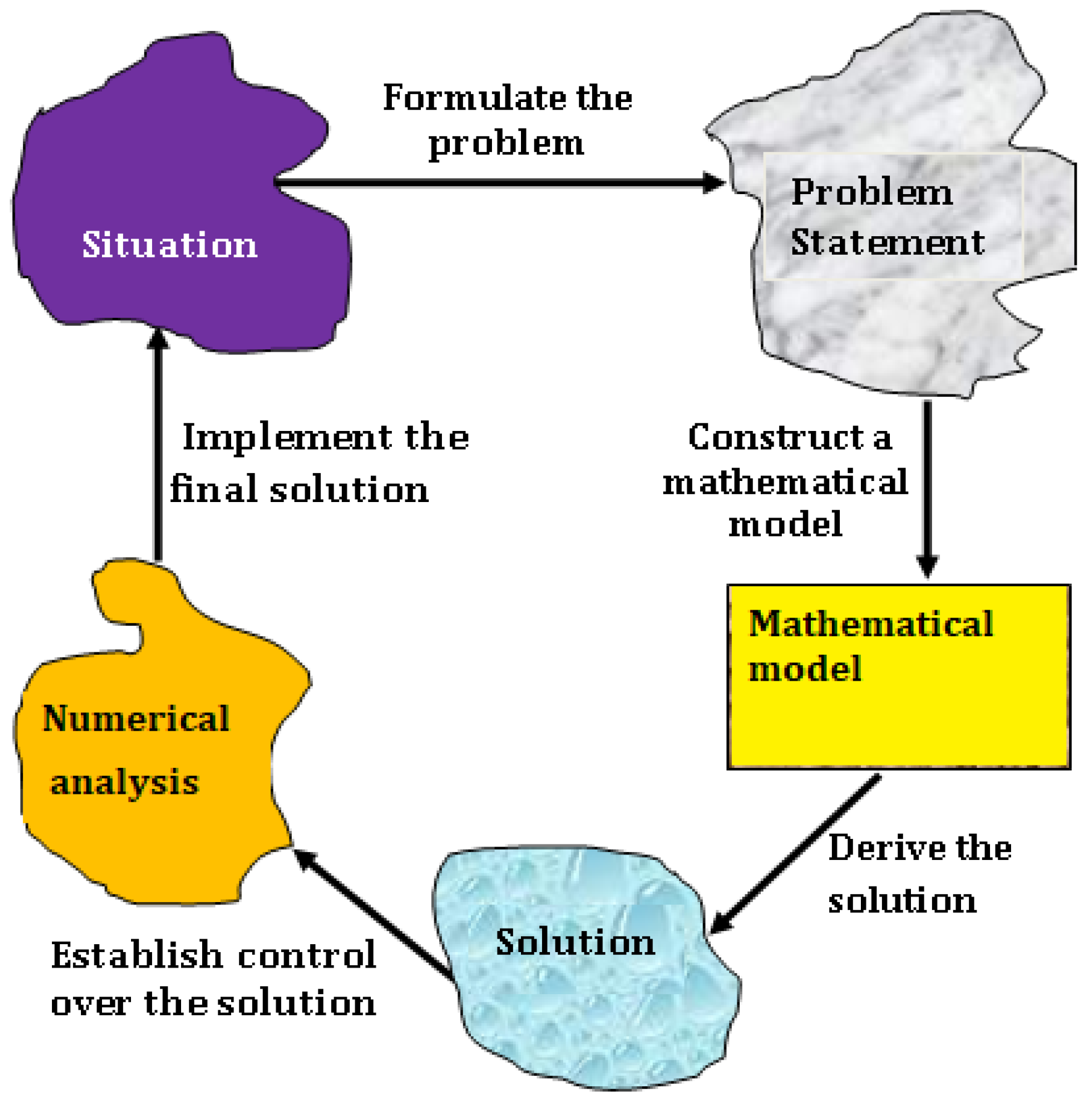
1.3. Research Methodology
- Description of the problem
- Mathematical model formulation
- Solution procedure
- Numerical Analysis
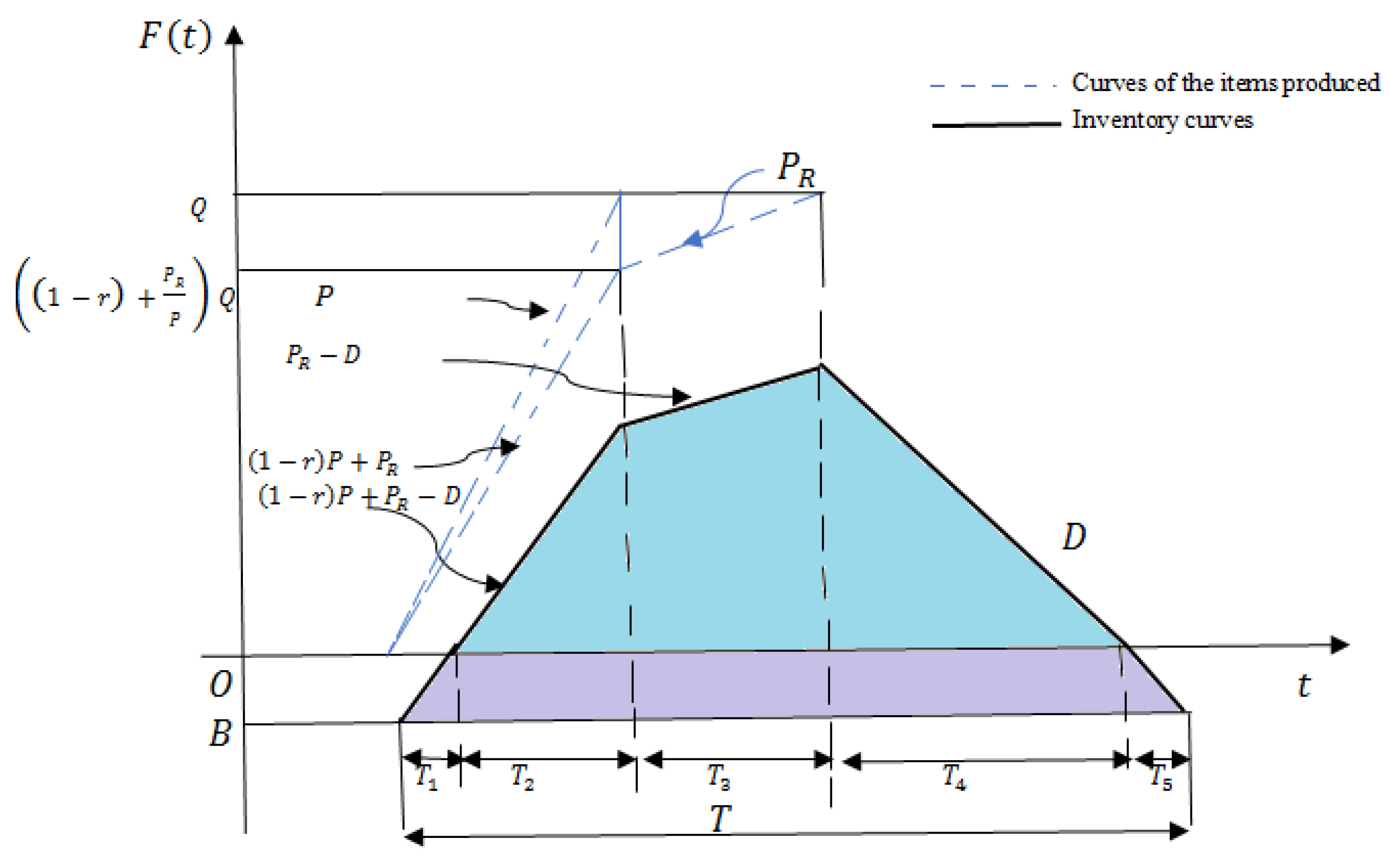
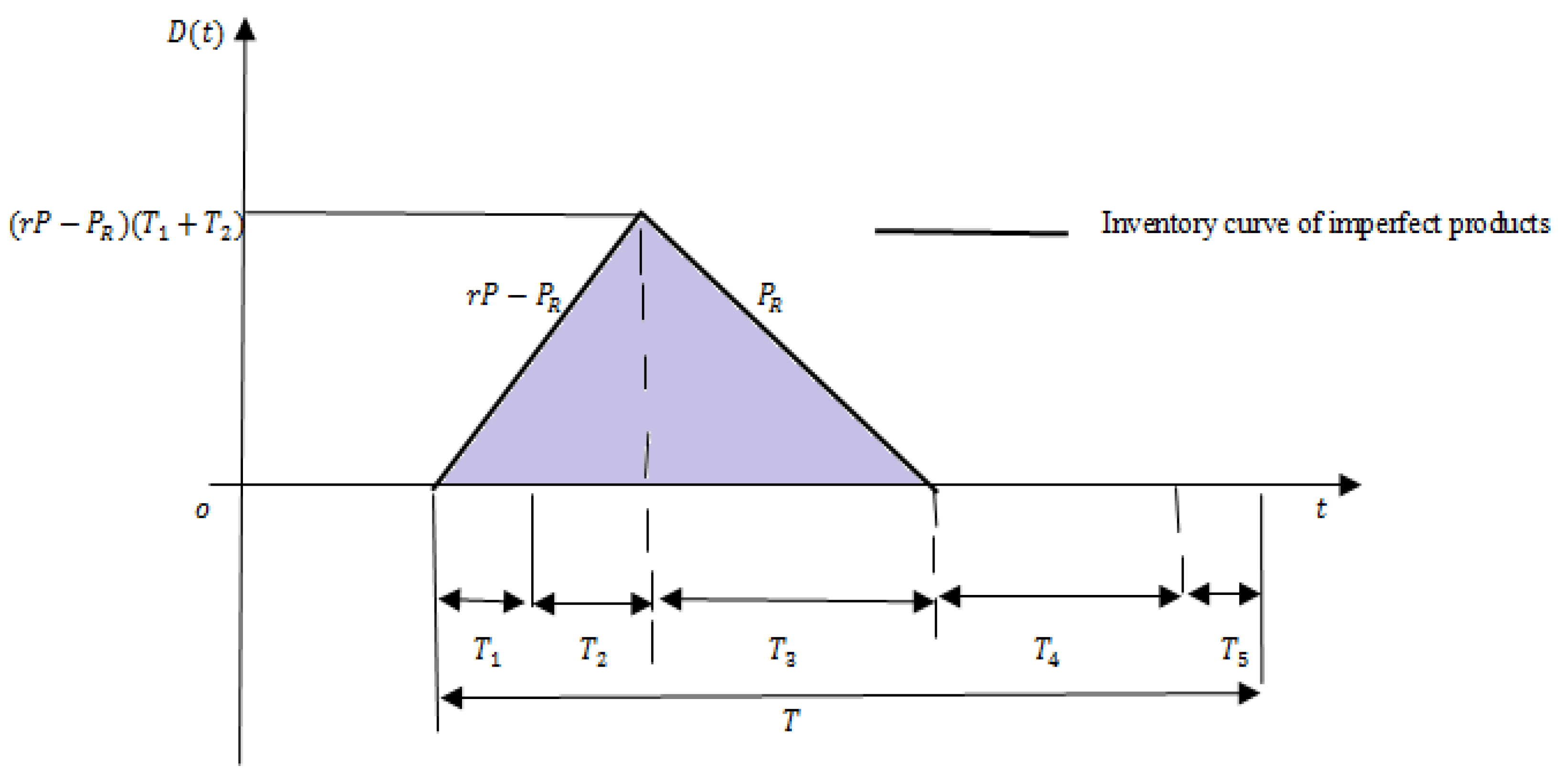
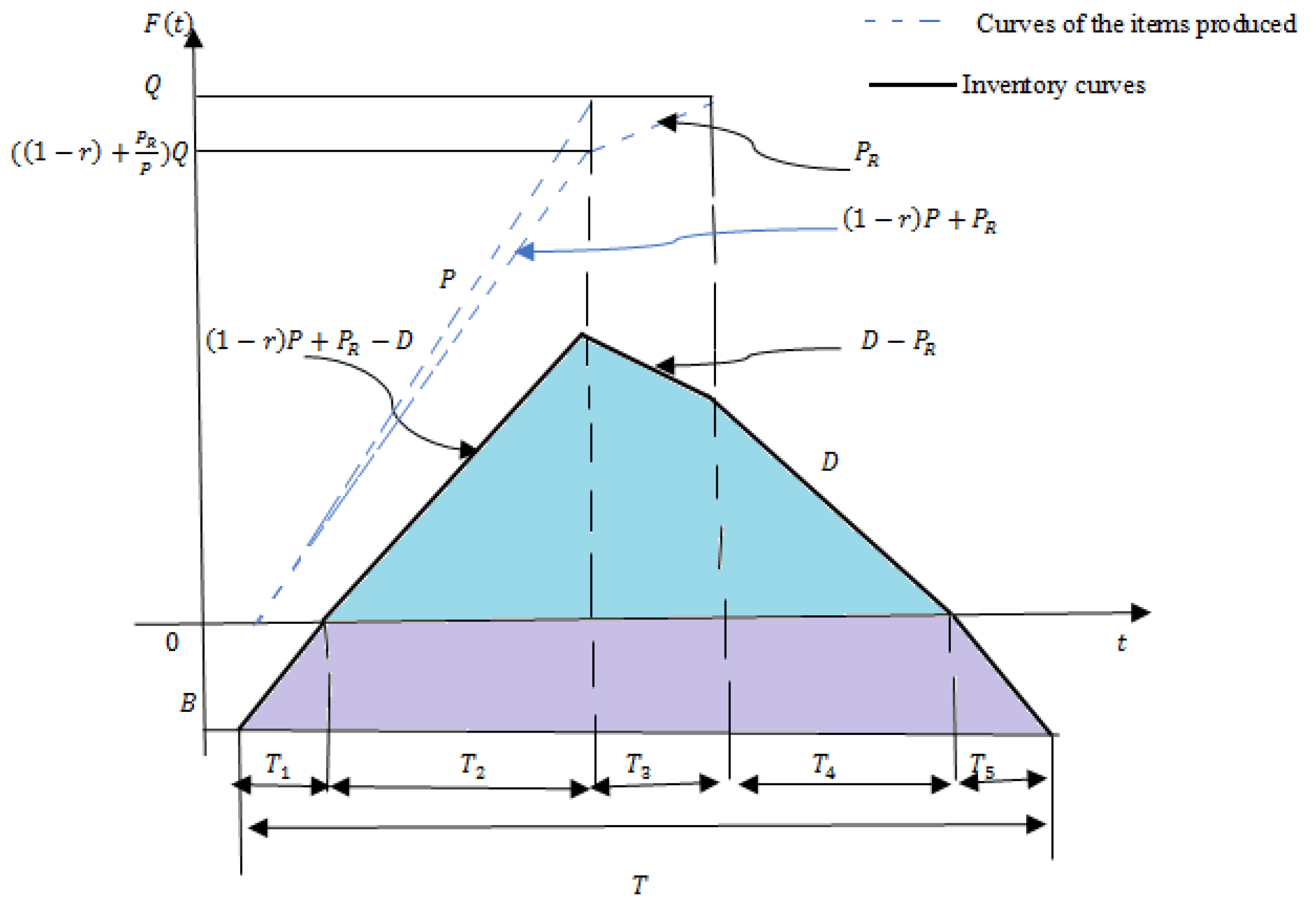
2. Descriptions of Problem
Assumptions
- Consumer requirement(demand) and production rate are constant.
- CO2 are generated from the process of production, transportation, and storage.
- There are two primary forms that green technology might reduce CO2:
- (i)
- , where stands for the offsetting CO2 reduction factor and for the CO2 reduction efficiency factor (Huang et al. [32]).
- (ii)
- where stands for the effectiveness of greener technology in decreasing CO2, is a proportion of CO2 after investment in green technology, and F is a fraction of average CO2 reduction (Mishra et al. [33]).
- The relationship between setup cost reduction and capital investment may be defined using the logarithmic investment cost function. Therefore, S and the capital expenditure for S reduction () may be recorded as for where , is the fractional cut in S\dollar rise in .
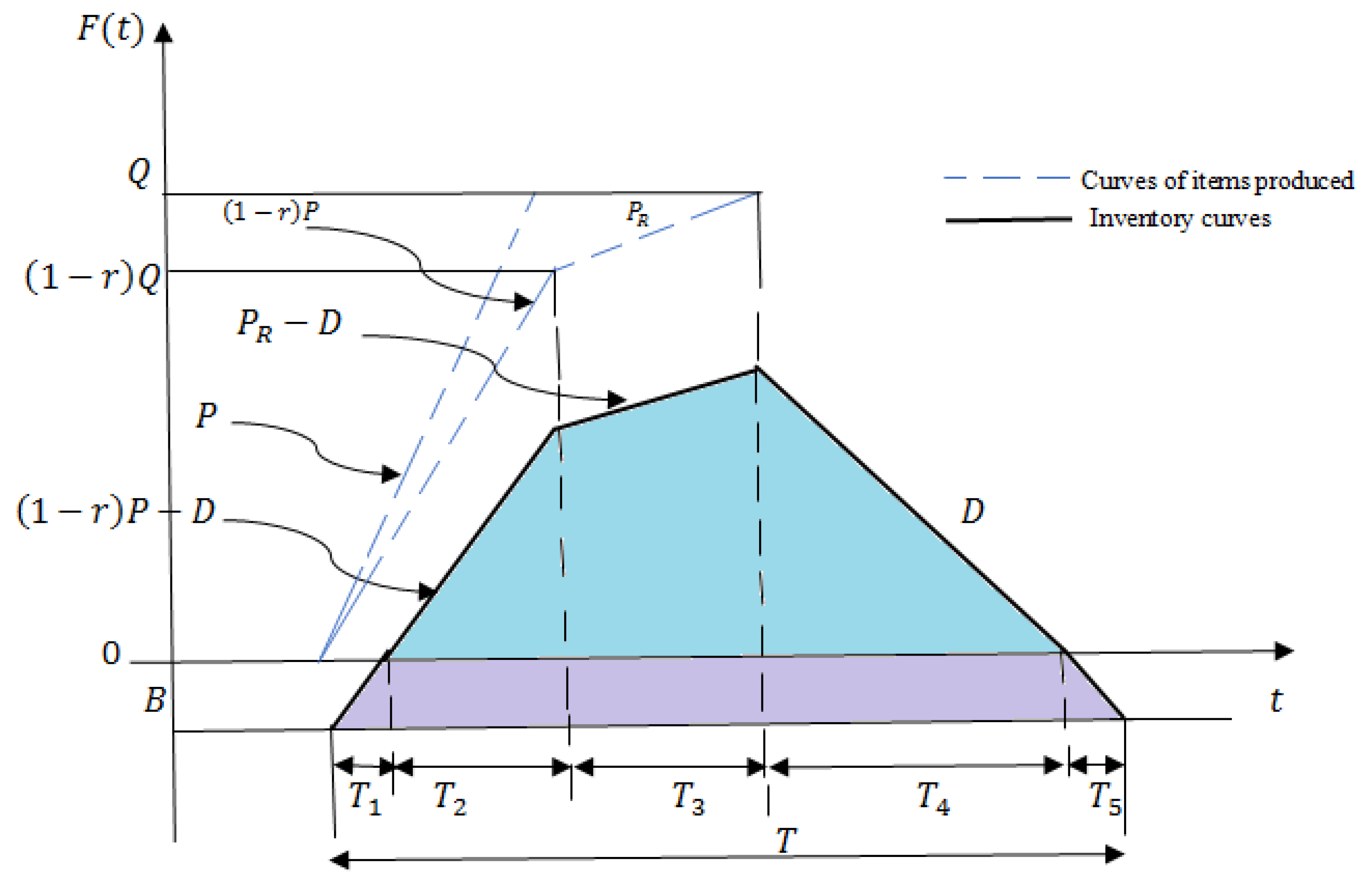
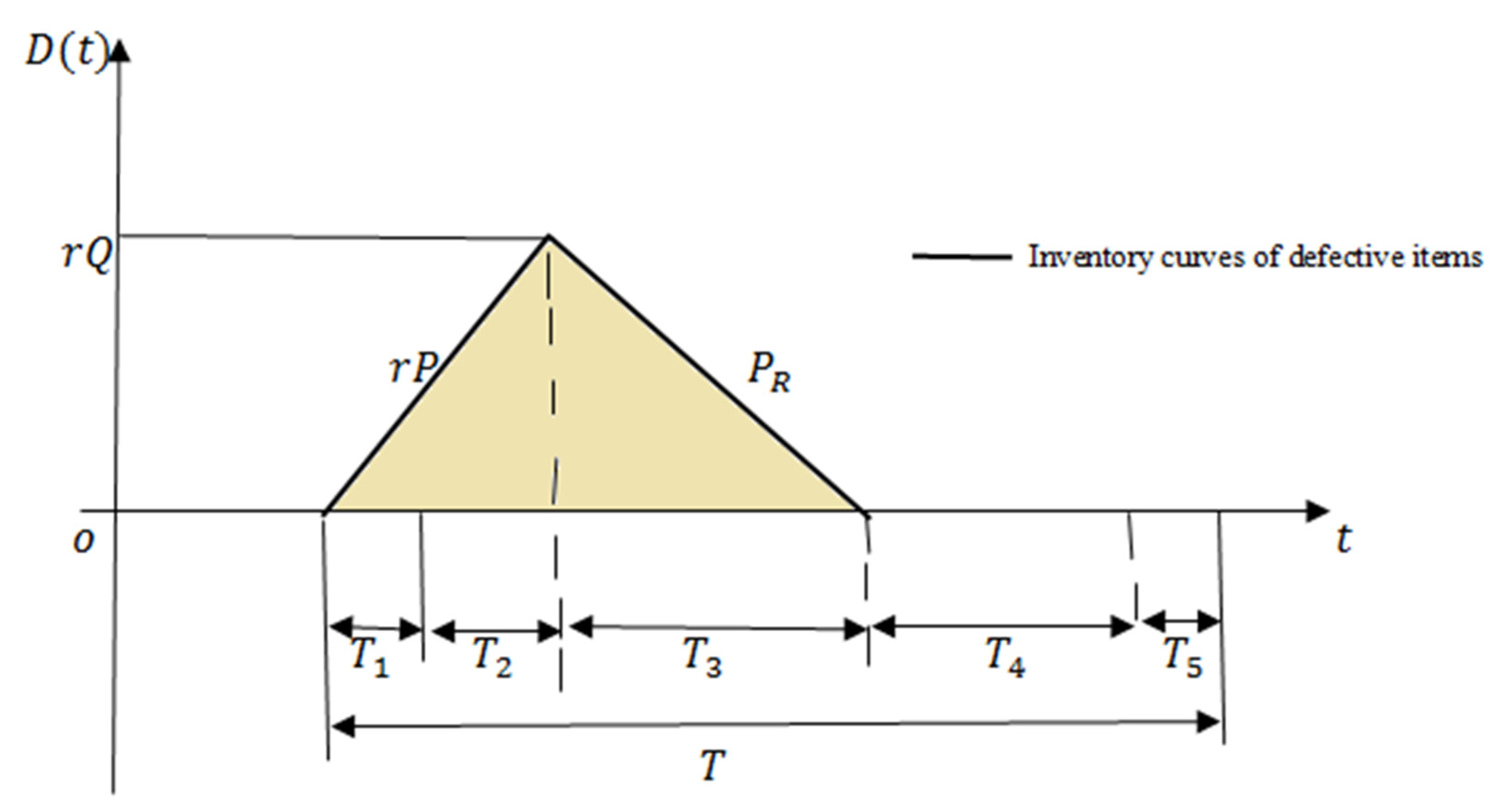
3. Production Scheduling with Asynchronous Rework
3.1. The PR Is Higher than D (PR > D)
3.1.1. Carbon Tax with Quadratic Form of Green Investment Function
| Algorithm 1. Optimal Solution for the Quadratic Case. |
| Step 1. Determine G from Equation (5) Step 2. Loop step (1.1)–(1.3) until the values Q, B and S have converged, and the solutions signify by . (1.1) Start with and . (1.2) Replacing B1 and S1 into Equation (3) calculates Q1. (1.3) Applying Q1 find B1 by Equation (3) and S2 from Equation (4). Step 3. Compare with
(2.1) Let and (2.2) Substitute B1 in Equation (2) (switch S by S0) to obtain the new Q1. (2.3) Utilizing Q1 determines B1 by Equation (3). Step 5. Compute by Equation (1), set is an optimal solution. |
3.1.2. Carbon Tax with Exponential form of Green Investment Function
| Algorithm 2. Optimal Solution for the Exponential Case. |
have converged, and the solutions represented by .
(2.1) Let (2.2) Substitute B1 and G1 in Equation (8) (replace S by S0) to obtain the new Q1. (2.3) Utilizing Q1 determines B1 and G1 by Equations (9) and (10). is an optimal solution. |
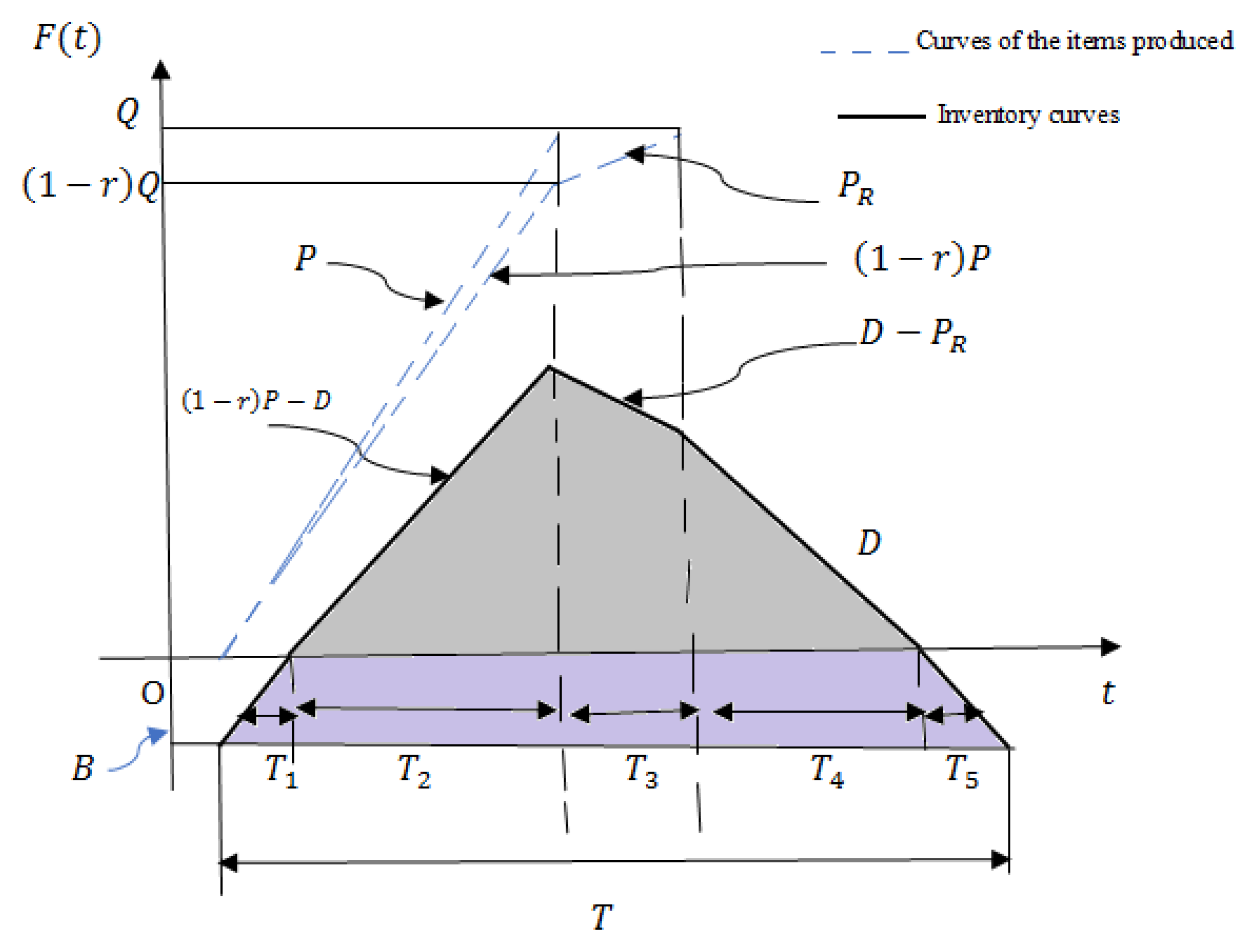
3.2. The PR Is Lower than
3.2.1. Carbon Tax with Quadratic Form of Green Investment
3.2.2. Carbon Tax with Exponential form of Green Investment function
4. Production Scheduling with Synchronous Rework
4.1. The Is Higher than D
4.1.1. Carbon Tax with Quadratic form of Green Investment Function
4.1.2. Carbon Tax with Exponential form of Green Investment Function
4.2. The Is Lower than D
4.2.1. Carbon Tax with Quadratic form of Green Investment Function
4.2.2. Carbon Tax with Exponential form of Green Investment Function
5. Numerical and Sensitivity Assessment
5.1. Asynchronous Rework
5.2. Synchronous Rework
5.3. Discussion and Comparison of Findings
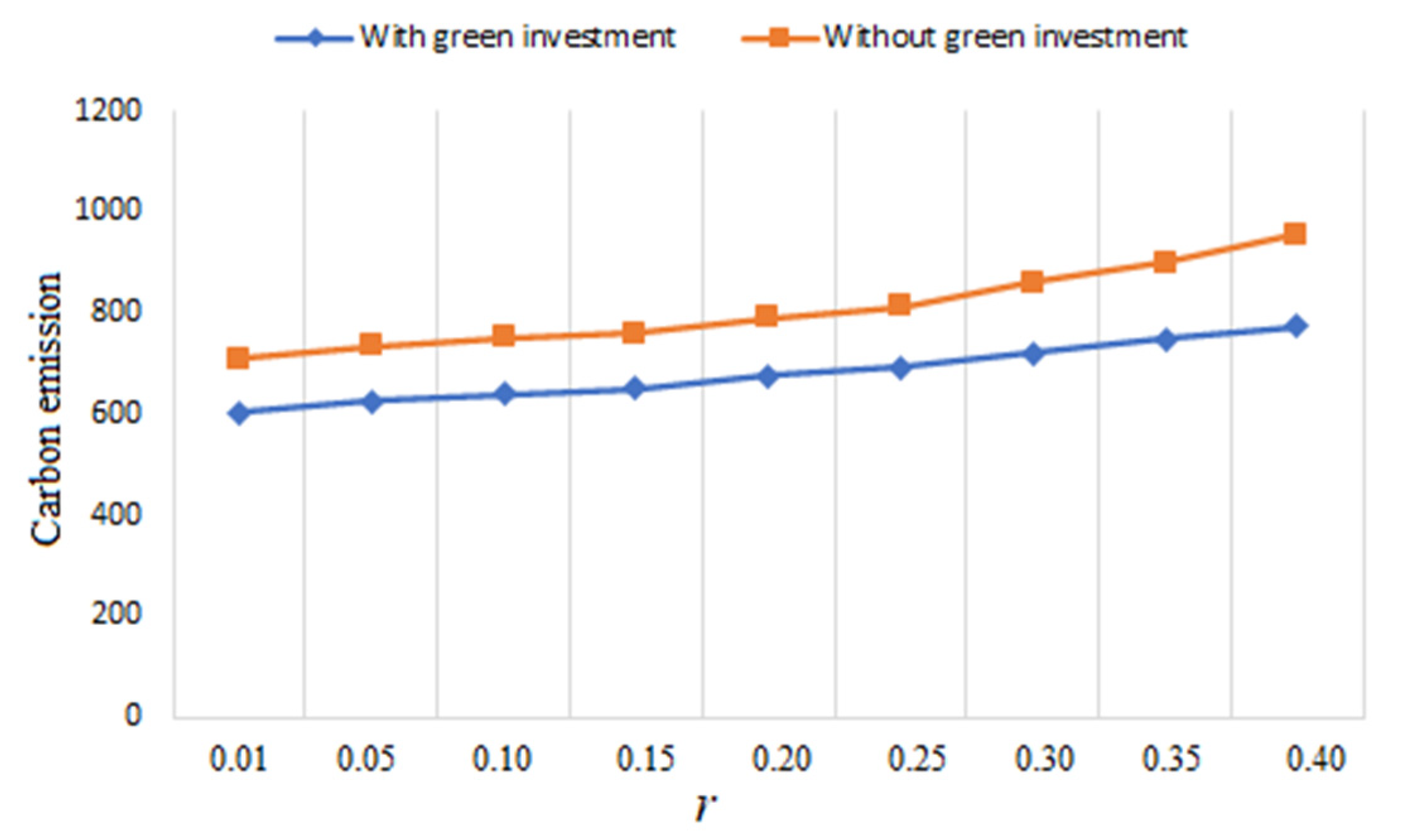
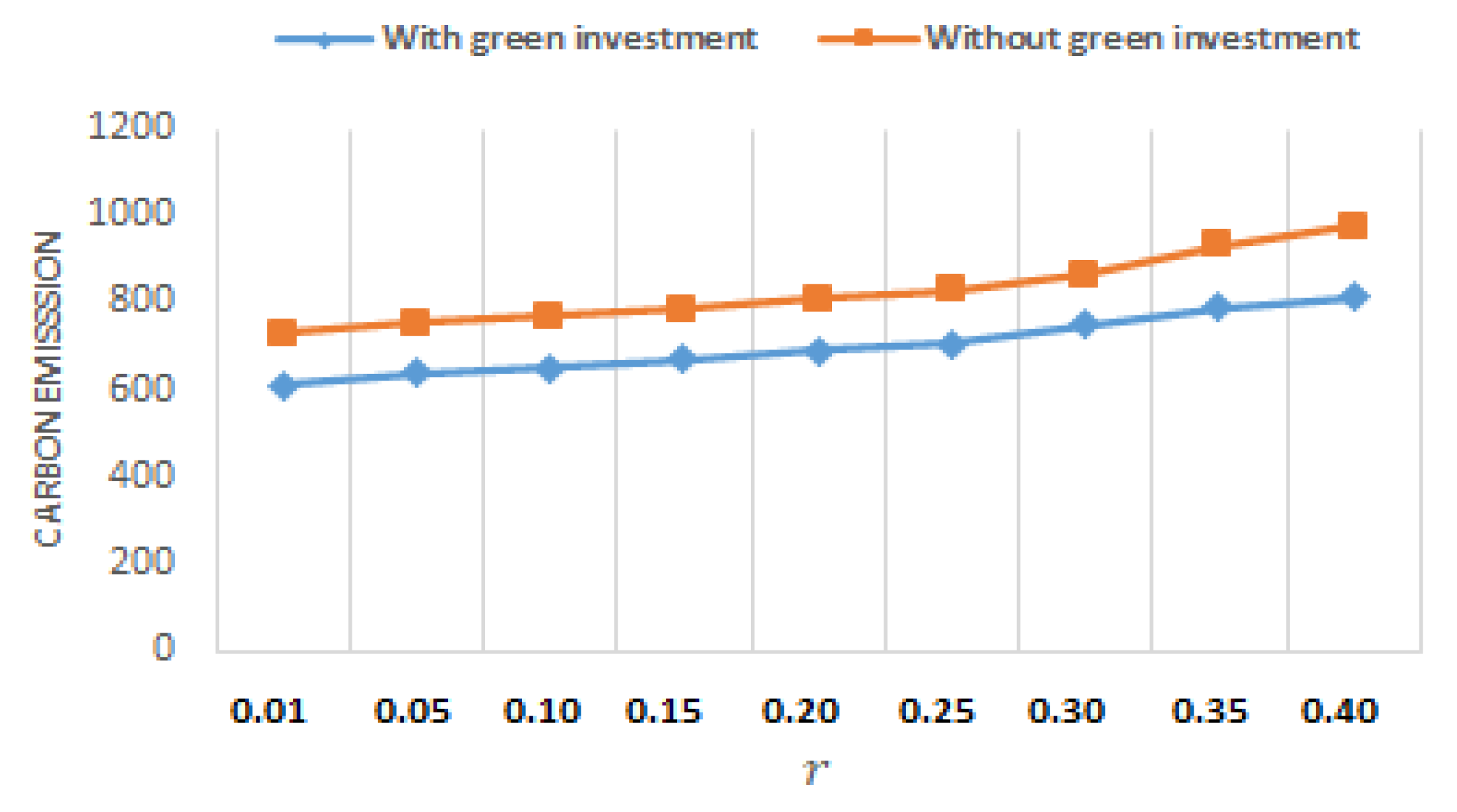
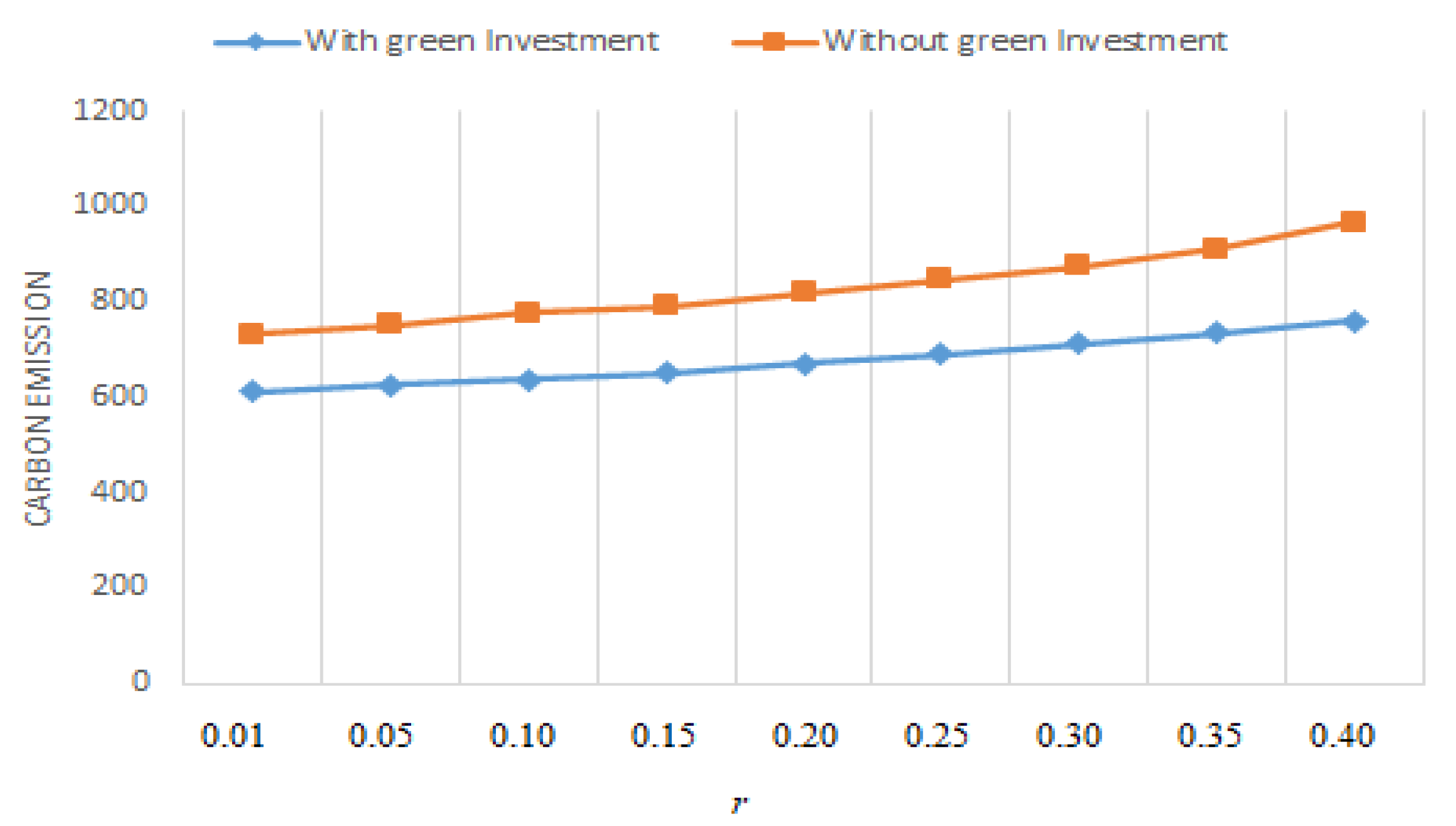
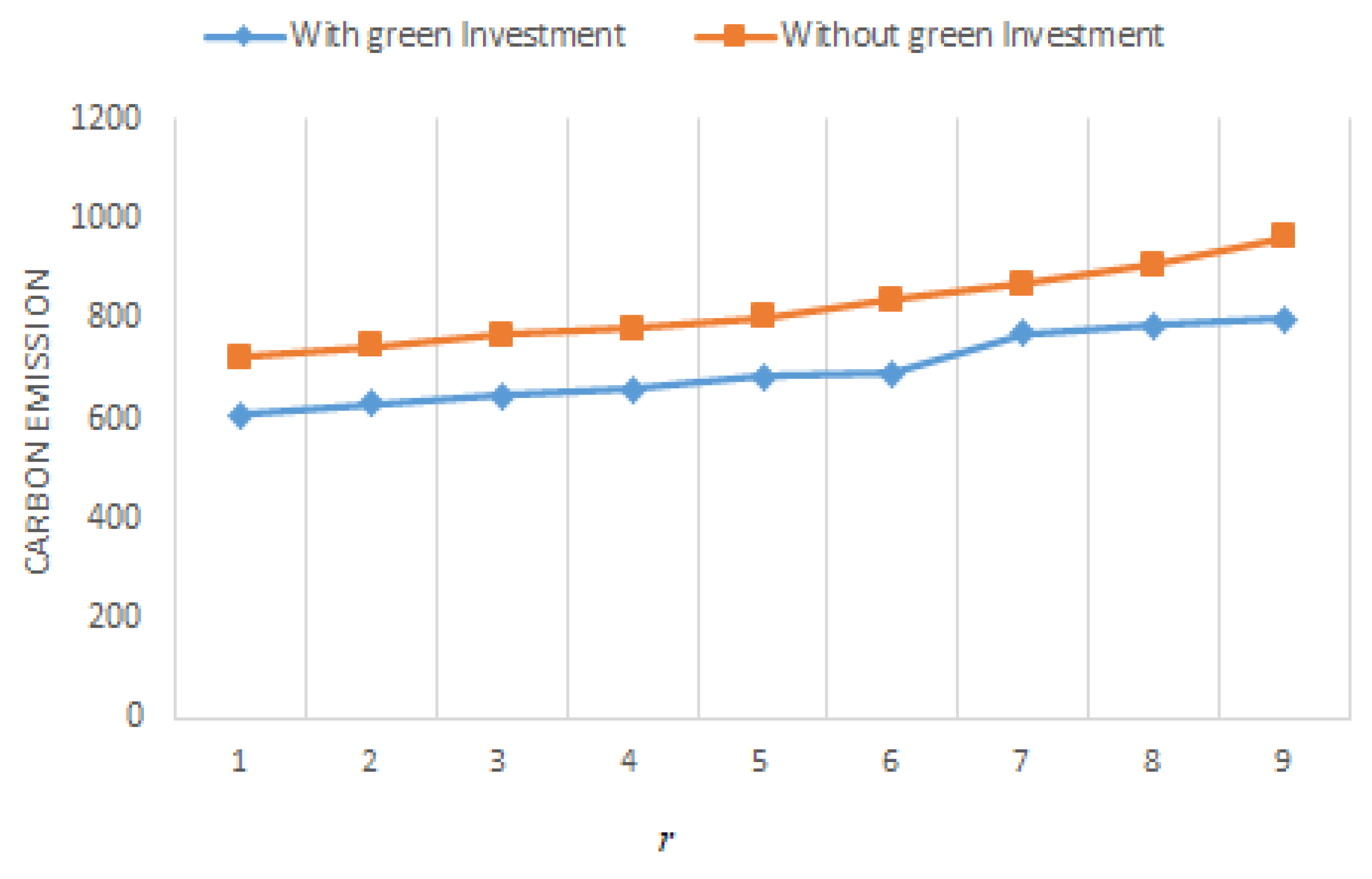
- According to Table 2, Table 3, Table 4 and Table 5 and Figure 13 and Figure 14, Al-Salamah’s [17] model performs similarly to ours, with the exception that the optimum lotsizes ( increase and backorders decrease more quickly. It should be noted that Al-Salamah’s [17] model disregards green investments as a means of reducing CO2 and setup costs. Moreover, if green technology is not employed to lower setup costs and CO2, costs and CO2 increase. A firm may save between 8.4% and 25.5% in costs when it invests in green technology to lower setup and CO2 emissions. Green technology therebydecreases the system’s overall cost of production and cuts CO2.
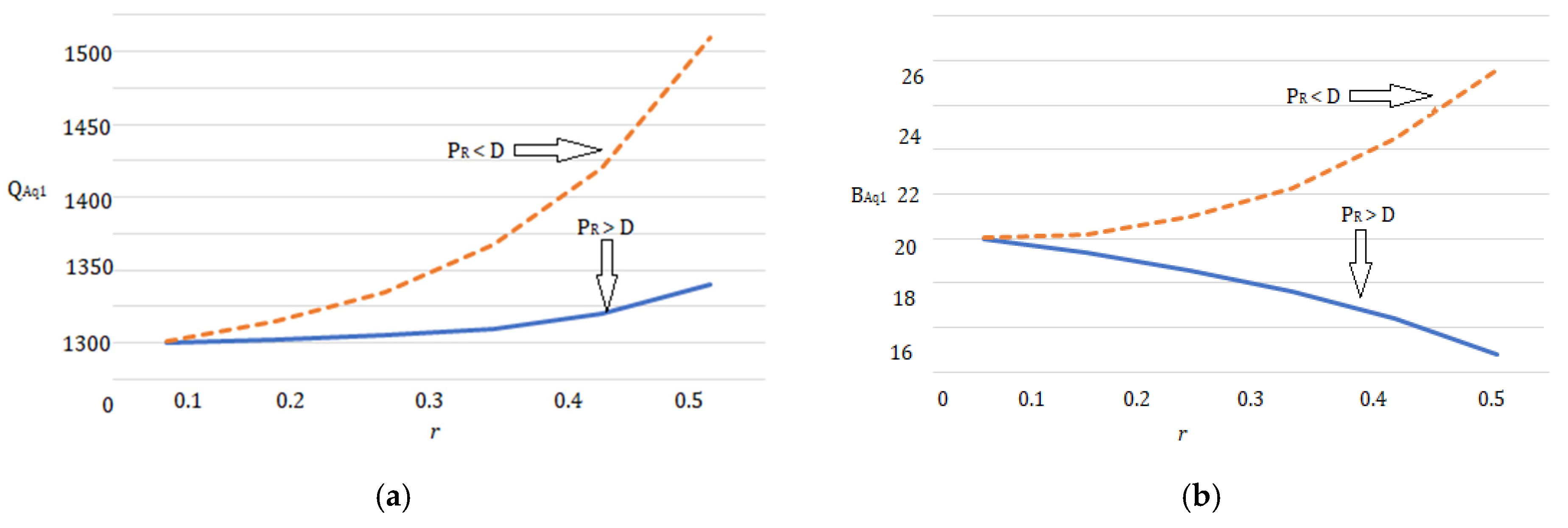
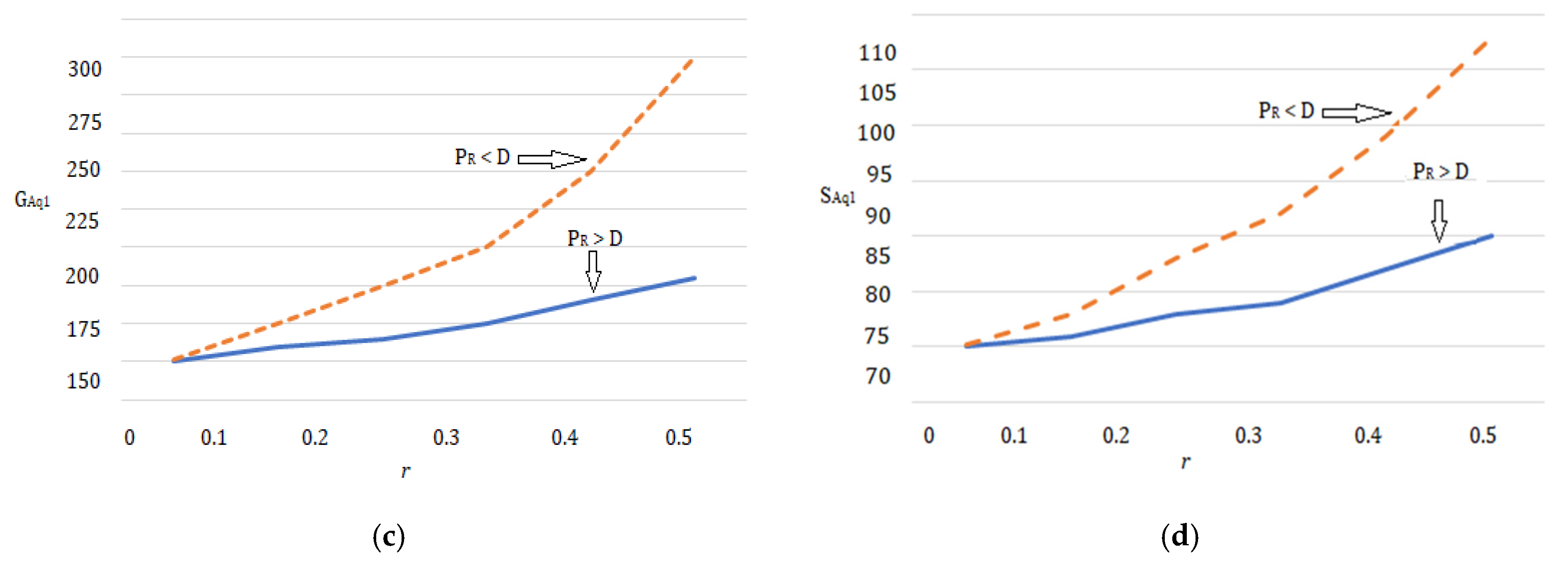
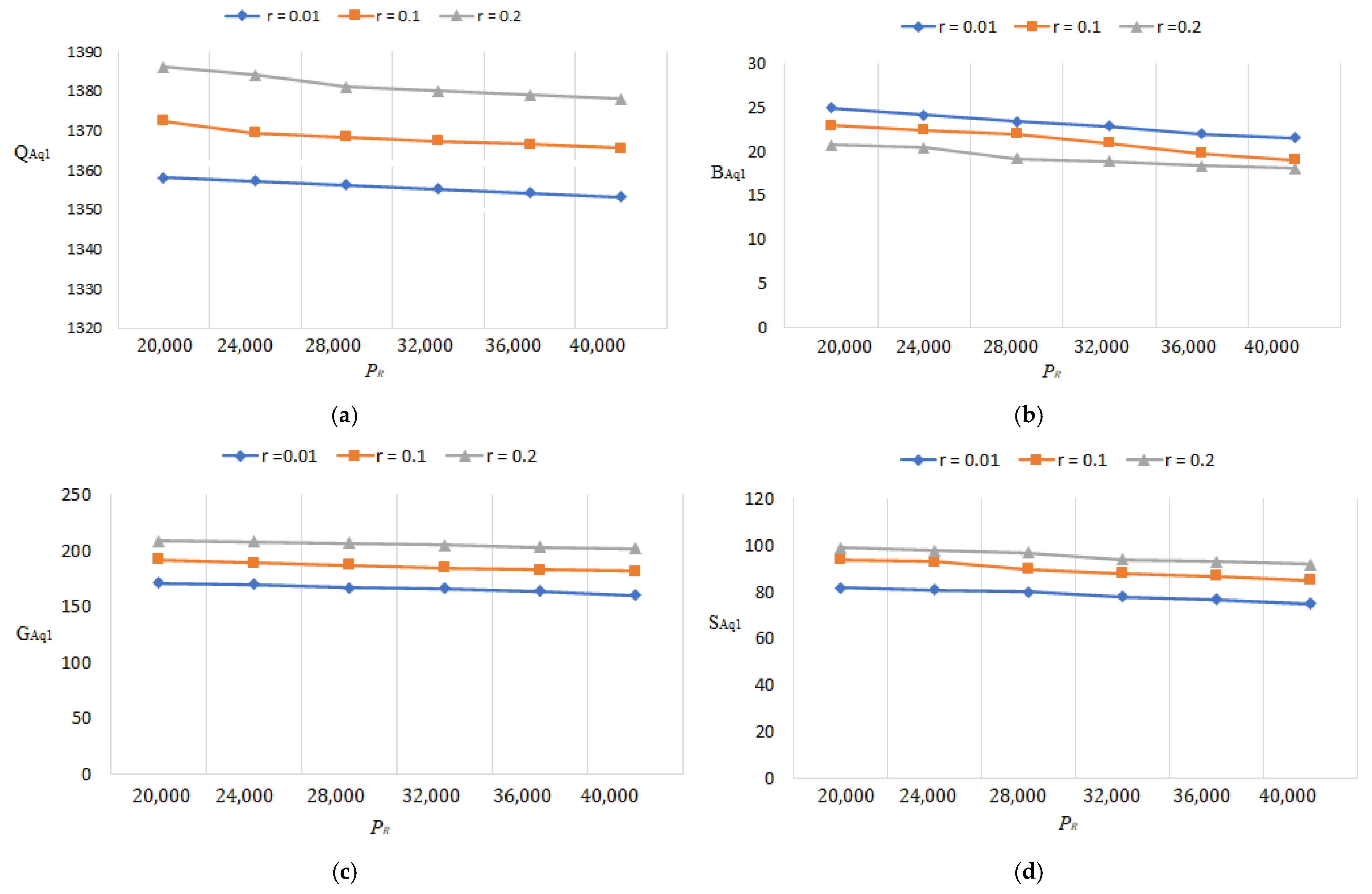
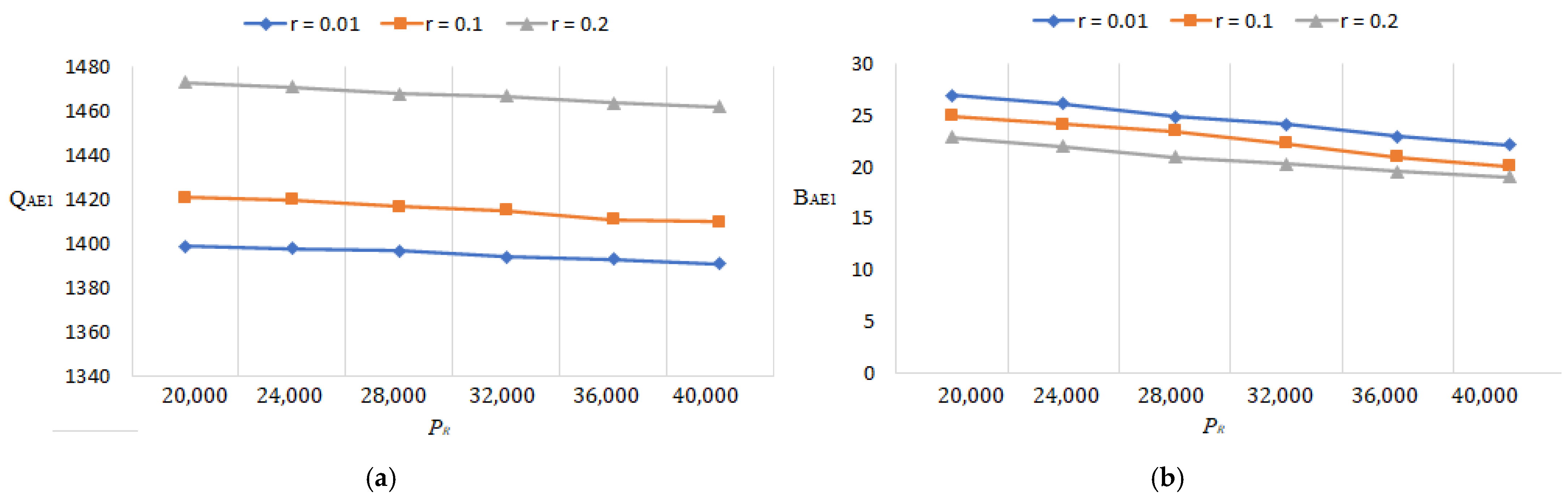
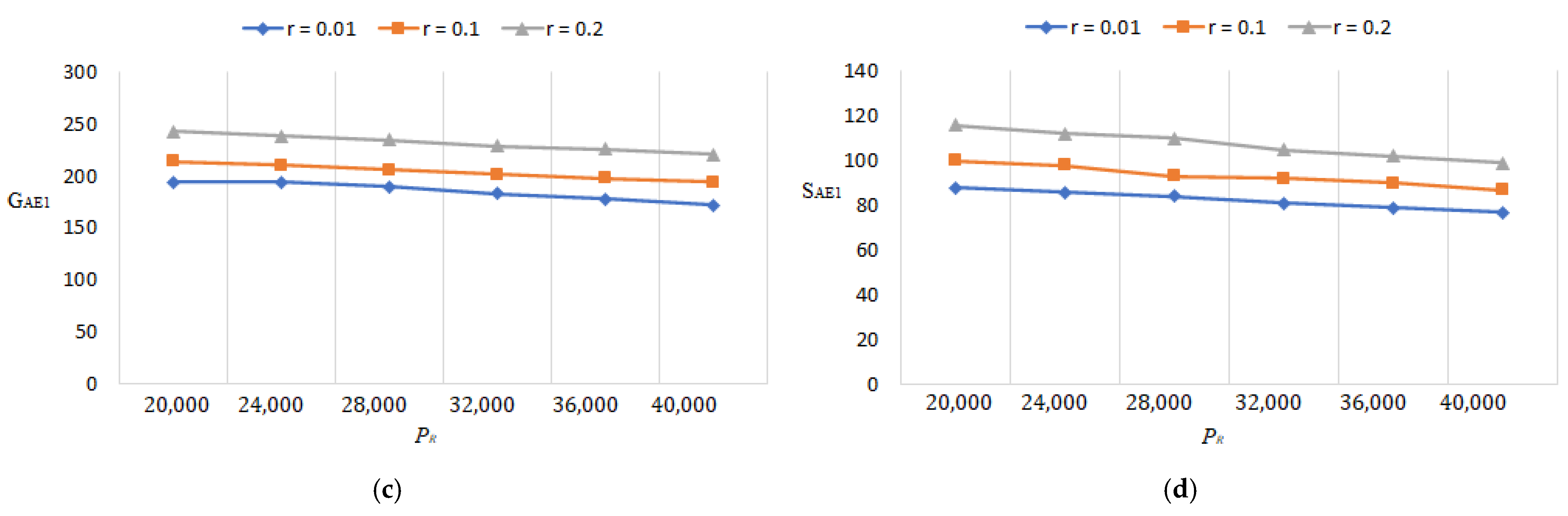
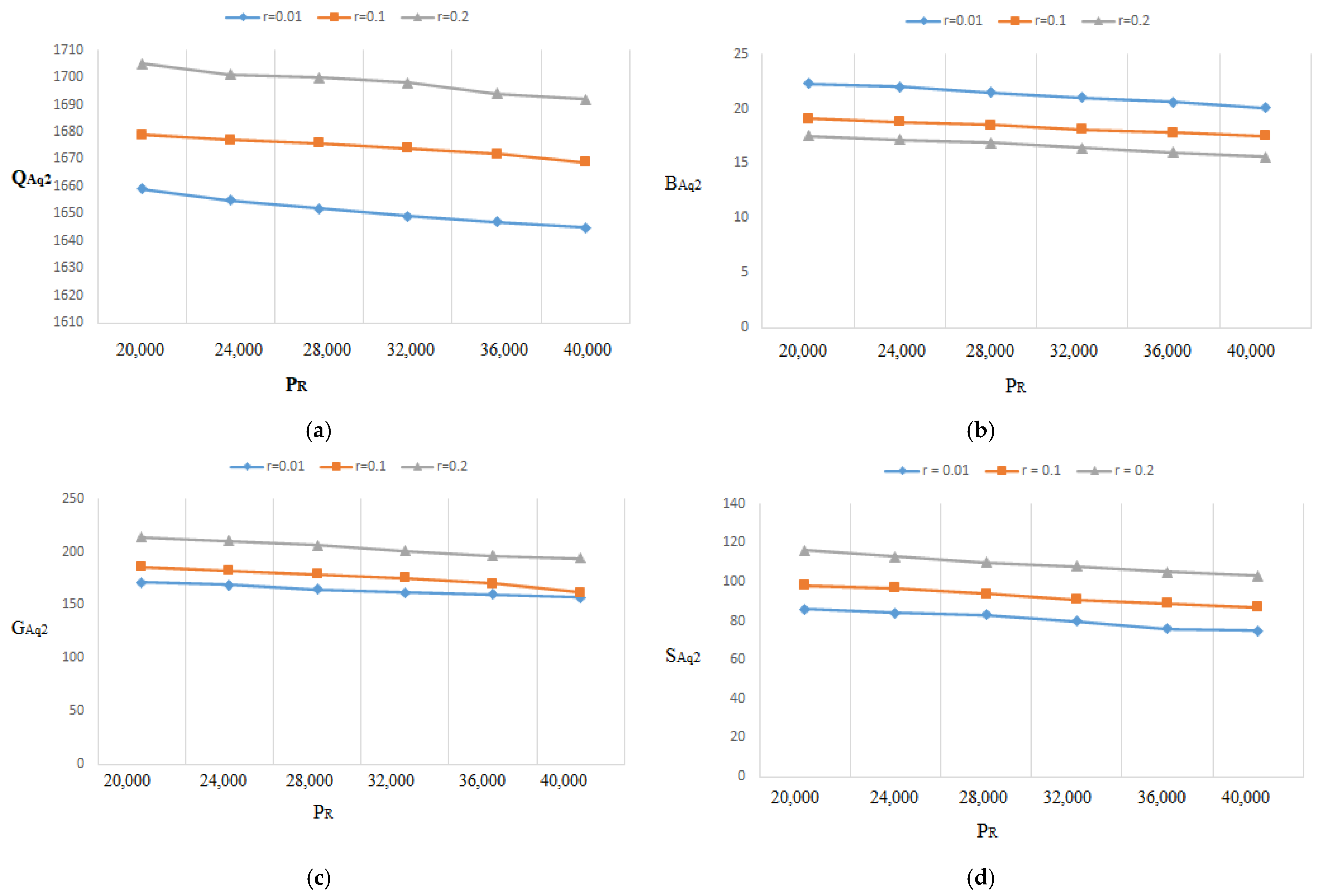
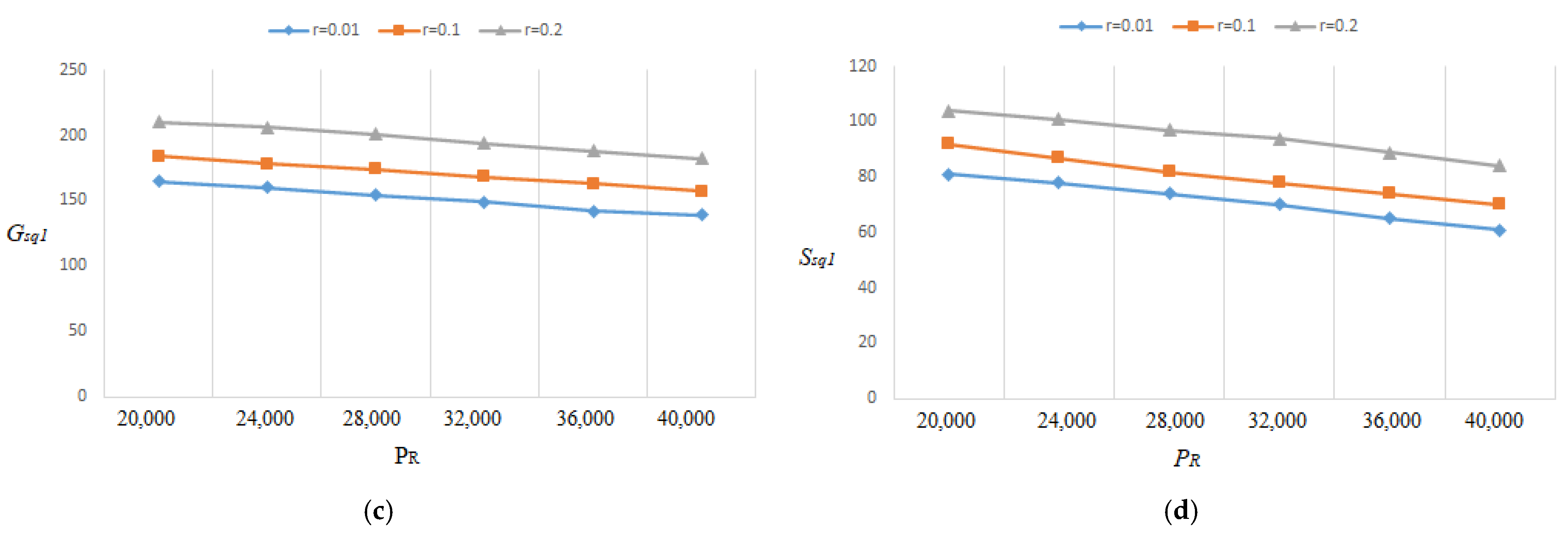
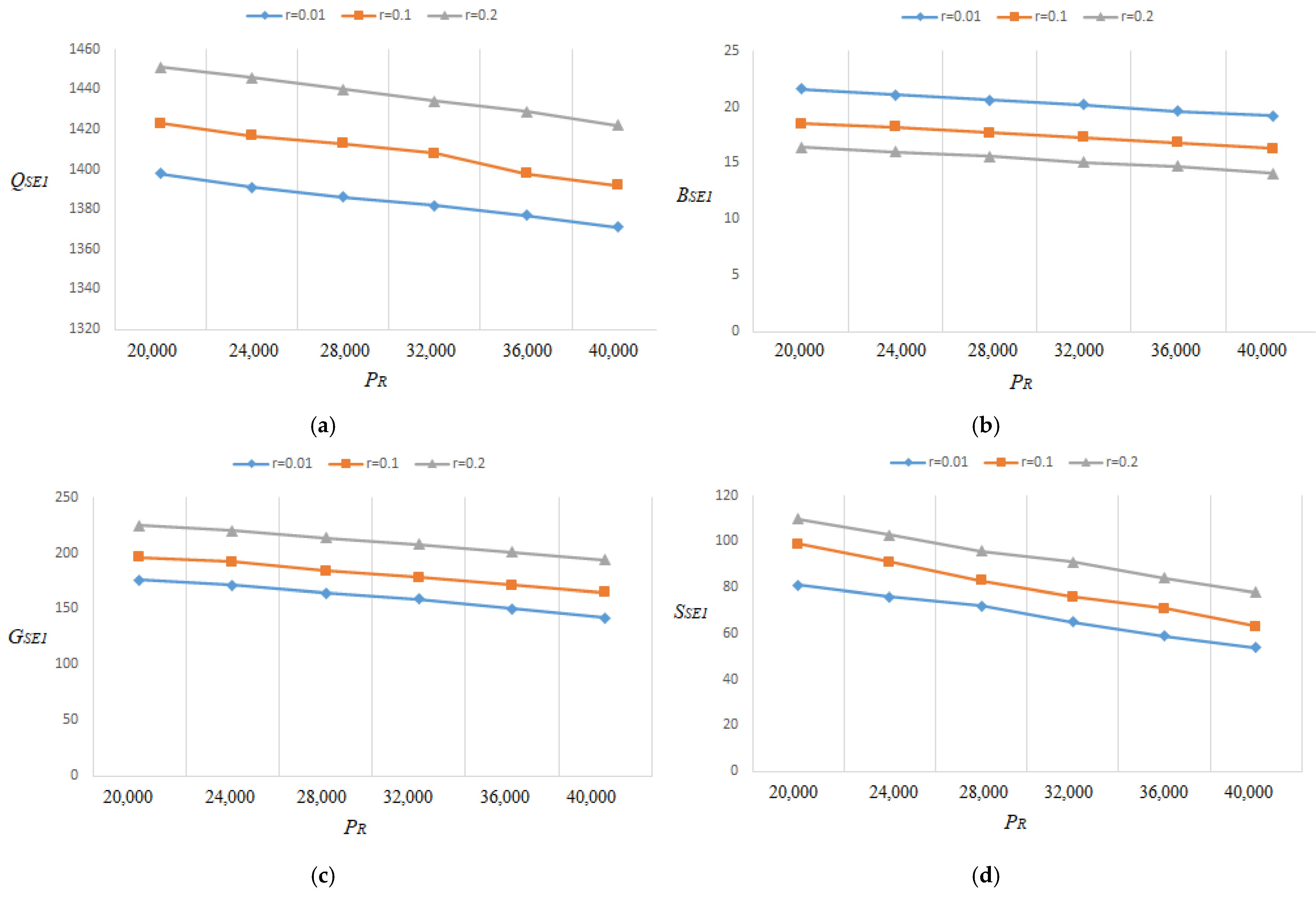
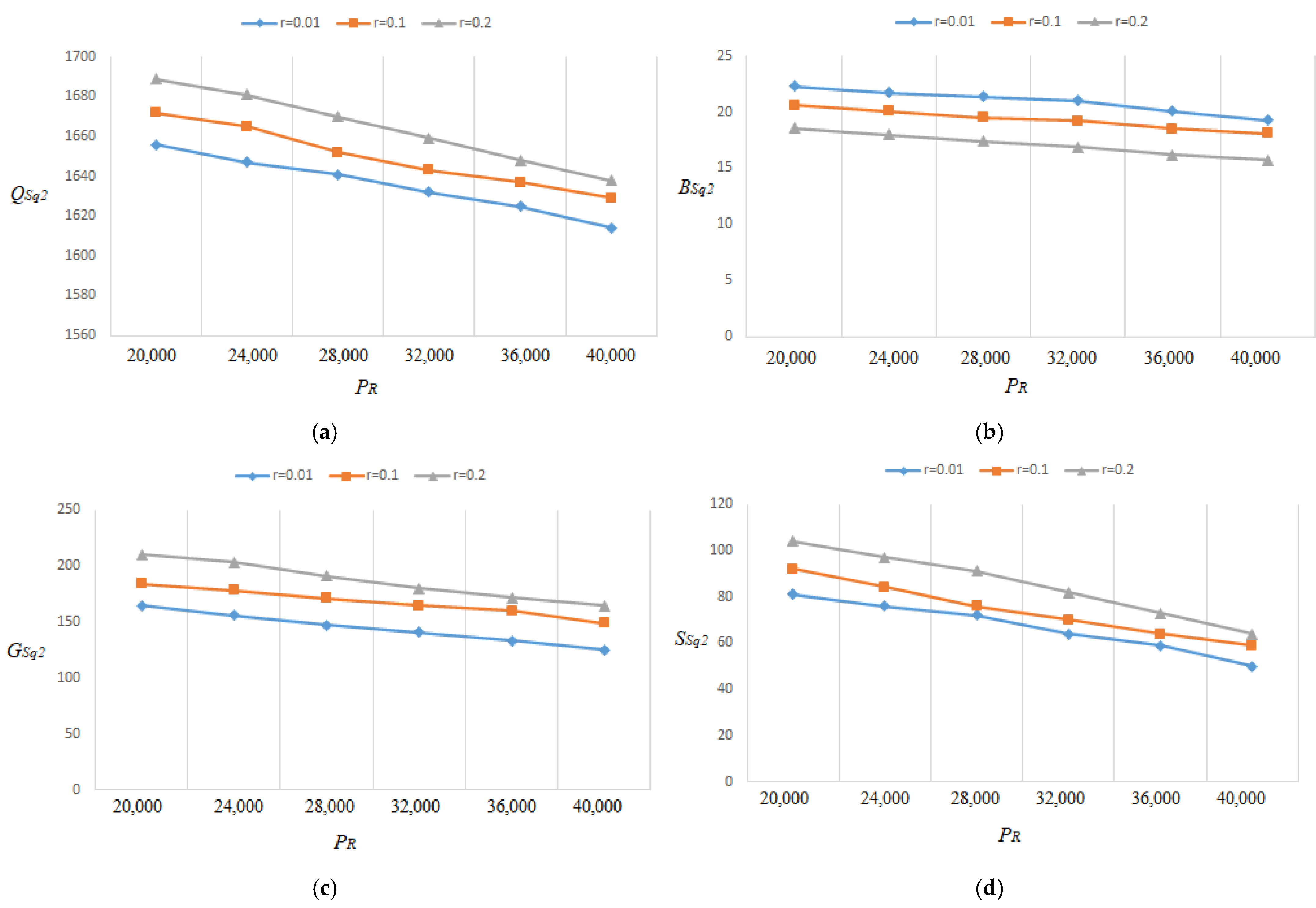
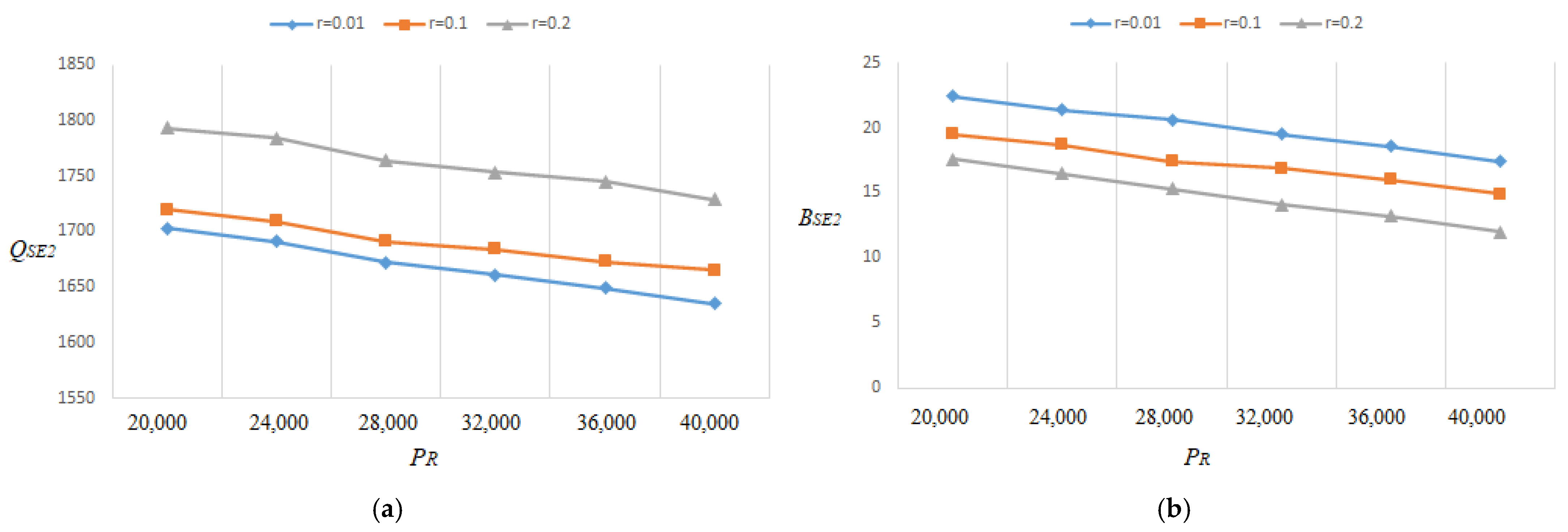
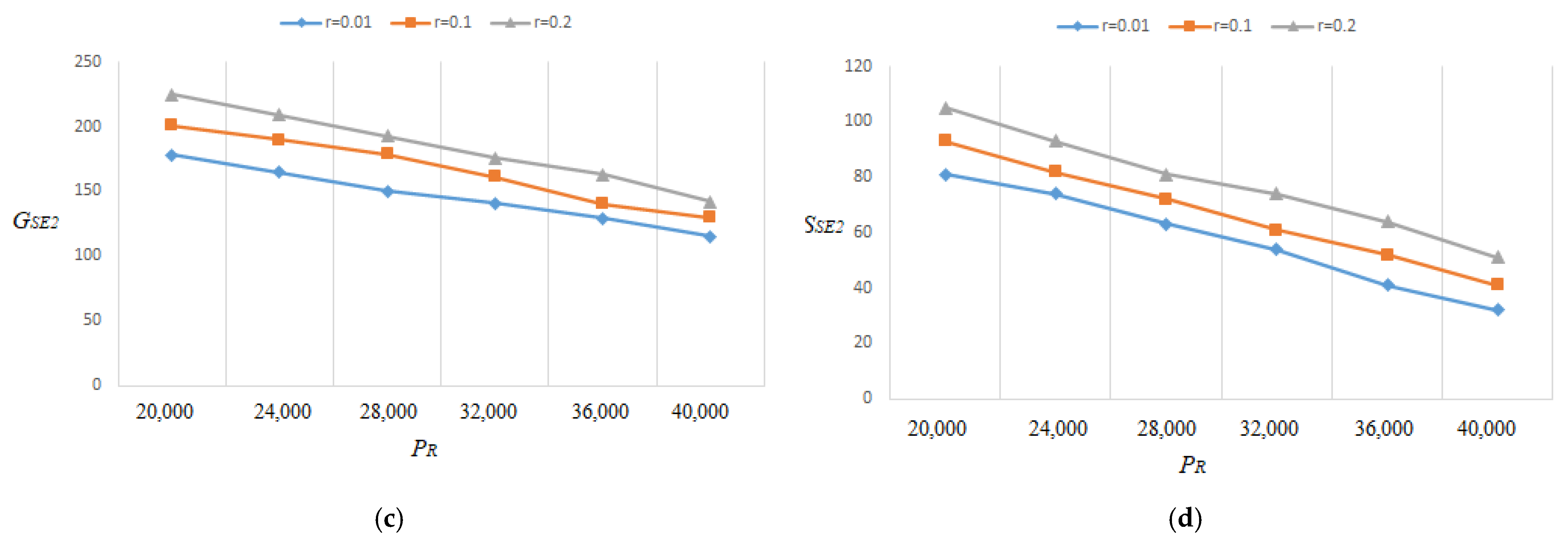
- Since the optimal lot size raises as the percentage of flawed rises, Figure 15a, Figure 16a, Figure 17a, Figure 18a, Figure 19a, Figure 20a, Figure 21a and Figure 22a explore the combined effects of both r and on lot-sizes (. For large values of r, the optimum lot sizes ( are more sensitive to changes in the for high values of r than for small values of , as seen in the picture. As a result, when r > 0.1, it is claimed that lot sizes ( decreases as increases. Green investments (, on the other hand, are less sensitive to changes in the for large values of r than when the percentage is small (), as shown in Figure 15c, Figure 16c, Figure 17c, Figure 18c, Figure 19c, Figure 20c, Figure 21c and Figure 22c. Backorder size behavior leads to a similar conclusion. Figure 15b, Figure 16b, Figure 17b, Figure 18b, Figure 19b, Figure 20b, Figure 21b, and Figure 22b indicate that a rise in induces a big fall in ( for values of .
- The lot-sizes () green investments () under the asynchronous rework model are slightly lower than the lot sizes () under the synchronous rework model for the range of r values indicated in Table 2, Table 3, Table 4 and Table 5. When the rework is asynchronous, the backorder is much higher than when it is synchronous for most values of r; though the differences between the backorders are minor, and certain backorders are almost equal for r = 0.4.
- Our research found that increasing lowers CO2 levels. The findings of Dwicahyani et al. [40] and Hasanov et al. [41], who found that tariffs had a beneficial effect on CO2 reduction, are consistent with this conclusion. The firm has new options for lowering CO2 produced by industrial operations with the use of green technology. The firm will gain from less CO2 even though green technology has higher direct costs. Studies, including Bai et al. [42] and others, have produced results that are similar.
- According to the findings (Table 2, Table 3, Table 4 and Table 5), the optimal , and grow continuously as r increases, whereas progressively decreases as the fraction of defectives rises. The model of Al-Salamah [17] shows a similar pattern, with the exception that the optimal lot size grows faster, and the backorder decreases more slowly than ours. It is worth noting that Al-Salamah’s [17] approach ignores green investment in terms of CO2 and setup costs. In addition, CO2 and total cost increase when green technology is not used for both CO2 and setup costs.
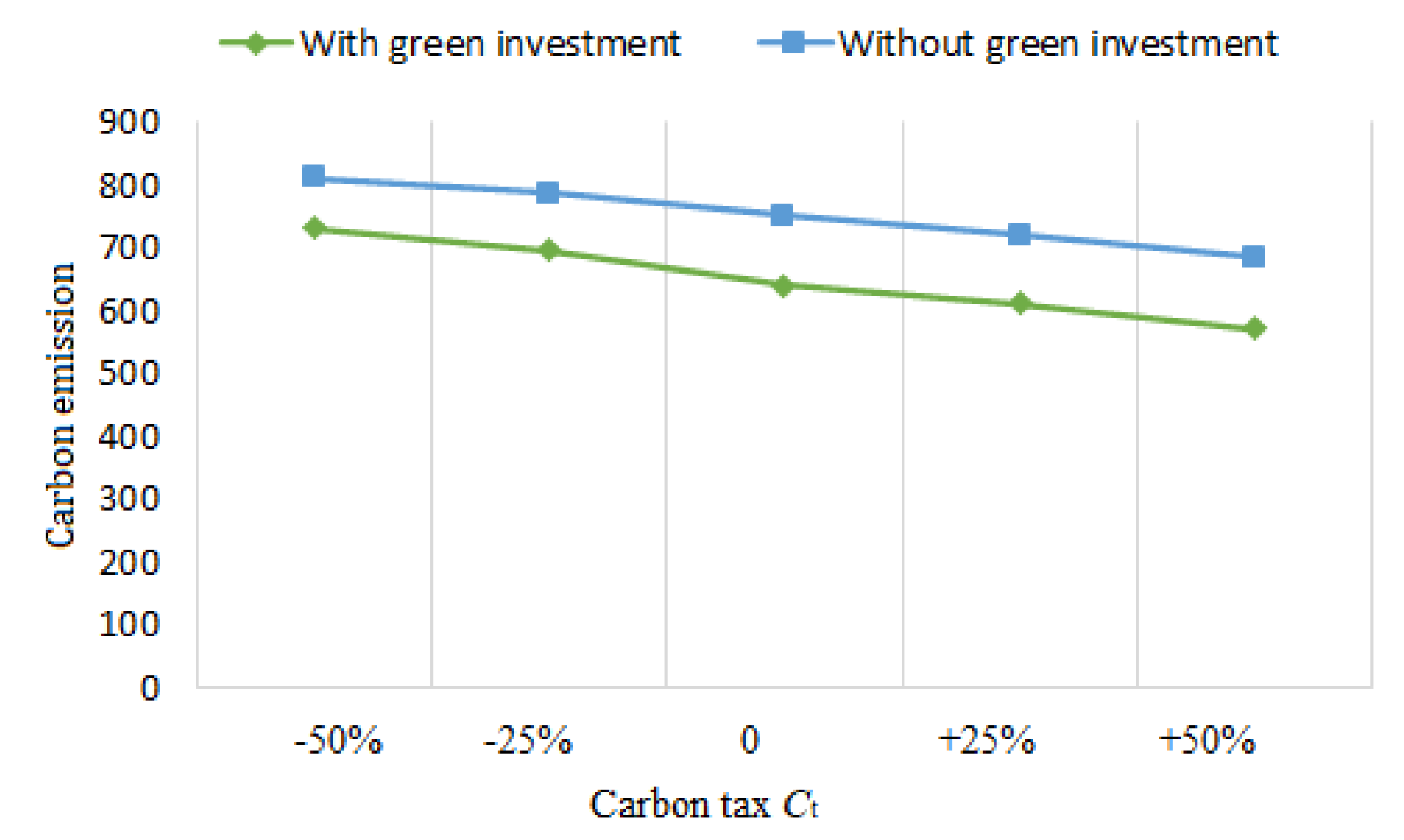
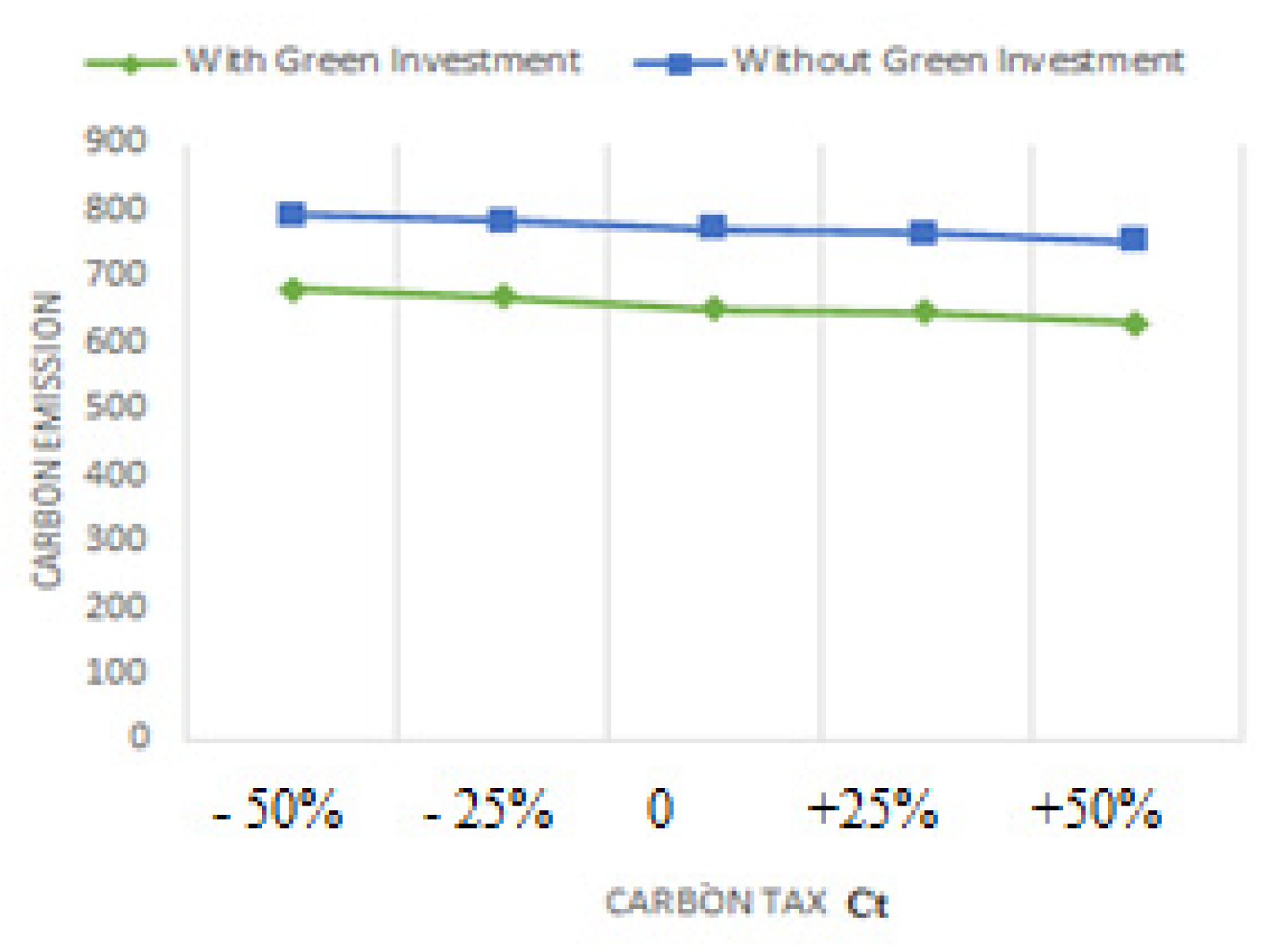
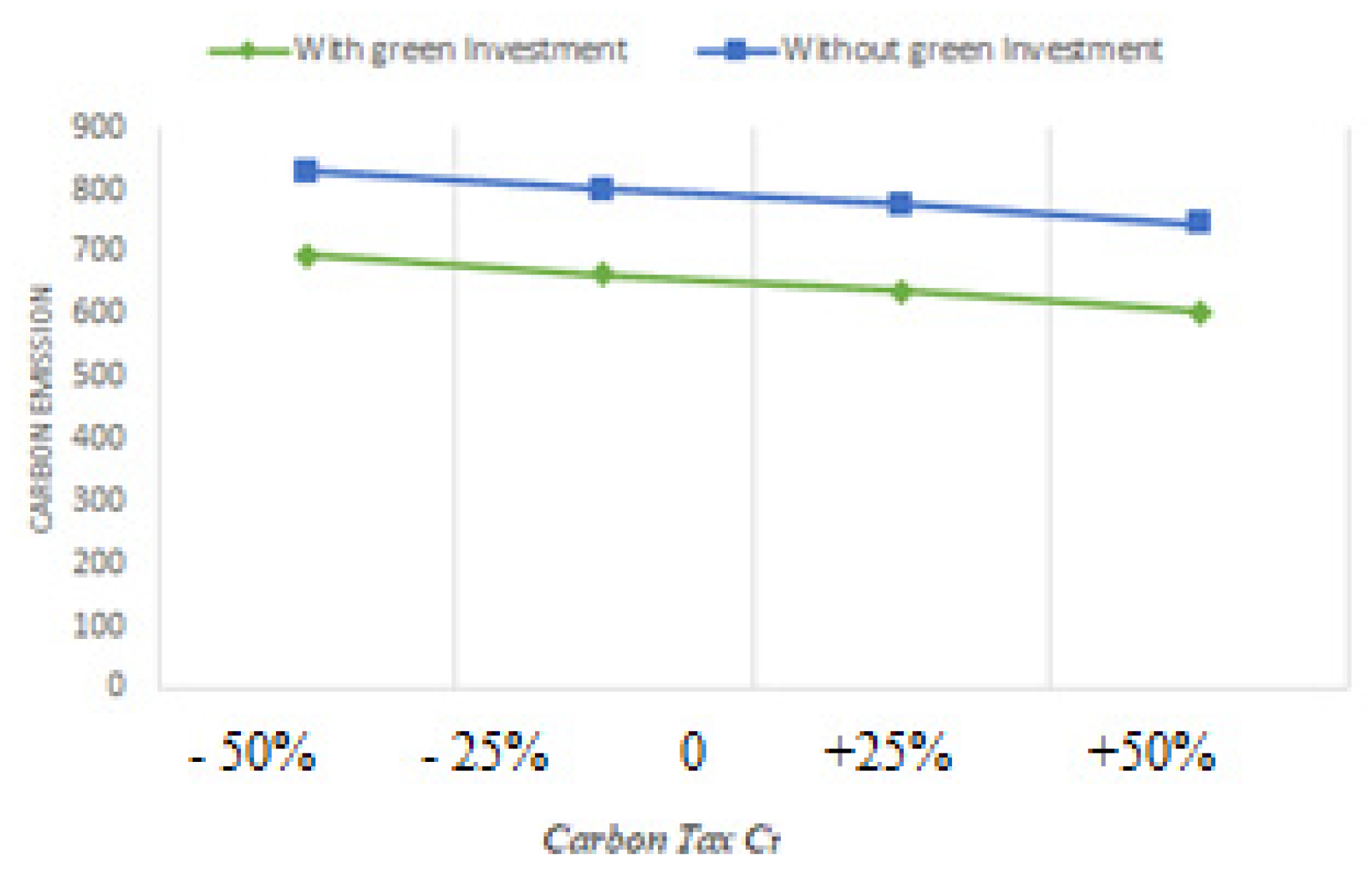
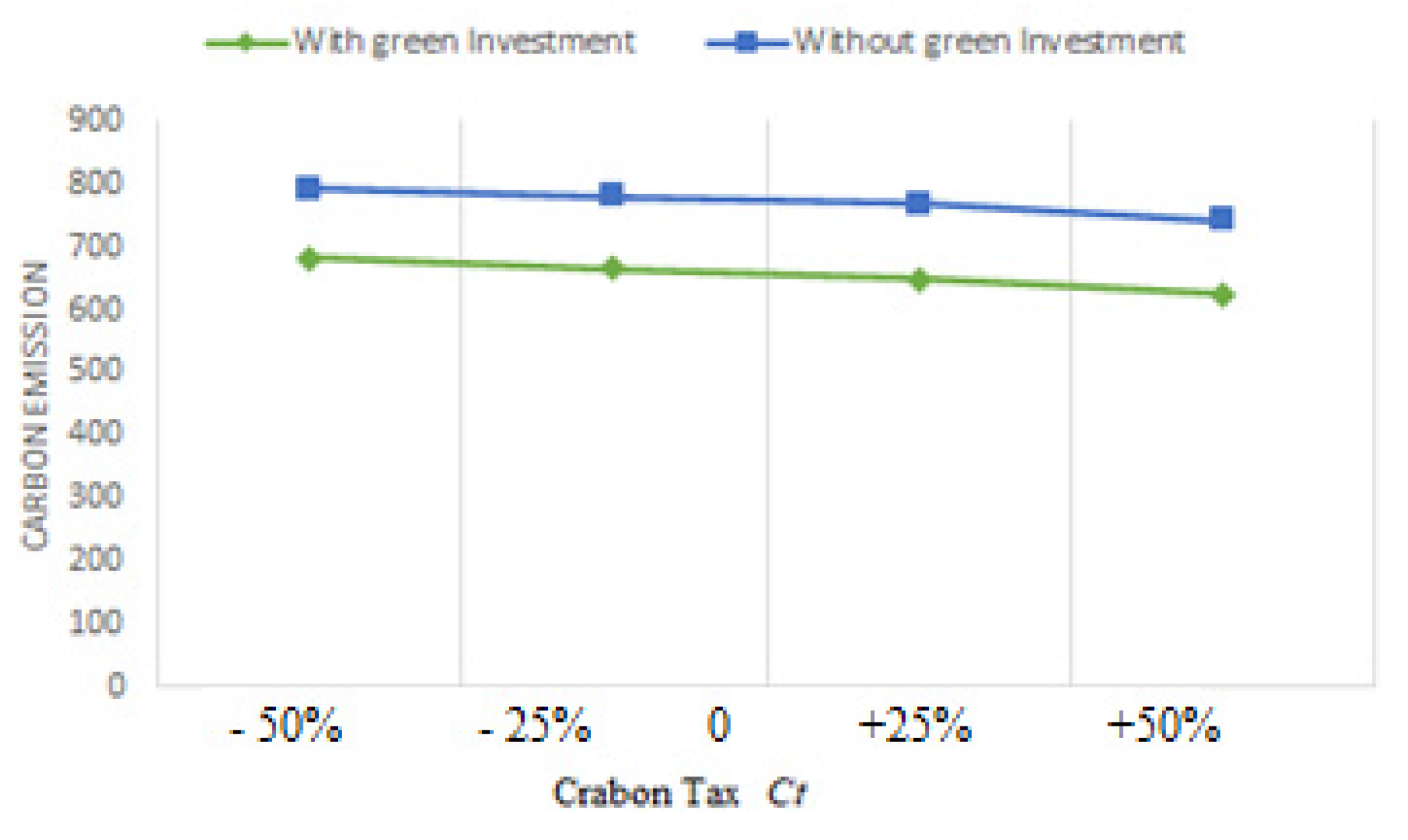
- We may look at Table 4 and Figure 18 and Figure 24 to see how the optimal solutions react when assumptions fluctuate. When r is increased, it is shown that for rises more quickly than for does if units/year. The optimal backorders respond in a number of ways when r’s value rises. declines when r rises, as was previously discovered. On the other hand, raising the value of r causes to rise. Additionally, Figure 12 and Figure 24 provide a visual comparison of tax and CO2 with and without green investment vs. r when .
- Table 5 and Figure 22 and Figure 26 show how the optimal solutions change when the assumption changes. When units/year, it is seen that, similar to the asynchronous situation when r is increased, for raises faster than for . The optimal backorders react in a number of ways as the value of r increases. As previously discovered, lessens as r rises. In contrast, increasing the value of r results in an increase in . Besides, Figure 12 and Figure 26 depict a visual contrast of CO2 and taxes with and without green investment vs. r when .
5.4. Insights and Implications for the Industry
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Notations
| Lot-size | |
| Green investment amount | |
| Backorder | |
| Set up cost | |
| S0 | The initial setup cost |
| Capital fractional opportunity cost | |
| Demand rate | |
| Rate of production | |
| Proportion of the flawed/or faulty products | |
| Rework rate | |
| Cycle Length | |
| Production time | |
| Rework period | |
| Production and inspection cost | |
| Rework cost of flawed products | |
| Backorder cost per unit of time | |
| Backorder cost per item | |
| Holding cost for perfect items | |
| Holding cost for defective products | |
| Transportation distance | |
| CO2 during production setup | |
| CO2 from production phase | |
| CO2 through transportation | |
| CO2 while having perfect items | |
| CO2 by keeping defective items | |
| Carbon tax per unit item | |
| Cap on CO2 |
Appendix A
Appendix B
Appendix C
Appendix D
Appendix E
Appendix F
Appendix G
Appendix H
References
- Rosenblatt, M.J.; Lee, H.L. Economic Production Cycles with Imperfect Production Processes. IIE Trans. 1986, 18, 48–55. [Google Scholar] [CrossRef]
- Khouja, M.; Abraham, M. An economic production lot size model with imperfect quality and variable production rate. J. Oper. Res. Soc. 1994, 45, 1405–1417. [Google Scholar] [CrossRef]
- Brojeswar, P.; Shib, S.S.; Kripasindhu, C. A mathematical model on EPQ for stochastic demand in an imperfect production system. J. Manuf. Syst. 2013, 32, 260–270. [Google Scholar]
- Hsu, J.-T.; Hsu, L.-F. Two EPQ models with imperfect production processes, inspection errors, planned backorders, and sales returns. Comput. Industr. Eng. 2013, 64, 389–402. [Google Scholar] [CrossRef]
- Taleizadeh, A.A.; Cárdenas-Barrón, L.E.; Mohammadi, B. A deterministic multi product single machine EPQ model with backordering, scraped products, rework and interruption in manufacturing process. Int. J. Prod. Econ. 2014, 150, 9–27. [Google Scholar] [CrossRef]
- Hsu, L.-F.; Hsu, J.-T. Economic production quantity (EPQ) models under an imperfect production process with shortages backordered. Int. J. Syst. Sci. 2014, 47, 852–867. [Google Scholar] [CrossRef]
- Ganesan, S.; Uthayakumar, R. EPQ models for an imperfect manufacturing system considering warm-up production run, shortages during hybrid maintenance period and partial backordering. Adv. Ind. Manuf. Eng. 2020, 1, 100005. [Google Scholar] [CrossRef]
- De Sujit, K.; Nayak, P.K.; Khan, A.; Bhattacharya, K.; Smarandache, F. Solution of an EPQ model for imperfect production process under game and neutrosophic fuzzy approach. Appl. Soft Comput. 2020, 93, 106397. [Google Scholar]
- Dipankar, B.; Apratim, G. Economic production lot sizing under imperfect quality, on-line inspection, and inspection errors: Full vs. sampling inspection. Comput. Industr. Eng. 2021, 160, 107565. [Google Scholar]
- Liu, J.J.; Yang, P. Optimal lot-sizing in an imperfect production system with homogeneous reworkable jobs. Eur. J. Oper. Res. 1996, 91, 517–527. [Google Scholar] [CrossRef]
- Hayek, P.A.; Salameh, M.K. Production lot sizing with the reworking of imperfect quality items produced. Prod. Plan. Control 2001, 12, 584–590. [Google Scholar] [CrossRef]
- Liao, G.-L.; Chen, Y.H.; Sheu, S.-H. Optimal economic production quantity policy for imperfect process with imperfect repair and maintenance. Eur. J. Oper. Res. 2009, 195, 348–357. [Google Scholar] [CrossRef]
- Liao, G.-L.; Sheu, S.-H. Economic production quantity model for randomly failing production process with minimal repair and imperfect maintenance. Int. J. Prod. Econ. 2011, 130, 118–124. [Google Scholar] [CrossRef]
- Krishnamoorthi, C.; Panayappan, S. An EPQ Model with Imperfect Production Systems with Rework of Regular Production and Sales Return. Am. J. Oper. Res. 2012, 2, 225–234. [Google Scholar] [CrossRef] [Green Version]
- Shah, N.H.; Patel, D.G.; Shah, D.B. EPQ model for returned/reworked inventories during imperfect production process under price-sensitive stock-dependent demand. Oper. Res. 2018, 18, 343–359. [Google Scholar] [CrossRef]
- Nihar, S.; Marianthi, I.; John, W. Synchronous and asynchronous decision-making strategies in supply chains. Comput. Chem. Eng. 2013, 71, 116–129. [Google Scholar]
- Al-Salamah, M. Economic production quantity in an imperfect manufacturing process with synchronous and asynchronous flexible rework rates. Oper. Res. Perspect. 2019, 6, 100103. [Google Scholar] [CrossRef]
- Coates, E.R.; Sarker, B.R.; Ray, T.G. Manufacturing setup cost reduction. Comput. Industr. Eng. 1996, 31, 111–114. [Google Scholar] [CrossRef]
- Sarkar, B.; Moon, I. Improved quality, setup cost reduction, and variable backorder costs in an imperfect production process. Int. J. Prod. Econ. 2014, 155, 204–213. [Google Scholar] [CrossRef]
- Porteus, E.L. Optimal Lot Sizing, Process Quality Improvement and Setup Cost Reduction. Oper. Res. 1986, 34, 137–144. [Google Scholar] [CrossRef]
- Hou, K.-L. An EPQ model with setup cost and process quality as functions of capital expenditure. Appl. Math. Model. 2007, 31, 10–17. [Google Scholar] [CrossRef]
- Freimer, M.; Thomas, D.; Tyworth, J. The value of setup cost reduction and process improvement for the economic production quantity model with defects. Eur. J. Oper. Res. 2006, 173, 241–251. [Google Scholar] [CrossRef]
- Nye, T.J.; Jewkes, E.M.; Dilts, D.M. Optimal investment in setup reduction in manufacturing systems with WIP inventories. Eur. J. Oper. Res. 2002, 135, 128–141. [Google Scholar] [CrossRef]
- Sarkar, B.; Chaudhuri, K.; Moon, I. Manufacturing setup cost reduction and quality improvement for the distribution free continuous-review inventory model with a service level constraint. J. Manuf. Syst. 2015, 34, 74–82. [Google Scholar] [CrossRef]
- Tiwari, S.; Kazemi, N.; Modak, N.M.; Cárdenas-Barrón, L.E.; Sarkar, S. The effect of human errors on an integrated stochastic supply chain model with setup cost reduction and backorder price discount. Int. J. Prod. Econ. 2020, 226, 107643. [Google Scholar] [CrossRef]
- Bouchery, Y.; Ghaffari, A.; Jemai, Z.; Dallery, Y. Including sustainability criteria into inventory models. Eur. J. Oper. Res. 2012, 222, 229–240. [Google Scholar] [CrossRef] [Green Version]
- Benjaafar, S.; Li, Y.; Daskin, M. Carbon Footprint and the Management of Supply Chains: Insights From Simple Models. IEEE Trans. Autom. Sci. Eng. 2013, 10, 99–116. [Google Scholar] [CrossRef]
- Toptal, A.; Özlü, H.; Konur, D. Joint decisions on inventory replenishment and emission reduction investment under different emission regulations. Int. J. Prod. Res. 2014, 52, 243–269. [Google Scholar] [CrossRef] [Green Version]
- Dye, C.-Y.; Yang, C.-T. Sustainable trade credit and replenishment decisions with credit-linked demand under carbon emission constraints. Eur. J. Oper. Res. 2015, 244, 187–200. [Google Scholar] [CrossRef]
- Qin, J.; Bai, X.; Xia, L. Sustainable Trade Credit and Replenishment Policies under the Cap-And-Trade and Carbon Tax Regulations. Sustainability 2015, 7, 16340–16361. [Google Scholar] [CrossRef] [Green Version]
- Datta, T.K. Effect of Green Technology Investment on a Production-Inventory System with Carbon Tax. Adv. Oper. Res. 2017, 2017, 4834839. [Google Scholar] [CrossRef] [Green Version]
- Huang, Y.-S.; Fang, C.-C.; Lin, Y.-A. Inventory management in supply chains with consideration of Logistics, green investment and different carbon emissions policies. Comput. Ind. Eng. 2019, 139, 106207. [Google Scholar] [CrossRef]
- Mishra, U.; Wu, J.-Z.; Sarkar, B. A sustainable production-inventory model for a controllable carbon emissions rate under shortages. J. Clean. Prod. 2020, 256, 120268. [Google Scholar] [CrossRef]
- Hasan, R.; Roy, T.C.; Daryanto, Y.; Wee, H.-M. Optimizing inventory level and technology investment under a carbon tax, cap-and-trade and strict carbon limit regulations. Sustain. Prod. Consum. 2020, 25, 604–621. [Google Scholar] [CrossRef]
- Kaswan, M.S.; Rathi, R.; Reyes, J.A.G.; Antony, J. Exploration and Investigation of Green Lean Six Sigma Adoption Barriers for Manufacturing Sustainability. IEEE Trans. Eng. Manag. 2021, 1–15. [Google Scholar] [CrossRef]
- Kaswan, M.S.; Rathi, R.; Garza-Reyes, J.A.; Antony, J. Green lean six sigma sustainability–oriented project selection and implementation framework for manufacturing industry. Int. J. Lean Six Sigma 2022. [Google Scholar] [CrossRef]
- Rathi, R.; Kaswan, M.S.; Garza-Reyes, J.A.; Antony, J.; Cross, J. Green Lean Six Sigma for improving manufacturing sustainability: Framework development and validation. J. Clean. Prod. 2022, 345, 131130. [Google Scholar] [CrossRef]
- Mohan, J.; Rathi, R.; Kaswan, M.S.; Nain, S.S. Green lean six sigma journey: Conceptualization and realization. Mater. Today Proc. 2021, 50, 1991–1998. [Google Scholar] [CrossRef]
- Ouyang, L.-Y.; Chen, C.-K.; Chang, H.-C. Quality improvement, setup cost and lead-time reductions in lot size reorder point models with an imperfect production process. Comput. Oper. Res. 2002, 29, 1701–1717. [Google Scholar] [CrossRef]
- Dwicahyani, A.R.; Jauhari, W.A.; Rosyidi, C.N.; Laksono, P.W. Inventory decisions in a two-echelon system with remanufacturing, carbon emission and energy effects. Cogent Eng. 2017, 4, 1–17. [Google Scholar] [CrossRef]
- Hasanov, P.; Jaber, M.; Tahirov, N. Four-level closed loop supply chain with remanufacturing. Appl. Math. Model. 2019, 66, 141–155. [Google Scholar] [CrossRef]
- Bai, Q.; Xua, J.; Chauhan, S.C. Effects of sustainability investment and risk aversion on a two-stage supply chain coordination under a carbon tax policy. Comp. Industr. Eng. 2020, 142, 106324. [Google Scholar] [CrossRef]




| Author(s) | Rework | Synchronous and Asynchronous | Setup Cost Reduction | Backorders | CO2 | Green Investment |
|---|---|---|---|---|---|---|
| Hsu et al. [4] | ✓ | |||||
| Taleizadeh et al. [5] | ✓ | ✓ | ||||
| Hsu et al. [6] | ✓ | |||||
| Ganesan et al. [7] | ||||||
| Sujit et al. [8] | ✓ | ✓ | ||||
| Liu et al. [10] | ✓ | ✓ | ||||
| Hayek et al. [11] | ✓ | |||||
| Liao et al. [12] | ✓ | |||||
| Liao et al. [13] | ✓ | |||||
| Krishnamurthy et al. [14] | ✓ | ✓ | ||||
| Shah et al. [15] | ✓ | |||||
| Nihar et al. [16] | ✓ | ✓ | ||||
| Al-Salamah [17] | ✓ | ✓ | ✓ | |||
| Sarkar et al. [19] | ✓ | |||||
| Ouyang et al. [39] | ✓ | |||||
| Hou et al. [21] | ✓ | ✓ | ||||
| Freimer et al. [22] | ✓ | |||||
| Nye et al. [23] | ✓ | |||||
| Tiwari et al. [25] | ✓ | |||||
| Bouchery et al. [26] | ✓ | |||||
| Benjaafar et al. [27] | ✓ | |||||
| Toptal et al. [28] | ✓ | ✓ | ||||
| Dye et al. [29] | ✓ | |||||
| Qin et al. [30] | ✓ | |||||
| Datta [31] | ✓ | |||||
| Huang et al. [32] | ✓ | ✓ | ||||
| Mishra et al. [33] | ✓ | ✓ | ||||
| Kaswan et al. [36] | ✓ | ✓ | ||||
| This paper | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ |
| Asynchronous Rework | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Quadratic Green Investment Function | |||||||||||||
| With Green Investment | Without Green Investment | ||||||||||||
| r | Savings (%) | ||||||||||||
| 0.01 | 1343 | 21.6 | 160 | 75 | 602 | 309,276 | 1398 | 23.8 | - | - | 711 | 335,231 | 8.4 |
| 0.05 | 1352 | 20.4 | 171 | 81 | 625 | 317,634 | 1426 | 22.4 | - | - | 735 | 354,374 | 11.6 |
| 0.10 | 1361 | 19.1 | 182 | 85 | 641 | 324,569 | 1456 | 21.6 | - | - | 751 | 372,371 | 14.7 |
| 0.15 | 1369 | 18.9 | 196 | 87 | 650 | 331,548 | 1471 | 20.8 | - | - | 761 | 385,365 | 16.2 |
| 0.20 | 1378 | 18.1 | 202 | 92 | 676 | 339,876 | 1498 | 20.1 | - | - | 790 | 400,273 | 17.7 |
| 0.25 | 1386 | 17.6 | 216 | 94 | 693 | 347,984 | 1516 | 19.5 | - | - | 813 | 415,076 | 19.3 |
| 0.30 | 1392 | 16.7 | 231 | 100 | 721 | 356,654 | 1535 | 18.7 | - | - | 861 | 434,067 | 21.7 |
| 0.35 | 1410 | 15.1 | 253 | 102 | 748 | 362,098 | 1550 | 17.7 | - | - | 899 | 448,071 | 23.7 |
| 0.40 | 1423 | 14.7 | 271 | 104 | 774 | 384,876 | 1574 | 16.6 | - | - | 957 | 481,379 | 25.1 |
| Exponential Green Investment Function | |||||||||||||
| With Green Investment | Without Green Investment | ||||||||||||
| r | Savings (%) | ||||||||||||
| 0.01 | 1391 | 22.2 | 172 | 77 | 602 | 309,316 | 1391 | 22.4 | - | - | 711 | 336,132 | 8.6 |
| 0.05 | 1402 | 20.9 | 183 | 85 | 625 | 317,743 | 1402 | 21.3 | - | - | 735 | 354,794 | 11.7 |
| 0.10 | 1410 | 20.1 | 194 | 87 | 641 | 324,641 | 1410 | 20.8 | - | - | 751 | 372,729 | 14.8 |
| 0.15 | 1448 | 19.8 | 208 | 89 | 650 | 331,678 | 1448 | 20.5 | - | - | 761 | 386,481 | 16.5 |
| 0.20 | 1462 | 19.1 | 221 | 99 | 676 | 339,991 | 1462 | 20.1 | - | - | 790 | 401,104 | 17.9 |
| 0.25 | 1516 | 18.2 | 231 | 102 | 693 | 348,220 | 1516 | 19.5 | - | - | 813 | 417,026 | 19.7 |
| 0.30 | 1542 | 17.4 | 243 | 104 | 721 | 356,743 | 1542 | 18.1 | - | - | 861 | 436,071 | 22.2 |
| 0.35 | 1571 | 16.1 | 269 | 106 | 748 | 362,142 | 1571 | 17.6 | - | - | 899 | 448,631 | 23.8 |
| 0.40 | 1598 | 15.3 | 281 | 109 | 774 | 384,966 | 1598 | 17.1 | - | - | 957 | 483,003 | 25.5 |
| Synchronous Rework | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Quadratic Green Investment Function | |||||||||||||
| With Green Investment | Without Green Investment | ||||||||||||
| r | Savings (%) | ||||||||||||
| 0.01 | 1364 | 22.3 | 165 | 81 | 612 | 317,964 | 1432 | 24.6 | - | - | 732 | 349,941 | 10.1 |
| 0.05 | 1371 | 21.4 | 176 | 86 | 627 | 324,587 | 1464 | 23.5 | - | - | 753 | 365,248 | 12.5 |
| 0.10 | 1379 | 20.6 | 184 | 92 | 638 | 339,641 | 1494 | 22.7 | - | - | 778 | 385,742 | 13.6 |
| 0.15 | 1385 | 19.5 | 193 | 98 | 652 | 348,423 | 1531 | 21.2 | - | - | 791 | 401,345 | 15.2 |
| 0.20 | 1394 | 18.6 | 210 | 104 | 671 | 356,214 | 1549 | 20.1 | - | - | 820 | 418,476 | 17.5 |
| 0.25 | 1399 | 17.2 | 219 | 109 | 690 | 367,198 | 1563 | 19.5 | - | - | 847 | 436,546 | 18.9 |
| 0.30 | 1411 | 16.7 | 236 | 114 | 712 | 376,347 | 1585 | 18.3 | - | - | 876 | 451,253 | 19.9 |
| 0.35 | 1420 | 15.4 | 254 | 117 | 735 | 383,695 | 1598 | 17.6 | - | - | 910 | 470,197 | 22.6 |
| 0.40 | 1432 | 14.7 | 278 | 121 | 760 | 394,322 | 1627 | 16.4 | - | - | 968 | 488,752 | 24.0 |
| Exponential green investment function | |||||||||||||
| With green investment | Without green investment | ||||||||||||
| r | Savings (%) | ||||||||||||
| 0.01 | 1398 | 21.6 | 176 | 81 | 612 | 309,867 | 1442 | 24.9 | - | - | 732 | 342,954 | 10.7 |
| 0.05 | 1416 | 20.3 | 187 | 92 | 627 | 319,675 | 1456 | 22.8 | - | - | 753 | 361,056 | 13.0 |
| 0.10 | 1423 | 18.5 | 196 | 99 | 638 | 328,542 | 1479 | 20.5 | - | - | 778 | 380,864 | 15.9 |
| 0.15 | 1439 | 17.1 | 201 | 105 | 652 | 339,671 | 1493 | 19.3 | - | - | 791 | 402,217 | 18.4 |
| 0.20 | 1451 | 16.4 | 225 | 110 | 671 | 344,755 | 1513 | 18.2 | - | - | 820 | 411,245 | 19.3 |
| 0.25 | 1476 | 15.7 | 251 | 114 | 690 | 359,876 | 1532 | 17.8 | - | - | 847 | 430,976 | 19.8 |
| 0.30 | 1586 | 14.9 | 269 | 118 | 712 | 367,423 | 1580 | 16.9 | - | - | 876 | 443,547 | 20.7 |
| 0.35 | 1594 | 14.1 | 282 | 121 | 735 | 372,547 | 1612 | 16.4 | - | - | 910 | 454,245 | 21.9 |
| 0.40 | 1607 | 13.5 | 290 | 125 | 760 | 389,451 | 1635 | 16.1 | - | - | 968 | 486,547 | 24.9 |
| Quadratic Green Investment Function | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| With Green Investment | Without Green Investment | ||||||||||||
| r | Savings (%) | ||||||||||||
| 0.01 | 1659 | 22.3 | 171 | 82 | 611 | 311,564 | 1721 | 24.5 | - | - | 731 | 341,165 | 9.5 |
| 0.05 | 1668 | 21.5 | 179 | 89 | 637 | 319,785 | 1739 | 23.6 | - | - | 755 | 357,874 | 11.9 |
| 0.10 | 1679 | 19.1 | 186 | 95 | 651 | 330,219 | 1770 | 22.4 | - | - | 771 | 376,247 | 13.9 |
| 0.15 | 1691 | 18.4 | 195 | 102 | 672 | 338,425 | 1782 | 21.7 | - | - | 786 | 390,014 | 15.2 |
| 0.20 | 1705 | 17.5 | 214 | 109 | 689 | 342,100 | 1798 | 19.7 | - | - | 811 | 406,570 | 18.8 |
| 0.25 | 1716 | 16.2 | 231 | 115 | 706 | 348,589 | 1817 | 18.5 | - | - | 829 | 418,214 | 20.0 |
| 0.30 | 1723 | 15.1 | 245 | 119 | 750 | 360,210 | 1836 | 18.0 | - | - | 864 | 441,429 | 22.6 |
| 0.35 | 1728 | 14.3 | 271 | 124 | 789 | 375,674 | 1860 | 17.4 | - | - | 932 | 465,478 | 23.9 |
| 0.40 | 1739 | 13.8 | 292 | 134 | 814 | 396,574 | 1895 | 17.3 | - | - | 976 | 495,425 | 24.9 |
| Exponential green investment function | |||||||||||||
| With green investment | Without green investment | ||||||||||||
| r | Savings (%) | ||||||||||||
| 0.01 | 1668 | 22.6 | 181 | 86 | 611 | 312,458 | 1712 | 24.6 | - | - | 731 | 343,214 | 9.8 |
| 0.05 | 1718 | 21.3 | 189 | 92 | 637 | 325,013 | 1741 | 23.6 | - | - | 755 | 358,478 | 10.3 |
| 0.10 | 1730 | 20.4 | 211 | 98 | 651 | 342,480 | 1769 | 22.7 | - | - | 771 | 379,987 | 11.0 |
| 0.15 | 1759 | 19.1 | 224 | 111 | 672 | 351,245 | 1784 | 21.8 | - | - | 786 | 397,163 | 13.1 |
| 0.20 | 1831 | 18.3 | 230 | 116 | 689 | 359,654 | 1821 | 21.0 | - | - | 811 | 411,245 | 14.3 |
| 0.25 | 1870 | 17.4 | 241 | 120 | 706 | 368,412 | 1830 | 19.3 | - | - | 829 | 425,741 | 15.6 |
| 0.30 | 1892 | 15.8 | 263 | 125 | 750 | 375,147 | 1854 | 18.4 | - | - | 864 | 438,320 | 16.8 |
| 0.35 | 1915 | 14.9 | 280 | 129 | 789 | 385,430 | 1876 | 17.3 | - | - | 932 | 462,147 | 19.9 |
| 0.40 | 1956 | 14.1 | 291 | 134 | 814 | 396,478 | 1899 | 16.9 | - | - | 976 | 489,217 | 23.4 |
| Quadratic Green Investment Function | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| With Green Investment | Without Green Investment | ||||||||||||
| r | Savings (%) | ||||||||||||
| 0.01 | 1656 | 21.9 | 162 | 78 | 609 | 310,387 | 1715 | 24.1 | - | - | 723 | 340,124 | 9.5 |
| 0.05 | 1663 | 20.7 | 173 | 84 | 632 | 319,978 | 1733 | 23.3 | - | - | 747 | 361,248 | 12.9 |
| 0.10 | 1672 | 18.4 | 184 | 89 | 648 | 325,741 | 1762 | 22.5 | - | - | 768 | 375,687 | 15.3 |
| 0.15 | 1680 | 17.6 | 198 | 94 | 659 | 336,425 | 1777 | 21.8 | - | - | 781 | 392,755 | 16.7 |
| 0.20 | 1689 | 17.1 | 211 | 97 | 685 | 352,413 | 1794 | 19.9 | - | - | 804 | 415,547 | 17.9 |
| 0.25 | 1698 | 16.2 | 225 | 101 | 692 | 361,214 | 1812 | 19.1 | - | - | 839 | 429,578 | 18.9 |
| 0.30 | 1706 | 15.1 | 241 | 104 | 770 | 372,457 | 1832 | 18.4 | - | - | 871 | 445,874 | 19.7 |
| 0.35 | 1718 | 14.5 | 264 | 107 | 786 | 385,424 | 1857 | 17.6 | - | - | 910 | 463,856 | 20.4 |
| 0.40 | 1732 | 13.9 | 282 | 110 | 799 | 389,842 | 1883 | 17.1 | - | - | 964 | 476,254 | 22.2 |
| Exponential green investment function | |||||||||||||
| With green investment | Without green investment | ||||||||||||
| r | Savings (%) | ||||||||||||
| 0.01 | 1703 | 22.4 | 178 | 81 | 609 | 311,457 | 1405 | 22.8 | - | - | 723 | 341,547 | 9.6 |
| 0.05 | 1712 | 20.6 | 189 | 89 | 632 | 321,654 | 1418 | 20.3 | - | - | 747 | 359,734 | 11.8 |
| 0.10 | 1720 | 19.5 | 201 | 93 | 648 | 332,158 | 1423 | 19.4 | - | - | 768 | 374,247 | 12.7 |
| 0.15 | 1752 | 18.3 | 212 | 98 | 659 | 339,868 | 1456 | 18.2 | - | - | 781 | 388,542 | 14.2 |
| 0.20 | 1793 | 17.6 | 225 | 105 | 685 | 347,654 | 1516 | 17.6 | - | - | 804 | 399,345 | 14.9 |
| 0.25 | 1843 | 17.0 | 240 | 109 | 692 | 359,873 | 1547 | 16.9 | - | - | 839 | 416,541 | 15.8 |
| 0.30 | 1872 | 16.2 | 252 | 113 | 770 | 367,871 | 1578 | 16.1 | - | - | 871 | 428,278 | 16.4 |
| 0.35 | 1889 | 15.8 | 275 | 115 | 786 | 378,453 | 1591 | 15.4 | - | - | 910 | 449,802 | 18.9 |
| 0.40 | 1913 | 15.1 | 287 | 119 | 799 | 389,871 | 1621 | 14.9 | - | - | 964 | 479,847 | 23.1 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Udayakumar, R.; Priyan, S.; Mittal, M.; Jirawattanapanit, A.; Rajchakit, G.; Kaewmesri, P. A Sustainable Production Scheduling with Backorders under Different Forms of Rework Process and Green Investment. Sustainability 2022, 14, 16999. https://doi.org/10.3390/su142416999
Udayakumar R, Priyan S, Mittal M, Jirawattanapanit A, Rajchakit G, Kaewmesri P. A Sustainable Production Scheduling with Backorders under Different Forms of Rework Process and Green Investment. Sustainability. 2022; 14(24):16999. https://doi.org/10.3390/su142416999
Chicago/Turabian StyleUdayakumar, R., S. Priyan, Mandeep Mittal, Anuwat Jirawattanapanit, Grienggrai Rajchakit, and Pramet Kaewmesri. 2022. "A Sustainable Production Scheduling with Backorders under Different Forms of Rework Process and Green Investment" Sustainability 14, no. 24: 16999. https://doi.org/10.3390/su142416999
APA StyleUdayakumar, R., Priyan, S., Mittal, M., Jirawattanapanit, A., Rajchakit, G., & Kaewmesri, P. (2022). A Sustainable Production Scheduling with Backorders under Different Forms of Rework Process and Green Investment. Sustainability, 14(24), 16999. https://doi.org/10.3390/su142416999






