Solar Photovoltaic Power Forecasting: A Review
Abstract
1. Introduction
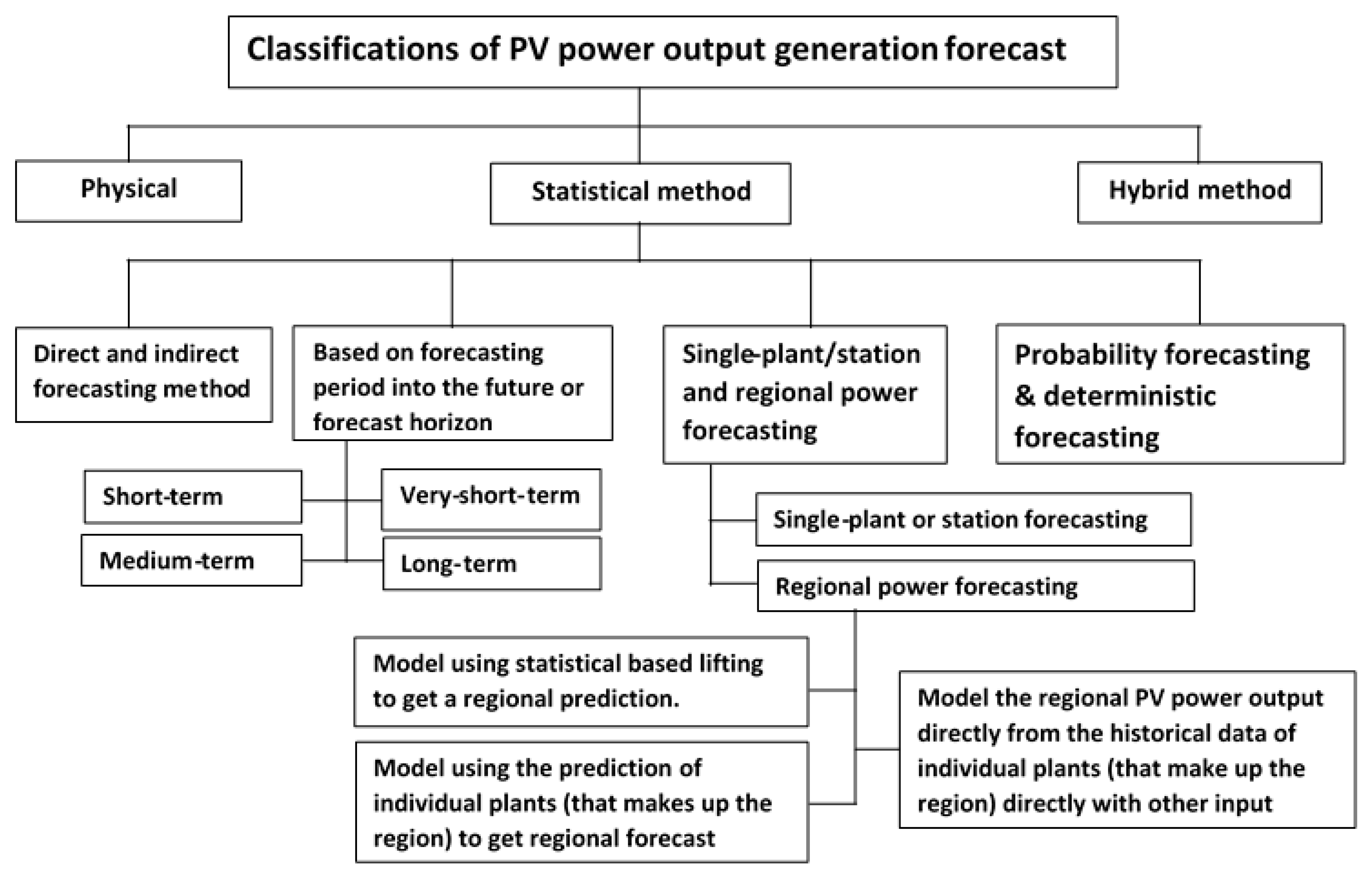
2. Classifying PV Output Power Prediction Models Based on the Forecasting Method
2.1. Physical Approach
2.1.1. Forecasting Approach Based on Temporal Information
2.1.2. Forecasting Approach Based on Spatial and Temporal Information
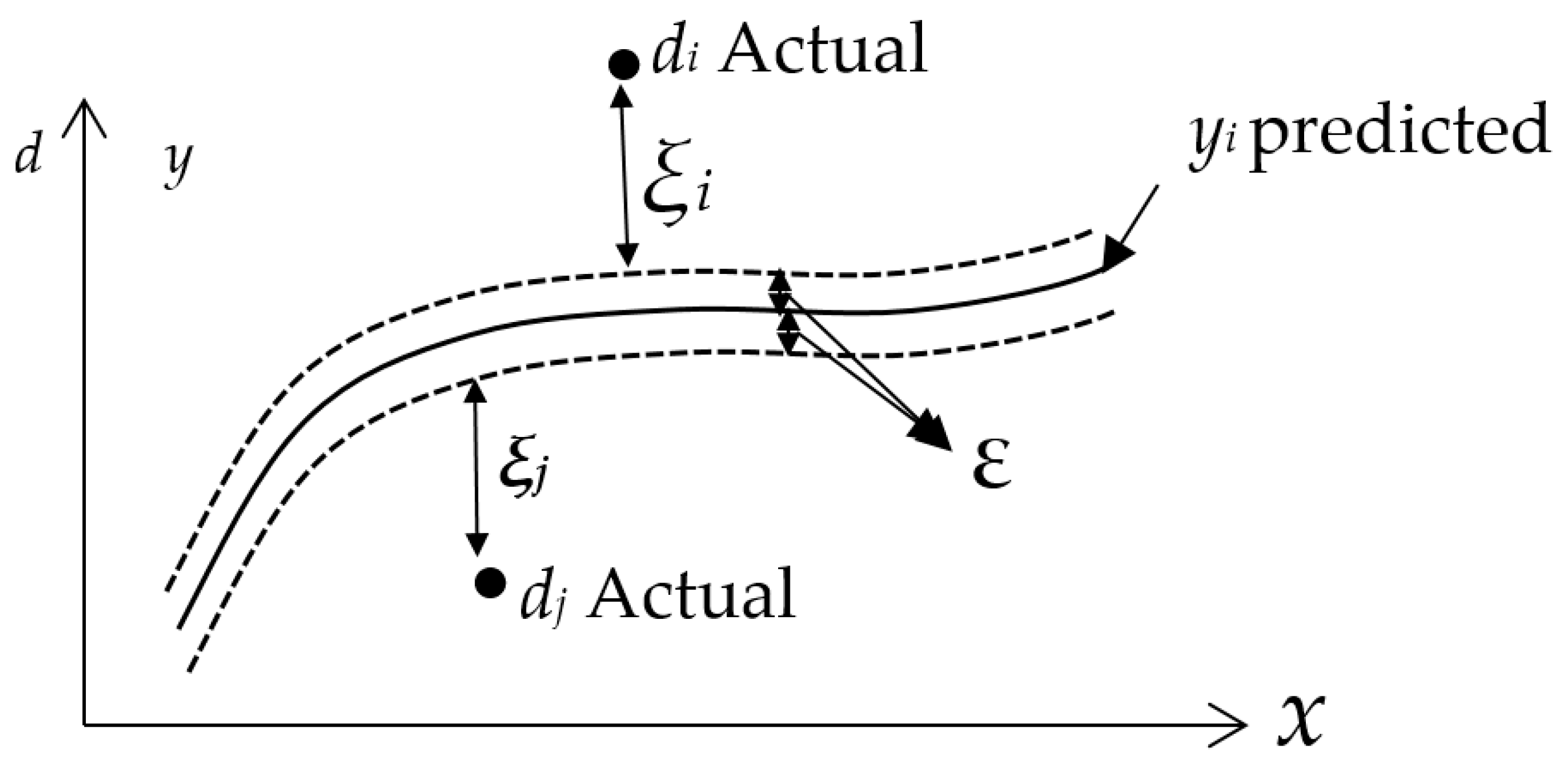
2.2. Statistical Technique
2.2.1. Direct and Indirect Forecasting Models
2.2.2. Classification of PV Power Forecasting Based on the Forecast Horizon
2.2.3. Single Plant and Regional Power Forecasting
- Summation of the results (or predictions) produced by the models of the individual stations that make up the region or area to make a prediction [49].
- Modeling the PV output power for the region using combined historical data of the individual stations that make up the region.
2.2.4. Probabilistic and Deterministic Forecasting Methods
2.3. Hybrid Method
3. Data Analytics
3.1. Input Data
3.2. Forecasting Models and Algorithms
3.2.1. The Persistence Model
3.2.2. Autoregressive Moving Average Technique
3.2.3. Regression Technique and Exponential Smoothing Technique
3.2.4. The Artificial Neural Network
3.2.5. Support Vector Machine
3.2.6. Deep Learning Neural Networks
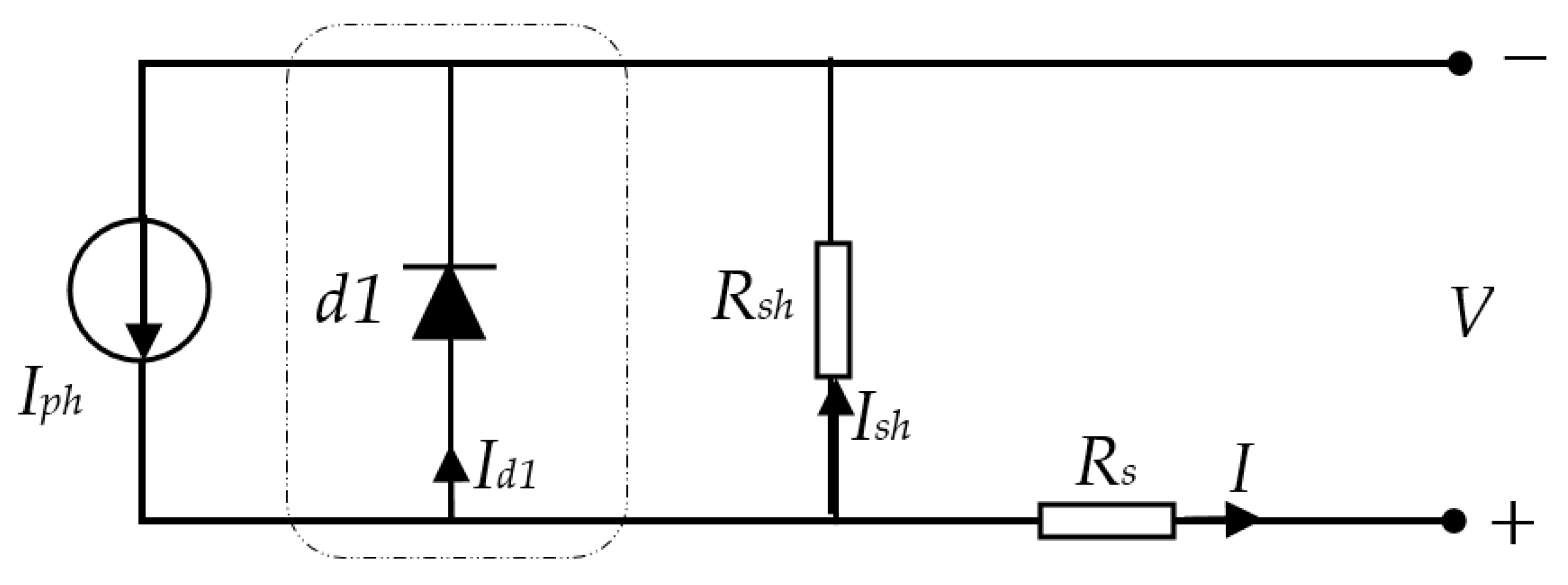
3.2.7. Parameter Extraction of Solar PV Models
4. Performance Evaluation
4.1. Matrices for Model Performance Evaluation
4.2. Evaluating the Performance of Some Selected Forecasting Models
5. Model Optimization
6. Challenges of Photovoltaic Power Forecasting
7. Conclusions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- IEA. 2022 Solar PV Report. Available online: https://www.iea.org/reports/solar-pv (accessed on 13 August 2022).
- Woyte, A.; Thong, V.; Belmans, R.; Nijs, J. Voltage fluctuations on distribution level introduced by photovoltaic systems. IEEE Trans. Energy Convers. 2006, 21, 202–209. [Google Scholar] [CrossRef]
- Strzalka, A.; Alam, N.; Duminil, E.; Coors, V.; Eicker, U. Large scale integration of photovoltaics in cities. Appl. Energy 2012, 93, 413–421. [Google Scholar] [CrossRef]
- Das, U.; Tey, K.; Idna Idris, M.; Mekhilef, S. Maximum Power Flow Management for Stand-alone PV Based Battery Charging System. In Proceedings of the 10th International Conference Power Electron, Busan, Republic of Korea, 27–30 May 2019. [Google Scholar] [CrossRef]
- Feilat, E.; Azzam, S.; Al-Salaymeh, A. Impact of large PV and wind power plants on voltage and frequency stability of Jordan’s national grid. Sustain. Cities Soc. 2018, 36, 257–271. [Google Scholar] [CrossRef]
- Gensler, A.; Henze, J.; Sick, B.; Raabe, N. Deep Learning for solar power forecasting—An approach using AutoEncoder and LSTM Neural Networks. In Proceedings of the IEEE International Conference on Systems, Man, and Cybernetics (SMC), Budapest, Hungary, 9–12 October 2016. [Google Scholar] [CrossRef]
- Tuohy, A.; Zack, J.; Haupt, S.; Sharp, J.; Ahlstrom, M.; Dise, S.; Grimit, E.; Mohrlen, C.; Lange, M.; Casado, M.; et al. Solar Forecasting: Methods, Challenges, and Performance. IEEE Power Energy Mag. 2015, 13, 50–59. [Google Scholar] [CrossRef]
- El Hendouzi, A.; Bourouhou, A. Solar Photovoltaic Power Forecasting. J. Electr. Comput. Eng. 2020, 2020, 8819925. [Google Scholar] [CrossRef]
- Das, K.; Tey, K.; Seyedmahmoudian, M.; Mekhilef, S.; Idris, M.; Deventer, W.; Horan, B.; Stojcevski, A. Forecasting of photovoltaic power generation and model optimization: A review. Renew. Sustain. Energy Rev. 2018, 81, 912–928. [Google Scholar] [CrossRef]
- Mellit, A.; Pavan, A.; Ogliari, E.; Leva, S.; Lughi, V. Advanced Methods for Photovoltaic Output Power Forecasting: A Review. Appl. Sci. 2020, 10, 487. [Google Scholar] [CrossRef]
- Li, P.; Zhou, K.; Yang, S. Photovoltaic Power Forecasting: Models and Methods. In Proceedings of the 2nd IEEE Conference Energy Internet Energy System Integration, Beijing, China, 20–22 October 2018. [Google Scholar] [CrossRef]
- Dolara, A.; Grimaccia, F.; Leva, S.; Mussetta, M.; Ogliari, E. A Physical Hybrid Artificial Neural Network for Short Term Forecasting of PV Plant Power Output. Energies 2015, 8, 1138–1153. [Google Scholar] [CrossRef]
- Monteiro, C.; Alfredo Fernandez-Jimenez, L.; Ramirez-Rosado, I.; Muñoz-Jimenez, A.; Lara-Santillan, P. Short-Term Forecasting Models for Photovoltaic Plants: Analytical versus Soft-Computing Techniques. Math. Probl. Eng. 2013, 2013, 767284. [Google Scholar] [CrossRef]
- Massidda, L.; Marrocu, M. Use of Multilinear Adaptive Regression Splines and numerical weather prediction to forecast the power output of a PV plant in Borkum, Germany. Sol. Energy 2017, 146, 141–149. [Google Scholar] [CrossRef]
- Soman, S.; Zareipour, H.; Malik, O.; Mandal, P. A review of wind power and wind speed forecasting methods with different time horizons. In Proceedings of the North American Power Symposium, Arlington, TX, USA, 26–28 September 2010. [Google Scholar] [CrossRef]
- Zhang, J.; Florita, A.; Hodge, B.; Lu, S.; Hamann, H.; Banunarayanan, V.; Brockway, A. A suite of metrics for assessing the performance of solar power forecasting. Sol. Energy 2015, 111, 157–175. [Google Scholar] [CrossRef]
- Blanc, P.; Remund, J.; Vallance, L. Short-term solar power forecasting based on satellite images. In Renewable Energy Forecasting from Model to Applications; Woodhead Publishing: Cambridge, UK, 2017; pp. 179–198. [Google Scholar] [CrossRef]
- Gueymard, C. Clear-sky irradiance predictions for solar resource mapping and large-scale applications: Improved validation methodology and detailed performance analysis of 18 broadband radiative models. Sol. Energy 2012, 86, 2145–2169. [Google Scholar] [CrossRef]
- Sengupta, M.; Habte, A.; Wilbert, S.; Gueymard, C.; Remund, J. Best Practices Handbook for the Collection and Use of Solar Resource Data for Solar Energy Applications, 3rd ed.; National Renewable Energy Laboratory: Golden, CO, USA, 2021. [Google Scholar] [CrossRef]
- Boilley, A.; Thomas, C.; Marchand, M.; Wey, E.; Blanc, P. The Solar Forecast Similarity Method: A New Method to Compute Solar Radiation Forecasts for the Next Day. Energy Procedia 2016, 91, 1018–1023. [Google Scholar] [CrossRef]
- Dambreville, R.; Blanc, P.; Chanussot, J.; Boldo, D. Very short term forecasting of the Global Horizontal Irradiance using a spatio-temporal autoregressive model. Renew. Energy 2014, 72, 291–300. [Google Scholar] [CrossRef]
- Voyant, C.; Haurant, P.; Muselli, M.; Paoli, C.; Nivet, M.L. Time series modeling and large scale global solar radiation forecasting from geostationary satellites data. Sol. Energy 2014, 102, 131–142. [Google Scholar] [CrossRef]
- Pedro, H.; Coimbra, C. Assessment of forecasting techniques for solar power production with no exogenous inputs. Sol. Energy 2012, 86, 2017–2028. [Google Scholar] [CrossRef]
- Kleissi, J. Current State of the Art in Solar Power Forecasting. California Renewable Energy Forecasting, Resource Data and Mapping. 2010. Available online: https://escholarship.org/uc/item/4fx8983f (accessed on 13 October 2022).
- Diagne, M.; David, M.; Lauret, P.; Boland, J.; Schmutz, N. Review of solar irradiance forecasting methods and a proposition for small-scale insular grids. Renew. Sustain. Energy Rev. 2013, 27, 65–76. [Google Scholar] [CrossRef]
- Coimbra, F.; Kleissl, J.; Marquez, R. Overview of solar-forecasting methods and a metric for accuracy evaluation. In Solar Energy Forecasting and Resource Assessment, 1st ed.; Kleissl, J., Ed.; Academic Press: Cambridge, MA, USA, 2013; pp. 171–194. [Google Scholar]
- Lorenz, E.; Hammer, A.; Heinemann, D. Short term forecasting of solar radiation based on satellite data. In Proceedings of the ISES Europe Solar Congress, Freiburg, Germany, 20 June 2004. [Google Scholar]
- Wang, G.; Su, Y.; Shu, L. One-day-ahead daily power forecasting of photovoltaic systems based on partial functional linear regression models. Renew. Energy 2016, 96, 469–478. [Google Scholar] [CrossRef]
- Wang, H.; Yi, H.; Peng, J.; Wang, G.; Liu, Y.; Jiang, H.; Liu, W. Deterministic and probabilistic forecasting of photovoltaic power based on deep convolutional neural network. Energy Convers. Manag. 2017, 153, 409–422. [Google Scholar] [CrossRef]
- Cervone, G.; Clemente-Harding, L.; Alessandrini, S.; Delle Monache, L. Short-term photovoltaic power forecasting using Artificial Neural Networks and an Analog Ensemble. Renew. Energy 2017, 108, 274–286. [Google Scholar] [CrossRef]
- Kudo, M.; Takeuchi, A.; Nozaki, Y.; Endo, H.; Sumita, J. Forecasting Electric Power Generation in a Photovoltaic Power System for an Energy Network. Electr. Energy Jpn. 2009, 167, 16–23. [Google Scholar] [CrossRef]
- Zhen, Z.; Fei, W.; Sun, Y.; Zengqiang, M.; Liu, C.; Wang, B.; Jing, L. SVM based cloud classification model using total sky images for PV power forecasting. In Proceedings of the IEEE Power Energy Society Innovative Smart Grid Technologies Conference, Washington, DC, USA, 18–20 February 2015. [Google Scholar] [CrossRef]
- Abdel-Nasser, M.; Mahmoud, K. Accurate photovoltaic power forecasting models using deep LSTM-RNN. Neural Comput. Appl. 2019, 31, 2727–2740. [Google Scholar] [CrossRef]
- Qing, X.; Niu, Y. Hourly day-ahead solar irradiance prediction using weather forecasts by LSTM. Energy 2018, 148, 461–468. [Google Scholar] [CrossRef]
- Thevenard, D.; Pelland, S. Estimating the uncertainty in long-term photovoltaic yield predictions. Sol. Energy 2013, 91, 432–445. [Google Scholar] [CrossRef]
- Yang, H.T.; Huang, C.M.; Huang, Y.C.; Pai, Y.S. A weather-based hybrid method for 1-day ahead hourly forecasting of PV power output. IEEE Trans. Sustain. Energy 2014, 5, 917–926. [Google Scholar] [CrossRef]
- Yang, X.; Ren, J.; Yue, H. Photovoltaic power forecasting with a rough set combination method. In Proceedings of the 11th UKACC International Conference Control, Belfast, UK, 31 August–2 September 2016. [Google Scholar] [CrossRef]
- Tanaka, K.; Uchida, K.; Ogimi, K.; Goya, T.; Yona, A.; Senjyu, T.; Funabashi, T.; Kim, C.H. Optimal operation by controllable loads based on smart grid topology considering insolation forecasted error. IEEE Trans. Smart Grid. 2011, 2, 438–444. [Google Scholar] [CrossRef]
- Senjyu, T.; Toshiaki, K.; Atsushi, Y.; Naomitsu, U.; Toshihisa, F.; Fujihiro, Y.; Shigeyuki, S. Output power control for large wind power penetration in small power system. In Proceedings of the IEEE Power Engineering Society General Meeting, Tampa, FL, USA, 24–28 June 2007. [Google Scholar] [CrossRef]
- Zhang, P.; Takano, H.; Murata, J. Daily solar radiation prediction based on wavelet analysis. In Proceedings of the SICE Annual Conference, Tokyo, Japan, 13–18 September 2011. [Google Scholar]
- Capizzi, G.; Napoli, C.; Bonanno, F. Innovative second-generation wavelets construction with recurrent neural networks for solar radiation forecasting. IEEE Trans. Neural Netw. Learn. Syst. 2012, 23, 1805–1815. [Google Scholar] [CrossRef]
- Cao, S.; Weng, W.; Chen, J.; Liu, W.; Yu, G.; Cao, J. Forecast of solar irradiance using chaos optimization neural networks. In Proceedings of the Asia-Pacific Power Energy Engineering Conference, Wuhan, China, 27–31 March 2009. [Google Scholar] [CrossRef]
- Wang, F.; Mi, Z.; Su, S.; Zhao, H. Short-Term Solar Irradiance Forecasting Model Based on Artificial Neural Network Using Statistical Feature Parameters. Energies 2012, 5, 1355–1370. [Google Scholar] [CrossRef]
- Hocaoǧlu, F.O.; Gerek, Ö.N.; Kurban, M. Hourly solar radiation forecasting using optimal coefficient 2-D linear filters and feed-forward neural networks. Sol. Energy 2008, 82, 714–726. [Google Scholar] [CrossRef]
- Patarau, T.; Petreus, D.; Etz, R. Analysis and optimization of a geothermal, biomass, solar hybrid system: An application of PV Sol software. In Proceedings of the 38th International Spring Seminar on Electronics Technology (ISSE), Eger, Hungary, 6–10 May 2015. [Google Scholar] [CrossRef]
- Kandasamy, C.; Prabu, P.; Niruba, K. Solar potential assessment using PVSYST software. In Proceedings of the International Conference on Green Computing, Communication and Conservation of Energy (ICGCE), Chennai, India, 12–14 December 2013. [Google Scholar] [CrossRef]
- Umer, F.; Aslam, M.; Rabbani, M.; Hanif, M.; Naeem, N.; Abbas, M. Design and Optimization of Solar Carport Canopies for Maximum Power Generation and Efficiency at Bahawalpur. Int. J. Photoenergy 2019, 2019, 6372503. [Google Scholar] [CrossRef]
- Gandoman, F.; Raeisi, F.; Ahmadi, A. A literature review on estimating of PV-array hourly power under cloudy weather conditions. Renew. Sustain. Energy Rev. 2016, 63, 579–592. [Google Scholar] [CrossRef]
- Da Silva Fonseca, J.; Oozeki, T.; Ohtake, H.; Takashima, T.; Ogimoto, K. Regional forecasts of photovoltaic power generation according to different data availability scenarios: A study of four methods. Prog. Photovolt. Res. Appl. 2015, 23, 1203–1218. [Google Scholar] [CrossRef]
- Saint-Drenan, Y.; Good, G.; Braun, M.; Freisinger, T. Analysis of the uncertainty in the estimates of regional PV power generation evaluated with the upscaling method. Sol. Energy 2016, 135, 536–550. [Google Scholar] [CrossRef]
- Huang, Y.; Lu, J.; Liu, C.; Xu, X.; Wang, W.; Zhou, X. Comparative study of power forecasting methods for PV stations. In Proceedings of the 2010 International Conference on Power System Technology (POWERCON2010), Zhejiang, China, 24–28 October 2010. [Google Scholar] [CrossRef]
- Bracale, A.; Caramia, P.; Carpinelli, G.; Rita, A.; Fazio, D.; Ferruzzi, G. A Bayesian Method for Short-Term Probabilistic Forecasting of Photovoltaic Generation in Smart Grid Operation and Control. Energies 2013, 6, 733–747. [Google Scholar] [CrossRef]
- Alessandrini, S.; Delle Monache, L.; Sperati, S.; Cervone, G. An analog ensemble for short-term probabilistic solar power forecast. Appl. Energy 2015, 157, 95–110. [Google Scholar] [CrossRef]
- Alfadda, A.; Adhikari, R.; Kuzlu, M.; Rahman, S. Hour-ahead solar PV power forecasting using SVR based approach. In Proceedings of the IEEE Power & Energy Society Innovative Smart Grid Technologies Conference (ISGT), Washington, DC, USA, 23–26 April 2017. [Google Scholar] [CrossRef]
- Alhakeem, D.; Mandal, P.; Haque, A.; Yona, A.; Senjyu, T.; Tseng, T. A new strategy to quantify uncertainties of wavelet-GRNN-PSO based solar PV power forecasts using bootstrap confidence intervals. In Proceedings of the 2015 IEEE Power & Energy Society General Meeting, Denver, CO, USA, 26–30 July 2015. [Google Scholar]
- Catalão, J.; Pousinho, H.; Mendes, V. Hybrid wavelet-PSO-ANFIS approach for short-term electricity prices forecasting. IEEE Trans. Power Syst. 2011, 26, 137–144. [Google Scholar] [CrossRef]
- Conejo, A.; Plazas, M.; Espínola, R.; Molina, A. Day-ahead electricity price forecasting using the wavelet transform and ARIMA models. IEEE Trans. Power Syst. 2005, 20, 1035–1042. [Google Scholar] [CrossRef]
- Azadeh, A.; Ghaderi, S.F.; Sohrabkhani, S. Forecasting electrical consumption by integration of Neural Network, time series and ANOVA. Appl. Math. Comput. 2007, 186, 1753–1761. [Google Scholar] [CrossRef]
- Raza, M.; Nadarajah, M.; Ekanayake, C. On recent advances in PV output power forecast. Sol. Energy 2016, 136, 124–144. [Google Scholar] [CrossRef]
- Shi, J.; Lee, W.J.; Liu, Y.; Yang, Y.; Wang, P. Forecasting power output of photovoltaic systems based on weather classification and support vector machines. IEEE Trans. Ind. Appl. 2012, 48, 1064–1069. [Google Scholar] [CrossRef]
- Perez, R.; Kivalov, S.; Schlemmer, J.; Hemker, K.; Renné, D.; Hoff, T. Validation of short and medium term operational solar radiation forecasts in the US. Sol. Energy 2010, 84, 2161–2172. [Google Scholar] [CrossRef]
- Antonanzas, J.; Osorio, N.; Escobar, R.; Urraca, R.; Martinez-de-Pison, F.; Antonanzas-Torres, F. Review of photovoltaic power forecasting. Sol. Energy 2016, 136, 78–111. [Google Scholar] [CrossRef]
- Huang, R.; Huang, T.; Gadh, R.; Li, N. Solar generation prediction using the ARMA model in a laboratory-level micro-grid. In Proceedings of the IEEE 3rd International Conference on Smart Grid Communications, Tainan, China, 5–8 November 2012. [Google Scholar] [CrossRef]
- Rajagopalan, S.; Santoso, S. Wind power forecasting and error analysis using the autoregressive moving average modeling. In Proceedings of the 2009 IEEE Power & Energy Society General Meeting, Calgary, AB, Canada, 26–30 July 2009. [Google Scholar] [CrossRef]
- Boland, J. Time series modelling of solar radiation. In Modeling Solar Radiation at the Earth’s Surface; Badescu, V., Ed.; Springer: Berlin/Heidelberg, Germany, 2008; pp. 283–312. [Google Scholar] [CrossRef]
- Box, G.; Jenkins, G.; Reinsel, G.; Ljung, G. Time Series Analysis: Forecasting and Control, 5th ed.; Wiley: Hoboken, NJ, USA, 2015. [Google Scholar]
- Wan Ahmad, W.; Ahmad, S. Arima model and exponential smoothing method: A comparison. In Proceedings of the AIP Conference Proceedings, Sydney, Australia, 27–29 November 2013. [Google Scholar] [CrossRef]
- Oudjana, S.; Hellal, A.; Mahamed, I. Short term photovoltaic power generation forecasting using neural network. In Proceedings of the 11th International Conference on Environment and Electrical Engineering (EEEIC), Venice, Italy, 18–25 May 2012. [Google Scholar] [CrossRef]
- Ostertagova, E.; Ostertag, O. Forecasting using simple exponential smoothing method. Acta Electrotech. Inform. 2012, 12, 62–66. [Google Scholar] [CrossRef]
- Holt, C. Forecasting seasonals and trends by exponentially weighted moving averages. Int. J. Forecast. 2004, 20, 5–10. [Google Scholar] [CrossRef]
- Kalekar, P. Time series Forecasting using Holt-Winters Exponential Smoothing. Kanwal Rekhi Sch. Inf. Technol. 2004, 4329008, 1–13. [Google Scholar]
- Winters, P. Forecasting Sales by Exponentially Weighted Moving Averages. Manag. Sci. 1960, 6, 324–342. [Google Scholar] [CrossRef]
- Dolara, A.; Leva, S.; Manzolini, G. Comparison of different physical models for PV power output prediction. Sol. Energy 2015, 119, 83–99. [Google Scholar] [CrossRef]
- Chu, Y.; Urquhart, B.; Gohari, S.; Pedro, H.; Kleissl, J.; Coimbra, C. Short-term reforecasting of power output from a 48 MWe solar PV plant. Sol. Energy 2015, 112, 68–77. [Google Scholar] [CrossRef]
- Aminzadeh, F.; De Groot, P. Neural Networks and Other Soft Computing Techniques with Applications in the Oil Industry; Eage Publications: Lancaster, OH, USA, 2006. [Google Scholar]
- Hossain, M.; Ong, Z.; Ismail, Z.; Noroozi, S.; Khoo, S. Artificial neural networks for vibration based inverse parametric identifications: A review. Appl. Soft Comput. 2017, 52, 203–219. [Google Scholar] [CrossRef]
- Mellit, A.; Kalogirou, S. Artificial intelligence techniques for photovoltaic applications: A review. Prog. Energy Combust. Sci. 2008, 34, 574–632. [Google Scholar] [CrossRef]
- Isa, I.; Omar, S.; Saad, Z.; Noor, N.; Osman, M. Weather forecasting using photovoltaic system and Neural Network. In Proceedings of the 2nd International Conference on Computational Intelligence, Communication Systems and Networks, Liverpool, UK, 28–30 July 2010. [Google Scholar] [CrossRef]
- Zhang, Y.; Chen, G.; Malik, O.; Hope, G. An Artificial Neural Network Based Adaptive Power System Stabilizer. IEEE Trans. Energy Convers. 1993, 8, 71–77. [Google Scholar] [CrossRef]
- Tasre, M.; Bedekar, P.; Ghate, V. Daily peak load forecasting using ANN. In Proceedings of the Nirma University International Conference on Engineering NUiCONE, Ahmedabad, India, 8–10 December 2011. [Google Scholar] [CrossRef]
- Malki, H.; Karayiannis, N.; Balasubramanian, M. Short-term electric power load forecasting using feedforward neural networks. Expert Syst. 2004, 21, 157–167. [Google Scholar] [CrossRef]
- Gupta, M.; Jin, L.; Homma, N. Static and Dynamic Neural Networks: From Fundamentals to Advanced Theory; John Wiley & Sons: Hoboken, NJ, USA, 2004. [Google Scholar]
- Mandal, P.; Madhira, S.T.S.; Ul Haque, A.; Meng, J.; Pineda, R.L. Forecasting Power Output of Solar Photovoltaic System Using Wavelet Transform and Artificial Intelligence Techniques. Procedia Comput. Sci. 2012, 12, 332–337. [Google Scholar] [CrossRef]
- Halden, U.; Cali, U.; Dynge, M.; Stekli, J.; Bai, L. DLT-based equity crowdfunding on the techno-economic feasibility of solar energy investments. Sol. Energy 2021, 227, 137–150. [Google Scholar] [CrossRef]
- Li, H.; Guo, S.; Li, C.; Sun, J. A hybrid annual power load forecasting model based on generalized regression neural network with fruit fly optimization algorithm. Knowl.-Based Syst. 2013, 37, 378–387. [Google Scholar] [CrossRef]
- Ibrić, S.; Djuriš, J.; Parojčić, J.; Djurić, Z. Artificial Neural Networks in Evaluation and Optimization of Modified Release Solid Dosage Forms. Pharmaceutics 2012, 4, 531–550. [Google Scholar] [CrossRef]
- Sözen, A.; Arcaklioǧlu, E.; Özalp, M.; Kanit, E.G. Use of artificial neural networks for mapping of solar potential in Turkey. Appl. Energy 2004, 77, 273–286. [Google Scholar] [CrossRef]
- Ding, M.; Wang, L.; Bi, R. An ANN-based Approach for Forecasting the Power Output of Photovoltaic System. Procedia Environ. Sci. 2011, 11, 1308–1315. [Google Scholar] [CrossRef]
- Bizzarri, F.; Bongiorno, M.; Brambilla, A.; Gruosso, G.; Gajani, G.S. Model of photovoltaic power plants for performance analysis and production forecast. IEEE Trans. Sustain. Energy 2013, 4, 278–285. [Google Scholar] [CrossRef]
- Smolensky, P.; Mozer, M.; Rumelhart, D. Mathematical Perspectives on Neural Networks, 1st ed.; Taylor and Francis: Philadelphia, PA, USA, 2013; ISBN 9780203772966. [Google Scholar]
- Srisaeng, P.; Baxter, G.; Wild, G. An adaptive neuro-fuzzy inference system for forecasting Australia’s domestic low cost carrier passenger demand. Vilnius Gedim. Tech. Univ. 2015, 19, 150–163. [Google Scholar] [CrossRef]
- Yun, Z.; Quan, Z.; Caixin, S.; Shaolan, L.; Yuming, L.; Yang, S. RBF neural network and ANFIS-based short-term load forecasting approach in real-time price environment. IEEE Trans. Power Syst. 2008, 23, 853–858. [Google Scholar]
- Awadallah, M.; Soliman, H.; Ehab, M.; Bayoumi, H.; Soliman, H. Adaptive deadbeat controllers for brushless dc drives using PSO and ANFIS techniques. J. Electr. Eng. 2009, 60, 3–11. [Google Scholar]
- Raza, M.Q.; Khosravi, A. A review on artificial intelligence-based load demand forecasting techniques for smart grid and buildings. Renew. Sustain. Energy Rev. 2015, 50, 1352–1372. [Google Scholar] [CrossRef]
- De Giorgi, M.; Malvoni, M.; Congedo, P. Comparison of strategies for multi-step ahead photovoltaic power forecasting models based on hybrid group method of data handling networks and least square support vector machine. Energy 2016, 107, 360–373. [Google Scholar] [CrossRef]
- Schölkopf, B.; Smola, A.; Müller, K. Kernel principal component analysis. In Artificial Neural Networks; Gerstner, W., Germond, A., Hasler, M., Nicoud, J., Eds.; Springer: Berlin/Heidelberg, Germany, 1997; Volume 1327, pp. 583–588. [Google Scholar] [CrossRef]
- Vapnik, V. The Nature of Statistical Learning Theory, 2nd ed.; Springer: New York, NY, USA, 1999. [Google Scholar]
- Hu, J.; Gao, P.; Yao, Y.; Xie, X. Traffic flow forecasting with particle swarm optimization and support vector regression. In Proceedings of the 17th International IEEE Conference on Intelligent Transportation Systems (ITSC), Qindao, China, 8–11 October 2014. [Google Scholar] [CrossRef]
- Zhang, F.; Deb, C.; Lee, S.; Yang, J.; Shah, K. Time series forecasting for building energy consumption using weighted Support Vector Regression with differential evolution optimization technique. Energy Build. 2016, 126, 94–103. [Google Scholar] [CrossRef]
- Hong, W. Electric load forecasting by support vector model. Appl. Math. Model 2009, 33, 2444–2454. [Google Scholar] [CrossRef]
- Müller, K.; Smoła, A.; Rätsch, G.; Schölkopf, B.; Kohlmorgen, J.; Vapnik, V. Predicting time series with support vector machines. In Artificial Neural Networks; Gerstner, W., Germond, A., Hasler, M., Nicoud, J., Eds.; Springer: Berlin, Germany, 1997; Volume 1327, pp. 999–1004. [Google Scholar] [CrossRef]
- Tang, Y.; Zhou, J. The performance of PSO-SVM in inflation forecasting. In Proceedings of the 12th International Conference on Service Systems and Service Management (ICSSSM), Guangzhou, China, 22–24 June 2015. [Google Scholar] [CrossRef]
- Mao, M.; Gong, W.; Chang, L. Short-term photovoltaic output forecasting model for economic dispatch of power system incorporating large-scale photovoltaic plant. In Proceedings of the IEEE Energy Conversion Congress and Exposition, Denver, CO, USA, 15–19 September 2013. [Google Scholar] [CrossRef]
- Lin, K.; Pai, P. Solar power output forecasting using evolutionary seasonal decomposition least-square support vector regression. J. Clean. Prod. 2016, 134, 456–462. [Google Scholar] [CrossRef]
- Cherkassky, V.; Ma, Y. Practical selection of SVM parameters and noise estimation for SVM regression. Neural Netw. 2004, 17, 113–126. [Google Scholar] [CrossRef]
- Yona, A.; Senjyu, T.; Funabashi, T.; Kim, C. Determination method of insolation prediction with fuzzy and applying neural network for long-term ahead PV power output correction. IEEE Trans. Sustain. Energy 2013, 4, 527–533. [Google Scholar] [CrossRef]
- Chen, S.; Chang, Y.; Chen, Z.; Chen, C. Multiple fuzzy rules interpolation with weighted antecedent variables in sparse fuzzy rule-based systems. Int. J. Pattern Recognit. Artif. Intell. 2013, 27, 1359002. [Google Scholar] [CrossRef]
- Colak, T.; Qahwaji, R. Automatic sunspot classification for real-time forecasting of solar activities. In Proceedings of the 2007 3rd International Conference on Recent Advances in Space Technologies RAST, Istanbul, Turkey, 14–16 June 2007. [Google Scholar] [CrossRef]
- Liu, J.; Fang, W.; Zhang, X.; Yang, C. Photovoltaic Power Forecasting with a Hybrid Deep Learning Approach. IEEE Access 2020, 8, 175871–175880. [Google Scholar] [CrossRef]
- Ali, M.; Mahmoud, K.; Lehtonen, M.; Access, M.D.-I. An efficient fuzzy-logic based variable-step incremental conductance MPPT method for grid-connected PV systems. IEEE Access 2021, 9, 26420–26430. [Google Scholar] [CrossRef]
- Ali, M.; Mahmoud, K.; Lehtonen, M.; Sensors, M.D. Promising MPPT methods combining metaheuristic, fuzzy-logic and ANN techniques for grid-connected photovoltaic. Sensors 2021, 21, 1244. [Google Scholar] [CrossRef] [PubMed]
- Bayoumi, A.; El-Sehiemy, R.; Sciences, K.M.-A. Assessment of an improved three-diode against modified two-diode patterns of MCS solar cells associated with soft parameter estimation paradigms. Appl. Sci. 2021, 13, 1055. [Google Scholar] [CrossRef]
- Abbas, A.S.; El-Sehiemy, R.A.; Abou El-Ela, A.; Ali, E.S.; Mahmoud, K.; Lehtonen, M.; Darwish, M.M.F. Optimal Harmonic Mitigation in Distribution Systems with Inverter Based Distributed Generation. Appl. Sci. 2021, 11, 774. [Google Scholar] [CrossRef]
- Qais, M.H.; Hasanien, H.M.; Alghuwainem, S. Transient search optimization for electrical parameters estimation of photovoltaic module based on datasheet values. Energy Convers. Manag. 2020, 214, 112904. [Google Scholar] [CrossRef]
- Said, M.; Shaheen Abdullah, M.; Ginidi, A.R.; El-Sehiemy, R.A.; Mahmoud, K.; Lehtonen, M.; Darwish, M.M.F. Estimating Parameters of Photovoltaic Models Using Accurate Turbulent Flow of Water Optimizer. Processes 2021, 9, 627. [Google Scholar] [CrossRef]
- Sudhakar Babu, T.; Prasanth Ram, J.; Sangeetha, K.; Laudani, A.; Rajasekar, N. Parameter extraction of two diode solar PV model using Fireworks algorithm. Sol. Energy 2016, 140, 265–276. [Google Scholar] [CrossRef]
- Khanna, V.; Das, B.K.; Bisht, D.; Vandana; Singh, P.K. A three diode model for industrial solar cells and estimation of solar cell parameters using PSO algorithm. Renew. Energy 2015, 78, 105–113. [Google Scholar] [CrossRef]
- AlRashidi, M.R.; AlHajri, M.F.; El-Naggar, K.M.; Al-Othman, A.K. A new estimation approach for determining the I–V characteristics of solar cells. Sol. Energy 2011, 85, 1543–1550. [Google Scholar] [CrossRef]
- Lin, P.; Cheng, S.; Yeh, W.; Chen, Z.; Wu, L. Parameters extraction of solar cell models using a modified simplified swarm optimization algorithm. Sol. Energy 2017, 144, 594–603. [Google Scholar] [CrossRef]
- Elsisi, M.; Mahmoud, K.; Lehtonen, M.; Access, M.D.-I. An improved neural network algorithm to efficiently track various trajectories of robot manipulator arms. IEEE Access 2021, 9, 11911–11920. [Google Scholar] [CrossRef]
- Elsisi, M.; Mahmoud, K.; Lehtonen, M.; Sensors, M.D. Reliable industry 4.0 based on machine learning and IOT for analyzing, monitoring, and securing smart meters. Sensors 2021, 21, 487. [Google Scholar] [CrossRef] [PubMed]
- Mansour, D.A.; Abdel-Gawad, N.M.; El Dein, A.Z.; Ahmed, H.M.; Darwish, M.M.F.; Lehtonen, M. Recent advances in polymer nanocomposites based on polyethylene and polyvinylchloride for power cables. Materials 2020, 14, 66. [Google Scholar] [CrossRef]
- Abouelatta, M.; Ward, S.; Sayed, A.; Mahmoud, K. Fast corona discharge assessment using FDM integrated with full multigrid method in HVDC transmission lines considering wind impact. IEEE Access 2020, 8, 225872–225883. [Google Scholar] [CrossRef]
- Ghoneim, S.; Mahmoud, K.; Lehtonen, M. Enhancing diagnostic accuracy of transformer faults using teaching-learning-based optimization. IEEE Access 2021, 9, 30817–30832. [Google Scholar] [CrossRef]
- Abaza, A.; El-Sehiemy, R.A.; Mahmoud, K.; Lehtonen, M.; Darwish, M.M.F. Optimal estimation of proton exchange membrane fuel cells parameter based on coyote optimization algorithm. Appl. Sci. 2021, 11, 2052. [Google Scholar] [CrossRef]
- Lun, S.X.; Wang, S.; Yang, G.H.; Guo, T.T. A new explicit double-diode modeling method based on Lambert W-function for photovoltaic arrays. Sol. Energy 2015, 116, 69–82. [Google Scholar] [CrossRef]
- Et-torabi, K.; Nassar-eddine, I.; Obbadi, A.; Errami, Y.; Rmaily, R.; Sahnoun, S.; El Fajri, A.; Agunaou, M. Parameters estimation of the single and double diode photovoltaic models using a Gauss–Seidel algorithm and analytical method: A comparative study. Energy Convers. Manag. 2017, 148, 1041–1054. [Google Scholar] [CrossRef]
- Kanimozhi, G.; Kumar, H. Modeling of solar cell under different conditions by Ant Lion Optimizer with LambertW function. Appl. Soft Comput. 2018, 71, 141–151. [Google Scholar]
- Toledo, F.; Blanes, J.; Galiano, V. Two-step linear least-squares method for photovoltaic single-diode model parameters extraction. IEEE Trans. Ind. Electron. 2018, 65, 6301–6308. [Google Scholar] [CrossRef]
- Ayang, A.; Wamkeue, R.; Ouhrouche, M.; Djongyang, N.; Essiane Salomé, N.; Pombe, J.K.; Ekemb, G. Maximum likelihood parameters estimation of single-diode model of photovoltaic generator. Renew. Energy 2019, 130, 111–121. [Google Scholar] [CrossRef]
- Guo, L.; Meng, Z.; Sun, Y.; Wang, L. Parameter identification and sensitivity analysis of solar cell models with cat swarm optimization algorithm. Energy Convers. Manag. 2016, 108, 520–528. [Google Scholar] [CrossRef]
- Ebrahimi, S.M.; Salahshour, E.; Malekzadeh, M.; Gordillo, F. Parameters identification of PV solar cells and modules using flexible particle swarm optimization algorithm. Energy 2019, 179, 358–372. [Google Scholar] [CrossRef]
- Abbassi, R.; Abbassi, A.; Heidari, A.A.; Mirjalili, S. An efficient salp swarm-inspired algorithm for parameters identification of photovoltaic cell models. Energy Convers. Manag. 2019, 179, 362–372. [Google Scholar] [CrossRef]
- Xiong, G.; Zhang, J.; Yuan, X.; Shi, D.; He, Y.; Yao, G. Parameter extraction of solar photovoltaic models by means of a hybrid differential evolution with whale optimization algorithm. Sol. Energy 2018, 176, 742–761. [Google Scholar] [CrossRef]
- Gao, X.; Cui, Y.; Hu, J.; Xu, G.; Wang, Z.; Qu, J.; Wang, H. Parameter extraction of solar cell models using improved shuffled complex evolution algorithm. Energy Convers. Manag. 2018, 157, 460–479. [Google Scholar] [CrossRef]
- Liang, J.; Qiao, K.; Yu, K.; Ge, S.; Qu, B.; Xu, R.; Li, K. Parameters estimation of solar photovoltaic models via a self-adaptive ensemble-based differential evolution. Sol. Energy 2020, 207, 336–346. [Google Scholar] [CrossRef]
- Abbassi, A.; Abbassi, R.; Heidari, A.A.; Oliva, D.; Chen, H.; Habib, A.; Jemli, M.; Wang, M. Parameters identification of photovoltaic cell models using enhanced exploratory salp chains-based approach. Energy 2020, 198, 117333. [Google Scholar] [CrossRef]
- Yu, K.; Liang, J.J.; Qu, B.Y.; Cheng, Z.; Wang, H. Multiple learning backtracking search algorithm for estimating parameters of photovoltaic models. Appl. Energy 2018, 226, 408–422. [Google Scholar] [CrossRef]
- Zhang, H.; Heidari, A.A.; Wang, M.; Zhang, L.; Chen, H.; Li, C. Orthogonal Nelder-Mead moth flame method for parameters identification of photovoltaic modules. Energy Convers. Manag. 2020, 211, 112764. [Google Scholar] [CrossRef]
- Zaky, A.A.; El Sehiemy, R.A.; Rashwan, Y.I.; Elhossieni, M.A.; Gkini, K.; Kladas, A.; Falaras, P. Optimal Performance Emulation of PSCs using the Elephant Herd Algorithm Associated with Experimental Validation. ECS J. Solid State Sci. Technol. 2019, 8, Q249–Q255. [Google Scholar] [CrossRef]
- Jian, X.; Weng, Z. A logistic chaotic JAYA algorithm for parameters identification of photovoltaic cell and module models. Optik 2020, 203, 164041. [Google Scholar] [CrossRef]
- Chen, H. An opposition-based sine cosine approach with local search for parameter estimation of photovoltaic models. Energy Convers. Manag. 2019, 195, 927–942. [Google Scholar] [CrossRef]
- Oliva, D.; Ewees, A.A.; Abd El Aziz, M.; Hassanien, A.E.; Cisneros, M.P. A chaotic improved artificial bee colony for parameter estimation of photovoltaic cells. Energies 2017, 10, 865. [Google Scholar] [CrossRef]
- Niu, Q.; Zhang, H.; Li, K. An improved TLBO with elite strategy for parameters identification of PEM fuel cell and solar cell models. Int. J. Hydrogen Energy 2014, 39, 3837–3854. [Google Scholar] [CrossRef]
- Allam, D.; Yousri, D.A.; Eteiba, M.B. Parameters extraction of the three diode model for the multi-crystalline solar cell/module using Moth-Flame Optimization Algorithm. Energy Convers. Manag. 2016, 123, 535–548. [Google Scholar] [CrossRef]
- Ghasemi, M. A novel and effective optimization algorithm for global optimization and its engineering applications: Turbulent Flow of Water-based Optimization (TFWO). Eng. Appl. Artif. Intell. 2020, 92, 10366. [Google Scholar] [CrossRef]
- Abdollahzadeh, B.; Soleimanian Gharehchopogh, F.; Mirjalili, S. Artificial gorilla troops optimizer: A new nature-inspired metaheuristic algorithm for global optimization problems. Int. J. Intell. Syst. 2021, 36, 5887–5958. [Google Scholar] [CrossRef]
- Ginidi, A.R.; Shaheen, A.M.; El-Sehiemy, R.A.; Elattar, E. Supply demand optimization algorithm for parameter extraction of various solar cell models. Energy Rep. 2021, 7, 5772–5794. [Google Scholar] [CrossRef]
- Askari, Q.; Saeed, M.; Younas, I. Heap-based optimizer inspired by corporate rank hierarchy for global optimization. Expert Syst. Appl. 2020, 161, 113702. [Google Scholar] [CrossRef]
- Chin, V.J.; Salam, Z. Coyote optimization algorithm for the parameter extraction of photovoltaic cells. Sol. Energy 2019, 194, 656–670. [Google Scholar] [CrossRef]
- Ginidi, A.; Shaheen, A.; El-Sehiemy, R.; El-Fergany, A. Gorilla troops optimizer for electrically based single and double-diode models of solar photovoltaic systems. Sustainability 2021, 13, 9459. [Google Scholar] [CrossRef]
- Liu, J.; Fang, W.; Zhang, X.; Yang, C. An Improved Photovoltaic Power Forecasting Model with the Assistance of Aerosol Index Data. IEEE Trans. Sustain. Energy 2015, 6, 434–442. [Google Scholar] [CrossRef]
- Yang, C.; Thatte, A.; Xie, L. Multitime-scale data-driven spatio-temporal forecast of photovoltaic generation. IEEE Trans. Sustain. Energy 2015, 6, 104–112. [Google Scholar] [CrossRef]
- Leva, S.; Dolara, A.; Grimaccia, F.; Mussetta, M.; Ogliari, E. Analysis and validation of 24 hours ahead neural network forecasting of photovoltaic output power. Math. Comput. Simul. 2017, 131, 88–100. [Google Scholar] [CrossRef]
- Mashud, M.; Koprinska, I.; Georgios Agelidis, V.; Rana, M.; Agelidis, V. Forecasting solar power generated by grid connected PV systems using ensembles of neural networks. In Proceedings of the International Joint Conference on Neural Networks (IJCNN), Killarney, Ireland, 12–17 July 2015. [Google Scholar] [CrossRef]
- Almeida, M.; Perpinan, O.; Narvarte, L. PV power forecast using a nonparametric PV model. Sol. Energy 2015, 115, 354–368. [Google Scholar] [CrossRef]
- Reikard, G. Predicting solar radiation at high resolutions: A comparison of time series forecasts. Sol. Energy 2009, 83, 342–349. [Google Scholar] [CrossRef]
- Ghofrani, M.; Ghayekhloo, M.; Azimi, R. A novel soft computing framework for solar radiation forecasting. Appl. Soft Comput. 2016, 48, 207–216. [Google Scholar] [CrossRef]
- Gupta, A.; Chauhan, Y.; Pachauri, R. A comparative investigation of maximum power point tracking methods for solar PV system. Sol. Energy 2016, 136, 236–253. [Google Scholar] [CrossRef]
- Law, E.; Prasad, A.; Kay, M.; Taylor, R. Direct normal irradiance forecasting and its application to concentrated solar thermal output forecasting—A review. Sol. Energy 2014, 108, 287–307. [Google Scholar] [CrossRef]
- Chen, P.; Yuan, L.; He, Y.; Luo, S. An improved SVM classifier based on double chains quantum genetic algorithm and its application in analogue circuit diagnosis. Neurocomputing 2016, 211, 202–211. [Google Scholar] [CrossRef]
- Li, Y.; He, Y.; Su, Y.; Shu, L. Forecasting the daily power output of a grid-connected photovoltaic system based on multivariate adaptive regression splines. Appl. Energy 2016, 180, 392–401. [Google Scholar] [CrossRef]
- Lauret, P.; Voyant, C.; Soubdhan, T.; David, M.; Poggi, P. A benchmarking of machine learning techniques for solar radiation forecasting in an insular context. Sol. Energy 2015, 112, 446–457. [Google Scholar] [CrossRef]
- Mojumder, J.; Ong, H.; Chong, W.; Shamshirband, S.; Al-Mamoon, A. Application of support vector machine for prediction of electrical and thermal performance in PV/T system. Energy Build. 2016, 111, 267–277. [Google Scholar] [CrossRef]
- Daye, T. Managing intermittency: Standards and recommended practices in solar power forecasting. ERCOT Emerg. Technol. 2011. Available online: https://energy.mit.edu/wp-content/uploads/2012/03/MITEI-RP-2011-001.pdf (accessed on 13 October 2022).
- Ratshilengo, M.; Sigauke, C.; Bere, A. Short-Term Solar Power Forecasting Using Genetic Algorithms: An Application Using South African Data. Appl. Sci. 2021, 11, 4214. [Google Scholar] [CrossRef]
- Zhang, J.; Verschae, R.; Nobuhara, S.; Lalonde, J. Deep photovoltaic nowcasting. Sol. Energy 2018, 176, 267–276. [Google Scholar] [CrossRef]
- El Hendouzi, A.; Bourouhou, A.; Ansari, O. The Importance of Distance between Photovoltaic Power Stations for Clear Accuracy of Short-Term Photovoltaic Power Forecasting. J. Electr. Comput. Eng. 2020, 2020, 9586707. [Google Scholar] [CrossRef]
- Luo, X.; Zhang, D.; Zhu, X. Deep learning based forecasting of photovoltaic power generation by incorporating domain knowledge. Energy 2021, 225, 120240. [Google Scholar] [CrossRef]
- Dawan, P.; Sriprapha, K.; Kittisontirak, S.; Boonraksa, T.; Junhuathon, N.; Titiroongruang, W.; Niemcharoen, S. Comparison of Power Output Forecasting on the Photovoltaic System Using Adaptive Neuro-Fuzzy Inference Systems and Particle Swarm Optimization-Artificial Neural Network Model. Energies 2020, 13, 351. [Google Scholar] [CrossRef]
- Bessa, R.J.; Trindade, A.; Silva, C.S.P.; Miranda, V. Probabilistic solar power forecasting in smart grids using distributed information. Int. J. Electr. Power Energy Syst. 2015, 72, 16–23. [Google Scholar] [CrossRef]
- Chupong, C.; Plangklang, B. Forecasting power output of PV grid connected system in Thailand without using solar radiation measurement. Energy Procedia 2011, 9, 230–237. [Google Scholar] [CrossRef]
- Semero, Y.; Zhang, J.; Zheng, D. PV power forecasting using an integrated GA-PSO-ANFIS approach and Gaussian process regression based feature selection strategy. CSEE J. Power Energy Syst. 2018, 4, 210–218. [Google Scholar] [CrossRef]
- Zhu, H.; Li, X.; Sun, Q.; Nie, L.; Yao, J.; Zhao, G. A Power Prediction Method for Photovoltaic Power Plant Based on Wavelet Decomposition and Artificial Neural Networks. Energies 2016, 9, 11. [Google Scholar] [CrossRef]
- Xu, Q.; He, D.; Zhang, N.; Kang, C.; Xia, Q.; Bai, J.; Huang, J. A short-term wind power forecasting approach with adjustment of numerical weather prediction input by data mining. IEEE Trans. Sustain. Energy 2015, 6, 1283–1291. [Google Scholar] [CrossRef]
- Zamo, M.; Mestre, O.; Arbogast, P.; Pannekoucke, O. A benchmark of statistical regression methods for short-term forecasting of photovoltaic electricity production. Part II: Probabilistic forecast of daily production. Sol. Energy 2014, 105, 804–816. [Google Scholar] [CrossRef]
- Chen, C.; Duan, S.; Cai, T.; Liu, B. Online 24-h solar power forecasting based on weather type classification using artificial neural network. Sol. Energy 2011, 85, 2856–2870. [Google Scholar] [CrossRef]
- Haque, A.; Nehrir, M.; Mandal, P. Solar PV power generation forecast using a hybrid intelligent approach. In Proceedings of the IEEE Power Energy Society General Meeting, Vancouver, BC, Canada, 21–25 July 2013. [Google Scholar] [CrossRef]
- Tao, Y.; Chen, Y. Distributed PV power forecasting using genetic algorithm based neural network approach. In Proceedings of the International Conference on Advanced Mechatronic Systems ICAMechS, Kumamoto, Japan, 10–12 August 2014. [Google Scholar] [CrossRef]
- Ramsami, P.; Oree, V. A hybrid method for forecasting the energy output of photovoltaic systems. Energy Convers. Manag. 2015, 95, 406–413. [Google Scholar] [CrossRef]
- Nagi, J.; Yap, K.; Tiong, S.; Ahmed, S. Electrical power load forecasting using hybrid self-organizing maps and support vector machines. In Proceedings of the International Power Engineering and Optimization Conference, Selangor, Malaysia, 4–5 June 2008. [Google Scholar]
- Xu, R.; Chen, H.; Sun, X. Short-term photovoltaic power forecasting with weighted support vector machine. In Proceedings of the IEEE International Conference on Automation and Logistics ICAL, Zhengzhou, China, 15–17 August 2012. [Google Scholar]
- Qiongbing, Z.; Lixin, D. A new crossover mechanism for genetic algorithms with variable-length chromosomes for path optimization problems. Expert Syst. Appl. 2016, 60, 183–189. [Google Scholar] [CrossRef]
- Bashir, Z.A.; El-Hawary, M.E. Applying wavelets to short-term load forecasting using PSO-based neural networks. IEEE Trans. Power Syst. 2009, 24, 20–27. [Google Scholar] [CrossRef]
- Hong, W. Electric load forecasting by seasonal recurrent SVR (support vector regression) with chaotic artificial bee colony algorithm. Energy 2011, 36, 5568–5578. [Google Scholar] [CrossRef]
- Bao, Y.; Liu, Z. A Fast Grid Search Method in Support Vector Regression Forecasting Time Series. In Intelligent Data Engineering and Automated Learning; Corchado, E., Yin, H., Botti, V., Fyfe, C., Eds.; Springer: Berlin, Germany, 2006; Volume 4224, pp. 504–511. [Google Scholar]
- Hong, W. Application of chaotic ant swarm optimization in electric load forecasting. Energy Policy 2010, 38, 5830–5839. [Google Scholar] [CrossRef]
- Niu, D.; Wang, Y.; Wu, D. Power load forecasting using support vector machine and ant colony optimization. Expert Syst. Appl. 2010, 37, 2531–2539. [Google Scholar] [CrossRef]
- Ye, H.; Yang, B.; Han, Y.; Chen, N. State-Of-The-Art Solar Energy Forecasting Approaches: Critical Potentials and Challenges. Front. Energy Res. 2022, 10, 268. [Google Scholar]



| Forecast Horizon | Time/Period | Application/Benefits |
|---|---|---|
| Very short-term | <1 min | Controlling power distribution |
| Short-term | 1–many hours | Ensures commitment, scheduling, and dispatch |
| Medium-term | 1 week–1 month | Smooths the planning of power system and maintenance schedule |
| Long-term | 1 month–1 year | Helpful for power generation transmission and distribution |
| Ref. | Forecast Horizon | Forecast Method | Forecast Error |
|---|---|---|---|
| [167] | Short-term | RNN | RMSE = 56.89%, MAE = 20.18%, rRME = 7.54%, rMAE = 4.49% |
| KNN | RMSE = 57.48%, MAE = 20.94%, rRME = 7.58%, rMAE = 4.58% | ||
| GA | RMSE = 35.50%, MAE = 26.74%, rRME = 5.95%, rMAE = 5.17% | ||
| [168] | Very short-term | Persistence, MPL, CNN, LSTM | RMSE = 15.3% |
| [169] | Short-term | Similarity algorithm, KNN, NARX, and smart persistence models | RMSE = 2.3% |
| [121] | Short-term | Physics-constrained long-term memory (PC-LSTM) network | MAE = 3.13% |
| [170] | Short-term | Adaptive-network-based fuzzy inference system (ANFIS) and PSO-ANN models. | RMSE = 0.1184% |
| [171] | Short-term | Vector AR exogenous | NRMSE = 8.5% |
| [73] | Short-term | Physical model | Normalized MAE (NMAE) < 1% & weighted MAE < 2% |
| [155] | Short-term | Back-propagation based ANN model | MAPE = 7.65% |
| [172] | Short-term | Elman NN | Mean absolute percentage error (MAPE) = 16.83% |
| [173] | Short-term | GA+ PSO + ANFIS | NRMSE = 5.48% |
| [8] | Short-term | RF, fuzzy C-means (FCM), sparse Gaussian process (SPGP), and improved grey wolf optimizer | RMSE = 6.5% |
| [174] | Short-term | Hybrid model of wavelet decomposition and ANN | RMSE value between 7.193% and 19.663% |
| [156] | Short-term | Non–parametric model | cv-Mean bias error < 1.3% |
| [175] | Short-term | K-means clustering method | MAPE ≈ 11% |
| [176] | Short-term | Statistical methods based on multiple regression analysis and Elman ANN | NMAE values between 6.50% and 19.49% and nRMSE values between 10.91% and 23.99% |
| [177] | Short-term | SOM and RBFNN | MAPE values between 8.29% and 10.80% |
| [178] | Short-term | WT, fuzzy ARTMAP, and firefly | MAPE 3.38−11.83% and nRMSE 12.11−13.13% |
| [179] | Short-term | GA-based NN | Error 8.00% |
| [88] | Short-term | ANN and similar day selection algorithm | MAPE of 10.06% (on sunny day) and 18.89% (on rainy day) |
| [180] | Short-term | Stepwise regression, GRNN, FFNN, and MLR | RMSE = 2.74% |
| [83] | Short-term | WT and RBFNN | MAPE 2.38% (on sunny day) and 4.08% (on cloudy day) |
| [174] | Short-term | Hybrid model of wavelet decomposition and ANN | RMSE values between 7.193−19.663% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Iheanetu, K.J. Solar Photovoltaic Power Forecasting: A Review. Sustainability 2022, 14, 17005. https://doi.org/10.3390/su142417005
Iheanetu KJ. Solar Photovoltaic Power Forecasting: A Review. Sustainability. 2022; 14(24):17005. https://doi.org/10.3390/su142417005
Chicago/Turabian StyleIheanetu, Kelachukwu J. 2022. "Solar Photovoltaic Power Forecasting: A Review" Sustainability 14, no. 24: 17005. https://doi.org/10.3390/su142417005
APA StyleIheanetu, K. J. (2022). Solar Photovoltaic Power Forecasting: A Review. Sustainability, 14(24), 17005. https://doi.org/10.3390/su142417005





