Study on Failure Mechanism of Soil–Rock Slope with FDM-DEM Method
Abstract
1. Introduction
2. FDM-DEM Coupled Simulation Method
2.1. FDM-DEM Coupled Theory
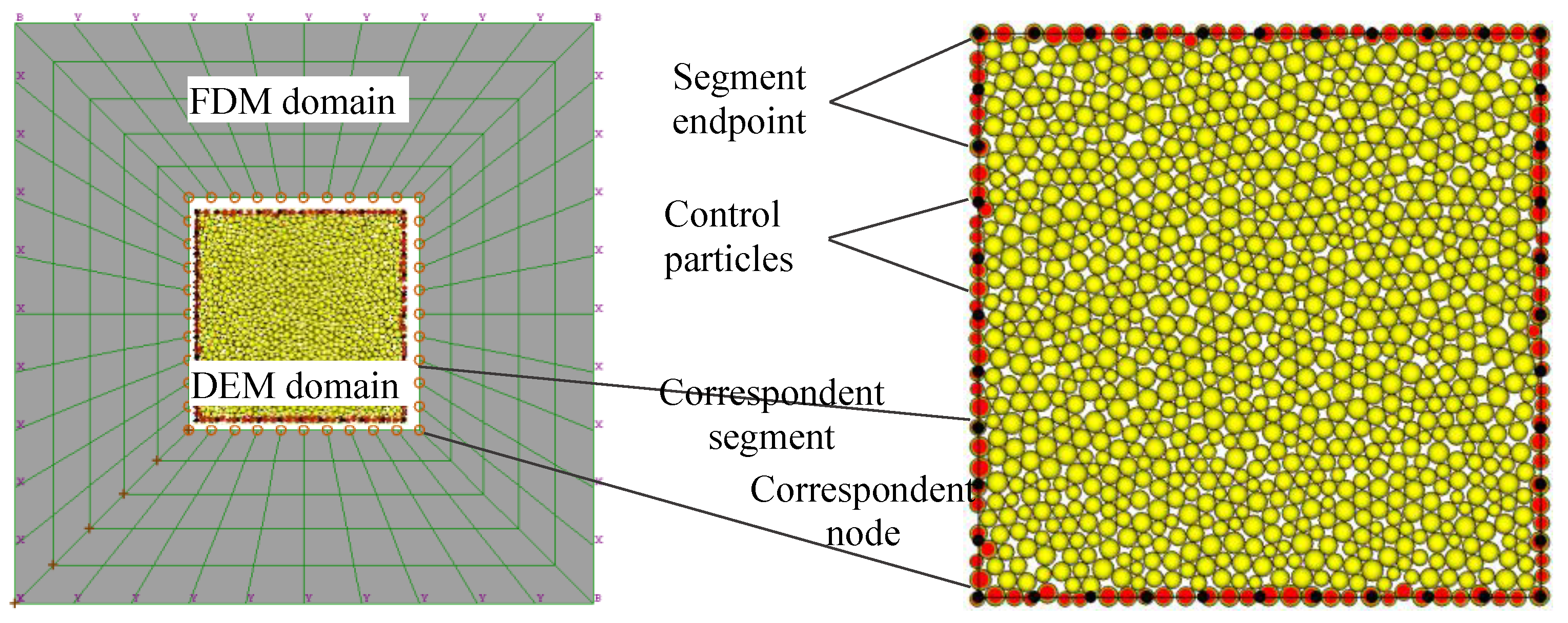
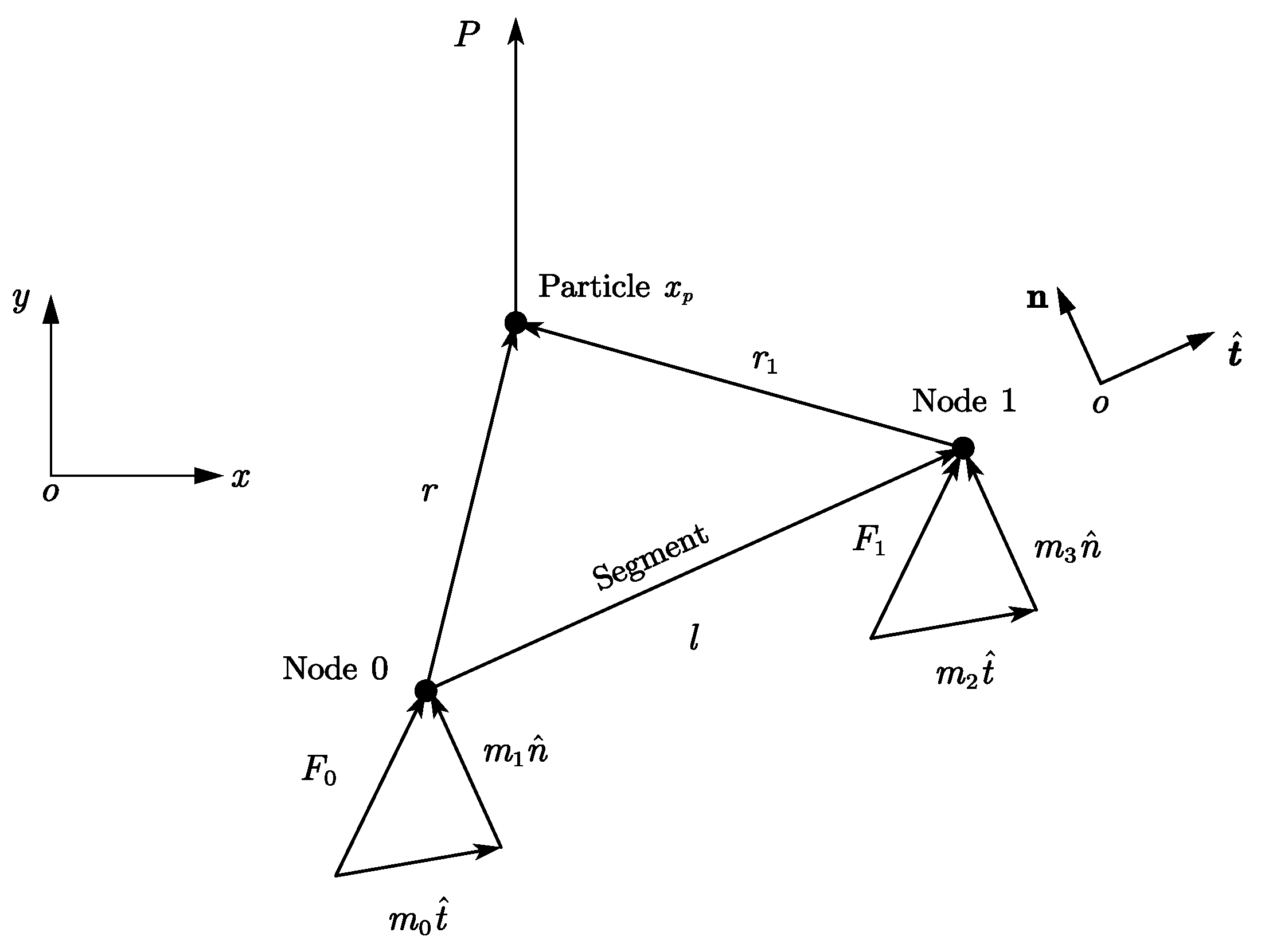
2.1.1. Theory of Mapping Control Particle Force to Segment Node
2.1.2. Theory of Mapping Segment Velocity to Control Particles
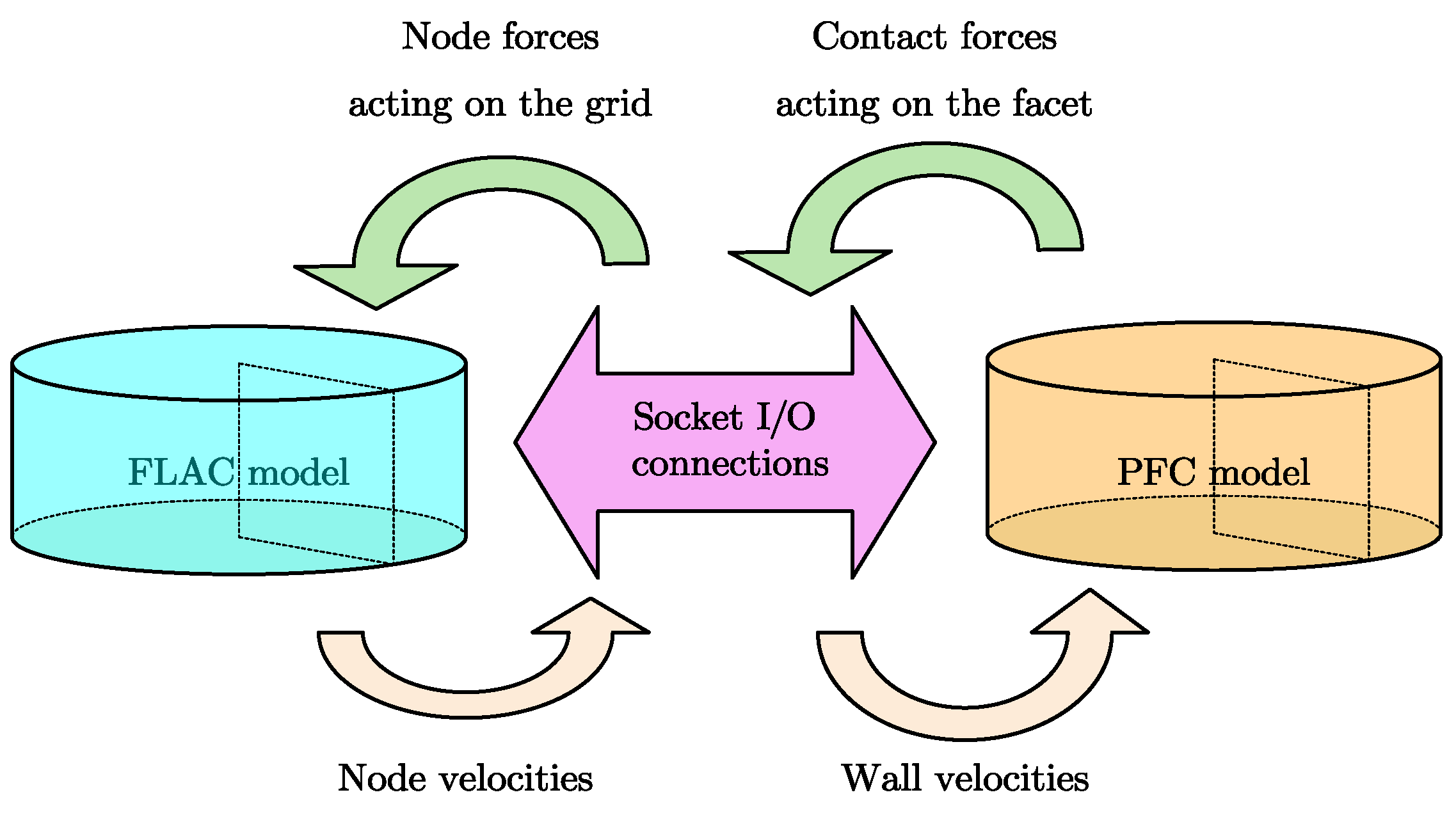
2.2. Realization of PFC/FLAC Coupled Method
3. Generation of Irregular Stone Blocks
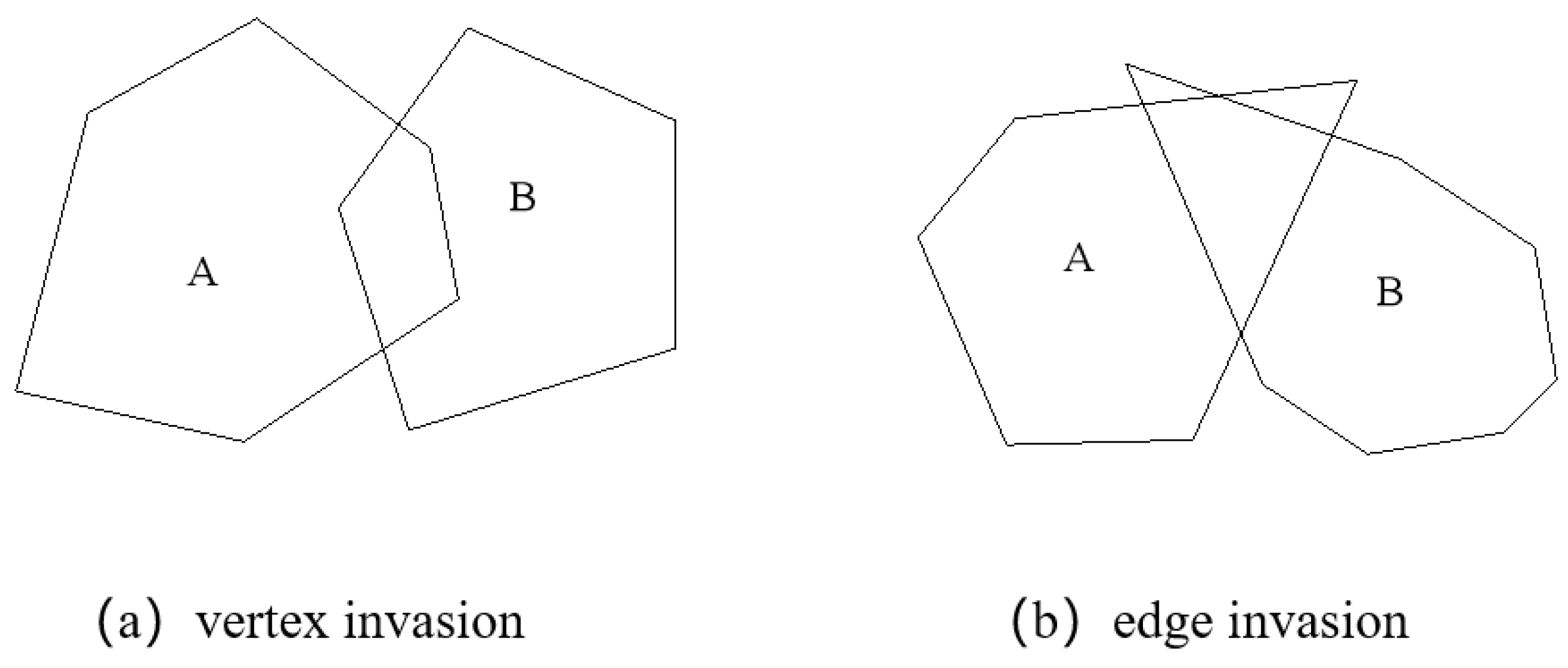
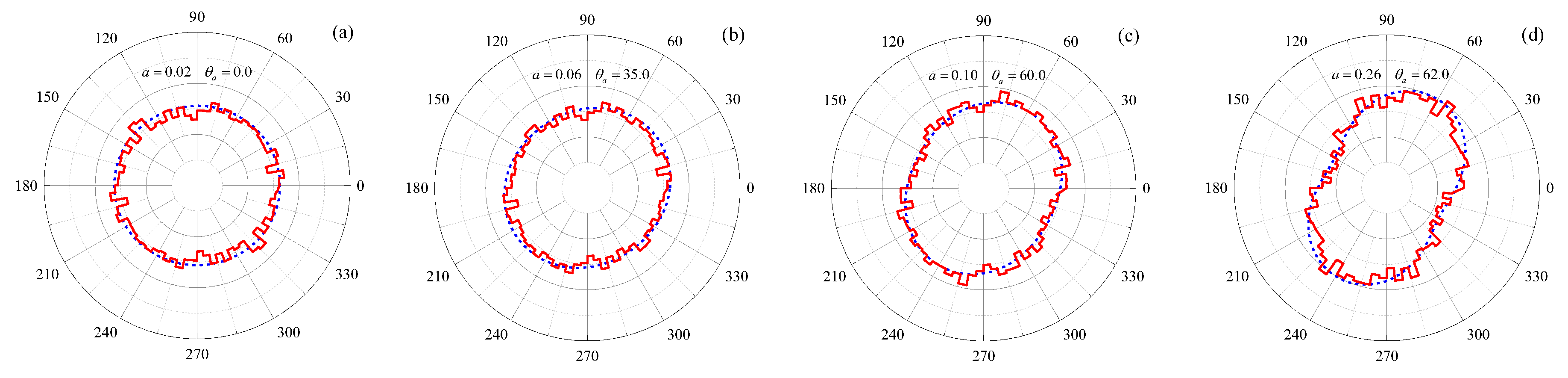
3.1. Development of Irregular Stone Blocks
3.2. Construction Process of Random Mesostructure
4. Numerical Simulation
4.1. Calibration of Micro- and Macro-Parameters
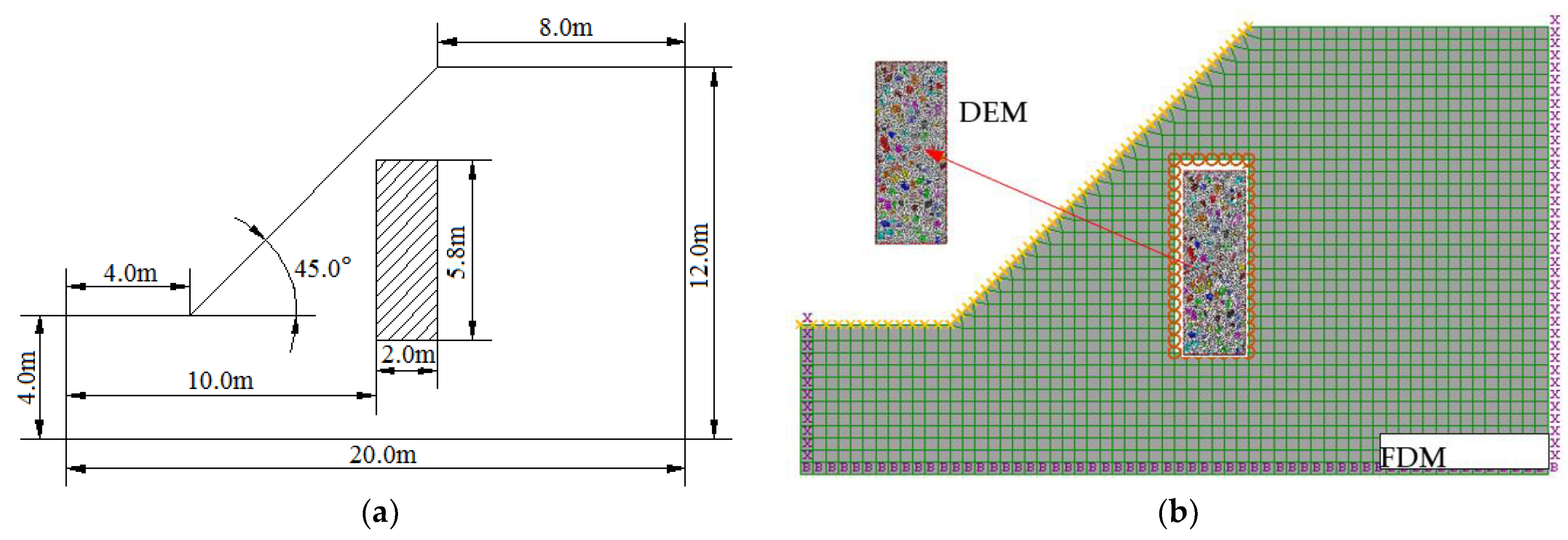
4.2. Establishment of FDM-DEM SRM Slop Model
5. Results and Discussion
5.1. Validation of the Model
5.2. Failure Process of Slope
5.3. Evolution of Meso-Contact between Stone Particles
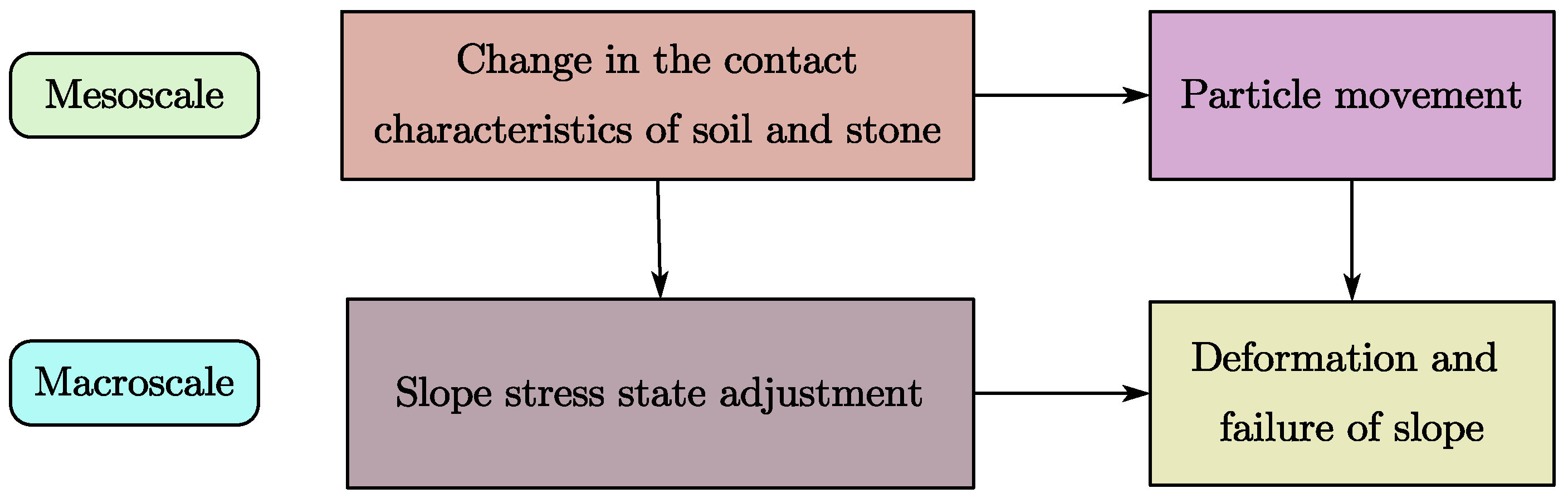
5.4. Macro and Meso Deformation and Failure Mechanism of SRM Slope
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Jia, C.; Zhang, Q.; Lei, M.; Yu, J.; Wang, R.; Liu, J. Study on the mechanical properties of outwash deposits with random structure method. Transp. Saf. Environ. 2021, 3, tdab014. [Google Scholar] [CrossRef]
- Lin, Y.; Yin, Z.-Y.; Wang, X.; Huang, L. A systematic 3D simulation method for geomaterials with block inclusions from image recognition to fracturing modelling. Theor. Appl. Fract. Mech. 2022, 117, 103194. [Google Scholar] [CrossRef]
- Yu, J.; Jia, C.; Xu, W.; Zhang, Q.; Wu, C. Granular discrete element simulation of the evolution characteristics of the shear band in soil–rock mixture based on particle rotation analysis. Environ. Earth Sci. 2021, 80, 213. [Google Scholar] [CrossRef]
- Sarma Sarada, K. Stability Analysis of Embankments and Slopes. J. Geotech. Eng. Div. 1979, 105, 1511–1524. [Google Scholar] [CrossRef]
- Spencer, E. A Method of analysis of the Stability of Embankments Assuming Parallel Inter-Slice Forces. Geotechnique 1967, 17, 11–26. [Google Scholar] [CrossRef]
- Bishop, A.W.; Morgenstern, N. Stability Coefficients for Earth Slopes. Geotechnique 1960, 10, 129–153. [Google Scholar] [CrossRef]
- Taylor, D.W. Stability of earth slopes. J. Boston Soc. Civ. Eng. 1937, 24, 197–247. [Google Scholar]
- Matsui, T.; San, K.-C. Finite Element Slope Stability Analysis by Shear Strength Reduction Technique. Soils Found. 1992, 32, 59–70. [Google Scholar] [CrossRef]
- Dawson, E.M.; Roth, W.H.; Drescher, A. Slope stability analysis by strength reduction. Geotechnique 1999, 49, 835–840. [Google Scholar] [CrossRef]
- Wang, H.; Liu, S.; Xu, W.; Yan, L.; Qu, X.; Xie, W.-C. Numerical investigation on the sliding process and deposit feature of an earthquake-induced landslide: A case study. Landslides 2020, 17, 2671–2682. [Google Scholar] [CrossRef]
- Zhou, J.-W.; Cui, P.; Yang, X.-G. Dynamic process analysis for the initiation and movement of the Donghekou landslide-debris flow triggered by the Wenchuan earthquake. J. Asian Earth Sci. 2013, 76, 70–84. [Google Scholar] [CrossRef]
- Wang, X.; Yu, P.; Yu, J.; Yu, Y.; Lv, H. Simulated Crack and Slip Plane Propagation in Soil Slopes with Embedded Discontinuities Using XFEM. Int. J. Geomech. 2018, 18, 04018170. [Google Scholar] [CrossRef]
- Wang, W.; Yin, K.; Chen, G.; Chai, B.; Han, Z.; Zhou, J. Practical application of the coupled DDA-SPH method in dynamic modeling for the formation of landslide dam. Landslides 2019, 16, 1021–1032. [Google Scholar] [CrossRef]
- Vallejo, L.E.; Mawby, R. Porosity influence on the shear strength of granular material–clay mixtures. Eng. Geol. 2000, 58, 125–136. [Google Scholar] [CrossRef]
- Zhang, Z.-L.; Xu, W.-J.; Xia, W.; Zhang, H.-Y. Large-scale in-situ test for mechanical characterization of soil–rock mixture used in an embankment dam. Int. J. Rock Mech. Min. Sci. 2016, 86, 317–322. [Google Scholar] [CrossRef]
- Huang, S.; Ding, X.; Zhang, Y.; Cheng, W. Triaxial Test and Mechanical Analysis of Rock-Soil Aggregate Sampled from Natural Sliding Mass. Adv. Mater. Sci. Eng. 2015, 2015, 238095. [Google Scholar] [CrossRef][Green Version]
- Dong, H.; Peng, B.; Gao, Q.-F.; Hu, Y.; Jiang, X. Study of hidden factors affecting the mechanical behavior of soil–rock mixtures based on abstraction idea. Acta Geotech. 2021, 16, 595–611. [Google Scholar] [CrossRef]
- Zhang, J.-C.; Li, Y.; Xu, B.; Meng, Q.-X.; Zhang, Q.; Wang, R.-B. Testing and constitutive modelling of the mechanical behaviours of gravelly soil material. Arab. J. Geosci. 2020, 13, 523. [Google Scholar] [CrossRef]
- Lin, Y.; Wang, X.; Ma, J.; Huang, L. A systematic framework for the 3D finite-discrete modelling of binary mixtures considering irregular block shapes and cohesive block-matrix interfaces. Powder Technol. 2022, 398, 117070. [Google Scholar] [CrossRef]
- Lin, Y.; Wang, X.; Ma, J.; Huang, L. A finite-discrete element based appoach for modelling the hydraulic fracturing of rocks with irregular inclusions. Eng. Fract. Mech. 2022, 261, 108209. [Google Scholar] [CrossRef]
- Nakashima, H.; Oida, A. Algorithm and implementation of soil–tire contact analysis code based on dynamic FE–DE method. J. Terramech. 2004, 41, 127–137. [Google Scholar] [CrossRef]
- Cai, M.; Kaiser, P.K.; Morioka, H.; Minami, M.; Maejima, T.; Tasaka, Y.; Kurose, H. FLAC/PFC coupled numerical simulation of AE in large-scale underground excavations. Int. J. Rock Mech. Min. Sci. 2007, 44, 550–564. [Google Scholar] [CrossRef]
- Saiang, D. Stability analysis of the blast-induced damage zone by continuum and coupled continuum–discontinuum methods. Eng. Geol. 2010, 116, 1–11. [Google Scholar] [CrossRef]
- Jia, M.; Yang, Y.; Liu, B.; Wu, S. PFC/FLAC coupled simulation of dynamic compaction in granular soils. Granul. Matter 2018, 20, 76. [Google Scholar] [CrossRef]
- Meng, Q.; Wang, H.; Cai, M.; Xu, W.; Zhuang, X.; Rabczuk, T. Three-dimensional mesoscale computational modeling of soil-rock mixtures with concave particles. Eng. Geol. 2020, 277, 105802. [Google Scholar] [CrossRef]
- Wang, Z.M.; Kwan, A.K.H.; Chan, H.C. Mesoscopic study of concrete I: Generation of random aggregate structure and finite element mesh. Comput. Struct. 1999, 70, 533–544. [Google Scholar] [CrossRef]
- He, J.; Li, X.; Li, S.; Gu, J.; Yin, Y. Numerical Study of Rock-Soil Aggregate by Discrete Element Modeling. In Proceedings of the 2009 Sixth International Conference on Fuzzy Systems and Knowledge Discovery, Tianjin, China, 14–16 August 2009. [Google Scholar]
- Coetzee, C.J.; Els, D.N.J. Calibration of granular material parameters for DEM modelling and numerical verification by blade–granular material interaction. J. Terramech. 2009, 46, 15–26. [Google Scholar] [CrossRef]
- Leung, C.F.; Zhou, Y. Rock Mechanics in Underground Construction-Proceedings of the 4th Asian and International Rock Mechanics Symposium 2006 (with Cd-Rom); World Scientific Publishing Company: Singapore, 2006; Available online: https://books.google.com.hk/books?id=x6nICgAAQBAJ (accessed on 8 November 2022).
- Rothenburg, L.; Bathurst, R. Analytical study of induced anisotropy in idealized granular materials. Geotechnique 1989, 39, 601–614. [Google Scholar] [CrossRef]











| Density (kg/m3) | Bulk Modulus (GPa) | Shear Modulus (GPa) | Frictional Angle (°) | Cohesion (kPa) | Tensile Strength (kPa) |
|---|---|---|---|---|---|
| 2700 | 0.5 | 0.15 | 30.0 | 50.0 | 0.1 |
| Material | Density (kg/m3) | Stiffness (N/m) | Cohesion (N) | Friction Coefficient | ||
|---|---|---|---|---|---|---|
| Soil | 2000 | 5.0 × 107 | 2.0 × 107 | 1.5 × 103 | 3.5 × 103 | 0.55 |
| Stone | 2700 | 5.0 × 108 | 5.0 × 108 | 1.0 × 106 | 1.0 × 106 | 1.0 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zheng, Y.; Zheng, L.; Zhan, H.; Huang, Q.; Jia, C.; Li, Z. Study on Failure Mechanism of Soil–Rock Slope with FDM-DEM Method. Sustainability 2022, 14, 17015. https://doi.org/10.3390/su142417015
Zheng Y, Zheng L, Zhan H, Huang Q, Jia C, Li Z. Study on Failure Mechanism of Soil–Rock Slope with FDM-DEM Method. Sustainability. 2022; 14(24):17015. https://doi.org/10.3390/su142417015
Chicago/Turabian StyleZheng, Yanni, Lifeng Zheng, Huyue Zhan, Qingfu Huang, Chaojun Jia, and Zhong Li. 2022. "Study on Failure Mechanism of Soil–Rock Slope with FDM-DEM Method" Sustainability 14, no. 24: 17015. https://doi.org/10.3390/su142417015
APA StyleZheng, Y., Zheng, L., Zhan, H., Huang, Q., Jia, C., & Li, Z. (2022). Study on Failure Mechanism of Soil–Rock Slope with FDM-DEM Method. Sustainability, 14(24), 17015. https://doi.org/10.3390/su142417015





