Solar Chimney Power Plants: A Review of the Concepts, Designs and Performances

Abstract

This research presents a comprehensive review of solar chimney power plants (SCPP) as a reliable source of renewable electricity generation. Solar chimney power plants differ from other renewable energy technologies because thermal and momentum effects result in 24-h electricity generation. However, they are influenced by a wide range of design, geometrical and operational parameters, and environmental conditions. This review evaluates the design aspects and the theoretical, numerical, experimental, and performance findings in previous works holistically and concisely. The study also extensively discusses the various optimization strategies, advantages, disadvantages, and limitations of solar chimney power plants. Energy storage aspects and hybrid system designs are also addressed in the present review in order to overcome the known handicaps and limitations of solar chimney power plants. The performance figures of the technology are clearly demonstrated as a function of the design and operational conditions, and future prospects are discussed in detail. It is hoped that designers and policymakers will gain valuable insight into the technological features and advancements of solar chimney power plants, assisting them in making a better-informed decision.

1. Introduction

Recently, electricity consumption has increased per capita due to technological developments and their impact on human life. The vast majority of the world’s population lives with technological devices, such that this union causes the need for electricity to increase day by day. Fossil fuel is the primary source to meet the energy demand. The increase in the energy demand due to population has increased the use of fossil fuels, bringing serious environmental pollution and CO₂ emissions. Technology has brought comfort and prosperity into our lives, but it negatively impacts our health due to pollutants. In the last ten years alone (2008–2018), CO₂ emissions have increased by more than 10% across the world (

Table 1. The amount of CO₂ emissions between 2008 and 2018 [1].

Year	2008	2009	2010	2011	2012	2013	2014	2015	2016	2017	2018
Million Tonnes of CO2	30,336.7	29,719.4	31,057.9	31,978.3	32,316.7	32,799.9	32,844.8	32,804.4	32,913.5	33,242.5	33,890.8

) [1].

The other negative point of burning fossil fuels is their production limitation, leading researchers to seek clean and alternative energy. Renewable energy sources have fewer concerns regarding CO₂ emissions and pollutants. Especially in recent years, with technological developments, the diversity and use of alternative energy sources have increased worldwide. When we look at the energy produced from renewable energy sources in the last ten years, it has increased from 124.1 million tons of oil equivalent in 2008 to 561.4 million tons of oil equivalent in 2018, which is over 3.5-times growth in a decade [1]. Among the renewable energy sources, solar energy, wind energy, and hydroelectric energy have increased in their potential over the last few years [2]. In particular, the development of solar panels with technological developments and the decrease in costs have been effective in their spread.

There are various renewable energy sources, such as wind, solar, hydroelectric, geothermal, and biomass; however, in recent years, solar energy has become a popular source because of its availability throughout the year and worldwide. The central concept of systems that harvest solar energy is similar. They are based on the principle of capturing the solar radiation coming through the darkened absorber surface, where there is direct or indirect contact between the absorbent system surface and the working fluid [3]. Generally, solar energy has been used in two main ways: as thermodynamic systems and as photovoltaic systems. Solar energy is converted directly into electricity through semiconductor materials called photovoltaic cells in photovoltaic systems. In thermodynamic systems, the sun acts as a thermal source in which the solar radiation is converted into heat energy; then, the heat can be transferred into different materials. The most common use of the solar energy converted into heat is space heating and hot water supply. Solar energy has been used as available thermal energy in several applications [4]:

• solar cookers,
• solar dryers,
• solar ponds,
• solar air conditioning,
• solar stills, water purification and distillation,
• solar chimneys, and
• solar power plants.

Some of these systems use solar thermal energy directly, while others contain different mechanisms to generate electricity. This study is about solar chimney power plants, which use the sun’s thermal energy to generate electricity according to the fundamental laws of physics. The theoretical emergence and history of solar chimney power plants are presented. A comprehensive review of the system’s operating mechanism, structure, and main elements are also carried out. In addition to the fundamental principles of the operation of solar chimneys, experimental and numerical studies are investigated. By considering the existing technology, each design’s advantages and disadvantages are discussed in order to fill the gaps in this area. Finally, several suggestions are presented for future studies. In this review, unlike other publications, the effect of geometric parameters on the system is evaluated by comparing existing studies in the literature. This comparison is made by evaluating the mathematical, theoretical and CFD studies separately for designs of different sizes. In this way, readers have the opportunity to compare different studies together with the numerical data.

2. Description of Solar Chimney Power Plants (SCPP)

2.1. History

Although the first application of solar chimney power plants was in the 1980s, theoretically, the idea was first accepted as the smoke jack designed by Leonardo Da Vinci in the 1450–1500s [5]. However, the idea of generating electricity from solar chimneys was first put forward by Spanish engineer Isidoro Cabanyes in 1903 [5]. By considering the current definition of solar chimney systems, Professor Bernard Dubos designed the idea of solar chimney power plants in 1926 to be built on a mountain slope in North Africa. Besides this, the system’s working principles and elements are included in the Dubos study [5]. Although the researchers carried out different studies in the following process, Robert Lucier made a detailed patent application in 1975, and this application was accepted in 1981 [5]. In 1982, he produced a prototype with a height of 200 m and a maximum power output of 50 kW in Manzanares, Spain, with the German team of Jörg Schlaich [6]. Since the first prototype’s production, researchers’ interest in solar chimney power plants has increased, and there are many such power plants installed in the world nowadays.

2.2. Working Principle

Although solar chimney power plants can be seen as large-scale complex structures, their working principle is based on simple and fundamental physical laws. The system is based on the upward buoyancy of fluids depending on their density difference and movements, which depend on their pressure difference. Due to the semi-permeable feature of the collector, which is the part of the system exposed to the sun, it transfers the solar radiation falling on it. The mechanism starts to function when it is transmitted to the ground. The solar radiation transferred to the system causes the air to heat because the collector acts as a cover. The decrease in the density of the heated air causes the air under the collector to move towards the collector. In addition, the solar radiation reaching the ground from the semi-permeable collector causes an increase in the temperature on the ground due to the opaque structure. Due to the temperature difference on the ground, the system’s air under the collector is exposed to the force of upward buoyancy. These forces push the air below the collector to the center of the collector, where it can only move. The pressure difference occurring at the entrance and exit of a long chimney placed vertically in the center of the collector creates a vacuum effect on the system’s air. It forces the system’s air to be drawn up through the chimney. With all of these effects, an increase occurs in the kinetic energy of the system’s air, the temperature and speed of which increase. There is a turbine in the chimney at a certain height from the ground. The kinetic energy of the system’s air hitting the turbine blades is converted into electrical energy, and power output is obtained from the system. The simplified mechanism of the system is given in Figure 1.

3. Solar Chimney Components: Construction and Materials

3.1. Tower

Although solar chimney power plants are large-scale structures, they consist of three main parts. These are the collector where the solar radiation is transferred to the system, the high chimney causing the pressure difference, and the turbine that provides the power output. The cylindrical pipe, called a tower or chimney, is positioned in the collector’s center (Figure 2) [7].

The chimney acts as a kind of motor in the system, allowing the system’s air—which heats up in the collector and increases in its kinetic energy—to be evacuated from the system by accelerating upward. It does not need any additional mechanism. There is a difference in height at the entrance and exit of the tower. The pressure difference caused by this height difference creates a vacuum effect in the collector’s center, which is the tower’s entrance, which evacuates the system’s air.

The chimney is the element that creates the pressure difference in the system. The total pressure difference in the chimney is directly proportional to the chimney’s height, and is calculated as follows [6]:

$$\Delta {\mathrm{p}}_{\mathrm{tot}}=\mathrm{g}{{\displaystyle \int }}_0^{{\mathrm{H}}_{\mathrm{tow}}}\left({\mathsf{\rho }}_{\mathrm{a}}-{\mathsf{\rho }}_{\mathrm{tow}}\right)\mathrm{dz}$$

(1)

Due to the low-temperature difference in the system, some researchers renew Equation (1) based on the Boussinesq approach [7]:

$$\Delta {\mathrm{p}}_{\mathrm{tot}}={\mathsf{\rho }\mathsf{\beta }\mathrm{gH}}_{\mathrm{tow}}\Delta \mathrm{T}$$

(2)

Schlaich claims that the efficiency of the chimney is directly dependent on the chimney height and the initial temperature, which can be given as follows [6]:

$${\mathsf{\eta }}_{\mathrm{tow}}=\frac{{\mathrm{gH}}_{\mathrm{tow}}}{{\mathrm{c}}_{\mathrm{p}}{\mathrm{T}}_{\mathrm{a}}}$$

(3)

In traditional solar chimneys, the cross-sectional area does not change with the height [9]. Von Backström and Gannon [10] claimed that increasing the chimney’s cross-section area from the chimney inlet to the chimney outlet will improve the system’s power output. Similarly, Motoyama et al. [11] also showed that the system’s power output would increase by increasing the chimney’s cross-sectional area towards the chimney outlet. On the contrary, other researchers examined the effect of designs in which the cross-sectional area decreases towards the chimney outlet on the system’s performance (Figure 3) [12]. When the existing solar chimney power plants are examined, it is seen that they mostly contain a chimney with a fixed cross-sectional area.

The chimney, which forms the main part of solar chimney power plants, is a large structure due to its height and diameter. Although the chimney’s height causes some structural difficulties, it can be dangerous due to environmental factors after the construction of the system is completed. Although this seemed like a problem in the first prototypes, technological developments allowed the construction of safer high-rise structures. Solar chimneys with a chimney height exceeding 1000 m could be built (Figure 4) [13]. Researchers stated that solar chimneys could be built with strong ring reinforcement such as internal wire, or wirelessly for higher chimneys’ economy, safety, and stability. They can be made reliably without any ring reinforcement up to 500 m in height [13]. The wall thicknesses vary according to the height of the solar chimneys. Von Backström et al. [13] designed a 1000-m high solar chimney for a 200 MW electric power output. The concrete chimney’s diameter was 260 m on the floor, the chimney diameter in the middle of the chimney was 133.4 m, and the diameter at the top of the chimney was 145 m. They designed the chimney with a wall thickness of 0.65 m at the base and 0.25 m at the top. Some researchers have recommended the measurement of different structural wind speeds and wind drag forces before installation [14].

Zhou et al. [15], considering the cost and strength calculations, designed an experimental solar chimney power plant using standard PVC drainage pipes with a diameter of 0.3 m and a height of 8 m as a chimney (Figure 5a). Some researchers used polycarbonate pipes with high temperature and impact resistance in their studies [16]. Ucgul and Koyun [17] used a solar chimney power plant with a height of 15 m and a cross-section of 1.92 m² for experimental purposes. The chimney was made of steel, in one piece (Figure 5b).

3.2. Collector

In solar chimney power plants, the collector is the facility’s base part, where the solar radiation is transferred to the system’s air. The air entering the system from the open part of the collector is warmed up by the solar radiation falling on the collector; therefore, the collector acts as a starter. The collector is made of a glass or plastic film (Figure 6a) [18]. These materials are used because they are transparent. The collecting material is positioned at a certain height from the ground [18].

The majority of the solar radiation passes through the collector, and a fraction of the radiation is directly absorbed by the system’s air. The soil and the system’s air emit long-wavelength radiation due to the solar radiation that is absorbed and trapped, and due to the collector, which is almost opaque to this long-wavelength radiation (transmittance 0.01), generating a greenhouse effect. The radiation effect under the collector increases the system temperature (Figure 6b and Figure 7a) [5]. Continuous heat transfer occurs between the collector, the system’s air, and the ground (Figure 7b) [19].

Due to the heating process in the collector, the temperature gradient forces the system’s air under the collector to move upwards in the central chimney. These effects cause the air to accelerate upwards due to the buoyant force and the conventional effect [20]. The collectors of solar chimney power plants are constructed to rise from the entrance to the collector outlet in order to support this air’s upward movement. For this reason, the collector height is greater at the chimney entrance. The temperature growth of the air in the channel can be calculated as follows:

$$\Delta \mathrm{T}=\frac{\stackrel{.}{\mathrm{Q}}}{{\mathrm{c}}_{\mathrm{p}}\stackrel{.}{\mathrm{m}}}$$

(4)

where $\stackrel{.}{\mathrm{Q}}$ is the thermal power of the system, which depends on the solar radiation coming directly to the collector and the collector’s efficiency. ∆T is the temperature increase in the system’s air at the inlet and outlet of the collector. The absorption coefficient measures how much sunlight penetrates the collector before passing through the system. If the absorption coefficient is known, the thermal power of the system can be obtained from the energy balance as follows [21]:

$$\stackrel{.}{\mathrm{Q}}=\left(\mathsf{\tau }\mathsf{\alpha }\right){\mathrm{A}}_{\mathrm{coll}}\mathrm{I}-{\mathrm{UA}}_{\mathrm{coll}}\left({\mathrm{T}}_{\mathrm{gr}}-{\mathrm{T}}_{\mathrm{a}}\right)$$

(5)

The system’s air remaining under the collector is exposed to heat transfer between the ground, solar radiation, and the collector, which triples from the collector inlet to the collector outlet. The flow characteristic can change continuously as the air, the temperature of which increases, accelerates towards the chimney inlet. Generally speaking, the characteristic of the flow can be estimated from the Rayleigh number (Ra):

$$\mathrm{Ra}=\frac{\mathrm{g}\mathsf{\beta }\left({\mathrm{T}}_{\max }-{\mathrm{T}}_{\mathrm{a}}\right){\mathrm{H}}_{\mathrm{coll}}{}^3}{\mathsf{\alpha }\mathsf{\nu }}$$

(6)

It is understood that the Ra in SCPP systems is greater than the critical 10⁹ number, such that the researchers emphasized that the entire flow in the system can be considered to be turbulent [22]. In the equation, β is the volumetric expansion coefficient, which is given as

$$\mathsf{\beta }=\frac{1}{\mathsf{\upsilon }}{\left(\frac{\partial \mathsf{\upsilon }}{\partial \mathrm{T}}\right)}_{\mathrm{P}}=-\frac{1}{\mathsf{\rho }}{\left(\frac{\partial \mathsf{\rho }}{\partial \mathrm{T}}\right)}_{\mathrm{P}}$$

(7)

Because the temperature change in solar chimney power plants is not very large, the researchers suggested using the Boussinesq approach [23]. Accordingly, the equation can be rewritten as follows:

$${\mathsf{\rho }}_{\mathrm{a}}-\mathsf{\rho }=\mathsf{\rho }\mathsf{\beta }\left(\mathrm{T}-{\mathrm{T}}_{\mathrm{a}}\right)$$

(8)

Pretorius and Kröger [24] showed that using quality glass as a collector material means better transparency and improves the system’s performance. The collector efficiency is the measure of how much solar radiation falling on the collector is transferred to the system’s air, and is given as follows:

$${\mathsf{\eta }}_{\mathrm{coll}}=\frac{\stackrel{.}{\mathrm{Q}}}{{\mathrm{I}\mathrm{A}}_{\mathrm{coll}}}$$

(9)

Alternatively, in terms of the collector’s material properties and the collector loss coefficient, some researchers state the collector efficiency as follows, and indicate that it will typically be between 40% and 60% [25]:

$${\mathsf{\eta }}_{\mathrm{coll}}=\left(\mathsf{\tau }\mathsf{\alpha }\right)-\frac{\mathrm{U}\Delta \mathsf{T}}{\mathrm{I}}$$

(10)

In solar chimney power plants, the collector is the main element that transfers solar energy to the system. Therefore, the efficiency of the collector is significant. Although the collector’s efficiency is influenced by its geometric parameters, it depends on the collector’s material and harvested solar radiation. Haaf [26], in his theoretical and experimental work on the Spanish prototype built in Manzanares, showed that the collector efficiency changes with the solar radiation (

Table 2. Comparison between the measured data from Manzanares, Spain, and theoretical results [26].

Time	8:00	10:00	12:00	14:00	16:00
I (W/m2)	413	742.5	848	755.6	461
${\mathsf{\eta }}_{coll}$Calculated (%)	6.54	20	26.12	30.98	33.83
${\mathsf{\eta }}_{coll}$Measured (%)	20.02	22.73	29.27	25.94	25.41

).

Because the solar radiation falling on the collector in the morning hours passes directly to the system’s air, the measured value of the collector’s efficiency is higher than its theoretical value. Researchers made studies to increase the system’s thermal power by using solar radiation with different collector designs. Bernardes et al. [27] modeled a solar chimney with a collector consisting of two parallel plates. Eryener et al. [28] showed that a glazed and transparent solar collector system is three times more efficient than conventional glass and plastic collectors. Before the manufacturing step, a detailed cost analysis should be carried out to determine the collector size. If a low collector cost is called into question by comparing the chimney collector costs, high-power-output systems can be installed with shorter chimney lengths using large-diameter collectors [29].

3.3. Turbine

In the collector, the part where the kinetic energy of the system’s air’s temperature and speed increases due to the acceleration of the system’s air with the pressure difference created by the chimney and the transfer of solar energy into thermal energy, is the turbine. Because it is the production-oriented part of the system, it is a crucial component. Although the turbine could be installed in the system in different positions, in traditional layouts, one turbine is used inside the chimney at a certain height parallel to the ground (Figure 8a) [30]. Researchers have claimed that solar chimneys may contain more than one axial or vertically positioned turbine (Figure 8b) [31].

Although the air velocities are identical, the turbines used in solar chimneys differ from wind turbines and gas turbines due to differences in the pressures at the turbine inlet and outlet. Therefore, the Betz limit does not comply with pressure-graded SCPP turbines [32]. The Betz limit for turbines in SCPP systems is theoretically 100%. In addition, the pressure drop is approximately ten times greater than that of wind turbines [13]. In SCPP systems, because the turbine is the component where the energy absorbed from the sun is transmitted to the generator, its efficiency directly affects the system. The turbine efficiency is affected by many variables, such as the design, location, and number of the blades. By evaluating the turbine and generator components of the system together, its efficiency can be calculated as follows:

$${\mathsf{\eta }}_{\mathrm{tur}-\mathrm{gen}}=\frac{{\mathrm{P}}_{\mathrm{o}}}{{\stackrel{.}{\mathrm{V}}\mathsf{\Delta }\mathrm{P}}_{\mathrm{tur}}}$$

(11)

∆P is the turbine pressure drop, which directly determines the system’s power output with the volumetric flow rate [33]. Although there are similar comments in the literature for the turbine pressure drop, in general, the turbine pressure drop is equal to the difference between the potential pressure difference and the pressure drop losses [34] (

Table 3. Pressure drops types in SCPP systems [34].

Inlet form pressure drop	$\Delta {\mathrm{P}}_{\mathrm{in}}={\mathrm{K}}_{\mathrm{in}}\frac{\mathsf{\rho }}{2}{\stackrel{.}{\mathrm{V}}}^2$
Frictional pressure drop	$\Delta {\mathrm{P}}_{\mathrm{f}}=\mathrm{f}\frac{{\mathrm{H}}_{\mathrm{tow}}}{{\mathrm{d}}_{\mathrm{e}}}\frac{\mathsf{\rho }}{2}{\stackrel{.}{\mathrm{V}}}^2$
Acceleration pressure drop	$\Delta {\mathrm{P}}_{\mathrm{a}}=\frac{{\stackrel{.}{\mathrm{m}}}^2}{2\mathsf{\rho }}\left(\frac{1}{{\mathrm{A}}_2{}^2}-\frac{1}{{\mathrm{A}}_1{}^2}\right)$
Outlet from pressure drop	$\Delta {\mathrm{P}}_{\mathrm{out}}={\mathrm{K}}_{\mathrm{out}}\frac{\mathsf{\rho }}{2}{\stackrel{.}{\mathrm{V}}}^2$

):

$$\Delta {\mathrm{P}}_{\mathrm{tur}}=\Delta {\mathrm{P}}_{\mathrm{tot}}-\Delta {\mathrm{P}}_{\mathrm{drop}}$$

(12)

This can be considered reversible and adiabatic by assuming constant entropy on the turbine by applying Bernoulli’s equation throughout the turbine. Because the airflow rate is not higher than the speed of sound if the density of the air in the turbine is considered constant, Hamdan [35] gave the pressure difference at the turbine inlet and outlet using the following equations:

$$\Delta {\mathrm{P}}_{\mathrm{tur}}={\mathsf{\rho }}_{\mathrm{tur}-\mathrm{i}}{\mathrm{gh}}_{\mathrm{t}}$$

(13)

$${\mathrm{s}}_{\mathrm{tur}-\mathrm{i}}={\mathrm{s}}_{\mathrm{tur}-\mathrm{o}}$$

(14)

Taking the air as the ideal gas and considering only the buoyancy effect in the chimney, Zhou et al. [36] calculated the total pressure difference in the system as follows:

$$\Delta {\mathrm{P}}_{\mathrm{tot}}=0.00353{\mathrm{gH}}_{\mathrm{tow}}\left(\frac{{\mathrm{A}}_{\mathrm{coll}}{\mathsf{\eta }}_{\mathrm{coll}}}{{\mathrm{c}}_{\mathrm{p}}\stackrel{.}{\mathrm{m}}}-\frac{\mathrm{g}}{2{\mathrm{c}}_{\mathrm{p}}}{\mathrm{H}}_{\mathrm{tow}}+\frac{1}{2}{\mathsf{\gamma }}_{\mathrm{a}}{\mathrm{H}}_{\mathrm{tow}}\right)$$

(15)

Using the potential pressure difference obtained from this equation, they gave the turbine pressure drop as follows [36]:

$$\Delta {\mathrm{P}}_{\mathrm{tot}}=\Delta {\mathrm{P}}_{\mathrm{t}}+\Delta {\mathrm{P}}_{\mathrm{f}}+\Delta {\mathrm{P}}_{\mathrm{in}}+\Delta {\mathrm{P}}_{\mathrm{out}}$$

(16)

They stated that the pressure losses in the equation could be calculated with specific coefficients, as reported in

Table 4. Pressure drop factors in SCPP systems [36].

Fractional pressure drop	$\Delta {\mathrm{P}}_{\mathrm{f}}=\mathrm{f}\frac{{\mathrm{H}}_{\mathrm{tow}}}{{\mathrm{D}}_{\mathrm{tow}}}\frac{1}{2}{\mathsf{\rho }\mathrm{v}}^2$	f = 0.008428
Inlet pressure drop	$\Delta {\mathrm{P}}_{\mathrm{in}}={\mathsf{\epsilon }}_{\mathrm{in}}\frac{1}{2}{\mathsf{\rho }\mathrm{v}}^2$	εin = 0.056
Outlet pressure drop	$\Delta {\mathrm{P}}_{\mathrm{out}}={\mathsf{\epsilon }}_{\mathrm{out}}\frac{1}{2}{\mathsf{\rho }}_{\mathrm{tow}-\mathrm{o}}{\mathrm{v}}^2$	εout = 1.058

f = wall friction factors, ε_in = collector entrance loss coefficient, ε_out = exit kinetic energy loss coefficient.

[36].

In SCPP systems, the air—of which the temperature and speed increases at the chimney inlet—is lighter than the ambient atmosphere above the chimney, exposing it to an upward driving force from the chimney floor to the chimney outlet. The turbine pressure drops due to this driving force; Bernardes et al. [27] expressed it as follows:

$$\Delta {\mathrm{P}}_{\mathrm{tur}}=\Delta {\mathrm{P}}_{\mathrm{tot}}-\frac{1}{2}{\mathsf{\rho }\mathrm{v}}_{\mathrm{tow}-\mathrm{o}}{}^2$$

(17)

They gave the total pressure difference between the chimney floor and the chimney outlet in the following equation:

$$\Delta {\mathrm{P}}_{\mathrm{tot}}={{\displaystyle \int }}_0^{{\mathrm{H}}_{\mathrm{toe}}}\left({\mathsf{\rho }}_{\mathrm{a}}-\mathsf{\rho }\right)\mathrm{gdz}$$

(18)

In Equation (18), v_tow-o is the chimney outlet velocity, which they calculated as

$${\mathrm{v}}_{\mathrm{tow}-\mathrm{o}}={\mathrm{v}}_{\mathrm{ideal}}\sqrt{1-\mathrm{x}}$$

(19)

where ${\mathrm{v}}_{\mathrm{ideal}}$ is the ideal velocity x turbine pressure drop when friction losses are neglected. With these equations, they obtained the theoretical power that can be taken by the turbine ${\mathrm{P}}_{\mathrm{o}}$:

$${\mathrm{P}}_{\mathrm{o}}=\Delta {\mathrm{P}}_{\mathrm{tot}}{\mathrm{A}}_{\mathrm{tow}}{\mathrm{v}}_{\mathrm{ideal}}{\mathrm{n}}_{\mathrm{t}}\mathrm{x}\sqrt{1-\mathrm{x}}$$

(20)

The turbine pressure drop in SCPP systems has been studied extensively by researchers, and has different applications in the literature. Theoretically, the turbine pressure drop ratio

$$\mathrm{x}=\frac{\Delta {\mathrm{P}}_{\mathrm{tur}}}{\Delta {\mathrm{P}}_{\mathrm{tot}}}$$

(21)

can be found by equality.

Guo et al. [37], in their experimental work, claimed that there was the following relationship between the turbine pressure drop and the upward air velocity at the chimney inlet:

$$\Delta {\mathrm{P}}_{\mathrm{tur}}=18.87{\mathrm{v}}_{\mathrm{tow}-\mathrm{i}}-57.59$$

(22)

There are many studies in the literature on the turbine pressure drop and turbine efficiency (

Table 5. Values of the turbine pressure drop and turbine–generator efficiency in the literature.

Reference	Pressure Drop Value	Efficiency
[38]	2/3	tur = 0.83
[37]	$\Delta {\mathrm{P}}_{\mathrm{tur}}=18.87{\mathrm{v}}_{\mathrm{tow}-\mathrm{i}}-57.59$	tur = 0.80
[9]	2/3	tur-gen = 0.83
[39]	16/27	tur-gen = 0.80
[27]	0.80–0.09	tur-gen = 0.75
[25]	2/3	tur = 0.85, gen = 0.90
[40] a	Variable	tur = 0.85, gen = 0.90
[41]	2/3	tur = 0.80
[42]	2/3	tur = 0.40–0.90
[43]	2/3	tur = 0.83
[44]	16/27	-
[45]	0.80–0.92	tur = 0.90
[46] b	$\frac{\left(\mathrm{n}-\mathrm{m}\right)}{\left(\mathrm{n}+1\right)}$	-
[47]	0.85	tur-gen = 0.80
[48] c	Variable	tur-gen = 0.80
[33]	Variable	tur = 0.80
[34]	0.66	-

In constant pressure potential, the optimum pressure drop is 2/3, but it is variable according to the system’s geometry and the solar radiation. Ref. [40] ^a For a proposed design with a 200 m collector radius and a 400 m chimney height, the optimum turbine pressure drop is 0.84. In Table 5 [46] ^b the optimum pressure drop as $\frac{\mathrm{n}-\mathrm{m}}{\mathrm{n}+1}$. Here, m is the pressure potential exponent, and n is the pressure loss exponent. Ref. [48] ^c The optimum value of the turbine pressure drop is 0.90, but it is variable during the day, and the lowest value is 0.52.

).

Only a fraction of the total pressure difference can drive the turbine in SCPP systems. Guo et al. [49] showed the relationship between the volumetric flow rate, pressure, and turbine pressure drop in Figure 9a. Figure 9b shows the effect of the turbine pressure drop on the upward airflow velocity and temperature increase at the chimney inlet.

Guo et al. [49] analyzed the optimum turbine pressure drop in SCPP systems with the analytical and numerical work they developed. They expressed the turbine pressure drop as follows:

$${\mathrm{x}}_{\mathrm{opt}}=1-\frac{\mathrm{m}+1}{3}$$

(23)

In Equation (23), m is the collector temperature rise exponent, but it practically approaches the potential pressure exponent. The Manzanares prototype was used to compare the turbine pressure drop values for different irradiation intensities in analytical and numerical studies (

Table 6. The optimal turbine pressure drop ratio is compared between the theoretical and numerical results [49].

Solar Radiation (W/m2)	m	xopt from the Theoretical Model	xopt from Numerical Simulation
200	−0.7340	0.9110	0.9134
400	−0.7678	0.9226	0.9051
600	−0.7808	0.9269	0.8942
800	−0.7889	0.9296	0.8782

).

Although there are different explanations of the turbine pressure drop and turbine efficiency in the literature, the general opinion is the same in the calculation of the power output and system efficiency of SCPP systems. The power output is given by researchers as the following [23,24,34,36,49]:

$${\mathrm{P}}_{\mathrm{o}}={\mathsf{\eta }}_{\mathrm{tur}-\mathrm{gen}}\Delta {\mathrm{P}}_{\mathrm{tur}}\stackrel{.}{\mathrm{V}}$$

(24)

The efficiency of the system expresses how much of the total solar radiation entering the system is converted into electrical energy, and its equation is

$${\mathsf{\eta }}_{\mathrm{SCPP}}=\frac{{\mathrm{P}}_{\mathrm{o}}}{{\mathrm{A}}_{\mathrm{coll}}\mathrm{I}}$$

(25)

The efficiency expression can also be defined as a function of the efficiency of the collector, chimney, and turbine, which are the three main components of the system:

$${\mathsf{\eta }}_{\mathrm{SCPP}}={\mathsf{\eta }}_{\mathrm{coll}}{\mathsf{\eta }}_{\mathrm{tow}}{\mathsf{\eta }}_{\mathrm{tur}-\mathrm{gen}}$$

(26)

4. Performance Assessment of SCPP

The first experimental study on SCPP systems was carried out by Haaf [26]. They compared theoretical studies with 24-h experimental results (Figure 10a). They measured the floor temperature during the day, and the temperatures at different depths under the floor (Figure 10b).

They measured the change in the solar radiation and ambient temperature during the day (Figure 10c). Air velocity and temperature changes within the system form part of the 24-h measurement (Figure 10d). The results obtained from the pilot plant in Manzanares shed light on many researchers’ work, and contribute to the development of new theoretical models. Zhou et al. [50] conducted experimental measurements by designing a small-scale SCPP system. A numerical model was generated using the experimental data to calculate the power output of different radiation intensities. They compared the effect of a change in the collector radius and chimney height on the power output at 850 W/m² constant radiation intensity with experimental and simulation results (Figure 11a,b). Some researchers carried out radiation, temperature, and velocity measurements at different hours during the day with the small-scale SCPP systems they established [12,15,51,52,53,54,55,56,57]. Atit [58] conducted a detailed experimental study and compared the effect of the fixed diameter chimney and the divergent chimney on the system (Figure 12a,b). Furthermore, the convergent and divergent collector comparison was studied considering a constant chimney entrance height. He compared the experimental results with the CFD model. Some researchers have examined the effect of the system’s speed and temperature by changing the collector inlet height after measuring the temperature and velocity distribution of SCPP systems with an experimental study [16,59]. Bugutekin [60] set up an SCPP facility and measured the change of the temperature–velocity values in the collector and chimney with the energy storage application throughout the day. They also studied the ground temperature change during the day.

He claimed that the temperature increase during the day at the outlet of the collector was 21–26 °C. By establishing experimental SCPP systems, some researchers analyzed the effects of changes in geometric dimensions such as the chimney height, collector radius and collector height on the system using mathematical, CFD and analytical models they developed with the experimental results [61,62,63,64]. Motoyama et al. [11] compared the temperature and velocity values of the SCPP system with a divergent chimney in a laboratory environment compared to the SCPP system with a fixed-diameter chimney. They stated that the SCPP system with a divergent chimney gave five times more power output at a 35 °C temperature difference. They compared the temperature and speed of the turbine and the non-turbine systems. Kalash et al. [65] analyzed the performance of an SCPP system they built on sloping ground (Figure 13a). They measured the temperature and speed within the system for 24 h. They stated that the temperature increase reached 19 °C even in winter, and the upward airflow velocity was 2.9 m/s.

Eryener et al. [28] claimed that smaller collectors could be used for the same power output with an application that would increase the collector efficiency of SCPP systems. They emphasized that the collector efficiency was increased by covering a part of the collector with polycarbonate (Figure 13b). They measured the effect of a change in the wind flow on the thermal efficiency, and measured the temperature, radiation, and airflow rate throughout the day. They claimed that the collector’s efficiency was between 60% and 80%, and that it was two times more efficient than regular collectors. Ayadi et al. [66] investigated the effect of the collector height on the system by constructing a small-scale model prototype. They compared the temperature and velocity distribution in the collector with the experimental results with the CFD model they developed. They examined the effect of the collector height on the system. They stated that the system’s power output will decrease with the collector height, and that the power output at a 0.005 m collector height is 50% more than the power output at a collector height of 0.02 m.

Experimental performance figures of solar chimneys are comparatively listed in

Table 7. Experimental studies on solar chimneys.

Location	Collector Diameter (m)	Tower Height (m)	Chimney Diameter (m)	Vmax (m/s)	Temp. Inc. (∆T)	Collector Material	Ref.
Manzanares, Spain	122	194.6	5.08	15	20	Plastic and glass	[38]
Florida, USA	18.3	7.92	2.44	4	28	Plastic	[12]
Hust, China	10	8	0.3	-	24.1	Fiberglass and Plastic	[15]
Botswana	-	22	2	4	7.5	Glass	[53]
Thailand	8.2	8	2	-	-	Plastic	[58]
Zanjan, Iran	10	12	0.25	4	27	Plastic	[63]
Karak, Jordan	6.8	4	0.58	-	-	Plastic	[52]
Turkey	27	17.15	0.8	5.5	21–26	Glass	[60]
Kerman, Iran	40	60	3	-	-	Glass	[61]
Nanjing, China	-	2.5	0.08	-	14	Glass	[53]
Texas, USA	11.58	4.88	0.19	2	-	Plastic	[54]
Damascus, Syria	-	9	0.31	2.9	19	Glass	[65]
Tehran, Iran	3	2	0.2	1.3	26.3	Glass	[16]
Zanja, Iran	10	12	0.25	3	25	Plastic	[59]
Edirne, Turkey	-	16.5	0.96	7	16–18	PC and glass	[28]
Eqypt	6	6	0.15	-	-	Plastic	[55]
Sfax, Tunisia	2.75	3	0.32	1.32	13	Plastic	[66]
Warangal, India	3.5	6	0.6	5.5	11.4	Glass	[56]
Erbil, Iraq	18	7.55	0.3	2.1	11.2	Glass	[57]
Japan	3	2	0.32	3	20–35	Acrylic Sheet	[11]
El-Beida, Libya a	2	2	0.11	8	10	Plastic	[67]
Sfax, Tunisia	3.7	2.95	0.16	2.2	18	P. Film	[68]
Petronas, Malaysia	3	6.3	0.32	2.25	-	Perspex	[69]
Japan	3	2	0.32	3	-	Acrylic Sheet	[70]
Kota, India b	12	8	0.2	6	12.2	Polyethylene	[71]
Suva, Fiji c	3.2	3.8	0.12–0.37	4.67	20	Perpex	[72]
Baghdad, Iraq	6	4	0.2	2.309	22	Plastic	[73]
Kompotades, Greece	-	25	2.5	5	-	Plastic	[74]
Tafresh, Iran	2.25	1.94	0.1	0.33	23.6	Glass	[75]
Isparta, Turkey	16	15	1.2	4.5	23	Glass	[17,76]

^a Vamb is 4 m/s. ^b Vamb is 4.5 m/s. ^c The tower inlet radius is 0.12 m, and 0.37 is the tower outlet radius. PC is polycarbonate, ∆T is the temperature increase, and P. is plastic.

.

5. Collector and Chimney Design Parameters

The collector is where solar radiation is absorbed in SCPP systems. The change in the collector’s geometry and design affects the system’s performance, as it will directly change the thermal energy entering the system. The studies in the literature will be examined separately according to their geometric and design effects. In SCPP systems, the chimney is the element of the structure positioned in the center of the collector; it creates a pressure difference due to its height. Thanks to the pressure difference it creates, it acts as a kind of system engine. The pressure difference is an essential factor because the power output of solar chimneys is directly caused by the system’s volumetric flow rate and pressure difference. The chimney and air velocity cause the pressure difference in the system. However, because the main component of the pressure difference is the chimney, the increase in the chimney’s height directly increases the pressure difference compared to Equation (2). In this section, firstly, studies in the literature will be given regarding the effect of the chimney height on the system. Because the change in the chimney’s diameter will affect the flow rate of the air in the system, the results of the difference in the diameter of the chimney will be included, and then the chimney profile will be continued.

5.1. Collector Radius

In the literature, the effect of the change in the collector radius on the system’s performance parameters, such as temperature, airflow rate, efficiency, and power output, has been repeatedly analyzed by many researchers. Considering the studies conducted, and given that changing the collector radius of the experimentally installed power plant is not allowed in most cases, the researchers mostly calculated the collector radius change’s effect on SCPP systems using mathematical, theoretical, and numerical analyses. Zhou et al. [50] conducted experimental measurements on a small-scale SCPP model with 8-m high and 0.7 m diameter. By changing the collector radius at 850 W/m² radiation intensity, they claimed that the power output, which was 2.087 W at a 2-m collector radius, increased by 140% to 5.01 W in a collector with a 5-m radius. Ghalamchi et al. [16] emphasized that the collector diameter increases the power output for the same geometry with their experimental data results. They stated that an SCPP system with a 500-m high chimney could give 468 kW power output with a collector of 420-m diameter. Al-Azawiey et al. [69] experimentally studied an SCPP prototype with a 6.3-m high and 0.32-m diameter chimney, with collector diameters of 3 m and 6 m. They stated that the chimney’s air velocity was 1.56 m/s for a 3-m collector diameter and 806 W/m² radiation intensity, and 2.25 m/s at the chimney for a 6-m collector diameter and 808 W/m² radiation intensity. Although the radiation intensity is almost the same for both measurements, doubling the chimney’s diameter increases the airflow rate in the chimney by approximately 44.23%. Larbi et al. [77] performed a performance analysis of a possible SCPP system installed in the Adrar region, which has a higher radiation intensity than other areas of Algeria, using a mathematical model. They claimed that the 200-m high, 10-m diameter chimney and a 500-m diameter collector SCPP system would provide between 140 and 200 kW of energy throughout the year. Designed with an 800 W/m² constant irradiance value and 30 °C initial temperature, the system gives a power output of approximately 142 kW with a collector diameter of 444 m; if the collector diameter is set to 690 m, the power output will increase by 140% to about 342 kW. Zhou et al. [78] developed a simple mathematical model to analyze the SCPP system’s performance installed on the Qinghai–Tibet plateau. They claimed that a 1000 m high, 80-m diameter chimney and a 5650-m diameter collector system would give 100 MW power output at 800 W/m² radiation at 20 °C atmospheric temperature. The system, which has a 1000-m high chimney, gives 10 MW power output with a 1750-m diameter collector under the same conditions. It reaches 50 MW power output by providing four times more power output with a 3935-m diameter collector. Koonsrisuk et al. [7] analyzed the Manzanares prototype with the detailed mathematical and CFD models. They compared the effect of the change in the chimney height ratio to the square of the collector radius on the system with two different models. The CFD model shows that the Manzanares prototype’s power output is 67–80 kW. They claimed that if the prototype H/R² ratio was 0.013 and the collector radius was 197.28 m at a fixed chimney height, the H/R² ratio would be 0.005 and the power output would be about 165 kW for both models. Similarly, they emphasized that the system’s mass flow rate will increase by 30%, from 765 kg/s in the reference state to 996 kg/s. Li et al. [79] analyzed the Manzanares prototype’s performance when powered by a turbine, using a theoretical model they developed. They stated that while giving 53.5 kW power output at a 122-m collector radius in the reference conditions at 1000 W/m² radiation, if the collector radius is set to 244 m, the power output will increase by 120.5% to approximately 118 kW. They claimed that increasing the collector radius above 500.5 m would not increase the system’s power output.

Hamdan [80] evaluated SCPP systems’ performance using the assumption of constant density, and compared the constant density model with a more realistic numerical discrete model that cares about the density change in the chimney. They showed that an SCPP system with a height of 1000 m and a chimney of a 100-m diameter would give a 35 MW power output with a collector of 1412-m diameter at 303 K ambient temperature with 263 W/m² radiation. If the collector diameter was set to 1778 m, the power output would be 50 MW. Gholamalizadeh and Mansouri [81] analyzed solar chimneys using a comprehensive numerical model. In the results they obtained from the Kerman plant, they claimed that if the collector diameter was increased from 40 m to 80 m with a 60-m high and 3-m diameter chimney at 800 W/m² radiation, the mass flow would increase by approximately 43%, and the power output would increase by 233%. They emphasized that increasing the collector diameter will decrease the energy unit cost. Guo et al. [82] analzed the performance of a large-scale solar chimney power plant that could be installed in Hami, China, which has the longest sunshine duration in a year, with a comprehensive theoretical model. They claimed that an SCPP system with a height of 1000 m and a chimney 120 m in diameter would deliver 100 MW of power output with a collector diameter of 5500 m at 300 K ambient temperature and 1000 W/m² radiation intensity. They showed that if the collector diameter was increased to 8000 m, the power output would increase by 51% to approximately 151 MW under the same conditions. Ngala et al. [83] developed a mathematical model to estimate an SCPP system’s likely performance if it was to be installed in semi-arid regions of Nigeria, and analyzed the impact of geometric and environmental factors on the system. They stated that the system, installed with 700-m high, 10-m diameter chimney, can give 3.9 × 10⁹ W power output with 800 W/m² radiation intensity and a 300-m collector diameter at 35 °C. They claimed that under the same conditions, the 600-m collector diameter power output could be 15.6 × 10⁹ W. They also predicted that the system would produce an average of 3000 MW power per month throughout the year with a collector diameter of 700 m. Khelifi et al. [84] developed a mathematical model based on one-dimensional heat and mass transfer within the system to describe, optimize and evaluate SCPP systems’ performance (Figure 14). They claimed that an SCPP model with a 100 m chimney height would deliver 0.25 MW of power with a 150 m radius collector at 1000 W/m² radiation and 298 K ambient temperature. They stated that the power output would be 1 MW with a 300 m radius collector under the same conditions. Choi et al. [34] developed an analytical model to analyze the effect of geometric parameters and energy storage units on SCPP systems’ performance. The effect of the collector radius change on an SCPP system’s power output with a 1000-m high, 200-m diameter chimney and a 5-m collector entrance height on 1000 W/m² solar radiation and 20 °C stable climate conditions were analyzed. They claimed that under the same conditions when the collector radius was 1500 m, the power output, which was 51 MW, would be approximately 109.5 MW if the collector radius was set to 3000 m, thus exceeding the power output twice. They also stated that the increase in the collector radius would decrease the rate of increase in the system’s power output after 3000 m, and would have a negative effect on the system after a certain point. Nouar et al. [85] analyzed SCPP systems using a theoretical model they developed. The chief predicted the power output to be established with Manzanares’ data in the Algeria region under the region’s climatic conditions. In June, they claimed that at noon in Manzanares’ geometry, it would give 71 kW of power with a 100-m collector radius, and 106 kW at a 122-m prototype radius; at a 200-m collector radius, the power output would exceed 260 kW. Ikhlef and Larbi [86] used a numerical model of the Manzanares prototype to analyze the effect of the use of energy storage units in SCPP systems on system performance. Adrar claimed that in the simulations carried out in Algerian climatic conditions, the power output—which was approximately 50 kW at a collector radius of 120 m—would quadruple to reach 200 kW when the collector radius is 240 m. Ming et al. [87] analyzed the Manzanares prototype with a 3D numerical study. They showed that with a collector radius of 120 m in the reference geometry, the driving force is 167 Pa. The efficiency of the system is 0.715%. If the collector radius is 200 m, the driving force will be 272 Pa, and the efficiency will be 0.751%. Kalantar and Zare [88] calculated the possible power output of the SCPP system installed in Yazd, Iran, with a 3D five-degree CFD model they developed from the Manzanares prototype. Unlike the reference geometry, they claimed that the system’s power output with a collector radius of 60 m was 28 kW. The collector radius was 240 m. It would exceed 110 kW, which is approximately four times the power output.

Karimi-Pour-Fard and Beheshti [89] conducted a CFD study referencing the Manzanares pilot plant for optimum sizing, examining the energy storage unit and its geometric parameters’ effects on SCPP systems. Then, the model was evaluated for 24-h simulations of the climatic conditions in Isfahan, Iran. They claimed that the system gave 42 kW power output with 122 m collectors in Isfahan in July; however, with a 244-m collector radius, the power output would triple to approximately 126 kW. The reverse situation is the case for the efficiency of the system. They emphasized that while the overall efficiency is 0.68% in the reference geometry, when the radius is 244 m the overall efficiency will decrease by 35% to 0.44%. Rajput et al. [90] developed a 2D model for the design and performance analysis of SCPP systems, and conducted a CFD study referencing the Manzanares prototype. They claimed that increasing the collector radius would improve the system’s mass flow, turbine pressure drop, air velocity at the turbine inlet, and power output. With a 122-m collector radius, the output power would be 48 kW. They emphasized that if the collector radius were 200 m under the same conditions, the power output would exceed 103 kW (Figure 15). Bhoraniye et al. [22] developed a CFD model to examine the effect of geometric parameters on SCPP systems’ performance. Referring to the Manzanares prototype’s dimensions, they claimed that increasing the collector radius up to 320 m at 1000 W/m² radiation intensity and 302 K ambient temperature would increase the airflow rate and the system’s power output. However, they claimed that the collector radius size of 395 m was the maximum power output point of the system; increasing the collector radius after this radius length would not improve the system’s performance.

Figure 14. Different collector radius effects for a 100-m high chimney SCPP power output. Toghraie et al. [91] and Khelifi et al. [84].

Figure 14. Different collector radius effects for a 100-m high chimney SCPP power output. Toghraie et al. [91] and Khelifi et al. [84].

Toghraie et al. [91] analyzed the effect of geometric parameters on SCPP systems’ performance using the 3D CFD model they developed. They said that a solar chimney with 100 m height, a 8-m diameter chimney, and a 2-m height horizontal collector will obtain approximately 78 kW power output with 308 K ambient temperature under constant conditions with a 100-m collector radius in 800 W/m² solar radiation. They claimed that if the collector radius was set to 200 m under the same conditions, the power output would increase by 233% to approximately 260 kW. They emphasized that the contrary is in question for efficiency with a collector radius of 100 m under the same climatic conditions; the efficiency will decrease by 13%, and will be 0.26% at a collector radius of 0.3% and 200 m. They stated that the increase in the collector radius would increase the temperature in the collector. The comparative power outputs of the researchers studying the collector radius effect of an SCPP system with a 100-m high chimney are shown in Figure 16. Similarly, the comparative graph of the power outputs for different collector radii is shown in Figure 17 by taking the researchers’ Manzanares pilot plant’s measurements as a reference. The comparison of the studies in which some researchers analyzed the effect of the collector radius in different geometries and climate conditions for the system with a chimney of 1000-m height is given in Figure 18. The researchers found that the change in the system’s collector radius affects the power output and other parameters. Esfidani et al. [92] studied the effect of the design parameters on the system’s performance with a mathematical model developed based on the geometric dimensions of the Manzanares pilot plant. They stated that increasing the collector radius at 300 K ambient temperature will boost the system’s power output. The opposite is true for the efficiency; they claimed that the efficiency of 0.536% at the reference collector radius of 122 m would decrease by 40% to 0.3195% if the collector radius was set to 240 m (Figure 17).

5.2. Collector Height

The collector is where both solar radiation and air enter the system. The change in the collector height is an essential geometric parameter determining SCPP systems’ performance. It affects the design’s airflow and the solar radiation transmitted to the ground. Najmi et al. [61] evaluated the performance of SCPP systems with a MATLAB code they developed. Their analysis with Kerman prototype measurements stated that when the collector height is 1.5 m, the temperature difference in the system is 1 °C higher than the 2-m collector height. Ayadi et al. [66] developed a CFD model to investigate the collector height’s effect on the temperature, pressure and velocity distribution by making the collector height 0.05, 0.10, 0.15 and 0.20 m. They claimed that increasing the collector height at 306 K ambient temperature and 800 W/m² constant radiation would reduce the chimney inlet velocity from 2.4 m/s to 1.85 m/s, and reduce the power output by 33%. Cottam et al. [93] designed a large-scale SCPP system with a 1000-m high, 55-m radius chimney and a 2150-m radius, 4-m entrance height collector, and analyzed the effect of the collector profile on the system using a steady-state analytical model. They stated that when the height of the horizontal collector is 4 m, the power output is 48.92 MW; when the collector height is 8 m, the power output will increase by 30% to 63.59 MW.

Dhahri et al. [94] investigated the effect of geometric parameters on the Manzanares pilot plant system with a CFD study. At a constant 293 K ambient temperature and 800 W/m² radiation intensity, when the collector height is 1 m, the system temperature increase is 22.3 °C, and the mass flow is 949 kg/s; when the collector height is 3 m, the temperature increase decreases to 5.5 °C, while the mass flow is 1087 kg/s. They stressed that it would be released. Karimi-Pour-Fard and Beheshti [89] Isfahan stated that increasing the collector height for the Manzanares prototype-sized SCPP system in Iranian climatic conditions would reduce the power output and efficiency of the system. They said that a system with a 2-m collector height in the reference state would have a 44 kW power output and 0.68% efficiency. They claimed that if the collector height is set to 3 m, the power output will decrease by 11.4% to 35.96 kW, and the efficiency would be reduced by 17.64% to 0.56%. Toghraie et al. [91] stated that, in the CFD model, 800 W/m² and 600 W/m² radiation values show that increasing the collector height decreases the power output, efficiency, pressure, and temperature change the system. They stated that in 800 W/m² constant radiation, 78.61 kW power output could be obtained with a 2-m collector height. They emphasized that when the collector height is set to 4 m, the power output will decrease by 23.6% to 60 kW; similarly, the system’s efficiency will decrease from 0.30% to 0.23%. Esfinadi et al. [92] stated that increasing the collector height in the non-inclined collector will reduce the system’s power output and efficiency. The system’s efficiency is 0.79% at the reference height, and its power output is 298.387 kW. They claimed that if the collector height is set to 4 m, its efficiency would decrease by 26.6% to 0.55%, and the power output would be 211.29 kW, decreasing by 29.1%. Researchers generally accept that the collector height reduces the system’s efficiency in the analysis of the collector height of the Manzanares prototype. The comparative graphic is given in Figure 19.

5.3. Collector SLOPE

Kasaeian et al. [59] designed a small-scale system with a fixed collector outlet height of 1 m in an experimental study to analyze the effect of a change in the collector inlet height on SCPP systems. They stated that if the chimney entrance speed is 2.78 m/s at the collector entrance height of 5 cm at 25 °C ambient temperature, and if the collector entrance height is set to 15 cm, the chimney entry speed decreases by 16% and the temperature in the chimney decreases from 47.16 °C to 38.57 °C. Ghalamchi et al. [16] measured the system’s effect with a fixed collector outlet height of 6 cm with a small-scale experimental SCPP system by setting the collector entrance heights at 6 cm, 8 cm and 12 cm. They stated that increasing the collector inlet height decreases the flowing air temperature, airflow rate and power output. Ayadi et al. [95] analyzed the effect of collector slopes of 1, −1 and −1.5 degrees on the system with the CFD model with a collector of 2.75-m diameter and 0.05-m height and a chimney of 0.16-m diameter and 2.75-m height. They stressed that the divergent collector negatively affects the system at 800 W/m² constant radiation compared to the non-inclined collector. They emphasized that while the maximum air velocity was 2.13 m/s in the horizontal collector, it decreased to 1.89 m/s in a 1-degree divergent collector. However, they claimed that the convergent collector increased the maximum air velocity compared to the non-inclined collector with 2.31 m/s at −1 degree and 2.36 m/s at −1.5 degrees. They showed that a similar situation is valid for temperature and pressure distributions. Al-Kayiem and Al-Nakeeb [96] evaluated the impact of the collector slope on the collector efficiency for four different seasons using the finite difference technique. They claimed that the −1 degree convergent-type collector’s collector efficiency was 124% higher in winter and 57.4% higher in summer than the horizontal collector. Gitan et al. [97] studied the impact of the collector slope on the performance of a possible SCPP system in Malaysian climatic conditions based on the Manzanares pilot facility’s geometric measurements. They claimed the highest power output was obtained using a 10-degree collector, which is 3.5 kW more than that of the horizontal collector. They showed that the collector efficiency was 51% of the maximum, and the system’s efficiency was 0.165% of the maximum. Cottam et al. [93] analyzed the impact of the collector profile on the SCPP system’s performance (Figure 20). They designed a large-scale solar chimney with a 2150-m radius collector, 1000-m high, and a 55-m radius chimney with 4-m collector entrance height. In the calculations made with the steady-state analytical model, they claimed in Figure 20 that the exponential and sloped collector gave a higher power output compared to the non-inclined collector. Still, it was an optimum point in both cases; after this point, the increase in the collector output height decreased the power output.

Choi et al. [34] estimated the effect of the collector outlet height on a large-scale SCPP system’s performance. They stated that the system’s power output would be 27.81 MW for the non-inclined collector at a 5-m collector input height. They claimed that by making the collector output 25 m (collector slope = 0.380), the system’s power output would approximately triple, reaching 109.73 MW. Semai et al. [98], based on the Manzanares pilot plant’s geometric dimensions, conducted a numerical study to analyze the impact of the collector structure and the use of an additional energy storage layer ground on the performance of the SCPP system. The model Adrar, which was verified with the pilot plant’s experimental data, was predicted for the possible system to be established in the region by using the climatic conditions of Algeria. By making the collector inlet and outlet heights 2 m and 4 m, the convergent- and divergent-type collectors’ effects on the system were compared. Data for a 24-h power output are given in Figure 21 [98], comparing the performance of the SCPP1 tilt collector, the SCPP2 divergent collector, and the SCPP3 convergent collector. They claimed that the highest power output would be achieved in the convergent-type collector; compared to the non-slope condition, the maximum power output would be approximately 5% higher. They stated that a similar situation would be valid for the system’s efficiency as well. The convergent-type collector’s highest efficiency value is 0.45% at 17:00 during the day, and this value is approximately 18% more than the non-inclined collector. Gholamalizadeh and Kim [99] studied the effect of the collector slope on SCPP systems by maintaining the collector inlet at a constant height of 1.85 m and changing the collector outlet height CFD model developed using the measurements of the Manzanares pilot plant. For a horizontal collector with a constant 300 K ambient temperature, 850 W/m² radiation intensity and a 1.85-m collector outlet height, the mass flow rate will be 727.31 kg/s, the collector efficiency will be 32.1%, and the power output will be 50.94 kW. They claimed that if the system’s collector outlet height was set to 3 m, the mass flow would increase to 759.63 kg/s, the collector efficiency would increase by 34.8%, and the power output would increase to 55.05 kW. They showed that increasing the collector outlet height from 3 m to 5 m would not affect the system. Karimi-Pour-Fard and Beheshti [89] stated that by making the Manzanares pilot plant’s collector slope 2 degrees, the system’s power output would increase by 55%, from 44 kW to 70 kW. Hassan et al. [100] conducted a CFD study of the Manzanares pilot plant’s measurements in order to examine the effect of the collector slope on the SCPP system. They claimed that assuming an ambient temperature of 303 K for 1 June at 13:00, increasing the collector slope would increase the airflow rate and the system’s mass flow.

Ahirwar and Sharma [101] developed a CFD model with the Manzanares pilot plant’s geometric dimensions. The CFD model claimed the highest power output at a height of 190 m by applying a heat flux of 500 W/m² to the ground in the ground, and by changing the chimney height by 180–205 m. They investigated the effect of changing the collector slope in the range of 2–10 degrees, on the airflow rate and power output at the system’s chimney inlet. They claimed that if the system’s collector slope, which a had a 37.084 kW power output and a 9.31 m/s chimney input speed, was set to 40, the chimney input speed would increase by 13.69% to 10.38 m/s, and the power output would increase by 34.72% to 49.96 kW. They claimed that increasing the slope would adversely affect the system, reducing the power output and chimney entry speed. Gholamalizadeh and Kim [102], in a geometric optimization study on previously established SCPP systems with mathematical modeling, claimed that using inclined collectors would give 15.85% more power output in the Kerman prototype and 27.73% more power in the Manzanares prototype. For the SCPP system with a height of 1000 m, the comparison of the power outputs of two systems with different chimney diameters and different collector radii according to the change of the collector output heights for 4-m and 5-m collector input heights is given in Figure 22. There are various studies with different findings in the literature for the collector slope. In general, it is seen that there are different evaluations for the maximum performance according to the system geometry.

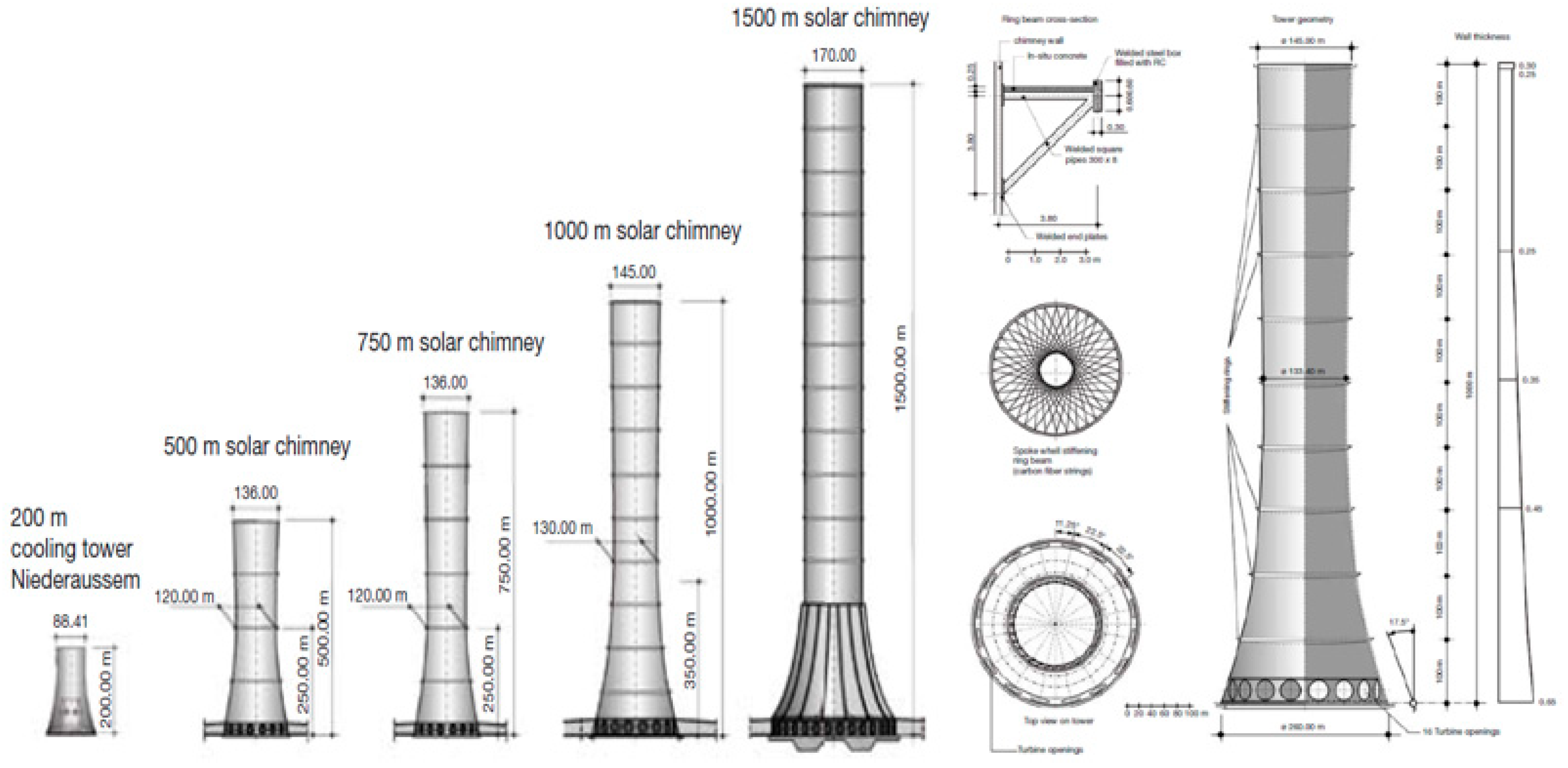
5.4. Chimney Height

Zhou et al. [50] investigated the effect of the chimney height change of a small-scale SCPP system with a 0.7-m diameter chimney and a 5-m collector radius on the power output at a constant 850 W/m² radiation intensity using a mathematical model developed based on the experimental results. They stated that the power is 2.26 W at a 4-m chimney height, and if the chimney height is set to 8 m, the power output will increase by 118% to 4.94 W. Kasaeian et al. [62] reported, in their experimental study, that the airflow velocity of 1.3 m/s at a 2-m chimney height was 4% more than the 1.354 m/s at a 3-m chimney height. Papageorgiou (2016) stated that the 15-m high and 2.5-m diameter SCPP system he built reached a maximum airspeed of 5 m/s with a collector area of 1020 m². He also indicated that the maximum airspeed becomes 6 m/s when the chimney’s height is increased to 24 m. Bernardes et al. [27] developed an analytical and numerical comprehensive model that described solar chimneys’ performances. They stated that when the system’s chimney has a 3.5-m entrance height and a 4100-m diameter collector, a 1000-m height and 120-m diameter chimney is increased by 50%, and the daily power output would be 0.929 GWh. They also claimed that by increasing the chimney height by 100%, the daily power output would become 2016 GWh. Nizetic et al. [42] developed a simplified model for the calculation of the power output that SCPP systems can generate in the Mediterranean region. They showed that the system’s chimney efficiency with a 200-m chimney with a collector diameter of 1250 m at 288 K ambient temperature is 0.698%, while the chimney efficiency will be 3.411% if the chimney height is set to 1000 m. Zhou et al. [36] developed a theoretical model and analyzed the effect of the change in the Manzanares prototype’s height on the system. In experimental measurements, they claimed that at 1040 W/m² constant radiation, which is the highest radiation intensity, increasing the chimney height will increase the system’s power output up to 615 m and then reduce the power output. They emphasized that the maximum power output will be 102 kW at 615 m. Larbi et al. [77] evaluated the effect of chimney height and collector diameter changes on the system, and designed a model with a 10-m diameter chimney and a 2.5-m collector height. They showed that the system would give 342 kW of power with a constant 800 W/m² radiation intensity, 600-m collector diameter, 250-m chimney height, and 300 K ambient temperature. They claimed that with a chimney height of 483 m, the power output would increase by 116.95% to 742 kW under the same conditions. They showed the increase in power output for different chimney heights and different collector diameters (Figure 23a) [77]. Sangi [103] evaluated the SCPP system’s performance that was likely to be established in different cities in Iran using a simple numerical model depending on environmental and geometric variables. Figure 23b [103] shows that the power output will increase directly with the chimney height and the collector diameter, and that the high power outputs will occur with both parameters on a large scale. Koonsrisuk et al. [7] only changed the chimney height and examined its effect on the system by maintaining the Manzanares prototype constant’s geometric parameters. They claimed that increasing the chimney’s height increases the system’s power output, and if the height is set to 296 m, the power output would be 180 kW. Al Alawin et al. [104] simulated the effect of the chimney height on an SCPP system for Jordan’s geographic conditions. They stated that increasing the chimney height increases the volume flow, pressure difference, efficiency and airflow rate of a system with a 40-m collector diameter and a 3.5-m chimney diameter. They claimed that the power output would increase similarly, but that a maximum power output of 85 kW was obtained at the height of 210 m, after which an increase in chimney height would reduce the power output of the system. Li et al. [79] claimed that the Manzanares prototype’s power output was 53.5 kW at 1000 W/m² constant radiation, and if the chimney height was set to 400 m, the power output would be 123.6 kW, increasing by 131%. Similarly, they showed that the higher the height, the higher the power output, exponentially. Hamdan [80] stated that a system with a 100-m diameter chimney and a 2000-m collector diameter would give 5.81 MW power output with a 400-m high chimney at a constant radiation intensity of 263 W/m² and an ambient temperature of 303 K. They claimed that if the chimney height of the system was set to 800 m, the power output would increase by 179.8% to 16.26 MW. Similarly, Figure 24a [80] shows that the chimney’s height directly increases the power output in a constant radiation intensity. The 35 MW, constant power output shows the relationship between the collector radius and the chimney height in different radiation intensities in Figure 24b [80].

Ngala et al. [83] stated that a SCPP system with a 700-m diameter collector and a 10 m fixed chimney diameter would deliver 1.5 × 10⁹ W power output with a 300-m chimney at 350 °C ambient temperature and a constant 800 W/m² radiation intensity. With a chimney height of 600 m, the power output would be approximately 100% more than 3.02 × 10⁹ W.

Nouar et al. [85] estimated the Manzanares pilot plant’s performance in Chlef, Algeria, using a theoretical model. They claimed that the facility, if it were to be established in the region, would give 49.34 kW power output with a 100-m chimney at noon in June, while the power output would double this at 200 m, i.e., 99 kW. They emphasized that the power output will increase with the chimney’s height. Ikhlef and Larbi [86] argued that an SCPP system likely to be installed in the size of the Manzanares pilot facility in the Algeria region would increase its performance by increasing the chimney height. They stated that it will give a power output of 52.5 kW at a height of 200 m, and a power output of 111.66 kW at a height of 300 m. Dhahri et al. [94] analyzed the mass flow rate for different chimney heights of the Manzanares pilot plant at an ambient temperature of 293 K and a radiation intensity of 800 W/m² under constant climatic conditions. They emphasized that the mass flow, which is 1075.56 kg/s at a height of 200 m, would increase by 13.4% at 300 m and 1220 kg/s. Karimi-Pour-Fard and Beheshti [89] claimed that an increase in the Manzanares’s chimney height for Iranian climatic conditions would increase the system’s power output and efficiency up to 685 m; increasing the height would reduce the performance of the system. They explained that the system, which has a power output of 40.35 kW and an efficiency of 0.66% with a 200-m chimney, would achieve 60.85 kW power output and 0.98% efficiency at a height of 400 m. Shahi et al. [105] developed a CFD model based on Manzanares’ geometry. They stated that it would give a power output of 48.04 kW at 1000 W/m² irradiance and 291.65 K ambient temperature. They emphasized that increasing the system’s chimney height would increase the mass flow, turbine pressure drop, turbine input speed, and power output. They claimed that at a 400-m chimney height, the power output would increase by 138% to 114,352 kW, while the mass flow would increase by 30% to 1,038,593 kg/s. Toghraie et al. [91] developed a CFD model with a 100-m collector radius and an 8-m chimney diameter. They emphasized that increasing the chimney height at a constant 800 W/m² radiation intensity and 308 K ambient temperature of the SCPP system would increase the power output, efficiency, pressure difference and mass flow. They claimed that the power output of 24 kW at a 25-m chimney height would be 313.5 kW at a 500-m chimney height. Cuce et al. [106] analyzed the effect of the chimney height on the system’s output by studying the Manzanares pilot plant. They showed that an increase in the chimney height increases the power output, efficiency, mass flow rate and pressure difference, and reduces the collector’s temperature increase. The change in the range of 100–500 m of the chimney height with 1000 W/m² radiation intensity and 293.15 K ambient temperature on the system is given in

Table 8. SCPP system of the chimney height for Manzanares, Spain [106].

Chimney Height (m)	Mass Flow Rate (kg/s)	Temperature Rise in Collector (K)	Power Output (kW)	Pressure Difference Around the Turbine (Pa)	Efficiency (%)
100	886.756	19.207	27.792	67.222	0.153
200	1133.16	16.252	54.872	110.375	0.3
300	1279.4	14.625	81.952	147.239	0.438
400	1414.128	13.729	109.032	176.056	0.566
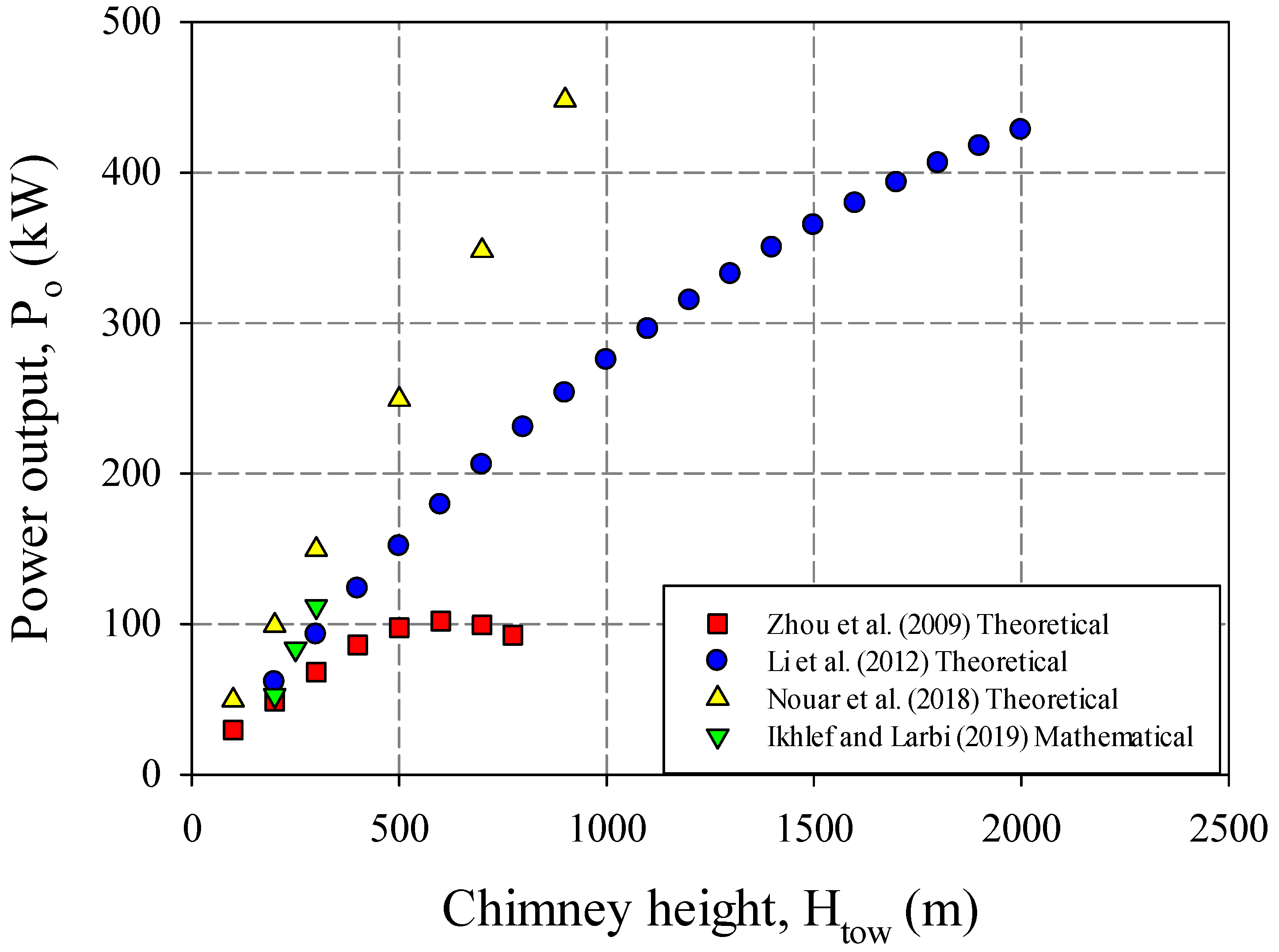
500	1496.348	13.235	136.112	202.818	0.674

. Based on the Manzanares prototype, the effect of the researchers’ chimney height on the system’s power output is shown in Figure 25 with theoretical and mathematical studies. Similarly, a comparison of the CFD studies is given in Figure 26. The study results of different researchers regarding the effect of the chimney height on the system’s mass flow and efficiency are presented in Figure 27.

Khelifi et al. [84] stated, in a numerical model, that the power output would be 1852.57 kW with a constant 1000 W/m² radiation intensity and a 200-m chimney at 298 K ambient temperature. They claimed that if the chimney were 400 m, the power output would be doubled to 3696.44 kW. Their results showed that the chimney’s height increases the power output linearly. Choi et al. [34] argued in an analytical study that the power output of a large-scale SCPP system with a 100 m radius chimney and a 3000 m radius collector at a constant 1000 W/m² radiation intensity and 20 °C ambient temperature would increase with the chimney height. They stated that with a height of 500 m, the power output would be 42.25, and with a doubled height (1000 m), the power output would increase by 160% to 110 MW.

Similarly, researchers show that the increase in the chimney height increases the system’s performance with systems with different geometries [107,108].

5.5. Chimney Diameter

The researchers also emphasized that this change in the flue radius would increase the chimney cost from €100 M to €150 M at the same power output, while reducing the collector cost from €1700 M to €975 M, thus reducing the total cost. Choi et al. [34] designed a solar chimney with a 1000-m chimney height, a 3000-m collector radius and a 100-m chimney diameter, with a maximum power output of 85 MW in an analytical model. They stated that increasing the chimney diameter exponentially increases the system’s power output to a certain level, decreasing the effect. They claimed that setting a chimney diameter of 200 m would increase the power output by 100% and provide about 170 MW. Ikhlef and Larbi [86] examined the effect of chimney diameter change on the system’s performance with a mathematical model based on the Manzanares prototype. They argued that changing a chimney diameter of 10 m to 30 m would increase the power output from 51.86 kW to 82.8 kW, i.e., by 60%. Karimi-Pour-Fard and Beheshti [89] studied the impact of the chimney diameter on the Manzanares pilot plant’s possible performance in Isfahan, Iran, using the Ansys Fluent engineering software. They claimed that the maximum power output could be acheived at a chimney radius of 6.17 m and 45.48 kW, which was 3.7% more than the reference power value as shown in Figure 28. Similarly, they argued that the system’s efficiency would increase by 4.5% to 0.69%.

Hamdan [35] examined the chimney’s diameter’s impact on solar chimneys’ power output with numerical analysis, and argued that increasing the chimney diameter would not affect the system’s power output and efficiency after a certain point. The research stated that the system, which gives a 10.1 MW power output with a 20-m chimney diameter, would provide 13 MW power output by increasing by 28.7% when the chimney diameter was set to 60 m. Toghraie et al. [91] showed the impact of the chimney diameter of the model they designed with the finite element method on the system’s power output and efficiency. They stated that the maximum power output and efficiency peaked at a certain point, and increasing the chimney diameter after this point had a negative effect on the system, and a similar effect was also seen on the system’s mass flow and pressure as shown in Figure 29.

Gholamalizadeh and Mansouri [81] claimed that by increasing the chimney diameter from 3 m to 5 m with the CFD model of the Iran solar chimney, Kerman, the mass flow rate of the system could increase up to 150%.

5.6. Convergent and Divergent Chimney Design

The design parameters affect the performance of solar chimney power plants as much as the geometric parameters. This situation was understood from the slope of the collector. Similarly, the chimney design affects the performance of the system. The chimney diameter not being fixed causes effects on the system’s performance, as this affects the airflow. This is clear in different studies as shown in Figure 30, Figure 31, Figure 32, Figure 33, Figure 34, Figure 35, Figure 36, Figure 37 and Figure 38.

Motoyama et al. [11] conducted an experimental design in a laboratory environment. They claimed that the divergent flue air velocity would be 50% higher than the cylindrical chimney design under the same conditions, and the rotation speed would likewise be 44.4% higher. Ohya et al. [70] experimentally showed that the divergent chimney structure’s power output was 4–5 times more than that in the cylinder chimney structure under the same conditions. When they compared the chimney angle outputs for 2, 4 and 6 degrees, they emphasized that the highest power output and airflow velocity were in the 4-degree chimney design.

Nasroui et al. [68] compared the outputs of the exponential divergent chimney models with the cylindrical chimney model using the computational fluid dynamics method with the developed model based on a small-scale solar chimney model. When the temperature, pressure and velocity distributions of the divergent chimney design were examined compared to the cylindrical model, they showed that the divergent design provided a better performance output.

Al-Kayiem and Al-Nakeeb [96] examined the effect of divergent and convergent chimney design on the system according to a cylindrical chimney design using the Finite Difference Technique. They compared the hydrothermal efficiencies for all four seasons, and they claimed that the convergent chimney’s hydrothermal efficiency was two times that of the other designs.

Hu et al. [109] developed a CFD model and analyzed the effect of the change in the chimney exit area ratio to the chimney entrance area on solar chimneys’ performance. They explored the system’s effect on the airflow rate, temperature increase, diving potential, and power output by changing the chimney exit area between 1 and 32 times, taking the Manzanares pilot facility’s geometric dimensions as a reference, with the chimney entrance being constant. They claimed that an ideal value for the chimney exit area’s ratio (AR) to the chimney entrance area for the pilot plant was about 10. They claimed that the performance of the system at this value was the maximum. Similarly, for 100-m, 200-m and 300-m chimney heights, they provided a normalized result comparing the AR and the divergent flue angle. They emphasized that increasing the AR after this point, where it is the current peak in every situation, would have a negative effect on the system.

Hassan et al. [100] investigated the effect of the divergent flue angle on the system by measuring the Manzanares pilot plant numerically. They claimed that if the system’s divergent flue angle, which gives 34 kW power output with a cylindrical flue in the reference case, is set to 1 degree, the power output would increase by approximately 100%. They argued that if the chimney angle was set to 2 degrees, the power output would be 65 kW; if it was set to 3 degrees, it would be 59 kW, which is the peak point for 1-degree power output. Ahirwar and Sharma [101] claimed that the maximum power output with an inclined collector would be in a 190-m chimney based on the Manzanares pilot plant’s dimensions. They stated that increasing the chimney inclination angle at a 190-m chimney height would increase the system’s power. They emphasized that if the power output’s divergent chimney angle, which is 37.08 kW in the non-inclined condition, is set to 6 degrees, the power output would increase by 95% to 72.33 kW. Pattanashetti and Madhukeshwara [110] analyzed a solar chimney with a radius of 100 m and a chimney height of 100 m using a 1-degree isometric CFD model. They fixed the chimney inlet diameter at 4 m and made performance comparisons for different area ratios by proportioning the chimney exit area to the chimney entrance area for values varying between 2.83- and 16-m chimney outlet diameters. They showed that for an area ratio (AR) of 9, the system gave the maximum performance, and higher AR values had a negative effect on the system. They claimed that up to 100 times more kinetic energy could be obtained with different designs at 800 W/m² radiation intensity. Ghorbani et al. [111] designed a hybrid dry cooling tower with a height of 200 m and a collector radius of 100 m in a solar chimney format. They claimed that the system with a diverging flue angle of 1.5 degrees in the chimney design would increase the air velocity on the radiators from 5.65 m/s to 6 m/s, which is an increase of 6.2% compared to the non-inclined chimney.

Das and Candramohan [112] designed small-scale solar chimney models with heights of 7 m and 3.5 m using a 3D computational model. They evaluated the performance of the CFD model in different chimney structures. They showed that the maximum power output and airflow velocity would be achieved with a 2-degree divergent chimney design. In this respect, the design with large angles would negatively affect the system’s performance. In CFD studies based on the Manzanares pilot plant’s geometric dimensions, Xu and Zhou [113] analyzed the effect of a divergent flue angle on the system by increasing the chimney outlet diameter to keeping the chimney inlet diameter constant. They determined the power output and airflow rate by matching the chimney exit area ratio to the chimney entrance area (COAR) with the divergent flue angle. They conducted a CFD study involving the total pressure potential (TPP), which consists in the working method, buoyancy and static pressure recovery using the effective pressure potential recovery coefficient (EPPRC). They claim that the maximum performance data would be obtained when the COAR is 8.7. They emphasized that when the area ratio is 8.7, the power output would increase 10.9 times to 231.7 kW compared to the reference situation. They stated that COAR values greater than 8.7 cause a reverse flow in the chimney, which would reduce the power output and airflow velocity, which adversely affects the system. Koonsrisuk and Chitsomboon [114] designed a solar chimney model with a 100-m high chimney, a 100-m radius and a collector 2 m above the ground, using computational fluids. They fixed the chimney inlet diameter to 4 m, and they performed simulations in different situations by proportioning the chimney exit area to the chimney entrance area (AR) for values ranging from 2.83 m to 16 m for the chimney exit radius. When they compared the results obtained from the 5-degree axial symmetric CFD model, they claimed that when the AR value was 16, the system’s power output would increase to 94.29 times that given in the reference situation efficiency system, which would reach 25%.

Figure 37. EPPRCs of different cases and the distribution of the axial velocity along the specified diameter of the chimney cross-section at a height of 190 m for different COARs [113]. (Adapted with permission from ref. [113]. Copyright 2018 Elsevier.)

Figure 37. EPPRCs of different cases and the distribution of the axial velocity along the specified diameter of the chimney cross-section at a height of 190 m for different COARs [113]. (Adapted with permission from ref. [113]. Copyright 2018 Elsevier.)

Figure 38. Streamlines of a divergent chimney for different COARs of (a) 8.7, (b) 11.9, (c) 15.5 and (d) 24.2, and (e) velocity vectors of the chimney outlet (COAR = 24.2) [113]. (Adapted with permission from ref. [113]. Copyright 2018 Elsevier.)

Figure 38. Streamlines of a divergent chimney for different COARs of (a) 8.7, (b) 11.9, (c) 15.5 and (d) 24.2, and (e) velocity vectors of the chimney outlet (COAR = 24.2) [113]. (Adapted with permission from ref. [113]. Copyright 2018 Elsevier.)

6. Energy Storage Systems

SCPP systems are systems that are made open to the environment by their structure. Taking advantage of this feature, the researchers argued that the system’s ground could be used for performance enhancement and energy storage. The features claim that performance can be achieved by transferring the energy to be stored on the ground during daylight hours to the system when the sun is not present. Guo et al. [115] developed a theoretical model for the thermodynamic behavior and power estimation of a heat storage SCPP system (Figure 39). They dealt with the convection effects in the system and the heat conduction in the ground as if they were one-dimensional. They claimed that a floor thickness of 4 m was sufficient, assuming that the physical properties of the heat storage layer remained constant. Their study based on the Manzanares pilot plant showed that the daily electricity production, which was 229.1 kWh in the reference case, would increase by 31.26% to 333.3 kWh with the heat storage system. They worked with the three different soil materials shown in

Table 9. Thermal properties of the selected soil materials [115].

Type	Density ρ (kg⋅m−3)	Specific Heat Capacity Cp (J⋅kg−1⋅K−1)	Thermal Conductivity λ (W⋅m−1⋅K−1)	Thermal Inertia (W⋅s0.5 m−2⋅K−1)
A	1587.32	1464.80	1.24	1697.98
B	1442	837	0.35	649.95
C	1440	1700	2.6	2522.86

. They emphasized that the temperature did not change much with the power from 1 m below the ground. They also stated that there would be less fluctuation in the power output during the day with a soil heat storage material with a high specific heat capacity and thermal conductivity. They mentioned that this would benefit the turbine operation and the network system.

Choi et al. [34] developed an analytical model to evaluate the impact of water storage system implementation on the performance of SCPP systems. The model validated by the Manzanares pilot plant was then used to estimate the possible power output of a large-scale SCPP system with a chimney height of 1000 m and a collector radius of 3000 m. The analysis using the iterative MATLAB code showed that the pilot plant has a power output of 35 kW in the middle of the day when there is no water storage system, but it drops below 25 kW when the water storage system is used. However, when we look at the 24-h total production, it is seen that the use of the water storage system allows for power output even in the absence of the sun, and that it increases the total electricity production. As the thickness of the water storage system increases, the fluctuation in the electricity generation during the day decreases as shown in Figure 40. A similar situation exists in the large-scale system. A maximum power output exceeding 80 MW without a storage system drops below 60 MW when using the storage system. It was stated that the water storage system is advantageous in terms of the total production throughout the day.

Fadaei et al. [116] experimentally studied the effect of latent heat storage in the solar chimney on the system as shown in Figure 41. They compared the data of two separate systems, with and without phase-change material (PCM). They claimed that the absorbent surface temperature at midday is 69 °C in the PCM-free system, and that it is 72 °C in the PCM-containing system. They also showed that the solar chimney containing PCM has a higher air flow rate in the system. They emphasized that the use of PCM increases the mass flow rate of the system by 8.33%. They argued that the use of PCM in SCPP systems would have a performance-enhancing effect on the system.

Yaswanthkumar and Chandramohan [117] evaluated the effect of the thermal energy storage (TES) unit on the performance of the SCPP system using a 3D CFD model as shown in Figure 42. They interpreted flow parameters such as velocity, pressure, density and temperature on a small-scale system with a 3.5-m collector radius and a 6-m chimney height. They claimed that because the design with thermal energy storage (TES) would store some of the energy entering the system, the air pressure, temperature and velocity in the system would be lower than those in the design without it.

Pretorius and Kröger [24] designed and numerically analyzed a large-scale SCPP system with a collector diameter of 7000 m and a chimney height of 1500. In the study, where different design effects were interpreted, a granite floor was included in the reference case. When the effect of different floor materials on the system was evaluated, the system’s outputs were almost similar to granite floors when limestone and sandstone were used as floor materials. The average physical properties of three different materials are given in

Table 10. Different ground types’ average properties [24].

Ground Type	Density [kg/m3]	Specific Heat Capacity [J/kg K]	Thermal Conductivity [W/m K]	Heat Penetration Coefficient bp [W s1/2/K m2]
Limestone	2500	900	1.26	1684
Sandstone	2160	710	1.83	1675
Granite	2640	820	1.73	1935

. The 24-h power output of the system is given in Figure 43 for July and December.

Attig-Bahar et al. [118] evaluated the effect of the use of heat storage systems in the ground on the performance of the SCPP system using a 3D CFD model as shown in Figure 44. In their study based on the measurements of the Manzanares pilot plant, they estimated the possible power output of a possible power plant to be built in Tozeur, in the south of Tunisia, and interpreted the effect of using 5-m thick soil, gravel and sand as energy storage materials on the system’s performance. The average physical properties of three different materials are given in

Table 11. Thermal properties of the heat storage media [118].

Properties	Soil	Gravel	Sand
Average density (kg/m3)	1700	2555	1700
Average heat capacity (kJ/kg K)	2.016	0.814	1.3
Thermal conductivity (W/m k)	0.78	2.00	1.00

. They claim that the annual total power output of 150 MWh in the SCPP system where the energy storage system is not used would increase by 35% when the storage system is used. They stated that the maximum electricity production would be achieved when soil is used as the energy storage material.

Karimi-Pour-Fard and Beheshti [119] created a 3D CFD model that referenced the dimensions of the Manzanares pilot plant. With this model, they interpreted the energy storage unit’s effect on the SCPP system’s performance. First, they used 1-m thick rock as the energy storage material. They then used water of different thicknesses as an energy storage system. The visuals of the energy storage unit are given in Figure 45. Details of five different cases are given in

Table 12. Different types of thermal energy storage case studies [119].

Case Study No.	Thermal Energy Storage
1	1 m depth stone
2	10 cm depth water container (3112 m3 totally)
3	15 cm depth water container (4668 m3 totally)
4	20 cm depth water container (6224 m3 totally)
5	15 cm depth water container and1 m depth stone

. They claim that the system without an energy storage unit in the reference state would give a maximum power output of 50 kW in the middle of the day, or a power output of 40 kW with 1 m of energy storage unit (stone). However, the energy storage unit shows that the power output would not fall below 10 kW during the hours when there is no sun. They emphasized that storing energy in water would provide a greater power output for the system. They showed that the best-case scenario would be obtained from the combination of water and stone environments, with the optimum water thickness being 15 cm. They stated that 10% more power output would be obtained at night in the optimum situation. The 24-h power output for six different situations is given in Figure 46.

Senbeto [120] evaluated the effect of energy storage unit usage on SCPP performance by taking the Manzanares pilot plant as a reference in a 2D CFD model as shown in Figure 47. They claimed that with the use of the energy storage system, power output could be obtained from the system in the evening hours. They showed that the use of water tubes for energy storage on the ground would give an average of 10–15 kW of power output during the hours when the sun is not shining on the pilot plant. They emphasized that when gravel is used on the ground, a higher surface temperature could be achieved than when soil is used.

Based on the Manzanares pilot plant, Semai and Bouhdjar [121] estimated the performance of a possible SCPP plant in Adrar, in the southwestern region of Algeria. In addition to the pilot plant, they evaluated the effect of a floating chimney and an additional energy storage unit on the system, and analyzed the optimum power output. They repeated the CFD models they verified with experimental data in order to establish the facility in Adrar. For this, they used the temperature and solar radiation values of Adrar for July. They used 0.1-m thick water covered with permeable plastic as the energy storage unit. Systems with different chimney inclination angles and without water storage are given in

Table 13. Physical model for configurations with and without water storage [121].

Case Name without Water Storage	Inclined Chimney Angle	Case Name with Water Storage	Inclined Chimney Angle
SCPP1	Vertical	SCPP2	Vertical
SCPP1-a	15°	SCPP2-a	15°
SCPP1-b	22°	SCPP2-b	22°
SCPP1-c	30°	SCPP2-c	30°

. The maximum power output at midday is approximately 180 kW in the design that does not use water as an energy storage unit, but it is 160 kW in the system that uses water. However, it can be seen that the power output does not fall below 30 kW in the model where water is used as the energy storage unit during the hours when there is no sun. They claimed that the use of water as an energy storage unit increases the total daily power output. The 24-h power output graphs for eight different designs are given in Figure 48. They also emphasize that this is the optimum angle for the chimney inclination, and that the power output is reduced at high angles.

A comparative view of SCPPs in terms of energy storage studies is given in

Table 14. Other studies of energy storage.

Content of the Study	Working Method and Geometry	Energy Storage Materials and Study	Results	Reference
The effect of the energy storage unit on the flow and heat transfer characteristics of solar chimney plants	CFD—Manzanares pilot plant	Soil and gravel	The heat storage ratio of the energy storage layer is changed with solar radiation and storage material. Gravel’s storage ratio is more than soil.	[122]
Effect of thermal energy storage layer porosity on SCPP performance	CFD—Manzanares pilot plant	Soil—soil porosity	The increase in soil porosity reduces the power output and efficiency of the system. For the pilot plant, reducing the soil pore efficiency from 0.4 to 0.1 increases the power output by 3.04%.	[123]
The thermal effects of soil as a natural storage unit and the effect of soil compaction rate on the system	CFD—Manzanares pilot plant	Soil—soil compaction	Energy storage unit is an effective method for the continuity of energy. Power output can be improved by 10% by increasing the degree of soil compaction.	[124]
With the CFD method, the effect of solid materials and PCMs as energy storage units on SC performance is evaluated over a 12-month period.	CFD—Manzanares pilot plant	Autoclaved aerated concrete (AAC)—Brick—Concrete—Limestone—Sand—Sandy clay—Sandstone—Different PCM materials	The use of solid materials as energy storage material provides better performance for SC than the use of PCM. It is seen that the use of sandstone as an energy storage material provides higher power output and efficiency than other materials.	[125]
Investigate the effect of using an energy storage system on the performance of the SCPP system with an experimental prototype.	Experimental—Small scale	Water and paraffin	They emphasized that the highest production will be achieved with paraffin, that the maximum air flow rate in the system is lower when paraffin is used, and this will extend the turbine life.	[126]

.

7. Hybrid Systems

When the studies on SCPP systems were examined in recent years, it was seen that combined systems were used to increase the performance of the system. These structures, called “HYBRID” systems, aim to increase the performance of SCPP systems, which have low efficiency compared to other solar energy systems. When the hybrid systems in the literature are examined, it can be seen that they can generally be grouped under the following headings:

• Integrated PV systems,
• Seawater desalination,
• Integrated geothermal systems,
• Integrated flue-gas flow,
• Gas turbine add-on systems,
• Integrated heat exchanger, and
• Hot gas injection.

Singh et al. [127] designed a small-scale SCPP system with a collector diameter of 300 cm and a chimney height of 300 cm. In the CFD study, the system’s floor was covered with a PV module, and performance analysis was performed for different geometries (Figure 49 and Figure 50). They claimed that the PV panel efficiency increased by 7% with the current system. It was also predicted that 80% of the collector area would decrease by 10–12. It appeared to be an effective zone for cooling PV modules.

Akbarzadeh et al. [128] designed a system consisting of a chimney and a solar pool integrated with the aim of generating power. The visual of the system design is given in Figure 51. The thermal energy stored at the bottom of the solar pool is used to heat the air in the chimney. The flue in the right position uses a direct non-contact heat exchanger, while the flue unit in the left position uses a direct-contact heat exchanger. In the latter case, some make-up water is needed to recoup the water that has evaporated due to the contact between the air and the water. In the study on the dimensions of the Manzanares pilot plant, a larger collector area than the reference collector area was considered. They claimed that when the air temperature in the chimney rises from 20 °C to 50 °C, 60 kW would be the output, and when it rises to 60 °C, 90 kW would be the output. They emphasized that the system efficiency would also reach 0.4%.

Zuo et al. [129] introduced a solar chimney power system with integrated seawater desalination to generate electricity and fresh water. The SSCS and the integrated system involved a one-dimensional flow, and were evaluated with two mathematical models. Based on the reference facility dimensions, a storage layer of 40 m was included in the system. The visual of the system is given in Figure 52. It was claimed to be more efficient than other combined systems with less than 1% solar utilization. They stated that the efficiency of land use is high, and that raw salt would be obtained from the system along with the energy production and drinking water.

Kashiwa and Kashiwa [43] claimed that atmospheric water can be collected by placing an expansion cyclone separator in the SCPP system. They performed a numerical study to show this. The general view of the system and the location of the cyclone separator are given in Figure 53. Condensed water due to dew is collected using a water film that rotates with centrifugal movement due to intense turbulence. The detailed scheme of the system is given in Figure 54. They claimed that if a high separation efficiency could be achieved, the use of a water pool for solar energy storage would increase the fresh water production three times and the electricity production ten times.

Al-Kayiem et al. [130] evaluated the effect of adding an external heat source to the SCPP system with an experimental study. The scheme of the system and the experimental solar chimney are given in Figure 55. The system had a collector diameter of 6 m and a chimney height of 6.65 m. After the experimental data were obtained, they compared the CFD results with the study. According to the CFD results, they claimed that the inclusion of 116 °C flue gas in the system with a flow rate of 0.0015 kg/s increased the collector efficiency by 64%. They emphasized that 24/7 power output can be obtained with the system.

Mokrani et al. [131] analyzed the effect of using geothermal water as an external heat source on the SCPP system with an experimental study as shown in Figure 56. The effects of geothermal water passed through the spiral pipe placed on the ground on the temperature and velocity values in the system were monitored experimentally. They claimed that during the day, the air temperature in the system reaches 80 °C, and the air flow rate reaches 7.1 m/s, due to both the collector’s preservation of the solar radiation and the geothermal water. These values are 68.3 °C and 5.8 m/s when there is no geothermal water source. They emphasized that the system is very suitable for arid regions under geothermal/solar heating.

Kiwan and Salim [132] developed a hybrid system to increase the economy of SCPP systems with a mathematical model as depicted in Figure 57. The PV module was first integrated into the SCPP system in the traditional pilot plant dimensions. Then, cooling was aimed for by immersing the PV module in the water pool. A PV module was also integrated into the outer part of the collector. In this way, while the power output was taken from the chimney, as in the traditional system, a power output was also obtained from the PV system. While the water pool lowers the temperature of the PV module, the evaporating water condenses on the chimney wall, and fresh water is obtained. They claimed that the hybrid system gives 45.35% more power output than the standalone PV system in Jordan’s conditions. They emphasized that while the utilization factor of traditional SCPP systems is 0.51%, that of the hybrid system is 4.37%. They stated that the efficiency of the traditional system would increase by 757% with the hybrid system.

Other hybrid studies on SCPPs are comparatively presented in

Table 15. Other hybrid studies on SCPP systems.

Content of the Study	Hybrid System Details	Working Method and Geometry	Results	Reference
Integrates with SCPP system with CFD work. Evaluates the effect of different location and sizing of the PV module on the system.	Integrated PV moduler	CFD—small scale	Combination of PV panels with chimney reduces PV temperature by 5 °C. The best configuration for PV panels and solar chimney is to arrange 50 cm wide panels at the collector inlet.	[133]
In SCPP, they evaluate the outputs of the hybrid system they have created by integrating the PV modules into the collector with an experimental study. Compare results with stand-alone PV systems.	Integrated PV moduler	Experimental—Small scale	They show that the new design is 2% more efficient than stand-alone PV systems. Compared to conventional SCPP systems, the efficiency is 100 times higher in the hybrid system and is in the range of about 16–18%.	[134]
They discuss the effect of different PV module areas on PV/T system with mathematical study. They compare the PV modules placed on the ground at different area ratios.	Solar chimney PV/T power plant	Mathematical model—Large scale	They indicate that the PV field ratio is less than 0.055 for the optimum condition. They claim that the power output with the combined system is 4.42% higher than with conventional designs.	[135]
Experimentally, a hybrid system is created by integrating a PV module into the SCPP system. The system is mainly installed for air cleaning and CFD work is done with the data obtained. Forecast for a large-scale hybrid system.	Integrated PV moduler and air cleaning system	Experimental and CFD—Small scale	The new design increases the efficiency of the 250 MW system by over 0.5%. With the design, it is seen that the heat of the hot flue gas and the heat of the radiators are recovered and the formation of greenhouse gases is prevented. For a large-scale system, using PV modules 40 m above and below the collector reduces the volumetric flow, but increases the power output by 50 times.	[136]
It integrates a transparent PV module into the collector of the traditional SCPP system with a one-dimensional mathematical study. They also develop a hybrid system that aims to separate the salt water from the salt by placing a water basin on the ground. They make optimizations with the aim of increasing the system efficiency and using the land effectively.	Transparent PV module and water basin integrated SCPP system	Mathematical model—Manzanares	It is seen that the hybrid system with desalination integrated with transparent PV module is on average 30% more efficient than the integrated PV module or SCPP systems with desalination alone. With geometric optimization, it is stated that the efficiency of the hybrid system is 35–36% more efficient than other combined systems.	[137]
Based on the geometric dimensions of the Manzanares pilot plant, the desalination performance of the SCPP is interpreted by the CFD study.	Seawater desalination	CFD—Manzanares	More fresh water can be supplied by increasing the relative humidity of the air inside the chimney. This can reduce costs by reducing the height of the chimney.	[138]
A hybrid system is created by desalination with a small-scale SCPP system. With the CFD study, the effect of geometric parameters on the system is evaluated.	Hybrid system of solar chimney and water desalination	CFD—Small scale	Chimney design is very important for the performance of the hybrid system. With a collector of 30 m diameter and a chimney of 30 m height, a hybrid system will be able to produce fresh water while giving power output. A total power output of 8.8 kWh can be obtained while obtaining 598 kg of fresh water per day in a place with sufficient sun.	[139]
In a SCPP system, a desalination system is integrated under the collector. In conventional systems, the floor is completely covered with the desalination system, while the entire floor is not covered in the operation.	Desalination and power generation	Numerical study—Large scale	Partial coverage of the floor for desalination appears to be more beneficial. Separate analysis is required for each system.	[140]
A new concept combines a thermal steam power plant with a dry cooling tower and a chimney. Peripheral injection was adopted in the study with CFD. The hot flue gas is injected in the chimney.	A dry cooling tower system and a solar chimney are recombined.	CFD—Manzanares	The new design increases the efficiency of the 250 MW system by over 0.5%. With the design, it is seen that the heat of the hot flue gas and the heat of the radiators are recovered and the formation of greenhouse gases is prevented.	[111]
With the CFD method, an external heat source is used for uninterrupted power output by placing flue gas channels on the collector. A hybrid system with a collector diameter of 6 m and a chimney height of 6.65 m is created. 0.0015 kg/s flow rate and 116 °C flue gases are integrated into the system and its performance is compared with the traditional SCPP system.	External Thermal Source Hybrid Solar Chimney System (flue gas)	CFD—Small scale	Compared to the traditional SCPP model, it is seen that the mass flow and efficiency in the hybrid system will be 7.63% and 11.48% higher, respectively. It is also emphasized that 24/7 power output can be obtained.	[141]
With the heat exchanger placed in the chimney instead of the collector in the traditional design, the temperature of the system air is increased and its upward movement is aimed.	SCPP with chimney concept with heat exchanger	CFD—Small scale	More power output is obtained than the traditional system. With geometric optimization, it is seen that the efficiency is 95% at the ideal slenderness ratio.	[142]
Due to the low efficiency of the solar chimney at night, they designed a solid oxide fuel cell and solid oxide electrolysis cell integrated hybrid system to increase performance.	Hybrid SCPP design with solid oxide electrolysis and fuel cell	Numerical—Large scale	It is seen that the excess energy during the daytime can be stored as hydrogen and used to meet the energy demand at night. It is also emphasized that more power output can be obtained with the system in summer.	[143]
Waste heat is applied on the floor of the SCPP system with desalination concept, which includes wind supercharger at the chimney outlet.	Wind supercharging, waste heat and seawater distillation integrated into the SCPP system	CFD—Manzanares	A hybrid system with a wind supercharger is claimed to be 15% more efficient than a system without it. It is emphasized that with the system, 15 tons of fresh water can be produced per hour. With the hybrid system, the height of the chimney can be reduced by 21%.	[144,145]

.

8. SWOT Analysis of the SCPP

A general description of SWOT analysis is given in Figure 58. Although the idea of SCPPs goes back a long time, they are solar energy systems of which the implementation goes back to recent history. They are promising systems considering the increasing electricity consumption in the 21st century.

8.1. Strengths (Internal, Positive Factors)

• Uses abundant solar energy: SCPPs make use of a natural source of solar energy, which is abundant in tropical areas. It is particularly well-suited to the generation of electricity in desert basins and other areas with plenty of sunlight [146].
• Efficient energy storage and generation: The pressure difference provided by the high chimney in its structure allows power to be generated even when there is no sun [147,148,149]. The direct and diffuse solar radiation are useful for the energy conversion caused by the collector. The ground beneath the transparent collector acts as a natural means of storing radiant energy.
• Simple technology: The maintenance and repair costs are low due to its simple structure. Solar chimney power plants have a simple design with only three essential components: a collector, a turbine, and a chimney. This simple and strong structure ensures a smooth operation [150,151].
• Creates jobs and drives the economy: There are no high-tech manufacturing unit requirements, such that they can be developed in less industrially developed nations. The local resources, including labour, can be used to construct SCPPs without incurring significant foreign exchange. This provides green jobs while significantly lowering the capital cost of the project.
• Cheap materials: The building materials required for solar updraft towers are concrete, steel, glass, and other transparent materials, which are easily obtained in any region. In fact, in the desert, the stone and sand can be used to implement SCPP on-site.
• Less emissions: Because solar chimneys do not use any resources, they do not pollute the environment or emit carbon dioxide [152,153,154].
• No cooling requirements: SCPPS do not require a cooling mechanism, as other traditional power generation systems do. This is a potential advantage for several sun-belt regions where water supply is already a major issue.
• Long life: The main structural element of the building, the chimney, is long-lasting because it can be made from reinforced concrete.
• Fewer operational and maintenance issues: Except for security, there are no functional issues in comparison to other plants. Because the collector creates a temperature-controlled environment, the area beneath it can be used for greenhouse purposes.

8.2. Weaknesses (Internal, Negative Factors)

• Large area requirements: Large-scale systems necessitate a large installation area. The efficiency of an SCPP is primarily determined by the collector area size and the tower height. This means that huge plant dimensions are required in order to increase the collector area.
• The electricity generation costs are high: SCPPs do necessitate a significant initial investment, and the cost per unit of energy production is 0.62 US $/kWh (0.56 €/kWh) [155]. Economical generation can be achieved only by optimizing the structure, efficiency, and construction costs.
• Immature technology: The demonstration of the technology is on a smaller scale, and has a short track record. The lack of reliable experimental data is a major hindrance to commercial-scale deployment.
• Lack of adequate expertise and awareness: The installation of an SCPP necessitates a high level of engineering and technical knowledge. Another barrier is a lack of technological awareness.
• Weak regulatory and policy instruments: The initial growth phase was slow due to a lack of proper regulation and limited investment opportunities. As a result, early market penetration was low.
• Safety issues: Because the elements of SCPPs are large, risk situations may arise during natural disasters such as cyclones or earthquakes. The industrial viability and investor acceptance are dependent on a highly accurate design and low uncertainties [156].
• Lower efficiency: SCPPS are inefficient to install in areas with less sunlight. The main limitation is the low efficiency compared to other systems. The combined collector, the tower, and the turbine efficiency play significant roles in the system’s performance.

8.3. Opportunities (External, Positive Factors)

• Intensifying inventions in solar chimney technology: The growing number of patents and publications provides opportunities for innovation in SCPPs [157].
• Immense potential and growing awareness: In hot and humid climates, technology has enormous potential. There has been an increasing awareness of solar chimney technology, which is evident from the publications.
• Joint ventures and collaboration: The growing partnership between industry and academia at the global, national, and local levels may spur growth in SCPP.
• The diversification of renewable energy: Concerns about climate change, carbon neutrality, and energy transitions are driving researchers to investigate various renewable energy options. The subsequent growth of a newer energy source provides a positive boost to many nations’ economic and environmental benefits across the world.
• Distributed generation: The technology has the potential to significantly improve the energy mix for small communities, and to alleviate environmental concerns.
• Scaling up: For large plants, the thermodynamic calculations for the collector, tower, and turbine are also very reliable. The size can be optimized based on the most cost-effective key dimensions and components.
• Emergence of new markets: Renewable energy investments in developing countries like India, China, Turkey, Australia, Brazil, Mexico, South Africa and Iran have increased.

8.4. Threats (External, Negative Factors)

• Seasonal variability: Seasonal variations in the amount of solar energy and the availability of sunshine hours are major limiting factors for solar technology, including SCPPs [158].
• Faster depreciation: The assets depreciate faster during the plant’s early operational period, posing a significant threat to the development.
• Technology readiness: The technological readiness level is lower, posing a higher risk to project development.
• The lack of R&D support and policies: Another major concern is the lack of R&D investment and policies that support the deployment of SCPP technology.
• The decrease of PV prices: Other development challenges include technological advancements in solar module technology, a reduction of solar cell prices, and the dominance of solar photovoltaic technology for power generation.
• Huge maintenance and repair: In an unexpected weather event, the maintenance of the parts is too complex and time-consuming.

9. Future Projections and the Evaluation of the Reviews of SCPPs in Terms of Energy Storage, Hybrid System Design and the Traditional Approach

It can be seen that there has been extensive literature published on solar chimneys in recent years. Especially, small-scale experimental studies and numerical studies are in the majority. When the literature reviews are examined, it can be seen that the existing studies are generally included, and the important points of the studies are mentioned. Some compilations and their contents are given in Table 16. The current reviews explain solar chimneys’ historical development, parts, and working principles. They also give information to researchers by including previous studies on the parameters affecting the system. They aim to illuminate further works by showing the effects of new designs and hybrid systems on the functioning and performance of the plants. In the study which was carried out, all of the system parameters were handled separately, and numerical performance comparisons were presented for the first time in the literature. In addition, this study aimed to give an idea for new studies for the future by including energy storage and hybrid systems.

Guo et al. [82] showed that this would reduce the cost. Geometric analysis to increase the performance of the system has been performed by researchers many times. In recent years, new designs to increase the efficiency with hybrid systems shed light on the future of SCPP systems. Some researchers have developed a hybrid solar chimney model that can be obtain fresh water from seawater while creating a power output from the system [159,160,161,162,163]. Solar chimneys are used not only for power output but also for different industrial purposes. Dried foods have had an important place in the food industry in recent years. Researchers have shown that solar chimneys can be used to dry food [164,165,166]. Increasing the human population and vertical construction created ventilation, heating and cooling problems. It is essential to meet these needs directly or indirectly from fossil fuels regarding clean energy and CO₂ emissions. Some researchers have conducted studies by integrating solar chimneys into enclosed spaces and building structures [167,168,169,170,171,172,173,174]. The most significant limitation of solar energy systems is that they cannot provide power output during hours without sunshine. SCPPs differ from other solar power systems in this regard. With the energy storage units installed on the ground, they can store energy during the sunlit hours and transfer it to the system when there is no sun. In this way, SCPP systems can give a 24-h power output. Some researchers have analyzed the system’s performance using different energy storage units [47,89,128,175]. The energy input to the SCPP system is from the collector part. The basic logic of the system is that the air under the collector is heated, and thus moves. Some researchers have created hybrid designs using geothermal water to contribute to the air heating under the collector, and to provide energy to the system when there is no sunshine [131,176]. The collecting part of solar chimneys is made at a large scale in order to increase the sun’s absorption. This large area can be used for different purposes.

By installing PV systems in this usable-ground part of solar chimney power plants, researchers have shown that a power output can be obtained from both systems simultaneously [127]. Researchers have worked with a wide variety of designs that would improve the performance of SCPP systems. Bilgen and Rheault [177] analyzed the system’s performance at high latitudes with a collector that they placed on a slope. The efficiency of PV systems is positively affected by the temperature. Solar chimneys provide ventilation by natural convection. Some researchers have used this feature of solar chimneys for the cooling of PV systems to increase their efficiency [178].

Table 16. Reviews of SCPPs in the literature.

References	Review Article	Study Content
[5]	A Review of solar Chimney Power Generation Technology	The physical structure and history of solar chimneys are given. Hybrid and different systems are interpreted.
[157]	Historic and recent progress in solar chimney power plant enhancing technologies	The studies on solar chimney power plants are evaluated and the effects that increase the performance of the system are interpreted.
[179]	A review of solar chimney power technology	The physical structure of traditional solar chimneys and the studies in the literature about the system are examined. Hybrid and innovative approaches are discussed.
[180]	Review on the Enhancement Techniques and Introduction of an Alternate Enhancement Technique of Solar Chimney Power Plant	The working principle of the system and publications in the literature are included.
[181]	Review of Solar Chimney Power Technology and Its Potentials in Semi-Arid Region of Nigeria	The development process and structure of solar chimneys are included. It estimates the performance of SCPP for the semi-arid region of Nigeria, including experimental studies.
[182]	Mathematical Correlations Developed for Solar Chimney Power Plant—A Critical Review	It offers researchers the opportunity to build a mathematical model to evaluate the performance of solar chimneys. In addition aims at the segregation of the different mathematical models.
[183]	Solar chimney power plant—A review	It presents the studies and developments about solar chimneys in various parts of the world with a critical review. It also analyzes important aspects of studies.
[184]	Research and development in solar chimney power plant technologies: a review	Evaluation is made on the design and analysis of solar chimneys. Innovations in the literature are presented to researchers.
[185]	A Brief Review on Solar Updraft Power Plant	The components of the system and its working principle are explained. Experimental and numerical studies are evaluated and analyzes are made to improve the system.
[186]	A review on solar chimney systems	Experimental and numerical studies on solar chimneys in the last 30 years are included in the study. Hybrid systems and innovative applications.
[187]	Solar updraft power plant system: A brief review and a case study on a new system with radial partition walls in its collector	Information about experimental studies, thermodynamic analyzes and new developments is given. The system is evaluated with chimney design, energy storage, mathematical models and CFD simulations. Special applications and the effect of ambient wind on SCPP are interpreted.
[188]	Past to Present: Solar Chimney Power Technologies	Solar chimneys are introduced and their basic principles are explained. Experimental and theoretical studies are examined and presented to the readers.
[189]	Questions and current understanding about solar chimney power plant: A review	With 7 questions, solar chimneys are evaluated by bringing a different perspective with the studies in the literature.
[190]	Evaluating the performance of solar chimney power plant	In the study, the performance parameters of solar chimney power plants are evaluated based on the literature.
[191]	Use of Solar Chimney in renewable energy applications—A review	The historical process and development of solar chimneys are interpreted. Working principle, components and innovative approaches about solar chimneys are presented to the readers.
[192]	Design and performance analysis of solar chimney power plant (SCPP): A review	Parameters affecting the performance of solar chimneys are interpreted. It presents new designs to the readers by making recommendations to increase the performance of the system.

Table 16. Reviews of SCPPs in the literature.

References	Review Article	Study Content
[5]	A Review of solar Chimney Power Generation Technology	The physical structure and history of solar chimneys are given. Hybrid and different systems are interpreted.
[157]	Historic and recent progress in solar chimney power plant enhancing technologies	The studies on solar chimney power plants are evaluated and the effects that increase the performance of the system are interpreted.
[179]	A review of solar chimney power technology	The physical structure of traditional solar chimneys and the studies in the literature about the system are examined. Hybrid and innovative approaches are discussed.
[180]	Review on the Enhancement Techniques and Introduction of an Alternate Enhancement Technique of Solar Chimney Power Plant	The working principle of the system and publications in the literature are included.
[181]	Review of Solar Chimney Power Technology and Its Potentials in Semi-Arid Region of Nigeria	The development process and structure of solar chimneys are included. It estimates the performance of SCPP for the semi-arid region of Nigeria, including experimental studies.
[182]	Mathematical Correlations Developed for Solar Chimney Power Plant—A Critical Review	It offers researchers the opportunity to build a mathematical model to evaluate the performance of solar chimneys. In addition aims at the segregation of the different mathematical models.
[183]	Solar chimney power plant—A review	It presents the studies and developments about solar chimneys in various parts of the world with a critical review. It also analyzes important aspects of studies.
[184]	Research and development in solar chimney power plant technologies: a review	Evaluation is made on the design and analysis of solar chimneys. Innovations in the literature are presented to researchers.
[185]	A Brief Review on Solar Updraft Power Plant	The components of the system and its working principle are explained. Experimental and numerical studies are evaluated and analyzes are made to improve the system.
[186]	A review on solar chimney systems	Experimental and numerical studies on solar chimneys in the last 30 years are included in the study. Hybrid systems and innovative applications.
[187]	Solar updraft power plant system: A brief review and a case study on a new system with radial partition walls in its collector	Information about experimental studies, thermodynamic analyzes and new developments is given. The system is evaluated with chimney design, energy storage, mathematical models and CFD simulations. Special applications and the effect of ambient wind on SCPP are interpreted.
[188]	Past to Present: Solar Chimney Power Technologies	Solar chimneys are introduced and their basic principles are explained. Experimental and theoretical studies are examined and presented to the readers.
[189]	Questions and current understanding about solar chimney power plant: A review	With 7 questions, solar chimneys are evaluated by bringing a different perspective with the studies in the literature.
[190]	Evaluating the performance of solar chimney power plant	In the study, the performance parameters of solar chimney power plants are evaluated based on the literature.
[191]	Use of Solar Chimney in renewable energy applications—A review	The historical process and development of solar chimneys are interpreted. Working principle, components and innovative approaches about solar chimneys are presented to the readers.
[192]	Design and performance analysis of solar chimney power plant (SCPP): A review	Parameters affecting the performance of solar chimneys are interpreted. It presents new designs to the readers by making recommendations to increase the performance of the system.

In future studies, it would be possible to design SCPPs as cogent systems. In this respect, some parts of the collector area, specifically the parts close to collector inlet, might be replaced with thin-film PV cells such as heat insulation solar glass (HISG) or thermally resistive PV glazing (TRPVG) [193,194,195]. By doing so, the conventional collector part is redesigned as a secondary power generating source, and the overall system efficiency is improved. Another issue regarding the SCPPs is the notable heat losses from the collector area due to the poor thermal resistance characteristics of collector materials. In order to be able to preserve the greenhouse effects beneath the collector, and to make maximum use of the thermal energy of system’s air, alternative thermally resistive and airtight glazing structures such as vacuum and aerogel glazing [196,197,198] can be considered, especially for small-scale power plants. This would improve the buoyant effects even under low solar radiation conditions, and would yield notably better velocity and power output figures.

10. Conclusions

The present study focused on the comprehensive literature on the various concepts, designs and performances of SCPPs. Most of the research work carried out to date was focused on numerical simulation using the CFD model. In the light of all of these studies, it was seen that there are many gaps in the literature regarding SCPP systems.

• The driving force of the system, the chimney, should be designed safely for enhanced power output, operation and efficiency.
• In addition, the weakness and threats of the SCPP technology need to be examined closely with the changing environment for steady development. The best performing SCPP configuration has to be identified for the commercial application.
• The temperature, pressure, and flow profile have been studied using numerical turbulence model computation.
• The power output can be maximized using innovative approaches in collector and chimney design which are appropriate to the local geographical conditions.
• The critical design parameters of the SCPP are the collector area, height, diameter, and slope; the chimney height; and the turbine pressure drop, which affect the efficiency of the plant.
• Continued research efforts in collector, chimney and hybrid design are strongly recommended in order to maximize the SCPP technology’s benefits.
• Technology developments in the hybrid models of SCPPs are encouraged for cost-effectiveness and commercial application.
• Despite its drawbacks, SCPP technology can provide decentralized energy solutions.
• According to the SWOT analysis results, hybrid system design can be considered to improve the poor efficiency range of SCPP technology. For example, some collector parts built by conventional glazing can be replaced with thin-film PV modules, notably near the collector inlet. By doing so, the PV modules can be cooled down due to the natural suction of cool air, which yields better electrical power output from the PVs. This also yields shorter payback periods for the SCPPs and improves the practicality of the technology due to dual electricity generation.
• Another output of the SWOT analysis is the use of the land under the collectors of SCPPs for agriculture and livestock activities. In doing so, the land is harnessed for multiple purposes, which improves the power plant’s functionality.