Digitalization Platform for Mechanistic Modeling of Battery Cell Production
Abstract
:1. Introduction
1.1. Motivation for a Model-Based Digitalization Platform
1.2. Existing Approaches to Make Cause–Effect Relations Transparent
2. Methodology
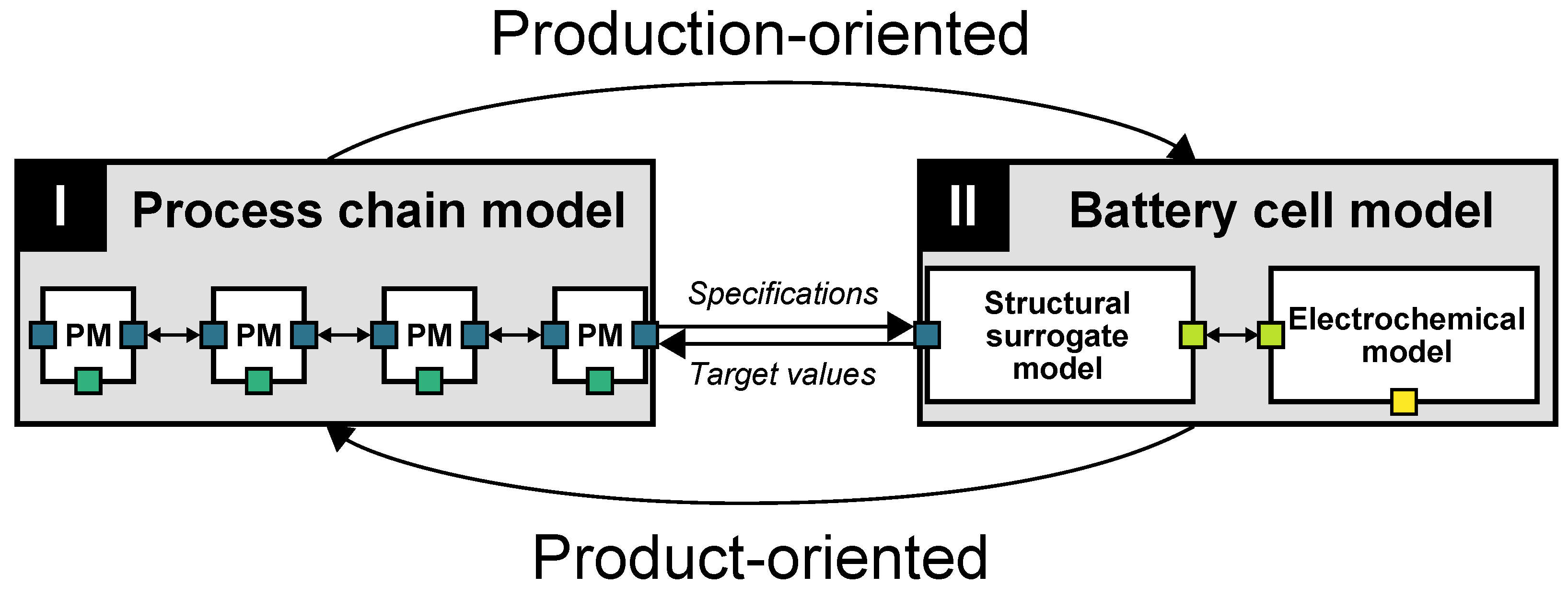
2.1. Concept of the Modeling Framework
2.2. Process Chain Model (I)
2.2.1. Meta-Modeling of Bottom-Up Models
2.2.2. Combining Process Models to Formulate the Process Chain Model
2.3. Battery Cell Model (II)
2.4. Analysis (III)
3. Use Case
3.1. Exemplary Implementation
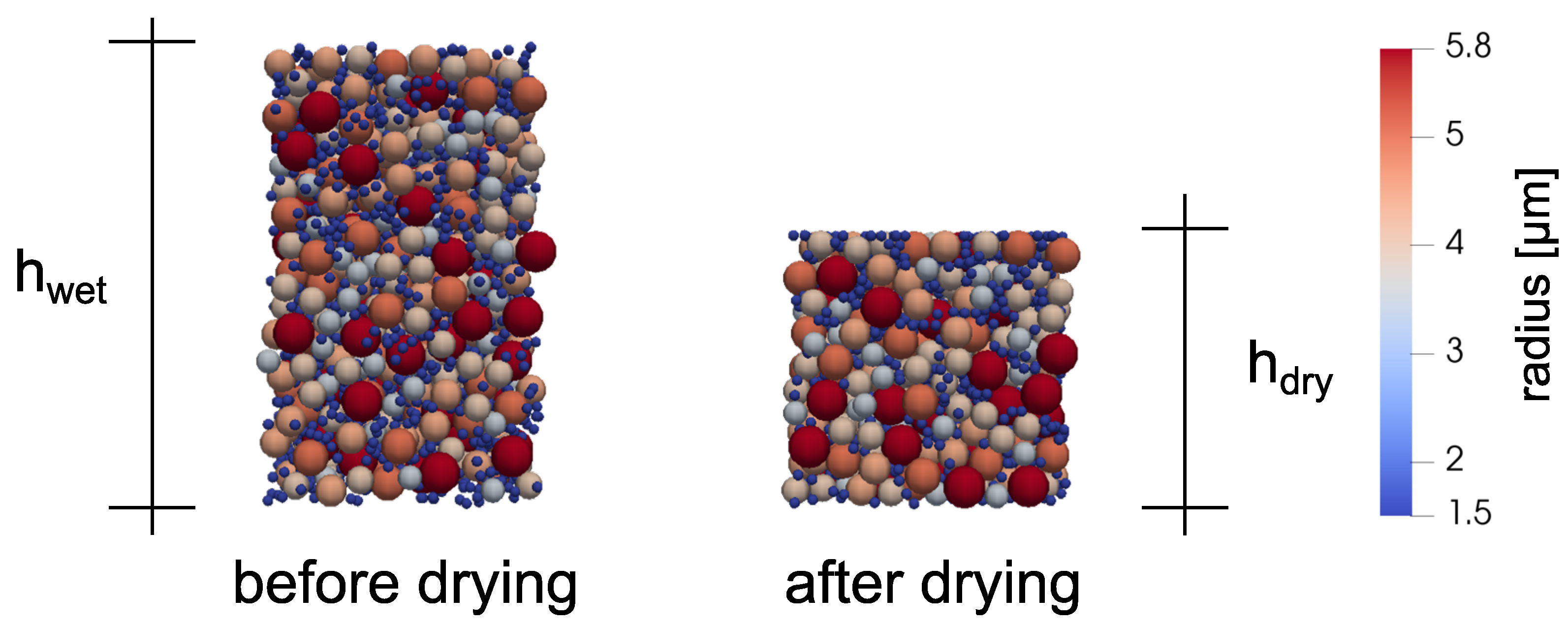
3.2. Process Chain Model
3.3. Battery Cell Model
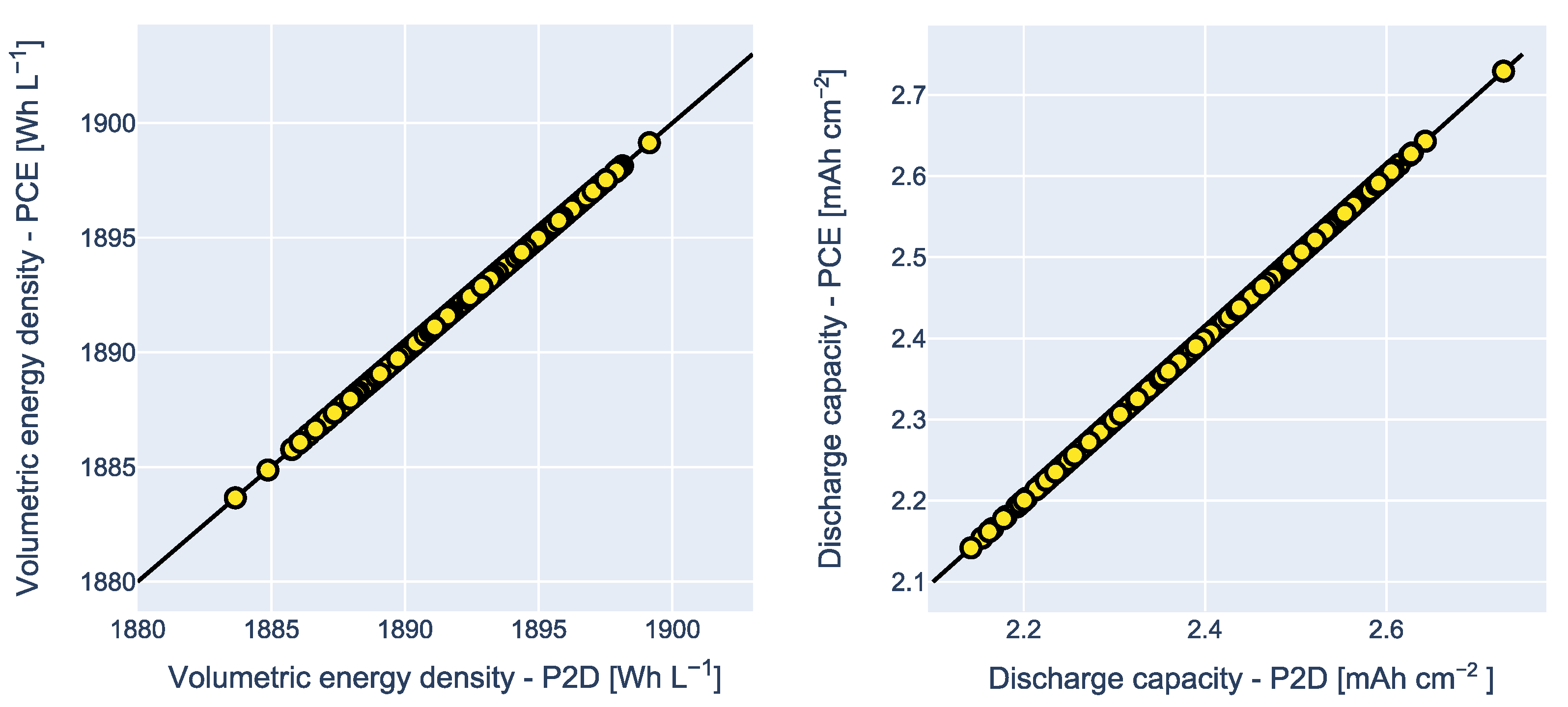
3.4. Analysis
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
| Parameter | Unit | Results | |
|---|---|---|---|
| Formulation | - | 0.94 ± 1.0% | |
| - | 0.03 ± 1.0% | ||
| - | 0.03 ± 1.0% | ||
| - | 0.7 ± 1.0% | ||
| Raw material | g cm−3 | 4.75 | |
| g cm−3 | 1.80 | ||
| g cm−3 | 1.70 | ||
| g cm−3 | 1.03 | ||
| Mixing | g cm−3 | 4.31 ± 0.9% | |
| Dispersion | g cm−3 | 2.20 ± 1.2% | |
| Coating | cm3 h−1 | 696 ± 1.0% | |
| v | m min−1 | 1.0 ± 1.0% | |
| w | mm | 125 ± 1.0% | |
| µm | 92.8 ± 1.7% | ||
| mg cm−2 | 20.5 ± 2.1% | ||
| Drying | % | 43.9 ± 0.3% | |
| mg cm−2 | 14.3 ± 2.8% | ||
| µm | 59.2 ± 2.6% | ||
| g cm−3 | 2.42 ± 0.9% | ||
| Calendering | N mm−1 | 84 ± 1.0% | |
| % | 17.6 ± 0.3% | ||
| N mm−1 | 129 ± 2.4% | ||
| % | 31.5 ± 0.4% | ||
| µm | 48.5 ± 3.0% | ||
| g cm−3 | 2.95 ± 0.9% | ||
| - | 0.58 ± 0.3% | ||
| - | 0.05 ± 1.3% | ||
| - | 0.05 ± 1.2% |
| Parameter | Symbol | Unit | Separator | Cathode |
|---|---|---|---|---|
| Coating thickness | m | - | 4.85 × 10−5 | |
| Porosity | - | 0.5 | 0.315 | |
| Particle size | m | - | 5.5 × 10−6 | |
| Tortuosity | - | 1 | 5.9449 | |
| Maximum capacity solid | mol m−3 | - | 4.3221 × 104 | |
| Initial capacity solid | mol m−3 | - | 1.5467 × 104 | |
| Initial capacity electrolyte | mol m−3 | - | 1 × 103 | |
| Diffusion coefficient solid | m2 s−1 | - | 9.5594 × 10−15 | |
| Diffusion coefficient electrolyte | m2 s−1 | - | [48] | |
| Electronic conductivity AM | S m−1 | - | 0.0309 | |
| Electronic conductivity CBM * | S m−1 | - | 760 | |
| Ionic conductivity | S m−1 | - | [48] | |
| Transference number | - | - | [48] | |
| Charge transfer coefficient | - | - | 0.5 | |
| Reaction rate constant | k | s−1 | - | 1.1717 × 10−9 |
| Double layer capacitance | F m−2 | - | 0.2 |
References
- IEA. Tracking Transport 2020; Technical Report; IEA: Paris, France, 2020. [Google Scholar]
- Niestadt, M.; Bjørnåvold, A. Electric Road Vehicles in the European Union Trends, Impacts and Policies; Technical Report April; European Parliament Briefing: Strasbourg, France, 2019. [Google Scholar]
- WEF. A Vision for a Sustainable Battery Value Chain in 2030 Unlocking the Full Potential to Power Sustainable Development and Climate Change Mitigation; World Economic Forum: Geneva, Switzerland, 2019. [Google Scholar]
- Henze, V. Battery Pack Prices Cited below $100/kWh for the First Time in 2020, While Market Average Sits at $137/kWh; Bloomberg New Energy Finance: New York, NY, USA, 2020. [Google Scholar]
- Michaelis, S.; Rahimzei, E. Roadmap Batterie-Produktionsmittel 2030–Update 2020; VDMA: Frankfurt am Main, Germany, 2020. [Google Scholar]
- Kwade, A.; Haselrieder, W.; Leithoff, R.; Modlinger, A.; Dietrich, F.; Droeder, K. Current status and challenges for automotive battery production technologies. Nat. Energy 2018, 3, 290–300. [Google Scholar] [CrossRef]
- Primo, E.N.; Touzin, M.; Franco, A.A. Analyzing the Link Between Process Parameters and Electrode Properties by Advanced Statistics. Batter. Supercaps 2021, 4, 834–844. [Google Scholar] [CrossRef]
- Turetskyy, A.; Thiede, S.; Thomitzek, M.; Drachenfels, N.V.; Pape, T.; Herrmann, C. Toward Data-Driven Applications in Lithium-Ion Battery Cell Manufacturing. Energy Technol. 2020, 8, 1900136. [Google Scholar] [CrossRef] [Green Version]
- Schmidt, O.; Thomitzek, M.; Röder, F.; Thiede, S.; Herrmann, C.; Krewer, U. Modeling the Impact of Manufacturing Uncertainties on Lithium-Ion Batteries Modeling the Impact of Manufacturing Uncertainties on Lithium- Ion Batteries. J. Electrochem. Soc. 2020, 167, 60501. [Google Scholar] [CrossRef]
- Kornas, T.; Knak, E.; Daub, R.; Bührer, U.; Lienemann, C.; Kampker, A.; Thiede, S.; Herrmann, C. A Multivariate KPI-Based Method for Quality Assurance in Lithium-Ion-Battery Production. Procedia CIRP 2019, 81, 75–80. [Google Scholar] [CrossRef]
- Ngandjong, A.C.; Lombardo, T.; Primo, E.N.; Chouchane, M.; Shodiev, A.; Arcelus, O.; Franco, A.A. Investigating electrode calendering and its impact on electrochemical performance by means of a new discrete element method model: Towards a digital twin of Li-Ion battery manufacturing. J. Power Sources 2021, 485, 229320. [Google Scholar] [CrossRef]
- Giménez, C.S.; Schilde, C.; Froböse, L.; Ivanov, S. Mechanical, Electrical, and Ionic Behavior of Lithium-Ion Battery Electrodes via Discrete Element Method Simulations. Energy Technol. 2019, 8, 1900180. [Google Scholar] [CrossRef]
- Turetskyy, A.; Wessel, J.; Herrmann, C.; Thiede, S. Data-driven cyber-physical System for Quality Gates in Lithium-ion Battery Cell Manufacturing. Procedia CIRP 2020, 93, 168–173. [Google Scholar] [CrossRef]
- Hoffmann, L.; Grathwol, J.K.; Haselrieder, W.; Leithoff, R.; Jansen, T.; Dilger, K.; Dröder, K.; Kwade, A.; Kurrat, M. Capacity Distribution of Large Lithium-Ion Battery Pouch Cells in Context with Pilot Production Processes. Energy Technol. 2020, 8, 1900196. [Google Scholar] [CrossRef]
- Hitzmann, B.; Herwig, C.; Remelhe, M.P.; Ulonska, S.; Wuerth, L.; Prata, A.; Steckenreiter, T. Between the Poles of Data-Driven and Mechanistic Modeling for Process Operation Do. Chem. Ing. Tech. 2017, 89, 542–561. [Google Scholar] [CrossRef]
- Fuller, T.F.; Soc, J.E.; Fuller, T.F.; Doyle, M.; Newman, J. Simulation and optimization of the dual lithium ion insertion cell. Electrochem. Soc. 1994, 141, 1. [Google Scholar] [CrossRef] [Green Version]
- Newman, J.; Thomas, K.E.; Hafezi, H.; Wheeler, D.R. Modeling of lithium-ion batteries. J. Power Sources 2003, 121, 838–843. [Google Scholar] [CrossRef]
- Witt, D.; Wilde, D.; Baakes, F.; Belkhir, F.; Röder, F.; Krewer, U. Myth and Reality of a Universal Lithium-Ion Battery Electrode Design Optimum: A Perspective and Case Study. Energy Technol. 2021, 9, 2000989. [Google Scholar] [CrossRef]
- Lenze, G.; Röder, F.; Bockholt, H.; Haselrieder, W.; Kwade, A.; Krewer, U. Simulation-Supported Analysis of Calendering Impacts on the Performance of Lithium-Ion-Batteries. J. Electrochem. Soc. 2017, 164, A1223. [Google Scholar] [CrossRef]
- Thomitzek, M.; Schmidt, O.; Röder, F.; Krewer, U.; Herrmann, C.; Thiede, S. Simulating Process-Product Interdependencies in Battery Production Systems. Procedia CIRP 2018, 72, 346–351. [Google Scholar] [CrossRef]
- Giménez, C.S.; Schilde, C.; Fröbose, L.; Finke, B.; Kwade, A. Numerical simulation of the behavior of lithium-ion battery electrodes during the calendaring process via the discrete element method. Powder Technol. 2019, 349, 1–11. [Google Scholar] [CrossRef]
- Mayer, J.K.; Almar, L.; Asylbekov, E.; Haselrieder, W.; Kwade, A.; Weber, A.; Nirschl, H. Influence of the Carbon Black Dispersing Process on the Microstructure and Performance of Li-Ion Battery Cathodes. Energy Technol. 2020, 8, 1900161. [Google Scholar] [CrossRef]
- Kumberg, J.; Baunach, M.; Eser, J.C.; Altvater, A.; Scharfer, P.; Schabel, W. Investigation of Drying Curves of Lithium-Ion Battery Electrodes with a New Gravimetrical Double-Side Batch Dryer Concept Including Setup Characterization and Model Simulations. Energy Technol. 2021, 9, 2000889. [Google Scholar] [CrossRef]
- Meyer, C.; Bockholt, H.; Haselrieder, W.; Kwade, A. Characterization of the calendering process for compaction of electrodes for lithium-ion batteries. J. Mater. Process. Technol. 2017, 249, 172–178. [Google Scholar] [CrossRef]
- Meyer, C.; Kosfeld, M.; Haselrieder, W.; Kwade, A. Process modeling of the electrode calendering of lithium-ion batteries regarding variation of cathode active materials and mass loadings. J. Energy Storage 2018, 18, 371–379. [Google Scholar] [CrossRef]
- Meyer, C.; Weyhe, M.; Haselrieder, W.; Kwade, A. Heated Calendering of Cathodes for Lithium-Ion Batteries with Varied Carbon Black and Binder Contents. Energy Technol. 2019, 8, 1900175. [Google Scholar] [CrossRef]
- Laue, V.; Schmidt, O.; Dreger, H.; Xie, X.; Röder, F.; Schenkendorf, R.; Kwade, A.; Krewer, U. Model-Based Uncertainty Quantification for the Product Properties of Lithium-Ion Batteries. Energy Technol. 2020, 8, 1900201. [Google Scholar] [CrossRef]
- Doyle, M.; Fuller, T.F.; Newman, J. Modeling of Galvanostatic Charge and Discharge of the Modeling of Galvanostatic Charge and Discharge of the Lithium/Polymer/Insertion Cell. J. Electrochem. Soc. 1993, 140, 1526. [Google Scholar] [CrossRef]
- Colclasure, A.M.; Kee, R.J. Thermodynamically consistent modeling of elementary electrochemistry in lithium-ion batteries. Electrochim. Acta 2010, 55, 8960–8973. [Google Scholar] [CrossRef]
- Legrand, N.; Raël, S.; Knosp, B.; Hinaje, M.; Desprez, P.; Lapicque, F. Including double-layer capacitance in lithium-ion battery mathematical models. J. Power Sources 2014, 251, 370–378. [Google Scholar] [CrossRef]
- Hein, S.; Feinauer, J.; Westhoff, D.; Manke, I.; Schmidt, V.; Latz, A. Stochastic microstructure modeling and electrochemical simulation of lithium-ion cell anodes in 3D. J. Power Sources 2016, 336, 161–171. [Google Scholar] [CrossRef] [Green Version]
- Laue, V.; Röder, F.; Krewer, U. Joint structural and electrochemical modeling: Impact of porosity on lithium-ion battery performance. Electrochim. Acta 2019, 314, 20–31. [Google Scholar] [CrossRef]
- Laue, V.; Wolff, N.; Röder, F.; Krewer, U. Modeling the Influence of Mixing Strategies on Microstructural Properties of All-Solid-State Electrodes. Energy Technol. 2020, 8, 1801049. [Google Scholar] [CrossRef]
- Bruggeman, D. Berechnung verschiedener physikalischer Konstanten von heterogenen Substanzen. Annalen der Physik 1935, 416, 636–664. [Google Scholar] [CrossRef]
- Thomitzek, M.; Schmidt, O.; Abraham, T.; Cerdas, F.; Röder, F.; Krewer, U.; Herrmann, C. Model-based identification of production tolerances in battery production. Procedia CIRP 2021, 104, 1059–1064. [Google Scholar] [CrossRef]
- Li, G.; Rabitz, H.; Yelvington, P.E.; Oluwole, O.O.; Bacon, F.; Kolb, C.E. Global Sensitivity Analysis for Systems with Independent and/or Correlated Inputs. J. Phys. Chem. A 2010, 114, 6022–6032. [Google Scholar] [CrossRef] [PubMed]
- Caniou, Y. Global Sensitivity Analysis for Nested and Multiscale Modelling; Université Blaise Pascal-Clermont-Ferrand II: Clermont-Ferrand, France, 2012. [Google Scholar]
- Schmitt, M. Slot Die Coating of Lithium-Ion Battery Electrodes; KIT Scientific Publishing: Karlsruhe, Germany, 2015. [Google Scholar]
- Bockholt, H.; Haselrieder, W.; Kwade, A. Intensive powder mixing for dry dispersing of carbon black and its relevance for lithium-ion battery cathodes. Powder Technol. 2016, 297, 266–274. [Google Scholar] [CrossRef]
- Jaiser, S.; Friske, A.; Baunach, M.; Scharfer, P.; Schabel, W. Development of a three-stage drying profile based on characteristic drying stages for lithium-ion battery anodes. Dry. Technol. 2017, 35, 1266–1275. [Google Scholar] [CrossRef]
- Conforto, G.; Ruess, R.; Schröder, D.; Trevisanello, E.; Fantin, R.; Richter, F.H.; Janek, J. Editors’ Choice—Quantification of the Impact of Chemo-Mechanical Degradation on the Performance and Cycling Stability of NCM-Based Cathodes in Solid-State Li-Ion Batteries. Electrochem. Soc. 2021, 168, 070546. [Google Scholar] [CrossRef]
- Baudin, M.; Dutfoy, A.; Iooss, B.; Popelin, A.L. OpenTURNS: An industrial software for uncertainty quantification in simulation. In Handbook of Uncertainty Quantification; Ghanem, R., Higdon, D., Owhadi, H., Eds.; Springer International Publishing: Cham, Switzerland, 2016. [Google Scholar]
- Marelli, S.; Sudret, B. UQLab: A framework for uncertainty quantification in Matlab. In Vulnerability, Uncertainty, and Risk: Quantification, Mitigation, and Management; American Society of Civil Engineers: Reston, VA, USA, 2014; pp. 2554–2563. [Google Scholar]
- Wiener, N. The Homogeneous Chaos. Am. J. Math. 1938, 60, 897–936. [Google Scholar] [CrossRef]
- Sudret, B. Global sensitivity analysis using polynomial chaos expansions. Reliab. Eng. Syst. Saf. 2008, 93, 964–979. [Google Scholar] [CrossRef]
- Lin, N.; Xie, X.; Schenkendorf, R.; Krewer, U. Efficient Global Sensitivity Analysis of 3D Multiphysics Model for Li-Ion Batteries. Electrochem. Soc. 2018, 165, A1169. [Google Scholar] [CrossRef] [Green Version]
- Ventura, G.; Thomitzek, M.; Abraham, T.; Herrmann, C. Bottleneck reduction strategies for energy efficiency in the battery manufacturing. Procedia CIRP 2021, 104, 1017–1022. [Google Scholar]
- Kremer, L.S.; Hoffmann, A.; Danner, T.; Hein, S.; Pri, B.; Westhoff, D.; Dreer, C.; Latz, A.; Schmidt, V.; Wohlfahrt-Mehrens, M. Manufacturing Process for Improved Ultra-Thick Cathodes in High-Energy Lithium-Ion Batteries. Energy Technol. 2020, 8, 1900167. [Google Scholar] [CrossRef]







| Vol. Energy Density | Discharge Capacity | |||||
|---|---|---|---|---|---|---|
| 0.76 | 0.77 | −0.01 | 0.25 | 0.23 | 0.02 | |
| 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | |
| 0.00 | 0.00 | 0.00 | 0.75 | 0.72 | 0.03 | |
| 0.24 | 0.24 | 0.00 | 0.00 | 0.00 | 0.00 | |
| ∑ | 1.00 | 1.01 | −0.01 | 1.00 | 0.95 | 0.05 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Thomitzek, M.; Schmidt, O.; Ventura Silva, G.; Karaki, H.; Lippke, M.; Krewer, U.; Schröder, D.; Kwade, A.; Herrmann, C. Digitalization Platform for Mechanistic Modeling of Battery Cell Production. Sustainability 2022, 14, 1530. https://doi.org/10.3390/su14031530
Thomitzek M, Schmidt O, Ventura Silva G, Karaki H, Lippke M, Krewer U, Schröder D, Kwade A, Herrmann C. Digitalization Platform for Mechanistic Modeling of Battery Cell Production. Sustainability. 2022; 14(3):1530. https://doi.org/10.3390/su14031530
Chicago/Turabian StyleThomitzek, Matthias, Oke Schmidt, Gabriela Ventura Silva, Hassan Karaki, Mark Lippke, Ulrike Krewer, Daniel Schröder, Arno Kwade, and Christoph Herrmann. 2022. "Digitalization Platform for Mechanistic Modeling of Battery Cell Production" Sustainability 14, no. 3: 1530. https://doi.org/10.3390/su14031530
APA StyleThomitzek, M., Schmidt, O., Ventura Silva, G., Karaki, H., Lippke, M., Krewer, U., Schröder, D., Kwade, A., & Herrmann, C. (2022). Digitalization Platform for Mechanistic Modeling of Battery Cell Production. Sustainability, 14(3), 1530. https://doi.org/10.3390/su14031530









